10.5 : Forme polaire des nombres complexes
- Page ID
- 195510
- Tracez des nombres complexes dans le plan complexe.
- Détermine la valeur absolue d'un nombre complexe.
- Écrivez des nombres complexes sous forme polaire.
- Convertissez un nombre complexe de forme polaire en nombre rectangulaire.
- Trouvez des produits de nombres complexes sous forme polaire.
- Trouvez des quotients de nombres complexes sous forme polaire.
- Trouvez les pouvoirs des nombres complexes sous forme polaire.
- Trouvez les racines de nombres complexes sous forme polaire.
« Dieu a créé les nombres entiers ; tout le reste est l'œuvre de l'homme. » Cette citation assez célèbre du mathématicien allemand du XIXe siècle Leopold Kronecker ouvre la voie à cette section consacrée à la forme polaire d'un nombre complexe. Les nombres complexes ont été inventés par des humains et représentent plus de mille ans de recherches et de luttes continues menées par des mathématiciens tels que Pythagore, Descartes, De Moivre, Euler, Gauss et d'autres. Les nombres complexes répondaient à des questions qui, depuis des siècles, intriguaient les plus grands esprits scientifiques.
Nous avons rencontré des nombres complexes pour la première fois dans la section sur les nombres complexes. Dans cette section, nous nous concentrerons sur la mécanique du travail avec des nombres complexes : traduction de nombres complexes de la forme polaire à la forme rectangulaire et vice versa, interprétation des nombres complexes dans le schéma des applications et application du théorème de De Moivre.
Tracé de nombres complexes dans le plan complexe
Tracer un nombre complexe\(a+bi\) est similaire au tracé d'un nombre réel, sauf que l'axe horizontal représente la partie réelle du nombre et que l'axe vertical représente la partie imaginaire du nombre,\(bi\).\(a\)
- Étiquetez l'axe horizontal comme axe réel et l'axe vertical comme axe imaginaire.
- Tracez le point dans le plan complexe en déplaçant les\(a\) unités dans le sens horizontal et les\(b\) unités dans le sens vertical.
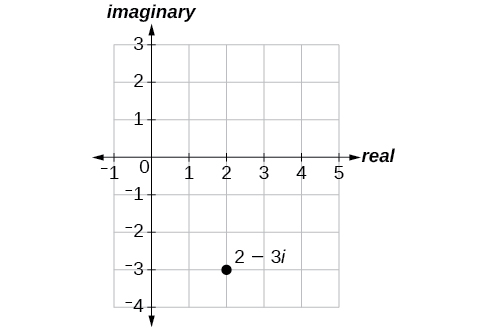
Tracez le nombre complexe\(2−3i\) dans le plan complexe.
Solution
À partir de l'origine, déplacez deux unités dans le sens horizontal positif et trois unités dans le sens vertical négatif. Voir la figure\(\PageIndex{1}\).
Tracez le point\(1+5i\) dans le plan complexe.
- Réponse
-
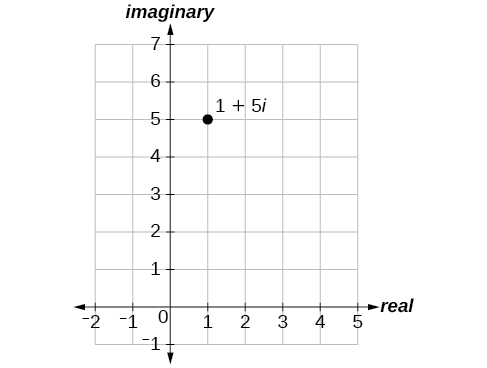
Figurine\(\PageIndex{2}\)
Déterminer la valeur absolue d'un nombre complexe
La première étape pour travailler avec un nombre complexe sous forme polaire est de trouver la valeur absolue. La valeur absolue d'un nombre complexe est identique à sa magnitude, ou\(| z |\). Il mesure la distance entre l'origine et un point du plan. Par exemple, le graphique de\(z=2+4i\), sur la figure\(\PageIndex{3}\), montre\(| z |\).
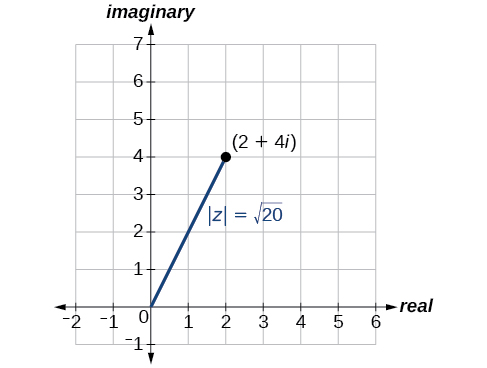
Étant donné qu'\(z=x+yi\)il s'agit d'un nombre complexe, la valeur absolue de\(z\) est définie comme
\[| z |=\sqrt{x^2+y^2}\]
C'est la distance entre l'origine et le point\((x,y)\).
Notez que la valeur absolue d'un nombre réel indique la distance entre le nombre et l'origine\(0\), tandis que la valeur absolue d'un nombre complexe indique la distance entre le nombre et l'origine\((0, 0)\).
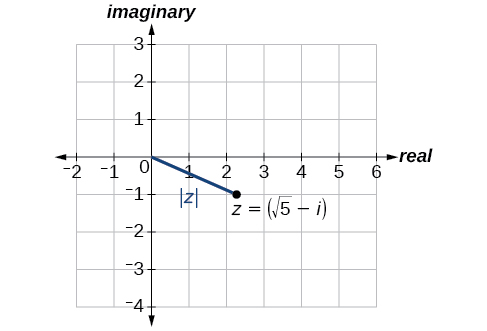
Détermine la valeur absolue de\(z=\sqrt{5}−i\).
Solution
En utilisant la formule, nous avons
\[\begin{align*} |z| &= \sqrt{x^2+y^2} \\ |z| &= \sqrt{{(\sqrt{5})}^2+{(-1)}^2} \\ |z| &= \sqrt{5+1} \\ |z| &= \sqrt{6} \end{align*}\]
Voir la figure\(\PageIndex{4}\).
Détermine la valeur absolue du nombre complexe\(z=12−5i\).
- Réponse
-
\(13\)
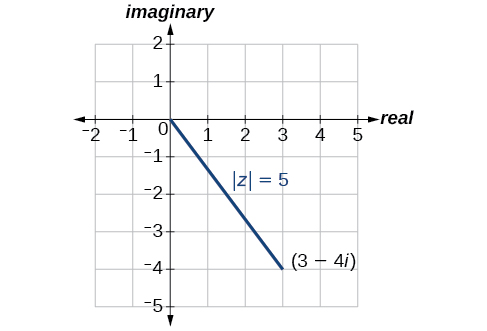
Donné\(z=3−4i\), trouvez\(| z |\).
Solution
En utilisant la formule, nous avons
\[\begin{align*} | z | &= \sqrt{x^2+y^2} \\ | z | &= \sqrt{{(3)}^2+{(-4)}^2} \\ | z | &= \sqrt{9+16} \\ | z | &= \sqrt{25} \\ | z | &= 5 \end{align*}\]
La valeur absolue\(z\) est\(5\). Voir la figure\(\PageIndex{5}\).
Donné\(z=1−7i\), trouvez\(| z |\).
- Réponse
-
\(| z |=\sqrt{50}=5\sqrt{2}\)
Écrire des nombres complexes sous forme polaire
La forme polaire d'un nombre complexe exprime un nombre en termes d'angle\(\theta\) et de distance par rapport à l'origine\(r\). Étant donné un nombre complexe sous forme rectangulaire exprimé en\(z=x+yi\), nous utilisons les mêmes formules de conversion que pour écrire le nombre sous forme trigonométrique :
\[\begin{align*} x &= r \cos \theta \\ y &= r \sin \theta \\ r &= \sqrt{x^2+y^2} \end{align*}\]
Nous passons en revue ces relations dans la Figure\(\PageIndex{6}\).
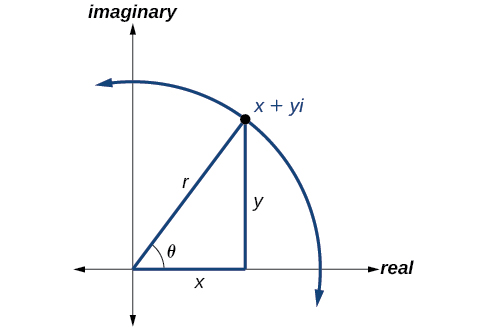
Nous utilisons le terme module pour représenter la valeur absolue d'un nombre complexe, ou la distance entre l'origine et le point\((x,y)\). Le module est donc le même que\(r\) le rayon sous forme polaire. Nous l'utilisons\(\theta\) pour indiquer l'angle de direction (comme pour les coordonnées polaires). En remplacement, nous avons
\[\begin{align*} z &= x+yi \\ z &= r \cos \theta+(r \sin \theta)i \\ z &= r(\cos \theta+i \sin \theta) \end{align*}\]
L'écriture d'un nombre complexe sous forme polaire implique les formules de conversion suivantes :
\[\begin{align} x &= r \cos \theta \\ y &= r \sin \theta \\ r &= \sqrt{x^2+y^2} \end{align}\]
En effectuant une substitution directe, nous avons
\[\begin{align} z &= x+yi \\ z &= (r \cos \theta)+i(r \sin \theta) \\ z &= r(\cos \theta+i \sin \theta) \end{align}\]
où\(r\) est le module et\(\theta\) l'argument. Nous utilisons souvent l'abréviation\(r\; cis \theta\) pour représenter\(r(\cos \theta+i \sin \theta)\).
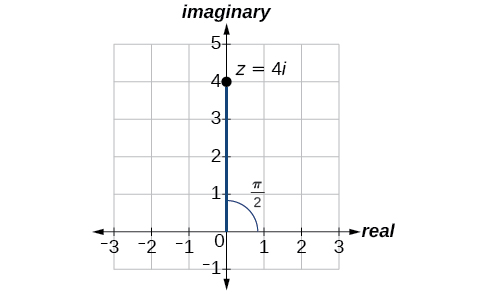
Exprime le nombre complexe\(4i\) à l'aide de coordonnées polaires.
Solution
Sur le plan complexe, le nombre\(z=4i\) est le même que\(z=0+4i\). En l'écrivant sous forme polaire, il faut d'\(r\)abord calculer.
\[\begin{align*} r &= \sqrt{x^2+y^2} \\ r &= \sqrt{0^2+4^2} \\ r &= \sqrt{16} \\ r &= 4 \end{align*}\]
Ensuite, nous examinons\(x\). Si\(x=r \cos \theta\), et\(x=0\), alors\(\theta=\dfrac{\pi}{2}\). En coordonnées polaires, le nombre complexe\(z=0+4i\) peut être écrit sous la forme\(z=4\left(\cos\left(\dfrac{\pi}{2}\right)+i \sin\left(\dfrac{\pi}{2}\right)\right) \text{ or } 4\; cis\left( \dfrac{\pi}{2}\right)\). Voir la figure\(\PageIndex{7}\).
\(z=3i\)\(r\space cis \theta\)Exprimez-la sous forme polaire.
- Réponse
-
\(z=3\left(\cos\left(\dfrac{\pi}{2}\right)+i \sin\left(\dfrac{\pi}{2}\right)\right)\)
Trouvez la forme polaire de\(−4+4i\).
Solution
Tout d'abord, trouvez la valeur de\(r\).
\[\begin{align*} r &= \sqrt{x^2+y^2} \\ r &= \sqrt{{(−4)}^2+(4^2)} \\ r &= \sqrt{32} \\ r &= 4\sqrt{2} \end{align*}\]
Trouvez l'angle\(\theta\) à l'aide de la formule :
\[\begin{align*} \cos \theta &= \dfrac{x}{r} \\ \cos \theta &= \dfrac{−4}{4\sqrt{2}} \\ \cos \theta &= −\dfrac{1}{\sqrt{2}} \\ \theta &= {\cos}^{−1} \left(−\dfrac{1}{\sqrt{2}}\right)\\ &= \dfrac{3\pi}{4} \end{align*}\]
La solution est donc\(4\sqrt{2}\space cis \left(\dfrac{3\pi}{4}\right)\).
Écrivez\(z=\sqrt{3}+i\) sous forme polaire.
- Réponse
-
\(z=2\left(\cos\left(\dfrac{\pi}{6}\right)+i \sin\left(\dfrac{\pi}{6}\right)\right)\)
Conversion d'un nombre complexe de forme polaire en nombre rectangulaire
La conversion d'un nombre complexe de la forme polaire à la forme rectangulaire consiste à évaluer ce qui est donné et à utiliser la propriété distributive. En d'autres termes, étant donné\(z=r(\cos \theta+i \sin \theta)\), évaluez d'abord les fonctions trigonométriques\(\cos \theta\) et\(\sin \theta\). Ensuite, multipliez par\(r\).
Convertissez la forme polaire du nombre complexe donné en forme rectangulaire :
\(z=12\left(\cos\left(\dfrac{\pi}{6}\right)+i \sin\left(\dfrac{\pi}{6}\right)\right)\)
Solution
Nous commençons par évaluer les expressions trigonométriques.
\[\begin{align*} \cos\left(\dfrac{\pi}{6}\right)&= \dfrac{\sqrt{3}}{2} \text{ and } \sin(\dfrac{\pi}{6})=\dfrac{1}{2}\\ \text {After substitution, the complex number is}\\ z&= 12\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i\right) \end{align*}\]
Nous appliquons la propriété distributive :
\[\begin{align*} z &= 12\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i\right) \\ &= (12)\dfrac{\sqrt{3}}{2}+(12)\dfrac{1}{2}i \\ &= 6\sqrt{3}+6i \end{align*}\]
La forme rectangulaire du point donné sous forme complexe est\(6\sqrt{3}+6i\).
Trouvez la forme rectangulaire du nombre complexe donné\(r=13\) et\(\tan \theta=\dfrac{5}{12}\).
Solution
Si\(\tan \theta=\dfrac{5}{12}\), et\(\tan \theta=\dfrac{y}{x}\), nous déterminons d'abord\(r=\sqrt{x^2+y^2}=\sqrt{122+52}=13\). Nous trouvons ensuite\(\cos \theta=\dfrac{x}{r}\) et\(\sin \theta=\dfrac{y}{r}\).
\[\begin{align*} z &= 13\left(\cos \theta+i \sin \theta\right) \\ &= 13\left(\dfrac{12}{13}+\dfrac{5}{13}i\right) \\ &=12+5i \end{align*}\]
La forme rectangulaire du nombre donné sous forme complexe est\(12+5i\).
Convertissez le nombre complexe en forme rectangulaire :
\(z=4\left(\cos \dfrac{11\pi}{6}+i \sin \dfrac{11\pi}{6}\right)\)
- Réponse
-
\(z=2\sqrt{3}−2i\)
Recherche de produits de nombres complexes sous forme polaire
Maintenant que nous pouvons convertir des nombres complexes en forme polaire, nous allons apprendre à effectuer des opérations sur des nombres complexes sous forme polaire. Pour le reste de cette section, nous travaillerons avec des formules développées par le mathématicien français Abraham de Moivre (1667-1754). Ces formules ont rendu le travail avec les produits, les quotients, les puissances et les racines de nombres complexes beaucoup plus simple qu'il n'y paraît. Les règles sont basées sur la multiplication des modules et l'ajout des arguments.
Si\(z_1=r_1(\cos \theta_1+i \sin \theta_1)\) et\(z_2=r_2(\cos \theta_2+i \sin \theta_2)\), alors le produit de ces nombres est donné comme suit :
\[\begin{align} z_1z_2 &= r_1r_2[ \cos(\theta_1+\theta_2)+i \sin(\theta_1+\theta_2) ] \\ z_1z_2 &= r_1r_2\space cis(\theta_1+\theta_2) \end{align}\]
Notez que le produit nécessite de multiplier les modules et d'ajouter les angles.
Trouvez le produit de\(z_1z_2\), donné\(z_1=4(\cos(80°)+i \sin(80°))\) et\(z_2=2(\cos(145°)+i \sin(145°))\).
Solution
Suivez la formule
\[\begin{align*} z_1z_2 &= 4⋅2[\cos(80°+145°)+i \sin(80°+145°)] \\ z_1z_2 &= 8[\cos(225°)+i \sin(225°)] \\ z_1z_2 &= 8\left[\cos\left(\dfrac{5\pi}{4}\right)+i \sin\left(\dfrac{5\pi}{4}\right) \right] \\ z_1z_2 &= 8\left[−\dfrac{\sqrt{2}}{2}+i\left(−\dfrac{\sqrt{2}}{2}\right) \right] \\ z_1z_2 &= −4\sqrt{2}−4i\sqrt{2} \end{align*}\]
Trouver des quotients de nombres complexes sous forme polaire
Le quotient de deux nombres complexes sous forme polaire est le quotient des deux modules et la différence des deux arguments.
Si\(z_1=r_1(\cos \theta_1+i \sin \theta_1)\) et\(z_2=r_2(\cos \theta_2+i \sin \theta_2)\), alors le quotient de ces nombres est
\[\dfrac{z_1}{z_2}=\dfrac{r_1}{r_2}[\cos(\theta_1−\theta_2)+i \sin(\theta_1−\theta_2) ],\space z_2≠0\]
\[\dfrac{z_1}{z_2}=\dfrac{r_1}{r_2}\space cis(\theta_1−\theta_2),\space z_2≠0\]
Notez que les modules sont divisés et que les angles sont soustraits.
- Diviser\(\dfrac{r_1}{r_2}\).
- Trouve\(\theta_1−\theta_2\).
- Remplacez les résultats dans la formule :\(z=r(\cos \theta+i \sin \theta)\). Remplacez\(r\) par\(\dfrac{r_1}{r_2}\), et remplacez\(\theta\) par\(\theta_1−\theta_2\).
- Calculez les nouvelles expressions trigonométriques et multipliez-les par\(r\).
Détermine le quotient de\(z_1=2(\cos(213°)+i \sin(213°))\) et\(z_2=4(\cos(33°)+i \sin(33°))\).
Solution
En utilisant la formule, nous avons
\[\begin{align*} \dfrac{z_1}{z_2} &= \dfrac{2}{4}[\cos(213°−33°)+i \sin(213°−33°)] \\ \dfrac{z_1}{z_2} &= \dfrac{1}{2}[\cos(180°)+i \sin(180°)] \\ \dfrac{z_1}{z_2} &= \dfrac{1}{2}[−1+0i] \\ \dfrac{z_1}{z_2} &= −\dfrac{1}{2}+0i \\ \dfrac{z_1}{z_2} &= −\dfrac{1}{2} \end{align*}\]
Trouvez le produit et le quotient de\(z_1=2\sqrt{3}(\cos(150°)+i \sin(150°))\) et\(z_2=2(\cos(30°)+i \sin(30°))\).
- Réponse
-
\(z_1z_2=−4\sqrt{3}\);\(\dfrac{z_1}{z_2}=−\dfrac{\sqrt{3}}{2}+\dfrac{3}{2}i\)
Déterminer les pouvoirs des nombres complexes sous forme polaire
La recherche des pouvoirs des nombres complexes est grandement simplifiée à l'aide du théorème de De Moivre. Il indique que, pour un entier positif\(n\),\(z^n\) est obtenu en élevant le module à la\(n^{th}\) puissance et en multipliant l'argument par\(n\). C'est la méthode standard utilisée en mathématiques modernes.
S'il s'\(z=r(\cos \theta+i \sin \theta)\)agit d'un nombre complexe, alors
\[\begin{align} z^n &= r^n[\cos(n\theta)+i \sin(n\theta) ] \\ z^n &= r^n\space cis(n\theta) \end{align}\]
où\(n\) est un entier positif.
Évaluez l'expression\({(1+i)}^5\) à l'aide du théorème de De Moivre.
Solution
Puisque le théorème de De Moivre s'applique aux nombres complexes écrits sous forme polaire, nous devons d'abord écrire\((1+i)\) sous forme polaire. Laissez-nous trouver\(r\).
\[\begin{align*} r &= \sqrt{x^2+y^2} \\ r &= \sqrt{{(1)}^2+{(1)}^2} \\ r &= \sqrt{2} \end{align*}\]
Ensuite, on trouve\(\theta\). L'utilisation de la formule\(\tan \theta=\dfrac{y}{x}\) donne
\[\begin{align*} \tan \theta &= \dfrac{1}{1} \\ \tan \theta &= 1 \\ \theta &= \dfrac{\pi}{4} \end{align*}\]
Utilisez le théorème de De Moivre pour évaluer l'expression.
\[\begin{align*} {(a+bi)}^n &= r^n[\cos(n\theta)+i \sin(n\theta)] \\ {(1+i)}^5 &= {(\sqrt{2})}^5\left[ \cos\left(5⋅\dfrac{\pi}{4}\right)+i \sin\left(5⋅\dfrac{\pi}{4}\right) \right] \\ {(1+i)}^5 &= 4\sqrt{2}\left[ \cos\left(\dfrac{5\pi}{4}\right)+i \sin\left(\dfrac{5\pi}{4}\right) \right] \\ {(1+i)}^5 &= 4\sqrt{2}\left[ −\dfrac{\sqrt{2}}{2}+i\left(−\dfrac{\sqrt{2}}{2}\right) \right] \\ {(1+i)}^5 &= −4−4i \end{align*}\]
Trouver les racines des nombres complexes sous forme polaire
Pour trouver la\(n^{th}\) racine d'un nombre complexe sous forme polaire, nous utilisons le théorème\(n^{th}\) racine ou le théorème de De Moivre et élevons le nombre complexe à une puissance avec un exposant rationnel. Il existe plusieurs manières de représenter une formule permettant de trouver\(n^{th}\) les racines de nombres complexes sous forme polaire.
Pour trouver la\(n^{th}\) racine d'un nombre complexe sous forme polaire, utilisez la formule donnée comme
\[z^{\tfrac{1}{n}}=r^{\tfrac{1}{n}}\left[ \cos\left(\dfrac{\theta}{n}+\dfrac{2k\pi}{n}\right)+i \sin\left(\dfrac{\theta}{n}+\dfrac{2k\pi}{n}\right) \right]\]
où\(k=0, 1, 2, 3, . . . , n−1\). Nous\(\dfrac{2k\pi}{n}\) l'ajoutons\(\dfrac{\theta}{n}\) afin d'obtenir les racines périodiques.
Évaluez les racines cubiques de\(z=8\left(\cos\left(\frac{2\pi}{3}\right)+i\sin\left(\frac{2\pi}{3}\right)\right)\).
Solution
Nous avons
\[\begin{align*} z^{\frac{1}{3}} &= 8^{\frac{1}{3}}\left[ \cos\left(\frac{\frac{2\pi}{3}}{3}+\frac{2k\pi}{3}\right)+i \sin\left(\frac{\frac{2\pi}{3}}{3}+\frac{2k\pi}{3}\right) \right] \\ z^{\frac{1}{3}} &= 2\left[ \cos\left(\frac{2\pi}{9}+\frac{2k\pi}{3}\right)+i \sin\left(\frac{2\pi}{9}+\frac{2k\pi}{3}\right) \right] \end{align*}\]
Il y aura trois racines :\(k=0, 1, 2\). Quand\(k=0\), nous avons
\(z^{\frac{1}{3}}=2\left(\cos\left(\dfrac{2\pi}{9}\right)+i \sin\left(\dfrac{2\pi}{9}\right)\right)\)
Quand\(k=1\), nous avons
\[\begin{align*} z^{\frac{1}{3}} &=2\left[ \cos\left(\dfrac{2\pi}{9}+\dfrac{6\pi}{9}\right)+i \sin\left(\dfrac{2\pi}{9}+\dfrac{6\pi}{9}\right) \right] \;\;\;\;\;\;\;\;\; \text{Add }\dfrac{2(1)\pi}{3} \text{ to each angle.} \\ z^{\frac{1}{3}} &= 2\left(\cos\left(\dfrac{8\pi}{9}\right)+i \sin\left(\dfrac{8\pi}{9}\right)\right) \end{align*}\]
Quand\(k=2\), nous avons
\[\begin{align*} z^{\frac{1}{3}} &= 2\left[ \cos\left(\dfrac{2\pi}{9}+\dfrac{12\pi}{9}\right)+i \sin\left(\dfrac{2\pi}{9}+\dfrac{12\pi}{9}\right) \right] \;\;\;\;\;\;\; \text{Add }\dfrac{2(2)\pi}{3} \text{ to each angle.} \\ z^{\frac{1}{3}} &= 2\left(\cos\left(\dfrac{14\pi}{9}\right)+i \sin\left(\dfrac{14\pi}{9}\right)\right) \end{align*}\]
N'oubliez pas de trouver le dénominateur commun pour simplifier les fractions dans des situations comme celle-ci. \(k=1\)En effet, la simplification de l'angle est
\[\begin{align*} \dfrac{\dfrac{2\pi}{3}}{3}+\dfrac{2(1)\pi}{3} &= \dfrac{2\pi}{3}(\dfrac{1}{3})+\dfrac{2(1)\pi}{3}\left(\dfrac{3}{3}\right) \\ &=\dfrac{2\pi}{9}+\dfrac{6\pi}{9} \\ &=\dfrac{8\pi}{9} \end{align*}\]
Trouvez les quatre quatrièmes racines de\(16(\cos(120°)+i \sin(120°))\).
- Réponse
-
\(z_0=2(\cos(30°)+i \sin(30°))\)
\(z_1=2(\cos(120°)+i \sin(120°))\)
\(z_2=2(\cos(210°)+i \sin(210°))\)
\(z_3=2(\cos(300°)+i \sin(300°))\)
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur les formes polaires des nombres complexes.
- Le produit et le quotient des nombres complexes sous forme trigonométrique
- Théorème de De Moivre
Concepts clés
- Les nombres complexes du formulaire\(a+bi\) sont tracés dans le plan complexe de la même manière que les coordonnées rectangulaires sont tracées dans le plan rectangulaire. Étiquetez l'\(x\)axe -comme étant l'axe réel et l'axe\(y\) - comme étant l'axe imaginaire. Voir l'exemple\(\PageIndex{1}\).
- La valeur absolue d'un nombre complexe est identique à sa magnitude. C'est la distance entre l'origine et le point :\(| z |=\sqrt{a^2+b^2}\). Voir Exemple\(\PageIndex{2}\) et Exemple\(\PageIndex{3}\).
- Pour écrire des nombres complexes sous forme polaire, nous utilisons les formules\(x=r \cos \theta\)\(y=r \sin \theta\), et\(r=\sqrt{x^2+y^2}\). Ensuite,\(z=r(\cos \theta+i \sin \theta)\). Voir Exemple\(\PageIndex{4}\) et Exemple\(\PageIndex{5}\).
- Pour passer de la forme polaire à la forme rectangulaire, évaluez d'abord les fonctions trigonométriques. Ensuite, multipliez par\(r\). Voir Exemple\(\PageIndex{6}\) et Exemple\(\PageIndex{7}\).
- Pour trouver le produit de deux nombres complexes, multipliez les deux modules et additionnez les deux angles. Évaluez les fonctions trigonométriques et multipliez-les à l'aide de la propriété distributive. Voir l'exemple\(\PageIndex{8}\).
- Pour déterminer le quotient de deux nombres complexes sous forme polaire, trouvez le quotient des deux modules et la différence des deux angles. Voir l'exemple\(\PageIndex{9}\).
- Pour trouver la puissance d'un nombre complexe\(z^n\),\(r\) augmentez la puissance\(n\) et multipliez\(\theta\) par\(n\). Voir l'exemple\(\PageIndex{10}\).
- Trouver les racines d'un nombre complexe revient à élever un nombre complexe à une puissance, mais en utilisant un exposant rationnel. Voir l'exemple\(\PageIndex{11}\).


