10.4 : Coordonnées polaires - Graphiques

Last updated
Save as PDF

Page ID: 195533

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Testez la symétrie des équations polaires.
Tracez des équations polaires en traçant des points.

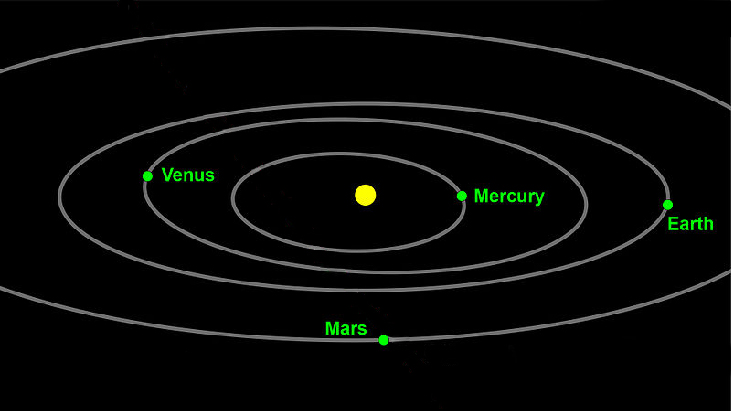
La première loi du mouvement planétaire de Keplar soutient que les planètes se déplacent dans l'espace sur des orbitales elliptiques périodiques autour du soleil, comme le montre la figure$\PageIndex{1}$. Ils sont en mouvement constant, donc fixer la position exacte de n'importe quelle planète n'est valable que pour un instant. En d'autres termes, nous ne pouvons fixer que la position instantanée d'une planète. Il s'agit d'une application des coordonnées polaires, représentée par$(r,\theta)$. Nous l'interprétons$r$ comme la distance par rapport au soleil et$\theta$ comme l'orientation angulaire de la planète, ou sa direction à partir d'un point fixe sur le soleil. Dans cette section, nous allons nous concentrer sur le système polaire et les graphes générés directement à partir des coordonnées polaires.

Illustration du système solaire avec le soleil au centre et les orbites des planètes Mercure, Vénus, Terre et Mars illustrées. — Figure$\PageIndex{1}$ : Les planètes suivent des trajectoires elliptiques lorsqu'elles orbitent autour du Soleil. (crédit : modification des travaux par la NASA/JPL-Caltech)

Test de symétrie d'équations polaires

Tout comme une équation rectangulaire qui$y=x^2$ décrit la relation entre$x$ et$y$ sur une grille cartésienne, une équation polaire décrit une relation entre$r$ et$\theta$ sur une grille polaire. Rappelez-vous que la paire de coordonnées$(r,\theta)$ indique que nous nous déplaçons dans le sens antihoraire depuis l'axe polaire ($x$axe positif) d'un angle de$\theta$ et que nous étendons un rayon à partir des$r$ unités polaires (origine) dans la direction de$\theta$. Tous les points qui répondent à l'équation polaire figurent sur le graphique.

La symétrie est une propriété qui nous aide à reconnaître et à tracer le graphe de n'importe quelle équation. Si une équation possède un graphique symétrique par rapport à un axe, cela signifie que si nous plions le graphique en deux sur cet axe, la partie du graphique d'un côté coïncidera avec la partie de l'autre côté. En effectuant trois tests, nous verrons comment appliquer les propriétés de symétrie aux équations polaires. De plus, nous utiliserons la symétrie (en plus de tracer les points clés, les zéros et les maximums de$r$) pour déterminer le graphe d'une équation polaire.

Dans le premier test, nous prenons en compte la symétrie par rapport à la ligne$\theta=\dfrac{\pi}{2}$ ($y$axe). Nous la$(r,\theta)$ remplaçons par$(−r,−\theta)$ pour déterminer si la nouvelle équation est équivalente à l'équation d'origine. Supposons, par exemple, qu'on nous donne l'équation$r=2 \sin \theta$ ;

\[\begin{align*} r&= 2 \sin \theta \\ -r&= 2 \sin -\theta \qquad \text{Replace } (r,\theta) \text{ with }(-r,-\theta). \\ -r&= -2 \sin \theta \qquad \text{Identity: }\sin(-\theta)=-\sin \theta. \\ r&= 2 \sin \theta \qquad \text{Multiply both sides by }-1 \end{align*}\]

Cette équation présente une symétrie par rapport à la droite$\theta=\dfrac{\pi}{2}$.

Dans le second test, nous prenons en compte la symétrie par rapport à l'axe polaire ($x$axe -). Nous la$(r,\theta)$ remplaçons par$(r,−\theta)$ ou$(−r,\pi−\theta)$ pour déterminer l'équivalence entre l'équation testée et l'équation d'origine. Supposons, par exemple, qu'on nous donne l'équation$r=1−2 \cos \theta$.

\[\begin{align*} r&= 1-2 \cos \theta \\ r&= 1-2 \cos(-\theta)\qquad \text{Replace }(r,\theta) \text{ with }(r,-\theta). \\ r&= 1-2 \cos \theta \qquad \text{Even/Odd identity} \end{align*}\]

Le graphique de cette équation présente une symétrie par rapport à l'axe polaire.

Dans le troisième test, nous considérons la symétrie par rapport au pôle (origine). Nous la$(r,\theta)$ remplaçons par$(−r,\theta)$ pour déterminer si l'équation testée est équivalente à l'équation d'origine. Supposons, par exemple, qu'on nous donne l'équation$r=2 \sin(3\theta)$.

$r=2 \sin(3\theta)$

$−r=2 \sin(3\theta)$

L'équation a échoué au test de symétrie, mais cela ne signifie pas qu'elle n'est pas symétrique par rapport au pôle. La réussite d'un ou de plusieurs tests de symétrie permet de vérifier que la symétrie sera affichée sur un graphique. Cependant, l'échec des tests de symétrie n'indique pas nécessairement qu'un graphe ne sera pas symétrique par rapport à la ligne$\theta=\dfrac{\pi}{2}$, à l'axe polaire ou au pôle. Dans ces cas, nous pouvons confirmer l'existence d'une symétrie en traçant les points réfléchissants le long de l'axe de symétrie apparent ou du pôle. Le test de symétrie est une technique qui simplifie la représentation graphique des équations polaires, mais son application n'est pas parfaite.

Remarque : TESTS DE SYMÉTRIE

Une équation polaire décrit une courbe sur la grille polaire. Le graphique d'une équation polaire peut être évalué pour trois types de symétrie, comme le montre la figure$\PageIndex{2}$.

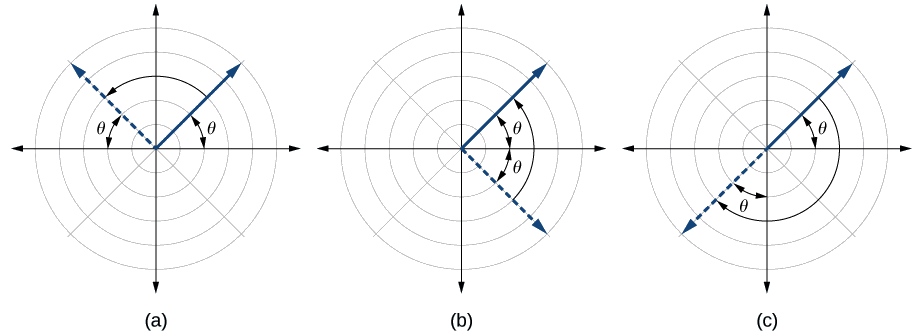
3 graphiques côte à côte. (A) montre un rayon s'étendant dans Q 1 et sa version symétrique dans Q 2. (B) montre un rayon s'étendant dans Q 1 et sa version symétrique dans Q 4. (C) montre un rayon s'étendant dans Q 1 et sa version symétrique dans Q 3. Voir la légende pour plus d'informations. — Figure$\PageIndex{2}$ : (a) Un graphique est symétrique par rapport à la ligne$\theta=\dfrac{\pi}{2}$ (axe Y) si le remplacement$(r,\theta)$ par$(−r,−\theta)$ donne une équation équivalente. (b) Un graphique est symétrique par rapport à l'axe polaire (axe x) s'il est remplacé par$(r,\theta)$ une équation équivalente$(r,−\theta)$ ou si elle$(−r,\pi−\theta)$ donne lieu à une équation équivalente. (c) Un graphique est symétrique par rapport au pôle (origine) si le remplacement$(r,\theta)$ par$(−r,\theta)$ donne une équation équivalente.

Mode d'emploi : À partir d'une équation polaire, testez la symétrie.

Remplacez la combinaison appropriée de composants pour$(r,\theta)$ :$(−r,−\theta)$ pour la$\theta=\dfrac{\pi}{2}$ symétrie ;$(r,−\theta)$ pour la symétrie de l'axe polaire ; et$(−r,\theta)$ pour la symétrie par rapport au pôle.
Si les équations obtenues sont équivalentes dans un ou plusieurs tests, le graphique produit la symétrie attendue.

Exemple$\PageIndex{1}$: Testing a Polar Equation for Symmetry

Testez la symétrie$r=2 \sin \theta$ de l'équation.

Solution

Testez chacun des trois types de symétrie.

1) Le remplacement$(r,\theta)$ par$(−r,−\theta)$ donne le même résultat. Ainsi, le graphe est symétrique par rapport à la droite$\theta=\dfrac{\pi}{2}$.

$−r=2 \sin(−\theta)$

$−r=−2 \sin \theta$Une identité encore plus étrange

$r=2 \sin \theta$Multipliez par$−1$

Passé

2) Le remplacement$\theta$ par$−\theta$ ne donne pas la même équation. Par conséquent, le graphique échoue au test et peut être symétrique ou non par rapport à l'axe polaire.

$r=2 \sin(−\theta)$

$r=−2 \sin \theta$Une identité encore plus étrange

$r=−2 \sin \theta ≠ 2 \sin \theta$

Échec

3) Le remplacement$r$ par$–r$ modifie l'équation et échoue au test. Le graphe peut être symétrique ou non par rapport au pôle.

$−r=2 \sin \theta$

$r=−2 \sin \theta ≠2 \sin \theta$

Échec

Analyse

À l'aide d'une calculatrice graphique, nous pouvons voir que l'équation$r=2 \sin \theta$ est un cercle centré sur un rayon$r=1$ et qu'elle est effectivement symétrique à la droite$\theta=\dfrac{\pi}{2}$.$(0,1)$ Nous pouvons également voir que le graphique n'est pas symétrique par rapport à l'axe polaire ou au pôle. Voir la figure$\PageIndex{3}$.

Représentation graphique du cercle donné sur la grille de coordonnées polaires. Le centre est à (0,1) et son rayon est de 1. — Figurine$\PageIndex{3}$

Exercice$\PageIndex{1}$

Testez la symétrie de l'équation :$r=−2 \cos \theta$.

Réponse: L'équation échoue au test de symétrie par rapport à la ligne$\theta=\dfrac{\pi}{2}$ et par rapport au pôle. Il passe le test de symétrie de l'axe polaire.

Représentation graphique d'équations polaires en traçant des points

Pour représenter graphiquement le système de coordonnées rectangulaires, nous construisons une table de$y$ valeurs$x$ et de valeurs. Pour représenter graphiquement le système de coordonnées polaires, nous construisons une table de$r$ valeurs$\theta$ et de valeurs. Nous entrons les valeurs de$\theta$ dans une équation polaire et calculons$r$. Cependant, l'utilisation des propriétés de symétrie et la détermination des valeurs clés de$\theta$ et$r$ signifie que moins de calculs seront nécessaires.

Trouver des zéros et des maxima

Pour trouver les zéros d'une équation polaire, nous résolvons les valeurs de$\theta$ ce résultat dans$r=0$. Rappelez-vous que, pour trouver les zéros des fonctions polynomiales, nous définissons l'équation à zéro, puis nous résolvons pour$x$. Nous utilisons le même processus pour les équations polaires. Définissez$r=0$ et résolvez pour$\theta$.

Pour la plupart des formes que nous allons rencontrer, la valeur maximale d'une équation polaire est déterminée en substituant les valeurs de$\theta$ dans l'équation qui donnent la valeur maximale des fonctions trigonométriques. Considérez$r=5 \cos \theta$ que la distance maximale entre la courbe et le pôle est exprimée en$5$ unités. La valeur maximale de la fonction cosinus est$1$ quand$\theta=0$, donc notre équation polaire l'est$5 \cos \theta$, et la valeur$\theta=0$ donnera le maximum$| r |$.

De même, la valeur maximale de la fonction sinusoïdale est le$1$ moment où$\theta=\dfrac{\pi}{2}$, et si notre équation polaire l'est$r=5 \sin \theta$, la valeur$\theta=\dfrac{\pi}{2}$ donnera le maximum$| r |$. Nous pouvons trouver des informations supplémentaires en calculant les valeurs de$r$ quand$\theta=0$. Ces points seraient des points d'intersection de l'axe polaire, ce qui peut être utile pour dessiner le graphique et identifier la courbe d'une équation polaire.

Exemple$\PageIndex{2}$: Finding Zeros and Maximum Values for a Polar Equation

À l'aide de l'équation de l'exemple$\PageIndex{1}$, trouvez les zéros$| r |$ et le maximum et, si nécessaire, l'axe polaire intercepte de$r=2 \sin \theta$.

Solution

Pour trouver les zéros, définissez une$r$ valeur égale à zéro et résolvez pour$\theta$.

\[\begin{align*} 2 \sin \theta &= 0 \\ \sin \theta &= 0 \\ \theta &= {\sin}^{-1} 0 \\ \theta &= n\pi \qquad \text{where n is an integer} \end{align*}\]

Remplacez n'importe laquelle des$\theta$ valeurs dans l'équation. Nous utiliserons$0$.

\[\begin{align*} r&= 2 \sin(0) \\ r&= 0 \end{align*}\]

Les points$(0,0)$ et$(0,\pm n\pi)$ sont les zéros de l'équation. Ils coïncident tous, de sorte qu'un seul point est visible sur le graphique. Ce point est également la seule intersection de l'axe polaire.

Pour trouver la valeur maximale de l'équation, examinez la valeur maximale de la fonction trigonométrique$\sin \theta$, qui se produit lorsque le$\theta=\dfrac{\pi}{2}\pm 2k\pi$ résultat est$\sin\left(\dfrac{\pi}{2}\right)=1$. Substitut$\dfrac{\pi}{2}$ de$\theta$.

\[\begin{align*} r&= 2 \sin\left(\dfrac{\pi}{2}\right) \\ r&= 2(1) \\ r&= 2 \end{align*}\]

Analyse

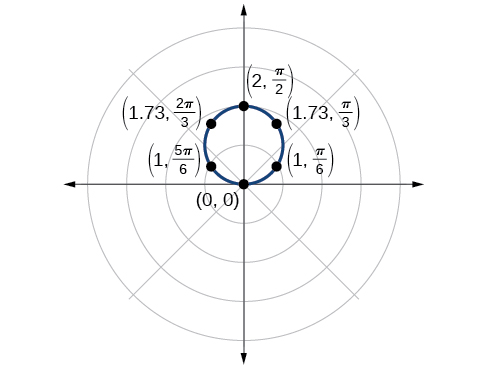
Le point$\left(2,\dfrac{\pi}{2}\right)$ sera la valeur maximale sur le graphique. Tracons quelques points supplémentaires pour vérifier le graphe d'un cercle. Voir le tableau$\PageIndex{1}$ et la figure$\PageIndex{4}$.

Tableau$\PageIndex{1}$
$\theta$	$r=2 \sin \theta$	$r$
\ (\ thêta \) « >$0$	\ (r=2 \ sin \ thêta \) « >$r=2 \sin(0)=0$	\ (r \) « >$0$
\ (\ thêta \) « >$\dfrac{\pi}{6}$	\ (r=2 \ sin \ thêta \) « >$r=2 \sin\left(\dfrac{\pi}{6}\right)=1$	\ (r \) « >$1$
\ (\ thêta \) « >$\dfrac{\pi}{3}$	\ (r=2 \ sin \ thêta \) « >$r=2 \sin\left(\dfrac{\pi}{3}\right)≈1.73$	\ (r \) « >$1.73$
\ (\ thêta \) « >$\dfrac{pi}{2}$	\ (r=2 \ sin \ thêta \) « >$r=2 \sin\left(\dfrac{\pi}{2}\right)=2$	\ (r \) « >$2$
\ (\ thêta \) « >$\dfrac{2\pi}{3}$	\ (r=2 \ sin \ thêta \) « >$r=2 \sin\left(\dfrac{2\pi}{3}\right)≈1.73$	\ (r \) « >$1.73$
\ (\ thêta \) « >$\dfrac{5\pi}{6}$	\ (r=2 \ sin \ thêta \) « >$r=2 \sin\left(\dfrac{5\pi}{6}\right)=1$	\ (r \) « >$1$
\ (\ thêta \) « >$\pi$	\ (r=2 \ sin \ thêta \) « >$r=2 \sin(\pi)=0$	\ (r \) « >$0$

Représentation graphique du cercle sur la grille de coordonnées polaires. Le centre est à (0,1) et son rayon est de 1. Six points le long de la circonférence sont marqués : (0,0), (1, pi/6), (1,3, pi/3), (2, pi/2), (1,73, 2pi/3) et (1, 5pi/6). — Figurine$\PageIndex{4}$

Exercice$\PageIndex{2}$

Sans convertir en coordonnées cartésiennes, testez la symétrie de l'équation donnée et trouvez les zéros et les valeurs maximales de$| r |$ :$r=3 \cos \theta$.

Réponse: Les tests révéleront la symétrie par rapport à l'axe polaire. Le zéro est$\left(0,\dfrac{\pi}{2}\right)$ et la valeur maximale est$(3,0)$.

Circles d'enquête

Nous avons maintenant vu l'équation d'un cercle dans le système de coordonnées polaires. Dans les deux derniers exemples, la même équation a été utilisée pour illustrer les propriétés de symétrie et montrer comment trouver les zéros, les valeurs maximales et les points tracés qui ont produit les graphes. Cependant, le cercle n'est qu'une des nombreuses formes de l'ensemble des courbes polaires.

Il existe cinq courbes polaires classiques : les cardioïdes, les limaons, les lemniscates, les courbes de rose et les spirales d'Archimède. Nous aborderons brièvement les formules polaires du cercle avant de passer aux courbes classiques et à leurs variations.

FORMULES POUR L'ÉQUATION D'UN CERCLE

Certaines des formules qui produisent le graphe d'un cercle en coordonnées polaires sont données par$r=a \cos \theta$ et$r=a \sin \theta$, où a est le diamètre du cercle ou la distance entre le pôle et le point le plus éloigné de la circonférence. Le rayon est$\dfrac{|a|}{2}$ égal ou égal à la moitié du diamètre. Pour$r=a \cos \theta$, le centre est$\left(\dfrac{a}{2},0\right)$. Pour$r=a \sin \theta$, le centre est$\left(\dfrac{a}{2},\pi\right)$. La figure$\PageIndex{5}$ montre les graphes de ces quatre cercles.

Quatre graphiques côte à côte. Tous ont une valeur absolue de rayon de a/2. Le premier est r=acos (thêta), a — Figurine$\PageIndex{5}$

Exemple$\PageIndex{3}$: Sketching the Graph of a Polar Equation for a Circle

Esquissez le graphique de$r=4 \cos \theta$.

Solution

Tout d'abord, en testant la symétrie de l'équation, nous constatons que le graphique est symétrique par rapport à l'axe polaire. Ensuite, nous trouvons les zéros et le maximum$| r |$ pour$r=4 \cos \theta$. Tout d'abord$r=0$, définissez et résolvez$\theta$. Ainsi, un zéro apparaît à$\theta=\dfrac{\pi}{2}\pm k\pi$. Un point clé à tracer est$\left(0,\dfrac{\pi}{2}\right)$.

Pour déterminer la valeur maximale de$r$, notez que la valeur maximale de la fonction cosinus est$1$ quand$\theta=0\pm 2k\pi$. Substituer$\theta=0$ dans l'équation :

\[\begin{align*} r&= 4 \cos \theta\\ r&= 4 \cos(0)\\ r&= 4(1)\\ &= 4 \end{align*}\]

La valeur maximale de l'équation est$4$. Un point clé à tracer est$(4, 0)$.

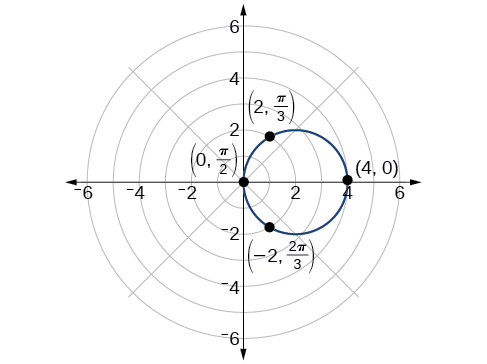
Comme$r=4 \cos \theta$ c'est symétrique par rapport à l'axe polaire, il suffit de calculer les$r$ valeurs -pour l'ensemble$θ$ de l'intervalle$[0, \pi]$. Les points du quadrant supérieur peuvent ensuite être réfléchis vers le quadrant inférieur. Créez un tableau de valeurs similaire à Tableau$\PageIndex{2}$. Le graphique est illustré dans la figure$\PageIndex{6}$.

Tableau$\PageIndex{2}$
$\theta$	$0$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$\dfrac{2\pi}{3}$	$\dfrac{3\pi}{4}$	$\dfrac{5\pi}{6}$	$\pi$
$r$	$4$	$3.46$	$2.83$	$2$	$0$	$−2$	$−2.83$	$−3.46$	$4$

Graphe de 4=4cos (thêta) en coordonnées polaires. Les points (0, pi/2), (-2, 2pi/3), (4,0) et (2, pi/3) sont marqués sur la circonférence. — Figurine$\PageIndex{6}$

Étudier les cardioïdes

Bien que la conversion des coordonnées polaires en coordonnées cartésiennes puisse sembler plus simple dans certains cas, la représentation graphique des courbes classiques est en fait moins compliquée dans le système polaire. La courbe suivante est appelée cardioïde, car elle ressemble à un cœur. Cette forme fait souvent partie de la famille des courbes appelées limaçons, mais nous aborderons ici la cardioïde en tant que telle.

FORMULES POUR UN CARDIOÏDE

Les formules qui produisent les graphes d'un cardioïde sont données par$r=a\pm b \cos \theta$ et$r=a\pm b \sin \theta$ où$a>0$$b>0$, et$\dfrac{a}{b}=1$. Le graphe cardioïde passe par le pôle, comme on peut le voir sur la figure$\PageIndex{7}$.

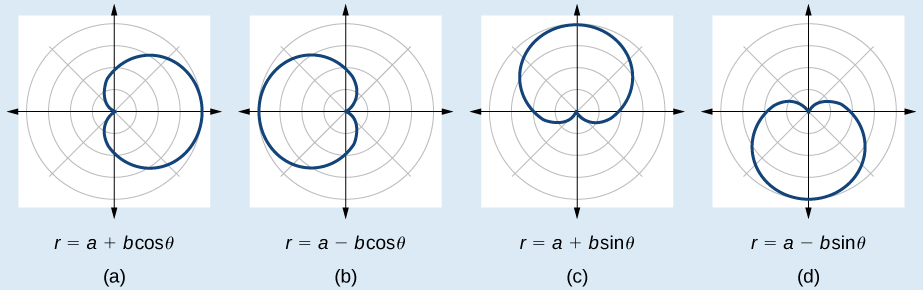
Graphique de quatre cardioïdes. (A) est r = a+ bcos (thêta). Cardioïde s'étendant vers la droite. (B) est r=a-bcos (thêta). Cardioïde s'étendant vers la gauche. (C) est r=a+bsin (thêta). Cardioïde s'étendant vers le haut (D) est r=a-bsin (thêta). Cardioïde s'étendant vers le bas — Figurine$\PageIndex{7}$

Comment : À partir de l'équation polaire d'un cardioïde, esquisser son graphique

Vérifiez l'équation pour les trois types de symétrie.
Trouve les zéros. Set$r=0$.
Détermine la valeur maximale de l'équation en fonction de la valeur maximale de l'expression trigonométrique.
Créez un tableau de valeurs pour$r$ et$\theta$.
Tracez les points et esquissez le graphique.

Exemple$\PageIndex{4}$: Sketching the Graph of a Cardioid

Esquissez le graphique de$r=2+2 \cos \theta$.

Solution

Tout d'abord, en testant la symétrie de l'équation, nous constatons que le graphe de cette équation sera symétrique par rapport à l'axe polaire. Ensuite, nous trouvons les zéros et les maximums. Cadre$r=0$, nous l'avons fait$\theta=\pi+2k\pi$. Le zéro de l'équation est situé à$(0,\pi)$. Le graphique passe par ce point.

La valeur maximale de$r=2+2 \cos \theta$ se produit lorsque$\cos \theta$ est un maximum, c'est-à-dire quand$\cos \theta=1$ ou quand$\theta=0$. $\theta=0$Substituez dans l'équation et résolvez pour$r$.

\[\begin{align*} r&= 2+2 \cos(0)\\ r&= 2+2(1)\\ &= 4 \end{align*}\]

Le point$(4,0)$ est la valeur maximale sur le graphique.

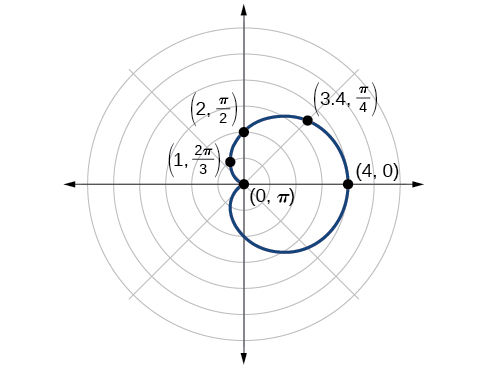
Nous avons constaté que l'équation polaire est symétrique par rapport à l'axe polaire, mais comme elle s'étend aux quatre quadrants, nous devons tracer les valeurs sur l'intervalle$[0, \pi]$. La partie supérieure du graphique est ensuite réfléchie sur l'axe polaire. Ensuite, nous créons un tableau de valeurs, comme dans Tableau$\PageIndex{3}$, puis nous traçons les points et dessinons le graphique. Voir la figure$\PageIndex{8}$.

Tableau$\PageIndex{3}$
θ	0	$\dfrac{π}{4}$	$\dfrac{π}{2}$	$\dfrac{2π}{3}$	$π$
r	4	3,41	2	1	0

Graphe de r=2+2cos (thêta). Cardioïde s'étendant vers la droite. Les points situés sur l'arête (0, pi), (4,0), (3,4, pi/4), (2, pi/2) et (1, 2pi/3) sont affichés. — Figurine$\PageIndex{8}$

Investiguer sur Limaçons

Le mot limaçon signifie « escargot » en vieux français, un nom qui décrit la forme du graphique. Comme mentionné précédemment, le cardioïde fait partie de la famille des limaçons, et nous pouvons voir les similitudes dans les graphiques. Les autres images de cette catégorie incluent le limaçon à une boucle et le limaçon à deux boucles (ou boucle intérieure). Les limaçons à boucle unique sont parfois appelés limaçons alvéolés quand$1<\dfrac{a}{b}<2$ et limaçons convexes quand$\dfrac{a}{b}≥2$.

FORMULES POUR LIMAÇONS À BOUCLE UNIQUE

Les formules qui produisent le graphique d'un limaçon à boucle unique alvéolé sont données par$r=a\pm b \cos \theta$ et$r=a\pm b \sin \theta$ où$a>0$$b>0$, et$1<ab<2$. Les quatre graphiques sont présentés dans la figure$\PageIndex{9}$.

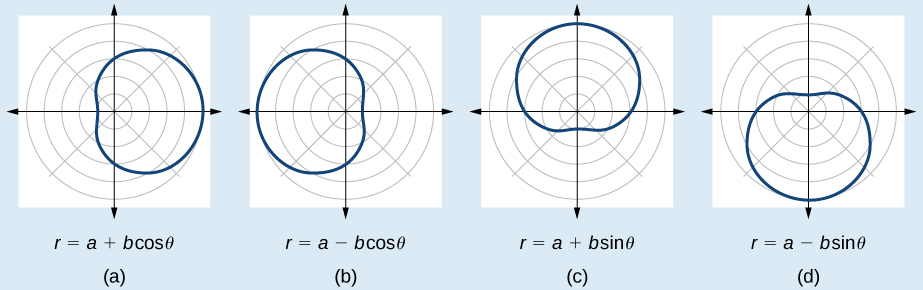
Quatre limaçons alvéolés côte à côte. (A) est r=a+bcos (thêta). S'étendant vers la droite. (B) est r=a-bcos (thêta). S'étendant vers la gauche. (C) est r=a+bsin (thêta). S'étendre vers le haut (D) est r=a-bsin (thêta). S'étendant vers le bas — Figurine$\PageIndex{9}$

Comment : À partir d'une équation polaire pour un limaçon à boucle unique, esquisser le graphique

Testez la symétrie de l'équation. N'oubliez pas que l'échec d'un test de symétrie ne signifie pas que la forme ne présentera pas de symétrie. Souvent, la symétrie peut se révéler lorsque les points sont tracés.
Trouve les zéros.
Trouvez les valeurs maximales en fonction de l'expression trigonométrique.
Fabriquez une table.
Tracez les points et esquissez le graphique.

Exemple$\PageIndex{5}$: Sketching the Graph of a One-Loop Limaçon

Tracez l'équation$r=4−3 \sin \theta$.

Solution

Tout d'abord, en testant la symétrie de l'équation, nous constatons qu'elle échoue aux trois tests de symétrie, ce qui signifie que le graphe peut présenter ou non une symétrie. Nous ne pouvons donc pas utiliser la symétrie pour nous aider à le tracer. Cependant, cette équation possède un graphique qui montre clairement la symétrie par rapport à la droite$\theta=\dfrac{\pi}{2}$, mais elle échoue aux trois tests de symétrie. Une calculatrice graphique illustrera immédiatement la qualité de réflexion du graphique.

Ensuite, nous trouvons les zéros et les maximums, et nous tracons les points réfléchissants pour vérifier toute symétrie. Le réglage a$r=0$ pour résultat$\theta$ d'être indéfini. Qu'est-ce que cela signifie ? Comment$\theta$ pourrait-on ne pas le définir ? L'angle n'$\theta$est pas défini quelle que soit la valeur de$\sin \theta>1$. Par conséquent, n'$\theta$est pas défini car il n'existe aucune valeur$\theta$ pour laquelle$\sin \theta>1$. Par conséquent, le graphe ne passe pas par le pôle. Peut-être que le graphique traverse l'axe polaire, mais pas au pôle. Nous pouvons étudier d'autres interceptions en calculant$r$ quand$\theta=0$.

\[\begin{align*} r(0)&= 4-3 \sin(0)\\ r&= 4-3\cdot 0\\ &= 4 \end{align*}\]

Il y a donc au moins une intersection de l'axe polaire à$(4,0)$.

Ensuite, comme la valeur maximale de la fonction sinusoïdale est$1$ quand$\theta=\dfrac{\pi}{2}$, nous allons la remplacer$\theta=\dfrac{\pi}{2}$ dans l'équation et résoudre pour$r$. Ainsi,$r=1$.

Créez un tableau des coordonnées similaire à Tableau$\PageIndex{4}$.

Tableau$\PageIndex{4}$
$\theta$	$0$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$\dfrac{2\pi}{3}$	$\dfrac{5\pi}{6}$	$\pi$	$\dfrac{7\pi}{6}$	$\dfrac{4\pi}{3}$	$\dfrac{3\pi}{2}$	$\dfrac{5\pi}{3}$	$\dfrac{11\pi}{6}$	$2\pi$
$r$	$4$	$2.5$	$1.4$	$1$	$1.4$	$2.5$	$4$	$5.5$	$6.6$	$7$	$6.6$	$5.5$	$4$

Le graphique est illustré dans la figure$\PageIndex{10}$.

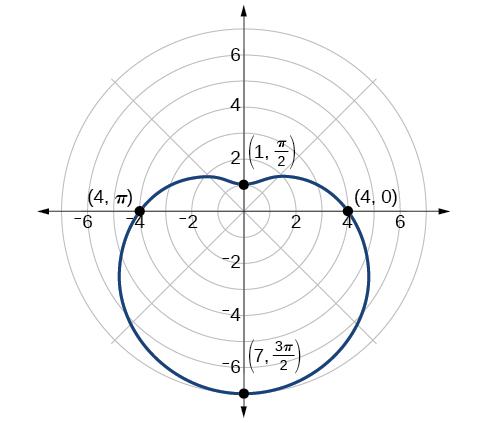
Graphe du limaçon r=4-3sin (thêta). S'étendant vers le bas Les points du bord sont affichés : (1, pi/2), (4,0), (4, pi) et (7, 3pi/2). — Figure$\PageIndex{10}$ : Limaçon à boucle unique

Analyse

Il s'agit d'un exemple de courbe pour laquelle la création d'un tableau de valeurs est essentielle pour produire un graphique précis. Les tests de symétrie échouent ; le zéro n'est pas défini. Bien qu'il puisse sembler évident qu'une équation impliquant$\sin \theta$ est probablement symétrique par rapport à la droite$\theta=\dfrac{\pi}{2}$, l'évaluation d'un plus grand nombre de points permet de vérifier que le graphique est correct.

Exercice$\PageIndex{3}$

Esquissez le graphique de$r=3−2 \cos \theta$.

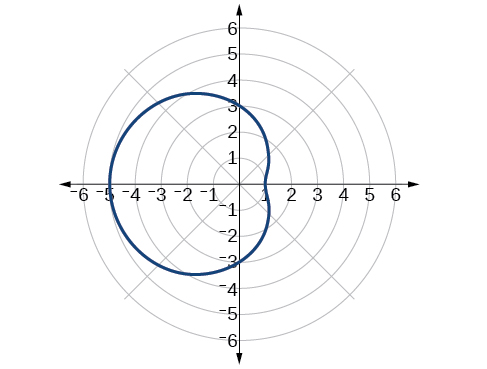
Réponse: $Graphe du limaçon r=3-2cos (thêta). S'étendant vers la gauche.$
Figurine$\PageIndex{11}$

Un autre type de limaçon, le limaçon à boucle intérieure, doit son nom à la boucle formée à l'intérieur de la forme générale du limaçon. Il a été découvert par l'artiste allemand Albrecht Dürer (1471-1528), qui a révélé une méthode pour dessiner le limaçon en boucle intérieure dans son livre de 1525 Underweysung der Messing. Un siècle plus tard, le père du mathématicien Blaise Pascal, Étienne Pascal (1588-1651), l'a redécouvert.

FORMULES POUR LIMAÇONS À BOUCLE INTÉRIEURE

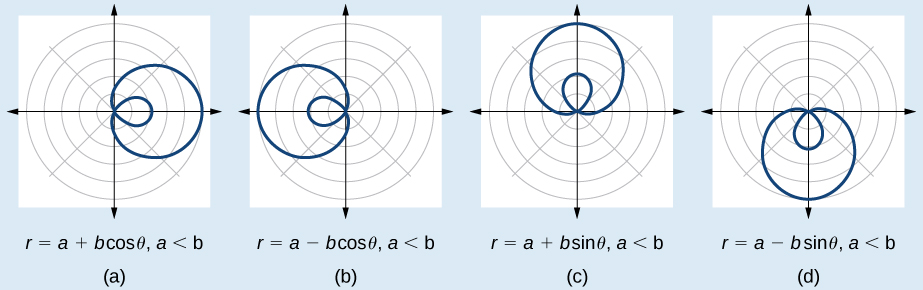
Les formules qui génèrent les limaçons de la boucle interne sont données par$r=a\pm b\cos \theta$ et$r=a\pm b \sin \theta$ où$a>0$$b>0$, et$a<b$. Le graphe du limaçon de la boucle intérieure passe deux fois par le pôle : une fois pour la boucle extérieure et une fois pour la boucle intérieure. Voir la Figure 10.5.12 pour les graphiques.

Graphe de quatre limaçons en boucle intérieure côte à côte. (A) est r=a+bcos (thêta), a<b. Étendu vers la droite. (B) est a-bcos (thêta), a<b. S'étend vers la gauche. (C) est r=a+bsin (thêta), a<b. S'étend vers le haut. (D) est r=a-bsin (thêta), a<b. S'étend vers le bas. — Figurine$\PageIndex{12}$

Exemple$\PageIndex{6}$: Sketching the Graph of an Inner-Loop Limaçon

Esquissez le graphique de$r=2+5 \cos \theta$.

Solution

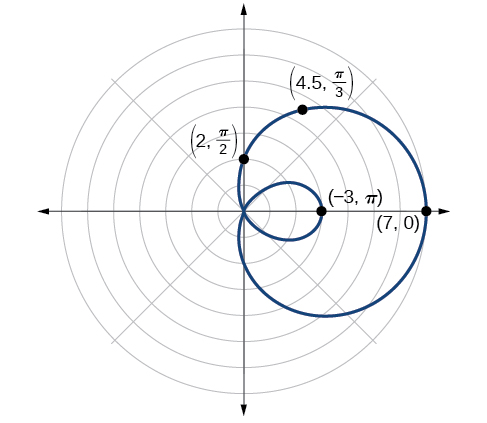
En testant la symétrie, nous constatons que le graphe de l'équation est symétrique par rapport à l'axe polaire. Ensuite, trouver les zéros révèle que lorsque$r=0$,$\theta=1.98$. Le maximum$| r |$ est trouvé quand$\cos \theta=1$ et quand$\theta=0$. Ainsi, le maximum est trouvé au point$(7, 0)$.

Même si nous avons trouvé la symétrie, le zéro et le maximum, le fait de tracer un plus grand nombre de points aidera à définir la forme, puis un motif apparaîtra. Voir le tableau$\PageIndex{5}$.

Tableau$\PageIndex{5}$
$\theta$	$0$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$\dfrac{2\pi}{3}$	$\dfrac{5\pi}{6}$	$\pi$	$\dfrac{7\pi}{6}$	$\dfrac{4\pi}{3}$	$\dfrac{3\pi}{2}$	$\dfrac{5\pi}{3}$	$\dfrac{11\pi}{6}$	$2\pi$
$r$	$7$	$6.3$	$4.5$	$2$	$−0.5$	$−2.3$	$−3$	$−2.3$	$−0.5$	$2$	$4.5$	$6.3$	$7$

Comme prévu, les valeurs commencent à se répéter par la suite$\theta=\pi$. Le graphique est illustré dans la figure$\PageIndex{13}$.

Graphique du limaçon de la boucle interne r=2+5cos (thêta). S'étend vers la droite. Les points sur l'arête tracés sont (7,0), (4,5, pi/3), (2, pi/2) et (-3, pi). — Figure$\PageIndex{13}$ : Limaçon à boucle intérieure

Enquête sur les lemniscates

La lemniscate est une courbe polaire qui ressemble au symbole de l'infini$\infty$ ou à une figure$8$. Centrée au pôle, une lemniscate est symétrique par définition.

FORMULES POUR LEMNISCATS

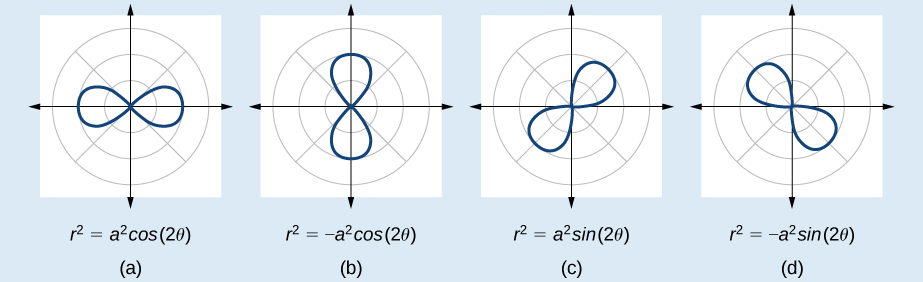
Les formules qui génèrent le graphe d'une lemniscate sont données par$r^2=a^2 \cos 2\theta$ et$r^2=a^2 \sin 2\theta$ où$a≠0$. La formule$r^2=a^2 \sin 2\theta$ est symétrique par rapport au pôle. La formule$r^2=a^2 \cos 2\theta$ est symétrique par rapport au pôle, à la ligne$\theta=\dfrac{\pi}{2}$ et à l'axe polaire. Voir la figure$\PageIndex{14}$ pour les graphiques.

Quatre graphes représentant des lemniscates côte à côte. (A) est r^2 = a^2 * cos (2thêta). Figure huit horizontale, sur l'axe X. (B) est r^2 = - a^2 * cos (2thêta). Figure huit verticale, sur l'axe Y. (C) est r^2 = a^2 * sin (2thêta). Figure huit en diagonale sur la ligne y=x. (D) est r^2 = -a^2 *sin (2thêta). Figure huit en diagonale sur la ligne y=-x. — Figurine$\PageIndex{14}$

Exemple$\PageIndex{7}$: Sketching the Graph of a Lemniscate

Esquissez le graphique de$r^2=4 \cos 2\theta$.

Solution

L'équation présente une symétrie par rapport à la ligne$\theta=\dfrac{\pi}{2}$, à l'axe polaire et au pôle.

Trouvons les zéros. Cela devrait être une routine maintenant, mais nous allons aborder cette équation un peu différemment en effectuant la substitution$u=2\theta$.

\[\begin{align*} 0 &= 4 \cos 2\theta \\ 0 &= 4 \cos u \\ 0 &= \cos u \\ {\cos}^{-1} 0 &= \dfrac{\pi}{2} \\ u &= \dfrac{\pi}{2} \qquad \text{Substitute } 2\theta \text{ back in for } u. \\ 2\theta &= \dfrac{\pi}{2} \\ \theta &= \dfrac{\pi}{4} \end{align*}\]

Donc, le point$\left(0,\dfrac{\pi}{4}\right)$ est un zéro de l'équation.

Trouvons maintenant la valeur maximale. Depuis le maximum de$\cos u=1$ quand$u=0$, le maximum de$\cos 2\theta=1$ quand$2\theta=0$. Ainsi,

\[\begin{align*} r^2 &= 4 \cos(0) \\ r^2 &= 4(1)\\ r^2&= 4 \\ r&= \pm 4\\ &=2 \end{align*}\]

Nous avons un maximum à$(2, 0)$. Comme ce graphique est symétrique par rapport au pôle, à la ligne$\theta=\dfrac{\pi}{2}$ et à l'axe polaire, il suffit de tracer les points du premier quadrant.

Créez un tableau similaire à Tableau$\PageIndex{6}$.

Tableau$\PageIndex{6}$
$\theta$	$0$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$
$r$	$2$	$\sqrt{2}$	$0$	$\sqrt{2}$	$0$

Tracez les points sur le graphique, comme celui illustré sur la figure$\PageIndex{15}$.

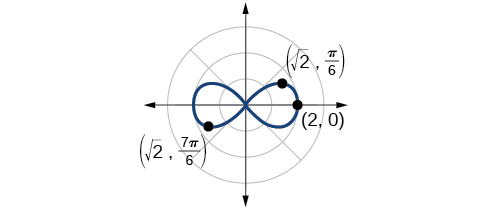
Graphe de r^2 = 4cos (2thêta). Lemniscate horizontale, le long de l'axe X. Les points sur l'arête tracés sont (2,0), (rad2, pi/6), (rad2 7pi/6). — Figurine$\PageIndex{15}$ : Lenniscate

Analyse

Faire une substitution telle que$u=2\theta$ c'est une pratique courante en mathématiques car cela peut simplifier les calculs. Cependant, il ne faut pas oublier de remplacer le terme de substitution par le terme d'origine à la fin, puis de résoudre l'inconnu.

Certains points de ce graphique peuvent ne pas apparaître à l'aide de la fonction Trace de la calculatrice graphique TI-84, et le tableau de la calculatrice peut afficher une erreur pour ces mêmes points de$r$. Cela est dû au fait qu'il n'existe pas de véritables racines carrées pour ces valeurs de$θ$. En d'autres termes, les$r$ valeurs -correspondantes de$\sqrt{4 \cos(2\theta)}$ sont des nombres complexes car il y a un nombre négatif sous le radical.

Étude de Rose Curves

Le type suivant d'équation polaire produit une forme en forme de pétale appelée courbe en rose. Bien que les graphiques semblent complexes, une simple équation polaire génère le motif.

ROSES CURVES

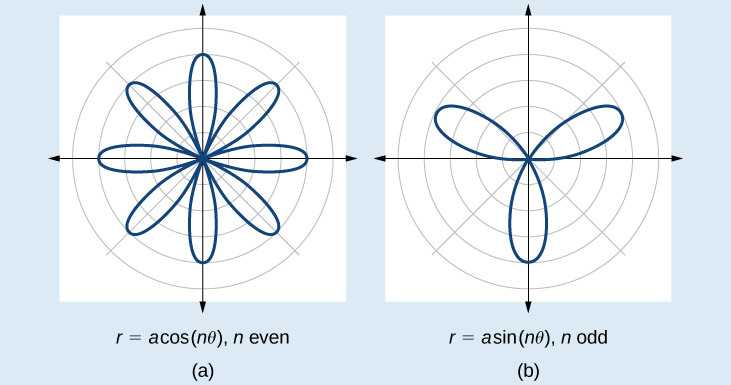
Les formules qui génèrent le graphique d'une courbe en rose sont données par$r=a \cos n\theta$ et$r=a \sin n\theta$ où$a≠0$. Si elle$n$ est uniforme, la courbe comporte$2n$ des pétales. Si$n$ c'est étrange, la courbe comporte$n$ des pétales. Voir la figure$\PageIndex{16}$.

Graphe de deux courbes de roses côte à côte. (A) est r=acos (ntheta), où n est pair. Huit pétales s'étendent à partir de leur origine, régulièrement espacés. (B) est r=asin (ntheta) où n est impair. Trois pétales s'étendent à partir de l'origine, régulièrement espacés. — Figurine$\PageIndex{16}$

Exemple$\PageIndex{8}$: Sketching the Graph of a Rose Curve ($n$ Even)

Esquissez le graphique de$r=2 \cos 4\theta$.

Solution

En testant la symétrie, nous constatons encore une fois que les tests de symétrie ne disent pas tout. Le graphe est non seulement symétrique par rapport à l'axe polaire, mais également par rapport à la ligne$\theta=\dfrac{\pi}{2}$ et au pôle.

Nous allons maintenant trouver les zéros. Effectuez d'abord la substitution$u=4\theta$.

\[\begin{align*} 0 &= 2 \cos 4\theta \\ 0 &= \cos 4\theta \\ 0 &= \cos u \\ {\cos}^{-1} 0 &=u \\ u &= \dfrac{\pi}{2} \\ 4\theta &= \dfrac{\pi}{2} \\ \theta &=\dfrac{\pi}{8} \end{align*}\]

Le zéro est$\theta=\dfrac{\pi}{8}$. Le point$\left(0,\dfrac{\pi}{8}\right)$ se trouve sur la courbe.

Ensuite, nous trouvons le maximum$| r |$. Nous savons que c'est la valeur maximale de$\cos u=1$ quand$\theta=0$. Ainsi,

\[\begin{align*} r &=2 \cos(4\cdot 0) \\ r &=2 \cos(0) \\ r &=2(1)\\ &= 2 \end{align*}\]

Le point$(2,0)$ se trouve sur la courbe.

Le graphique de la courbe de rose possède des propriétés uniques, qui sont révélées dans le tableau$\PageIndex{7}$.

Tableau$\PageIndex{7}$
$\theta$	$0$	$\dfrac{\pi}{8}$	$\dfrac{\pi}{4}$	$\dfrac{3\pi}{8}$	$\dfrac{\pi}{2}$	$5π8$	$3π4$
$r$	$2$	$0$	$−2$	$0$	$2$	$0$	$−2$

Comme$r=0$ lorsque$\theta=\dfrac{\pi}{8}$, il est logique de diviser les valeurs du tableau par$\dfrac{\pi}{8}$ unités. Un schéma précis se dégage. Regardez la plage de$r$ valeurs :$2, 0, −2, 0$ et ainsi de suite. Cela représente le développement de la courbe, un pétale à la fois. À partir de$r=0$, chaque pétale s'étend sur une distance de$r=2$, puis revient à zéro$2n$ fois pour un total de huit pétales. Voir le graphique dans la figure$\PageIndex{17}$.

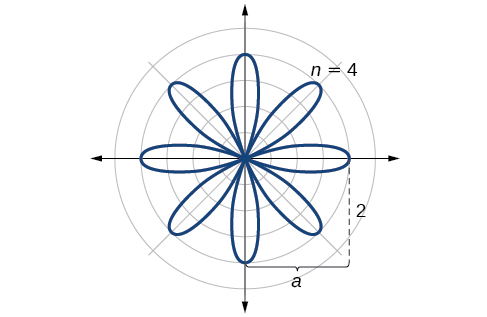
Croquis de la courbe de rose r=2*cos (4 thêta). Dépasse une distance de 2 pour chaque pétale 2 n fois (ici 2*4 = 8 fois). — Figure$\PageIndex{17}$ : Courbe de rose,$n$ paire

Analyse

Lorsque ces courbes sont dessinées, il est préférable de tracer les points dans l'ordre, comme dans le tableau$\PageIndex{7}$. Cela nous permet de voir comment le graphique atteint un maximum (la pointe d'un pétale), revient en boucle en traversant le pôle, atteint le maximum opposé et revient en boucle vers le pôle. L'action est continue jusqu'à ce que tous les pétales soient dessinés.

Exercice$\PageIndex{4}$

Esquissez le graphique de$r=4 \sin(2\theta)$.

Réponse: Le graphique est une courbe en rose,$n$ égale

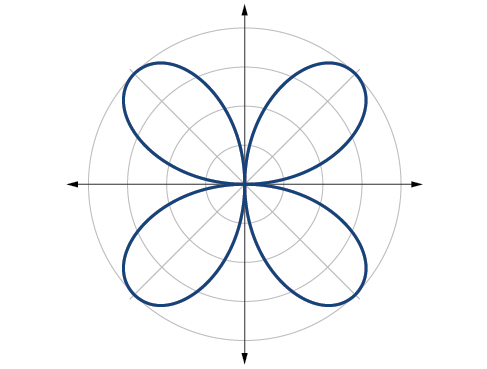
$Graphique de la courbe de rose r=4 sin (2 thêta). Paire : quatre pétales régulièrement espacés, chacun d'une longueur de 4.$
Figurine$\PageIndex{18}$

Exemple$\PageIndex{9}$: Sketching the Graph of a Rose Curve ($n$ Odd)

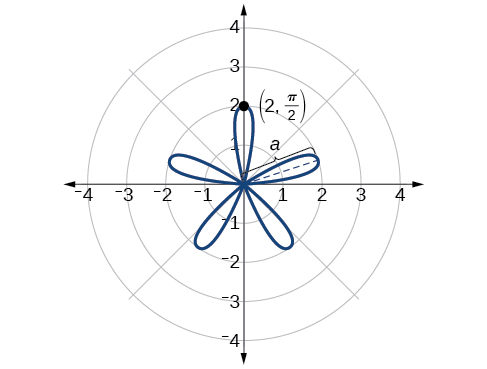
Esquissez le graphique de$r=2 \sin(5\theta)$.

Solution

Le graphique de l'équation montre la symétrie par rapport à la droite$\theta=\dfrac{\pi}{2}$. Ensuite, trouvez les zéros et le maximum. Nous voudrons effectuer la substitution$u=5\theta$.

\[\begin{align*} 0 &=2 \sin(5\theta) \\ 0 &=\sin u \\ {\sin}^{-1} 0 &=0 \\ u &=0 \\ 5\theta &=0 \\ \theta &=0 \end{align*}\]

La valeur maximale est calculée à l'angle où$\sin \theta$ est un maximum. Par conséquent,

\[\begin{align*} r&= 2 \sin\left(5\cdot \dfrac{\pi}{2}\right) \\ r&= 2(1)\\ &= 2 \end{align*}\]

Ainsi, la valeur maximale de l'équation polaire est$2$. Il s'agit de la longueur de chaque pétale. Comme la courbe des$n$ paires donne le même nombre de pétales que$n$, il y aura cinq pétales sur le graphique. Voir la figure$\PageIndex{19}$.

Créez une table de valeurs similaire à Table$\PageIndex{8}$.

Tableau$\PageIndex{8}$
$\theta$	$0$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$\dfrac{2\pi}{3}$	$\dfrac{5\pi}{6}$	$\pi$
$r$	\ (0 \ 0)	$1$	$−1.73$	$2$	$−1.73$	$1$	$0$

Graphique de la courbe de rose r=2sin (5thêta). Cinq pétales régulièrement espacés autour de leur origine. Le point (2, pi/2) sur l'arête est marqué. — Figure$\PageIndex{19}$ : Courbe de rose,$n$ impaire

Exercice$\PageIndex{5}$

Esquissez le graphique de$r=3 \cos(3\theta)$.

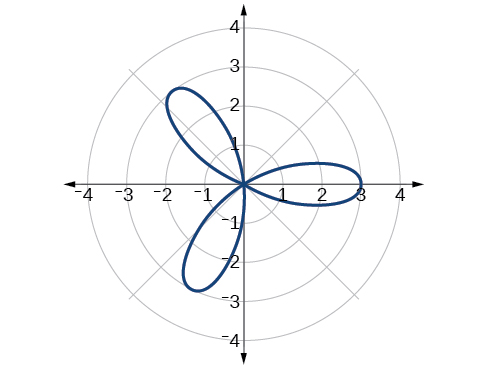
Réponse: $Graphique de la courbe de rose r=3cos (3thêta). Trois pétales régulièrement espacés par rapport à leur origine.$
Figurine$\PageIndex{20}$

Courbe de rose,$n$ impaire

Enquête sur la spirale d'Archimède

La dernière équation polaire dont nous discuterons est la spirale d'Archimède, nommée en l'honneur de son découvreur, le mathématicien grec Archimède (vers 287 avant notre ère - vers 212 avant notre ère), à qui on attribue de nombreuses découvertes dans les domaines de la géométrie et de la mécanique.

SPIRALE D'ARCHIMÈDE

La formule qui génère le graphe de la spirale d'Archimède est donnée par$r=\theta$ for$\theta≥0$. Au fur et à$r$ mesure qu'il$\theta$ augmente, augmente à un rythme constant sur une trajectoire toujours plus large, sans fin et en spirale. Voir la figure$\PageIndex{21}$.

Comment faire : étant donné la fin de la spirale d'Archimède$[ 0,2\pi ]$,sketch the graph

Créez un tableau de valeurs pour$r$ et$\theta$ sur le domaine donné.
Tracez les points et esquissez le graphique.

Exemple$\PageIndex{10}$: Sketching the Graph of an Archimedes’ Spiral

Esquissez le graphique de$r=\theta$ plus$[0,2\pi]$.

Solution

Comme$r$ il est égal à$\theta$, le tracé de la spirale d'Archimède commence au pôle au point$(0, 0)$. Bien que le graphique indique une symétrie, il n'y a aucune symétrie formelle en ce qui concerne la réussite des tests de symétrie. De plus, il n'y a pas de valeur maximale, sauf si le domaine est restreint.

Créez un tableau tel que Tableau$\PageIndex{9}$.

Tableau$\PageIndex{9}$
$\theta$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\pi$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2\pi$
$r$	$0.785$	$1.57$	$3.14$	$4.71$	$5.50$	$6.28$

Notez que les valeurs r sont simplement la forme décimale de l'angle mesuré en radians. Nous pouvons les voir sur un graphique de la figure$\PageIndex{22}$.

Graphe de la spirale r=thêta d'Archimède sur [0,2pi]. Commence à l'origine et sort en spirale en une boucle dans le sens antihoraire. Les points (pi/4, pi/4), (pi/2, pi/2), (pi, pi), (5 pi/4, 5 pi/4), (7 pi/4, pi/4) et (2 pi, 2 pi) sont marqués. — Figure$\PageIndex{22}$ : La spirale d'Archimède

Analyse

Le domaine de cette courbe polaire est$[ 0,2\pi ]$. En général, cependant, le domaine de cette fonction est$(−\infty,\infty)$. Représenter graphiquement l'équation de la spirale d'Archimède est assez simple, même si l'image donne l'impression que ce serait complexe.

Exercice$\PageIndex{6}$

Esquissez le graphique de$r=−\theta$ l'intervalle$[ 0,4\pi ]$.

Réponse: $alt$
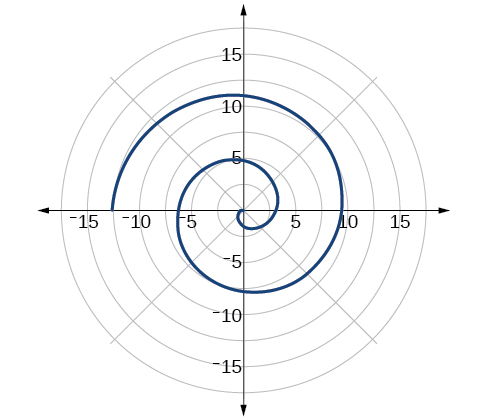
Figurine$\PageIndex{23}$

Résumé de Curves

Nous avons exploré un certain nombre de courbes polaires apparemment complexes dans cette section. La figure$\PageIndex{24}$ et la figure$\PageIndex{25}$ résument les graphiques et les équations pour chacune de ces courbes.

Quatre graphiques côte à côte - un résumé. (A) est un cercle : r=asin (thêta) ou r=acos (thêta). (B) est un cardioïde : r= a + ou - bcos (thêta), ou r = a + ou - b sin (thêta). a — Figurine$\PageIndex{24}$

Quatre graphiques côte à côte - un résumé. (A) est lemniscate. R^2 = a^2cos (2thêta), ou r^2=a^2sin (2thêta). a n'est pas égal à 0. (B) est une courbe ascendante (paire). R = acos (nthêta) ou r=asin (nthêta). N est pair et il y a 2n pétales. (C) est une courbe en rose (pas impaire). R = acos (nthêta) ou r=asin (thêta). N est impair et il n'y a pas de pétales. (D) est une spirale d'Archimède. R=thêta et thêta — Figurine$\PageIndex{25}$

Médias

Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires avec des graphiques de coordonnées polaires.

Représentation graphique des équations polaires, partie 1
Représentation graphique des équations polaires, partie 2
Animation : Les graphes des équations polaires
Représentation graphique d'équations polaires sur le TI-84

Concepts clés

Il est plus facile de représenter graphiquement des équations polaires si nous pouvons tester la symétrie des équations par rapport à la ligne$\theta=\dfrac{\pi}{2}$, à l'axe polaire ou au pôle.
Trois tests de symétrie indiquent si le graphe d'une équation polaire présentera une symétrie. Si une équation échoue à un test de symétrie, le graphe peut présenter ou non une symétrie. Voir l'exemple$\PageIndex{1}$.
Les équations polaires peuvent être représentées graphiquement en créant un tableau de valeurs pour$\theta$ et$r$.
La valeur maximale d'une équation polaire est déterminée en substituant la valeur$\theta$ qui conduit à la valeur maximale de l'expression trigonométrique.
Les zéros d'une équation polaire sont déterminés en définissant$r=0$ et en résolvant pour$\theta$. Voir l'exemple$\PageIndex{2}$.
Certaines formules qui produisent le graphe d'un cercle en coordonnées polaires sont données par$r=a \cos \theta$ et$r=a \sin \theta$. Voir l'exemple$\PageIndex{3}$.
Les formules qui produisent les graphes d'un cardioïde sont données par$r=a\pm b \cos \theta$ et$r=a\pm b \sin \theta$, pour$a>0$$b>0$, et$ab=1$. Voir l'exemple$\PageIndex{4}$.
Les formules qui produisent les graphes d'un limaçon à boucle unique sont données par$r=a\pm b \cos \theta$ et$r=a\pm b \sin \theta$ pour$1<ab<2$. Voir l'exemple$\PageIndex{5}$.
Les formules qui produisent les graphes d'un limaçon en boucle interne sont données par$r=a\pm b \cos \theta$ et$r=a\pm b \sin \theta$ pour$a>0$$b>0$, et$a<b$. Voir l'exemple$\PageIndex{6}$.
Les formules qui produisent les graphes d'une lemniscate sont données par$r^2=a^2 \cos 2\theta$ et$r^2=a^2 \sin 2\theta$, où.$a≠0$ Voir l'exemple$\PageIndex{7}$.
Les formules qui produisent les graphes des courbes de rose sont données par$r=a \cos n\theta$ et$r=a \sin n\theta$, où$a≠0$ ; si$n$ c'est pair, il y a des$2n$ pétales, et si$n$ c'est impair, il y a n pétales. Voir Exemple$\PageIndex{8}$ et Exemple$\PageIndex{9}$.
La formule qui produit le graphe d'une spirale d'Archimède est donnée par$r=\theta$,$\theta≥0$. Voir l'exemple$\PageIndex{10}$.

\(\theta\)	\(r=2 \sin \theta\)	\(r\)
\ (\ thêta \) « >\(0\)	\ (r=2 \ sin \ thêta \) « >\(r=2 \sin(0)=0\)	\ (r \) « >\(0\)
\ (\ thêta \) « >\(\dfrac{\pi}{6}\)	\ (r=2 \ sin \ thêta \) « >\(r=2 \sin\left(\dfrac{\pi}{6}\right)=1\)	\ (r \) « >\(1\)
\ (\ thêta \) « >\(\dfrac{\pi}{3}\)	\ (r=2 \ sin \ thêta \) « >\(r=2 \sin\left(\dfrac{\pi}{3}\right)≈1.73\)	\ (r \) « >\(1.73\)
\ (\ thêta \) « >\(\dfrac{pi}{2}\)	\ (r=2 \ sin \ thêta \) « >\(r=2 \sin\left(\dfrac{\pi}{2}\right)=2\)	\ (r \) « >\(2\)
\ (\ thêta \) « >\(\dfrac{2\pi}{3}\)	\ (r=2 \ sin \ thêta \) « >\(r=2 \sin\left(\dfrac{2\pi}{3}\right)≈1.73\)	\ (r \) « >\(1.73\)
\ (\ thêta \) « >\(\dfrac{5\pi}{6}\)	\ (r=2 \ sin \ thêta \) « >\(r=2 \sin\left(\dfrac{5\pi}{6}\right)=1\)	\ (r \) « >\(1\)
\ (\ thêta \) « >\(\pi\)	\ (r=2 \ sin \ thêta \) « >\(r=2 \sin(\pi)=0\)	\ (r \) « >\(0\)

\(\theta\)	\(0\)	\(\dfrac{\pi}{6}\)	\(\dfrac{\pi}{4}\)	\(\dfrac{\pi}{3}\)	\(\dfrac{\pi}{2}\)	\(\dfrac{2\pi}{3}\)	\(\dfrac{3\pi}{4}\)	\(\dfrac{5\pi}{6}\)	\(\pi\)
\(r\)	\(4\)	\(3.46\)	\(2.83\)	\(2\)	\(0\)	\(−2\)	\(−2.83\)	\(−3.46\)	\(4\)

θ	0	\(\dfrac{π}{4}\)	\(\dfrac{π}{2}\)	\(\dfrac{2π}{3}\)	\(π\)
r	4	3,41	2	1	0

\(\theta\)	\(0\)	\(\dfrac{\pi}{6}\)	\(\dfrac{\pi}{3}\)	\(\dfrac{\pi}{2}\)	\(\dfrac{2\pi}{3}\)	\(\dfrac{5\pi}{6}\)	\(\pi\)	\(\dfrac{7\pi}{6}\)	\(\dfrac{4\pi}{3}\)	\(\dfrac{3\pi}{2}\)	\(\dfrac{5\pi}{3}\)	\(\dfrac{11\pi}{6}\)	\(2\pi\)
\(r\)	\(4\)	\(2.5\)	\(1.4\)	\(1\)	\(1.4\)	\(2.5\)	\(4\)	\(5.5\)	\(6.6\)	\(7\)	\(6.6\)	\(5.5\)	\(4\)

\(\theta\)	\(0\)	\(\dfrac{\pi}{6}\)	\(\dfrac{\pi}{3}\)	\(\dfrac{\pi}{2}\)	\(\dfrac{2\pi}{3}\)	\(\dfrac{5\pi}{6}\)	\(\pi\)	\(\dfrac{7\pi}{6}\)	\(\dfrac{4\pi}{3}\)	\(\dfrac{3\pi}{2}\)	\(\dfrac{5\pi}{3}\)	\(\dfrac{11\pi}{6}\)	\(2\pi\)
\(r\)	\(7\)	\(6.3\)	\(4.5\)	\(2\)	\(−0.5\)	\(−2.3\)	\(−3\)	\(−2.3\)	\(−0.5\)	\(2\)	\(4.5\)	\(6.3\)	\(7\)

Remarque : TESTS DE SYMÉTRIE

Mode d'emploi : À partir d'une équation polaire, testez la symétrie.

Exemple\(\PageIndex{1}\): Testing a Polar Equation for Symmetry

Exercice\(\PageIndex{1}\)

Exemple\(\PageIndex{2}\): Finding Zeros and Maximum Values for a Polar Equation

Exercice\(\PageIndex{2}\)

Circles d'enquête

FORMULES POUR L'ÉQUATION D'UN CERCLE

Exemple\(\PageIndex{3}\): Sketching the Graph of a Polar Equation for a Circle

Étudier les cardioïdes

FORMULES POUR UN CARDIOÏDE

Comment : À partir de l'équation polaire d'un cardioïde, esquisser son graphique

Exemple\(\PageIndex{4}\): Sketching the Graph of a Cardioid

Investiguer sur Limaçons

FORMULES POUR LIMAÇONS À BOUCLE UNIQUE

Comment : À partir d'une équation polaire pour un limaçon à boucle unique, esquisser le graphique

Exemple\(\PageIndex{5}\): Sketching the Graph of a One-Loop Limaçon

Exercice\(\PageIndex{3}\)

FORMULES POUR LIMAÇONS À BOUCLE INTÉRIEURE

Exemple\(\PageIndex{6}\): Sketching the Graph of an Inner-Loop Limaçon

Enquête sur les lemniscates

FORMULES POUR LEMNISCATS

Exemple\(\PageIndex{7}\): Sketching the Graph of a Lemniscate

Étude de Rose Curves

ROSES CURVES

Exemple\(\PageIndex{8}\): Sketching the Graph of a Rose Curve (\(n\) Even)

Exercice\(\PageIndex{4}\)

Exemple\(\PageIndex{9}\): Sketching the Graph of a Rose Curve (\(n\) Odd)

Exercice\(\PageIndex{5}\)

Enquête sur la spirale d'Archimède

SPIRALE D'ARCHIMÈDE

Comment faire : étant donné la fin de la spirale d'Archimède\([ 0,2\pi ]\),sketch the graph

Exemple\(\PageIndex{10}\): Sketching the Graph of an Archimedes’ Spiral

Exercice\(\PageIndex{6}\)

Médias

\(\theta\)	\(0\)	\(\dfrac{\pi}{8}\)	\(\dfrac{\pi}{4}\)	\(\dfrac{3\pi}{8}\)	\(\dfrac{\pi}{2}\)	\(5π8\)	\(3π4\)
\(r\)	\(2\)	\(0\)	\(−2\)	\(0\)	\(2\)	\(0\)	\(−2\)

Tableau\(\PageIndex{9}\)
\(\theta\)	\(\dfrac{\pi}{4}\)	\(\dfrac{\pi}{2}\)	\(\pi\)	\(\dfrac{3\pi}{2}\)	\(\dfrac{7\pi}{4}\)	\(2\pi\)
\(r\)	\(0.785\)	\(1.57\)	\(3.14\)	\(4.71\)	\(5.50\)	\(6.28\)