10.1 : Triangles non droits - Loi des sinus
- Page ID
- 195476
- Utilisez la loi des sinus pour résoudre des triangles obliques.
- Déterminez l'aire d'un triangle oblique à l'aide de la fonction sinus.
- Résolvez des problèmes appliqués en utilisant la loi des sinus.
Supposons que deux stations radar situées à des\(20\) kilomètres l'une de l'autre détectent un aéronef entre elles. L'angle d'élévation mesuré par la première station est de\(35\) degrés, tandis que l'angle d'élévation mesuré par la seconde station est de\(15\) degrés. Comment déterminer l'altitude de l'avion ? Nous voyons sur la figure\(\PageIndex{1}\) que le triangle formé par l'avion et les deux stations n'est pas un triangle droit, nous ne pouvons donc pas utiliser ce que nous savons des triangles droits. Dans cette section, nous allons découvrir comment résoudre les problèmes impliquant des triangles non droits.
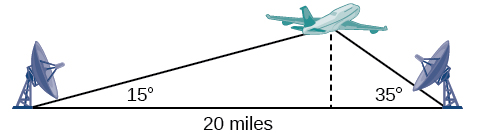
Figurine\(\PageIndex{1}\)
Utiliser la loi des sinus pour résoudre des triangles obliques
Dans n'importe quel triangle, nous pouvons tracer une altitude, une ligne perpendiculaire allant d'un sommet au côté opposé, formant deux triangles droits. Il serait toutefois préférable de disposer de méthodes que nous pouvons appliquer directement aux triangles non droits sans avoir à créer au préalable des triangles droits.
Tout triangle qui n'est pas un triangle droit est un triangle oblique. Pour résoudre un triangle oblique, il faut trouver les mesures des trois angles et des trois côtés. Pour ce faire, nous devons commencer par au moins trois de ces valeurs, y compris au moins l'un des côtés. Nous étudierons trois situations problématiques possibles liées aux triangles obliques :
ASA (angle-side-angle) Nous connaissons les mesures de deux angles et du côté inclus. Voir la figure\(\PageIndex{2}\).
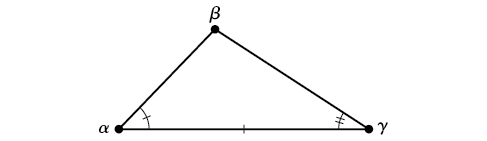
Figurine\(\PageIndex{2}\)
AAS (angle-angle-side) Nous connaissons les mesures de deux angles et d'un côté qui ne se trouve pas entre les angles connus. Voir la figure\(\PageIndex{3}\).
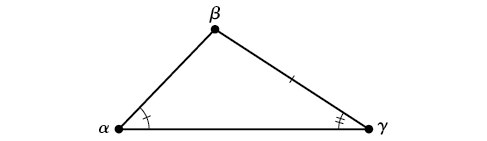
Figurine\(\PageIndex{3}\)
SSA (side-side-angle) Nous connaissons les mesures de deux côtés et d'un angle qui ne se situe pas entre les côtés connus. Voir la figure\(\PageIndex{4}\).
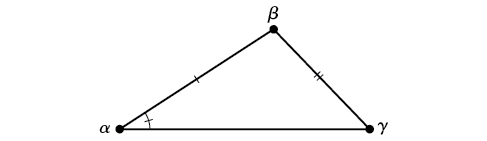
Figurine\(\PageIndex{4}\)
Savoir aborder chacune de ces situations nous permet de résoudre des triangles obliques sans avoir à laisser tomber une perpendiculaire pour former deux triangles droits. Au lieu de cela, nous pouvons utiliser le fait que le rapport entre la mesure de l'un des angles et la longueur de son côté opposé sera égal aux deux autres rapports entre la mesure de l'angle et le côté opposé. Voyons comment cette déclaration est dérivée en considérant le triangle illustré dans la figure\(\PageIndex{5}\).
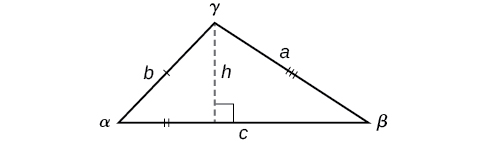
Figurine\(\PageIndex{5}\)
En utilisant les bonnes relations triangulaires, nous savons que\(\sin \alpha=\dfrac{h}{b}\) et\(\sin \beta=\dfrac{h}{a}\). La résolution des deux équations pour\(h\) donne deux expressions différentes pour\(h\).
\(h=b \sin \alpha\)et\(h=a \sin \beta\)
Nous mettons ensuite les expressions égales les unes aux autres.
\[\begin{align*} b \sin \alpha&= a \sin \beta\\ \left(\dfrac{1}{ab}\right)\left(b \sin \alpha\right)&= \left(a \sin \beta\right)\left(\dfrac{1}{ab}\right)\qquad \text{Multiply both sides by } \dfrac{1}{ab}\\ \dfrac{\sin \alpha}{a}&= \dfrac{\sin \beta}{b} \end{align*}\]
De même, nous pouvons comparer les autres ratios.
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \gamma}{c}\)et\(\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\)
Collectivement, ces relations sont appelées la loi des sinus.
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\)
Notez la méthode standard pour étiqueter les triangles : l'angle\(\alpha\) (alpha) est le côté opposé\(a\) ; l'angle\(\beta\) (bêta) est le côté opposé\(b\) ; et l'angle\(\gamma\) (gamma) est le côté opposé\(c\). Voir la figure\(\PageIndex{6}\).
Lorsque vous calculez les angles et les côtés, veillez à intégrer les valeurs exactes à la réponse finale. En général, les réponses finales sont arrondies au dixième le plus proche, sauf indication contraire.
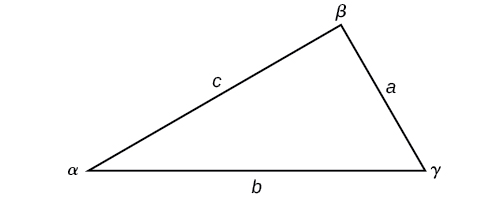
Figurine\(\PageIndex{6}\)
Dans le cas d'un triangle avec des angles et des côtés opposés étiquetés comme sur la figure\(\PageIndex{6}\), le rapport entre la mesure d'un angle et la longueur de son côté opposé sera égal aux deux autres rapports entre la mesure de l'angle et le côté opposé. Toutes les proportions seront égales. La loi des sinus est basée sur les proportions et est présentée symboliquement de deux manières.
\[\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\]
\[\dfrac{a}{\sin \alpha}=\dfrac{b}{\sin \beta}=\dfrac{c}{\sin \gamma}\]
Pour résoudre un triangle oblique, utilisez n'importe quelle paire de ratios applicables.
Résolvez le triangle illustré sur la figure\(\PageIndex{7}\) au dixième près.
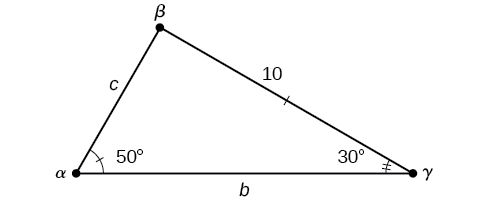
Figurine\(\PageIndex{7}\)
Solution
La somme des trois angles doit atteindre 180 degrés. À partir de là, nous pouvons déterminer que
\[\begin{align*} \beta &= 180^{\circ} - 50^{\circ} - 30^{\circ}\\ &= 100^{\circ} \end{align*}\]
Pour trouver un côté inconnu, nous devons connaître l'angle correspondant et un ratio connu. Nous connaissons cet angle\(\alpha=50°\) et son côté correspondant\(a=10\). Nous pouvons utiliser la proportion suivante de la loi des sinus pour trouver la longueur de\(c\).
\[\begin{align*} \dfrac{\sin(50^{\circ})}{10}&= \dfrac{\sin(30^{\circ})}{c}\\ c\dfrac{\sin(50^{\circ})}{10}&= \sin(30^{\circ})\qquad \text{Multiply both sides by } c\\ c&= \sin(30^{\circ})\dfrac{10}{\sin(50^{\circ})}\qquad \text{Multiply by the reciprocal to isolate } c\\ c&\approx 6.5 \end{align*}\]
De même, pour résoudre le problème\(b\), nous avons défini une autre proportion.
\[\begin{align*} \dfrac{\sin(50^{\circ})}{10}&= \dfrac{\sin(100^{\circ})}{b}\\ b \sin(50^{\circ})&= 10 \sin(100^{\circ})\qquad \text{Multiply both sides by } b\\ b&= \dfrac{10 \sin(100^{\circ})}{\sin(50^{\circ})}\qquad \text{Multiply by the reciprocal to isolate }b\\ b&\approx 12.9 \end{align*}\]
Par conséquent, l'ensemble complet des angles et des côtés est
\(\begin{matrix} \alpha=50^{\circ} & a=10\\ \beta=100^{\circ} & b\approx 12.9\\ \gamma=30^{\circ} & c\approx 6.5 \end{matrix}\)
Résolvez le triangle illustré sur la figure\(\PageIndex{8}\) au dixième près.
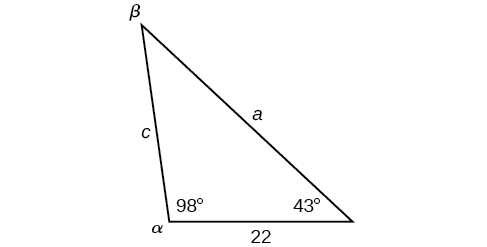
Figurine\(\PageIndex{8}\)
- Réponse
-
\(\begin{matrix} \alpha=98^{\circ} & a=34.6\\ \beta=39^{\circ} & b=22\\ \gamma=43^{\circ} & c=23.8 \end{matrix}\)
Utiliser la loi des sinus pour résoudre les triangles SSA
Nous pouvons utiliser la loi des sinus pour résoudre n'importe quel triangle oblique, mais certaines solutions peuvent ne pas être simples. Dans certains cas, plus d'un triangle peut répondre aux critères donnés, ce que nous décrivons comme un cas ambigu. Les triangles classés SSA, ceux dans lesquels nous connaissons la longueur de deux côtés et la mesure de l'angle opposé à l'un des côtés donnés, peuvent aboutir à une ou deux solutions, voire à aucune solution.
Les triangles obliques de la catégorie SSA peuvent avoir quatre résultats différents. La figure\(\PageIndex{9}\) illustre les solutions avec les côtés\(a\)\(b\) et l'angle connus\(\alpha\).
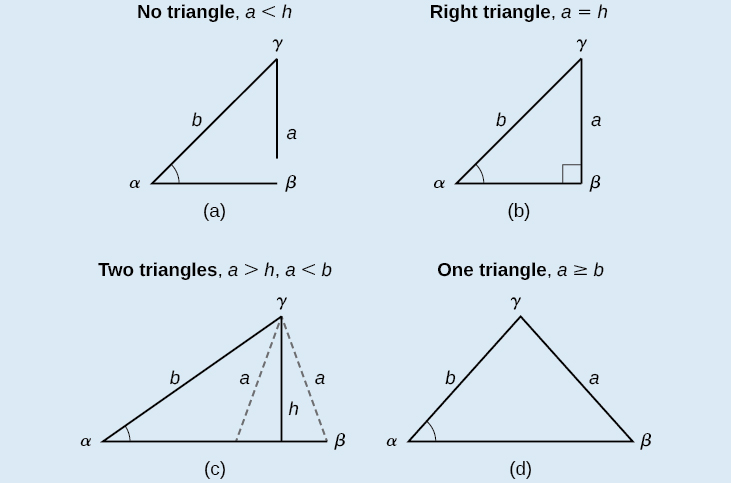
Figurine\(\PageIndex{9}\)
Résolvez le triangle de la Figure\(\PageIndex{10}\) pour le côté manquant et trouvez l'angle manquant mesuré au dixième le plus proche.
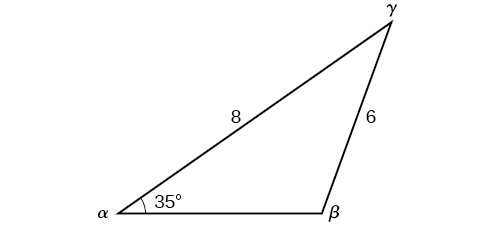
Figurine\(\PageIndex{10}\)
Solution
Utilisez la loi des sinus pour trouver l'angle\(\beta\) et l'angle\(\gamma\), puis le côté\(c\). En résolvant\(\beta\), nous avons la proportion
\[\begin{align*} \dfrac{\sin \alpha}{a}&= \dfrac{\sin \beta}{b}\\ \dfrac{\sin(35^{\circ})}{6}&= \dfrac{\sin \beta}{8}\\ \dfrac{8 \sin(35^{\circ})}{6}&= \sin \beta\\ 0.7648&\approx \sin \beta\\ {\sin}^{-1}(0.7648)&\approx 49.9^{\circ}\\ \beta&\approx 49.9^{\circ} \end{align*}\]
Toutefois, sur le diagramme, l'angle\(\beta\) semble être un angle obtus et peut être supérieur à\(90°\). Comment avons-nous obtenu un angle aigu et comment en trouvons-nous la mesure\(\beta\) ? Enquêtons plus en profondeur. En laissant tomber une perpendiculaire\(\gamma\) et en regardant le triangle depuis une perspective à angle droit, nous avons la Figure\(\PageIndex{11}\). Il semble qu'il puisse y avoir un deuxième triangle qui correspondra aux critères donnés.
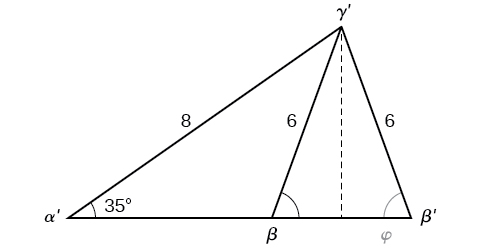
Figurine\(\PageIndex{11}\)
L'angle supplémentaire à\(\beta\) est approximativement égal à\(49.9°\), ce qui signifie que\(\beta=180°−49.9°=130.1°\). (N'oubliez pas que la fonction sinusoïdale est positive à la fois dans le premier et le deuxième quadrant.) Pour résoudre ce problème\(\gamma\), nous avons
\[\begin{align*} \gamma&= 180^{\circ}-35^{\circ}-130.1^{\circ}\\ &\approx 14.9^{\circ} \end{align*}\]
Nous pouvons ensuite utiliser ces mesures pour résoudre l'autre triangle. Puisque\(\beta′\) vient s'ajouter à\(\beta\), nous avons
\[\begin{align*} \gamma^{'}&= 180^{\circ}-35^{\circ}-49.5^{\circ}\\ &\approx 95.1^{\circ} \end{align*}\]
Maintenant, nous devons trouver\(c\) et\(c′\).
Nous avons
\[\begin{align*} \dfrac{c}{\sin(14.9^{\circ})}&= \dfrac{6}{\sin(35^{\circ})}\\ c&= \dfrac{6 \sin(14.9^{\circ})}{\sin(35^{\circ})}\\ &\approx 2.7 \end{align*}\]
Enfin,
\[\begin{align*} \dfrac{c'}{\sin(95.1^{\circ})}&= \dfrac{6}{\sin(35^{\circ})}\\ c'&= \dfrac{6 \sin(95.1^{\circ})}{\sin(35^{\circ})}\\ &\approx 10.4 \end{align*}\]
Pour résumer, il existe deux triangles avec un angle de 8\(35°\), un côté adjacent de 8 et un côté opposé de 6, comme le montre la figure\(\PageIndex{12}\).
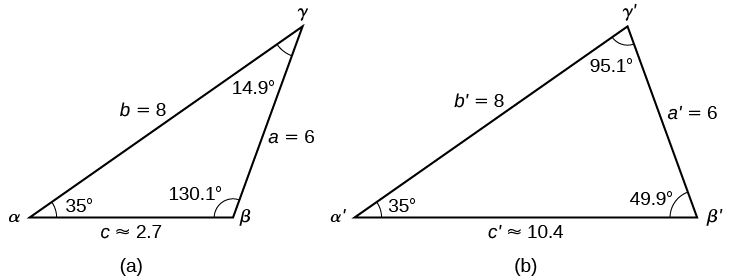
Figurine\(\PageIndex{12}\)
Cependant, nous recherchions les valeurs du triangle avec un angle obtus\(\beta\). Nous pouvons les voir dans le premier triangle (a) de la figure\(\PageIndex{12}\).
Étant donné\(\alpha=80°\)\(a=120\), et\(b=121\), trouvez le côté et les angles manquants. S'il existe plusieurs solutions possibles, affichez les deux.
- Réponse
-
Solution 1
\(\begin{matrix} \alpha=80^{\circ} & a=120\\ \beta\approx 83.2^{\circ} & b=121\\ \gamma\approx 16.8^{\circ} & c\approx 35.2 \end{matrix}\)
Solution 2
\(\begin{matrix} \alpha '=80^{\circ} & a'=120\\ \beta '\approx 96.8^{\circ} & b'=121\\ \gamma '\approx 3.2^{\circ} & c'\approx 6.8 \end{matrix}\)
Dans le triangle illustré sur la figure\(\PageIndex{13}\), résolvez le côté et les angles inconnus. Arrondissez vos réponses au dixième le plus proche.
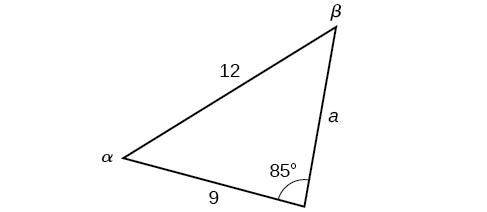
Figurine\(\PageIndex{13}\)
Solution
Pour choisir la paire de ratios de la loi des sinus à utiliser, examinez les informations fournies. Dans ce cas, nous connaissons l'angle\(\gamma=85°\), et son côté correspondant\(c=12\), et nous connaissons le côté\(b=9\). Nous utiliserons cette proportion pour résoudre\(\beta\).
\[\begin{align*} \dfrac{\sin(85^{\circ})}{12}&= \dfrac{\sin \beta}{9}\qquad \text{Isolate the unknown.}\\ \dfrac{9 \sin(85^{\circ})}{12}&= \sin \beta \end{align*}\]
Pour le trouver\(\beta\), appliquez la fonction sinusoïdale inverse. Le sinus inverse produira un résultat unique, mais gardez à l'esprit qu'il peut y avoir deux valeurs pour\(\beta\). Il est important de vérifier le résultat, car il peut y avoir deux solutions viables, une seule solution (cas habituel) ou aucune solution.
\[\begin{align*} \beta&= {\sin}^{-1}\left(\dfrac{9 \sin(85^{\circ})}{12}\right)\\ \beta&\approx {\sin}^{-1} (0.7471)\\ \beta&\approx 48.3^{\circ} \end{align*}\]
Dans ce cas, si nous soustrayons\(\beta\) de\(180°\), nous constatons qu'il peut y avoir une deuxième solution possible. Ainsi,\(\beta=180°−48.3°≈131.7°\). Pour vérifier la solution, soustrayez les deux angles\(131.7°\) et\(85°\) de\(180°\). Cela donne
\[\begin{align*} \alpha&= 180^{\circ}-85^{\circ}-131.7^{\circ}\\ &\approx -36.7^{\circ} \end{align*}\]
ce qui est impossible, et ainsi de suite\(\beta≈48.3°\).
Pour trouver les valeurs manquantes restantes, nous calculons\(\alpha=180°−85°−48.3°≈46.7°\). Maintenant, seul le côté\(a\) est nécessaire. Utilisez la loi des sinus pour calculer\(a\) par l'une des proportions.
\[\begin{align*} \dfrac{\sin(85°)}{12}&= \dfrac{\sin(46.7^{\circ})}{a}\\ a\dfrac{\sin(85^{\circ})}{12}&= \sin(46.7^{\circ})\\ a&=\dfrac{12\sin(46.7^{\circ})}{\sin(85^{\circ})}\\ &\approx 8.8 \end{align*}\]
L'ensemble complet de solutions pour le triangle donné est
\(\begin{matrix} \alpha\approx 46.7^{\circ} & a\approx 8.8\\ \beta\approx 48.3^{\circ} & b=9\\ \gamma=85^{\circ} & c=12 \end{matrix}\)
Étant donné\(\alpha=80°\),\(a=100\),\(b=10\), trouvez le côté et les angles manquants. S'il existe plusieurs solutions possibles, affichez les deux. Arrondissez vos réponses au dixième le plus proche.
- Réponse
-
\(\beta≈5.7°\),\(\gamma≈94.3°\),\(c≈101.3\)
Trouvez tous les triangles possibles si un côté a une longueur\(4\) opposée à un angle de\(50°\) et qu'un second côté a une longueur\(10\).
Solution
En utilisant les informations données, nous pouvons résoudre l'angle opposé au côté de la longueur\(10\). Voir la figure\(\PageIndex{14}\).
\[\begin{align*} \dfrac{\sin \alpha}{10}&= \dfrac{\sin(50^{\circ})}{4}\\ \sin \alpha&= \dfrac{10 \sin(50^{\circ})}{4}\\ \sin \alpha&\approx 1.915 \end{align*}\]
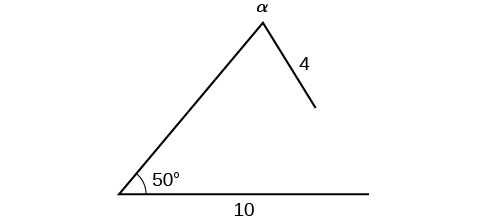
Figurine\(\PageIndex{14}\)
Nous pouvons nous arrêter ici sans trouver la valeur de\(\alpha\). Comme la plage de la fonction sinus est\([ −1,1 ]\), il est impossible que la valeur du sinus soit égale à\(1.915\). En fait, la saisie\({\sin}^{−1}(1.915)\) dans une calculatrice graphique génère un DOMAINE D'ERREUR. Par conséquent, aucun triangle ne peut être dessiné avec les dimensions fournies.
Déterminez le nombre de triangles possibles étant donné\(a=31\),\(b=26\),\(\beta=48°\).
- Réponse
-
deux
Déterminer l'aire d'un triangle oblique à l'aide de la fonction sinusoïdale
Maintenant que nous pouvons résoudre un triangle pour les valeurs manquantes, nous pouvons utiliser certaines de ces valeurs et la fonction sinus pour trouver l'aire d'un triangle oblique. Rappelez-vous que la formule de l'aire d'un triangle est donnée sous la forme\(Area=\dfrac{1}{2}bh\), où\(b\) sont la base et\(h\) la hauteur. Pour les triangles obliques, nous devons trouver\(h\) avant de pouvoir utiliser la formule de surface. En observant les deux triangles de la figure\(\PageIndex{15}\), l'un aigu et l'autre obtus, nous pouvons laisser tomber une perpendiculaire pour représenter la hauteur, puis appliquer la propriété trigonométrique\(\sin \alpha=\dfrac{opposite}{hypotenuse}\) pour écrire une équation pour l'aire dans les triangles obliques. Dans le triangle aigu, nous avons\(\sin \alpha=\dfrac{h}{c}\) ou\(c \sin \alpha=h\). Cependant, dans le triangle obtus, nous laissons tomber la perpendiculaire à l'extérieur du triangle et étendons la base\(b\) pour former un triangle droit. L'angle utilisé dans le calcul est\(\alpha′\), ou\(180−\alpha\).
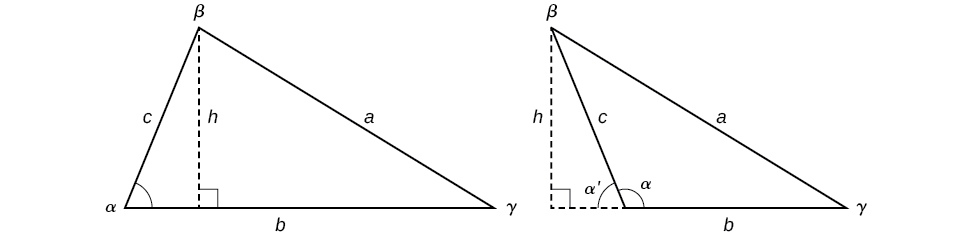
Figurine\(\PageIndex{15}\)
Ainsi,
\(Area=\dfrac{1}{2}(base)(height)=\dfrac{1}{2}b(c \sin \alpha)\)
De même,
\(Area=\dfrac{1}{2}a(b \sin \gamma)=\dfrac{1}{2}a(c \sin \beta)\)
La formule pour l'aire d'un triangle oblique est donnée par
\[Area=\dfrac{1}{2}bc \sin \alpha\]
\[Area=\dfrac{1}{2}ac \sin \beta\]
\[Area=\dfrac{1}{2}ab \sin \gamma\]
Cela équivaut à la moitié du produit des deux côtés et au sinus de leur angle inclus.
Détermine l'aire d'un triangle avec\(a=90\) des\(b=52\) côtés et un angle\(\gamma=102°\). Arrondissez la surface à l'entier le plus proche.
Solution
En utilisant la formule, nous avons
\[\begin{align*} Area&= \dfrac{1}{2}ab \sin \gamma\\ Area&= \dfrac{1}{2}(90)(52) \sin(102^{\circ})\\ Area&\approx 2289\; \text{square units} \end{align*}\]
Détermine l'aire du triangle donné\(\beta=42°\),\(a=7.2 ft\),\(c=3.4 ft\). Arrondissez la zone au dixième le plus proche.
- Réponse
-
environ pieds\(8.2\) carrés
Résoudre des problèmes appliqués à l'aide de la loi des sinus
Plus nous étudions les applications trigonométriques, plus nous découvrons que les applications sont innombrables. Certaines sont des situations plates de type diagramme, mais de nombreuses applications en calcul, en ingénierie et en physique impliquent trois dimensions et un mouvement.
Déterminez l'altitude de l'avion dans le problème présenté au début de cette section, illustré à la figure\(\PageIndex{16}\). Arrondissez l'altitude au dixième de mille le plus proche.
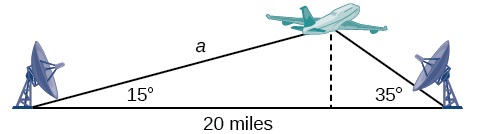
Figurine\(\PageIndex{16}\)
Solution
Pour déterminer l'altitude de l'avion, nous déterminons d'abord la distance entre une station et l'avion, telle que le côté\(a\), puis nous utilisons des relations triangulaires droites pour déterminer la hauteur de l'avion\(h\).
Comme les angles du triangle s'additionnent en\(180\) degrés, l'angle inconnu doit l'être\(180°−15°−35°=130°\). Cet angle est opposé au côté de la longueur\(20\), ce qui nous permet d'établir une relation selon la loi des sinus.
\[\begin{align*} \dfrac{\sin(130^{\circ})}{20}&= \dfrac{\sin(35^{\circ})}{a}\\ a \sin(130^{\circ})&= 20 \sin(35^{\circ})\\ a&= \dfrac{20 \sin(35^{\circ})}{\sin(130^{\circ})}\\ a&\approx 14.98 \end{align*}\]
La distance entre une station et l'avion est d'environ\(14.98\) miles.
Maintenant que nous le savons\(a\), nous pouvons utiliser les relations du triangle droit pour résoudre\(h\).
\[\begin{align*} \sin(15^{\circ})&= \dfrac{opposite}{hypotenuse}\\ \sin(15^{\circ})&= \dfrac{h}{a}\\ \sin(15^{\circ})&= \dfrac{h}{14.98}\\ h&= 14.98 \sin(15^{\circ})\\ h&\approx 3.88 \end{align*}\]
L'avion se trouve à une altitude d'environ\(3.9\) miles.
Le diagramme de la figure\(\PageIndex{17}\) représente la hauteur d'un dirigeable survolant un stade de football. Déterminez la hauteur du dirigeable si l'angle d'élévation à la zone d'extrémité sud, point A\(70°\), est égal à l'angle d'élévation par rapport à la zone d'extrémité nord, point B, est\(62°\), et si la distance entre les points de vue des deux zones d'extrémité est de\(145\) mètres.
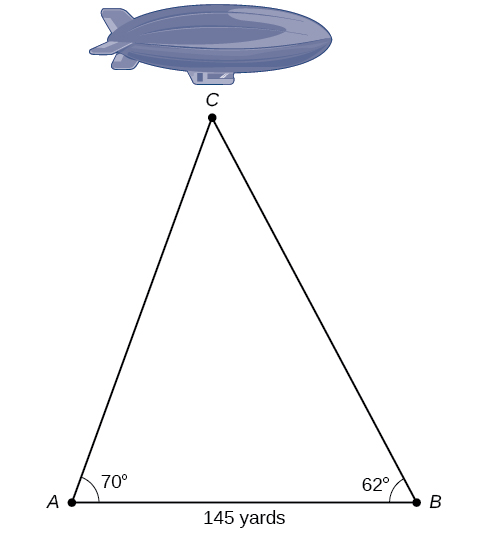
Figurine\(\PageIndex{17}\)
- Réponse
-
\(161.9\)yd.
Médias
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires avec les applications trigonométriques.
Équations clés
| Loi des Sines |
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\) \(\dfrac{a}{\sin \alpha}=\dfrac{b}{\sin \beta}=\dfrac{c}{\sin \gamma}\) |
| Zone pour triangles obliques |
\(Area=\dfrac{1}{2}bc \sin \alpha\) \(=\dfrac{1}{2} ac \sin \beta\) \(=\dfrac{1}{2} ab \sin \gamma\) |
Concepts clés
- La loi des sinus peut être utilisée pour résoudre des triangles obliques, qui sont des triangles non droits.
- Selon la loi de Sines, le rapport entre la mesure de l'un des angles et la longueur de son côté opposé est égal aux deux autres rapports entre la mesure de l'angle et le côté opposé.
- Trois cas sont possibles : ASA, AAS, SSA. En fonction des informations fournies, nous pouvons choisir l'équation appropriée pour trouver la solution demandée. Voir l'exemple\(\PageIndex{1}\).
- Le cas ambigu se présente lorsqu'un triangle oblique peut avoir des résultats différents.
- Trois cas peuvent découler d'un arrangement SSA : une solution unique, deux solutions possibles et aucune solution. Voir Exemple\(\PageIndex{2}\) et Exemple\(\PageIndex{3}\).
- La loi des sinus peut être utilisée pour résoudre des triangles avec des critères donnés. Voir l'exemple\(\PageIndex{4}\).
- La formule de surface générale pour les triangles se traduit par des triangles obliques en trouvant d'abord la valeur de hauteur appropriée. Voir l'exemple\(\PageIndex{5}\).
- Il existe de nombreuses applications trigonométriques. Ils peuvent souvent être résolus en dessinant d'abord un diagramme des informations données, puis en utilisant l'équation appropriée. Voir l'exemple\(\PageIndex{6}\).


