9.5 : Résolution d'équations trigonométriques
- Page ID
- 195375
- Résolvez des équations trigonométriques linéaires en sinus et en cosinus.
- Résolvez des équations impliquant une seule fonction trigonométrique.
- Résolvez des équations trigonométriques en utilisant une calculatrice
- Résolvez des équations trigonométriques de forme quadratique.
- Résolvez des équations trigonométriques en utilisant des identités fondamentales
- Résolvez des équations trigonométriques sous plusieurs angles.
- Résolvez les problèmes du triangle droit
Thalès de Milet (environ 625—547 av. J.-C.) est connu comme le fondateur de la géométrie. La légende raconte qu'il a calculé la hauteur de la Grande Pyramide de Gizeh en Égypte en utilisant la théorie des triangles similaires, qu'il a développée en mesurant l'ombre de son bâton. Basée sur les proportions, cette théorie a des applications dans de nombreux domaines, notamment la géométrie fractale, l'ingénierie et l'architecture. Souvent, l'angle d'élévation et l'angle de dépression sont déterminés à l'aide de triangles similaires.

Dans les sections précédentes de ce chapitre, nous avons examiné les identités trigonométriques. Les identités sont vraies pour toutes les valeurs du domaine de la variable. Dans cette section, nous commençons notre étude des équations trigonométriques afin d'étudier des scénarios réels tels que la détermination des dimensions des pyramides.
Résolution d'équations trigonométriques linéaires en sinus et en cosinus
Les équations trigonométriques sont, comme leur nom l'indique, des équations qui impliquent des fonctions trigonométriques. Semblable à bien des égards à la résolution d'équations polynomiales ou d'équations rationnelles, seules des valeurs spécifiques de la variable seront des solutions, s'il existe des solutions. Nous allons souvent résoudre une équation trigonométrique sur un intervalle spécifié. Cependant, tout aussi souvent, on nous demandera de trouver toutes les solutions possibles, et comme les fonctions trigonométriques sont périodiques, les solutions se répètent au cours de chaque période. En d'autres termes, les équations trigonométriques peuvent avoir un nombre infini de solutions. De plus, à l'instar des équations rationnelles, le domaine de la fonction doit être pris en compte avant de supposer qu'une solution est valide. La période de la fonction sinusoïdale et de la fonction cosinus est\(2\pi\). En d'autres termes, pour chaque\(2\pi\) unité, les valeurs y se répètent. Si nous devons trouver toutes les solutions possibles, nous devons ajouter\(2\pi k\), où\(k\) est un entier, à la solution initiale. Rappelons la règle qui donne le format pour énoncer toutes les solutions possibles pour une fonction où le point est\(2\pi\) :
\[\sin \theta=\sin(\theta \pm 2k\pi)\]
Il existe des règles similaires pour indiquer toutes les solutions possibles pour les autres fonctions trigonométriques. La résolution d'équations trigonométriques nécessite les mêmes techniques que la résolution d'équations algébriques. Nous lisons l'équation de gauche à droite, horizontalement, comme une phrase. Nous recherchons des modèles connus, des facteurs, trouvons des dénominateurs communs et substituons certaines expressions par une variable pour simplifier le processus de résolution. Cependant, avec les équations trigonométriques, nous avons également l'avantage d'utiliser les identités que nous avons développées dans les sections précédentes.
Trouvez toutes les solutions exactes possibles pour l'équation\(\cos \theta=\dfrac{1}{2}\).
Solution
D'après le cercle des unités, nous savons que
\[ \begin{align*} \cos \theta &=\dfrac{1}{2} \\[4pt] \theta &=\dfrac{\pi}{3},\space \dfrac{5\pi}{3} \end{align*}\]
Ce sont les solutions dans l'intervalle\([ 0,2\pi ]\). Toutes les solutions possibles sont données par
\[\theta=\dfrac{\pi}{3} \pm 2k\pi \quad \text{and} \quad \theta=\dfrac{5\pi}{3} \pm 2k\pi \nonumber\]
où\(k\) est un entier.
Trouvez toutes les solutions exactes possibles pour l'équation\(\sin t=\dfrac{1}{2}\).
Solution
La résolution de toutes les valeurs possibles de\(t\) signifie que les solutions incluent des angles au-delà de la période de\(2\pi\). Dans la section sur les identités de somme et de différence, nous pouvons voir que les solutions sont\(t=\dfrac{\pi}{6}\) et\(t=\dfrac{5\pi}{6}\). Mais le problème est de demander toutes les valeurs possibles pour résoudre l'équation. Par conséquent, la réponse est
\[t=\dfrac{\pi}{6}\pm 2\pi k \quad \text{and} \quad t=\dfrac{5\pi}{6}\pm 2\pi k \nonumber\]
où\(k\) est un entier.
- Recherchez un modèle qui suggère une propriété algébrique, telle que la différence de carrés ou une opportunité de factorisation.
- Remplacez l'expression trigonométrique par une variable unique, telle que\(x\) ou\(u\).
- Résolvez l'équation de la même manière qu'une équation algébrique le serait.
- Remplacez l'expression trigonométrique par la variable dans les expressions résultantes.
- Résolvez pour l'angle.
Résolvez exactement l'équation :\(2 \cos \theta−3=−5\),\(0≤\theta<2\pi\).
Solution
Utilisez des techniques algébriques pour résoudre l'équation.
\[\begin{align*} 2 \cos \theta-3&= -5\\ 2 \cos \theta&= -2\\ \cos \theta&= -1\\ \theta&= \pi \end{align*}\]
Résolvez exactement l'équation linéaire suivante sur l'intervalle\([0,2\pi)\) :\(2 \sin x+1=0\).
- Réponse
-
\(x=\dfrac{7\pi}{6},\space \dfrac{11\pi}{6}\)
Résolution d'équations impliquant une seule fonction trigonométrique
Lorsque l'on nous donne des équations qui n'impliquent qu'une seule des six fonctions trigonométriques, leurs solutions impliquent l'utilisation de techniques algébriques et du cercle unitaire (voir [lien]). Nous devons prendre en compte plusieurs considérations lorsque l'équation implique des fonctions trigonométriques autres que le sinus et le cosinus. Les problèmes impliquant les réciproques des fonctions trigonométriques primaires doivent être considérés d'un point de vue algébrique. En d'autres termes, nous allons écrire la fonction réciproque et résoudre les angles à l'aide de la fonction. De plus, une équation impliquant la fonction tangente est légèrement différente d'une équation contenant une fonction sinusoïdale ou cosinusoïdale. Tout d'abord, comme nous le savons, la période de tangente l'est\(\pi\), non\(2\pi\). De plus, le domaine de la tangente est composé de tous les nombres réels à l'exception des multiples entiers impairs de\(\dfrac{\pi}{2}\), à moins, bien entendu, qu'un problème n'impose ses propres restrictions au domaine.
Résolvez exactement le problème :\(2 {\sin}^2 \theta−1=0\),\(0≤\theta<2\pi\).
Solution
Comme ce problème n'est pas facile à prendre en compte, nous allons le résoudre en utilisant la propriété de racine carrée. Tout d'abord, nous utilisons l'algèbre pour isoler\(\sin \theta\). Ensuite, nous trouverons les angles.
\ [\ begin {align*}
2 {\ sin} ^2 \ théta-1&= 0 \ \
2 {\ sin} ^2 \ theta&= 1 \ \
{\ sin} ^2 \ theta&= \ dfrac {1} {2} \
\ sqrt {\ sqrt {\ sin} ^2 \ theta} &= \ pm \ sqrt {\ dfrac {1} {2}} \
\ sin \ theta&= \ pm \ dfrac {1} {\ sqrt {2}} \ \
&= \ pm \ dfrac {\ sqrt {2}} {2} \ \
\ theta&= \ dfrac {\ pi} {4}, \ space \ dfrac {3 \ pi} {4}, \ space \ dfrac {5 \ pi} {4}, \ space \ dfrac {7 \ pi} {4}
\ end {align*} \]
Résolvez exactement l'équation suivante :\(\csc \theta=−2\),\(0≤\theta<4\pi\).
Solution
Nous voulons toutes les valeurs\(\theta\) pour lesquelles\(\csc \theta=−2\) sur l'intervalle\(0≤\theta<4\pi\).
\[\begin{align*} \csc \theta&= -2\\ \dfrac{1}{\sin \theta}&= -2\\ \sin \theta&= -\dfrac{1}{2}\\ \theta&= \dfrac{7\pi}{6},\space \dfrac{11\pi}{6},\space \dfrac{19\pi}{6}, \space \dfrac{23\pi}{6} \end{align*}\]
Analyse
Comme\(\sin \theta=−\dfrac{1}{2}\), notez que les quatre solutions se situent dans les troisième et quatrième quadrants.
Résolvez exactement l'équation :\(\tan\left(\theta−\dfrac{\pi}{2}\right)=1\),\(0≤\theta<2\pi\).
Solution
Rappelez-vous que la fonction tangente a une période de\(\pi\). Sur l'intervalle\([ 0,\pi )\) et à l'angle de\(\dfrac{\pi}{4}\), la tangente a une valeur de\(1\). Cependant, l'angle que nous voulons est\(\left(\theta−\dfrac{\pi}{2}\right)\). Ainsi, si\(\tan\left(\dfrac{\pi}{4}\right)=1\), alors
\[\begin{align*} \theta-\dfrac{\pi}{2}&= \dfrac{\pi}{4}\\ \theta&= \dfrac{3\pi}{4} \pm k\pi \end{align*}\]
Dans l'intervalle\([ 0,2\pi )\), nous avons deux solutions :
\(\theta=\dfrac{3\pi}{4}\)et\(\theta=\dfrac{3\pi}{4}+\pi=\dfrac{7\pi}{4}\)
Trouvez toutes les solutions pour\(\tan x=\sqrt{3}\).
- Réponse
-
\(\dfrac{\pi}{3}\pm \pi k\)
Identifiez toutes les solutions exactes à l'équation\(2(\tan x+3)=5+\tan x\),\(0≤x<2\pi\).
Solution
Nous pouvons résoudre cette équation en utilisant uniquement l'algèbre. Isolez l'expression\(\tan x\) sur le côté gauche du signe égal.
\[\begin{align*} 2(\tan x)+2(3)&= 5+\tan x\\ 2\tan x+6&= 5+\tan x\\ 2\tan x-\tan x&= 5-6\\ \tan x&= -1 \end{align*}\]
Le cercle unitaire comporte deux angles dont la valeur tangente est\(−1\) :\(\theta=\dfrac{3\pi}{4}\) et\(\theta=\dfrac{7\pi}{4}\).
Résoudre des équations trigonométriques en utilisant une calculatrice
Toutes les fonctions ne peuvent pas être résolues exactement en utilisant uniquement le cercle unitaire. Lorsque nous devons résoudre une équation impliquant un angle autre que l'un des angles spéciaux, nous devons utiliser une calculatrice. Assurez-vous qu'il est réglé sur le mode approprié, en degrés ou en radians, en fonction des critères du problème.
Utilisez une calculatrice pour résoudre l'équation\(\sin \theta=0.8\), où\(\theta\) est exprimé en radians.
Solution
Assurez-vous que le mode est réglé sur radians. Pour le trouver\(\theta\), utilisez la fonction sinusoïdale inverse. Sur la plupart des calculatrices, vous devez appuyer sur le bouton 2 ND puis sur le bouton SIN pour faire apparaître la\({\sin}^{−1}\) fonction. Ce qui s'affiche à l'écran est\({\sin}^{−1}\). La calculatrice est prête à être saisie entre parenthèses. Pour ce problème, nous entrons et\({\sin}^{−1}(0.8)\) appuyons sur ENTER. Ainsi, à quatre décimales,
\({\sin}^{−1}(0.8)≈0.9273\)
La solution est
\(\theta≈0.9273\pm 2\pi k\)
La mesure de l'angle en degrés est
\[\begin{align*} \theta&\approx 53.1^{\circ}\\ \theta&\approx 180^{\circ}-53.1^{\circ}\\ &\approx 126.9^{\circ} \end{align*}\]
Analyse
Notez qu'un calculateur ne renvoie qu'un angle en quadrants I ou IV pour la fonction sinus, car il s'agit de la plage du sinus inverse. L'autre angle est obtenu en utilisant\(\pi−\theta\).
Utilisez une calculatrice pour résoudre l'équation\( \sec θ=−4, \) donnant votre réponse en radians.
Solution
Nous pouvons commencer par un peu d'algèbre.
\[\begin{align*} \sec \theta&= -4\\ \dfrac{1}{\cos \theta}&= -4\\ \cos \theta&= -\dfrac{1}{4} \end{align*}\]
Vérifiez que le MODE est en radians. Utilisez maintenant la fonction cosinus inverse
\[\begin{align*}{\cos}^{-1}\left(-\dfrac{1}{4}\right)&\approx 1.8235\\ \theta&\approx 1.8235+2\pi k \end{align*}\]
Puisque\(\dfrac{\pi}{2}≈1.57\) et\(\pi≈3.14\),\(1.8235\) se trouve entre ces deux nombres, il\(\theta≈1.8235\) se trouve donc dans le quadrant II. Le cosinus est également négatif dans le quadrant III. Notez qu'un calculateur renvoie uniquement un angle en quadrants I ou II pour la fonction cosinus, car il s'agit de la plage du cosinus inverse. Voir la figure\(\PageIndex{2}\).
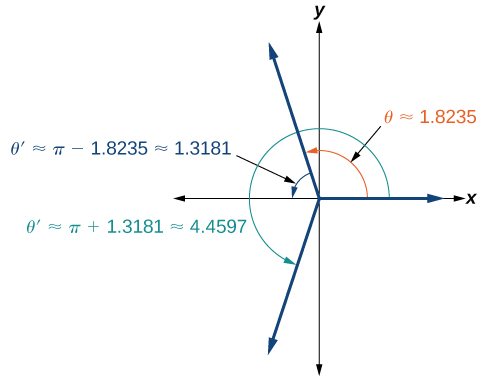
Nous devons donc également trouver la mesure de l'angle dans le quadrant III. Dans le quadrant III, l'angle de référence est\(\theta '≈\pi−1.8235≈1.3181\). L'autre solution dans le quadrant III est\(\theta '≈\pi+1.3181≈4.4597\).
Les solutions sont\(\theta≈1.8235\pm 2\pi k\) et\(\theta≈4.4597\pm 2\pi k\).
Résoudre\(\cos \theta=−0.2\).
- Réponse
-
\(\theta≈1.7722\pm 2\pi k\)et\(\theta≈4.5110\pm 2\pi k\)
Résolution d'équations trigonométriques sous forme quadratique
La résolution d'une équation quadratique peut être plus compliquée, mais encore une fois, nous pouvons utiliser l'algèbre comme nous le ferions pour n'importe quelle équation quadratique. Regardez le schéma de l'équation. Y a-t-il plus d'une fonction trigonométrique dans l'équation, ou y en a-t-il une seule ? Quelle fonction trigonométrique est au carré ? Si une seule fonction est représentée et que l'un des termes est au carré, pensez à la forme standard du quadratique. Remplacez la fonction trigonométrique par une variable telle que\(x\) ou\(u\). Si la substitution donne à l'équation l'apparence d'une équation quadratique, alors nous pouvons utiliser les mêmes méthodes pour résoudre les quadratiques afin de résoudre les équations trigonométriques.
Résolvez exactement l'équation :\({\cos}^2 \theta+3 \cos \theta−1=0\),\(0≤\theta<2\pi\).
Solution
Nous commençons par utiliser la substitution et le remplacer\(\cos \theta\) par\(x\). Il n'est pas nécessaire de recourir à la substitution, mais cela peut faciliter la résolution visuelle du problème. Laissez\(\cos \theta=x\). Nous avons
\(x^2+3x−1=0\)
L'équation ne peut pas être factorisée, nous utiliserons donc la formule quadratique :\(x=\dfrac{−b\pm \sqrt{b^2−4ac}}{2a}\).
\[\begin{align*} x&= \dfrac{ -3\pm \sqrt{ {(-3)}^2-4 (1) (-1) } }{2}\\ &= \dfrac{-3\pm \sqrt{13}}{2}\end{align*}\]
Remplacez\(x\) par\(\cos \theta \) et résolvez.
\[\begin{align*} \cos \theta&= \dfrac{-3\pm \sqrt{13}}{2}\\ \theta&= {\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right) \end{align*}\]
Notez que seul le signe + est utilisé. Cela est dû au fait que nous obtenons une erreur lorsque nous résolvons\(\theta={\cos}^{−1}\left(\dfrac{−3−\sqrt{13}}{2}\right)\) sur une calculatrice, puisque le domaine de la fonction cosinus inverse est\([ −1,1 ]\). Cependant, il existe une deuxième solution :
\[\begin{align*} \theta&= {\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right)\\ &\approx 1.26 \end{align*}\]
Ce côté terminal de l'angle se trouve dans le quadrant I. Comme le cosinus est également positif dans le quadrant IV, la deuxième solution est
\[\begin{align*} \theta&= 2\pi-{\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right)\\ &\approx 5.02 \end{align*}\]
Résolvez exactement l'équation :\(2 {\sin}^2 \theta−5 \sin \theta+3=0\),\(0≤\theta≤2\pi\).
Solution
En utilisant le regroupement, ce quadratique peut être factorisé. Soit effectuer la véritable substitution\(\sin \theta=u\), soit l'imaginer, en tenant compte des facteurs suivants :
\[\begin{align*} 2 {\sin}^2 \theta-5 \sin \theta+3&= 0\\ (2 \sin \theta-3)(\sin \theta-1)&= 0 \qquad \text {Now set each factor equal to zero.}\\ 2 \sin \theta-3&= 0\\ 2 \sin \theta&= 3\\ \sin \theta&= \dfrac{3}{2}\\ \sin \theta-1&= 0\\ \sin \theta&= 1 \end{align*}\]
Ensuite, résolvez\(\theta\) :\(\sin \theta≠\dfrac{3}{2}\), comme l'est la plage de la fonction sinusoïdale\([ −1,1 ]\). Cependant\(\sin \theta=1\), donner la solution\(\theta=\dfrac{\pi}{2}\).
Analyse
Assurez-vous de vérifier toutes les solutions du domaine donné, car certains facteurs n'ont pas de solution.
Résolvez\({\sin}^2 \theta=2 \cos \theta+2\),\(0≤\theta≤2\pi\). [Conseil : effectuez une substitution pour exprimer l'équation uniquement en termes de cosinus.]
- Réponse
-
\(\cos \theta=−1\),\(\theta=\pi\)
Résolvez exactement :\(2 {\sin}^2 \theta+\sin \theta=0;\space 0≤\theta<2\pi\)
Solution
Ce problème devrait vous sembler familier car il ressemble à un problème quadratique. Laissez\(\sin \theta=x\). L'équation devient\(2x^2+x=0\). Nous commençons par l'affacturage :
\ [\ begin {align*}
2x^2+x&= 0 \ \
x (2x+1) &= 0 \ qquad \ text {Définissez chaque facteur sur zéro.} \ \
x&= 0 \ \
2x+1&= 0 \ \
x&= - \ dfrac {1} {2} \ end {align*} \]
Ensuite, replacez dans l'équation l'expression d'origine\(\sin \theta \) pour\(x\). Ainsi,
\ [\ begin {align*} \ sin \ theta&= 0 \ \
\ theta&= 0, \ pi \ \
\ sin \ theta&= - \ dfrac {1} {2} \
\ theta&= \ dfrac {7 \ pi} {6}, \ dfrac {11 \ pi} {6}
\ end {align*} \]
Les solutions du domaine\(0≤\theta<2\pi\) sont\(\theta=0,\pi,\dfrac{7\pi}{6},\dfrac{11\pi}{6}\).
Si nous préférons ne pas la remplacer, nous pouvons résoudre l'équation en suivant le même schéma de factorisation et en attribuant à chaque facteur la valeur zéro.
\[\begin{align*} {\sin}^2 \theta+\sin \theta&= 0\\ \sin \theta(2\sin \theta+1)&= 0\\ \sin \theta&= 0\\ \theta&= 0,\pi\\ 2 \sin \theta+1&= 0\\ 2\sin \theta&= -1\\ \sin \theta&= -\dfrac{1}{2}\\ \theta&= \dfrac{7\pi}{6},\dfrac{11\pi}{6} \end{align*}\]
Analyse
Nous pouvons voir les solutions sur le graphique de la figure\(\PageIndex{3}\). Sur l'intervalle\(0≤\theta<2\pi\), le graphique traverse l'axe\(x\) - quatre fois, aux solutions notées. Notez que les équations trigonométriques sous forme quadratique peuvent donner jusqu'à quatre solutions au lieu des deux solutions attendues qui sont trouvées avec les équations quadratiques. Dans cet exemple, chaque solution (angle) correspondant à une valeur sinusoïdale positive produira deux angles qui donneraient cette valeur.
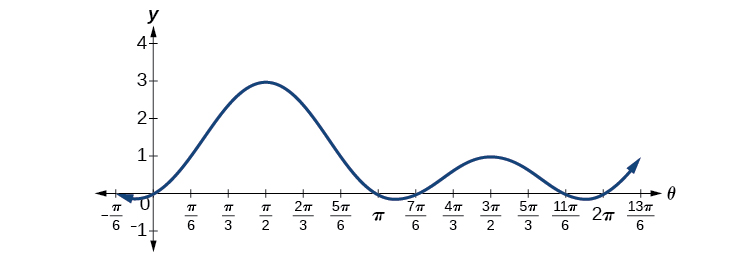
Nous pouvons également vérifier les solutions sur le cercle unitaire via le résultat dans la section sur les identités de somme et de différence.
Résolvez l'équation quadratique sous forme exacte :\(2 {\sin}^2 \theta−3 \sin \theta+1=0\),\(0≤\theta<2\pi\).
Solution
Nous pouvons factoriser en utilisant le regroupement. Les valeurs de solution de\(\theta\) peuvent être trouvées sur le cercle unitaire.
\[\begin{align*} (2 \sin \theta-1)(\sin \theta-1)&= 0\\ 2 \sin \theta-1&= 0\\ \sin \theta&= \dfrac{1}{2}\\ \theta&= \dfrac{\pi}{6}, \dfrac{5\pi}{6}\\ \sin \theta&= 1\\ \theta&= \dfrac{\pi}{2} \end{align*}\]
Résolvez l'équation quadratique\(2{\cos}^2 \theta+\cos \theta=0\).
- Réponse
-
\(\dfrac{\pi}{2}, \space \dfrac{2\pi}{3}, \space \dfrac{4\pi}{3}, \space \dfrac{3\pi}{2}\)
Résolution d'équations trigonométriques à l'aide d'identités fondamentales
Bien que l'algèbre puisse être utilisée pour résoudre un certain nombre d'équations trigonométriques, nous pouvons également utiliser les identités fondamentales car elles simplifient la résolution d'équations. N'oubliez pas que les techniques que nous utilisons pour résoudre les problèmes ne sont pas les mêmes que celles utilisées pour vérifier les identités. Les règles de base de l'algèbre s'appliquent ici, par opposition à la réécriture d'un côté de l'identité pour qu'il corresponde à l'autre côté. Dans l'exemple suivant, nous utilisons deux identités pour simplifier l'équation.
Utilisez les identités pour résoudre exactement l'équation trigonométrique sur l'intervalle\(0≤x<2\pi\).
\(\cos x \cos(2x)+\sin x \sin(2x)=\dfrac{\sqrt{3}}{2}\)
Solution
Notez que le côté gauche de l'équation est la formule de différence pour le cosinus.
\[\begin{align*} \cos x \cos(2x)+\sin x \sin(2x)&= \dfrac{\sqrt{3}}{2}\\ \cos(x-2x)&= \dfrac{\sqrt{3}}{2}\qquad \text{Difference formula for cosine}\\ \cos(-x)&= \dfrac{\sqrt{3}}{2}\qquad \text{Use the negative angle identity.}\\ \cos x&= \dfrac{\sqrt{3}}{2} \end{align*}\]
Dans le cercle des unités de la section sur les identités de somme et de différence, nous voyons\(\cos x=\dfrac{\sqrt{3}}{2}\) quand\(x=\dfrac{\pi}{6},\space \dfrac{11\pi}{6}\).
Résolvez l'équation exactement en utilisant une formule à double angle :\(\cos(2\theta)=\cos \theta\).
Solution
Nous avons trois choix d'expressions pour remplacer le double angle du cosinus. Comme il est plus simple de résoudre une fonction trigonométrique à la fois, nous allons choisir l'identité à double angle impliquant uniquement le cosinus :
\[\begin{align*} \cos(2\theta)&= \cos \theta\\ 2{\cos}^2 \theta-1&= \cos \theta\\ 2 {\cos}^2 \theta-\cos \theta-1&= 0\\ (2 \cos \theta+1)(\cos \theta-1)&= 0\\ 2 \cos \theta+1&= 0\\ \cos \theta&= -\dfrac{1}{2}\\ \cos \theta-1&= 0\\ \cos \theta&= 1 \end{align*}\]
Donc, si\(\cos \theta=−\dfrac{1}{2}\), alors\(\theta=\dfrac{2\pi}{3}\pm 2\pi k\) et\(\theta=\dfrac{4\pi}{3}\pm 2\pi k\) ; si\(\cos \theta=1\), alors\(\theta=0\pm 2\pi k\).
Résolvez l'équation exactement en utilisant une identité :\(3 \cos \theta+3=2 {\sin}^2 \theta\),\(0≤\theta<2\pi\).
Solution
Si nous réécrivons le côté droit, nous pouvons écrire l'équation en termes de cosinus :
\ [\ begin {align*}
3 \ cos \ théta+3&= 2 {\ sin} ^2 \ thêta \ \
3 \ cos \ théta+3&= 2 (1- {\ cos} ^2 \ thêta) \ \
3 \ cos \ théta+3&= 2-2 {\ cos} ^2 \ thêta \ \
2 {\ cos} ^2 \ théta+3 \ cos \ théta+1&= 0 \ \
(2 \ cos \ théta+1) (\ cos \ théta+1) &= 0 \ \
2 \ cos \ théta+1&= 0 \ \
\ cos \ theta&= - \ dfrac {1} {2} \ \
\ theta&= \ dfrac {2 \ pi} {3}, \ space \ dfrac {4 \ pi} {3} \ \ \ cos
\ théta+1&= 0 \ \ \ cos
\ théta&= -1 \ \
\ théta&= \ pi \ \ \
\ {end aligner*} \]
Nos solutions sont\(\theta=\dfrac{2\pi}{3},\space \dfrac{4\pi}{3},\space \pi\).
Résolution d'équations trigonométriques sous plusieurs angles
Parfois, il n'est pas possible de résoudre une équation trigonométrique avec des identités à angles multiples, telles que\(\sin(2x)\) ou\(\cos(3x)\). Lorsque vous êtes confronté à ces équations, rappelez-vous qu'\(y=\sin(2x)\)il s'agit d'une compression horizontale d'un facteur 2 de la fonction\(y=\sin x\). Sur un intervalle de\(2\pi\), nous pouvons représenter graphiquement deux périodes de\(y=\sin(2x)\), au lieu d'un cycle de\(y=\sin x\). Cette compression du graphique nous amène à penser qu'il peut y avoir deux fois plus de x -intercepts ou de solutions\(\sin(2x)=0\) par rapport à\(\sin x=0\). Ces informations nous aideront à résoudre l'équation.
Résolvez exactement :\(\cos(2x)=\dfrac{1}{2}\) non\([ 0,2\pi )\).
Solution
Nous pouvons voir que cette équation est l'équation standard avec un multiple d'angle. Si\(\cos(\alpha)=\dfrac{1}{2}\), nous le savons,\(\alpha\) se trouve dans les quadrants I et IV. Bien que cela ne\(\theta={\cos}^{−1} \dfrac{1}{2}\) produira des solutions que dans les quadrants I et II, nous reconnaissons que les solutions de l'équation\(\cos \theta=\dfrac{1}{2}\) se trouveront dans les quadrants I et IV.
Par conséquent, les angles possibles sont\(\theta=\dfrac{\pi}{3}\) et\(\theta=\dfrac{5\pi}{3}\). Donc,\(2x=\dfrac{\pi}{3}\) ou\(2x=\dfrac{5\pi}{3}\), ce qui signifie que\(x=\dfrac{\pi}{6}\) ou\(x=\dfrac{5\pi}{6}\). Est-ce que cela a du sens ? Oui, parce que\(\cos\left(2\left(\dfrac{\pi}{6}\right)\right)=\cos\left(\dfrac{\pi}{3}\right)=\dfrac{1}{2}\).
Y a-t-il d'autres réponses possibles ? Revenons à notre première étape.
Dans le quadrant I\(2x=\dfrac{\pi}{3}\),\(x=\dfrac{\pi}{6}\) comme indiqué. Tournons-nous à nouveau autour du cercle :
\ [\ begin {align*}
2x&= \ dfrac {\ pi} {3} +2 \ pi \ \
&= \ dfrac {\ pi} {3} + \ dfrac {6 \ pi} {3} \ \
&= \ dfrac {7 \ pi} {3} \ \
x&= \ dfrac {7 \ pi} {6} \ \
\ text {Une rotation de plus donne} \ \
2x&= \ dfrac {\ pi} {3} +4 \ pi \ \
& ; = \ dfrac {\ pi} {3} + \ dfrac {12 \ pi} {3} \ \
&= \ dfrac {13 \ pi} {3} \ \
\ end {align*} \]
\(x=\dfrac{13\pi}{6}>2\pi\), donc cette valeur pour\(x\) est supérieure à\(2\pi\), il ne s'agit donc pas d'une solution activée\([ 0,2\pi )\).
Dans le quadrant IV\(2x=\dfrac{5\pi}{3}\),\(x=\dfrac{5\pi}{6}\) comme indiqué. Tournons-nous à nouveau autour du cercle :
\[\begin{align*} 2x&= \dfrac{5\pi}{3}+2\pi\\ &= \dfrac{5\pi}{3}+\dfrac{6\pi}{3}\\ &= \dfrac{11\pi}{3} \end{align*}\]
donc\(x=\dfrac{11\pi}{6}\).
Une rotation de plus donne
\[\begin{align*} 2x&= \dfrac{5\pi}{3}+4\pi\\ &= \dfrac{5\pi}{3}+\dfrac{12\pi}{3}\\ &= \dfrac{17\pi}{3} \end{align*}\]
\(x=\dfrac{17\pi}{6}>2\pi\), donc cette valeur pour\(x\) est supérieure à\(2\pi\), il ne s'agit donc pas d'une solution activée\([ 0,2\pi )\).
Nos solutions sont\(x=\dfrac{\pi}{6}, \space \dfrac{5\pi}{6}, \space \dfrac{7\pi}{6}\), et\(\dfrac{11\pi}{6}\). Notez que chaque fois que nous résolvons un problème sous la forme de\(sin(nx)=c\), nous devons contourner l'unité de\(n\) temps du cercle.
Résoudre les problèmes du triangle droit
Nous pouvons maintenant utiliser toutes les méthodes que nous avons apprises pour résoudre des problèmes qui impliquent l'application des propriétés des triangles droits et du théorème de Pythagore. Nous commençons par le célèbre théorème de Pythagore,
\[a^2+b^2=c^2 \label{Pythagorean}\]
et modélisez une équation adaptée à une situation.
L'un des câbles qui ancre le centre de la grande roue London Eye au sol doit être remplacé. Le centre de la grande roue se trouve\(69.5\) à quelques mètres au-dessus du sol et le deuxième point d'ancrage au sol se trouve à\(23\) quelques mètres de la base de la grande roue. Quelle est la longueur approximative du câble et quel est l'angle d'élévation (du sol au centre de la grande roue) ? Voir la figure\(\PageIndex{4}\).
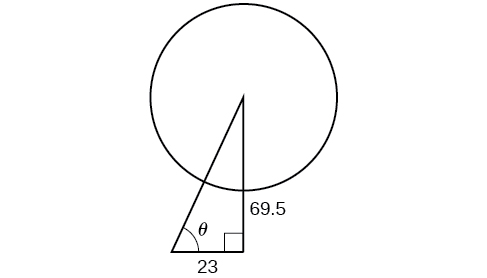
Solution
Utilisez le théorème de Pythagore (équation \ ref {Pythagore}) et les propriétés des triangles droits pour modéliser une équation qui répond au problème. En utilisant les informations fournies, nous pouvons dessiner un triangle droit. Nous pouvons trouver la longueur du câble avec le théorème de Pythagore.
\[\begin{align*} a^2+b^2&= c^2\\ {(23)}^2+{(69.5)}^2&\approx 5359\\ \sqrt{5359}&\approx 73.2\space m \end{align*}\]
L'angle d'élévation est\(\theta\) formé par le second ancrage au sol et le câble atteignant le centre de la roue. Nous pouvons utiliser la fonction tangente pour trouver sa mesure. Arrondir à deux décimales.
\[\begin{align*} \tan \theta&= 69.523\\ {\tan}^{-1}(69.523)&\approx 1.2522\\ &\approx 71.69^{\circ} \end{align*}\]
L'angle d'élévation est d'environ\(71.7°\) et la longueur du câble est de\(73.2\) mètres.
Les règles de sécurité de l'OSHA exigent que la base d'une échelle soit placée à un\(1\) pied du mur pour chaque\(4\) pied de la longueur de l'échelle. Déterminez l'angle qu'une échelle de n'importe quelle longueur forme avec le sol et la hauteur à laquelle l'échelle touche le mur.
Solution
Quelle que soit la longueur de l'échelle, la base doit se trouver à une distance du mur égale au quart de la longueur de l'échelle. De manière équivalente, si la base de l'échelle se trouve à « un » pied du mur, la longueur de l'échelle sera de\(4a\) pieds. Voir la figure\(\PageIndex{5}\).
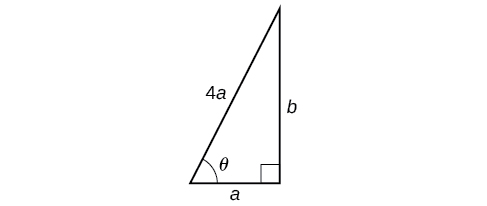
Le côté adjacent à l'\(\theta\)hypoténuse\(a\) et à l'hypoténuse est\(4a\). Ainsi,
\[\begin{align*} \cos \theta&= \dfrac{a}{4a}\\ &= \dfrac{1}{4}\\ {\cos}^{-1}\left (\dfrac{1}{4}\right )&\approx 75.5^{\circ} \end{align*}\]
L'élévation de l'échelle forme un angle\(75.5°\) avec le sol. La hauteur à laquelle l'échelle touche le mur peut être déterminée en utilisant le théorème de Pythagore :
\[\begin{align*} a^2+b^2&= {(4a)}^2\\ b^2&= {(4a)}^2-a^2\\ b^2&= 16a^2-a^2\\ b^2&= 15a^2\\ b&= a\sqrt{15} \end{align*}\]
Ainsi, l'échelle touche le mur à\(a\sqrt{15}\) pieds du sol.
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à résoudre des équations trigonométriques.
- Résolution d'équations trigonométriques I
- Résolution d'équations trigonométriques II
- Résolution d'équations trigonométriques III
- Résolution d'équations trigonométriques IV
- Résolution d'équations trigonométriques V
- Résolution d'équations trigonométriques VI
Concepts clés
- Pour résoudre des équations trigonométriques linéaires, nous pouvons utiliser des techniques algébriques tout comme nous le faisons pour résoudre des équations algébriques. Recherchez des modèles, tels que la différence entre les carrés, la forme quadratique ou une expression qui se prête bien à la substitution. Voir Exemple\(\PageIndex{1}\)\(\PageIndex{2}\), Exemple et Exemple\(\PageIndex{3}\).
- Les équations impliquant une seule fonction trigonométrique peuvent être résolues ou vérifiées à l'aide du cercle unitaire. Voir Exemple\(\PageIndex{4}\), Exemple\(\PageIndex{5}\)\(\PageIndex{6}\), Exemple et Exemple\(\PageIndex{7}\).
- Nous pouvons également résoudre des équations trigonométriques à l'aide d'un calculateur graphique. Voir Exemple\(\PageIndex{8}\) et Exemple\(\PageIndex{9}\).
- De nombreuses équations apparaissent de forme quadratique. Nous pouvons utiliser la substitution pour rendre l'équation plus simple, puis utiliser les mêmes techniques que celles que nous utilisons pour résoudre une quadratique algébrique : factorisation, formule quadratique, etc. Voir Exemple\(\PageIndex{10}\), Exemple\(\PageIndex{11}\)\(\PageIndex{12}\), Exemple et Exemple\(\PageIndex{13}\).
- Nous pouvons également utiliser les identités pour résoudre des équations trigonométriques. Voir Exemple\(\PageIndex{14}\)\(\PageIndex{15}\), Exemple et Exemple\(\PageIndex{16}\).
- Nous pouvons utiliser la substitution pour résoudre une équation trigonométrique à angles multiples, qui est une compression d'une fonction trigonométrique standard. Nous devrons prendre en compte la compression et vérifier que nous avons trouvé toutes les solutions dans l'intervalle donné. Voir l'exemple\(\PageIndex{17}\).
- Les scénarios du monde réel peuvent être modélisés et résolus à l'aide du théorème de Pythagore et des fonctions trigonométriques. Voir l'exemple\(\PageIndex{18}\).


