9.3 : Formules à double angle, demi-angle et réduction
- Page ID
- 195400
- Utilisez des formules à double angle pour trouver des valeurs exactes
- Utiliser des formules à double angle pour vérifier les identités
- Utiliser des formules de réduction pour simplifier une expression
- Utilisez des formules en demi-angle pour trouver des valeurs exactes
Les rampes pour vélos conçues pour la compétition (voir Figure\(\PageIndex{1}\)) doivent varier en hauteur en fonction du niveau de compétence des concurrents. Pour les concurrents avancés, l'angle formé par la rampe et le sol doit être\(\theta\) tel que\(\tan \theta=\dfrac{5}{3}\). L'angle est divisé en deux pour les novices. Quelle est la pente de la rampe pour les novices ? Dans cette section, nous étudierons trois catégories supplémentaires d'identités que nous pouvons utiliser pour répondre à des questions telles que celle-ci.
Utilisation de formules à double angle pour trouver des valeurs exactes
Dans la section précédente, nous avons utilisé des formules d'addition et de soustraction pour les fonctions trigonométriques. Maintenant, nous examinons à nouveau ces mêmes formules. Les formules à double angle sont un cas particulier des formules de somme, où\(\alpha=\beta\). La dérivation de la formule à double angle pour le sinus commence par la formule de somme,
\[\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\]
Si nous le laissons faire\(\alpha=\beta=\theta\), alors nous avons
\[\begin{align*} \sin(\theta+\theta)&= \sin \theta \cos \theta+\cos \theta \sin \theta\\[4pt] \sin(2\theta)&= 2\sin \theta \cos \theta \end{align*}\]
La dérivation du double angle pour le cosinus nous donne trois options. Tout d'abord, en partant de la formule de somme\(\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\), et en laissant\(\alpha=\beta=\theta\), nous avons
\[\begin{align*} \cos(\theta+\theta)&= \cos \theta \cos \theta-\sin \theta \sin \theta\\[4pt] \cos(2\theta)&= {\cos}^2 \theta - {\sin}^2 \theta \end{align*}\]
En utilisant les propriétés de Pythagore, nous pouvons étendre cette formule à double angle pour le cosinus et obtenir deux variantes supplémentaires. La première variante est la suivante :
\[\begin{align*} \cos(2\theta)&= {\cos}^2 \theta - {\sin}^2 \theta \\[4pt] &= (1-{\sin}^2 \theta)-{\sin}^2 \theta \end{align*}\]
La deuxième variante est la suivante :
\[\begin{align*} \cos(2\theta)&= {\cos}^2 \theta-{\sin}^2 \theta\\[4pt] &= {\cos}^2 \theta-(1-{\cos}^2 \theta)\\[4pt] &= 2 {\cos}^2 \theta-1 \end{align*}\]
De même, pour dériver la formule à double angle pour la tangente, le remplacement\(\alpha=\beta=\theta\) dans la formule de somme donne
\[\begin{align*} \tan(\alpha+\beta)&= \dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}\\[4pt] \tan(\theta+\theta)&= \dfrac{\tan \theta+\tan \theta}{1-\tan \theta \tan \theta}\\[4pt] \tan(2\theta)&= \dfrac{2\tan \theta}{1-{\tan}^2 \theta} \end{align*}\]
Les formules à double angle sont résumées comme suit :
\[\begin{align} \sin(2\theta)&= 2 \sin \theta \cos \theta\\[4pt] \cos(2\theta)&= {\cos}^2 \theta-{\sin}^2 \theta =1-2 {\sin}^2 \theta = 2{\cos}^2 \theta-1\\[4pt] \tan(2\theta)&= \dfrac{2 \tan \theta}{1-{\tan}^2\theta} \end{align}\]
- Tracez un triangle pour refléter les informations données.
- Déterminez la formule à double angle correcte.
- Substituez des valeurs dans la formule en fonction du triangle.
- Simplifiez.
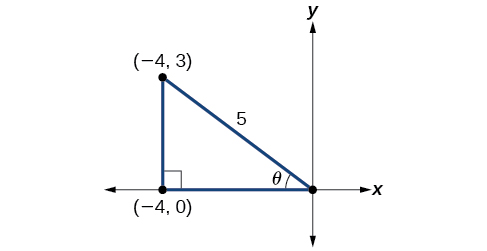
Compte tenu de cela\(\tan \theta=−\dfrac{3}{4}\) et\(\theta\) se trouve dans le quadrant II, trouvez ce qui suit :
- \(\sin(2\theta)\)
- \(\cos(2\theta)\)
- \(\tan(2\theta)\)
Solution
Si nous dessinons un triangle pour refléter les informations fournies, nous pouvons trouver les valeurs nécessaires pour résoudre les problèmes sur l'image. Nous sommes donnés\(\tan \theta=−\dfrac{3}{4}\), c'\(\theta\)est-à-dire dans le quadrant II. La tangente d'un angle est égale au côté opposé par rapport au côté adjacent, et comme il\(\theta\) se trouve dans le second quadrant, le côté adjacent se trouve sur l'axe x et est négatif. Utilisez le théorème de Pythagore pour déterminer la longueur de l'hypoténuse :
\[\begin{align*} {(-4)}^2+{(3)}^2&= c^2\\[4pt] 16+9&= c^2\\[4pt] 25&= c^2\\[4pt] c&= 5 \end{align*}\]
Nous pouvons maintenant dessiner un triangle similaire à celui illustré sur la figure\(\PageIndex{2}\).
- Commençons par écrire la formule à double angle pour le sinus.
\(\sin(2\theta)=2 \sin \theta \cos \theta\)
Nous voyons que nous devons trouver\(\sin \theta\) et\(\cos \theta\). Sur la base de la figure\(\PageIndex{2}\), nous voyons que l'hypoténuse est égale à\(5\)\(\sin θ=35\), donc\(\sin θ=35\), et\(\cos θ=−45\). Substituez ces valeurs dans l'équation et simplifiez.
Ainsi,
\[\begin{align*} \sin(2\theta)&= 2\left(\dfrac{3}{5}\right)\left(-\dfrac{4}{5}\right)\\[4pt] &= -\dfrac{24}{25} \end{align*}\]
- Écrivez la formule à double angle pour le cosinus.
\(\cos(2\theta)={\cos}^2 \theta−{\sin}^2 \theta\)
Encore une fois, remplacez les valeurs du sinus et du cosinus dans l'équation et simplifiez.
\[\begin{align*} \cos(2\theta)&= {\left(-\dfrac{4}{5}\right)}^2-{\left(\dfrac{3}{5}\right)}^2\\[4pt] &= \dfrac{16}{25}-\dfrac{9}{25}\\[4pt] &= \dfrac{7}{25} \end{align*}\]
- Écrivez la formule à double angle pour la tangente.
\(\tan(2\theta)=\dfrac{2 \tan \theta}{1−{\tan}^2\theta}\)
Dans cette formule, nous avons besoin de la tangente, qui nous a été donnée\(\tan \theta=−\dfrac{3}{4}\). Substituez cette valeur dans l'équation et simplifiez.
\ [\ begin {align*} \ tan (2 \ thêta) &= \ dfrac {2 \ left (- \ dfrac {3} {4} \ right)} {1- {\ left (- \ dfrac {3} {4} \ right)} ^2} \ \ [4 points]
&= \ dfrac {- \ dfrac {3} {2}} {1- \ dfrac {9} {16}} \ \ [4 points]
&= - \ dfrac {3} {2} \ gauche (\ dfrac {16} {7} \ droite) \ \ [4 points]
&= - \ dfrac {24} {7}
\ end {align*} \]
Étant donné\(\sin \alpha=\dfrac{5}{8}\), avec\(\theta\) dans le quadrant I, trouvez\(\cos(2\alpha)\).
- Réponse
-
\(\cos(2\alpha)=\dfrac{7}{32}\)
Utilisez la formule à double angle pour le cosinus pour écrire\(\cos(6x)\) en termes de\(cos(3x)\).
Solution
\[\begin{align*} \cos(6x)&= \cos(3x+3x)\\[4pt] &= \cos 3x \cos 3x-\sin 3x \sin 3x\\[4pt] &= {\cos}^2 3x-{\sin}^2 3x \end{align*}\]
Analyse
Cet exemple montre que nous pouvons utiliser la formule à double angle sans avoir de valeurs exactes. Il souligne que le modèle est ce dont nous devons nous souvenir et que les identités sont vraies pour toutes les valeurs du domaine de la fonction trigonométrique.
Utilisation de formules à double angle pour vérifier les identités
L'établissement des identités à l'aide des formules à double angle s'effectue selon les mêmes étapes que celles que nous avons utilisées pour dériver les formules de somme et de différence. Choisissez le côté le plus complexe de l'équation et réécrivez-le jusqu'à ce qu'il corresponde à l'autre côté.
Vérifiez l'identité suivante à l'aide de formules à double angle :
\[1+\sin(2\theta)={(\sin\theta+\cos\theta)}^2 \nonumber \]
Solution
Nous allons travailler sur le côté droit du signe égal et réécrire l'expression jusqu'à ce qu'elle corresponde au côté gauche.
\[\begin{align*} {(\sin \theta+\cos \theta)}^2&= {\sin}^2 \theta+2 \sin \theta \cos \theta+{\cos}^2 \theta\\[4pt] &= ({\sin}^2 \theta+{\cos}^2 \theta)+2 \sin \theta \cos \theta\\[4pt] &= 1+2 \sin \theta \cos \theta\\[4pt] &= 1+\sin(2\theta) \end{align*}\]
Analyse
Ce processus n'est pas compliqué, tant que l'on se souvient de la formule carrée parfaite issue de l'algèbre :
\[{(a\pm b)}^2=a^2\pm 2ab+b^2 \nonumber \]
où\(a=\sin \theta\) et\(b=\cos \theta\). Pour réussir en mathématiques, il faut notamment être capable de reconnaître des modèles. Bien que les termes ou les symboles puissent changer, l'algèbre reste cohérente.
Vérifiez l'identité :\({\cos}^4 \theta−{\sin}^4 \theta=\cos(2\theta)\).
- Réponse
-
\({\cos}^4 \theta−{\sin}^4 \theta=({\cos}^2 \theta+{\sin}^2 \theta)({\cos}^2 \theta−{\sin}^2 \theta)=\cos(2\theta)\)
Vérifiez l'identité :\(\tan(2 \theta)=2\cot \theta−\tan \theta\)
Solution
Dans ce cas, nous allons travailler avec le côté gauche de l'équation et le simplifier ou le réécrire jusqu'à ce qu'il soit égal au côté droit de l'équation.
\[\begin{align*} \tan(2\theta)&= \dfrac{2 \tan \theta}{1-{\tan}^2 \theta} \qquad \text{Double-angle formula}\\[4pt] &= \dfrac{2 \tan \theta\left (\dfrac{1}{\tan \theta}\right)}{(1-{\tan}^2 \theta)\left (\dfrac{1}{\tan \theta}\right )} \qquad \text{Multiply by a term that results in desired numerator}\\[4pt] &= \dfrac{2}{\dfrac{1}{\tan \theta}-\dfrac{ {\tan}^2 \theta}{\tan \theta}}\\[4pt] &= \dfrac{2}{\cot \theta-\tan \theta} \qquad \text {Use reciprocal identity for } \dfrac{1}{\tan \theta} \end{align*}\]
Analyse
Voici un cas où le côté le plus compliqué de l'équation initiale apparaissait sur la droite, mais nous avons choisi de travailler sur le côté gauche. Toutefois, si nous avions choisi le côté gauche pour réécrire, nous aurions travaillé à rebours pour arriver à l'équivalence. Supposons, par exemple, que nous souhaitions montrer
\[\begin{align*} \dfrac{2\tan \theta}{1-{\tan}^2 \theta}&= \dfrac{2}{\cot \theta-\tan \theta} \\[4pt] \text{Lets work on the right side}\\[4pt] \dfrac{2}{\cot \theta-\tan \theta}&= \frac{2}{\frac{1}{\tan \theta }-\tan \theta }\left ( \frac{\tan \theta }{\tan \theta } \right )\\[4pt] &= \dfrac{2 \tan \theta}{\dfrac{1}{\tan \theta}(\tan \theta)-\tan \theta(\tan \theta)}\\[4pt] &= \dfrac{2 \tan \theta}{1-{\tan}^2 \theta} \end{align*}\]
Lorsque vous utilisez les identités pour simplifier une expression trigonométrique ou résoudre une équation trigonométrique, plusieurs chemins mènent généralement au résultat souhaité. Il n'existe aucune règle précise quant au côté qui doit être manipulé. Toutefois, nous devrions commencer par les directives énoncées précédemment.
Vérifiez l'identité :\(\cos(2\theta)\cos \theta={\cos}^3 \theta−\cos \theta {\sin}^2 \theta\).
- Réponse
-
\(\cos(2 \theta)\cos \theta=({\cos}^2 \theta−{\sin}^2 \theta) \cos \theta={\cos}^3 \theta−\cos \theta {\sin}^2 \theta\)
Utiliser des formules de réduction pour simplifier une expression
Les formules à double angle peuvent être utilisées pour dériver les formules de réduction, qui sont des formules que nous pouvons utiliser pour réduire la puissance d'une expression donnée impliquant des puissances paires de sinus ou de cosinus. Ils nous permettent de réécrire les puissances paires du sinus ou du cosinus en fonction de la première puissance du cosinus. Ces formules sont particulièrement importantes dans les cours de mathématiques de niveau supérieur, en particulier le calcul. Également appelées formules de réduction de puissance, trois identités sont incluses et peuvent être facilement dérivées des formules à double angle.
Nous pouvons utiliser deux des trois formules à double angle pour le cosinus afin de dériver les formules de réduction pour le sinus et le cosinus. Commençons par\(\cos(2\theta)=1−2 {\sin}^2 \theta\). Résolvez pour\({\sin}^2 \theta\) :
\[\begin{align*} \cos(2\theta)&= 1-2 {\sin}^2 \theta\\[4pt] 2 {\sin}^2 \theta&= 1-\cos(2\theta)\\[4pt] {\sin}^2 \theta&= \dfrac{1-\cos(2\theta)}{2} \end{align*}\]
Ensuite, nous utilisons la formule\(\cos(2\theta)=2 {\cos}^2 \theta−1\). Résolvez pour\({\cos}^2 \theta\) :
\[\begin{align*} \cos(2\theta)&= 2 {\cos}^2 \theta-1\\[4pt] 1+\cos(2\theta)&= 2 {\cos}^2 \theta\\[4pt] \dfrac{1+\cos(2\theta)}{2}&= {\cos}^2 \theta \end{align*}\]
La dernière formule de réduction est dérivée en écrivant la tangente en termes de sinus et de cosinus :
\[\begin{align*} \tan^2 \theta &= \frac{\sin^2 \theta}{\cos^2 \theta} \\[4pt] &= \dfrac{\dfrac{1-\cos(2\theta)}{2}}{\dfrac{1+\cos(2\theta)}{2}} \qquad \tag{Substitute the reduction formulas} \\[4pt] &= \left(\dfrac{1-\cos(2 \theta)}{2}\right)\left(\dfrac{2}{1+\cos(2 \theta)}\right) \\[4pt] &= \dfrac{1-\cos(2 \theta)}{1+\cos(2 \theta)} \end{align*}\]
Les formules de réduction sont résumées comme suit :
\[{\sin}^2 \theta=\dfrac{1−\cos(2 \theta)}{2}\]
\[{\cos}^2 \theta=\dfrac{1+\cos(2 \theta)}{2}\]
\[{\tan}^2 \theta=\dfrac{1−\cos(2 \theta)}{1+\cos(2 \theta)}\]
Écrivez une expression équivalente\({\cos}^4 x\) qui n'implique aucune puissance de sinus ou de cosinus supérieure à\(1\).
Solution
Nous appliquerons la formule de réduction pour le cosinus deux fois.
\ [\ begin {align*}
{\ cos} ^4 x&= {({\ cos} ^2 x)} ^2 \ \ [4pt]
&= {\ left (\ dfrac {1+ \ cos (2x)} {2} \ right)} ^2 \ qquad \ text {Formule de réduction de remplacement} \ \ [4 points]
&= \ dfrac {1} {4} (1+2) \ cos (2 x) + {\ cos} ^2 (2)) \ \ [4 points]
&= \ dfrac {1} {4} + \ dfrac {1} {2} \ cos (2) + \ dfrac {1} {4} \ left (\ dfrac {1+ {\ cos} ^2 (2x)} {2} \ right) \ qquad \ text {Formule de réduction de remplacement pour} {\ cos} ^2 x \ \ [4pt]
&= \ dfrac {1} {4} + \ dfrac {1} {2} \ cos (2x) + \ dfrac {1} {8} + \ dfrac {1} {8} \ cos (4) \ \ [4 points]
&= \ dfrac {3} {8} + \ dfrac {1} {2} \ cos (2) + \ dfrac {1} {8} \ cos (4)
\ fin {align*} \]
Analyse
La solution est trouvée en utilisant deux fois la formule de réduction, comme indiqué, et la formule carrée parfaite issue de l'algèbre.
Utilisez les formules de réduction de puissance pour prouver\({\sin}^3(2x)=\left[ \dfrac{1}{2} \sin(2x) \right] [ 1−\cos(4x) \)
Solution
Nous travaillerons à simplifier le côté gauche de l'équation :
\[\begin{align*} {\sin}^3(2x)&= [\sin(2x)][{\sin}^2(2x)]\\[4pt] &= \sin(2x)\left [\dfrac{1-\cos(4x)}{2}\right ]\qquad \text{Substitute the power-reduction formula.}\\[4pt] &= \sin(2x)\left(\dfrac{1}{2}\right)[1-\cos(4x)]\\[4pt] &= \dfrac{1}{2}[\sin(2x)][1-\cos(4x)] \end{align*}\]
Analyse
Notez que dans cet exemple, nous avons remplacé\(\dfrac{1−\cos(4x)}{2}\)\({\sin}^2(2x)\). La formule indique\({\sin}^2 \theta=\dfrac{1−\cos(2\theta)}{2}\)
Nous avons laissé faire\(\theta=2x\), alors\(2\theta=4x\).
Utilisez les formules de réduction de puissance pour le prouver\(10{\cos}^4 x=\dfrac{15}{4}+5\cos(2x)+\dfrac{5}{4}\cos(4x)\).
- Réponse
-
\[\begin{align*} 10{\cos}^4 x&= 10{({\cos}^2x)}^2\\[4pt] &= 10{\left[\dfrac{ 1+\cos(2x)}{2} \right]}^2\qquad \text{Substitute reduction formula for } {\cos}^2x\\[4pt] &= \dfrac{10}{4}[1+2\cos(2x)+{\cos}^2(2x)]\\[4pt] &= \dfrac{10}{4}+\dfrac{10}{2}\cos(2x)+\dfrac{10}{4}\left(\dfrac{1+{\cos}^2(2x)}{2}\right)\qquad \text{ Substitute reduction formula for } {\cos}^2 x\\[4pt] &= \dfrac{10}{4}+\dfrac{10}{2} \cos(2x)+\dfrac{10}{8}+\dfrac{10}{8}\cos(4x)\\[4pt] &= \dfrac{30}{8}+5\cos(2x)+\dfrac{10}{8}\cos(4x)\\[4pt] &= \dfrac{15}{4}+5\cos(2x)+\dfrac{5}{4}\cos(4x) \end{align*}\]
Utilisation de formules en demi-angle pour trouver des valeurs exactes
L'ensemble d'identités suivant est l'ensemble de formules demi-angle, qui peuvent être dérivées des formules de réduction et que nous pouvons utiliser lorsque nous avons un angle qui est la moitié de la taille d'un angle spécial. Si nous la\(\theta\) remplaçons par\(\dfrac{\alpha}{2}\), la formule du demi-angle pour le sinus est trouvée en simplifiant l'équation et en résolvant pour\(\sin\left(\dfrac{\alpha}{2}\right)\). Notez que les formules en demi-angle sont précédées d'un\(\pm\) signe. Cela ne signifie pas que les expressions positives et négatives sont valides. Cela dépend plutôt du quadrant dans lequel\(\dfrac{\alpha}{2}\) se termine.
La formule du demi-angle pour le sinus est dérivée comme suit :
\[\begin{align*} {\sin}^2 \theta&= \dfrac{1-\cos(2\theta)}{2}\\[4pt] {\sin}^2\left(\dfrac{\alpha}{2}\right)&= \dfrac{1-\left(\cos 2\cdot \dfrac{\alpha}{2}\right)}{2}\\[4pt] &= \dfrac{1-\cos \alpha}{2}\\[4pt] \sin \left(\dfrac{\alpha}{2}\right)&= \pm \sqrt{\dfrac{1-\cos \alpha}{2}} \end{align*}\]
Pour dériver la formule du demi-angle pour le cosinus, nous avons
\[\begin{align*} {\cos}^2 \theta&= \dfrac{1+\cos(2\theta)}{2}\\[4pt] {\cos}^2\left(\dfrac{\alpha}{2}\right)&= \dfrac{1+\cos\left(2\cdot \dfrac{\alpha}{2}\right)}{2}\\[4pt] &= \dfrac{1+\cos \alpha}{2}\\[4pt] \cos\left(\dfrac{\alpha}{2}\right)&= \pm \sqrt{\dfrac{1+\cos \alpha}{2}} \end{align*}\]
Pour l'identité tangente, nous avons
\[\begin{align*} {\tan}^2 \theta&= \dfrac{1-\cos(2\theta)}{1+\cos(2\theta)}\\[4pt] {\tan}^2\left(\dfrac{\alpha}{2}\right)&= \dfrac{1-\cos\left(2\cdot \dfrac{\alpha}{2}\right)}{1+\cos\left(2\cdot \dfrac{\alpha}{2}\right)}\\[4pt] \tan\left(\dfrac{\alpha}{2}\right)&= \pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}} \end{align*}\]
Les formules du demi-angle sont les suivantes :
\[\begin{align} \sin\left(\dfrac{\alpha}{2}\right)&=\pm \sqrt{\dfrac{1-\cos \alpha}{2}} \label{halfsine} \\[4pt] \cos \left(\dfrac{\alpha}{2} \right) &=\pm \sqrt{\dfrac{1+\cos \alpha}{2}} \\[4pt] \tan\left(\dfrac{\alpha}{2}\right) &=\pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}} =\dfrac{\sin \alpha}{1+\cos \alpha} =\dfrac{1-\cos \alpha}{\sin \alpha}\end{align}\]
Utilisation d'une formule en demi-angle pour déterminer la valeur exacte d'une fonction sinusoïdale. Trouvez\(\sin(15°)\) à l'aide d'une formule en demi-angle.
Solution
Depuis\(15°=\dfrac{30°}{2}\), nous utilisons la formule du demi-angle pour le sinus (équation \ ref {halfsinus}) :
\ [\ begin {align*}
\ sin \ dfrac {30^ {\ circ}} {2} &= \ sqrt {\ dfrac {1- \ cos 30^ {\ circ}} {2}} \ \ [4pt]
&= \ sqrt {\ dfrac {1- \ dfrac {\ sqrt {3}} {2}} {2}} {2}} \ dfrac {1- \ dfrac {\ sqrt {3}} {2}} \ [4 points]
&= \ sqrt {\ dfrac {\ dfrac {2- \ sqrt {3}} {2}} {2}} \ \ [4 points]
&= \ sqrt {\ dfrac {2- \ sqrt {3}} {4}} \ \ [4 points]
&= \ dfrac {\ sqrt {2- \ sqrt {3}}} {2}
\ end {align*} \]
N'oubliez pas que nous pouvons vérifier la réponse à l'aide d'une calculatrice graphique.
Analyse
Notez que nous n'avons utilisé que la racine positive car elle\(\sin(15°)\) est positive.
- Tracez un triangle pour représenter les informations données.
- Déterminez la formule de demi-angle correcte.
- Substituez des valeurs dans la formule en fonction du triangle.
- Simplifiez.
Compte tenu de cela\(\tan \alpha=\dfrac{8}{15}\) et\(α\) se trouve dans le quadrant III, trouvez la valeur exacte de ce qui suit :
- \(\sin\left(\dfrac{\alpha}{2}\right)\)
- \(\cos\left(\dfrac{\alpha}{2}\right)\)
- \(\tan\left(\dfrac{\alpha}{2}\right)\)
Solution
En utilisant les informations données, nous pouvons dessiner le triangle illustré sur la figure\(\PageIndex{3}\). En utilisant le théorème de Pythagore, nous trouvons que l'hypoténuse est de 17. Par conséquent, nous pouvons calculer\(\sin \alpha=−\dfrac{8}{17}\) et\(\cos \alpha=−\dfrac{15}{17}\).
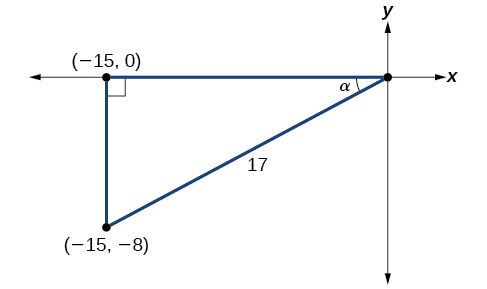
- Avant de commencer, nous devons nous rappeler que si\(α\) c'est dans le quadrant III, alors\(180°<\alpha<270°\), donc\(\dfrac{180°}{2}<\dfrac{\alpha}{2}<\dfrac{270°}{2}\). Cela signifie que le côté terminal de\(\dfrac{\alpha}{2}\) se trouve dans le quadrant II, depuis\(90°<\dfrac{\alpha}{2}<135°\). Pour le trouver\(\sin \dfrac{\alpha}{2}\), nous commençons par écrire la formule du demi-angle pour le sinus. Ensuite, nous substituons la valeur du cosinus que nous avons trouvée à partir du triangle de la figure\(\PageIndex{3}\) et simplifions. \[\begin{align*} \sin \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1-\cos \alpha}{2}}\\[4pt] &= \pm \sqrt{\dfrac{1-(-\dfrac{15}{17})}{2}}\\[4pt] &= \pm \sqrt{\dfrac{\dfrac{32}{17}}{2}}\\[4pt] &= \pm \sqrt{\dfrac{32}{17}\cdot \dfrac{1}{2}}\\[4pt] &= \pm \sqrt{\dfrac{16}{17}}\\[4pt] &= \pm \dfrac{4}{\sqrt{17}}\\[4pt] &= \dfrac{4\sqrt{17}}{17} \end{align*}\]Nous choisissons la valeur positive de\(\sin \dfrac{\alpha}{2}\) car l'angle se termine dans le quadrant II et le sinus est positif dans le quadrant II.
- Pour trouver\(\cos \dfrac{\alpha}{2}\), nous allons écrire la formule demi-angle pour le cosinus, remplacer la valeur du cosinus que nous avons trouvée à partir du triangle de la Figure\(\PageIndex{3}\) et simplifier. \[\begin{align*} \cos \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1+\cos \alpha}{2}}\\[4pt] &= \pm \sqrt{\dfrac{1+\left(-\dfrac{15}{17}\right)}{2}}\\[4pt] &= \pm \sqrt{\dfrac{\dfrac{2}{17}}{2}}\\[4pt] &= \pm \sqrt{\dfrac{2}{17}\cdot \dfrac{1}{2}}\\[4pt] &= \pm \sqrt{\dfrac{1}{17}}\\[4pt] &= -\dfrac{\sqrt{17}}{17} \end{align*}\]Nous choisissons la valeur négative de\(\cos \dfrac{\alpha}{2}\) parce que l'angle se trouve dans le quadrant II car le cosinus est négatif dans le quadrant II.
- Pour trouver\(\tan \dfrac{\alpha}{2}\), nous écrivons la formule du demi-angle pour la tangente. Encore une fois, nous substituons la valeur du cosinus que nous avons trouvée à partir du triangle de la figure\(\PageIndex{3}\) et simplifions. \[\begin{align*} \tan \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}}\\[4pt] &= \pm \sqrt{\dfrac{1-\left(-\dfrac{15}{17}\right)}{1+\left(-\dfrac{15}{17}\right)}}\\[4pt] &= \pm \sqrt{\dfrac{\dfrac{32}{17}}{\dfrac{2}{17}}}\\[4pt] &= \pm \sqrt{\dfrac{32}{2}}\\[4pt] &= -\sqrt{16}\\[4pt] &= -4 \end{align*}\]Nous choisissons la valeur négative de\(\tan \dfrac{\alpha}{2}\) car\(\dfrac{\alpha}{2}\) se trouve dans le quadrant II, et la tangente est négative dans le quadrant II.
Compte tenu de cela\(\sin \alpha=−\dfrac{4}{5}\) et\(\alpha\) se trouve dans le quadrant IV, trouvez la valeur exacte de\(\cos \left(\dfrac{\alpha}{2}\right)\).
- Réponse
-
\(-\dfrac{2}{\sqrt{5}}\)
Nous allons maintenant revenir au problème posé au début de la section. Une rampe à vélo est construite pour les compétitions de haut niveau avec un angle\(θ\) formé par la rampe et le sol. Une autre rampe doit être construite deux fois moins raide pour les compétitions novices. S'il s'agit\(tan θ=53\) d'une compétition de haut niveau, quelle est la mesure de l'angle pour la compétition pour les novices ?
Solution
Puisque l'angle de la compétition pour les débutants mesure la moitié de l'inclinaison de l'angle pour la compétition de haut niveau, et\(\tan \theta=\dfrac{5}{3}\) pour la compétition de haut niveau, nous pouvons le trouver\(\cos \theta\) à partir du triangle droit et du théorème de Pythagore afin de pouvoir utiliser les identités du demi-angle. Voir la figure\(\PageIndex{4}\).
\[\begin{align*} 3^2+5^2&=34\\[4pt] c&=\sqrt{34} \end{align*}\]
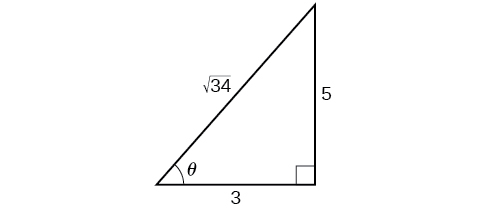
C'est ce que nous voyons\(\cos \theta=\dfrac{3}{\sqrt{34}}=\dfrac{3\sqrt{34}}{34}\). Nous pouvons utiliser la formule du demi-angle pour la tangente :\(\tan \dfrac{\theta}{2}=\sqrt{\dfrac{1−\cos \theta}{1+\cos \theta}}\). Puisque\(\tan \theta\) c'est dans le premier quadrant, il en va de même\(\tan \dfrac{\theta}{2}\).
\ [\ begin {align*}
\ tan \ dfrac {\ theta} {2} &= \ sqrt {\ dfrac {1- \ dfrac {3 \ sqrt {34}} {34}} {1+ \ dfrac {3 \ sqrt {34}}}} \ \ [4 points]
&= \ sqrt {\ dfrac {\ dfrac {\ dfrac {34-3 \ sqrt {34}} {34}} {\ dfrac {34+3 \ sqrt {34}}} \ \ [4 points]
&= \ sqrt {\ dfrac {34-3 \ sqrt {34}} {34+3 \ sqrt {34}}}} \ \ [4 points]
& \ environ 0,57
\ end {align*} \]
Nous pouvons prendre la tangente inverse pour trouver l'angle :\({\tan}^{−1}(0.57)≈29.7°\). Donc, l'angle de la rampe pour les compétitions novices est\(≈29.7°\).
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur les formules à double angle, demi-angle et réduction.
- Identités à double angle
- Identités en demi-angle
Équations clés
| formules à double angle |
\(\sin(2\theta)=2\sin \theta \cos \theta\) \(\cos(2\theta)={\cos}^2 \theta−{\sin}^2 \theta\) \(=1−2{\sin}^2 \theta\) \(=2{\cos}^2 \theta−1\) \(\tan(2\theta)=\dfrac{2\tan \theta}{1−{\tan}^2 \theta}\) |
| Des formules de réduction |
\({\sin}^2 \theta=\dfrac{1−\cos(2\theta)}{2}\) \({\cos}^2 \theta=\dfrac{1+\cos(2\theta)}{2}\) \({\tan}^2 \theta=\dfrac{1−\cos(2\theta)}{1+\cos(2\theta)}\) |
| Formules demi-angles |
\(\sin \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1−\cos \alpha}{2}}\) \(\cos \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1+\cos \alpha}{2}}\) \(\tan \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1−\cos \alpha}{1+\cos \alpha}}\) \(=\dfrac{\sin \alpha}{1+\cos \alpha}\) \(=\dfrac{1−\cos \alpha}{\sin \alpha}\) |
Concepts clés
- Les identités à double angle sont dérivées des formules de somme des fonctions trigonométriques fondamentales : sinus, cosinus et tangente. Voir Exemple\(\PageIndex{1}\), Exemple\(\PageIndex{2}\)\(\PageIndex{3}\), Exemple et Exemple\(\PageIndex{4}\).
- Les formules de réduction sont particulièrement utiles en calcul, car elles nous permettent de réduire la puissance du terme trigonométrique. Voir Exemple\(\PageIndex{5}\) et Exemple\(\PageIndex{6}\).
- Les formules de demi-angle nous permettent de déterminer la valeur des fonctions trigonométriques impliquant des demi-angles, que l'angle d'origine soit connu ou non. Voir Exemple\(\PageIndex{7}\)\(\PageIndex{8}\), Exemple et Exemple\(\PageIndex{9}\).


