9.1 : Résolution d'équations trigonométriques à l'aide d'identités
- Page ID
- 195358
- Vérifiez les identités trigonométriques fondamentales.
- Simplifiez les expressions trigonométriques à l'aide de l'algèbre et des identités.
Dans les films d'espionnage, nous voyons des espions internationaux munis de plusieurs passeports, chacun revendiquant une identité différente. Cependant, nous savons que chacun de ces passeports représente la même personne. Les identités trigonométriques agissent de la même manière que plusieurs passeports : il existe de nombreuses façons de représenter la même expression trigonométrique. Tout comme un espion choisit un passeport italien lorsqu'il voyage en Italie, nous choisissons l'identité qui s'applique au scénario donné lors de la résolution d'une équation trigonométrique.

Dans cette section, nous allons commencer à examiner les identités trigonométriques fondamentales, y compris comment les vérifier et comment les utiliser pour simplifier les expressions trigonométriques.
Vérification des identités trigonométriques fondamentales
Les identités nous permettent de simplifier des expressions complexes. Ce sont les outils de base de la trigonométrie utilisés pour résoudre des équations trigonométriques, tout comme la factorisation, la recherche de dénominateurs communs et l'utilisation de formules spéciales sont les outils de base pour résoudre des équations algébriques. En fait, nous utilisons constamment des techniques algébriques pour simplifier les expressions trigonométriques. Les propriétés et formules de base de l'algèbre, telles que la formule de différence de carrés et la formule des carrés parfaits, simplifieront le travail lié aux expressions et aux équations trigonométriques. Nous savons déjà que toutes les fonctions trigonométriques sont liées car elles sont toutes définies en termes de cercle unitaire. Par conséquent, toute identité trigonométrique peut être écrite de nombreuses manières.
Pour vérifier les identités trigonométriques, nous commençons généralement par le côté le plus complexe de l'équation et réécrivons essentiellement l'expression jusqu'à ce qu'elle soit transformée en la même expression que l'autre côté de l'équation. Parfois, nous devons factoriser des expressions, développer des expressions, trouver des dénominateurs communs ou utiliser d'autres stratégies algébriques pour obtenir le résultat souhaité. Dans cette première section, nous travaillerons sur les identités fondamentales : les identités pythagoriciennes, les identités paires, les identités réciproques et les identités quotientes.
Nous allons commencer par les identités pythagoriciennes (Tableau\(\PageIndex{1}\)), qui sont des équations impliquant des fonctions trigonométriques basées sur les propriétés d'un triangle droit. Nous avons déjà vu et utilisé le premier de ces identifiants, mais nous allons maintenant utiliser des identités supplémentaires.
| \({\sin}^2 \theta+{\cos}^2 \theta=1\) | \(1+{\cot}^2 \theta={\csc}^2 \theta\) | \(1+{\tan}^2 \theta={\sec}^2 \theta\) |
Les deuxième et troisième identités peuvent être obtenues en manipulant la première. L'identité\(1+{\cot}^2 \theta={\csc}^2 \theta\) est trouvée en réécrivant le côté gauche de l'équation en termes de sinus et de cosinus.
Prouvez :\(1+{\cot}^2 \theta={\csc}^2 \theta\)
\[\begin{align*} 1+{\cot}^2 \theta&= (1+\dfrac{{\cos}^2}{{\sin}^2})\qquad \text{Rewrite the left side}\\ &= \left(\dfrac{{\sin}^2}{{\sin}^2}\right)+\left (\dfrac{{\cos}^2}{{\sin}^2}\right)\qquad \text{Write both terms with the common denominator}\\ &= \dfrac{{\sin}^2+{\cos}^2}{{\sin}^2}\\ &= \dfrac{1}{{\sin}^2}\\ &= {\csc}^2 \end{align*}\]
De même, on\(1+{\tan}^2 \theta={\sec}^2 \theta\) peut l'obtenir en réécrivant le côté gauche de cette identité en termes de sinus et de cosinus. Cela donne
\[\begin{align*} 1+{\tan}^2 \theta&= 1+{\left(\dfrac{\sin \theta}{\cos \theta}\right )}^2\qquad \text{Rewrite left side}\\ &= {\left (\dfrac{\cos \theta}{\cos \theta}\right )}^2+{\left (\dfrac{\sin \theta}{\cos \theta}\right)}^2\qquad \text{Write both terms with the common denominator}\\ &= \dfrac{{\cos}^2 \theta+{\sin}^2 \theta}{{\cos}^2 \theta}\\ &= \dfrac{1}{{\cos}^2 \theta}\\ &= {\sec}^2 \theta \end{align*}\]
Rappelons que nous avons déterminé quelles fonctions trigonométriques sont impaires et lesquelles sont paires. Le prochain ensemble d'identités fondamentales est l'ensemble des identités paires et impaires. Les identités paires associent la valeur d'une fonction trigonométrique à un angle donné à la valeur de la fonction à l'angle opposé (Tableau\(\PageIndex{2}\)).
| \(\tan(−\theta)=−\tan \theta\) | \(\sin(−\theta)=−\sin \theta\) | \(\cos(−\theta)=\cos \theta\) |
| \(\cot(−\theta)=−\cot \theta\) | \(\csc(−\theta)=−\csc \theta\) | \(\sec(−\theta)=\sec \theta\) |
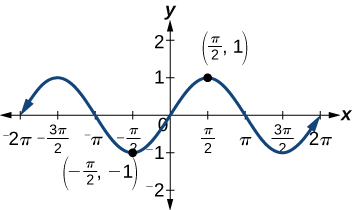
Rappelez-vous qu'une fonction étrange est une fonction dans laquelle,\(f(−x)= −f(x)\) pour tous\(x\), le domaine est désactivé. f. La fonction sinus est une fonction étrange parce que\(\sin(−\theta)=−\sin \theta\). Le graphe d'une fonction impaire est symétrique par rapport à l'origine. Par exemple, considérez les entrées correspondantes de\(\dfrac{\pi}{2}\) et\(−\dfrac{\pi}{2}\). La sortie de\(\sin\left (\dfrac{\pi}{2}\right )\) est opposée à la sortie de\(\sin \left (−\dfrac{\pi}{2}\right )\). Ainsi,
\[\begin{align*} \sin\left (\dfrac{\pi}{2}\right)&=1 \\[4pt] \sin\left (-\dfrac{\pi}{2}\right) &=-\sin\left (\dfrac{\pi}{2}\right) \\[4pt] &=-1 \end{align*}\]
Ceci est illustré dans la figure\(\PageIndex{2}\).
Rappelez-vous qu'une fonction paire est une fonction dans laquelle
\(f(−x)=f(x)\)pour tous\(x\) dans le domaine de\(f\)
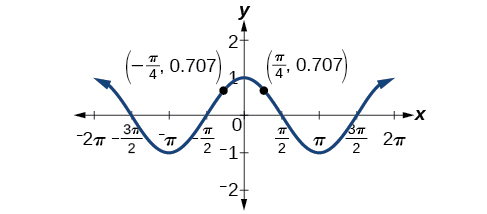
Le graphe d'une fonction paire est symétrique par rapport à l'axe y. La fonction cosinus est une fonction paire car\(\cos(−\theta)=\cos \theta\). Par exemple, considérez les entrées correspondantes\(\dfrac{\pi}{4}\) et\(−\dfrac{\pi}{4}\). La sortie de\(\cos\left (\dfrac{\pi}{4}\right)\) est identique à la sortie de\(\cos\left (−\dfrac{\pi}{4}\right)\). Ainsi,
\[\begin{align*} \cos\left (−\dfrac{\pi}{4}\right ) &=\cos\left (\dfrac{\pi}{4}\right) \\[4pt] &≈0.707 \end{align*}\]
Voir la figure\(\PageIndex{3}\).
Pour tous\(\theta\) ceux qui se situent respectivement dans le domaine des fonctions sinus et cosinus, on peut affirmer ce qui suit :
- Puisque\(\sin(−\theta)=−\sin \theta\), le sinus est une fonction étrange.
- Puisque\(\cos(−\theta)=\cos \theta\), le cosinus est une fonction uniforme.
Les autres identités paires découlent de la nature paire et impaire des fonctions sinus et cosinus. Par exemple, considérez l'identité tangente,\(\tan(−\theta)=−\tan \theta\). Nous pouvons interpréter la tangente d'un angle négatif comme
\[\tan (−\theta)=\dfrac{\sin (−\theta)}{\cos (−\theta)}=\dfrac{−\sin \theta}{\cos \theta}=−\tan \theta. \nonumber\]
La tangente est donc une fonction étrange, ce qui signifie que\(\tan(−\theta)=−\tan(\theta)\) pour tous\(\theta\) dans le domaine de la fonction tangente.
L'identité cotangente,\(\cot(−\theta)=−\cot \theta\), découle également des identités sinus et cosinus. Nous pouvons interpréter la cotangente d'un angle négatif comme
\[\cot(−\theta)=\dfrac{\cos(−\theta)}{\sin(−\theta)}=\dfrac{\cos \theta}{−\sin \theta}=−\cot \theta.\nonumber\]
La cotangente est donc une fonction étrange, ce qui signifie que\(\cot(−\theta)=−\cot(\theta)\) pour tous\(\theta\) dans le domaine de la fonction cotangente.
La fonction cosécante est l'inverse de la fonction sinusoïdale, ce qui signifie que la cosécante d'un angle négatif sera interprétée comme
\[\csc(−\theta)=\dfrac{1}{\sin(−\theta)}=\dfrac{1}{−\sin \theta}=−\csc \theta. \nonumber\]
La fonction cosécante est donc impaire.
Enfin, la fonction sécante est l'inverse de la fonction cosinus, et la sécante d'un angle négatif est interprétée comme
\[\sec(−\theta)=\dfrac{1}{\cos(−\theta)}=\dfrac{1}{\cos \theta}=\sec \theta. \nonumber\]
La fonction sécante est donc uniforme.
En résumé, seules deux des fonctions trigonométriques, le cosinus et la sécante, sont paires. Les quatre autres fonctions sont impaires, vérifiant les identités paires.
Le prochain ensemble d'identités fondamentales est l'ensemble des identités réciproques qui, comme leur nom l'indique, mettent en relation des fonctions trigonométriques réciproques les unes des autres. (Tableau\(\PageIndex{3}\)). Rappelons que nous avons rencontré ces identités pour la première fois lors de la définition de fonctions trigonométriques à angle droit en trigonométrie à angle droit.
| \(\sin \theta=\dfrac{1}{\csc \theta}\) | \(\csc \theta=\dfrac{1}{\sin \theta}\) |
| \(\cos \theta = \dfrac{1}{\sec \theta}\) | \(\sec \theta=\dfrac{1}{\cos \theta}\) |
| \(\tan \theta=\dfrac{1}{\cot \theta}\) | \(\cot \theta=\dfrac{1}{\tan \theta}\) |
Le dernier ensemble d'identités est l'ensemble des identités de quotient, qui définissent les relations entre certaines fonctions trigonométriques et peuvent être très utiles pour vérifier d'autres identités (Tableau\(\PageIndex{4}\)).
| \(\tan \theta=\dfrac{\sin \theta}{\cos \theta}\) | \(\cot \theta=\dfrac{\cos \theta}{\sin \theta}\) |
Les identités réciproques et quotientes sont dérivées des définitions des fonctions trigonométriques de base.
Les identités pythagoriciennes sont basées sur les propriétés d'un triangle droit.
\[{\cos}^2 \theta+{\sin}^2 \theta=1\]
\[1+{\cot}^2 \theta={\csc}^2 \theta\]
\[1+{\tan}^2 \theta={\sec}^2 \theta\]
Les identités paires et impaires relient la valeur d'une fonction trigonométrique à un angle donné à la valeur de la fonction à l'angle opposé.
\[\tan(−\theta)=−\tan \theta\]
\[\cot(−\theta)=−\cot \theta\]
\[\sin(−\theta)=−\sin \theta\]
\[\csc(−\theta)=−\csc \theta\]
\[\cos(−\theta)=\cos \theta\]
\[\sec(−\theta)=\sec \theta\]
Les identités réciproques définissent les réciproques des fonctions trigonométriques.
\[\sin \theta=\dfrac{1}{\csc \theta}\]
\[\cos \theta=\dfrac{1}{\sec \theta}\]
\[\tan \theta=\dfrac{1}{\cot \theta}\]
\[\csc \theta=\dfrac{1}{\sin \theta}\]
\[\sec \theta=\dfrac{1}{\cos \theta}\]
\[\cot \theta=\dfrac{1}{\tan \theta}\]
Les identités des quotients définissent la relation entre les fonctions trigonométriques.
\[\tan \theta=\dfrac{\sin \theta}{\cos \theta}\]
\[\cot \theta=\dfrac{\cos \theta}{\sin \theta}\]
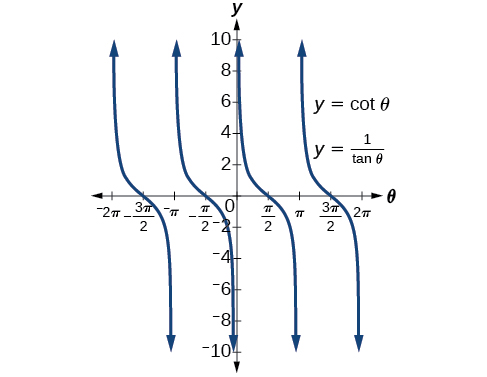
Tracez les deux côtés de l'identité\(\cot \theta=\dfrac{1}{\tan \theta}\). En d'autres termes, sur la calculatrice graphique, graphique\(y=\cot \theta\) et\(y=\dfrac{1}{\tan \theta}\).
Solution
Voir la figure\(\PageIndex{4}\).
Analyse
Nous ne voyons qu'un seul graphique car les deux expressions génèrent la même image. L'un est superposé à l'autre. C'est un bon moyen de prouver n'importe quelle identité. Si les deux expressions donnent le même graphe, il doit s'agir d'identités.
- Travaillez sur un côté de l'équation. Il est généralement préférable de commencer par le côté le plus complexe, car il est plus facile de simplifier que de construire.
- Recherchez des opportunités de factoriser des expressions, de mettre au carré un binôme ou d'ajouter des fractions.
- En notant quelles fonctions se trouvent dans l'expression finale, recherchez les opportunités d'utiliser les identités et d'effectuer les substitutions appropriées.
- Si ces étapes ne donnent pas le résultat souhaité, essayez de convertir tous les termes en sinus et en cosinus.
Vérifiez\(\tan \theta \cos \theta=\sin \theta\).
Solution
Nous allons commencer par le côté gauche, car c'est le côté le plus compliqué :
\[ \begin{align*} \tan \theta \cos \theta &=\left(\dfrac{\sin \theta}{\cos \theta}\right)\cos \theta \\[4pt] &=\sin \theta \end{align*}\]
Analyse
Cette identité était assez simple à vérifier, car elle ne nécessitait qu'une écriture\(\tan \theta\) en termes de\(\sin \theta\) et\(\cos \theta\).
Vérifiez l'identité\(\csc \theta \cos \theta \tan \theta=1\).
- Réponse
-
\[ \begin{align*} \csc \theta \cos \theta \tan \theta=\left(\dfrac{1}{\sin \theta}\right)\cos \theta\left(\dfrac{\sin \theta}{\cos \theta}\right) \\[4pt] & =\dfrac{\cos \theta}{\sin \theta}(\dfrac{\sin \theta}{\cos \theta}) \\[4pt] & =\dfrac{\sin \theta \cos \theta}{\sin \theta \cos \theta} \\[4pt] &=1 \end{align*}\]
Vérifiez l'équivalence suivante en utilisant les identités paires et impaires :
\((1+\sin x)[1+\sin(−x)]={\cos}^2 x\)
Solution
En travaillant sur le côté gauche de l'équation, nous avons
\( (1+\sin x)[1+\sin(−x)]=(1+\sin x)(1-\sin x)\)
Depuis
\[\begin{align*} \sin(-x)&= -\sin x \\ [5pt] &=1-{\sin}^2 x\qquad \text{Difference of squares} \\ [5pt] &={\cos}^2 x \\ {\cos}^2 x&= 1-{\sin}^2 x \\ \end{align*}\]
Vérifiez l'identité\(\dfrac{{\sec}^2 \theta−1}{{\sec}^2 \theta}={\sin}^2 \theta\)
Solution
Comme le côté gauche est plus compliqué, commençons par là.
\ [\ begin {align*}
\ dfrac {{\ sec} ^2 \ théta-1} {{\ sec} ^2 \ thêta} &= \ dfrac {({\ tan} ^2 \ thêta +1) -1} {{\ sec} ^2 \ thêta} \ \
{\ sec} ^2 \ theta&= {\ tan} ^2 \ thêta +1 \ \
&= \ dfrac frac {{\ tan} ^2 \ thêta} {{\ sec} ^2 \ thêta} \ \
&= {\ tan} ^2 \ thêta \ left (\ dfrac {1} {{\ sec} ^2 \ thêta} \ droite) \ \
&= {\ tan} ^2 \ thêta \ gauche ({\ cos} ^2 \ thêta \ droite) \ \
{\ cos} ^2 \ thêta&= \ dfrac {1} {{\ sec} ^2 \ thêta} \ \
&= \ left (\ dfrac {{\ sin} ^2 \ thêta} {\ cos} ^2 \ thêta} {\ cos} 2 \ thêta} \ right) \ \
{\ tan} ^2 \ theta&= \ dfrac {{\ sin} ^2 \ thêta} {{\ cos} ^2 \ thêta } \ \
&= {\ sin} ^2 \ thêta
\ end {align*} \]
Il existe plusieurs façons de vérifier une identité. Voici une autre possibilité. Encore une fois, nous pouvons commencer par le côté gauche.
\[\begin{align*} \dfrac{{\sec}^2 \theta-1}{{\sec}^2 \theta}&= \dfrac{{\sec}^2 \theta}{{\sec}^2 \theta}-\dfrac{1}{{\sec}^2 \theta}\\ &= 1-{\cos}^2 \theta\\ &= {\sin}^2 \theta \end{align*}\]
Analyse
Dans la première méthode, nous avons utilisé l'identité\({\sec}^2 \theta={\tan}^2 \theta+1\) et avons continué à simplifier. Dans la deuxième méthode, nous divisons la fraction en plaçant les deux termes du numérateur au-dessus du dénominateur commun. Ce problème montre qu'il existe plusieurs façons de vérifier une identité. Faire preuve de créativité peut parfois simplifier une procédure. Tant que les substitutions sont correctes, la réponse sera la même.
Montrez ça\(\dfrac{\cot \theta}{\csc \theta}=\cos \theta\).
- Réponse
-
\[\begin{align*} \dfrac{\cot \theta}{\csc \theta}&= \dfrac{\tfrac{\cos \theta}{\sin \theta}}{\dfrac{1}{\sin \theta}}\\ &= \dfrac{\cos \theta}{\sin \theta}\cdot \dfrac{\sin \theta}{1}\\ &= \cos \theta \end{align*}\]
Créez une identité pour l'expression\(2 \tan \theta \sec \theta\) en la réécrivant strictement en termes de sinus.
Solution
Il existe plusieurs façons de commencer, mais nous utiliserons ici le quotient et les identités réciproques pour réécrire l'expression :
\[\begin{align*} 2 \tan \theta \sec \theta&= 2\left (\dfrac{\sin \theta}{\cos \theta}\right )\left(\dfrac{1}{\cos \theta}\right )\\ &= \dfrac{2\sin \theta}{{\cos}^2 \theta}\\ &= \dfrac{2\sin \theta}{1-{\sin}^2 \theta}\qquad \text{Substitute } 1-{\sin}^2 \theta \text{ for } {\cos}^2 \theta \end{align*}\]
Ainsi,
\(2 \tan \theta \sec \theta=\dfrac{2 \sin \theta}{1−{\sin}^2 \theta}\)
Vérifiez l'identité :
\(\dfrac{{\sin}^2(−\theta)−{\cos}^2(−\theta)}{\sin(−\theta)−\cos(−\theta)}=\cos \theta−\sin \theta\)
Solution
Commençons par le côté gauche et simplifions-le :
\[\begin{align*} \dfrac{{\sin}^2(-\theta)-{\cos}^2(-\theta)}{\sin(-\theta)-\cos(-\theta)}&= \dfrac{{[\sin(-\theta)]}^2-{[\cos(-\theta)]}^2}{\sin(-\theta)-\cos(-\theta)}\\ &= \dfrac{{(-\sin \theta)}^2-{(\cos \theta)}^2}{-\sin \theta -\cos \theta} \;\; \; , \sin(-x) = -\sin\space x\text { and } \cos(-x)=\cos \space x\\ &= \dfrac{{(\sin \theta)}^2-{(\cos \theta)}^2}{-\sin \theta -\cos \theta}\qquad \text{Difference of squares}\\ &= \dfrac{(\sin \theta-\cos \theta)(\sin \theta+\cos \theta)}{-(\sin \theta+\cos \theta)}\\ &= \cos \theta-\sin \theta \end{align*}\]
Vérifiez l'identité\(\dfrac{{\sin}^2 \theta−1}{\tan \theta \sin \theta−\tan \theta}=\dfrac{\sin \theta+1}{\tan \theta}\).
- Réponse
-
\[\begin{align*} \dfrac{{\sin}^2 \theta-1}{\tan \theta \sin \theta-\tan \theta}&= \dfrac{(\sin \theta +1)(\sin \theta -1)}{\tan \theta(\sin \theta -1)}\\ &= \dfrac{\sin \theta+1}{\tan \theta} \end{align*}\]
Vérifiez l'identité :\((1−{\cos}^2 x)(1+{\cot}^2 x)=1\).
Solution
\[\begin{align*} (1-{\cos}^2 x)(1+{\cot}^2 x)&= (1-{\cos}^2 x)\left(1+\dfrac{{\cos}^2 x}{{\sin}^2 x}\right)\\ &= (1-{\cos}^2 x)\left(\dfrac{{\sin}^2 x}{{\sin}^2 x}+\dfrac{{\cos}^2 x}{{\sin}^2 x}\right )\qquad \text{Find the common denominator}\\ &= (1-{\cos}^2 x)\left(\dfrac{{\sin}^2 x +{\cos}^2 x}{{\sin}^2 x}\right)\\ &= ({\sin}^2 x)\left (\dfrac{1}{{\sin}^2 x}\right )\\ &= 1 \end{align*}\]
Utilisation de l'algèbre pour simplifier les expressions trigonométriques
Nous avons vu que l'algèbre est très importante pour vérifier les identités trigonométriques, mais qu'elle est tout aussi essentielle pour simplifier les expressions trigonométriques avant de les résoudre. La connaissance des propriétés et des formules de base de l'algèbre, telles que la formule de différence de carrés, la formule des carrés parfaits ou la substitution, simplifiera le travail lié aux expressions trigonométriques et aux équations.
Par exemple, l'équation\((\sin x+1)(\sin x−1)=0\) ressemble à l'équation\((x+1)(x−1)=0\), qui utilise la forme factorielle de la différence des carrés. L'utilisation de l'algèbre permet de trouver une solution simple et familière. Nous pouvons définir chaque facteur égal à zéro et résoudre. C'est un exemple de reconnaissance de modèles algébriques dans des expressions ou des équations trigonométriques.
Un autre exemple est la formule de différence de carrés\(a^2−b^2=(a−b)(a+b)\), largement utilisée dans de nombreux domaines autres que les mathématiques, tels que l'ingénierie, l'architecture et la physique. Nous pouvons également créer notre propre identité en élargissant continuellement une expression et en effectuant les substitutions appropriées. L'utilisation de propriétés et de formules algébriques facilite la compréhension et la résolution de nombreuses équations trigonométriques.
Écrivez l'expression trigonométrique suivante sous forme d'expression algébrique :\(2{\cos}^2 \theta+\cos \theta−1\).
Solution
Notez que le modèle affiché a la même forme qu'une expression quadratique standard,\(ax^2+bx+c\). Maintenant\(\cos \theta=x\), nous pouvons réécrire l'expression comme suit :
\(2x^2+x−1\)
Cette expression peut être prise en compte comme\((2x+1)(x−1)\). Si elle était fixée à zéro et que nous voulions résoudre l'équation, nous utiliserions la propriété du facteur zéro et résoudrions chaque facteur pour\(x\). À ce stade, nous remplacerions\(x\) par\(\cos \theta\) et résoudrions\(\theta\).
Réécrivez l'expression trigonométrique en utilisant la différence de carrés :\(4{cos}^2 \theta−1\).
Solution
Notez que le coefficient et l'expression trigonométrique du premier terme sont au carré et que le carré du chiffre 1 est 1. C'est la différence des carrés.
\[\begin{align*} 4{\cos}^2 \theta-1&= {(2\cos \theta)}^2-1\\ &= (2\cos \theta-1)(2\cos \theta+1) \end{align*}\]
Analyse
Si cette expression était écrite sous la forme d'un ensemble d'équations égal à zéro, nous pourrions résoudre chaque facteur en utilisant la propriété du facteur zéro. Nous pouvons également utiliser la substitution comme nous l'avons fait dans le problème précédent et laisser\(\cos \theta=x\), réécrire l'expression en tant que\(4x^2−1\) facteur\((2x−1)(2x+1)\). Remplacez ensuite\(x\) par\(\cos \theta\) et résolvez l'angle.
Réécrivez l'expression trigonométrique en utilisant la différence de carrés :\(25−9{\sin}^2 \theta\).
- Réponse
-
Il s'agit d'une formule de différence de carrés :\(25−9{\sin}^2 \theta=(5−3\sin \theta)(5+3\sin \theta)\).
Simplifiez l'expression en réécrivant et en utilisant des identités :
\({\csc}^2 \theta−{\cot}^2 \theta\)
Solution
Nous pouvons commencer par l'identité pythagoricienne.
\[\begin{align*} 1+{\cot}^2 \theta&= {\csc}^2 \theta\\ \text{Now we can simplify by substituting } 1+{\cot}^2 \theta \text{ for } {\csc}^2 \theta\\ {\csc}^2 \theta-{\cot}^2 \theta&= 1+{\cot}^2 \theta-{\cot}^2 \theta\\ &= 1 \end{align*}\]
Utilisez des techniques algébriques pour vérifier l'identité :\(\dfrac{\cos \theta}{1+\sin \theta}=\dfrac{1−\sin \theta}{\cos \theta}\).
(Conseil : multipliez le numérateur et le dénominateur sur le côté gauche par\(1−\sin \theta\).)
- Réponse
-
\[\begin{align*} \dfrac{\cos \theta}{1+\sin \theta}\left(\dfrac{1-\sin \theta}{1-\sin \theta}\right)&= \dfrac{\cos \theta (1-\sin \theta)}{1-{\sin}^2 \theta}\\ &= \dfrac{\cos \theta (1-\sin \theta)}{{\cos}^2 \theta}\\ &= \dfrac{1-\sin \theta}{\cos \theta} \end{align*}\]
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur les identités trigonométriques fondamentales.
- Identités trigonométriques fondamentales
- Vérification des identités trigonométriques
Équations clés
| Identités pythagoriciennes |
\({\cos}^2 \theta+{\sin}^2 \theta=1\) \(1+{\cot}^2 \theta={\csc}^2 \theta\) \(1+{\tan}^2 \theta={\sec}^2 \theta\) |
| Des identités encore plus étranges |
\(\tan(−\theta)=-\tan \theta\) \(\cot(-\theta)=-\cot \theta\) \(\sin(-\theta)=-\sin \theta\) \(\csc(-\theta)=-\csc \theta\) \(\cos(-\theta)=\cos \theta\) \(\sec(-\theta)=\sec \theta\) |
| Identités réciproques |
\(\sin \theta=\dfrac{1}{\csc \theta}\) \(\cos \theta=\dfrac{1}{\sec \theta}\) \(\tan \theta=\dfrac{1}{\cot \theta}\) \(\csc \theta=\dfrac{1}{\sin \theta}\) \(\sec \theta=\dfrac{1}{\cos \theta}\) \(\cot \theta=\dfrac{1}{\tan \theta}\) |
| Identités de quotient |
\(\tan \theta=\dfrac{\sin \theta}{\cos \theta}\) \(\cot \theta=\dfrac{\cos \theta}{\sin \theta}\) |
Concepts clés
- Il existe plusieurs manières de représenter une expression trigonométrique. La vérification des identités montre comment les expressions peuvent être réécrites pour simplifier un problème.
- Le fait de représenter graphiquement les deux côtés d'une identité permet de la vérifier. Voir l'exemple\(\PageIndex{1}\).
- Simplifier un côté de l'équation pour qu'il soit égal à l'autre est une autre méthode pour vérifier une identité. Voir Exemple\(\PageIndex{2}\) et Exemple\(\PageIndex{3}\).
- L'approche utilisée pour vérifier une identité dépend de la nature de l'identité. Il est souvent utile de commencer par le côté le plus complexe de l'équation. Voir l'exemple\(\PageIndex{4}\).
- Nous pouvons créer une identité puis la vérifier. Voir l'exemple\(\PageIndex{5}\).
- La vérification d'une identité peut impliquer l'algèbre avec les identités fondamentales. Voir Exemple\(\PageIndex{6}\) et Exemple\(\PageIndex{7}\).
- Les techniques algébriques peuvent être utilisées pour simplifier les expressions trigonométriques. Nous utilisons des techniques algébriques tout au long de ce texte, car elles constituent les règles fondamentales des mathématiques. Voir Exemple\(\PageIndex{8}\)\(\PageIndex{9}\), Exemple et Exemple\(\PageIndex{10}\).


