8.3 : Fonctions trigonométriques inverses

Objectifs d'apprentissage

• Comprenez et utilisez les fonctions sinus, cosinus et tangente inverses.
• Déterminez la valeur exacte des expressions impliquant les fonctions sinus, cosinus et tangente inverses.
• Utilisez une calculatrice pour évaluer les fonctions trigonométriques inverses.
• Trouvez les valeurs exactes des fonctions composites à l'aide de fonctions trigonométriques inverses.

Pour tout triangle droit, étant donné un autre angle et la longueur d'un côté, nous pouvons déterminer quels sont les autres angles et côtés. Mais que se passerait-il si l'on ne nous donnait que les deux côtés d'un triangle droit ? Nous avons besoin d'une procédure qui nous amène d'un rapport de côtés à un angle. C'est là que la notion d'inverse d'une fonction trigonométrique entre en jeu. Dans cette section, nous allons explorer les fonctions trigonométriques inverses.

Compréhension et utilisation des fonctions sinus, cosinus et tangente inverses

Pour utiliser des fonctions trigonométriques inverses, nous devons comprendre qu'une fonction trigonométrique inverse « annule » ce que « fait » la fonction trigonométrique d'origine, comme c'est le cas pour toute autre fonction et son inverse. En d'autres termes, le domaine de la fonction inverse est la plage de la fonction d'origine, et vice versa, comme résumé dans la Figure$\PageIndex{1}$.

Figurine$\PageIndex{1}$

Par exemple, si$f(x)=\sin\space x$, alors nous écririons$f^{−1}(x)={\sin}^{−1}x$. Sachez que cela${\sin}^{−1}x$ ne veut pas dire$\dfrac{1}{\sin\space x}$. Les exemples suivants illustrent les fonctions trigonométriques inverses :

• Depuis$\sin\left(\dfrac{\pi}{6}\right)=\dfrac{1}{2}$, alors$\dfrac{\pi}{6}={\sin}^{−1}\left(\dfrac{1}{2}\right)$.
• Depuis$\cos(\pi)=−1$, alors$\pi={\cos}^{−1}(−1)$.
• Depuis$\tan\left (\dfrac{\pi}{4}\right )=1$, alors$\dfrac{\pi}{4}={\tan}^{−1}(1)$.

Dans les sections précédentes, nous avons évalué les fonctions trigonométriques à différents angles, mais nous avons parfois besoin de savoir quel angle produirait une valeur de sinus, de cosinus ou de tangente spécifique. Pour cela, nous avons besoin de fonctions inverses. Rappelez-vous que, pour une fonction biunivoque, si$f(a)=b$, alors une fonction inverse satisferait$f^{−1}(b)=a$.

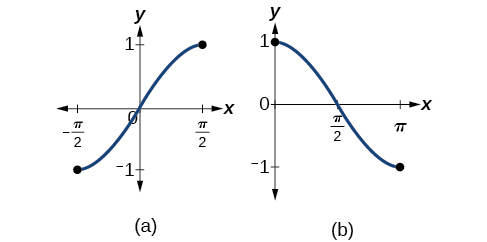
N'oubliez pas que les fonctions sinus, cosinus et tangente ne sont pas des fonctions biunivoques. Le graphe de chaque fonction échouerait au test de la ligne horizontale. En fait, aucune fonction périodique ne peut être biunivoque car chaque sortie de sa plage correspond à au moins une entrée dans chaque période, et il existe un nombre infini de périodes. Comme pour les autres fonctions qui ne sont pas un-à-un, nous devrons restreindre le domaine de chaque fonction pour obtenir une nouvelle fonction biunivoque. Nous choisissons un domaine pour chaque fonction qui inclut le numéro 0. La figure$\PageIndex{2}$ montre le graphe de la fonction sinusoïdale limitée à$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$ et le graphe de la fonction cosinus limitée à$[ 0,\pi ]$.

Figure$\PageIndex{2}$ : (a) Fonction sinusoïdale sur un domaine restreint de$\left[ −\dfrac{\pi}{2}, \dfrac{\pi}{2} \right]$ ; (b) Fonction cosinus sur un domaine restreint de$[ 0,\pi ]$

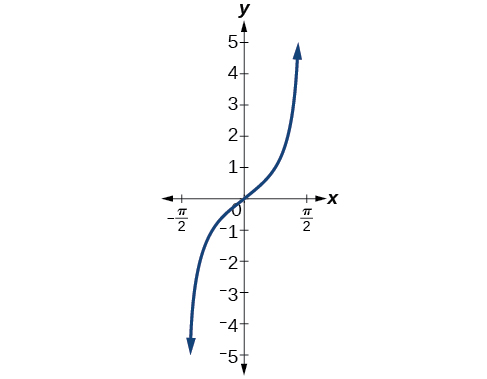
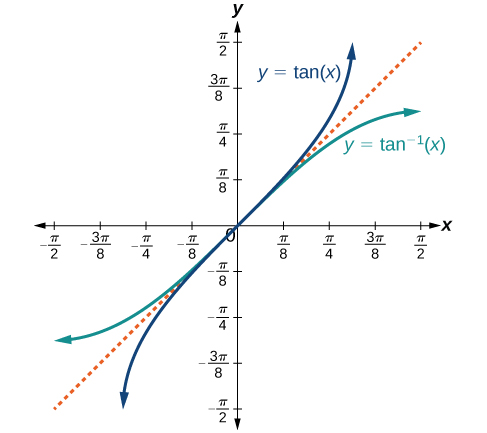
La figure$\PageIndex{3}$ montre le graphique de la fonction tangente limitée à$\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$.

Figure$\PageIndex{3}$ : Fonction tangente sur un domaine restreint de$\left (−\dfrac{\pi}{2},\dfrac{\pi}{2}\right )$

Ces choix classiques pour le domaine restreint sont quelque peu arbitraires, mais ils présentent des caractéristiques importantes et utiles. Chaque domaine inclut l'origine et certaines valeurs positives et, plus important encore, chacun aboutit à une fonction biunivoque inversible. Le choix classique pour le domaine restreint de la fonction tangente possède également la propriété utile de s'étendre d'une asymptote verticale à la suivante au lieu d'être divisée en deux parties par une asymptote.

Sur ces domaines restreints, nous pouvons définir les fonctions trigonométriques inverses.

• La fonction sinusoïdale inverse$y={\sin}^{−1}x$ signifie$x=\sin\space y$. La fonction sinusoïdale inverse est parfois appelée fonction arcsine et notée$\arcsin\space x$.

  $y={\sin}^{−1}x$possède un domaine$[−1,1]$ et une plage$\left[−\frac{\pi}{2},\frac{\pi}{2}\right]$

• La fonction cosinus inverse$y={\cos}^{−1}x$ signifie$x=\cos\space y$. La fonction cosinus inverse est parfois appelée fonction arccosine et notée$\arccos\space x$.

  $y={\cos}^{−1}x$possède un domaine$[−1,1]$ et une plage$[0,π]$

• La fonction tangente inverse$y={\tan}^{−1}x$ signifie$x=\tan\space y$. La fonction tangente inverse est parfois appelée fonction arctangente et notée$\arctan\space x$.

  $y={\tan}^{−1}x$possède un domaine$(−\infty,\infty)$ et une plage$\left(−\frac{\pi}{2},\frac{\pi}{2}\right)$

Les graphes des fonctions inverses sont présentés dans les figures$\PageIndex{4}$ -$\PageIndex{6}$. Notez que la sortie de chacune de ces fonctions inverses est un nombre, un angle en radian. Nous voyons qu'il${\sin}^{−1}x$ a un domaine$[ −1,1 ]$ et une plage$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$,${\cos}^{−1}x$ un domaine$[ −1,1 ]$ et une plage$[0,\pi]$, et qu'il${\tan}^{−1}x$ a un domaine de tous les nombres réels et de toutes les plages$\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$. Pour trouver le domaine et la plage des fonctions trigonométriques inverses, changez le domaine et la plage des fonctions d'origine. Chaque graphe de la fonction trigonométrique inverse est le reflet du graphe de la fonction d'origine autour de la droite$y=x$.

Figure$\PageIndex{4}$ : La fonction sinusoïdale et la fonction sinusoïdale inverse (ou arcsinus)

Figure$\PageIndex{5}$ : La fonction cosinus et la fonction cosinus inverse (ou arccosine)

Figure$\PageIndex{6}$ : La fonction tangente et la fonction tangente inverse (ou arctangente)

RELATIONS POUR LES FONCTIONS SINUS, COSINUS ET TANGENTES INVERSES

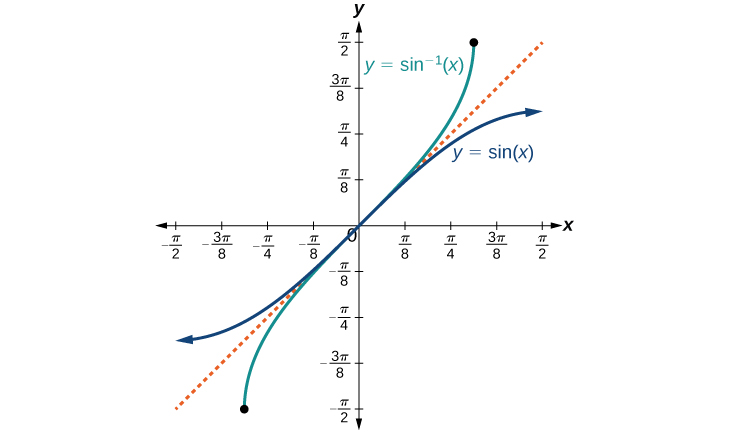
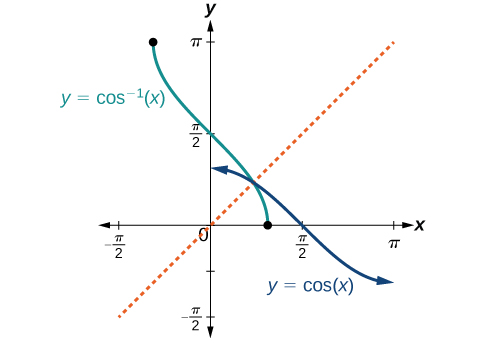
Pour les angles compris dans l'intervalle$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$, si$\sin y=x$, alors${\sin}^{−1}x=y$.

Pour les angles compris dans l'intervalle$[ 0,\pi ]$, si$\cos y=x$, alors${\cos}^{−1}x=y$.

Pour les angles compris dans l'intervalle$\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right )$, si$\tan y=x$, alors${\tan}^{−1}x=y$.

Exemple$\PageIndex{1}$: Writing a Relation for an Inverse Function

Étant donné$\sin\left(\dfrac{5\pi}{12}\right)≈0.96593$, écrivez une relation impliquant le sinus inverse.

Solution

Utilisez la relation pour le sinus inverse. Si$\sin y=x$, alors${\sin}^{−1}x=y$.

Dans ce problème$x=0.96593$, et$y=\dfrac{5\pi}{12}$.

${\sin}^{−1}(0.96593)≈\dfrac{5\pi}{12}$

Exercice$\PageIndex{1}$

Étant donné$\cos(0.5)≈0.8776$, écrivez une relation impliquant le cosinus inverse.

Réponse

$\arccos(0.8776)≈0.5$

Déterminer la valeur exacte des expressions impliquant les fonctions sinus, cosinus et tangente inverses

Maintenant que nous pouvons identifier les fonctions inverses, nous allons apprendre à les évaluer. Pour la plupart des valeurs de leurs domaines, nous devons évaluer les fonctions trigonométriques inverses à l'aide d'une calculatrice, en interpolant à partir d'un tableau ou en utilisant une autre technique numérique. Tout comme nous l'avons fait pour les fonctions trigonométriques d'origine, nous pouvons donner des valeurs exactes pour les fonctions inverses lorsque nous utilisons les angles spéciaux, en particulier$\dfrac{\pi}{6}$ (30°),$\dfrac{\pi}{4}$ (45°) et$\dfrac{\pi}{3}$ (60°), et leurs réflexions dans d'autres quadrants.

À partir d'une valeur d'entrée « spéciale », évaluez une fonction trigonométrique inverse.

1. Détermine l'angle$x$ pour lequel la fonction trigonométrique d'origine possède une sortie égale à l'entrée donnée pour la fonction trigonométrique inverse.
2. S'il ne$x$ se trouve pas dans la plage définie de l'inverse, trouvez un autre angle$y$ qui se trouve dans la plage définie et qui possède le même sinus, cosinus ou tangente que$x$, selon ce qui correspond à la fonction inverse donnée.

Exemple$\PageIndex{2}$: Evaluating Inverse Trigonometric Functions for Special Input Values

Évaluez chacun des éléments suivants.

1. ${\sin}^{−1}\left(\dfrac{1}{2}\right)$
2. ${\sin}^{−1}\left(−\dfrac{\sqrt{2}}{2}\right)$
3. ${\cos}^{−1}\left(−\dfrac{\sqrt{3}}{2}\right)$
4. ${\tan}^{−1}(1)$

Solution

1. L'évaluation${\sin}^{−1}\left(\dfrac{1}{2}\right)$ revient à déterminer l'angle qui aurait une valeur sinusoïdale de$\dfrac{1}{2}$. En d'autres termes, quel angle$x$ satisferait$\sin(x)=\dfrac{1}{2}$ ? Plusieurs valeurs peuvent satisfaire cette relation, telles que$\dfrac{\pi}{6}$ et$\dfrac{5\pi}{6}$, mais nous savons que nous avons besoin de l'angle dans l'intervalle$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$, donc la réponse sera${\sin}^{−1}\left (\dfrac{1}{2}\right)=\dfrac{\pi}{6}$. N'oubliez pas que l'inverse est une fonction, donc pour chaque entrée, nous obtiendrons exactement une sortie.
2. Pour évaluer${\sin}^{−1}\left(−\dfrac{\sqrt{2}}{2}\right)$, nous savons que$\dfrac{5\pi}{4}$ les$\dfrac{7\pi}{4}$ deux ont une valeur sinusoïdale de$-\dfrac{\sqrt{2}}{2}$, mais aucune n'est comprise dans l'intervalle$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$. Pour cela, nous avons besoin de l'angle négatif coterminal avec$\dfrac{7\pi}{4}$ :${\sin}^{−1}\left(−\dfrac{\sqrt{2}}{2}\right)=−\dfrac{\pi}{4}$.
3. Pour évaluer${\cos}^{−1}\left(−\dfrac{\sqrt{3}}{2}\right)$, nous recherchons un angle dans l'intervalle$[ 0,\pi ]$ avec une valeur de cosinus de$-\dfrac{\sqrt{3}}{2}$. L'angle qui répond à cela est${\cos}^{−1}\left(−\dfrac{\sqrt{3}}{2}\right)=\dfrac{5\pi}{6}$.
4. En évaluant${\tan}^{−1}(1)$, nous recherchons un angle dans l'intervalle$\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$ avec une valeur tangente de$1$. Le bon angle est${\tan}^{−1}(1)=\dfrac{\pi}{4}$.

Exercice$\PageIndex{2}$

Évaluez chacun des éléments suivants.

1. ${\sin}^{−1}(−1)$
2. ${\tan}^{−1}(−1)$
3. ${\cos}^{−1}(−1)$
4. ${\cos}^{−1}\left(\dfrac{1}{2}\right)$

Répondez à une

$-\dfrac{\pi}{2}$

Réponse b

$-\dfrac{\pi}{4}$

Réponse c

$\pi$

Réponse d

$\dfrac{\pi}{3}$

Utilisation d'une calculatrice pour évaluer les fonctions trigonométriques inverses

Pour évaluer les fonctions trigonométriques inverses qui n'impliquent pas les angles spéciaux discutés précédemment, nous devrons utiliser une calculatrice ou un autre type de technologie. La plupart des calculatrices scientifiques et des applications d'émulation de calculatrices disposent de touches ou de boutons spécifiques pour les fonctions du sinus inverse, du cosinus et de la tangente. Ils peuvent être étiquetés, par exemple, SIN-1, ARCSIN ou ASIN.

Dans le chapitre précédent, nous avons utilisé la trigonométrie sur un triangle droit afin de déterminer les côtés d'un triangle donné d'un côté et d'un angle supplémentaire. À l'aide des fonctions trigonométriques inverses, nous pouvons résoudre les angles d'un triangle droit à deux côtés, et nous pouvons utiliser une calculatrice pour trouver les valeurs à plusieurs décimales.

Dans ces exemples et exercices, les réponses seront interprétées comme des angles et nous les utiliserons$\theta$ comme variable indépendante. La valeur affichée sur le calculateur peut être en degrés ou en radians. Veillez donc à définir le mode approprié à l'application.

Exemple$\PageIndex{3}$: Evaluating the Inverse Sine on a Calculator

Évaluez${\sin}^{−1}(0.97)$ en utilisant une calculatrice.

Solution

Comme la sortie de la fonction inverse est un angle, le calculateur nous donnera une valeur en degrés en mode degrés et une valeur en radian en mode radian. Les calculateurs utilisent également les mêmes restrictions de domaine sur les angles que nous utilisons.

En mode radian,${\sin}^{−1}(0.97)≈1.3252$. En mode degrés,${\sin}^{−1}(0.97)≈75.93°$. Notez qu'en calcul et au-delà, nous utiliserons des radians dans presque tous les cas.

Exercice$\PageIndex{3}$

Évaluez${\cos}^{−1}(−0.4)$ en utilisant une calculatrice.

Réponse

$1.9823$ou$113.578^{\circ}$

À partir des deux côtés d'un triangle droit, comme celui illustré à la Figure 8.4.7, trouvez un angle.

Figurine$\PageIndex{7}$

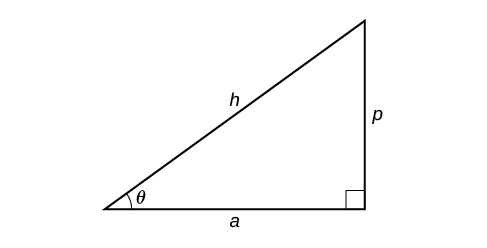
1. Si un côté donné est l'hypoténuse de la longueur$h$ et que le côté de la longueur$a$ adjacent à l'angle souhaité est donné, utilisez l'équation$\theta={\cos}^{−1}\left(\dfrac{a}{h}\right)$.
2. Si un côté donné est l'hypoténuse de la longueur$h$ et que le côté de la longueur$p$ opposé à l'angle souhaité est donné, utilisez l'équation$\theta={\sin}^{−1}\left(\dfrac{p}{h}\right)$.
3. Si les deux jambes (les côtés adjacents à l'angle droit) sont données, utilisez l'équation$\theta={\tan}^{−1}\left(\dfrac{p}{a}\right)$.

Exemple$\PageIndex{4}$: Applying the Inverse Cosine to a Right Triangle

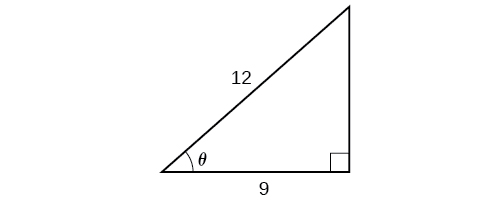
Résolvez le triangle de la figure$\PageIndex{8}$ pour l'angle$\theta$.

Figurine$\PageIndex{8}$

Solution

Comme nous connaissons l'hypoténuse et le côté adjacent à l'angle, il est logique que nous utilisions la fonction cosinus.

$$\begin{align*} \cos \theta&= \dfrac{9}{12}\\ \theta&= {\cos}^{-1}\left(\dfrac{9}{12}\right)\qquad \text{Apply definition of the inverse}\\ \theta&\approx 0.7227\qquad \text{or about } 41.4096^{\circ} \text{ Evaluate} \end{align*}$$

Exercice$\PageIndex{4}$

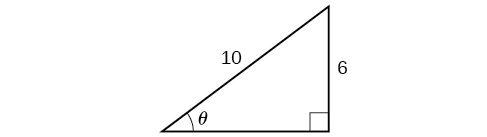
Résolvez le triangle de la figure$\PageIndex{9}$ pour l'angle$\theta$.

Figurine$\PageIndex{9}$

Réponse

${\sin}^{−1}(0.6)=36.87°=0.6435$radians

Trouver des valeurs exactes de fonctions composites à l'aide de fonctions trigonométriques inverses

Il y a des moments où nous devons composer une fonction trigonométrique avec une fonction trigonométrique inverse. Dans ces cas, nous pouvons généralement trouver des valeurs exactes pour les expressions résultantes sans recourir à une calculatrice. Même lorsque l'entrée de la fonction composite est une variable ou une expression, nous pouvons souvent trouver une expression pour la sortie. Pour aider à trier les différents cas,$f(x)$$g(x)$ supposons deux fonctions trigonométriques différentes appartenant à l'ensemble {$\sin(x)$,$\cos(x)$,$\tan(x)$} et laissez$f^{-1}(y)$ et$g^{-1}(y)$ soyez leurs inverses.

Évaluation de la composition du formulaire$f(f^{-1}(y))$ et$f^{-1}(f(x))$

Pour toute fonction trigonométrique,$f(f^{-1}(y))=y$ pour toutes les personnes$y$ se trouvant dans le domaine approprié pour la fonction donnée. Cela découle de la définition de l'inverse et du fait que la plage de$f$ a été définie comme étant identique au domaine de$f^{−1}$. Cependant, nous devons être un peu plus prudents avec les expressions de la forme$f^{-1}(f(x))$.

COMPOSITIONS D'UNE FONCTION TRIGONOMÉTRIQUE ET DE SON INVERSE

$$\begin{align*} \sin({\sin}^{-1}x)&= x\qquad \text{for } -1\leq x\leq 1\\ \cos({\cos}^{-1}x)&= x\qquad \text{for } -1\leq x\leq 1\\ \tan({\tan}^{-1}x)&= x\qquad \text{for } -\infty<x<\infty\\ {\sin}^{-1}(\sin x)&= x\qquad \text{only for } -\dfrac{\pi}{2}\leq x\leq \dfrac{\pi}{2}\\ {\cos}^{-1}(\cos x)&= x\qquad \text{only for } 0\leq x\leq \pi\\ {\tan}^{-1}(\tan x)& =x\qquad \text{only for } -\dfrac{\pi}{2}< x< \dfrac{\pi}{2} \end{align*}$$

QUESTIONS-RÉPONSES

Est-ce exact${\sin}^{−1}(\sin x)=x$ ?

Non Cette équation est correcte si x appartient au domaine restreint$\left[−\dfrac{\pi}{2},\dfrac{\pi}{2}\right]$, mais un sinus est défini pour toutes les valeurs d'entrée réelles, et$x$ en dehors de l'intervalle restreint, l'équation n'est pas correcte car son inverse renvoie toujours une valeur dans$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$. La situation est similaire pour le cosinus et la tangente et leurs inverses. Par exemple,${\sin}^{−1}\left(\sin\left(\dfrac{3\pi}{4}\right)\right)=\dfrac{\pi}{4}$.

Étant donné une expression de la forme$f^{-1}(f(\theta))$ where $f(\theta)=\sin \theta$, $\cos \theta$, or $\tan \theta$, evaluate.

1. S'il$\theta$ se trouve dans le domaine restreint de$f$, alors$f^{−1}(f(\theta))=\theta$.
2. Si ce n'est pas le cas, trouvez un angle$\phi$ dans le domaine restreint off f tel que$f(\phi)=f(\theta)$. Alors$f^{−1}(f(\theta))=\phi$.

Exemple$\PageIndex{5}$: Using Inverse Trigonometric Functions

Évaluez les éléments suivants :

1. ${\sin}^{−1}\left (\sin \left(\dfrac{\pi}{3}\right )\right )$
2. ${\sin}^{−1}\left (\sin \left(\dfrac{2\pi}{3}\right )\right )$
3. ${\cos}^{−1}\left (\cos \left (\dfrac{2\pi}{3}\right )\right )$
4. ${\cos}^{−1}\left (\cos \left (−\dfrac{\pi}{3}\right )\right )$

Solution

1. $\dfrac{\pi}{3}$est dedans$\left[−\dfrac{\pi}{2},\dfrac{\pi}{2}\right]$, donc${\sin}^{−1}\left(\sin\left(\dfrac{\pi}{3}\right)\right)=\dfrac{\pi}{3}$.
2. $\dfrac{2\pi}{3}$n'est pas$\left[−\dfrac{\pi}{2},\dfrac{\pi}{2}\right]$ là$sin\left(\dfrac{2\pi}{3}\right)=sin\left(\dfrac{\pi}{3}\right)$, mais donc${\sin}^{−1}\left(\sin\left(\dfrac{2\pi}{3}\right)\right)=\dfrac{\pi}{3}$.
3. $\dfrac{2\pi}{3}$est dedans$[ 0,\pi ]$, donc${\cos}^{−1}\left(\cos\left(\dfrac{2\pi}{3}\right)\right)=\dfrac{2\pi}{3}$.
4. $-\dfrac{\pi}{3}$n'est pas dedans$[ 0,\pi ]$, mais$\cos\left(−\dfrac{\pi}{3}\right)=\cos\left(\dfrac{\pi}{3}\right)$ parce que le cosinus est une fonction paire. $\dfrac{\pi}{3}$est dedans$[ 0,\pi ]$, donc${\cos}^{−1}\left(\cos\left(−\dfrac{\pi}{3}\right)\right)=\dfrac{\pi}{3}$.

Exercice$\PageIndex{5}$

Évaluez${\tan}^{−1}\left(\tan\left(\dfrac{\pi}{8}\right)\right)$ et${\tan}^{−1}\left(\tan\left(\dfrac{11\pi}{9}\right)\right)$.

Réponse

$\dfrac{\pi}{8}$;$\dfrac{2\pi}{9}$

Évaluation de la composition du formulaire$f^{-1}(g(x))$

Maintenant que nous pouvons composer une fonction trigonométrique avec son inverse, nous pouvons explorer comment évaluer la composition d'une fonction trigonométrique et l'inverse d'une autre fonction trigonométrique. Nous allons commencer par les compositions du formulaire$f^{-1}(g(x))$. Pour des valeurs spéciales de$x$, nous pouvons évaluer exactement la fonction interne puis la fonction inverse externe. Cependant, nous pouvons trouver une approche plus générale en examinant la relation entre les deux angles aigus d'un triangle droit où se trouve l'un$\theta$, créant l'autre.$\dfrac{\pi}{2}−\theta$ Considérez le sinus et le cosinus de chaque angle du triangle droit sur la figure$\PageIndex{10}$.

Figure$\PageIndex{10}$ : Triangle droit illustrant les relations de cofonctions

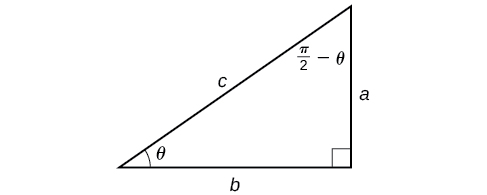
Parce$\cos \theta=\dfrac{b}{c}=sin\left(\dfrac{\pi}{2}−\theta\right)$ que nous l'${\sin}^{−1}(\cos \theta)=\dfrac{\pi}{2}−\theta$avons$0≤\theta≤\pi$. Si ce n'$\theta$est pas dans ce domaine, alors nous devons trouver un autre angle qui a le même cosinus$\theta$ et qui appartient au domaine restreint ; nous soustrayons ensuite cet angle de$\dfrac{\pi}{2}$ .De même$\sin \theta=\dfrac{a}{c}=\cos\left(\dfrac{\pi}{2}−\theta\right)$, donc${\cos}^{−1}(\sin \theta)=\dfrac{\pi}{2}−\theta$ si$−\dfrac{\pi}{2}≤\theta≤\dfrac{\pi}{2}$. Ce ne sont que les relations fonction-cofonction présentées d'une autre manière.

Fonctions données du formulaire${\sin}^{−1}(\cos x)$ and ${\cos}^{−1}(\sin x)$, evaluate them.

1. Si$x$ c'est dedans$[ 0,\pi ]$, alors${\sin}^{−1}(\cos x)=\dfrac{\pi}{2}−x$.
2. Si$x$ ce n'est pas dedans$[ 0,\pi ]$, alors trouvez un autre angle$y$ dans$[ 0,\pi ]$ lequel$\cos y=\cos x$.

   $${\sin}^{−1}(\cos x)=\dfrac{\pi}{2}−y$$

3. Si$x$ c'est dedans$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$, alors${\cos}^{−1}(\sin x)=\dfrac{\pi}{2}−x$.
4. Si$x$ ce n'est pas dedans$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$, alors trouvez un autre angle$y$ dans$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$ lequel$\sin y=\sin x$.

   $${\cos}^{−1}(\sin x)=\dfrac{\pi}{2}−y$$

Exemple$\PageIndex{6}$: Evaluating the Composition of an Inverse Sine with a Cosine

Évaluer${\sin}^{−1}\left(\cos\left(\dfrac{13\pi}{6}\right)\right)$

1. par évaluation directe.
2. par la méthode décrite précédemment.

Solution

1. Ici, nous pouvons évaluer directement l'intérieur de la composition. $$\begin{align*} \cos\left(\dfrac{13\pi}{6}\right)&= \cos\left (\dfrac{\pi}{6}+2\pi\right )\\ &= \cos\left (\dfrac{\pi}{6}\right )\\ &= \dfrac{\sqrt{3}}{2} \end{align*}$$ Nous pouvons maintenant évaluer la fonction inverse comme nous l'avons fait précédemment. $${\sin}^{−1}\left (\dfrac{\sqrt{3}}{2}\right )=\dfrac{\pi}{3}$$
2. Nous avons$x=\dfrac{13\pi}{6}$$y=\dfrac{\pi}{6}$, et $$\begin{align*} {\sin}^{-1}\left (\cos \left (\dfrac{13\pi}{6} \right ) \right )&= \dfrac{\pi}{2}-\dfrac{\pi}{6}\\ &= \dfrac{\pi}{3} \end{align*}$$

Exercice$\PageIndex{6}$

Évaluer${\cos}^{−1}\left (\sin\left (−\dfrac{11\pi}{4}\right )\right )$.

Réponse

$\dfrac{3\pi}{4}$

Évaluation de la composition du formulaire$f(g^{−1}(x))$

Pour évaluer les compositions de la forme$f(g^{−1}(x))$, où$f$ et$g$ sont deux des fonctions sinus, cosinus ou tangente et$x$ est une entrée dans le domaine de$g^{−1}$, nous avons des formules exactes, telles que$\sin({\cos}^{−1}x)=\sqrt{1−x^2}$. Lorsque nous avons besoin de les utiliser, nous pouvons dériver ces formules en utilisant les relations trigonométriques entre les angles et les côtés d'un triangle droit, ainsi que la relation de Pythagore entre les longueurs des côtés. Nous pouvons utiliser l'identité pythagoricienne pour résoudre l'un quand on lui donne l'autre.${\sin}^2 x+{\cos}^2 x=1$ Nous pouvons également utiliser les fonctions trigonométriques inverses pour trouver des compositions impliquant des expressions algébriques.

Exemple$\PageIndex{7}$: Evaluating the Composition of a Sine with an Inverse Cosine

Trouvez une valeur exacte pour$\sin\left({\cos}^{−1}\left(\dfrac{4}{5}\right)\right)$.

Solution

En commençant par l'intérieur, nous pouvons dire qu'il existe un angle tel que$\theta={\cos}^{−1}\left (\dfrac{4}{5}\right )$, ce qui signifie$\cos \theta=\dfrac{4}{5}$, et nous recherchons$\sin \theta$. Nous pouvons utiliser l'identité pythagoricienne pour cela.

$$\begin{align*} {\sin}^2 \theta+{\cos}^2 \theta&= 1\qquad \text{Use our known value for cosine}\\ {\sin}^2 \theta+{\left (\dfrac{4}{5} \right )}^2&= 1\qquad \text{Solve for sine}\\ {\sin}^2 \theta&= 1-\dfrac{16}{25}\\ \sin \theta&=\pm \dfrac{9}{25}\\ &= \pm \dfrac{3}{5} \end{align*}$$

Puisque$\theta={\cos}^{−1}\left (\dfrac{4}{5}\right )$ c'est dans le quadrant I,$\sin \theta$ doit être positif, donc la solution l'est$35$. Voir la figure$\PageIndex{11}$.

Figure$\PageIndex{11}$ : Triangle droit illustrant que si$\cos \theta=\dfrac{4}{5}$, alors$\sin \theta=\dfrac{3}{5}$

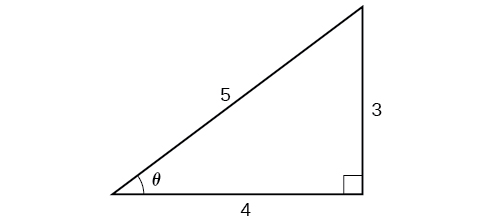
Nous savons que le cosinus inverse donne toujours un angle sur l'intervalle$[ 0,\pi ]$, donc nous savons que le sinus de cet angle doit être positif ; par conséquent$\sin \left ({\cos}^{−1}\left (\dfrac{4}{5} \right ) \right )=\sin \theta=\dfrac{3}{5}$.

Exercice$\PageIndex{7}$

Évaluer$\cos \left ({\tan}^{−1} \left (\dfrac{5}{12} \right ) \right )$.

Réponse

$\frac{12}{13}$

Exemple$\PageIndex{8}$: Evaluating the Composition of a Sine with an Inverse Tangent

Trouvez une valeur exacte pour$\sin\left({\tan}^{−1}\left(\dfrac{7}{4}\right)\right)$.

Solution

Bien que nous puissions utiliser une technique similaire à celle de l'exemple$\PageIndex{6}$, nous allons démontrer une technique différente ici. De l'intérieur, on sait qu'il existe un angle tel que$\tan \theta=\dfrac{7}{4}$. Nous pouvons l'imaginer comme les côtés opposés et adjacents d'un triangle droit, comme le montre la figure$\PageIndex{12}$.

Figure$\PageIndex{12}$ : Un triangle droit dont les deux côtés sont connus

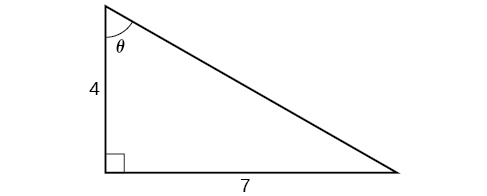
En utilisant le théorème de Pythagore, nous pouvons trouver l'hypoténuse de ce triangle.

\ [\ begin {align*}
4^2+7^2&= {hypoténuse} ^2 \ \
hypoténuse&= \ sqrt {65} \ \
 \ text {Maintenant, nous pouvons évaluer le sinus de l'angle comme étant le côté opposé divisé par l'hypoténuse.} \ \
 \ sin \ theta&= \ dfrac {7} {\ sqrt {65}} \ \
 \ text {Cela nous donne la composition souhaitée.} \
 \ sin \ left ({\ tan} ^ {-1} \ left (\ dfrac {7} {4} \ right) \ right) &= \ sin \ theta \ \
&= \ dfrac {7} {\ sqrt {65}} \ \
&= \ dfrac {7 \ sqrt {65}} {65}
 \ end {align*} \]

Exercice$\PageIndex{8}$

Évaluer$\cos\left({\sin}^{−1}\left(\dfrac{7}{9}\right)\right)$.

Réponse

$\dfrac{4\sqrt{2}}{9}$

Exemple$\PageIndex{9}$: Finding the Cosine of the Inverse Sine of an Algebraic Expression

Trouvez une expression simplifiée$\cos\left({\sin}^{−1}\left(\dfrac{x}{3}\right)\right)$ pour$−3≤x≤3$.

Solution

Nous savons qu'il existe un$\theta$ tel angle$\sin \theta=\dfrac{x}{3}$.

$$\begin{align*} {\sin}^2 \theta+{\cos}^2 \theta&= 1\qquad \text{Use the Pythagorean Theorem}\\ {\left (\dfrac{x}{3}\right )}^2+{\cos}^2 \theta&= 1\qquad \text{Solve for cosine}\\ {\cos}^2 \theta&= 1-\dfrac{x^2}{9}\\ \cos \theta &= \pm \sqrt{\dfrac{9-x^2}{9}}\\ &= \pm \sqrt{\dfrac{9-x^2}{3}} \end{align*}$$

Comme nous savons que le sinus inverse doit donner un angle sur l'intervalle$[ −\dfrac{\pi}{2},\dfrac{\pi}{2} ]$, nous pouvons en déduire que le cosinus de cet angle doit être positif.

$cos\left({\sin}^{−1}\left(\dfrac{x}{3}\right)\right)=\sqrt{\dfrac{9-x^2}{3}}$

Exercice$\PageIndex{9}$

Trouvez une expression simplifiée pour$\sin({\tan}^{−1}(4x))$ for $−\dfrac{1}{4}≤x≤\dfrac{1}{4}$.

Réponse

$\dfrac{4x}{\sqrt{16x^2+1}}$

Médias

Accédez à cette ressource en ligne pour obtenir des instructions et des exercices supplémentaires sur les fonctions trigonométriques inverses.

• Évaluer les expressions impliquant des fonctions trigonométriques inverses

Visitez ce site Web pour des questions pratiques supplémentaires sur Learningpod.

Concepts clés

• Une fonction inverse est une fonction qui « annule » une autre fonction. Le domaine d'une fonction inverse est la plage de la fonction d'origine et la plage d'une fonction inverse est le domaine de la fonction d'origine.
• Comme les fonctions trigonométriques ne sont pas univoques sur leurs domaines naturels, les fonctions trigonométriques inverses sont définies pour des domaines restreints.
• Pour toute fonction trigonométrique$f(x)$, si$x=f^{−1}(y)$, alors$f(x)=y$. Cependant, cela implique$f(x)=y$ uniquement qu'$x=f^{−1}(y)$$x$il appartient au domaine restreint de$f$. Voir l'exemple$\PageIndex{1}$.
• Les angles spéciaux sont les sorties des fonctions trigonométriques inverses pour des valeurs d'entrée spéciales ; par exemple,$\frac{\pi}{4}={\tan}^{−1}(1)$$\frac{\pi}{6}={\sin}^{−1}(\frac{1}{2})$ et. Voir exemple$\PageIndex{2}$.
• Un calculateur renverra un angle dans le domaine restreint de la fonction trigonométrique d'origine. Voir l'exemple$\PageIndex{3}$.
• Les fonctions inverses nous permettent de trouver un angle lorsqu'on leur donne les deux côtés d'un triangle droit. Voir l'exemple$\PageIndex{4}$.
• Dans la composition des fonctions, si la fonction interne est une fonction trigonométrique inverse, il existe des expressions exactes ; par exemple,$\sin({\cos}^{−1}(x))=\sqrt{1−x^2}$. Voir l'exemple$\PageIndex{5}$.
• Si la fonction interne est une fonction trigonométrique, les seules combinaisons possibles sont${\sin}^{−1}(\cos x)=\frac{\pi}{2}−x$ si$0≤x≤\pi$ et${\cos}^{−1}(\sin x)=\frac{\pi}{2}−x$ si$−\frac{\pi}{2}≤x≤\frac{\pi}{2}$. Voir Exemple$\PageIndex{6}$ et Exemple$\PageIndex{7}$.
• Lorsque vous évaluez la composition d'une fonction trigonométrique à l'aide d'une fonction trigonométrique inverse, tracez un triangle de référence pour aider à déterminer le rapport des côtés qui représente la sortie de la fonction trigonométrique. Voir l'exemple$\PageIndex{8}$.
• Lorsque vous évaluez la composition d'une fonction trigonométrique à l'aide d'une fonction trigonométrique inverse, vous pouvez utiliser des identités de trigonométrie pour aider à déterminer le rapport des côtés. Voir l'exemple$\PageIndex{9}$.