7.3 : Unit Circle

Objectifs d'apprentissage

• Trouvez des valeurs de fonction pour le sinus et le cosinus de 30°\((\frac{\pi}{6})\) ou, 45° ou\((\frac{\pi}{4})\), et 60° ou\((\frac{\pi}{3})\).
• Identifiez le domaine et l'étendue des fonctions sinusoïdales et cosinus.
• Trouvez des angles de référence.
• Utilisez des angles de référence pour évaluer les fonctions trigonométriques.

À la recherche de sensations fortes ? Envisagez ensuite une balade à bord du Singapore Flyer, la plus haute grande roue du monde. Située à Singapour, la grande roue culmine à 541 pieds, soit un peu plus d'un dixième de mile ! Décrit comme une roue d'observation, les cyclistes profitent de vues spectaculaires lorsqu'ils se déplacent du sol jusqu'au sommet et redescendent selon un schéma répétitif. Dans cette section, nous allons examiner ce type de mouvement de rotation autour d'un cercle. Pour ce faire, nous devons d'abord définir le type de cercle, puis placer ce cercle sur un système de coordonnées. Ensuite, nous pouvons discuter du mouvement circulaire en termes de paires de coordonnées.

Figure\(\PageIndex{1}\) : Le Singapore Flyer est la plus haute grande roue du monde. (crédit : « Vibin JK » /Flickr)

Recherche de valeurs de fonction pour le sinus et le cosinus

Pour définir nos fonctions trigonométriques, nous commençons par dessiner un cercle unitaire, un cercle centré à l'origine avec un rayon 1, comme indiqué sur la figure\(\PageIndex{2}\). L'angle (en radians) qui\(t\) intercepte forme un arc de longueur\(s\). En utilisant la formule\(s=rt\), et sachant cela\(r=1\), nous voyons que pour un cercle unitaire,\(s=t\).

Souvenez-vous que les axes x et y divisent le plan de coordonnées en quatre quarts appelés quadrants. Nous étiquetons ces quadrants pour imiter la direction qu'un angle positif balayerait. Les quatre quadrants sont étiquetés I, II, III et IV.

Pour n'importe quel angle,\(t,\) nous pouvons étiqueter l'intersection du côté terminal et du cercle unitaire par ses coordonnées,\((x,y)\). Les coordonnées\(x\) et\(y\) seront les sorties des fonctions trigonométriques\(f(t)= \cos t\) et\( f(t)= \sin t\), respectivement. Cela signifie\(x= \cos t\) et\(y= \sin t\).

Figure\(\PageIndex{2}\) : Cercle unitaire dont l'angle central est le\(t\) radians

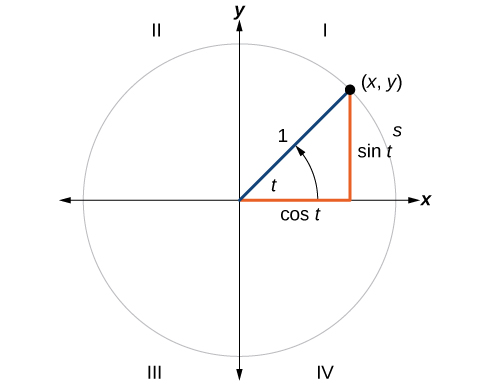
UNITÉ CIRCLE

Un cercle unitaire possède un centre\((0,0)\) et un rayon\(1\). La longueur de l'arc intercepté est égale à la mesure en radians de l'angle central\(t\).

\((x,y)\)Soit l'extrémité du cercle unitaire d'un arc de longueur d'arc\(s\). Les\((x,y)\) coordonnées de ce point peuvent être décrites en fonction de l'angle.

Définition des fonctions sinus et cosinus

Maintenant que notre cercle unitaire est étiqueté, nous pouvons apprendre comment les\((x,y)\) coordonnées sont liées à la longueur et à l'angle de l'arc. La fonction sinus associe un nombre réel\(t\) à la\(y\) coordonnée du point où l'angle correspondant intercepte l'unité de cercle. Plus précisément, le sinus d'un angle\(t\) est égal à la\(y\) valeur -de l'extrémité sur le cercle unitaire d'un arc de longueur\(t\). Dans la figure\(\PageIndex{3}\), le sinus est égal à\(y\). Comme toutes les fonctions, la fonction sinusoïdale possède une entrée et une sortie. Son entrée est la mesure de l'angle ; sa sortie est la\(y\) coordonnée du point correspondant sur l'unité de cercle.

La fonction cosinus d'un angle\(t\) est égale à la\(x\) valeur -de l'extrémité sur l'unité de cercle d'un arc de longueur\(t\). Dans la figure\(\PageIndex{1}\), le cosinus est égal à x.

Figurine\(\PageIndex{3}\)

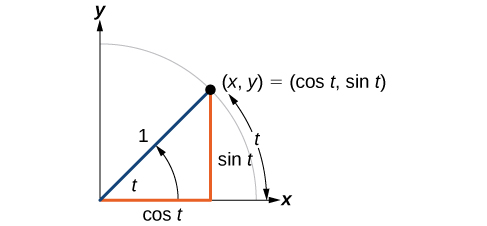
Comme il est entendu que le sinus et le cosinus sont des fonctions, il n'est pas toujours nécessaire de les écrire entre parenthèses :\(\sin t\) est identique à\(\sin (t)\) et\(\cos t\) est identique à\(\cos (t)\). De même,\(\cos ^2 t\) est une notation abrégée couramment utilisée pour\(( \cos (t))^2\). Sachez que de nombreuses calculatrices et ordinateurs ne reconnaissent pas la notation abrégée. En cas de doute, utilisez les parenthèses supplémentaires lorsque vous saisissez des calculs dans une calculatrice ou un ordinateur.

FONCTIONS SINUS ET COSINUS

Si\(t\) est un nombre réel et qu'un point\((x,y)\) du cercle unitaire correspond à un angle de\(t\), alors

$$$$

\[ \begin{align} \cos t & = x \\ \sin t & = y \end{align}\]

Comment faire : Avec un point\(P(x,y)\) on the unit circle corresponding to an angle of \( t\), find the sine and cosine

1. Le sinus de\(t\) est égal à la\(y\) coordonnée du point\(P\) :\( \sin t=y\).
2. Le cosinus de\(t\) est égal à la\(x\) coordonnée du point\(P\) :\( \cos t=x\).

Exemple\(\PageIndex{1}\): Finding Function Values for Sine and Cosine

\(P\)Le point est un point du cercle unitaire correspondant à un angle de\(t\), comme indiqué sur la figure\(\PageIndex{4}\). Trouvez\(\cos (t)\) et\(\sin (t)\).

Figurine\(\PageIndex{4}\)

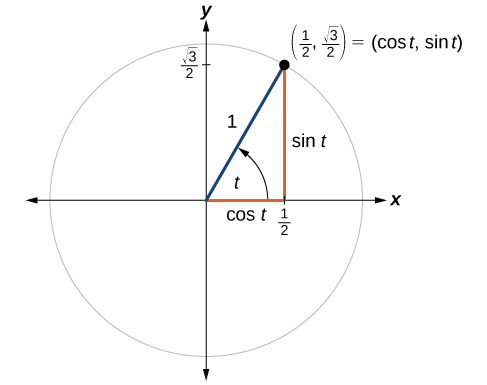
Solution

Nous savons qu'il\(\cos t \) s'agit de la\(x\) coordonnée du point correspondant sur le cercle unitaire et\(\sin t\) de la\(y\) coordonnée du point correspondant sur le cercle unitaire. Donc :

\(\begin{align*} x & = \cos t= \frac{1}{2} \\ y & = \sin t= \frac{\sqrt{3}}{2} \end{align*}\)

$$$$

Essayez-le\(\PageIndex{1}\)

Un certain angle\(t\) correspond à un point du cercle unitaire,\(\left(−\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2}\right)\) comme indiqué sur la figure\(\PageIndex{5}\). Trouvez\(\cos t\) et\(\sin t\).

Figurine\(\PageIndex{5}\)

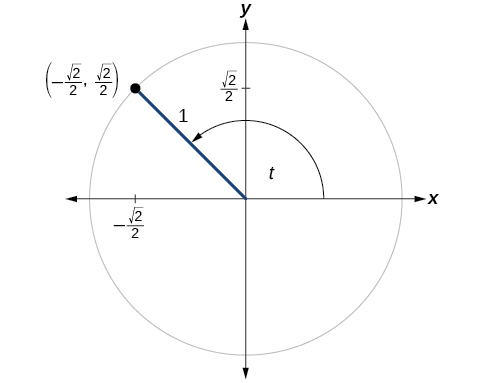
Réponse

\(\cos (t)=−\dfrac{ \sqrt{2} }{2}, \sin (t)=\dfrac {\sqrt{2}}{2} \)

Déterminer les sinus et les cosinus des angles sur un axe

Pour les angles quadrantraux, le point correspondant du cercle unitaire se trouve sur l'\(y\)axe\(x\) - ou. Dans ce cas, nous pouvons facilement calculer le cosinus et le sinus à partir des valeurs de\(x\) et\(y\).

Exemple\(\PageIndex{2}\): Calculating Sines and Cosines along an Axis

Trouvez\(\cos (90°)\) et\(\sin (90°).\)

Solution

Le fait de nous déplacer dans le\(90°\) sens antihoraire autour du cercle unitaire à partir de l'\(x\)axe positif nous amène au sommet du cercle, où les\((x,y)\) coordonnées sont (0, 1), comme indiqué sur la figure\(\PageIndex{6}\).

Figurine\(\PageIndex{6}\)

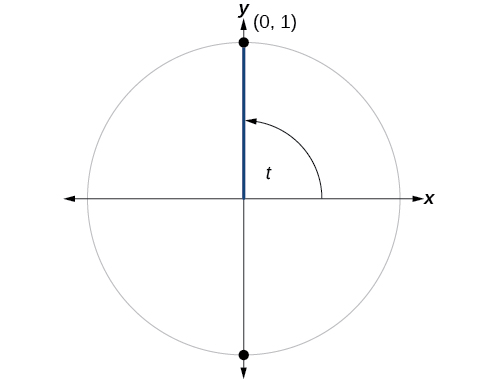
En utilisant nos définitions du cosinus et du sinus,

\(\begin{align*} x &= \cos t = \cos (90°) = 0 \\ y &= \sin t = \sin (90°) = 1 \end{align*} \)

$$$$

Le cosinus de 90° est 0 ; le sinus de 90° est 1.

Essayez-le\(\PageIndex{2}\)

Détermine le cosinus et le sinus de l'angle\(π\).

Réponse

\(\cos (π)=−1, \sin (π)=0\)

L'identité pythagoricienne

Maintenant que nous pouvons définir le sinus et le cosinus, nous allons apprendre comment ils sont liés entre eux et avec le cercle unitaire. Rappelez-vous que l'équation du cercle unitaire est\(x^2+y^2=1\). Parce que\(x= \cos t\) et\(y=\sin t\), nous pouvons remplacer\( x\) et\(y\) obtenir\(\cos ^2 t+ \sin ^2 t=1.\) Cette équation,\( \cos ^2 t+ \sin ^2 t=1,\) est connue sous le nom d'identité pythagoricienne. Voir la figure\(\PageIndex{7}\).

Figurine\(\PageIndex{7}\)

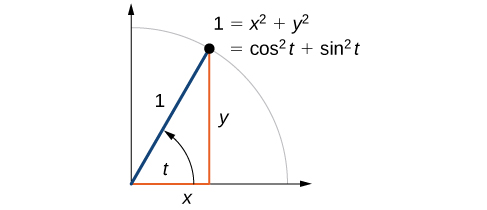
Nous pouvons utiliser l'identité pythagoricienne pour trouver le cosinus d'un angle si nous connaissons le sinus, ou vice versa. Cependant, comme l'équation donne deux solutions, nous avons besoin de connaissances supplémentaires sur l'angle pour choisir la solution avec le bon signe. Si nous connaissons le quadrant où se trouve l'angle, nous pouvons facilement choisir la bonne solution.

IDENTITÉ PYTHAGORICIENNE

L'identité pythagoricienne indique que, pour tout nombre réel\(t\),

\[ \cos^2 t+ \sin^2 t=1  \]

Procédure : étant donné le sinus d'un angle t et l'emplacement de son quadrant, trouvez le cosinus de t

1. Remplacez la valeur connue par\(\sin (t)\) dans l'identité pythagoricienne.
2. Résolvez pour\( \cos (t)\).
3. Choisissez la solution avec le signe approprié pour les\(x\) valeurs -dans le quadrant où se\(t\) trouve.

Exemple\(\PageIndex{3}\): Finding a Cosine from a Sine or a Sine from a Cosine

Si\(\sin (t)=\dfrac{3}{7}\) et\(t\) se trouve dans le deuxième quadrant, trouvez\( \cos (t)\).

Solution

Si nous déposons une ligne verticale à partir du point du cercle unitaire correspondant à\(t\), nous créons un triangle droit, à partir duquel nous pouvons voir que l'identité de Pythagore n'est qu'un cas du théorème de Pythagore. Voir la figure\(\PageIndex{8}\).

Figurine\(\PageIndex{8}\)

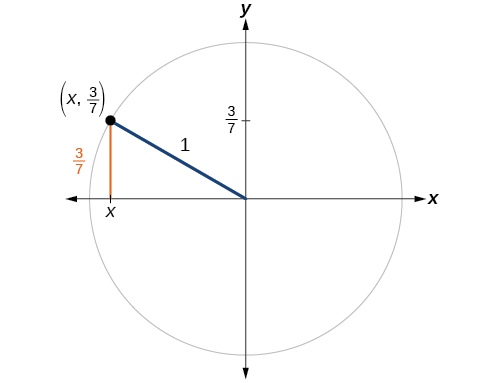
Substituer le sinus par la valeur connue dans l'identité pythagoricienne,

\[\begin{align*} \cos ^2 (t)+ \sin ^2(t) &=1 \\  \cos ^2(t)+\dfrac{9}{49} &=1 \\ \cos ^2(t) & = \dfrac{40}{49} \\  \cos (t) &=± \sqrt{\dfrac{40}{49}}=±\dfrac{\sqrt{40}}{7}=±\dfrac{2\sqrt{10}}{7} \end{align*}\]

Comme l'angle se trouve dans le deuxième quadrant, nous savons que la\(x\) valeur -est un nombre réel négatif, de sorte que le cosinus est également négatif. Donc

\[ \cos (t)=−\dfrac{2\sqrt{10}}{7} \nonumber \]

Essayez-le\(\PageIndex{3}\)

Si\(\cos (t)=\dfrac{24}{25}\) et\(t\) se trouve dans le quatrième quadrant, trouvez\( \sin (t)\).

Réponse

\(\sin (t)=−\dfrac{7}{25}\)

Trouver les sinus et les cosinus d'angles spéciaux

Nous avons déjà appris certaines propriétés des angles spéciaux, telles que la conversion des radians en degrés. Nous pouvons également calculer les sinus et les cosinus des angles spéciaux en utilisant l'identité pythagoricienne et notre connaissance des triangles.

Déterminer les sinus et les cosinus d'angles de 45°

Tout d'abord, nous examinerons les angles de\(45°\) ou\(\dfrac{π}{4}\), comme indiqué sur la figure\(\PageIndex{9}\). Un\(45°–45°–90°\) triangle est un triangle isocèle, de sorte que les\(y\) coordonnées\(x\) - et - du point correspondant sur le cercle sont les mêmes. Les valeurs x et\(y\) -étant identiques, les valeurs du sinus et du cosinus seront également égales.

Figurine\(\PageIndex{9}\)

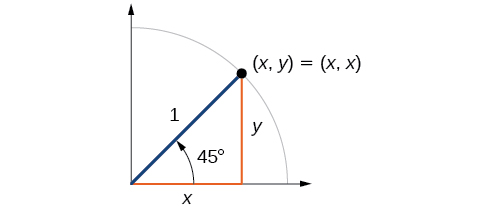
À\(t=\frac{π}{4}\), qui est de 45 degrés, le rayon du cercle unitaire divise le premier angle quadrantal en deux. Cela signifie que le rayon se situe le long de la ligne\(y=x\). Un cercle unitaire a un rayon égal à 1. Ainsi, le triangle droit formé sous la ligne\(y=x\) a des côtés\(x\) et\(y\) (avec\(y=x),\) et un rayon) = 1. Voir la figure\(\PageIndex{10}\).

Figurine\(\PageIndex{10}\)

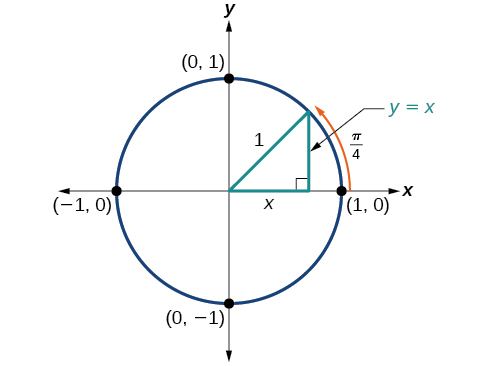
Du théorème de Pythagore, nous obtenons

\[x^2+y^2=1 \nonumber \]

\(y=x\)En remplaçant, nous obtenons

\[x^2+x^2=1 \nonumber \]

En combinant des termes similaires, on obtient

\[2x^2=1 \nonumber \]

Et en résolvant pour\(x\), nous obtenons

\[\begin{align*} x^2 &=\dfrac{1}{2} \\ x &=±\dfrac{1}{\sqrt{2}} \end{align*}  \]

Dans le quadrant I,\(x=\dfrac{1}{\sqrt{2}}\).

À\(t=\dfrac{π}{4}\) ou 45 degrés,

\[\begin{align*} (x,y) & =(x,x)=(\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}}) \\ x &= \dfrac{1}{\sqrt{2}}, \; y=\dfrac{1}{\sqrt{2}} \\ \cos t &= \dfrac{1}{\sqrt{2}}, \; \sin t=\dfrac{1}{\sqrt{2}} \end{align*}  \]

Si nous rationalisons ensuite les dénominateurs, nous obtenons

\[ \begin{align*} \cos t &= \dfrac{1}{\sqrt{2}}\dfrac{\sqrt{2}}{\sqrt{2}} \\ &= \dfrac{\sqrt{2}}{2} \\ \sin t &= \dfrac{1}{\sqrt{2}} \dfrac{\sqrt{2}}{\sqrt{2}}  \\ &=\dfrac{\sqrt{2}}{2} \end{align*}\]

Par conséquent, les\((x,y)\) coordonnées d'un point sur un cercle de rayon\(1\) à un angle de\(45°\) sont\(\left(\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2}\right)\).

Détermination des sinus et des cosinus d'angles de 30° et 60°

Ensuite, nous trouverons le cosinus et le sinus sous un angle de\(30°,\) ou\(\tfrac{π}{6}\). Tout d'abord, nous allons dessiner un triangle à l'intérieur d'un cercle avec un côté à un angle de\(30°,\) et un autre à un angle de,\(−30°,\) comme indiqué sur la figure\(\PageIndex{11}\). Si les deux triangles droits obtenus sont combinés en un seul grand triangle, notez que les trois angles de ce grand triangle seront\(60°,\) tels qu'illustrés sur la figure\(\PageIndex{12}\).

Figurine\(\PageIndex{11}\)

Figurine\(\PageIndex{12}\)

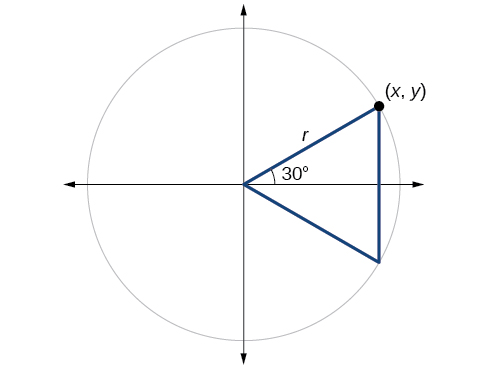
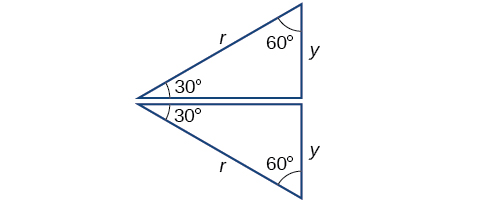
Comme tous les angles sont égaux, les côtés sont également égaux. La ligne verticale a une longueur\(2y\), et comme les côtés sont tous égaux, nous pouvons également en conclure que\(r=2y\) ou\(y=\frac{1}{2}r\). Depuis\( \sin t=y\),

\[ \sin \left(\frac{π}{6} \right)=\dfrac{1}{2} \nonumber \]

Et puisque\(r=1\) dans notre cercle d'unités,

\[\begin{align*} \sin \left(\frac{π}{6} \right) & = \dfrac{1}{2}(1) \\ &= \dfrac{1}{2} \end{align*}  \]

En utilisant l'identité pythagoricienne, nous pouvons trouver la valeur du cosinus.

\ (\ begin {aligné}
 \ cos^2 \ left (\ frac {π} {6} \ right) + \ sin^2 \ left (\ frac {π} {6} \ right) &= 1 && \
 \ \ cos^2 \ left (\ frac {π} {6} \ right) + \ left (\ dfrac {1} {2} \ right) ^2 &= 1 \ &&
 \ \ cos^2 \ left (\ frac {π} {6} \ right) &= \ drac {3} {4} && \ text { Utilisez la propriété de racine carrée.} \ \
 \ cos \ left (\ frac {π} {6} \ right) &= \ pm \ sqrt {\ dfrac {3} {4}} = \ dfrac {\ sqrt {3}} {2} && \ text {Puisque\(y\) c'est positif, choisissez la racine positive.} \ \
 \ end {aligné} \)

Les\((x,y)\) coordonnées du point sur un cercle de rayon\(1\) à un angle de\(30°\) sont\(\left(\dfrac{\sqrt{3}}{2},\dfrac{1}{2}\right)\). À\(t=\dfrac{π}{3}\) (60°), le rayon du cercle unitaire, 1, sert d'hypoténuse d'un triangle droit de 30 à 60 à 90 degrés,\(BAD,\) comme le montre la figure\(\PageIndex{13}\). L'angle\(A\) a une mesure de 60°. 60°. Au point,\(B,\) nous dessinons un angle\(ABC\) avec la mesure de\( 60°\). Nous connaissons la somme des angles d'un triangle\(180°\), de sorte que la mesure de l'angle\(C\) est également\(60°\). Nous avons maintenant un triangle équilatéral. Comme chaque côté du triangle\(ABC\) équilatéral a la même longueur et que nous savons que l'un des côtés correspond au rayon du cercle unitaire, tous les côtés doivent avoir une longueur de 1.

Figurine\(\PageIndex{13}\)

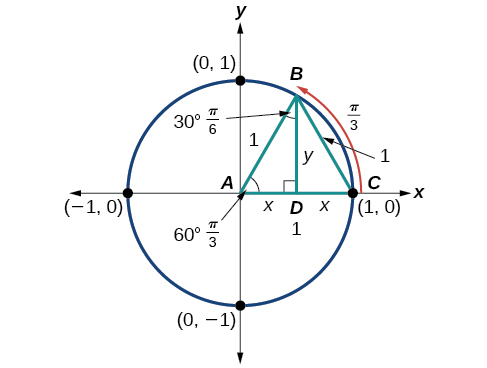
La mesure de l'angle\(ABD\) est de 30°. Donc, s'il est double, l'angle\(ABC\) est de 60°. \(BD\)est la bissectrice perpendiculaire de\(AC\), donc elle coupe\(AC\) en deux. Cela signifie qu'il\(AD\) s'agit\( \dfrac{1}{2}\) du rayon, ou\(\dfrac{1}{2}.\) Notice, de la\(x\) coordonnée du point\(B\), qui se trouve à l'intersection de l'angle de 60° et du cercle unitaire.\(AD\) Cela nous donne un triangle\(BAD\) avec une hypoténuse de 1 et un côté\(x\) de longueur\(\dfrac{1}{2}\).

Du théorème de Pythagore, nous obtenons

\[x^2+y^2=1 \nonumber \]

\(x=\frac{1}{2}\)En remplaçant, nous obtenons

\[ \left(  \dfrac{1}{2}  \right)^2+y^2=1 \nonumber \]

En résolvant\(y\), nous obtenons

\[\begin{align*} \dfrac{1}{4}+y^2 &=1 \\ y^2 &=1−\dfrac{1}{4} \\ y^2 &= \dfrac{3}{4} \\ y &=± \dfrac{\sqrt{3}}{2} \end{align*}\]

Puisque\(t=\dfrac{π}{3}\) le côté terminal se trouve dans le quadrant I où la\(y\) coordonnée -est positive, nous choisissons\(y=\dfrac{\sqrt{3}}{2}\) la valeur positive.

À\(t=\dfrac{π}{3}\) (60°), les\((x,y)\) coordonnées du point d'un cercle de rayon\(1\) à un angle de\(60°\) sont\(\left(\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)\), ce qui nous permet de trouver le sinus et le cosinus.

\( (x, y) = \left( \dfrac{1}{2}, \dfrac{ \sqrt{3} }{2} \right) \)

\( x = \dfrac{1}{2}, \; y = \dfrac{ \sqrt{3} }{2} \)

\( \cos t = \dfrac{1}{2}, \; \sin t = \dfrac{ \sqrt{3} }{2} \)

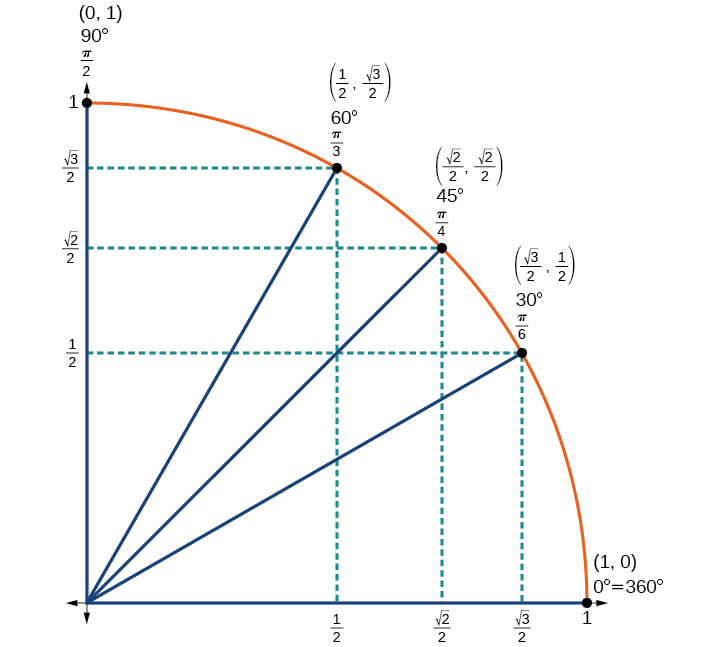
Nous avons maintenant trouvé les valeurs du cosinus et du sinus pour tous les angles les plus fréquemment rencontrés dans le premier quadrant du cercle unitaire. Le tableau\(\PageIndex{1}\) résume ces valeurs.

Tableau\(\PageIndex{1}\)

Angle	0	\(\dfrac{π}{6}\), ou 30	\(\dfrac{π}{4}\), ou 45°	\(\dfrac{π}{3}\), ou 60°	\(\dfrac{π}{2}\), ou 90°
Cosinus	1	\(\dfrac{\sqrt{3}}{2}\)	\(\dfrac{\sqrt{2}}{2}\)	\(\dfrac{1}{2}\)	0
Sinus	0	\(\dfrac{1}{2}\)	\(\dfrac{\sqrt{2}}{2}\)	\(\dfrac{\sqrt{3}}{2}\)	1

La figure\(\PageIndex{14}\) montre les angles communs dans le premier quadrant du cercle unitaire.

Figurine\(\PageIndex{14}\)

Utiliser une calculatrice pour trouver le sinus et le cosinus

Pour trouver le cosinus et le sinus des angles autres que les angles spéciaux, nous nous tournons vers un ordinateur ou une calculatrice. Attention : la plupart des calculateurs peuvent être réglés en mode « degré » ou « radian », qui indique au calculateur les unités de la valeur d'entrée. Lorsque nous évaluons\( \cos (30)\) sur notre calculatrice, elle l'évaluera comme le cosinus de 30 degrés si la calculatrice est en mode degrés, ou le cosinus de 30 radians si la calculatrice est en mode radian.

Procédure : à partir d'un angle en radians, utilisez une calculatrice graphique pour trouver le cosinus

1. Si la calculatrice possède le mode degrés et le mode radian, réglez-le sur le mode radian.
2. Appuyez sur la touche COS.
3. Entrez la valeur en radian de l'angle et appuyez sur la touche «) » entre parenthèses.
4. Appuyez sur ENTER.

Exemple\(\PageIndex{4}\): Using a Graphing Calculator to Find Sine and Cosine

Évaluez\( \cos \left(\dfrac{5π}{3}\right)\) à l'aide d'un calculateur graphique ou d'un ordinateur.

Solution

Entrez les touches suivantes :

\(\mathrm{COS( 5 × π ÷ 3 ) \; ENTER}\)

\[ \cos \left(\dfrac{5π}{3}\right)=0.5 \nonumber\]

Analyse

Nous pouvons trouver le cosinus ou le sinus d'un angle en degrés directement sur une calculatrice avec mode degrés. Pour les calculatrices ou les logiciels qui utilisent uniquement le mode radian, nous pouvons trouver le signe de\(20°\), par exemple, en incluant le facteur de conversion en radians dans l'entrée :

\[\mathrm{SIN( 20 × π ÷ 180 ) \; ENTER} \nonumber\]

Essayez-le\(\PageIndex{4}\)

Évaluer\(\sin \left( \dfrac{π}{3} \right) \).

Réponse

environ 0,866025403

Identifier le domaine et la plage des fonctions sinusoïdales et cosinusoïd

Maintenant que nous pouvons trouver le sinus et le cosinus d'un angle, nous devons discuter de leurs domaines et de leurs plages. Quels sont les domaines des fonctions sinus et cosinus ? Autrement dit, quels sont les nombres les plus petits et les plus grands qui peuvent être des entrées des fonctions ? Parce que les angles inférieurs à 0 et les angles supérieurs à 2π peuvent toujours être représentés graphiquement sur le cercle unitaire et avoir des valeurs réelles de\(x, \; y\)\(r\), et qu'il n'y a pas de limite inférieure ou supérieure aux angles pouvant être entrés dans les fonctions sinus et cosinus. L'entrée des fonctions sinus et cosinus est la rotation à partir de l'\(x\)axe positif, qui peut être n'importe quel nombre réel.

Quelles sont les plages des fonctions sinus et cosinus ? Quelles sont les valeurs les plus faibles et les plus élevées possibles pour leur sortie ? Nous pouvons voir les réponses en examinant le cercle unitaire, comme indiqué sur la figure\(\PageIndex{15}\). Les limites de la\(x\) coordonnée -sont\( [−1,1]\). Les limites de la\(y\) coordonnée -sont également\([−1,1]\). Par conséquent, la plage des fonctions sinus et cosinus est de\([−1,1]\).

Figurine\(\PageIndex{15}\)

Trouver des angles de référence

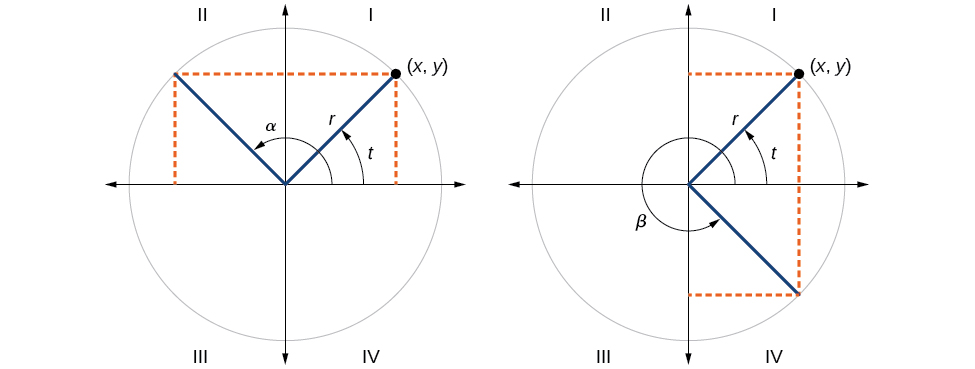
Nous avons discuté de la détermination du sinus et du cosinus pour les angles du premier quadrant, mais que se passe-t-il si notre angle se trouve dans un autre quadrant ? Pour tout angle donné dans le premier quadrant, il existe un angle dans le second quadrant avec la même valeur sinusoïdale. Comme la valeur du sinus est la\(y\) coordonnée sur le cercle unitaire, l'autre angle ayant le même sinus partagera la même\(y\) valeur, mais aura la\(x\) valeur opposée. Par conséquent, sa valeur de cosinus sera opposée à la valeur du cosinus du premier angle.

De même, il y aura un angle dans le quatrième quadrant avec le même cosinus que l'angle d'origine. L'angle ayant le même cosinus partagera la même\(x\) valeur -mais aura la\(y\) valeur opposée. Par conséquent, sa valeur sinusoïdale sera opposée à la valeur sinusoïdale de l'angle d'origine.

Comme le montre la figure\(\PageIndex{16}\), l'angle\(α\) a la même valeur sinusoïdale que l'angle\(t\) ; les valeurs du cosinus sont opposées. L'angle\(β\) a la même valeur de cosinus que l'angle\(t\) ; les valeurs des sinus sont opposées.

\ (\ begin {array} {ccc} \ sin (t) = \ sin (α) & \ text {et} & \ cos (t) = - \ cos (α) \ \
 \ sin (t) = - \ sin (β) & \ text {et} & \ cos (t) = \ cos (β) \ \
 \ end {tableau} \)

Figurine\(\PageIndex{16}\)

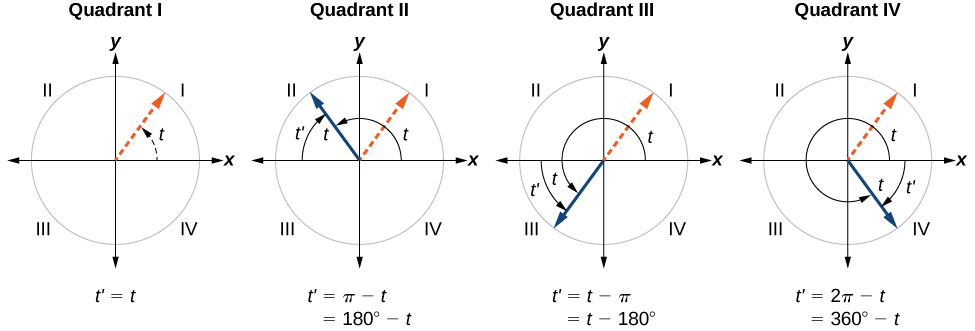
Rappelez-vous que l'angle de référence d'un angle est l'angle aigu\(t\), formé par le côté terminal de l'angle\(t\) et l'axe horizontal. Un angle de référence est toujours un angle compris entre\(0\) et\(90°\), ou\(0\) et\(\dfrac{π}{2}\) des radians. Comme nous pouvons le voir sur la figure\(\PageIndex{17}\), pour tout angle dans les quadrants II, III ou IV, il existe un angle de référence dans le quadrant I.

Figurine\(\PageIndex{17}\)

Mode d'emploi : étant donné un angle entre\(0\) and \(2π\), find its reference angle

1. Un angle dans le premier quadrant est son propre angle de référence.
2. Pour un angle situé dans le deuxième ou le troisième quadrant, l'angle de référence est\(|π−t|\) ou\(|180°−t|\).
3. Pour un angle situé dans le quatrième quadrant, l'angle de référence est\(2π−t\) ou\(360°−t.\)
4. Si un angle est inférieur\(0\) ou supérieur à,\(2π,\) ajoutez ou soustrayez\(2π\) autant de fois que nécessaire pour trouver un angle équivalent entre\(0\) et\(2π\).

Exemple\(\PageIndex{5}\): Finding a Reference Angle

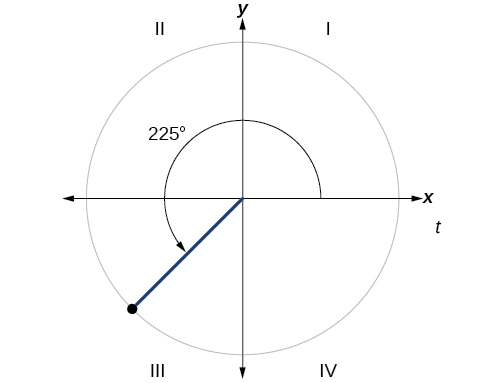
Trouvez l'angle de référence de\(225°\) comme indiqué sur la figure\(\PageIndex{18}\).

Figurine\(\PageIndex{18}\)

Solution

Comme\( 225°\) il se trouve dans le troisième quadrant, l'angle de référence est

\[|(180°−225°)|=|−45°|=45° \nonumber \]

Essayez-le\(\PageIndex{5}\)

Trouvez l'angle de référence de\(\frac{5π}{3}\).

Réponse

(\ dfrac {π} {3} \)

Utilisation des angles de référence

Prenons maintenant un moment pour reconsidérer la grande roue présentée au début de cette section. Supposons qu'un motard prenne une photo alors qu'il est arrêté à vingt pieds au-dessus du sol. Le cavalier effectue ensuite une rotation aux trois quarts du cercle. Quelle est la nouvelle altitude du pilote ? Pour répondre à des questions comme celle-ci, nous devons évaluer les fonctions sinusoïdales ou cosinusoïdales à des angles supérieurs à 90 degrés ou à un angle négatif. Les angles de référence permettent d'évaluer les fonctions trigonométriques pour les angles situés en dehors du premier quadrant. Ils peuvent également être utilisés pour trouver les\((x,y)\) coordonnées de ces angles. Nous utiliserons l'angle de référence de l'angle de rotation combiné au quadrant dans lequel se trouve le côté terminal de l'angle.

Utilisation d'angles de référence pour évaluer des fonctions trigonométriques

Nous pouvons trouver le cosinus et le sinus de n'importe quel angle dans n'importe quel quadrant si nous connaissons le cosinus ou le sinus de son angle de référence. Les valeurs absolues du cosinus et du sinus d'un angle sont les mêmes que celles de l'angle de référence. Le signe dépend du quadrant de l'angle d'origine. Le cosinus sera positif ou négatif selon le signe des\(x\) valeurs -dans ce quadrant. Le sinus sera positif ou négatif selon le signe des\(y\) valeurs -dans ce quadrant.

UTILISATION D'ANGLES DE RÉFÉRENCE POUR TROUVER LE COSINUS ET LE

Les angles ont des cosinus et des sinus ayant la même valeur absolue que les cosinus et les sinus de leurs angles de référence. Le signe (positif ou négatif) peut être déterminé à partir du quadrant de l'angle.

Procédure : à partir d'un angle en position standard, trouvez l'angle de référence, ainsi que le cosinus et le sinus de l'angle d'origine

1. Mesurez l'angle entre le côté terminal de l'angle donné et l'axe horizontal. C'est l'angle de référence.
2. Déterminez les valeurs du cosinus et du sinus de l'angle de référence.
3. Donnez au cosinus le même signe que les\(x\) valeurs -dans le quadrant de l'angle d'origine.
4. Donnez au sinus le même signe que les\(y\) valeurs -dans le quadrant de l'angle d'origine.

Exemple\(\PageIndex{6}\): Using Reference Angles to Find Sine and Cosine

1. À l'aide d'un angle de référence, déterminez la valeur exacte de\(\cos (150°)\) et\( \sin (150°)\).
2. À l'aide de l'angle de référence, recherchez\( \cos \dfrac{5π}{4}\) et\(\sin \frac{5π}{4}\).

Solution

Cela nous indique que 150° a les mêmes valeurs de sinus et de cosinus que 30°, à l'exception du signe. Nous savons que

Comme\(150°\) il se trouve dans le deuxième quadrant, la\(x\) coordonnée du point du cercle est négative, donc la valeur du cosinus est négative. La\(y\) coordonnée -est positive, donc la valeur sinusoïdale est positive.

\(\dfrac{5π}{4}\)se trouve dans le troisième quadrant. Son angle de référence est\( \left| \dfrac{5π}{4} - π \right| = \dfrac{π}{4} \). Le cosinus et le sinus de\(\dfrac{π}{4} \) sont à la fois\( \dfrac{\sqrt{2}}{2} \). Dans le troisième quadrant,\(x\) les deux\(y\) sont négatifs, donc :

\( \cos \dfrac{5π}{4} = -\dfrac{\sqrt{2}}{2} \)et\(\sin \dfrac{5π}{4} = -\dfrac{\sqrt{2}}{2} \)

Essayez-le\(\PageIndex{6}\)

1. Utilisez l'angle de référence de\(315°\) pour trouver\( \cos (315°) \) et\(\sin (315°)\).
2. Utilisez l'angle de référence de\(−\dfrac{π}{6}\) pour trouver\( \cos \left(−\dfrac{π}{6}\right) \) et\( \sin \left(−\dfrac{π}{6}\right)\)

Réponse

1. \( \cos (315°)= \dfrac{\sqrt{2}}{2}, \sin (315°)=\dfrac{–\sqrt{2}}{2}\)
2. \(\cos \left(−\dfrac{π}{6}\right)=\dfrac{\sqrt{3}}{2}, \sin \left(−\dfrac{π}{6}\right)=−\frac{1}{2} \)

Utilisation d'angles de référence pour trouver des coordonnées

Maintenant que nous avons appris à déterminer les valeurs du cosinus et du sinus pour les angles spéciaux du premier quadrant, nous pouvons utiliser la symétrie et les angles de référence pour renseigner les valeurs du cosinus et du sinus pour le reste des angles spéciaux du cercle unitaire. Ils sont illustrés sur la figure\(\PageIndex{19}\). Prenez le temps d'apprendre les\((x,y)\) coordonnées de tous les principaux angles du premier quadrant.

Figure\(\PageIndex{19}\) : Angles spéciaux et coordonnées des points correspondants sur le cercle unitaire

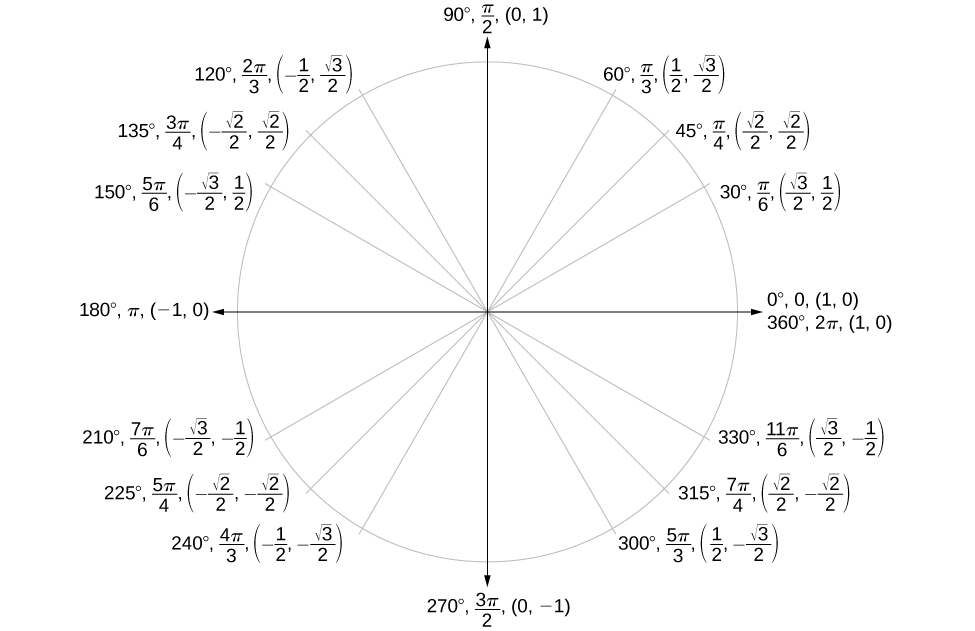
En plus d'apprendre les valeurs des angles spéciaux, nous pouvons utiliser les angles de référence pour trouver les\((x,y)\) coordonnées de n'importe quel point du cercle unitaire, en utilisant ce que nous savons des angles de référence et des identités

\[\begin{align*} x &= \cos t \\ y & = \sin t \end{align*}\]

Nous trouvons d'abord l'angle de référence correspondant à l'angle donné. Ensuite, nous prenons les valeurs du sinus et du cosinus de l'angle de référence et leur donnons les signes correspondant aux\(x\) valeurs\(y\) - et - du quadrant.

Comment faire : en fonction de l'angle d'un point sur un cercle et du rayon du cercle, trouvez\((x,y)\) coordinates of the point

1. Trouvez l'angle de référence en mesurant le plus petit angle par rapport à l'\(x\)axe.
2. Détermine le cosinus et le sinus de l'angle de référence.
3. Déterminez les signes appropriés pour\(x\) et\(y\) dans le quadrant donné.

Exemple\(\PageIndex{7}\): Using the Unit Circle to Find Coordinates

Trouvez les coordonnées du point sur le cercle unitaire à un angle de\(\dfrac{7π}{6}\).

Solution

Nous savons que l'angle\(\dfrac{7π}{6}\) se situe dans le troisième quadrant.

Trouvons d'abord l'angle de référence en mesurant l'angle par rapport à l'\(x\)axe. Pour trouver l'angle de référence d'un angle dont le côté terminal se trouve dans le quadrant III, on trouve la différence entre l'angle et\(π\).

\[\dfrac{7π}{6}−π=\dfrac{π}{6} \nonumber \]

Ensuite, nous allons trouver le cosinus et le sinus de l'angle de référence :

\[\cos \left( \dfrac{π}{6} \right) =\dfrac{3}{2} \;\;        \sin \left(\dfrac{π}{6}\right)=\dfrac{1}{2} \nonumber \]

Nous devons déterminer les signes appropriés pour\(x\) et\(y\) dans le quadrant donné. Parce que notre angle d'origine se situe dans le troisième quadrant, où les deux\(x\) et\(y\) sont négatifs, le cosinus et le sinus sont négatifs.

\[\begin{align*} \cos \left(\dfrac{7π}{6}\right) &=−\dfrac{\sqrt{3}}{2} \\ \sin \left(\dfrac{7π}{6}\right) & =−\dfrac{1}{2} \end{align*}\]

Nous pouvons maintenant calculer les\((x,y)\) coordonnées en utilisant les identités\(x= \cos θ\) et\(y= \sin θ\).

Les coordonnées du point se trouvent\(\left(−\dfrac{\sqrt{3}}{2},−\dfrac{1}{2}\right)\) sur le cercle unitaire.

Essayez-le\(\PageIndex{7}\)

Trouvez les coordonnées du point sur le cercle unitaire à un angle de\(\dfrac{5π}{3}\).

Réponse

\(  \left( \dfrac{1}{2},−\dfrac{\sqrt{3}}{2} \right) \)

médias

Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur les fonctions sinus et cosinus.

• Fonctions trigonométriques utilisant le cercle unitaire
• Sinus et cosinus du cercle unitaire
• Sinus et cosinus du cercle unitaire et multiples de Pi divisés par six
• Sinus et cosinus du cercle unitaire et multiples de Pi divisés par quatre
• Fonctions trigonométriques utilisant des angles de référence

Équations clés

Cosinus	\( \cos t=x\)
Sinus	\( \sin t=y\)
Identité pythagoricienne	\( \cos ^2 t+ \sin ^2 t=1\)

Concepts clés

• Pour trouver les valeurs de fonction pour le sinus et le cosinus, commencez par dessiner un cercle unitaire centré sur l'origine et ayant un rayon de 1 unité.
• En utilisant le cercle unitaire, le sinus d'un angle\(t\) est égal à la\(y\) valeur -de l'extrémité sur le cercle unitaire d'un arc de longueur,\(t\) tandis que le cosinus d'un angle\(t\) est égal à la\(x\) valeur -de l'extrémité. Voir l'exemple.
• Les valeurs du sinus et du cosinus sont déterminées le plus directement lorsque le point correspondant du cercle unitaire tombe sur un axe. Voir l'exemple.
• Lorsque le sinus ou le cosinus est connu, nous pouvons utiliser l'identité de Pythagore pour trouver l'autre. L'identité pythagoricienne est également utile pour déterminer les sinus et les cosinus d'angles particuliers. Voir l'exemple.
• Les calculateurs et les logiciels graphiques sont utiles pour trouver les sinus et les cosinus si la procédure appropriée pour saisir des informations est connue. Voir l'exemple.
• Le domaine des fonctions sinus et cosinus est constitué de nombres réels.
• La plage des fonctions sinus et cosinus est de\([−1,1]\).
• Le sinus et le cosinus d'un angle ont la même valeur absolue que le sinus et le cosinus de son angle de référence.
• Les signes du sinus et du cosinus sont déterminés à partir des\(y\) valeurs x et -dans le quadrant de l'angle d'origine.
• L'angle de référence d'un angle est l'angle\(t\) dimensionnel, formé par le côté terminal de l'angle\(t\) et l'axe horizontal. Voir l'exemple.
• Les angles de référence peuvent être utilisés pour déterminer le sinus et le cosinus de l'angle d'origine. Voir l'exemple.
• Les angles de référence peuvent également être utilisés pour trouver les coordonnées d'un point sur un cercle. Voir l'exemple.

Lexique

fonction cosinusoïdale

la\(x\) valeur -du point sur un cercle unitaire correspondant à un angle donné

Identité pythagoricienne

un corollaire du théorème de Pythagore selon lequel le carré du cosinus d'un angle donné plus le carré du sinus de cet angle est égal à 1

fonction sinusoïdale

la\(y\) valeur -du point sur un cercle unitaire correspondant à un angle donné

cercle d'unités

un cercle dont le centre\((0,0)\) et le rayon sont égaux à 1.