7.1 : Angles
- Page ID
- 195566
Objectifs d'apprentissage
- Tracez des angles en position standard.
- Convertissez les degrés en radians.
- Trouvez les angles coterminaux.
- Détermine la longueur d'un arc de cercle.
- Utilisez la vitesse linéaire et angulaire pour décrire le mouvement sur une trajectoire circulaire.
Un golfeur se balance pour frapper une balle au-dessus d'un piège à sable et sur le green. Un pilote de ligne manœuvre un avion vers une piste étroite. Une créatrice de vêtements crée les dernières tendances de la mode. Qu'est-ce qu'ils ont tous en commun ? Ils travaillent tous avec des angles, tout comme nous le faisons tous à un moment ou à un autre. Parfois, nous avons besoin de mesurer des angles avec précision avec des instruments. D'autres fois, nous les estimons ou les jugeons à l'œil nu. Quoi qu'il en soit, le bon angle peut faire la différence entre le succès et l'échec dans de nombreuses entreprises. Dans cette section, nous allons examiner les propriétés des angles.
Angles de dessin en position standard
Pour bien définir un angle, il faut d'abord définir un rayon. Un rayon se compose d'un point sur une ligne et de tous les points s'étendant dans une direction à partir de ce point. Le premier point est appelé point final du rayon. Nous pouvons faire référence à un rayon spécifique en indiquant son point final et tout autre point sur celui-ci. Le rayon de la figure\(\PageIndex{1}\) peut être nommé rayon EF ou sous forme de symbole\(\overrightarrow{EF}\).
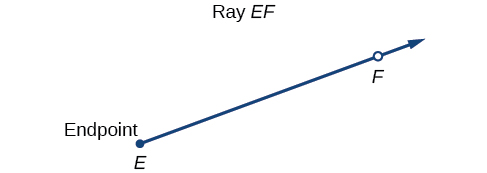
Un angle est l'union de deux rayons ayant un point final commun. Le point final est appelé sommet de l'angle, et les deux rayons sont les côtés de l'angle. L'angle de la figure\(\PageIndex{2}\) est formé à partir de\(\overrightarrow{ED}\) et\(\overrightarrow{EF}\). Les angles peuvent être nommés en utilisant un point sur chaque rayon et le sommet, tel que l'angle DEF, ou sous forme de symbole\(∠DEF.\)
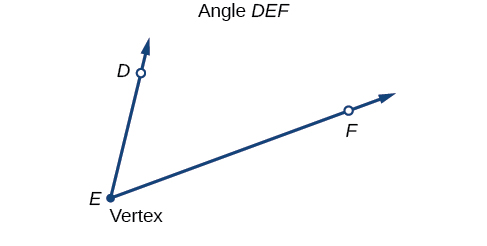
Les lettres grecques sont souvent utilisées comme variables pour la mesure d'un angle. Le tableau\(\PageIndex{1}\) est une liste de lettres grecques couramment utilisées pour représenter les angles, et un exemple d'angle est illustré sur la figure\(\PageIndex{3}\).
| \(θ\) | \(φ \text{ or }ϕ\) | \(α\) | \(β\) | \(γ\) |
| thêta | phi | alpha | bêta | gamma |
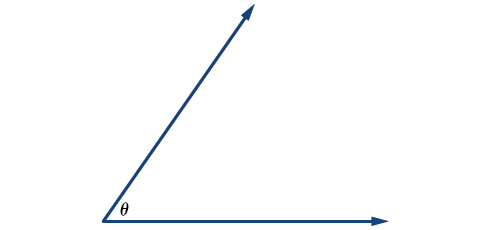
Figure \(\PageIndex{3}\): Angle thêta, représenté par\(∠θ\)
La création d'angles est un processus dynamique. Nous commençons par deux rayons superposés. Nous laissons l'un fixe en place et faisons pivoter l'autre. Le rayon fixe est le côté initial et le rayon pivoté est le côté terminal. Afin d'identifier les différents côtés, nous indiquons la rotation avec un petit arc et une flèche près du sommet, comme sur la figure\(\PageIndex{4}\).
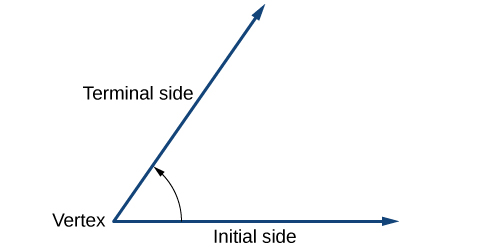
Comme nous l'avons vu au début de la section, il existe de nombreuses applications pour les angles, mais pour les utiliser correctement, nous devons être en mesure de les mesurer. La mesure d'un angle est la quantité de rotation entre le côté initial et le côté terminal. L'unité de mesure d'angle la plus connue est probablement le degré. Un \(\frac{1}{360}\)degré correspond à une rotation circulaire, donc une rotation circulaire complète contient 360 degrés. Un angle mesuré en degrés doit toujours inclure l'unité « degrés » après le nombre, ou inclure le symbole du degré°. Par exemple, 90 degrés = 90 degrés.
Pour formaliser notre travail, nous allons commencer par dessiner des angles sur un plan de coordonnées x - y. Les angles peuvent apparaître dans n'importe quelle position sur le plan de coordonnées, mais à des fins de comparaison, la convention consiste à les illustrer à la même position chaque fois que cela est possible. Un angle est en position standard si son sommet est situé à l'origine et que son côté initial s'étend le long de l'axe x positif. Voir la figure\(\PageIndex{5}\).
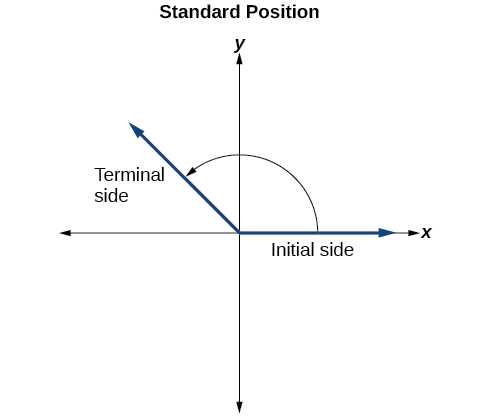
Si l'angle est mesuré dans le sens antihoraire entre le côté initial et le côté terminal, l'angle est considéré comme un angle positif. Si l'angle est mesuré dans le sens des aiguilles d'une montre, l'angle est considéré comme un angle négatif.
Le tracé d'un angle en position standard commence toujours de la même manière : dessinez le côté initial le long de l'axe X positif. Pour placer le côté terminal de l'angle, nous devons calculer la fraction d'une rotation complète que représente l'angle. Pour ce faire, nous divisons la mesure de l'angle en degrés par 360°. Par exemple, pour dessiner un angle de 90°, nous le calculons\(\frac{90°}{360°}=\frac{1}{4}\). Ainsi, le côté terminal se trouvera au quart du cercle, se déplaçant dans le sens antihoraire par rapport à l'axe X positif. Pour dessiner un angle de 360°, nous le calculons\(\frac{360°}{360°}=1\). Ainsi, le côté terminal effectuera une rotation complète autour du cercle, en se déplaçant dans le sens antihoraire à partir de l'axe X positif. Dans ce cas, le côté initial et le côté terminal se chevauchent. Voir la figure\(\PageIndex{6}\).
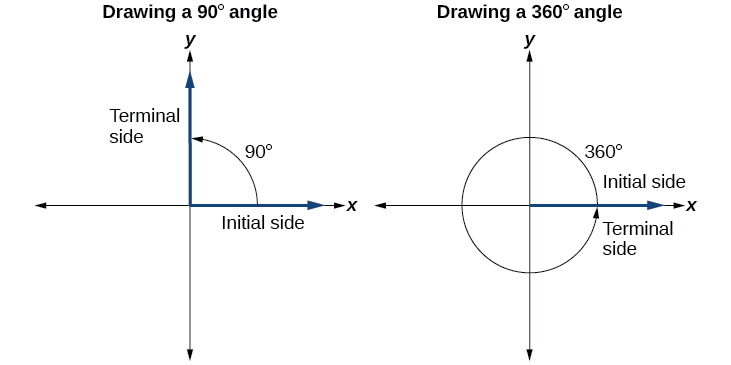
Puisque nous définissons un angle en position standard par son côté initial, nous avons un type spécial d'angle dont le côté terminal se trouve sur un axe, un angle quadrantal. Ce type d'angle peut avoir une mesure de 0°, 90°, 180°, 270° ou 360°. Voir la figure\(\PageIndex{7}\).
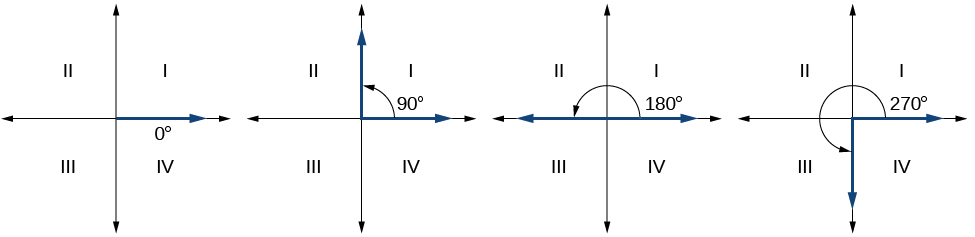
ANGLES QUADRANTAUX
Les angles quadrantaux sont des angles en position standard dont le côté terminal se trouve sur un axe, y compris 0°, 90°, 180°, 270° ou 360°.
À partir d'un angle mesuré en degrés, dessinez l'angle en position standard
- Exprimez la mesure de l'angle sous la forme d'une fraction de 360°.
- Réduisez la fraction à la forme la plus simple.
- Tracez un angle contenant la même fraction du cercle, en commençant par l'axe X positif et en vous déplaçant dans le sens antihoraire pour les angles positifs et dans le sens des aiguilles d'une montre pour les angles négatifs.
Exemple\(\PageIndex{1}\): Drawing an Angle in Standard Position Measured in Degrees
- Esquissez un angle de 30° en position standard.
- Esquissez un angle de −135° en position standard.
Solution
- Divisez la mesure de l'angle par 360°.
\[\dfrac{30°}{360°}=\dfrac{1}{12}\]
Pour réécrire la fraction en une fraction plus familière, nous pouvons reconnaître que
\[\dfrac{1}{12}=\dfrac{1}{3}(\frac{1}{4})\]
Un douzième équivaut à un tiers de quart, donc en divisant un quart de rotation en tiers, nous pouvons dessiner une ligne à 30° comme sur la figure\(\PageIndex{8}\).
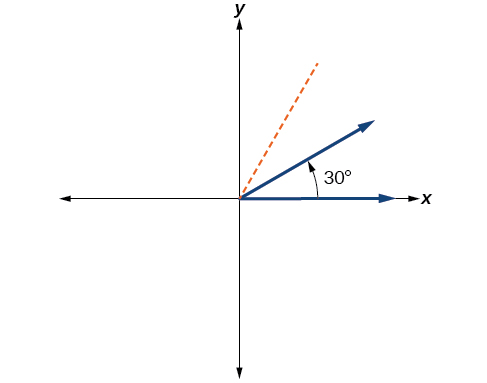
Figurine\(\PageIndex{8}\) - Divisez la mesure de l'angle par 360°.
\[\dfrac{−135°}{360°}=−\dfrac{3}{8}\]
Dans ce cas, nous pouvons reconnaître que
\[−\dfrac{3}{8}=−\dfrac{3}{2}(\dfrac{1}{4})\]
Les trois huitièmes négatifs correspondent à une fois et demie par quart. Nous plaçons donc une ligne en nous déplaçant dans le sens des aiguilles d'une montre d'un quart complet et de la moitié d'un autre quart, comme dans la Figure\(\PageIndex{9}\).
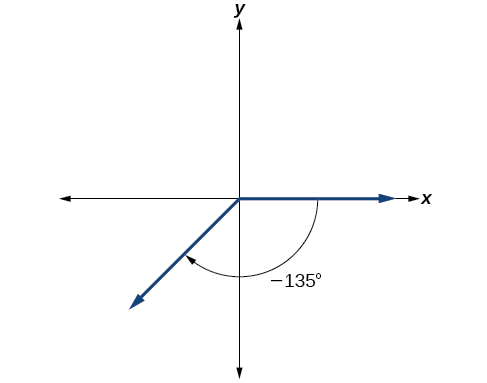
Figurine\(\PageIndex{9}\)
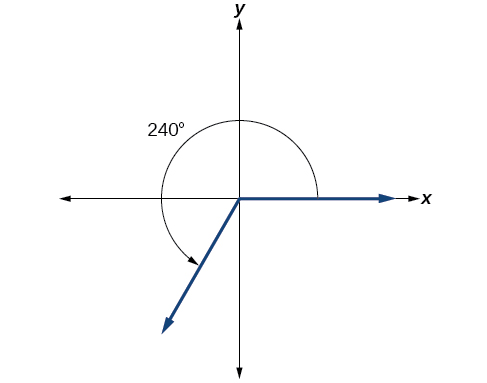
\(\PageIndex{1}\):
Afficher un angle de 240° sur un cercle en position standard.
Solution
Conversion entre degrés et radians
Diviser un cercle en 360 parties est un choix arbitraire, bien que cela crée la mesure des degrés familière. Nous pouvons choisir d'autres moyens de diviser un cercle. Pour trouver une autre unité, pensez au processus qui consiste à dessiner un cercle. Imaginez que vous vous arrêtez avant que le cercle ne soit terminé. La partie que vous avez dessinée est appelée arc. Un arc peut être une partie d'un cercle complet, un cercle complet ou plus d'un cercle complet, représenté par plusieurs rotations complètes. La longueur de l'arc autour d'un cercle entier est appelée la circonférence de ce cercle.
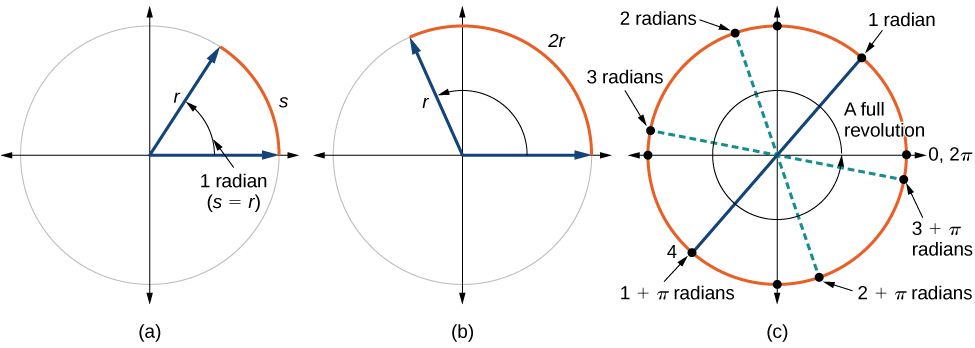
La circonférence d'un cercle est de\(C=2πr\). Si nous divisons les deux côtés de cette équation par\(r\), nous créons le rapport entre la circonférence et le rayon, qui est toujours\(2π\) indépendamment de la longueur du rayon. Ainsi, la circonférence d'un cercle est\(2π≈6.28\) multipliée par la longueur du rayon. Cela signifie que si nous prenions une corde aussi longue que le rayon et que nous l'utilisions pour mesurer des longueurs consécutives autour de la circonférence, il y aurait de la place pour six longueurs de corde complètes et un peu plus d'un quart de septième, comme le montre la figure\(\PageIndex{11}\).
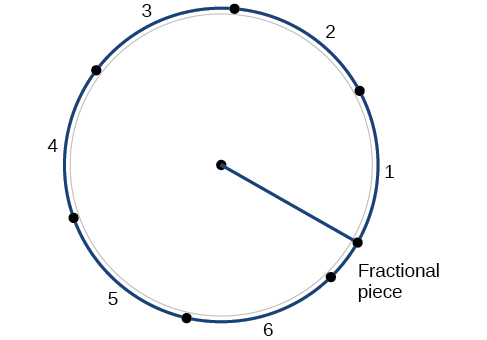
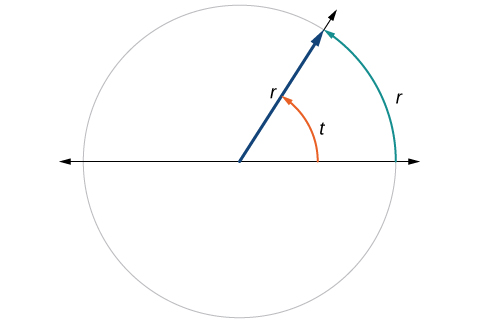
Cela nous amène à notre nouvelle mesure d'angle. Un radian est la mesure de l'angle central d'un cercle qui intercepte un arc de longueur égale au rayon de ce cercle. Un angle central est un angle formé au centre d'un cercle par deux rayons. Comme la circonférence totale est égale au\(2π\) multiplié par le rayon, une rotation circulaire complète est exprimée en\(2π\) radians. Donc
\[\begin{align} 2π \text{ radians } & =360^∘ \\ π \text{ radians } & =\dfrac{360^∘}{2}=180^∘ \\ 1 \text{ radian } & =\dfrac{180^∘}{π}≈57.3^∘ \end{align}\]
Voir la figure\(\PageIndex{12}\). Notez que lorsqu'un angle est décrit sans unité spécifique, il fait référence à la mesure du radian. Par exemple, une mesure d'angle de 3 indique 3 radians. En fait, la mesure du radian est sans dimension, puisqu'il s'agit du quotient d'une longueur (circonférence) divisé par une longueur (rayon) et les unités de longueur s'annulent.
Associer les longueurs d'arc au rayon
La longueur d'un arc\(s\) est la longueur de la courbe le long de l'arc. Tout comme la circonférence complète d'un cercle a toujours un rapport constant avec le rayon, la longueur de l'arc produite par un angle donné a également une relation constante avec le rayon, quelle que soit la longueur du rayon.
Ce rapport, appelé mesure du radian, est le même quel que soit le rayon du cercle ; il dépend uniquement de l'angle. Cette propriété nous permet de définir une mesure de n'importe quel angle comme le rapport entre la longueur de l'arc s s et le rayon\(r\). Voir la figure\(\PageIndex{13}\).
\[\begin{align} s &=rθ \\ θ &=\dfrac{s}{r} \end{align}\]
Si\( s=r\), alors\(θ=\frac{r}{r}= 1 \text{ radian.}\)
Pour approfondir cette idée, considérez deux cercles, l'un de rayon 2 et l'autre de rayon 3. Rappelez-vous que la circonférence d'un cercle est\(C=2πr\), où\(r\) est le rayon. Le plus petit cercle a alors une circonférence\(2π(2)=4π\) et le plus grand une circonférence\(2π(3)=6π\). Nous dessinons maintenant un angle de 45° sur les deux cercles, comme dans la Figure\(\PageIndex{14}\).
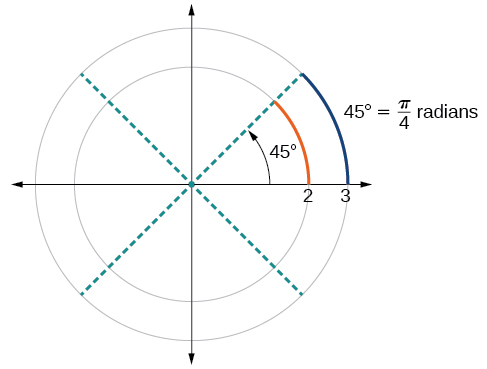
Remarquez ce qui se passe si nous trouvons le rapport entre la longueur de l'arc et le rayon du cercle.
\[\begin{align} \text{Smaller circle: } \dfrac{\frac{1}{2}π}{2} & =\dfrac{1}{4}π \\[2mm] \text{Larger circle: } \dfrac{\frac{3}{4}π}{3} & =\dfrac{1}{4}π \end{align}\]
Comme les deux ratios le sont\(\frac{1}{4}π\), les mesures d'angle des deux cercles sont les mêmes, même si la longueur et le rayon de l'arc diffèrent.
RADIANS
Un radian est la mesure de l'angle central d'un cercle de telle sorte que la longueur de l'arc entre le côté initial et le côté terminal soit égale au rayon du cercle. Un tour complet (360°) équivaut à\(2\pi\) des radians. Un demi-tour (180°) équivaut à des\(\pi\) radians.
La mesure en radians d'un angle est le rapport entre la longueur de l'arc sous-tendu par l'angle et le rayon du cercle. En d'autres termes, si\(s\) c'est la longueur d'un arc de cercle et\(r\) le rayon du cercle, alors l'angle central contenant cet arc mesure\(\frac{s}{r}\) les radians. Dans un cercle de rayon 1, la mesure du radian correspond à la longueur de l'arc.
Une mesure de 1 radian semble être d'environ 60°. Est-ce que c'est exact ?
Oui Il est d'environ 57,3°. Parce que \(2π\)les radians sont égaux à 360°,\(1\) radian est égal à\(\frac{360°}{2π}≈57.3°\).
Utiliser des radians
Comme la mesure du radian est le rapport entre deux longueurs, il s'agit d'une mesure sans unité. Par exemple, dans la figure\(\PageIndex{14}\), supposons que le rayon était de 2 pouces et que la distance le long de l'arc était également de 2 pouces. Lorsque nous calculons la mesure en radian de l'angle, les « pouces » s'annulent et nous obtenons un résultat sans unités. Il n'est donc pas nécessaire d'écrire l'étiquette « radians » après une mesure en radians, et si nous voyons un angle qui n'est pas étiqueté par « degrés » ou par le symbole du degré, nous pouvons supposer qu'il s'agit d'une mesure en radians.
Si l'on considère le cas le plus élémentaire, le cercle unitaire (un cercle de rayon 1), nous savons qu'une rotation équivaut à 360 degrés, 360°. Nous pouvons également suivre une rotation autour d'un cercle en trouvant la circonférence\(C=2πr\), et pour le cercle unitaire.\(C=2π.\) Ces deux méthodes différentes de rotation autour d'un cercle nous permettent de convertir des degrés en radians.
\[\begin{array}{clll} 1 \text{rotation } & =360° & =2π & \text{radians} \\[2mm] \dfrac{1}{2} \text{rotation } & =180° & =π & \text{radians} \\[2mm] \dfrac{1}{4} \text{rotation } & =90° & =\dfrac{π}{2} & \text{radians} \end{array}\]
Identification des angles spéciaux mesurés en radians
En plus de connaître les mesures en degrés et en radians d'un quart de révolution, d'un demi-tour et d'un tour complet, il existe d'autres angles fréquemment rencontrés dans un tour de cercle que nous devrions connaître. Il est fréquent de rencontrer des multiples de 30, 45, 60 et 90 degrés. Ces valeurs sont illustrées dans la figure\(\PageIndex{15}\). La mémorisation de ces angles sera très utile lorsque nous étudierons les propriétés associées aux angles.
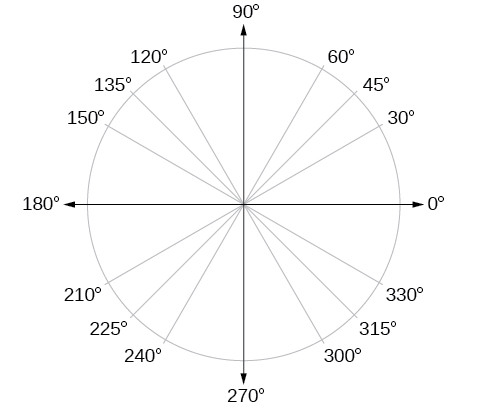
Nous pouvons maintenant répertorier les valeurs de radians correspondantes pour les mesures communes d'un cercle correspondant à celles répertoriées dans la figure\(\PageIndex{15}\), qui sont illustrées dans la figure\(\PageIndex{16}\). Assurez-vous de pouvoir vérifier chacune de ces mesures.
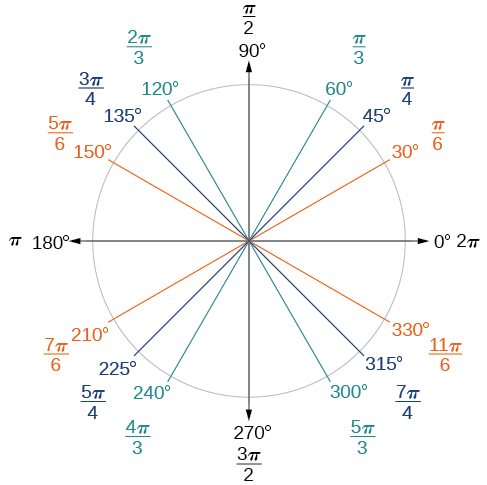
Exemple\(\PageIndex{2}\): Finding a Radian Measure
Détermine la mesure en radians d'un tiers d'une rotation complète.
Solution
Pour n'importe quel cercle, la longueur de l'arc le long d'une telle rotation serait égale au tiers de la circonférence. Nous savons que
\[1 \text{ rotation}=2πr\]
Donc,
\[\begin{align}s &= \dfrac{1}{3}(2πr) \\[2mm] &=\dfrac{2πr}{3} \end{align}\]
La mesure en radians serait la longueur de l'arc divisée par le rayon.
\[\begin{align} \text{radian measure} & = \dfrac{\frac{2πr}{3}}{r} \\[2mm] &= \dfrac{2πr}{3r} \\[2mm] & = \dfrac{2π}{3} \end{align}\]
\(\PageIndex{2}\)
Détermine la mesure en radians des trois quarts d'une rotation complète.
Solution
\[\dfrac{3π}{2}\]
Conversion entre radians et degrés
Comme les degrés et les radians mesurent tous deux des angles, nous devons être capables de les convertir. Nous pouvons facilement le faire en utilisant une proportion.
\[\dfrac{θ}{180}=\dfrac{θ^R}{π}\]
Cette proportion montre que la mesure de l'angle\(θ\) en degrés divisé par 180 est égale à la mesure de l'angle\(θ\) en radians divisée par\(π.\) Or, exprimé autrement, les degrés sont à 180 comme les radians sont à\(π\).
\[\dfrac{\text{Degrees}}{180}=\dfrac{Radians}{π} \]
CONVERSION ENTRE RADIANS ET DEGRÉS
Pour convertir les degrés en radians, utilisez la proportion
\[\dfrac{θ}{180}=\dfrac{θ^R}{π}\]
Exemple\(\PageIndex{3}\): Converting Radians to Degrees
Convertissez chaque mesure de radians en degrés.
- \(\frac{π}{6}\)
- 3
Solution
Comme on nous donne des radians et que nous voulons des degrés, nous devons établir une proportion et la résoudre.
- Nous utilisons la proportion en substituant les informations données.
\[\begin{align}\dfrac{θ}{180} &=\dfrac{θ^R}{π} \\[2mm] \dfrac{θ}{180} & =\dfrac{\frac{π}{6}}{π} \\ θ & =\dfrac{180}{6} \\ θ & =30^∘ \end{align}\]
- Nous utilisons la proportion en substituant les informations données.
\[\begin{align}\dfrac{θ}{180} &= \dfrac{θ^R}{π} \\ \dfrac{θ}{180} &=\dfrac{3}{π} \\ θ &= \dfrac{3(180)}{π} \\ θ & ≈172^∘ \end{align}\]
\(\PageIndex{3}\)
Convertissez\(−\frac{3π}{4}\) les radians en degrés.
Solution
−135°
Exemple\(\PageIndex{4}\): Converting Degrees to Radians
Convertissez les\(15\) degrés en radians.
Solution
Dans cet exemple, nous commençons par les degrés et voulons des radians. Nous redéfinissons donc une proportion et la résolvons, mais nous remplaçons les informations données dans une partie différente de la proportion.
\[\begin{align}\dfrac{θ}{180} &= \dfrac{θ^R}{π} \\ \dfrac{15}{180} &=\dfrac{θ^R}{π} \\ \dfrac{15π}{180} & =θ^R \\ \dfrac{π}{12} & =θ^R \end{align}\]
Analyse
Une autre façon de penser à ce problème est de s'en souvenir\(30^∘=\frac{π}{6}\). Parce que\(15^∘=\frac{1}{2}(30^∘)\), nous pouvons trouver que c'\(\frac{1}{2}(\frac{π}{6})\)est le cas\(\frac{π}{12}\).
\(\PageIndex{4}\)
Convertissez 126° en radians.
Solution
\(\frac{7π}{10}\)
Trouver des angles co-terminaux
La conversion entre les degrés et les radians peut faciliter l'utilisation des angles dans certaines applications. Pour d'autres applications, il se peut que nous ayons besoin d'un autre type de conversion. Les angles négatifs et les angles supérieurs à un tour complet sont plus difficiles à utiliser que ceux compris entre 0° et 360°, ou entre 0 et 0\(2π\). Il serait pratique de remplacer ces angles hors plage par un angle correspondant compris dans la plage d'un tour unique.
Il est possible que plusieurs angles aient le même côté terminal. Regardez Figure\(\PageIndex{17}\). L'angle de 140° est un angle positif, mesuré dans le sens antihoraire. L'angle de —220° est un angle négatif, mesuré dans le sens des aiguilles d'une montre. Mais les deux angles ont le même côté terminal. Si deux angles en position standard ont le même côté terminal, ce sont des angles co-terminaux. Chaque angle supérieur à 360° ou inférieur à 0° est co-terminal avec un angle compris entre 0° et 360°, et il est souvent plus pratique de trouver l'angle coterminal dans la plage de 0° à 360° que de travailler avec un angle situé en dehors de cette plage.
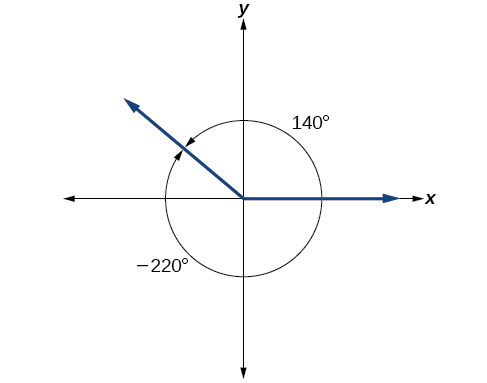
Chaque angle possède une infinité d'angles coterminaux, car chaque fois que nous ajoutons 360° à cet angle (ou que nous en soustrayons 360°), la valeur résultante a un côté terminal au même endroit. Par exemple, 100° et 460° sont coterminaux pour cette raison, tout comme -260°. Le fait de reconnaître que tout angle possède une infinité d'angles coterminaux explique la forme répétitive des graphes des fonctions trigonométriques.
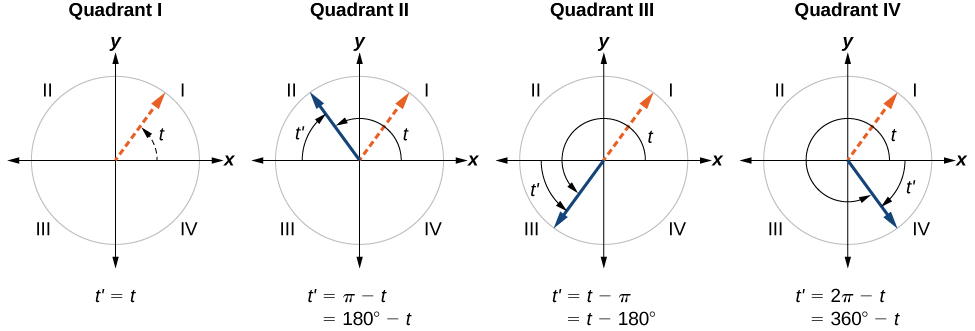
L'angle de référence d'un angle est la mesure du plus petit angle aigu positif\(t\) formé par le côté terminal de l'angle\(t\) et l'axe horizontal. Ainsi, les angles de référence positifs ont des côtés terminaux situés dans le premier quadrant et peuvent être utilisés comme modèles pour les angles situés dans d'autres quadrants. Voir la figure\(\PageIndex{18}\) pour des exemples d'angles de référence pour des angles dans différents quadrants.
ANGLES COTERMINAUX ET DE RÉFÉRENCE
- Les angles co-terminaux sont deux angles en position standard qui ont le même côté terminal.
- L'angle de référence d'un angle est la taille du plus petit angle aigu\(t′\), formé par le côté terminal de l'angle\(t\) et l'axe horizontal.
Étant donné un angle supérieur à 360°, trouvez un angle co-terminal compris entre 0° et 360°
- Soustrayez 360° de l'angle donné.
- Si le résultat est toujours supérieur à 360°, soustrayez à nouveau 360° jusqu'à ce que le résultat soit compris entre 0° et 360°.
- L'angle obtenu est coterminal avec l'angle d'origine.
Exemple\(\PageIndex{5}\): Finding an Angle Coterminal with an Angle of Measure Greater Than 360°
Détermine l'angle θ le moins positif qui soit coterminal avec un angle de 800°, où\(0°≤θ<360°\).
Solution
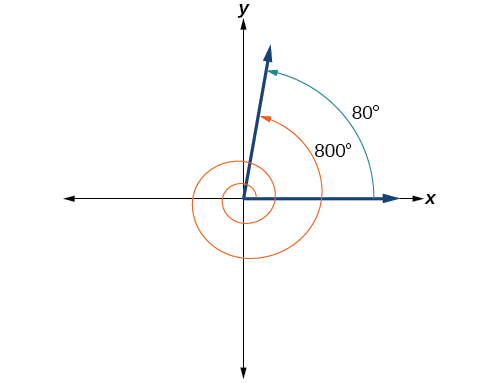
Un angle de mesure de 800° est co-terminal avec un angle de mesure 800 − 360 = 440°, mais 440° est toujours supérieur à 360°. Nous soustrayons donc à nouveau 360° pour trouver un autre angle coterminal : 440 − 360 = 80°.
L'angle\(θ=80°\) est co-terminal à 800°. En d'autres termes, 800° équivaut à 80° plus deux rotations complètes, comme le montre la figure\(\PageIndex{19}\).
\(\PageIndex{5}\)
Trouvez un angle\(α\) coterminal avec un angle de 870°, où\(0°≤α<360°\).
Solution
\(α=150°\)
Étant donné un angle dont la mesure est inférieure à 0°, trouvez un angle co-terminal ayant une mesure comprise entre 0° et 360°.
- Ajoutez 360° à l'angle donné.
- Si le résultat est toujours inférieur à 0°, ajoutez à nouveau 360° jusqu'à ce que le résultat soit compris entre 0° et 360°.
- L'angle obtenu est coterminal avec l'angle d'origine.
Exemple\(\PageIndex{6}\): Finding an Angle Coterminal with an Angle Measuring Less Than 0°
Montrez l'angle avec la mesure −45° sur un cercle et trouvez un angle coterminal α positif tel que 0° ≤ α < 360°.
Solution
Comme 45° est la moitié de 90°, nous pouvons commencer par l'axe horizontal positif et mesurer dans le sens des aiguilles d'une montre la moitié d'un angle de 90°.
Comme nous pouvons trouver des angles coterminaux en ajoutant ou en soustrayant une rotation complète de 360°, nous pouvons trouver un angle coterminal positif ici en ajoutant 360° :
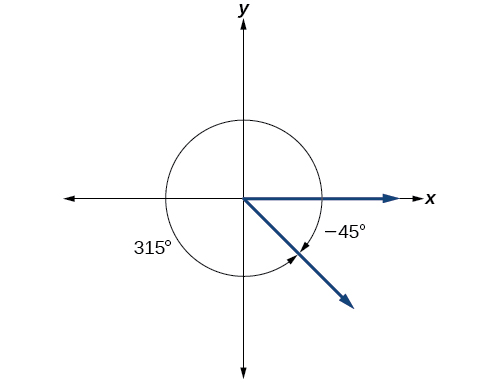
\[−45°+360°=315°\]
Nous pouvons ensuite montrer l'angle sur un cercle, comme dans la figure\(\PageIndex{20}\).
\(\PageIndex{6}\)
Trouvez un angle β qui est coterminal avec un angle de −300° tel que\(0°≤β<360°\).
Solution
\(β=60°\)
Déterminer les angles co-terminaux mesurés en radians
Nous pouvons trouver les angles coterminaux mesurés en radians de la même manière que nous les avons trouvés en degrés. Dans les deux cas, nous trouvons les angles coterminaux en ajoutant ou en soustrayant une ou plusieurs rotations complètes.
Étant donné un angle supérieur à\(2\pi\), find a coterminal angle between 0 and \(2\pi\).
- Soustrayez\(2π\) de l'angle donné.
- Si le résultat est toujours supérieur à\(2π\), soustrayez à\(2π\) nouveau jusqu'à ce que le résultat soit compris entre\(0\) et\(2π\).
- L'angle obtenu est coterminal avec l'angle d'origine.
Exemple\(\PageIndex{7}\): Finding Coterminal Angles Using Radians
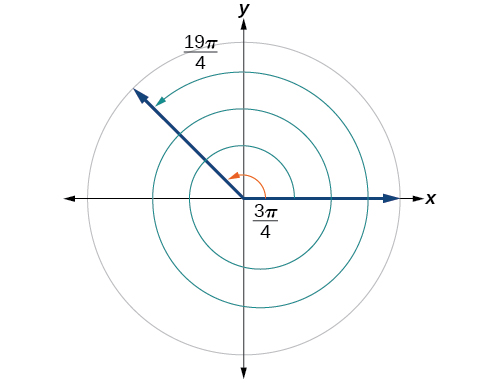
Trouvez un angle\(β\) coterminal avec\(\frac{19π}{4}\), où\(0≤β<2π.\)
Solution
Lorsque nous travaillions en degrés, nous avons trouvé des angles coterminaux en ajoutant ou en soustrayant 360 degrés, soit une rotation complète. De même, en radians, nous pouvons trouver les angles coterminaux en ajoutant ou en soustrayant les rotations complètes des\(2π\) radians :
\[\begin{align} \dfrac{19π}{4}−2π & =\dfrac{19π}{4}−\dfrac{8π}{4} \\ &=\dfrac{11π}{4} \end{align}\]
L'angle\(\frac{11π}{4}\) est coterminal, mais pas inférieur à\(2π\), donc on soustrait une autre rotation :
\[\begin{align} \dfrac{11π}{4}−2π &= \dfrac{11π}{4}−\dfrac{8π}{4} \\ &= \dfrac{3π}{4} \end{align}\]
L'angle\(\frac{3π}{4}\) est co-terminal avec\(\frac{19π}{4}\), comme le montre la figure\(\PageIndex{21}\).
\(\PageIndex{7}\)
Trouvez un angle de\(θ\) mesure coterminal avec un angle de mesure\(−\frac{17π}{6}\) où\(0≤θ<2π.\)
Solution
\(\frac{7π}{6}\)
Déterminer la longueur d'un arc
Rappelons que la mesure en\(θ\) radians d'un angle a été définie comme le rapport entre la longueur\(s\) de l'arc d'un arc circulaire et le rayon\(r\) du cercle,\(θ=\frac{s}{r}\). À partir de cette relation, nous pouvons trouver la longueur d'un arc le long d'un cercle, donné un angle.
LONGUEUR DE L'ARC SUR UN CERCLE
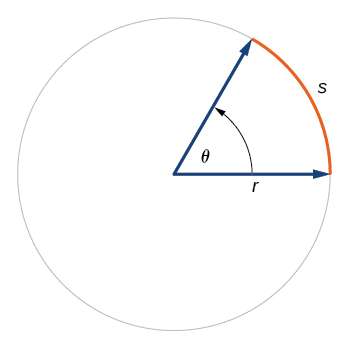
Dans un cercle de rayon r, la longueur d'un arc\(s\) sous-tendu par un angle avec une mesure\(θ\) en radians, illustrée sur la figure\(\PageIndex{22}\), est
\[s=rθ\]
Étant donné un cercle de rayon\(r,\) calculate the length \(s\) of the arc subtended by a given angle of measure \(θ\).
- Si nécessaire,\(θ\) convertissez-la en radians.
- Multipliez le rayon\(r\) par la mesure en radian de\(θ:s=rθ\).
Exemple\(\PageIndex{8}\): Finding the Length of an Arc
Supposons que l'orbite de Mercure autour du soleil forme un cercle parfait. Mercure se trouve à environ 36 millions de kilomètres du soleil.
- En un jour terrestre, Mercure effectue 0,0114 de sa révolution totale. Combien de kilomètres parcoure-t-il en une journée ?
- Utilisez votre réponse à la partie (a) pour déterminer la mesure en radian du mouvement de Mercure en un jour terrestre.
Solution
- Commençons par déterminer la circonférence de l'orbite de Mercure.
\[\begin{align} C &=2πr \\ &=2π(\text{36 million miles}) \\ &≈226 \text{ million miles} \end{align}\]
Puisque Mercure effectue 0,0114 de sa révolution totale en un jour terrestre, nous pouvons maintenant déterminer la distance parcourue :
\[(0.0114)226 \text{ million miles} = 2.58 \text{ million miles}\]
- Maintenant, nous convertissons en radians :
\[\begin{align} \text{radian} & = \dfrac{\text{arc length}}{\text{radius}} \\ &= \dfrac{2.58 \text{ million miles}}{36 \text{ million miles}} \\ & =0.0717 \end{align} \]
\(\PageIndex{8}\)
Détermine la longueur de l'arc le long d'un cercle de 10 unités de rayon sous-tendu par un angle de 215°.
Solution
\[\dfrac{215π}{18}=37.525 \text{ units} \]
Déterminer l'aire d'un secteur d'un cercle
En plus de la longueur de l'arc, nous pouvons également utiliser des angles pour déterminer l'aire d'un secteur d'un cercle. Un secteur est une région d'un cercle délimitée par deux rayons et l'arc intercepté, comme une tranche de pizza ou de tarte. Rappelez-vous que l'aire d'un cercle avec un rayon\(r\) peut être trouvée à l'aide de la formule\(A=πr^2\). Si les deux rayons forment un angle de\(θ\), mesuré en radians, alors\(\frac{θ}{2π}\) est le rapport entre l'angle mesuré et la mesure d'une rotation complète et est donc également le rapport entre l'aire du secteur et l'aire du cercle. Ainsi, la surface d'un secteur est la fraction\(\frac{θ}{2π}\) multipliée par l'ensemble de la surface. (N'oubliez pas que cette formule ne s'applique que si elle\(θ\) est exprimée en radians.)
\[\begin{align} \text{Area of sector} & =(\dfrac{θ}{2π})πr^2 \\ &=\dfrac{θπr^2}{2π} \\ & =\dfrac{1}{2}θr^2 \end{align}\]
SUPERFICIE D'UN SECTEUR
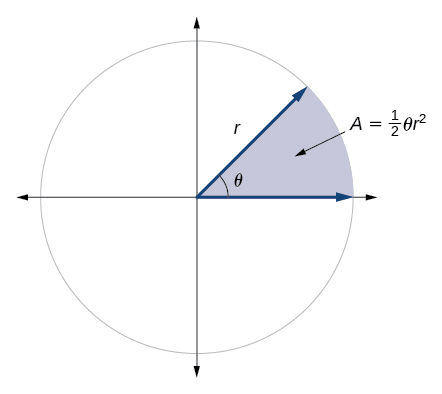
L'aire d'un secteur d'un cercle dont le rayon est\(r\) sous-tendu par un angle\(θ\), mesuré en radians, est
\[A=\dfrac{1}{2}θr^2\]
Voir la figure\(\PageIndex{23}\).
Étant donné un cercle de rayon\(r,\) find the area of a sector defined by a given angle \(θ.\)
- Si nécessaire,\(θ\) convertissez-la en radians.
- Multipliez la moitié de la mesure en\(θ\) radians de par le carré du rayon\(r: A=\frac{1}{2}θr^2.\)
Exemple\(\PageIndex{9}\): Finding the Area of a Sector
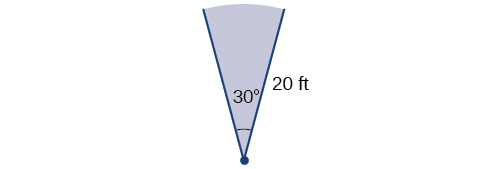
Un arroseur de pelouse automatique pulvérise sur une distance de 20 pieds tout en pivotant de 30 degrés, comme indiqué sur la figure\(\PageIndex{24}\). Quelle est la superficie du secteur d'herbe où se trouvent les eaux des arroseurs ?
Solution
Tout d'abord, nous devons convertir la mesure de l'angle en radians. Comme 30 degrés est l'un de nos angles spéciaux, nous connaissons déjà la mesure équivalente en radians, mais nous pouvons également convertir :
\[\begin{align} \text{30 degrees} &=30⋅\frac{π}{180} \\ &=\frac{π}{6} \text{ radians} \end{align}\]
La superficie du secteur est alors
\[\begin{align} \text{Area} &= \dfrac{1}{2}(\dfrac{π}{6})(20)^2 \\ & ≈104.72 \end{align}\]
Donc, la région est à peu près\(\mathrm{104.72 \; ft^2}\).
\(\PageIndex{9}\)
Dans l'irrigation à pivot central, un grand tuyau d'irrigation sur roues tourne autour d'un point central. Un agriculteur dispose d'un système de pivot central d'un rayon de 400 mètres. Si les restrictions d'eau ne lui permettent d'arroser que 150 000 mètres carrés par jour, quel angle doit-elle couvrir le système ? Écrivez la réponse en radians à deux décimales près.
Solution
1,88
Utiliser la vitesse linéaire et angulaire pour décrire le mouvement sur une trajectoire circulaire
En plus de déterminer l'aire d'un secteur, nous pouvons utiliser des angles pour décrire la vitesse d'un objet en mouvement. Un objet se déplaçant sur une trajectoire circulaire possède deux types de vitesse. La vitesse linéaire est la vitesse le long d'une trajectoire droite et peut être déterminée par la distance sur laquelle elle se déplace (son déplacement) dans un intervalle de temps donné. Par exemple, si une roue d'un rayon de 5 pouces tourne une fois par seconde, un point situé sur le bord de la roue se déplace sur une distance égale à la circonférence, soit 10 pouces π, chaque seconde. La vitesse linéaire du point est donc\(10π\) atteinte. /s. L'équation de la vitesse linéaire est la suivante, où\(v\) est la vitesse linéaire,\(s\) le déplacement et\(t\) le temps.
\[v=\dfrac{s}{t}\]
La vitesse angulaire résulte d'un mouvement circulaire et peut être déterminée par l'angle de rotation d'un point dans un intervalle de temps donné. En d'autres termes, la vitesse angulaire est la rotation angulaire par unité de temps. Ainsi, par exemple, si un engrenage effectue une rotation complète toutes les 4 secondes, nous pouvons calculer sa vitesse angulaire à\(\frac{360 \text{ degrees}}{4 \text{ seconds}}= \) 90 degrés par seconde. La vitesse angulaire peut être donnée en radians par seconde, en rotations par minute ou en degrés par heure par exemple. L'équation de la vitesse angulaire est la suivante, où\(ω\) (lue en oméga)\(θ\) est la vitesse angulaire, l'angle parcouru et\(t\) le temps.
\[ω=\dfrac{θ}{t}\]
En combinant la définition de la vitesse angulaire avec l'équation de la longueur de l'arc\(s=rθ\), nous pouvons trouver une relation entre les vitesses angulaires et linéaires. L'équation de la vitesse angulaire peut être résolue pour\(θ\), en\(θ=ωt.\) remplaçant cette équation dans l'équation de longueur de l'arc, on obtient :
\[\begin{align}s &=rθ \\ &=rωt \end{align}\]
En le remplaçant dans l'équation de vitesse linéaire, on obtient :
\[\begin{align} v & = \dfrac{s}{t} &=\dfrac{rωt}{t} &=rω \end{align}\]
VITESSE ANGULAIRE ET LINÉAIRE
Lorsqu'un point se déplace le long d'un cercle de rayon,\(r,\) sa vitesse angulaire\(ω\),, est la rotation angulaire\(θ\) par unité de temps,\(t\).
\[ω=\dfrac{θ}{t}\]
La vitesse linéaire. \(v\), du point peut être trouvé sous la forme de la distance parcourue, de la longueur de l'arc\(s\), par unité de temps,\(t.\)
\[v=\frac{s}{t}\]
Lorsque la vitesse angulaire est mesurée en radians par unité de temps, la vitesse linéaire et la vitesse angulaire sont liées par l'équation
\[v=rω\]
Cette équation indique que la vitesse angulaire en radians\(ω\), représentant la quantité de rotation se produisant dans une unité de temps, peut être multipliée par le rayon\(r\) pour calculer la longueur totale de l'arc parcouru en une unité de temps, qui est la définition de la vitesse linéaire.
Compte tenu de la quantité de rotation angulaire et du temps écoulé, calculez la vitesse angulaire
- Si nécessaire, convertissez la mesure d'angle en radians.
- Divisez l'angle en radians par le nombre d'unités de temps écoulées :\(ω=\frac{θ}{t}.\)
- La vitesse résultante sera exprimée en radians par unité de temps.
Exemple\(\PageIndex{10}\): Finding Angular Speed
Une roue hydraulique, illustrée à la figure\(\PageIndex{25}\), effectue 1 rotation toutes les 5 secondes. Détermine la vitesse angulaire en radians par seconde.
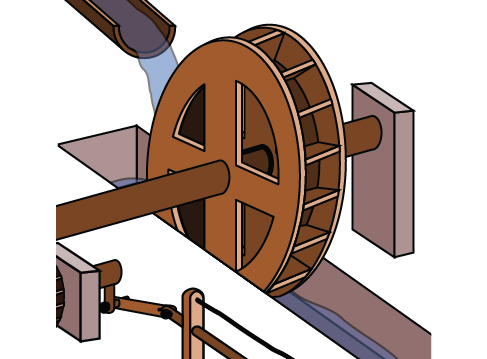
Solution
La roue effectue 1 rotation ou passe par un angle de\(2π\) radians en 5 secondes, de sorte que la vitesse angulaire serait de\(ω=\frac{2π}{5}≈1.257\) radians par seconde.
\(\PageIndex{10}\)
Un vieux disque vinyle est joué sur une platine tournant dans le sens des aiguilles d'une montre à raison de 45 rotations par minute. Détermine la vitesse angulaire en radians par seconde.
Solution
\(−\frac{3π}{2}\)rad/s
En fonction du rayon d'un cercle, de l'angle de rotation et de la durée écoulée, déterminez la vitesse linéaire
- Convertissez la rotation totale en radians si nécessaire.
- Divisez la rotation totale en radians par le temps écoulé pour trouver la vitesse angulaire : appliquez\(ω=\frac{θ}{t}\).
- Multipliez la vitesse angulaire par la longueur du rayon pour obtenir la vitesse linéaire, exprimée en termes d'unité de longueur utilisée pour le rayon et d'unité de temps utilisée pour le temps écoulé : appliquer\(v=rω\).
Exemple\(\PageIndex{11}\): Finding a Linear Speed
Un vélo a des roues de 28 pouces de diamètre. Un tachymètre détermine que les roues tournent à 180 tr/min (tours par minute). Déterminez la vitesse à laquelle le vélo roule sur la route.
Solution
Ici, nous avons une vitesse angulaire et nous devons trouver la vitesse linéaire correspondante, car la vitesse linéaire de l'extérieur des pneus est la vitesse à laquelle le vélo se déplace sur la route.
Nous commençons par convertir les rotations par minute en radians par minute. Il peut être utile d'utiliser les unités pour effectuer cette conversion :
\[\mathrm{180 \dfrac{\cancel{rotations}}{minute}⋅\dfrac{2π \; radians}{\cancel{rotation}}=360π\dfrac{radians}{minute}}\]
En utilisant la formule ci-dessus et le rayon des roues, nous pouvons trouver la vitesse linéaire :
\[\begin{align} v & =(14 \text{ inches})(360π \dfrac{\text{radians}}{\text{minute}}) \\ &=5040π \dfrac{\text{inches}}{\text{minute}} \end{align}\]
N'oubliez pas que les radians sont une mesure sans unité, il n'est donc pas nécessaire de les inclure. Mesure sans unité, il n'est donc pas nécessaire de les inclure.
Enfin, nous souhaiterons peut-être convertir cette vitesse linéaire en une mesure plus familière, comme les miles par heure.
\[\mathrm{5040π\dfrac{\cancel{inches}}{\cancel{minute}}⋅\dfrac{1 \; \cancel{ feet}}{12 \; \cancel{ inches}}⋅\dfrac{1 \; \cancel{ mile}}{5280 \cancel{ feet}}⋅\dfrac{60 \cancel{ minutes}}{1 \; hour}≈14.99 \; miles \; per \; hour \; (mph)}\]
![]() \(\PageIndex{11}\)
\(\PageIndex{11}\)
Un satellite tourne autour de la Terre à 0,25 radian par heure à une altitude de 242 km au-dessus de la Terre. Si le rayon de la Terre est de 6378 kilomètres, trouvez la vitesse linéaire du satellite en kilomètres par heure.
Solution
1655 kilomètres par heure
Médias
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires concernant les angles, la longueur des arcs et les zones des secteurs.
Équations clés
| longueur de l'arc | \(s=rθ\) |
| area of a sector | \(A=\frac{1}{2}θr^2\) |
| angular speed | \(ω=\frac{θ}{t}\) |
| linear speed | \(v=\frac{s}{t}\) |
| linear speed related to angular speed | \(v=rω\) |
Key Concepts
- An angle is formed from the union of two rays, by keeping the initial side fixed and rotating the terminal side. The amount of rotation determines the measure of the angle.
- An angle is in standard position if its vertex is at the origin and its initial side lies along the positive x-axis. A positive angle is measured counterclockwise from the initial side and a negative angle is measured clockwise.
- To draw an angle in standard position, draw the initial side along the positive x-axis and then place the terminal side according to the fraction of a full rotation the angle represents. See Example.
- In addition to degrees, the measure of an angle can be described in radians. See Example.
- To convert between degrees and radians, use the proportion \(\frac{θ}{180}=\frac{θ^R}{π}\). See Example and Example.
- Two angles that have the same terminal side are called coterminal angles.
- We can find coterminal angles by adding or subtracting 360° or \(2π\). See Example and Example.
- Coterminal angles can be found using radians just as they are for degrees. See Example.
- The length of a circular arc is a fraction of the circumference of the entire circle. See Example.
- The area of sector is a fraction of the area of the entire circle. See Example.
- An object moving in a circular path has both linear and angular speed.
- The angular speed of an object traveling in a circular path is the measure of the angle through which it turns in a unit of time. See Example.
- The linear speed of an object traveling along a circular path is the distance it travels in a unit of time. See Example.
Glossary
- angle
- the union of two rays having a common endpoint
- angular speed
- the angle through which a rotating object travels in a unit of time
- arc length
- the length of the curve formed by an arc
- area of a sector
- area of a portion of a circle bordered by two radii and the intercepted arc; the fraction \(\frac{θ}{2π}\) multiplied by the area of the entire circle
- coterminal angles
- description of positive and negative angles in standard position sharing the same terminal side
- degree
- a unit of measure describing the size of an angle as one-360th of a full revolution of a circle
- initial side
- the side of an angle from which rotation begins
- linear speed
- the distance along a straight path a rotating object travels in a unit of time; determined by the arc length
- measure of an angle
- the amount of rotation from the initial side to the terminal side
- negative angle
- description of an angle measured clockwise from the positive x-axis
- positive angle
- description of an angle measured counterclockwise from the positive x-axis
- quadrantal angle
- an angle whose terminal side lies on an axis
- radian measure
- the ratio of the arc length formed by an angle divided by the radius of the circle
- radian
- the measure of a central angle of a circle that intercepts an arc equal in length to the radius of that circle
- ray
- one point on a line and all points extending in one direction from that point; one side of an angle
- reference angle
- the measure of the acute angle formed by the terminal side of the angle and the horizontal axis
- standard position
- the position of an angle having the vertex at the origin and the initial side along the positive x-axis
- terminal side
- the side of an angle at which rotation ends
- vertex
- the common endpoint of two rays that form an angle


