6.2 : Graphiques de fonctions exponentielles
- Page ID
- 195658
- Tracez des fonctions exponentielles.
- Représentez des fonctions exponentielles sous forme graphique à
Comme nous l'avons vu dans la section précédente, les fonctions exponentielles sont utilisées pour de nombreuses applications du monde réel telles que la finance, la criminalistique, l'informatique et la plupart des sciences de la vie. Le fait de travailler avec une équation qui décrit une situation réelle nous donne une méthode pour faire des prédictions. Toutefois, la plupart du temps, l'équation elle-même ne suffit pas. Nous apprenons beaucoup de choses sur les choses en regardant leurs représentations picturales, et c'est exactement pourquoi la représentation graphique d'équations exponentielles est un outil puissant. Cela nous donne une autre couche d'informations pour prévoir les événements futurs.
Représentation graphique de fonctions exponentielles
Avant de commencer à dessiner des graphiques, il est utile de passer en revue le comportement de la croissance exponentielle. Rappelez le tableau des valeurs d'une fonction de la forme\(f(x)=b^x\) dont la base est supérieure à un. Nous allons utiliser la fonction\(f(x)=2^x\). Observez comment les valeurs de sortie du tableau\(\PageIndex{1}\) changent à mesure que l'entrée augmente de\(1\).
| \(x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|---|---|---|
| \(f(x)=2^x\) | \(\dfrac{1}{8}\) | \(\dfrac{1}{4}\) | \(\dfrac{1}{2}\) | \(1\) | \(2\) | \(4\) | \(8\) |
Chaque valeur de sortie est le produit de la sortie précédente et de la base,\(2\). Nous appelons la base\(2\) le ratio constant. En fait, pour toute fonction exponentielle avec la forme\(f(x)=ab^x\),\(b\) est le ratio constant de la fonction. Cela signifie que lorsque l'entrée augmente de\(1\), la valeur de sortie sera le produit de la base et de la sortie précédente, quelle que soit la valeur de\(a\).
Remarquez dans le tableau que
- les valeurs de sortie sont positives pour toutes les valeurs de\(x\) ;
- à mesure qu'elles\(x\) augmentent, les valeurs de sortie augmentent sans borne ; et
- à mesure qu'elles\(x\) diminuent, les valeurs de sortie diminuent et se rapprochent de zéro.
La figure\(\PageIndex{1}\) montre la fonction de croissance exponentielle\(f(x)=2^x\).
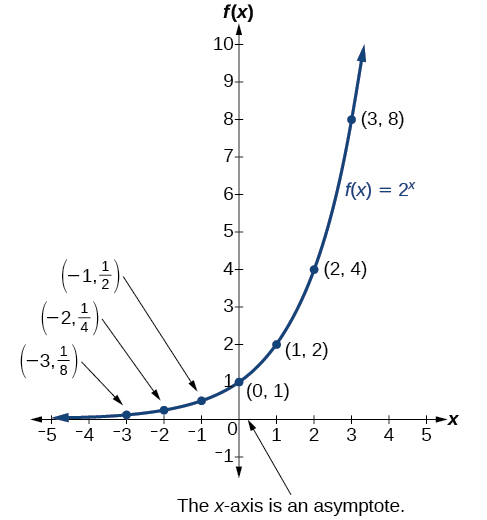
Le domaine de\(f(x)=2^x\) est composé uniquement de nombres réels, la plage est\((0,\infty)\) et l'asymptote horizontale est\(y=0\).
Pour avoir une idée du comportement de la décroissance exponentielle, nous pouvons créer une table de valeurs pour une fonction de la forme\(f(x)=b^x\) dont la base est comprise entre zéro et un. Nous allons utiliser la fonction\(g(x)={\left(\dfrac{1}{2}\right)}^x\). Observez comment les valeurs de sortie du tableau\(\PageIndex{2}\) changent à mesure que l'entrée augmente de\(1\).
| \(x\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|---|---|---|
| \(g(x)={\left(\dfrac{1}{2}\right)}^x\) | \(8\) | \(4\) | \(2\) | \(1\) | \(\dfrac{1}{2}\) | \(\dfrac{1}{4}\) | \(\dfrac{1}{8}\) |
Encore une fois, étant donné que l'entrée augmente de\(1\), chaque valeur de sortie est le produit de la sortie précédente et de la base, ou rapport constant\(\dfrac{1}{2}\).
Remarquez dans le tableau que
- les valeurs de sortie sont positives pour toutes les valeurs de\(x\) ;
- à mesure qu'elles\(x\) augmentent, les valeurs de sortie diminuent, se rapprochant de zéro ; et
- à mesure qu'elles\(x\) diminuent, les valeurs de sortie augmentent sans limite.
La figure\(\PageIndex{2}\) montre la fonction de décroissance exponentielle,\(g(x)={\left(\dfrac{1}{2}\right)}^x\).
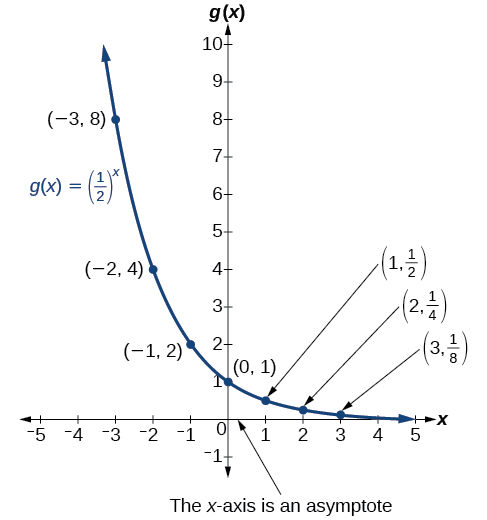
Le domaine de\(g(x)={(\dfrac{1}{2})}^x\) est composé uniquement de nombres réels, la plage est\((0,\infty)\) et l'asymptote horizontale est\(y=0\).
Une fonction exponentielle de la forme\(f(x)=b^x\),,\(b>0\)\(b≠1\), possède les caractéristiques suivantes :
- fonction un à un
- asymptote horizontale :\(y=0\)
- domaine :\((–\infty, \infty)\)
- gamme :\((0,\infty)\)
- x- Interception : aucune
- Interception y- :\((0,1)\)
- augmentant si\(b>1\)
- décroissant si\(b<1\)
La figure\(\PageIndex{3}\) compare les graphiques des fonctions de croissance exponentielle et de décroissance.
- Créez un tableau de points.
- Tracez au moins\(3\) un point de la table, y compris l'intersection\((0,1)\) y.
- Tracez une courbe lisse à travers les points.
- Indiquez le domaine\((−\infty,\infty)\), la plage et l'asymptote horizontale\(y=0\).\((0,\infty)\)
Esquissez un graphique de\(f(x)=0.25^x\). Indiquez le domaine, la plage et l'asymptote.
Solution
Avant de créer un graphique, identifiez le comportement et créez un tableau de points pour le graphique.
| \(x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|---|---|---|
| \(f(x)={0.25}^x\) | \(64\) | \(16\) | \(4\) | \(1\) | \(0.25\) | \ (0,0625 \ 0) | \(0.015625\) |
- Comme elle\(b=0.25\) est comprise entre zéro et un, nous savons que la fonction est décroissante. La queue gauche du graphique augmentera sans limite, et la queue droite s'approchera de l'asymptote\(y=0\).
- Créez un tableau de points comme dans Tableau\(\PageIndex{3}\).
- Tracez l'intersection y,\((0,1)\), ainsi que deux autres points. Nous pouvons utiliser\((−1,4)\) et\((1,0.25)\).
Tracez une courbe lisse reliant les points comme dans la figure\(\PageIndex{4}\).
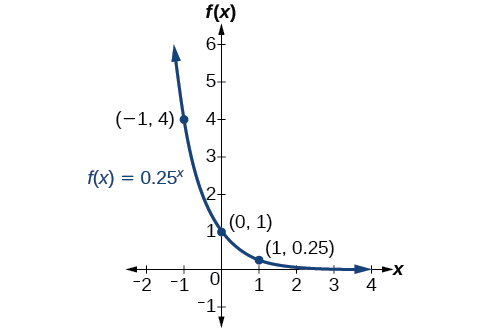
Le domaine est\((−\infty,\infty)\) ; la plage est\((0,\infty)\) ; l'asymptote horizontale est\(y=0\).
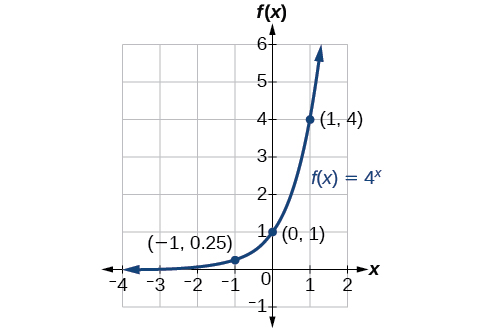
Esquissez le graphique de\(f(x)=4^x\). Indiquez le domaine, la plage et l'asymptote.
- Réponse
-
Le domaine est\((−\infty,\infty)\) ; la plage est\((0,\infty)\) ; l'asymptote horizontale est\(y=0\).
Représentation graphique des transformations de fonctions exponentielles
Les transformations des graphes exponentiels se comportent de la même manière que celles des autres fonctions. Comme pour les autres fonctions parentales, nous pouvons appliquer les quatre types de transformations (décalages, réflexions, étirements et compressions) à la fonction parent\(f(x)=b^x\) sans perte de forme. Par exemple, tout comme la fonction quadratique conserve sa forme parabolique lorsqu'elle est décalée, réfléchie, étirée ou comprimée, la fonction exponentielle conserve également sa forme générale quelles que soient les transformations appliquées.
Représentation graphique d'un décalage vertical
La première transformation se produit lorsque nous ajoutons une constante\(d\) à la fonction parent\(f(x)=b^x\), ce qui nous donne un décalage vertical d unités dans la même direction que le signe. Par exemple, si nous commençons par représenter graphiquement une fonction parent\(f(x)=2^x\), nous pouvons ensuite représenter graphiquement deux décalages verticaux le long de celle-ci, en utilisant\(d=3\) : le décalage vers le haut\(g(x)=2^x+3\) et le décalage vers le bas\(h(x)=2^x−3\). Les deux décalages verticaux sont illustrés sur la figure\(\PageIndex{5}\).
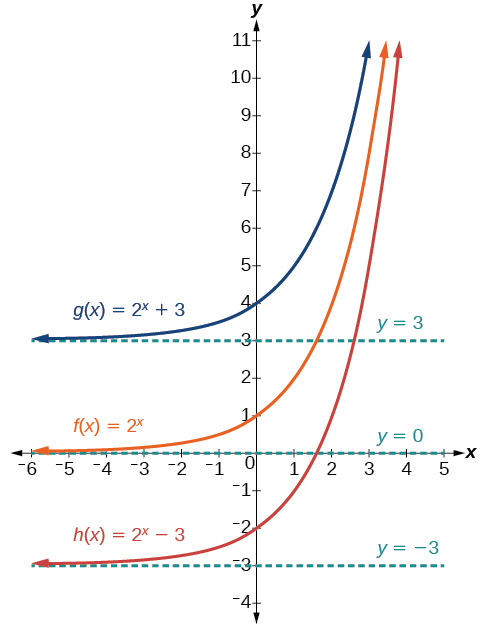
Observez les résultats du déplacement\(f(x)=2^x\) vertical :
- Le domaine\((−\infty,\infty)\) reste inchangé.
- Lorsque la fonction est déplacée vers le haut,\(3\) unités pour\(g(x)=2^x+3\) :
- L'intersection y déplace les\(3\) unités vers le haut vers\((0,4)\).
- L'asymptote déplace les\(3\) unités vers le haut vers\(y=3\).
- La gamme devient\((3,\infty)\).
- Lorsque la fonction est déplacée vers le bas, les\(3\) unités\(h(x)=2^x−3\) suivantes sont affichées
- L'intersection y déplace les\(3\) unités vers le bas vers\((0,−2)\).
- L'asymptote déplace également les\(3\) unités vers le bas vers\(y=−3\).
- La gamme devient\((−3,\infty)\).
Représentation graphique d'un décalage horizontal
La transformation suivante se produit lorsque nous ajoutons une constante\(c\) à l'entrée de la fonction parent\(f(x)=b^x\), ce qui nous donne un décalage horizontal des\(c\) unités dans la direction opposée au signe. Par exemple, si nous commençons par représenter graphiquement la fonction parent\(f(x)=2^x\), nous pouvons ensuite représenter graphiquement deux décalages horizontaux le long de celle-ci, en utilisant\(c=3\) : le décalage vers la gauche et le décalage vers la droite\(h(x)=2^{x−3}\).\(g(x)=2^{x+3}\) \(h(x)=2^{x−3}\). Les deux décalages horizontaux sont illustrés sur la figure\(\PageIndex{6}\).
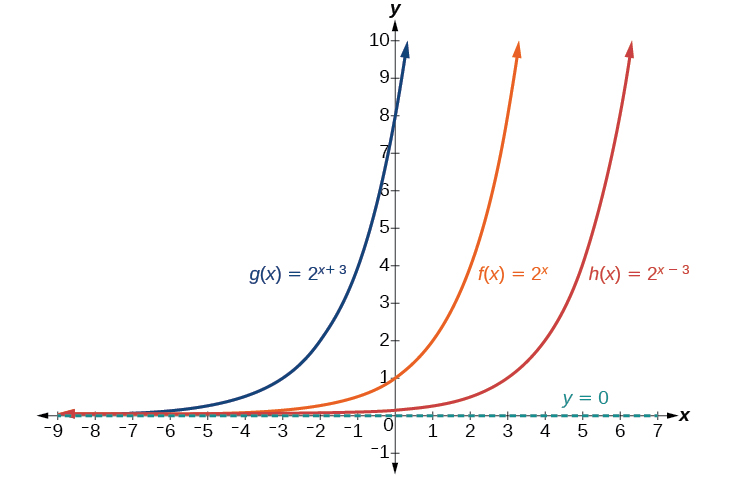
Observez les résultats du déplacement\(f(x)=2^x\) horizontal :
- Le domaine,\((−\infty,\infty)\), reste inchangé.
- L'asymptote,\(y=0\), reste inchangé.
- L'intersection y se déplace de telle sorte que :
- Lorsque la fonction est déplacée des\(3\) unités de gauche vers\(g(x)=2^{x+3}\), l'intersection y devient\((0,8)\). Cela est dû\(2^{x+3}=(8)2^x\) au fait que la valeur initiale de la fonction est donc\(8\).
- Lorsque la fonction est déplacée\(3\) d'unités\(h(x)=2^{x−3}\) droites vers, l'intersection y devient\((0,\dfrac{1}{8})\). Encore une fois, voyez cela\(2^{x−3}=(\dfrac{1}{8})2^x\), donc la valeur initiale de la fonction est\(\dfrac{1}{8}\).
Pour toutes les constantes\(c\) et\(d\), la fonction\(f(x)=b^{x+c}+d\) déplace la fonction parent\(f(x)=b^x\)
- \(d\)unités verticales, dans la même direction que le signe de\(d\).
- \(c\)unités horizontales, dans la direction opposée au signe de\(c\).
- L'intersection y devient\((0,b^c+d)\).
- L'asymptote horizontale devient\(y=d\).
- La gamme devient\((d,\infty)\).
- Le domaine,\((−\infty,\infty)\), reste inchangé.
- Dessine l'asymptote horizontale\(y=d\).
- Identifiez le quart de travail comme\((−c,d)\). Déplace le graphique des\(c\) unités de\(f(x)=b^x\) gauche si elle\(c\) est positive et des\(c\) unités de droite si elle\(c\) est négative.
- Déplace le graphique des\(d\) unités vers le\(f(x)=b^x\) haut si\(d\) c'est positif et des\(d\) unités vers le bas si\(d\) c'est négatif.
- Indiquez le domaine\((−\infty,\infty)\), la plage et l'asymptote horizontale\(y=d\).\((d,\infty)\)
Graphe\(f(x)=2^{x+1}−3\). Indiquez le domaine, la plage et l'asymptote.
Solution
Nous avons une équation exponentielle de la forme\(f(x)=b^{x+c}+d\), avec\(b=2\)\(c=1\), et\(d=−3\).
Dessinez l'asymptote horizontale\(y=d\), alors dessinez\(y=−3\).
Identifiez le quart de travail comme étant\((−c,d)\), ainsi, le quart de travail\((−1,−3)\).
Déplace le graphique des\(1\) unités\(f(x)=b^x\) gauches et des\(3\) unités descendantes.
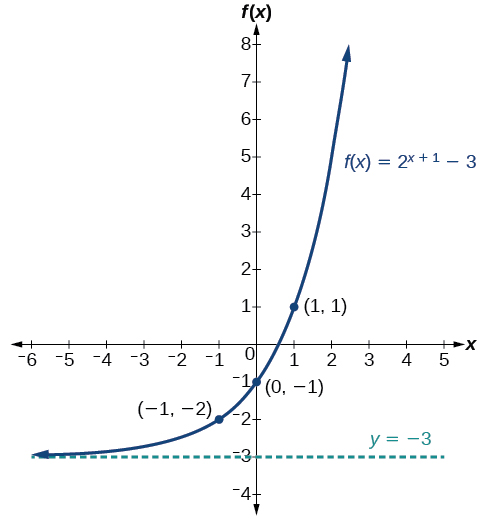
Le domaine est\((−\infty,\infty)\) ; la plage est\((−3,\infty)\) ; l'asymptote horizontale est\(y=−3\).
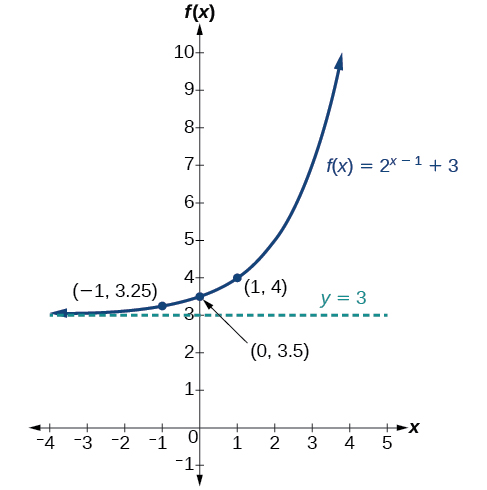
Graphe\(f(x)=2^{x−1}+3\). Domaine d'état, plage et asymptote.
- Réponse
-
Le domaine est\((−\infty,\infty)\) ; la plage est\((3,\infty)\) ; l'asymptote horizontale est\(y=3\).
- Appuyez sur [Y=]. Entrez l'équation exponentielle donnée sur la ligne intitulée « Y 1 = ».
- Entrez la valeur donnée pour f (x) f (x) dans la ligne intitulée « Y 2 = ».
- Appuyez sur [FENÊTRE]. Ajustez l'axe y de manière à ce qu'il inclue la valeur saisie pour « Y 2 = ».
- Appuyez sur [GRAPH] pour observer le graphique de la fonction exponentielle ainsi que la ligne correspondant à la valeur spécifiée off (x). f (x).
- Pour trouver la valeur de x, x, nous calculons le point d'intersection. Appuyez sur [2ND] puis sur [CALC]. Sélectionnez « Intersecter » et appuyez trois fois sur [ENTER]. Le point d'intersection donne la valeur de x pour la valeur indiquée de la fonction.
Résolvez\(42=1.2{(5)}^x+2.8\) graphiquement Arrondir au millième le plus proche.
Solution
Appuyez sur [Y=] et entrez à\(1.2{(5)}^x+2.8\) côté de Y 1 =. Entrez ensuite à\(42\) côté de Y2=. Pour une fenêtre, utilisez les valeurs\(–3\)\(3\) pour\(x\) et\(–5\)\(55\) pour\(y\). Appuyez sur [GRAPH]. Les graphes doivent se croiser à proximité\(x=2\).
Pour une meilleure approximation, appuyez sur [2ND] puis sur [CALC]. Sélectionnez [5 : intersection] et appuyez trois fois sur [ENTER]. La coordonnée x du point d'intersection s'affiche sous la forme\(2.1661943\). (Votre réponse peut être différente si vous utilisez une fenêtre différente ou si vous utilisez une valeur différente pour Guess ? ) Au millième le plus proche,\(x≈2.166\).
Résolvez\(4=7.85{(1.15)}^x−2.27\) graphiquement Arrondir au millième le plus proche.
- Réponse
-
\(x≈−1.608\)
Représenter graphiquement un étirement ou une compression
Alors que les décalages horizontaux et verticaux impliquent l'ajout de constantes à l'entrée ou à la fonction elle-même, un étirement ou une compression se produit lorsque nous multiplions la fonction parent\(f(x)=b^x\) par une constante\(|a|>0\). Par exemple, si nous commençons par représenter graphiquement la fonction parent\(f(x)=2^x\), nous pouvons ensuite représenter graphiquement l'étirement\(a=3\), en utilisant, pour obtenir\(g(x)=3{(2)}^x\) comme indiqué à gauche dans la Figure\(\PageIndex{8}\), et la compression, en utilisant\(a=\dfrac{1}{3}\), pour obtenir\(h(x)=\dfrac{1}{3}{(2)}^x\) comme indiqué à droite dans la Figure\(\PageIndex{8}\).
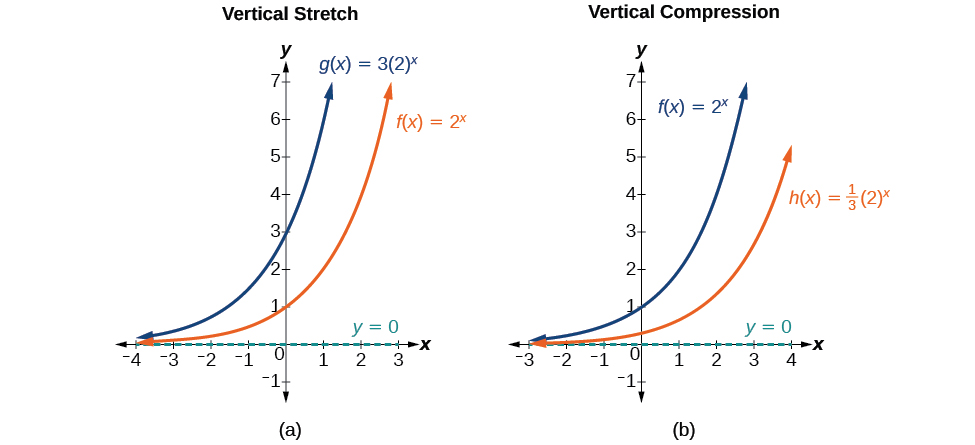
Quel que soit le facteur\(a>0\), la fonction\(f(x)=a{(b)}^x\)
- est étiré verticalement d'un facteur\(a\) if\(|a|>1\).
- est compressé verticalement d'un facteur\(a\) if\(|a|<1\).
- possède une intersection y de\((0,a)\).
- possède une asymptote horizontale à\(y=0\), une plage de\((0,\infty)\) et un domaine de\((−\infty,\infty)\), qui sont inchangés par rapport à la fonction parent.
Esquissez un graphique de\(f(x)=4{(\dfrac{1}{2})}^x\). Indiquez le domaine, la plage et l'asymptote.
Solution
Avant de créer un graphique, identifiez le comportement et les points clés du graphique.
- Comme\(b=\dfrac{1}{2}\) il est compris entre zéro et un, l'extrémité gauche du graphique augmentera sans limite à\(x\) mesure que la valeur diminue, et la queue droite s'approchera de l'axe des X lorsque la valeur\(x\) augmente.
- Puisque\(a=4\), le graphique de\(f(x)={(\dfrac{1}{2})}^x\) sera étiré d'un facteur de\(4\).
- Créez un tableau de points comme indiqué dans le tableau\(\PageIndex{4}\).
Tableau\(\PageIndex{4}\) \(x\) \(−3\) \(−2\) \(−1\) \(0\) \(1\) \(2\) \(3\) \(f(x)=4{(\dfrac{1}{2})}^x\) \(32\) \(16\) \(8\) \(4\) \(2\) \(1\) \(0.5\) - Tracez l'intersection y\((0,4)\), ainsi que deux autres points. Nous pouvons utiliser\((−1,8)\) et\((1,2)\).
Tracez une courbe lisse reliant les points, comme indiqué sur la figure\(\PageIndex{9}\).

Le domaine est\((−\infty,\infty)\) ; la plage est\((0,\infty)\) ; l'asymptote horizontale est\(y=0\).
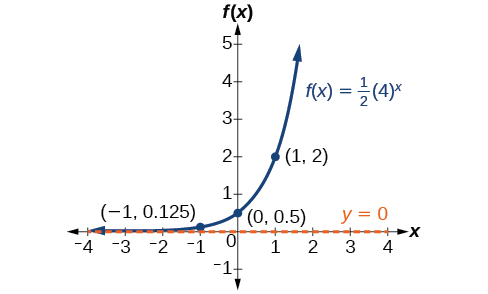
Esquissez le graphique de\(f(x)=\dfrac{1}{2}{(4)}^x\). Indiquez le domaine, la plage et l'asymptote.
- Réponse
-
Le domaine est\((−\infty,\infty)\) ; la plage est\((0,\infty)\) ; l'asymptote horizontale est\(y=0\).
Reflections graphiques
En plus de déplacer, de compresser et d'étirer un graphique, nous pouvons également le refléter autour de l'axe x ou de l'axe des y. Lorsque nous multiplions la fonction parent\(f(x)=b^x\) par\(−1\), nous obtenons une réflexion sur l'axe X. Lorsque nous multiplions l'entrée par\(−1\), nous obtenons une réflexion sur l'axe y. Par exemple, si nous commençons par représenter graphiquement la fonction parent\(f(x)=2^x\), nous pouvons ensuite représenter graphiquement les deux réflexions le long de celle-ci. La réflexion autour de l'axe x\(g(x)=−2^x\), est indiquée sur le côté gauche de la figure\(\PageIndex{10}\), et la réflexion sur l'axe y\(h(x)=2^{−x}\) est représentée sur le côté droit de la figure\(\PageIndex{10}\).
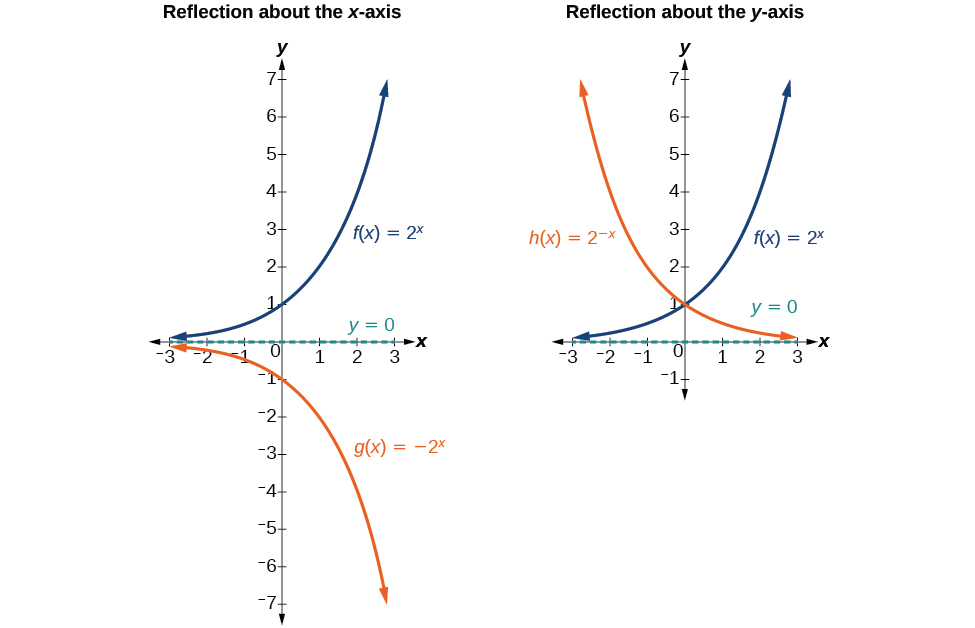
La fonction\(f(x)=−b^x\)
- reflète la fonction parent\(f(x)=b^x\) sur l'axe X.
- possède une intersection y de\((0,−1)\).
- propose une gamme de\((−\infty,0)\)
- possède une asymptote horizontale à\(y=0\) et un domaine de\((−\infty,\infty)\), qui sont inchangés par rapport à la fonction parent.
La fonction\(f(x)=b^{−x}\)
- reflète la fonction parent\(f(x)=b^x\) sur l'axe y.
- possède une intersection y\((0,1)\), une asymptote horizontale\(y=0\), une plage de et un domaine de\((0,\infty)\)\((−\infty,\infty)\), qui sont inchangés par rapport à la fonction parent.
Trouvez et représentez graphiquement l'équation d'une fonction\(g(x)\), qui se reflète\(f(x)={(\dfrac{1}{4})}^x\) autour de l'axe X. Indiquez son domaine, sa plage et son asymptote.
Solution
Puisque nous voulons refléter la fonction parent\(f(x)={(\dfrac{1}{4})}^x\) sur l'axe X, nous multiplions\(f(x)\) par\(−1\) pour obtenir,\(g(x)=−{(\dfrac{1}{4})}^x\). Ensuite, nous créons un tableau de points comme dans Tableau\(\PageIndex{5}\).
| \(x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|---|---|---|
| \(g(x)=−{(\dfrac{1}{4})}^x\) | \(−64\) | \(−16\) | \(−4\) | \(−1\) | \(−0.25\) | \(−0.0625\) | \(−0.0156\) |
Tracez l'intersection y\((0,−1)\), ainsi que deux autres points. Nous pouvons utiliser\((−1,−4)\) et\((1,−0.25)\).
Tracez une courbe lisse reliant les points :
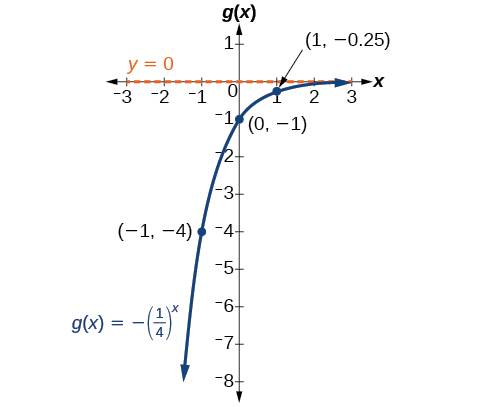
Le domaine est\((−\infty,\infty)\) ; la plage est\((−\infty,0)\) ; l'asymptote horizontale est\(y=0\).
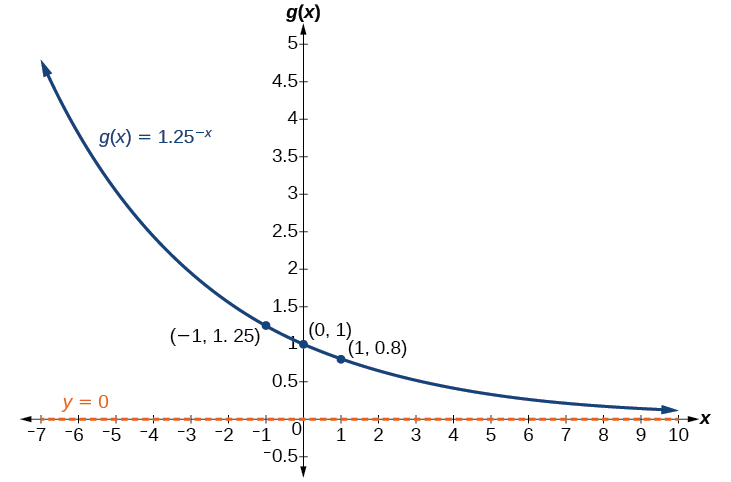
Trouvez et représentez graphiquement l'équation d'une fonction\(g(x)\), qui se reflète\(f(x)={1.25}^x\) autour de l'axe y. Indiquez son domaine, sa plage et son asymptote.
- Réponse
-
Le domaine est\((−\infty,\infty)\) ; la plage est\((0,\infty)\) ; l'asymptote horizontale est\(y=0\).
Synthèse des traductions de la fonction exponentielle
Maintenant que nous avons travaillé avec chaque type de translation pour la fonction exponentielle, nous pouvons les résumer dans le tableau\(\PageIndex{6}\) pour obtenir l'équation générale de traduction des fonctions exponentielles.
La traduction d'une fonction exponentielle a la forme
\(f(x)=ab^{x+c}+d\)
Où la fonction parent,\(y=b^x\),\(b>1\), est
- \(c\)unités horizontales décalées vers la gauche.
- étiré verticalement d'un facteur\(|a|\) if\(|a|>0\).
- compressé verticalement par un facteur\(|a|\) if\(0<|a|<1\).
- \(d\)unités décalées verticalement.
- reflété autour de l'axe X lorsque\(a<0\).
Notez que l'ordre des déplacements, des transformations et des réflexions suit l'ordre des opérations.
Écrivez l'équation de la fonction décrite ci-dessous. Indiquez l'asymptote horizontale, le domaine et la plage.
\(f(x)=e^x\)est étiré verticalement d'un facteur de\(2\), reflété sur l'axe y, puis décalé d'\(4\)unités vers le haut.
Solution
Nous voulons trouver une équation de la forme générale f (x) =abx+c+d. f (x) =abx+c+d. Nous utilisons la description fournie pour trouver a, a, b, b, c, c et d.
- On nous donne la fonction parentale\(f(x)=e^x\), donc\(b=e\).
- La fonction est étirée par un facteur de\(2\), donc\(a=2\).
- La fonction est reflétée autour de l'axe y. Nous\(x\) remplaçons par\(−x\) pour obtenir :\(e^{−x}\).
- Le graphique est décalé verticalement de 4 unités, donc\(d=4\).
En substituant dans la forme générale que nous obtenons,
\(f(x)=ab^{x+c}+d\)
\(=2e^{−x+0}+4\)
\(=2e^{−x}+4\)
Le domaine est\((−\infty,\infty)\) ; la plage est\((4,\infty)\) ; l'asymptote horizontale est\(y=4\).
Écrivez l'équation de la fonction décrite ci-dessous. Indiquez l'asymptote horizontale, le domaine et la plage.
\(f(x)=e^x\)est comprimé verticalement d'un facteur de\(\dfrac{1}{3}\), reflété sur l'axe x, puis décalé vers le bas\(2\) d'unités.
- Réponse
-
\(f(x)=−\dfrac{1}{3}e^{x}−2\); le domaine est\((−\infty,\infty)\) ; la plage est\((−\infty,2)\) ; l'asymptote horizontale est\(y=2\).
Accédez à cette ressource en ligne pour obtenir des instructions et des exercices supplémentaires sur la création graphique de fonctions exponentielles.
- Fonctions exponentielles du graphe
Équations clés
| Formulaire général pour la traduction de la fonction parent\(f(x)=b^x\) | \(f(x)=ab^{x+c}+d\) |
Concepts clés
- Le graphe de la fonction\(f(x)=b^x\) possède une intersection y à\((0, 1)\), un domaine\((−\infty, \infty)\), une plage\((0, \infty)\) et une asymptote horizontale\(y=0\). Voir l'exemple.
- Si\(b>1\), la fonction augmente. La queue gauche du graphique se rapprochera de l'asymptote\(y=0\), tandis que la queue droite augmentera sans limite.
- Si\(0<b<1\), la fonction est décroissante. La queue gauche du graphique augmentera sans limite, et la queue droite s'approchera de l'asymptote\(y=0\).
- L'équation\(f(x)=b^x+d\) représente un décalage vertical de la fonction parent\(f(x)=b^x\).
- L'équation\(f(x)=b^{x+c}\) représente un décalage horizontal de la fonction parent\(f(x)=b^x\). Voir l'exemple.
- Des solutions approximatives de l'équation\(f(x)=b^{x+c}+d\) peuvent être trouvées à l'aide d'une calculatrice graphique. Voir l'exemple.
- L'équation\(f(x)=ab^x\), où\(a>0\), représente un étirement vertical\(|a|>1\) ou une compression si\(0<|a|<1\) de la fonction parent\(f(x)=b^x\). Voir l'exemple.
- Lorsque la fonction parent\(f(x)=b^x\) est multipliée par\(−1\)\(f(x)=−b^x\), le résultat est un reflet de l'axe X. Lorsque l'entrée est multipliée par\(−1\), le résultat,\(f(x)=b^{−x}\), est une réflexion autour de l'axe y. Voir l'exemple.
- Toutes les traductions de la fonction exponentielle peuvent être résumées par l'équation générale\(f(x)=ab^{x+c}+d\). Voir le tableau.
- À l'aide de l'équation générale\(f(x)=ab^{x+c}+d\), nous pouvons écrire l'équation d'une fonction en fonction de sa description. Voir l'exemple.


