5.8 : Modélisation utilisant la variation
- Page ID
- 195584
Objectifs d'apprentissage
Dans cette section, vous allez :- Résolvez les problèmes de variation directe
- Résolvez les problèmes de variation inverse
- Résolvez les problèmes liés aux variations articulaires
Un fabricant de véhicules d'occasion vient de proposer à sa meilleure candidate, Nicole, un poste dans la vente. Le poste offre une commission de 16 % sur ses ventes. Ses revenus dépendent du montant de ses ventes. Par exemple, si elle vend un véhicule pour 4 600$, elle gagnera 736$. Elle veut évaluer l'offre, mais elle ne sait pas comment. Dans cette section, nous examinerons les relations, comme celle-ci, entre les bénéfices, les ventes et le taux de commission.
Résolution des problèmes de variation directe
Dans l'exemple ci-dessus, les revenus de Nicole peuvent être trouvés en multipliant ses ventes par sa commission. La formule nous\(e=0.16s\) indique ses revenus\(e\), proviennent du produit de 0,16, de sa commission et du prix de vente du véhicule. Si nous créons un tableau, nous observons qu'à mesure que le prix de vente augmente, les bénéfices augmentent également, ce qui devrait être intuitif. Voir le tableau 5.8.1.
| \(s\), prix de vente | \(e=0.16s\) | interprétation |
|---|---|---|
| \ (s \), prix de vente » class="lt-math-1351">9 200$ | \ (e=0,16 s \) » class="lt-math-1351">\(e=0.16(9,200)=1,472\) | La vente d'un véhicule de 9 200$ génère des revenus de 1 472$. |
| \ (s \), prix de vente » class="lt-math-1351">4 600$ | \ (e=0,16 s \) » class="lt-math-1351">\(e=0.16(4,600)=736\) | La vente d'un véhicule de 4 600$ génère des revenus de 736$. |
| \ (s \), prix de vente » class="lt-math-1351">18 400$ | \ (e=0,16 s \) » class="lt-math-1351">\(e=0.16(18,400)=2,944\) | La vente d'un véhicule de 18 400$ génère des revenus de 2 944$. |
Tableau 5.8.1
Notez que les revenus sont un multiple des ventes. À mesure que les ventes augmentent, les bénéfices augmentent de manière prévisible. Doublez les ventes du véhicule de 4 600$ à 9 200$, et nous doublons les revenus de 736$ à 1 472$. Lorsque l'entrée augmente, la sortie augmente en tant que multiple de l'entrée. Une relation dans laquelle une quantité est une constante multipliée par une autre est appelée variation directe. Chaque variable de ce type de relation varie directement avec l'autre.
La figure 5.8.1 représente les données relatives aux revenus potentiels de Nicole. Nous disons que les revenus varient directement en fonction du prix de vente de la voiture. La formule\(y=kx^n\) est utilisée pour la variation directe. La valeur\(k\) est une constante non nulle supérieure à zéro et est appelée constante de variation. Dans ce cas,\(k=0.16\) et\(n=1\). Nous avons vu des fonctions comme celle-ci lorsque nous avons discuté des fonctions de puissance.
La source de la figure n'est pas valide : image visible jusqu'à son enregistrement... src= »/@api /deki/pages/ =Bookshelves%252FPrecalculus%252FBook%25253A_Precalculus_ (OpenStax) %252F 03% 25253A_Polynomial_and_Rational_Functions%252F 3.9% 25253A_Modeling_Using_Variation/files/CNX_Precalc_Figure_03_09_001.jpg
Remarque générale : VARIATION DIRECTE
Si\(x\) et\(y\) sont liés par une équation de la forme
\(y=kx^n\)
ensuite, nous disons que la relation est une variation directe et\(y\) varie directement avec, ou est proportionnelle à,\(n\) la puissance de\(x\). Dans les relations de variation directe, il existe un ratio constant non nul\(k=\dfrac{y}{x^n}\)\(k\), appelé constante de variation, qui aide à définir la relation entre les variables.
À partir de la description d'un problème de variation directe, résolvez un problème inconnu.
- Identifiez l'entrée\(x\), et la sortie,\(y\).
- Déterminez la constante de variation. Vous devrez peut-être diviser\(y\) par la puissance spécifiée de\(x\) pour déterminer la constante de variation.
- Utilisez la constante de variation pour écrire une équation pour la relation.
- Substituez des valeurs connues dans l'équation pour trouver l'inconnu.
Exemple
Résolution d'un problème de variation directe
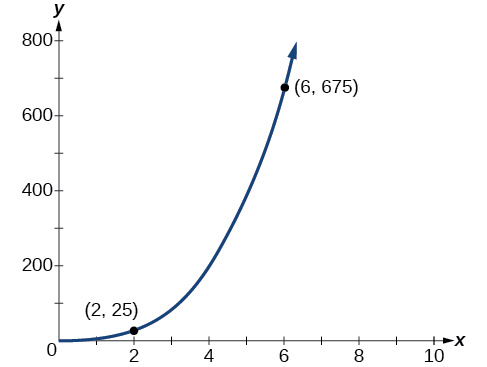
La quantité\(y\) varie directement avec le cube de\(x\). Si\(x\) c'est\(y=25\) quand\(x=2\), trouvez\(y\) quand\(6\).
Solution
La formule générale pour la variation directe avec un cube est\(y=kx^3\). La constante peut être trouvée en divisant\(y\) par le cube de\(x\).
\(k=\dfrac{y}{x^3}\)
\(=\dfrac{25}{2^3}\)
\(=\dfrac{25}{8}\)
Utilisez maintenant la constante pour écrire une équation qui représente cette relation.
\(y=\dfrac{25}{8}x^3\)
Remplacez\(x=6\) et résolvez par\(y\).
\(y=\dfrac{25}{8}{(6)}^3\)
\(=675\)
Analyse
Le graphique de cette équation est un cubique simple, comme le montre la Figure 5.8.2.
QUESTIONS-RÉPONSES
Les graphes de toutes les équations à variation directe ressemblent-ils à des exemples ?
Non. Les équations de variation directe sont des fonctions de puissance : elles peuvent être linéaires, quadratiques, cubiques, quartiques, radicales, etc. Mais tous les graphes passent par là\((0,0)\).
Exercice
La quantité\(y\) varie directement avec le carré de\(x\). Si\(y=24\) quand\(x=3\), trouvez\(y\) quand\(x\) est 4.
Solution
\(\frac{128}{3}\)
Résoudre les problèmes de variation inverse
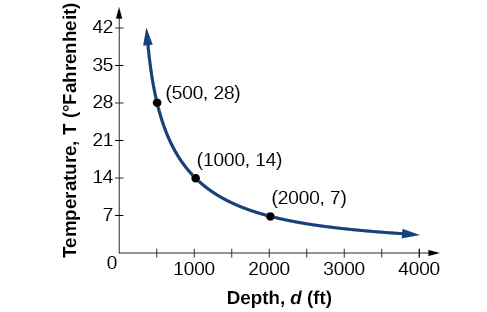
La température de l'eau d'un océan varie inversement en fonction de la profondeur de l'eau. La formule nous\(T=\frac{14,000}{d}\) donne la température en degrés Fahrenheit à une profondeur en pieds sous la surface de la Terre. Prenons l'exemple de l'océan Atlantique, qui couvre 22 % de la surface de la Terre. À un certain endroit, à une profondeur de 500 pieds, la température peut être de 28 °F.
Si nous créons le tableau 5.8.2, nous observons qu'à mesure que la profondeur augmente, la température de l'eau diminue.
| \(d\), profondeur | \(T=\frac{14,000}{d}\) | interprétation |
|---|---|---|
| \ (d \), profondeur » class="lt-math-1351">500 pieds | \ (T= \ frac {14 000} {d} \) » class="lt-math-1351">\(\frac{14,000}{500}=28\) | À une profondeur de 500 pieds, la température de l'eau est de 28 °F. |
| \ (d \), profondeur » class="lt-math-1351">1000 pieds | \ (T= \ frac {14 000} {d} \) » class="lt-math-1351">\(\frac{14,000}{1000}=14\) | À une profondeur de 1 000 pieds, la température de l'eau est de 14 °F. |
| \ (d \), profondeur » class="lt-math-1351">2000 pieds | \ (T= \ frac {14 000} {d} \) » class="lt-math-1351">\(\frac{14,000}{2000}=7\) | À une profondeur de 2 000 pieds, la température de l'eau est de 7 °F. |
Tableau 5.8.2
Nous remarquons dans la relation entre ces variables qu'à mesure qu'une quantité augmente, l'autre diminue. Les deux quantités sont dites inversement proportionnelles et chaque terme varie inversement par rapport à l'autre. Les relations inversement proportionnelles sont également appelées variations inverses.
Pour notre exemple, la Figure 5.8.3 décrit la variation inverse. Nous disons que la température de l'eau varie inversement avec la profondeur de l'eau car, à mesure que la profondeur augmente, la température diminue. Dans ce cas, la formule\(y=\frac{k}{x}\) de variation inverse utilise\(k=14,000\).
Remarque générale : VARIATION INVERSE
Si\(x\) et\(y\) sont liés par une équation de la forme
\(y=\frac{k}{x^n}\)
où\(k\) est une constante non nulle, alors on dit qu'elle\(y\) varie inversement avec\(n\) la puissance de\(x\). Dans les relations inversement proportionnelles, ou les variations inverses, il existe un multiple constant\(k=x^ny\).
Exemple
Écrire une formule pour une relation inversement proportionnelle
Un touriste prévoit de parcourir 160 km. Trouvez une formule pour la durée du trajet en fonction de la vitesse parcourue par le touriste.
Solution
Rappelez-vous que la multiplication de la vitesse par le temps donne de la distance. Si nous laissons\(t\) représenter le temps de trajet en heures et\(v\) la vitesse (vitesse ou vitesse) à laquelle le touriste se déplace, alors la\(vt=\) distance. Parce que la distance est fixée à 100 miles,\(vt=100\) donc\(t=\frac{100}{v}\). Comme le temps est fonction de la vélocité, nous pouvons écrire\(t(v)\).
\(t(v)=\frac{100}{v}\)
\(=100v^{−1}\)
Nous pouvons voir que la constante de variation est de 100 et, bien que nous puissions écrire la relation en utilisant l'exposant négatif, il est plus courant de la voir écrite sous forme de fraction. Nous disons que le temps varie inversement avec la vitesse.
À partir de la description d'un problème de variation indirecte, résolvez un problème inconnu.
- Identifiez l'entrée\(x\), et la sortie,\(y\).
- Déterminez la constante de variation. Il se peut que vous deviez multiplier\(y\) par la puissance spécifiée de\(x\) pour déterminer la constante de variation.
- Utilisez la constante de variation pour écrire une équation pour la relation.
- Substituez des valeurs connues dans l'équation pour trouver l'inconnu.
Exemple
Résolution d'un problème de variation inverse
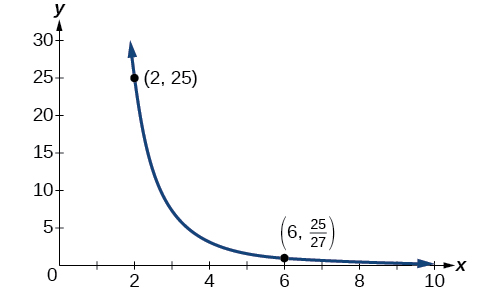
Une quantité\(y\) varie inversement avec le cube de\(x\). Si\(x\) c'est\(y=25\) quand\(x=2\), trouvez\(y\) quand\(6\).
Solution
La formule générale pour la variation inverse avec un cube est\(y=\frac{k}{x^3}\). La constante peut être trouvée en multipliant\(y\) par le cube de\(x\).
\(k=x^3y\)
\(=2^3⋅25\)
\(=200\)
Nous utilisons maintenant la constante pour écrire une équation qui représente cette relation.
\(y=\dfrac{k}{x^3}\),\( k=200\)
\(y=\dfrac{200}{x^3}\)
Remplacez\(x=6\) et résolvez par\(y\).
\(y=\dfrac{200}{6^3}\)
\(=\dfrac{25}{27}\)
Analyse
Le graphique de cette équation est une fonction rationnelle, comme le montre la Figure 5.8.4.
Exercice
Une quantité\(y\) varie inversement avec le carré de\(x\). Si\(x\) c'est\(y=8\) quand\(x=3\), trouvez\(y\) quand\(4\).
Solution
\(\frac{9}{2}\)
Résolution de problèmes impliquant des variations articulaires
De nombreuses situations sont plus compliquées qu'un modèle de base à variation directe ou inverse. Une variable dépend souvent de plusieurs autres variables. Lorsqu'une variable dépend du produit ou du quotient de deux variables ou plus, on parle de variation conjointe. Par exemple, le coût du transport en autobus des élèves pour chaque voyage scolaire varie en fonction du nombre d'élèves fréquentant l'école et de la distance qui les sépare de l'école. La variable\(c\), le coût, varie en fonction du nombre d'\(n\)étudiants et de la distance\(d\).
Remarque générale : VARIATION ARTICULAIRE
La variation conjointe se produit lorsqu'une variable varie directement ou inversement avec plusieurs variables.
Par exemple, cela\(x\) varie directement avec les deux\(y\) et\(z\), nous avons\(x=kyz\). Il\(x\) varie directement avec\(y\) et inversement avec\(z\), nous avons\(x=\frac{ky}{z}\). Notez que nous n'utilisons qu'une seule constante dans une équation de variation conjointe.
Exemple
Résolution de problèmes impliquant des variations articulaires
Une quantité\(x\) varie directement avec le carré de\(y\) et inversement avec la racine cubique de\(z\). Si\(x=6\)\(y=2\) et\(z=8\), trouvez\(x\) quand\(y=1\) et\(z=27\).
Solution
Commencez par écrire une équation pour montrer la relation entre les variables.
\(x=\dfrac{ky^2}{\sqrt[3]{z}}\)
\(y=2\)Substituez\(x=6\), et\(z=8\) pour trouver la valeur de la constante\(k\).
\(6=\dfrac{k2^2}{\sqrt[3]{8}}\)
\(6=\dfrac{4k}{2}\)
\(3=k\)
Nous pouvons maintenant remplacer la valeur de la constante dans l'équation de la relation.
\(x=\dfrac{3y^2}{\sqrt[3]{z}}\)
Pour déterminer\(x\) quand\(y=1\) et\(z=27\), nous allons substituer des valeurs à\(y\) et\(z\) dans notre équation.
\(x=\dfrac{3{(1)}^2}{\sqrt[3]{27}}\)
\(=1\)
Exercice
Une quantité\(x\) varie directement avec le carré de\(y\) et inversement avec\(z\). Si\(x=40\)\(y=4\) et\(z=2\), trouvez\(x\) quand\(y=10\) et\(z=25\).
Solution
\(x=20\)
Médias
Accédez à ces ressources en ligne pour obtenir des instructions et des pratiques supplémentaires en matière de variation directe et inverse.
Visitez ce site Web pour des questions pratiques supplémentaires sur Learningpod.
Équations clés
| Variation directe | \(y=kx^n\),\(k\) est une constante non nulle. |
| Variation inverse | \(y=\dfrac{k}{x^n}\),\(k\) est une constante non nulle. |
Concepts clés
- Une relation dans laquelle une quantité est une constante multipliée par une autre est appelée variation directe. Voir l'exemple.
- Deux variables directement proportionnelles l'une à l'autre auront un ratio constant.
- Une relation dans laquelle une quantité est une constante divisée par une autre est appelée variation inverse. Voir l'exemple.
- Deux variables inversement proportionnelles l'une à l'autre auront un multiple constant. Voir l'exemple.
- Dans de nombreux problèmes, une variable varie directement ou inversement avec plusieurs variables. Nous appelons ce type de relation variation conjointe. Voir l'exemple.


