5.4 : Division de polynômes

Last updated
Save as PDF

Page ID: 195576

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Utilisez la division longue pour diviser les polynômes.
Utilisez la division synthétique pour diviser les polynômes.

L'extérieur du Lincoln Memorial à Washington, D.C., est un grand solide rectangulaire d'une longueur en$61.5$ mètres (m), d'une largeur en$40$ m et d'une hauteur en$30$ m.$^1$

On peut facilement trouver le volume en utilisant la géométrie élémentaire.

\[\begin{align*} V&=l \; {\cdot} \; w \; {\cdot} \; h \\ &=61.5 \; {\cdot} \; 40 \; {\cdot} \; 30 \\ &=73,800 \end{align*}\]

Le volume est donc$73,800$ en mètres cubes ($m^3$).

alt — Figure$\PageIndex{1}$ : Lincoln Memorial, Washington, D.C. (crédit : Ron Cogswell, Flickr)

Supposons que nous connaissions le volume, la longueur et la largeur. On pourrait diviser pour trouver la hauteur.

\[\begin{align*} h&=\dfrac{V}{l{\cdot}w} \\&=\dfrac{73,800}{61.5{\cdot}40} \\ &=30 \end{align*}\]

Comme nous pouvons le confirmer à partir des dimensions ci-dessus, la hauteur est de 30 m. Nous pouvons utiliser des méthodes similaires pour trouver les dimensions manquantes. Nous pouvons également utiliser la même méthode si certaines ou toutes les mesures contiennent des expressions variables. Supposons, par exemple, que le volume d'un solide rectangulaire soit donné par le polynôme$3x^4−3x^3−33x^2+54x$. La longueur du solide est donnée par$3x$ ; la largeur est donnée par$x−2$.

Pour déterminer la hauteur du solide, nous pouvons utiliser la division polynomiale, qui est l'objet de cette section.

Utilisation de la division longue pour diviser des polynômes

Nous connaissons l'algorithme de division longue pour l'arithmétique ordinaire. Nous commençons par le diviser en chiffres du dividende qui ont la plus grande valeur de position. Nous divisons, multiplions, soustrayons, incluons le chiffre à la position de valeur de position suivante et répétons. Par exemple, divisons 178 par 3 en utilisant la division longue.

$alt$

Une autre façon de considérer la solution consiste à la considérer comme une somme de parties. Cela devrait vous sembler familier, car il s'agit de la même méthode que celle utilisée pour vérifier la division en arithmétique élémentaire.

\[\begin{align*} \text{dividend}&=(\text{divisor}{\cdot}\text{quotient})+\text{remainder} \\ 178&=(3{\cdot}59)+1 \\ &=177+1 \\ &=178\end{align*}\]

Nous appelons cela l'algorithme de division et nous en discuterons plus formellement après avoir examiné un exemple.

La division de polynômes contenant plus d'un terme présente des similitudes avec la division longue de nombres entiers. Nous pouvons écrire un dividende polynomial comme le produit du diviseur et du quotient ajouté au reste. Les termes de la division polynomiale correspondent aux chiffres (et aux valeurs de position) de la division numérique entière. Cette méthode permet de diviser deux polynômes. Par exemple, si nous devions diviser$2x^3−3x^2+4x+5$ en$x+2$ utilisant l'algorithme de division longue, cela ressemblerait à ceci :

\ [\ require {enclose} \ begin {array} {rll} \ large x+2 \ enclose {longdiv} {2x^3-3x^2+4x+5 \ phantom {0}} & \ qquad & \ large \ text {Configurez le problème de division.} \ \ [8pt]
\ large 2x^2 \ hspace {5.45em} & \ qquad & \ large2x^3 \ text {divisé par} x \ text {est} 2x^2. \ \ [-3pt]
\ large x+2 \ enfermer { longdiv} {2x^3-3x^2+4x+5 \ phantom {0}} & \ qquad & \ \ [8 points]
\ large 2x^2 \ hspace {5,45 em} & \ qquad & \ \ [-3 pt]
\ large x+2 \ enfermer {longdiv} {2x^3-3x^2+4x+5 \ phantom {0}} & \ qquad & \ \ [--3pt]
\ large \ underline {- \ left (2x^3 + 4x^2 \ right)} \ hspace {4,9em} & \ qquad & \ large \ text {Multipliez} x+2 \ text {par} 2x^2 \ text {et soustrayez.} \ \ [-3pt]
\ large -7x^2+4x \ hspace {2,8em} & \ qquad & \ large \ text {Réduisez le terme suivant.} \ \ [8pt]

\ large 2x^2 - 7x \ hspace {2,85em} & qqquad & \ large -7x^2 \ text {divisé par} x \ text {est} -7x. \ \ [-3 pt]
\ large x+2 \ enfermer {longdiv} {2x^3-3x^2+4x+5 \ phantom {0}} & \ qquad & \ \ [-3 points]
\ large \ souligner {- \ left (2x^3 + 4x^2 \ right)} \ hspace {4,9em} & \ qquad & \ \ [-3 pt]
\ grand -7x^2+4x \ hspace {2,8 em} & \ qquad & \ \ [-3 points]
\ large \ underline {- \ left (-7x^2 - 14x \ right)} \ hspace {2.0em} & \ qquad & \ large \ text {Multipliez} x+2 \ text {par} -7x. \ \ [-3pt]
\ large 18x+5 \ phantom {0} & \ qquad & \ large \ text {Soustrayez et réduisez le terme suivant.} \ \ [8pt]

\ large 2x^2 - 7x+18 et \ qquad & \ large 18x \ text {divisé par} x \ text {is} 18. \ \ [-3pt]
\ large x+2 \ enclose {longdiv} {2x^3-3x^2+4x+5 \ phantom {0}} & \ qquad & \ \ [-3pt] \ large \ underline {- \ left (2x^3 + 4x^2 \ right)} \ hspace {4,9pt]
\ large \ underline {- \ left (2x^3 + 4x^2 \ right)} \ hspace {4,9pt] \ large \ underline {- \ left (2x^3 + 4x^2 em} & \ qquad &
\ \ [-3 points] \ large -7x^2+4x \ hspace {2.8 em} & \ qquad & \ \ [-3 pt]
\ large \ underline {- \ left (-7x^2 - 14x \ right)} \ hspace {2.0em} & \ qquad & \ \ [-3 pt]
\ large 18x+ \ phantom {0} 5 & \ qquad & \ \ [-3 pt]
\ large \ underline {- \ left (18x+ 36 \ right)} hspace {-0,45em} et \ quad & \ large \ text {Multipliez} x+2 \ text {par} 18. \ \ [-3pt]
\ large -31 & \ qquad & \ large \ text {Soustrayez.} \ \ [8 points]
\ end {array} \ nonumber \]

Nous avons trouvé

\[\dfrac{2x^3−3x^2+4x+5}{x+2}=2x^2−7x+18−\dfrac{31}{x+2} \nonumber\]

\[ 2x^3−3x^2+4x+5=(x+2)(2x^2−7x+18)−31 \nonumber\]

Nous pouvons identifier le dividende, le diviseur, le quotient et le reste.

L'écriture du résultat de cette manière illustre l'algorithme de division.

L'algorithme de division

L'algorithme de division indique que, étant donné un dividende polynomial$f(x)$ et un diviseur polynomial non nul$d(x)$ où le degré de$d(x)$ est inférieur ou égal au degré de$f(x)$, il existe des polynômes uniques$q(x)$ et$r(x)$ tels que

\[f(x)=d(x)q(x)+r(x)\]

$q(x)$est le quotient et$r(x)$ est le reste. Le reste est égal à zéro ou a un degré strictement inférieur à$d(x)$.

Si$r(x)=0$, alors$d(x)$ se divise uniformément en$f(x)$. Cela signifie que, dans ce cas, les deux$d(x)$ et$q(x)$ sont des facteurs de$f(x)$.

Étant donné un polynôme et un binôme, utilisez la division longue pour diviser le polynôme par le binôme

Configurez le problème de division.
Déterminez le premier terme du quotient en divisant le terme principal du dividende par le terme principal du diviseur.
Multipliez la réponse par le diviseur et écrivez-la en dessous des termes similaires du dividende.
Soustrayez le binôme inférieur du binôme supérieur.
Réduisez le prochain terme du dividende.
Répétez les étapes 2 à 5 jusqu'à atteindre la dernière échéance du dividende.
Si le reste n'est pas nul, exprimez-le sous forme de fraction en utilisant le diviseur comme dénominateur.

Exemple$\PageIndex{1}$: Using Long Division to Divide a Second-Degree Polynomial

Divisez$5x^2+3x−2$ par$x+1$.

Solution

$alt$

Le quotient est$5x−2$. Le reste est égal à 0. Nous écrivons le résultat sous la forme

\[\dfrac{5x^2+3x−2}{x+1}=5x−2 \nonumber\]

\[5x^2+3x−2=(x+1)(5x−2) \nonumber\]

Analyse

Ce problème de division avait un reste de 0. Cela nous indique que le dividende est divisé équitablement par le diviseur et que le diviseur est un facteur du dividende.

Exemple$\PageIndex{2}$: Using Long Division to Divide a Third-Degree Polynomial

Divisez$6x^3+11x^2−31x+15$ par$3x−2$.

Solution

\ [\ require {enclose} \ begin {array} {rll}
\ large 2x^2 + \ phantom {0} 5x- \ phantom {0} 7 & \ qquad & \ large 6x^3 \ text {divisé par} 3x \ text {is} 2x^2. \ \ [-3pt]
\ large 3x-2 \ enclose {longdiv} {6x^3+11x^2. 2-31x+15} & \ qquad & \ \ [-3 points]
\ large \ souligné {- \ left (6x^3 - 4x^2) \ right)} \ hspace {5,8em} & \ qquad & \ large \ text {Multipliez} 3x-2 \ text {par} 2x^2. \ \ [-3pt]
\ large 15x^2-31x \ hspace {3,0em} & \ qquad & \ large \ text {Soustraire. Déclenchez le prochain trimestre.} 15x^2 \ text {divisé par} 3x \ text {est} 5x. \ \ [-3pt] \ large \ underline {-
\ left (15x^2 - 10x \ right)} \ hspace {2,5em} & \ qquad & \ large \ text {Multipliez} 3x-2 \ text {par} 5x. \ \ [-3pt] \ large -21xtext {Multipliez} 3x-2 \ text {par} 5x.
\ \ [-3pt] \ large +15 \ hspace {0,5 em} & \ qquad & \ large \ text {Soustraire. Déclenchez le prochain trimestre.} -21x \ text {divisé par} 3x \ text {is} -7. \ \ [-3pt]
\ large \ underline {- \ left (-21x + 14 \ right)} \ hspace {0.1em} & \ qquad & \ large \ text {Multipliez} 3x-2 \ text {par} -7. \ \ [-3pt]
\ large 1 \ {hspace 0,5 em} & \ qquad & \ large \ text {Soustraire. Le reste est 1.} \ \ [8pt]
\ end {array} \ nonumber \]

Il y a un reste de 1. Nous pouvons exprimer le résultat comme suit :

\[\dfrac{6x^3+11x^2−31x+15}{3x−2}=2x^2+5x−7+\dfrac{1}{3x−2} \nonumber\]

Analyse

Nous pouvons vérifier notre travail en utilisant l'algorithme de division pour réécrire la solution. Puis multipliez.

\[(3x−2)(2x^2+5x−7)+1=6x^3+11x^2−31x+15 \nonumber\]

Remarquez qu'au moment où nous écrivons notre résultat,

le dividende est$6x^3+11x^2−31x+15$
le diviseur est$3x−2$
le quotient est$2x^2+5x−7$
le reste est$1$

Essayez-le ! $\PageIndex{2}$

Divisez$16x^3−12x^2+20x−3$ par$4x+5$.

Solution: $4x^2−8x+15−\dfrac{78}{4x+5}$

Utilisation de la division synthétique pour diviser des polynômes

Comme nous l'avons vu, une division longue de polynômes peut impliquer de nombreuses étapes et être assez fastidieuse. La division synthétique est une méthode abrégée de division des polynômes dans le cas particulier de la division par un facteur linéaire dont le coefficient principal est$1.$

Pour illustrer le processus, rappelez-vous l'exemple au début de la section.

Divisez$2x^3−3x^2+4x+5$ en$x+2$ utilisant l'algorithme de division longue.

La forme finale du processus se présentait comme suit :

\ [\ require {enfermer} \ begin {array} {rl} \ large 2x^2 - 7x+18 & \ \ [-3 pt] \ large x+2
\ enfermer {longdiv} {2x^3-3x^2+4x+5 \ phantom {0}} & \ \ [-3 pt] \ large \ underline {- \ left (2x^3 + 4x^2 \ right)} \ {hspace]
\ large \ underline {- \ left (2x^3 + 4x^2 \ right)} \ {hspace 4,9em} &
\ \ [-3 points] \ large -7x^2+4x \ hspace {2,8 em} et \ \ [-3 points]
\ large \ underline {- \ left (-7x^2 - 14x \ right)} \ hspace {2.0em} & \ \ [-3pt]
\ large 18x+ \ phantom {0} 5 & \ \ [-3 pt]
\ large \ underline {- \ left (18x + 36 \ right)} \ hspace {-0,45em} & \ \ [-3 pt]
\ large -31 & \ [8pt]
\ end {array} \ nonnumber \]

Il y a beaucoup de répétitions dans le tableau. Si nous n'écrivons pas les variables mais que nous alignons leurs coefficients dans des colonnes sous le signe de division et que nous éliminons également les produits partiels, nous avons déjà une version plus simple de l'ensemble du problème.

$alt$

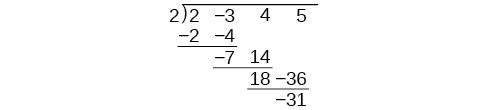
La division synthétique entraîne cette simplification de quelques étapes supplémentaires. Réduisez le tableau en déplaçant chacune des lignes vers le haut pour combler les places vacantes. De plus, au lieu de diviser par 2, comme nous le ferions dans une division de nombres entiers, puis de multiplier et de soustraire le produit intermédiaire, nous changeons le signe du « diviseur » en —2, multiplions et additionnons. Le processus commence par la réduction du coefficient principal.

$alt$

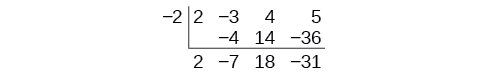
Nous le multiplions ensuite par le « diviseur » et l'ajoutons, en répétant ce processus colonne par colonne, jusqu'à ce qu'il ne reste plus d'entrées. La rangée du bas représente les coefficients du quotient ; la dernière entrée de la rangée du bas correspond au reste. Dans ce cas, le quotient est$2x^2–7x+18$ et le reste est.$–31.$ Le processus sera expliqué plus clairement dans l'exemple$\PageIndex{3}$.

Division synthétique

La division synthétique est un raccourci qui peut être utilisé lorsque le diviseur est un binôme dans le formulaire$x−k$. Dans la division synthétique, seuls les coefficients sont utilisés dans le processus de division.

Étant donné deux polynômes, utilisez la division synthétique pour diviser

Écrivez$k$ pour le diviseur.
Écrivez les coefficients du dividende.
Réduisez le coefficient de plomb.
Multipliez le coefficient de plomb par$k$. Inscrivez le produit dans la colonne suivante.
Ajoutez les termes de la deuxième colonne.
Multipliez le résultat par$k$. Inscrivez le produit dans la colonne suivante.
Répétez les étapes 5 et 6 pour les autres colonnes.
Utilisez les chiffres du bas pour écrire le quotient. Le nombre de la dernière colonne est le reste et a le degré 0, le nombre suivant en partant de la droite a le degré 1, le nombre suivant en partant de la droite a le degré 2, et ainsi de suite.

Exemple$\PageIndex{3}$: Using Synthetic Division to Divide a Second-Degree Polynomial

Utilisez une division synthétique pour diviser$5x^2−3x−36$ par$x−3$.

Solution

Commencez par mettre en place la division synthétique. Ecrivez$k$ et les coefficients.

$alt$

Réduisez le coefficient de plomb. Multipliez le coefficient de plomb par$k$.

$alt$

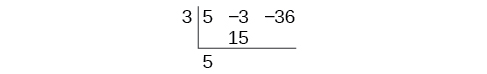
Continuez en ajoutant les chiffres dans la deuxième colonne. Multipliez le nombre obtenu par$k$ .Écrivez le résultat dans la colonne suivante. Ajoutez ensuite les chiffres dans la troisième colonne.

$alt$

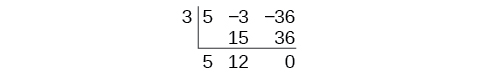
Le résultat est$5x+12$. Le reste est égal à 0. Il en$x−3$ va de même pour un facteur du polynôme d'origine.

Analyse

Comme pour la division longue, nous pouvons vérifier notre travail en multipliant le quotient par le diviseur et en ajoutant le reste.

\[(x−3)(5x+12)+0=5x^2−3x−36 \nonumber\]

Exemple$\PageIndex{4}$: Using Synthetic Division to Divide a Third-Degree Polynomial

Utilisez une division synthétique pour diviser$4x^3+10x^2−6x−20$ par$x+2$.

Solution

Le diviseur binomial est$x+2$ ainsi$k=−2$. Ajoutez chaque colonne, multipliez le résultat par —2 et répétez l'opération jusqu'à ce que la dernière colonne soit atteinte.

\ [\ large {\ begin {matrice} {c} -2 \ \ \ \ \ \
\ end {matrice}}
{\ begin {align*} & \ \ [0pt]
& {\ begin {matrice} {r|} \ \ [0pt]
\ \ [0pt] \ end {tableau}} \ \ [1 point]
& \ \ [2 points] & \ end {align*}} \ ! \ !
{\ begin {array} {rrrr}
1 et -1 et -11 et 18 \ \
& 2 et 2 et -18 \ \
\ hlignes 1 et 1 et -9 et 0
\ end {array}}
\ nonumber \]

Le résultat est$4x^2+2x−10$.

Le reste est égal à 0. Donc,$x+2$ est un facteur de$4x^3+10x^2−6x−20$.

Analyse

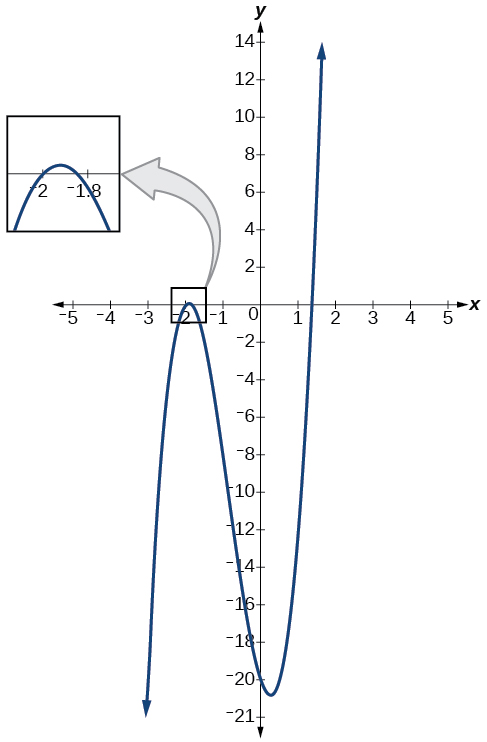
Le graphique de la fonction polynomiale$f(x)=4x^3+10x^2−6x−20$ de la figure$\PageIndex{2}$ montre un zéro à$x=k=−2$. Cela confirme que$x+2$ c'est un facteur de$4x^3+10x^2−6x−20$.

Exemple$\PageIndex{5}$: Using Synthetic Division to Divide a Fourth-Degree Polynomial

Utilisez une division synthétique pour diviser$−9x^4+10x^3+7x^2−6$ par$x−1$.

Solution

Notez qu'il n'y a pas de$x$ terme. Nous utiliserons un zéro comme coefficient pour ce terme.

\ [\ large {\ begin {matrice} {c} 1 \ \ \ \ \ \
\ end {matrice}}
{\ begin {align*} & \ \ [0pt]
& {\ begin {matrice} {r|} \ \ [0pt]
\ \ [0pt] \ end {tableau}} \ \ [1pt]
& \ \ [2pt] & \ end {align*}} \ ! \ !
{\ begin {array} {rrrrr}
-9 et 10 et 7 et 0 &-6 \ \
& -9 et 1 et 8 et 8 \ \
\ hline -9 et 1 & 1 & 8 et 8 et 2
\ end {tableau}}
\ nonumber \]

Le résultat est$−9x^3+x^2+8x+8+\dfrac{2}{x−1}$.

Essayez-le ! $\PageIndex{3}$

Utilisez une division synthétique pour diviser$3x^4+18x^3−3x+40$ par$x+7$.

Solution: $3x^3−3x^2+21x−150+\dfrac{1090}{x+7}$

Utilisation de la division polynomiale pour résoudre des problèmes d'application

La division polynomiale peut être utilisée pour résoudre divers problèmes d'application impliquant des expressions de surface et de volume. Nous avons examiné une application au début de cette section. Nous allons maintenant résoudre ce problème dans l'exemple suivant.

Exemple$\PageIndex{6}$: Using Polynomial Division in an Application Problem

Le volume d'un solide rectangulaire est donné par le polynôme$3x^4−3x^3−33x^2+54x$. La longueur du solide est donnée par$3x$ et la largeur est donnée par$x−2$. Détermine la hauteur$h$ du solide.

Solution

Il existe plusieurs manières d'aborder ce problème. Nous devons diviser l'expression du volume du solide par les expressions de longueur et de largeur. Laissez-nous créer un croquis comme dans la figure$\PageIndex{3}$. Soit$h$ égale à la hauteur de la boîte.

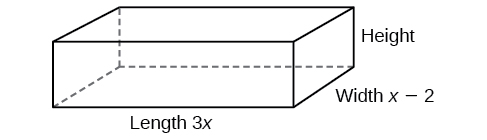
Nous pouvons maintenant écrire une équation en substituant les valeurs connues dans la formule du volume d'un solide rectangulaire.

\[\begin{align*} V&=l{\cdot}w{\cdot}h \\ 3x^4−3x^3−33x^2+54x&=3x{\cdot}(x−2){\cdot}h \end{align*}\]

Pour résoudre le problème$h$, divisez d'abord les deux côtés par$3x$.

\[\dfrac{3x{\cdot}(x−2){\cdot}h}{3x}=\dfrac{3x^4−3x^3−33x^2+54x}{3x} \nonumber\]

\[(x-2)h=\dfrac{x^3-x^2-11x+18}{x-2} \nonumber\]

Maintenant, résolvez d'$h$utiliser la division synthétique.

\[h=\dfrac{x^3−x^2−11x+18}{x−2} \nonumber\]

Le quotient est$x^2+x−9$ et le reste est$0.$ La hauteur du solide est$x^2+x−9$.

Essayez-le ! $\PageIndex{4}$

L'aire d'un rectangle est donnée par$3x^3+14x^2−23x+6$. La largeur du rectangle est donnée par$x+6$. Trouvez une expression pour la longueur du rectangle.

Solution: $3x^2−4x+1$

Équations clés

Algorithme$f(x)=d(x)q(x)+r(x)$ de division$q(x){\neq}0$

Concepts clés

La division polynomiale longue peut être utilisée pour diviser un polynôme par n'importe quel polynôme de degré égal ou inférieur.
L'algorithme de division nous indique qu'un dividende polynomial peut être écrit comme le produit du diviseur et du quotient ajouté au reste.
La division synthétique est un raccourci qui peut être utilisé pour diviser un polynôme par un binôme dans le formulaire$x−k.$
La division polynomiale peut être utilisée pour résoudre des problèmes d'application, notamment en termes de surface et de volume.

Notes

$^1$Service des parcs nationaux. « Statistiques du Lincoln Memorial Building ». www.nps.gov/linc/historycultu... statistics.htm. Consulté le 03/04/2014

Lexique

Algorithme de

étant donné un dividende polynomial$f(x)$ et un diviseur polynomial non nul$d(x)$ où le degré de$d(x)$ est inférieur ou égal au degré de$f(x)$, il existe des polynômes uniques$q(x)$ et$r(x)$ tels que$f(x)=d(x)q(x)+r(x)$ où$q(x)$ est le quotient et$r(x)$ est reste. Le reste est égal à zéro ou a un degré strictement inférieur à$d(x)$.

division synthétique

une méthode de raccourci qui peut être utilisée pour diviser un polynôme par un binôme de la forme$x−k$