5.3 : Graphiques des fonctions polynomiales

Last updated
Save as PDF

Page ID: 195561

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Reconnaître les caractéristiques des graphes de fonctions polynomiales.
Utilisez la factorisation pour trouver les zéros des fonctions polynomiales.
Identifiez les zéros et leurs multiplicités.
Déterminez le comportement final.
Comprenez la relation entre le degré et les points tournants.
Tracez les fonctions polynomiales.
Utilisez le théorème des valeurs intermédiaires.

Le chiffre d'affaires en millions de dollars d'un câblodistributeur fictif de 2006 à 2013 est indiqué dans le tableau$\PageIndex{1}$.

Tableau$\PageIndex{1}$
Année	2006	2007	2008	2009	2010	2011	2012	2013
Revenus	52,4	52,8	51,2	49,5	48,6	48,6	48,7	47,1

Le revenu peut être modélisé par la fonction polynomiale

\[R(t)=−0.037t^4+1.414t^3−19.777t^2+118.696t−205.332\]

où$R$ représente les recettes en millions de dollars et$t$ représente l'année,$t=6$ correspondant à 2006. À quels intervalles le chiffre d'affaires de l'entreprise augmente-t-il ? À quels intervalles le chiffre d'affaires de l'entreprise diminue-t-il ? Il est possible de répondre à ces questions, ainsi qu'à bien d'autres, en examinant le graphe de la fonction polynomiale. Nous avons déjà exploré le comportement local des quadratiques, un cas particulier de polynômes. Dans cette section, nous allons explorer le comportement local des polynômes en général.

Reconnaissance des caractéristiques des graphes de fonctions polynomiales

Les fonctions polynomiales de degré 2 ou plus ont des graphes qui n'ont pas d'angles vifs ; rappelons que ces types de graphes sont appelés courbes lisses. Les fonctions polynomiales affichent également des graphes sans interruption. Les courbes sans interruption sont appelées continues. La figure$\PageIndex{1}$ montre un graphe qui représente une fonction polynomiale et un graphe qui représente une fonction qui n'est pas un polynôme.

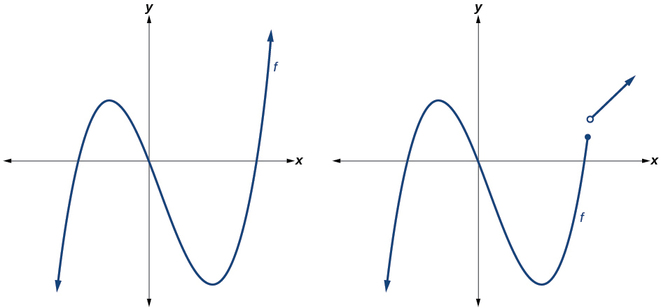
Graphique de f (x) =x^3-0,01x — Figure$\PageIndex{1}$ : Graphique de$f(x)=x^3-0.01x$.

Exemple$\PageIndex{1}$: Recognizing Polynomial Functions

Lequel des graphes de la figure$\PageIndex{2}$ représente une fonction polynomiale ?

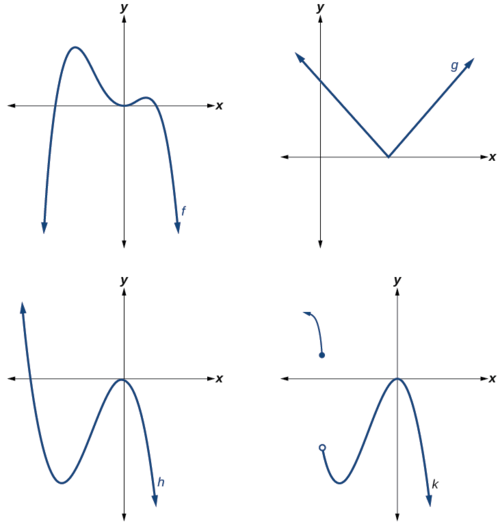
$Deux graphes dans lesquels l'un possède une fonction polynomiale et l'autre possède une fonction qui ressemble beaucoup à un polynôme mais qui ne l'est pas. Deux graphes dans lesquels l'un possède une fonction polynomiale et l'autre possède une fonction qui ressemble beaucoup à un polynôme mais qui ne l'est pas.$
Figurine$\PageIndex{2}$

Solution

Les graphes de$f$ et$h$ sont des graphes de fonctions polynomiales. Ils sont lisses et continus.
Les graphes de$g$ et$k$ sont des graphes de fonctions qui ne sont pas des polynômes. Le graphique de la fonction$g$ présente un angle pointu. Le graphe de la fonction n'$k$est pas continu.

QUESTIONS-RÉPONSES

Toutes les fonctions polynomiales ont-elles pour domaine tous les nombres réels ?

Oui. Tout nombre réel est une entrée valide pour une fonction polynomiale.

Utilisation de la factorisation pour trouver les zéros des fonctions polynomiales

Rappelez-vous qu'il s'$f$agit d'une fonction polynomiale dont les valeurs de$x$ pour$f(x)=0$ sont appelées zéros de$f$. Si l'équation de la fonction polynomiale peut être factorisée, nous pouvons définir chaque facteur égal à zéro et résoudre pour les zéros.

Nous pouvons utiliser cette méthode pour trouver les interceptions X, car aux interceptions X, nous trouvons les valeurs d'entrée lorsque la valeur de sortie est nulle. Pour les polynômes généraux, cette perspective peut être difficile. Alors que les quadratiques peuvent être résolus à l'aide de la formule quadratique relativement simple, les formules correspondantes pour les polynômes cubiques et du quatrième degré ne sont pas assez simples à retenir, et il n'existe pas de formules pour les polynômes généraux de degré supérieur. Par conséquent, nous nous limiterons à trois cas dans cette section :

Le polynôme peut être factorisé à l'aide de méthodes connues : le plus grand facteur commun et la factorisation trinomiale.
Le polynôme est donné sous forme factorielle.
La technologie est utilisée pour déterminer les interceptions.

HowTo : Compte tenu d'une fonction polynomiale$f$, find the x-intercepts by factoring

Set$f(x)=0$.
Si la fonction polynomiale n'est pas donnée sous forme factorielle :
1. Éliminez tous les facteurs monomiaux courants.
2. Factorisez tous les binômes ou trinômes factorisables.
Définissez chaque facteur sur zéro et résolvez pour trouver les interceptions X.

Exemple$\PageIndex{2}$: Finding the x-Intercepts of a Polynomial Function by Factoring

Trouvez les interceptions X de$f(x)=x^6−3x^4+2x^2$.

Solution

Nous pouvons essayer de factoriser ce polynôme pour trouver des solutions$f(x)=0$.

\[\begin{align*} x^6−3x^4+2x^2&=0 & &\text{Factor out the greatest common factor.} \\ x^2(x^4−3x^2+2)&=0 & &\text{Factor the trinomial.} \\ x^2(x^2−1)(x^2−2)&=0 & &\text{Set each factor equal to zero.} \end{align*}\]

\[\begin{align*} x^2&=0 & & & (x^2−1)&=0 & & & (x^2−2)&=0 \\ x^2&=0 & &\text{ or } & x^2&=1 & &\text{ or } & x^2&=2 \\ x&=0 &&& x&={\pm}1 &&& x&={\pm}\sqrt{2} \end{align*}\].

Cela nous donne cinq interceptions X :$(0,0)$$(1,0)$,$(−1,0)$,$(\sqrt{2},0)$, et$(−\sqrt{2},0)$ (Figure$\PageIndex{3}$). Nous pouvons voir qu'il s'agit d'une fonction uniforme.

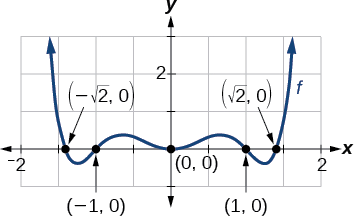
Exemple$\PageIndex{3}$: Finding the x-Intercepts of a Polynomial Function by Factoring

Trouvez les interceptions X de$f(x)=x^3−5x^2−x+5$.

Solution

Trouvez des solutions$f(x)=0$ par affacturage.

\[\begin{align*} x^3−5x^2−x+5&=0 &\text{Factor by grouping.} \\ x^2(x−5)−(x−5)&=0 &\text{Factor out the common factor.} \\ (x^2−1)(x−5)&=0 &\text{Factor the difference of squares.} \\ (x+1)(x−1)(x−5)&=0 &\text{Set each factor equal to zero.} \end{align*}\]

\[\begin{align*} x+1&=0 & &\text{or} & x−1&=0 & &\text{or} & x−5&=0 \\ x&=−1 &&& x&=1 &&& x&=5\end{align*}\]

Il existe trois interceptions X :$(−1,0)$$(1,0)$, et$(5,0)$ (Figure$\PageIndex{4}$).

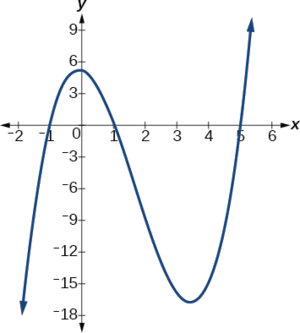
Graphe de f (x) =x^3-5x^2-x+5 avec ses trois interceptions (-1, 0), (1, 0) et (5, 0). — Figure$\PageIndex{4}$ : Graphique de$f(x)$.

Exemple$\PageIndex{4}$: Finding the y- and x-Intercepts of a Polynomial in Factored Form

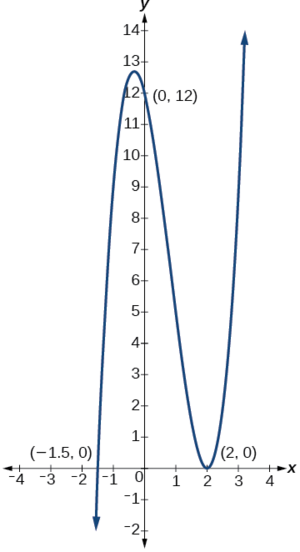
Trouvez les interceptions Y et X de$g(x)=(x−2)^2(2x+3)$.

Solution

L'intersection y peut être trouvée en évaluant$g(0)$.

\[\begin{align*} g(0)&=(0−2)^2(2(0)+3) \\ &=12 \end{align*}\]

Donc, l'intersection Y est$(0,12)$.

Les x-intercepts peuvent être trouvés en résolvant$g(x)=0$.

\[(x−2)^2(2x+3)=0\]

\[\begin{align*} (x−2)^2&=0 & & & (2x+3)&=0 \\ x−2&=0 & &\text{or} & x&=−\dfrac{3}{2} \\ x&=2 \end{align*}\]

Les x-intercepts sont donc$(2,0)$ et$\left(−\dfrac{3}{2},0\right)$.

Analyse

Nous pouvons toujours vérifier que nos réponses sont raisonnables en utilisant une calculatrice graphique pour représenter graphiquement le polynôme, comme indiqué sur la figure$\PageIndex{5}$.

Graphe de g (x) = (x-2) ^2 (2x+3) avec ses deux interceptions x (2, 0) et (-3/2, 0) et son intersection y (0, 12). — Figure$\PageIndex{5}$ : Graphique de$g(x)$.

Exemple$\PageIndex{5}$: Finding the x-Intercepts of a Polynomial Function Using a Graph

Trouvez les interceptions X de$h(x)=x^3+4x^2+x−6$.

Solution

Ce polynôme n'est pas factorisé, ne possède aucun facteur commun et ne semble pas être factorisable à l'aide des techniques discutées précédemment. Heureusement, nous pouvons utiliser la technologie pour trouver les interceptions. Gardez à l'esprit que certaines valeurs rendent la création graphique difficile à la main. Dans ces cas, nous pouvons tirer parti des utilitaires de création graphique.

En regardant le graphique de cette fonction, comme le montre la figure$\PageIndex{6}$, il apparaît qu'il existe des interceptions X à$x=−3,−2, \text{ and }1$.

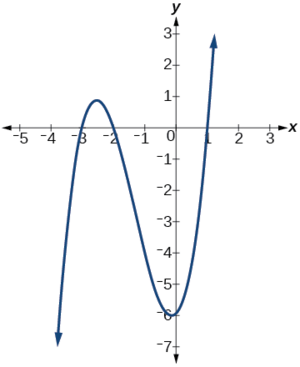
Graphique de h (x) =x^3+4x^2+x-6. — Figure$\PageIndex{6}$ : Graphique de$h(x)$.

Nous pouvons vérifier si elles sont correctes en les remplaçant par ces valeurs$x$ et en vérifiant que
\[h(−3)=h(−2)=h(1)=0. \nonumber\]

Depuis$h(x)=x^3+4x^2+x−6$, nous avons :

\[ \begin{align*} h(−3)&=(−3)^3+4(−3)^2+(−3)−6=−27+36−3−6=0 \\[4pt] h(−2) &=(−2)^3+4(−2)^2+(−2)−6 =−8+16−2−6=0 \\[4pt] h(1)&=(1)^3+4(1)^2+(1)−6=1+4+1−6=0 \end{align*}\]

Chaque intersection X correspond à un zéro de la fonction polynomiale et chaque zéro donne un facteur. Nous pouvons donc maintenant écrire le polynôme sous forme factorielle.

\[\begin{align*} h(x)&=x^3+4x^2+x−6 \\ &=(x+3)(x+2)(x−1) \end{align*}\]

Exercice$\PageIndex{1}$

Trouvez les interceptions y et x de la fonction$f(x)=x^4−19x^2+30x$.

Réponse

interception en Y$(0,0)$ ;
x-intercepts$(0,0)$$(–5,0)$,$(2,0)$, et$(3,0)$

Identifier les zéros et leurs multiplicités

Les graphes se comportent différemment selon les interceptions X. Parfois, le graphe passe au-dessus de l'axe horizontal à une intersection. D'autres fois, le graphique touchera l'axe horizontal et rebondira. Supposons, par exemple, que nous tracions la fonction

\[f(x)=(x+3)(x−2)^2(x+1)^3.\]

Remarquez dans la figure$\PageIndex{7}$ que le comportement de la fonction à chacune des interceptions en X est différent.

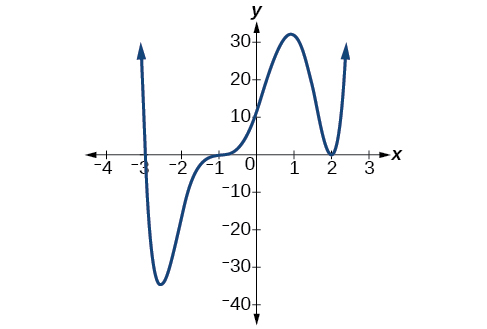
L'intersection x −3 est la solution de l'équation$(x+3)=0$. Le graphe passe directement par l'intersection x à$x=−3$. Le facteur est linéaire (il a un degré de 1), de sorte que le comportement à proximité de l'intersection est similaire à celui d'une ligne : il passe directement par l'intersection. Nous appelons cela un zéro unique car le zéro correspond à un seul facteur de la fonction.

Le x-intercept 2 est la solution répétée de l'équation$(x−2)^2=0$. Le graphique touche l'axe à l'intersection et change de direction. Le facteur étant quadratique (degré 2), le comportement à proximité de l'intersection ressemble à celui d'un quadratique : il rebondit sur l'axe horizontal à l'intersection.

\[(x−2)^2=(x−2)(x−2)\]

Le facteur est répété, c'est-à-dire qu'il$(x−2)$ apparaît deux fois. Le nombre de fois qu'un facteur donné apparaît sous la forme factorielle de l'équation d'un polynôme est appelé multiplicité. Le zéro associé à ce facteur,$x=2$, a une multiplicité de 2 car le facteur$(x−2)$ se produit deux fois.

L'intersection x -1 est la solution répétée du facteur$(x+1)^3=0$. Le graphe passe par l'axe à l'intersection, mais s'aplatit d'abord un peu. Ce facteur étant cubique (degré 3), le comportement à proximité de l'intersection ressemble à celui d'un cube, avec la même forme en S près de l'intersection que celle de la fonction de la boîte à outils$f(x)=x^3$. Nous appelons cela un triple zéro, ou un zéro avec une multiplicité de 3.

Pour les zéros avec des multiplicités paires, les graphes touchent l'axe des abscisses ou sont tangents à celui-ci. Pour les zéros avec des multiplicités impaires, les graphes croisent ou coupent l'axe X. Voir la figure$\PageIndex{8}$ pour des exemples de graphes de fonctions polynomiales avec multiplicité 1, 2 et 3.

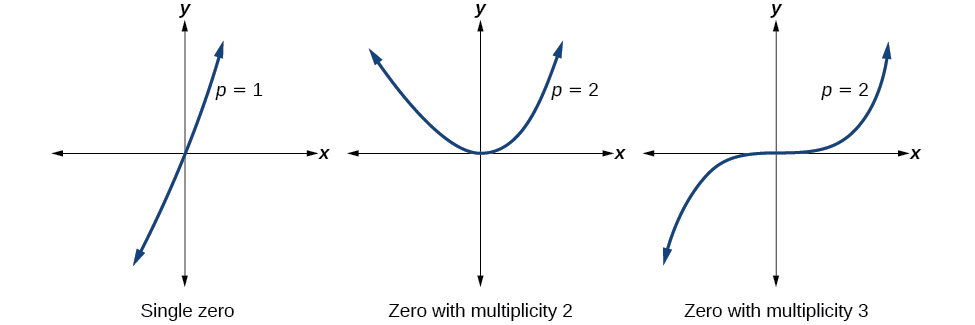
Figure$\PageIndex{8}$ : Trois graphes montrant trois fonctions polynomiales différentes avec une multiplicité de 1, 2 et 3.

Pour des puissances paires plus élevées, telles que 4, 6 et 8, le graphique se touchera toujours de l'axe horizontal et rebondira sur celui-ci, mais pour chaque puissance paire croissante, le graphique apparaîtra plus plat à mesure qu'il approche et quitte l'axe des abscisses.

Pour les puissances impaires supérieures, telles que 5, 7 et 9, le graphique traversera toujours l'axe horizontal, mais pour chaque puissance impaire croissante, le graphique apparaîtra plus plat à mesure qu'il approche et quitte l'axe des abscisses.

Comportement graphique des polynômes aux intersections X

Si un polynôme contient un facteur de la forme$(x−h)^p$, le comportement à proximité de l'intersection X est déterminé par la puissance$p$. Nous disons que$x=h$ c'est le zéro de la multiplicité$p$.

Le graphe d'une fonction polynomiale touchera l'axe X à des zéros avec des multiplicités paires. Le graphique traversera l'axe X à des zéros avec des multiplicités impaires.

La somme des multiplicités est le degré de la fonction polynomiale.

HOWTO : À partir d'un graphe d'une fonction polynomiale de degré$n$, identify the zeros and their multiplicities

Si le graphique croise l'axe des abscisses et apparaît presque linéaire à l'intersection, il s'agit d'un zéro unique.
Si le graphique touche l'axe X et rebondit sur cet axe, il s'agit d'un zéro avec une multiplicité uniforme.
Si le graphique croise l'axe X à zéro, il s'agit d'un zéro avec une multiplicité impaire.
La somme des multiplicités est de$n$.

Exemple$\PageIndex{6}$: Identifying Zeros and Their Multiplicities

Utilisez le graphique de la fonction du degré 6 dans la figure$\PageIndex{9}$ pour identifier les zéros de la fonction et leurs multiplicités possibles.

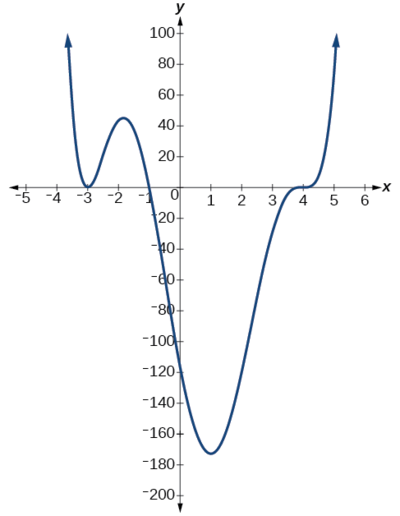
Graphe d'un polynôme pair de degré 6. — Figure$\PageIndex{9}$ : Graphique d'une fonction polynomiale de degré 5.

Solution

La fonction polynomiale est de degré$n$. La somme des multiplicités doit être$n$.

En partant de la gauche, le premier zéro apparaît à$x=−3$. Le graphique touche l'axe des abscisses, de sorte que la multiplicité du zéro doit être égale. Le zéro de -3 a une multiplicité de 2.

Le zéro suivant apparaît à$x=−1$. Le graphique semble presque linéaire à ce stade. Il s'agit d'un zéro unique de la multiplicité 1.

Le dernier zéro se trouve à$x=4$. Le graphique croise l'axe des abscisses, de sorte que la multiplicité du zéro doit être impaire. Nous savons que la multiplicité est probable de 3 et que la somme des multiplicités est probable de 6.

Exercice$\PageIndex{2}$

Utilisez le graphique de la fonction du degré 5 dans la figure$\PageIndex{10}$ pour identifier les zéros de la fonction et leurs multiplicités.

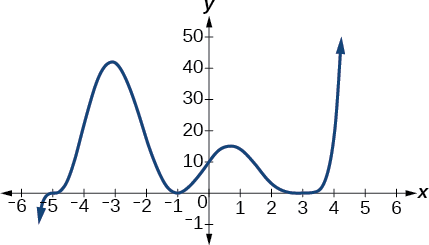
$Graphe d'une fonction polynomiale de degré 5.$

Figure$\PageIndex{10}$ : Graphique d'une fonction polynomiale de degré 5.

Réponse: Le graphe a un zéro de —5 avec une multiplicité de 1, un zéro de —1 avec une multiplicité de 2 et un zéro de 3 avec une multiplicité paire.

Déterminer le comportement final

Comme nous l'avons déjà appris, le comportement d'un graphe d'une fonction polynomiale de la forme

\[f(x)=a_nx^n+a_{n−1}x^{n−1}+...+a_1x+a_0\]

augmenteront ou diminueront en fin de compte sous forme d'$x$augmentations sans limites et augmenteront ou diminueront sous forme de$x$ diminutions sans limites. Cela est dû au fait que pour les entrées très volumineuses, par exemple 100 ou 1 000, le terme principal domine la taille de la sortie. Il en va de même pour les entrées très petites, par exemple —100 ou —1 000.

Rappelez-vous que nous appelons ce comportement le comportement final d'une fonction. Comme nous l'avons souligné lors de la discussion des équations quadratiques, lorsque le terme principal d'une fonction polynomiale est une fonction de puissance paire, qui$x$ augmente ou diminue sans limite,$f(x)$ augmente sans borne.$a_nx^n$ Lorsque le terme principal est une fonction de puissance impaire, lorsqu'il$x$ diminue sans limite, diminue$f(x)$ également sans limite ; lorsqu'il$x$ augmente sans borne, augmente$f(x)$ également sans borne. Si le terme principal est négatif, cela changera la direction du comportement final. La figure$\PageIndex{11}$ résume les quatre cas.

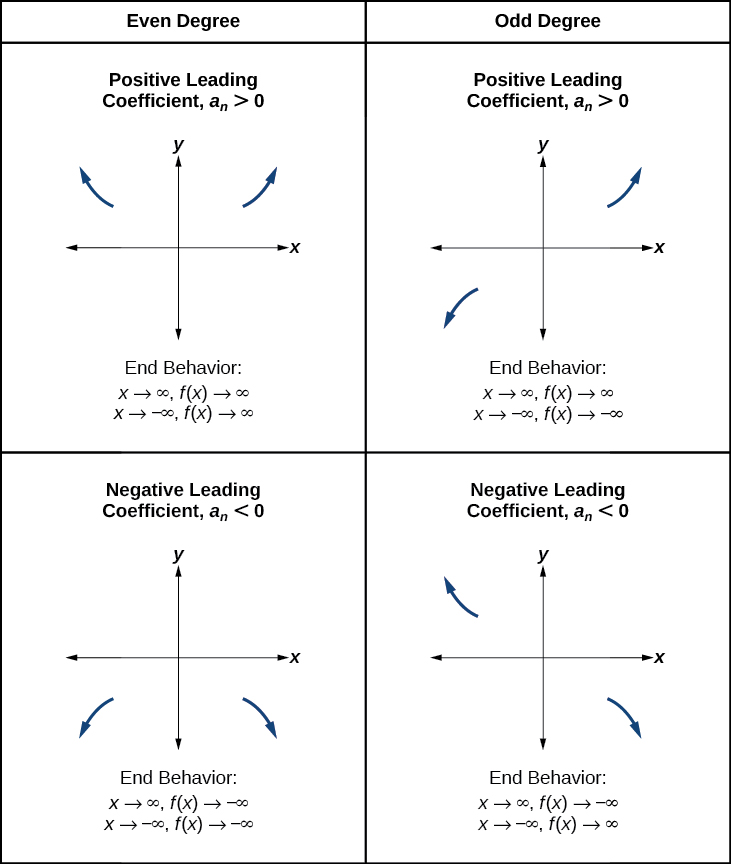
Tableau montrant le comportement final des polynômes pairs et impairs avec des coefficients positifs et négatifs — Chiffre$\PageIndex{11}$.

Comprendre la relation entre le degré et les points tournants

En plus du comportement final, rappelons que nous pouvons analyser le comportement local d'une fonction polynomiale. Il peut y avoir un point tournant où le graphique passe de l'augmentation à la baisse (de la hausse à la baisse) ou de la baisse à l'augmentation (de la baisse à la hausse). Regardez le graphique de la fonction polynomiale$f(x)=x^4−x^3−4x^2+4x$ dans la figure$\PageIndex{12}$. Le graphique présente trois points tournants.

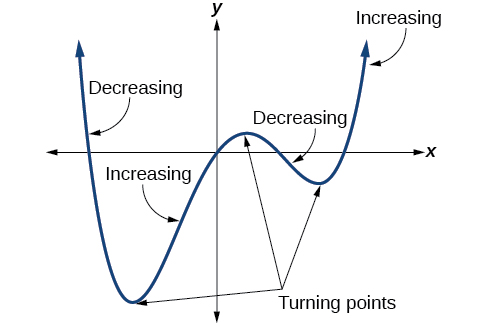
Graphique de f (x) =x^4-x^3-4x^2+4x qui indique où la fonction augmente et diminue et ses points de retournement. — Figure$\PageIndex{12}$ : Graphique de$f(x)=x^4-x^3-4x^2+4x$

Cette fonction$f$ est une fonction polynomiale du 4e degré et comporte 3 points de retournement. Le nombre maximum de points de retournement d'une fonction polynomiale est toujours inférieur d'un point au degré de la fonction.

Définition : Interpréter les tournants

Un point tournant est un point du graphique où le graphique passe de l'augmentation à la baisse (de la hausse à la baisse) ou de la baisse à l'augmentation (de la baisse à la hausse). Un polynôme de degré$n$ aura au plus des points de$n−1$ retournement.

Exemple$\PageIndex{7}$: Finding the Maximum Number of Turning Points Using the Degree of a Polynomial Function

Détermine le nombre maximum de points de retournement de chaque fonction polynomiale.

$f(x)=−x^3+4x^5−3x^2+1$
$f(x)=−(x−1)^2(1+2x^2)$

Solution

un.$f(x)=−x^3+4x^5−3x^2+1$

Tout d'abord, réécrivez la fonction polynomiale par ordre décroissant :$f(x)=4x^5−x^3−3x^2+1$

Identifiez le degré de la fonction polynomiale. Cette fonction polynomiale est de degré 5.

Le nombre maximum de points de retournement est de$5−1=4$.

b.$f(x)=−(x−1)^2(1+2x^2)$

Tout d'abord, identifiez le terme principal de la fonction polynomiale si la fonction a été étendue.

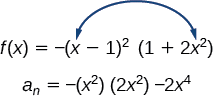
$imageedit_33_3540887475.png$

Ensuite, identifiez le degré de la fonction polynomiale. Cette fonction polynomiale est de degré 4.

Le nombre maximum de points de retournement est de$4−1=3$.

Représentation graphique de fonctions polynomiales

Nous pouvons utiliser ce que nous avons appris sur les multiplicités, le comportement final et les points de retournement pour esquisser des graphes de fonctions polynomiales. Rassemblons tout cela et examinons les étapes requises pour représenter graphiquement les fonctions polynomiales.

Procédure : à partir d'une fonction polynomiale, esquissez le graphe

Trouvez les interceptions.
Vérifiez la symétrie. Si la fonction est une fonction paire, son graphe est symétrique par rapport à l'axe Y, c'est-à-dire$f(−x)=f(x)$. Si une fonction est une fonction étrange, son graphe est symétrique par rapport à l'origine, c'est-à-dire$f(−x)=−f(x)$.
Utilisez les multiplicités des zéros pour déterminer le comportement du polynôme aux intersections X.
Déterminez le comportement final en examinant le terme principal.
Utilisez le comportement final et le comportement aux points d'intersection pour esquisser un graphique.
Assurez-vous que le nombre de points de retournement ne dépasse pas un point de moins que le degré du polynôme.
Vous pouvez également utiliser la technologie pour vérifier le graphique.

Exemple$\PageIndex{8}$: Sketching the Graph of a Polynomial Function

Esquissez un graphique de$f(x)=−2(x+3)^2(x−5)$.

Solution

Ce graphique comporte deux interceptions en X. At$x=−3$, le facteur est au carré, indiquant une multiplicité de 2. Le graphique rebondira à cette intersection X. At$x=5$, la fonction possède une multiplicité de un, ce qui indique que le graphe traversera l'axe à cette intersection.

L'intersection y est trouvée en évaluant$f(0)$.

\[\begin{align*} f(0)&=−2(0+3)^2(0−5) \\ &=−2⋅9⋅(−5) \\ &=90 \end{align*}\]

L'intersection Y est$(0,90)$.

De plus, nous pouvons voir que le terme principal, si ce polynôme était multiplié$−2x3$, serait donc le suivant : le comportement final serait celui d'un cube réfléchi verticalement, les sorties diminuant lorsque les entrées approchent de l'infini, et les sorties augmentant lorsque les entrées approchent de l'infini négatif. Voir la figure$\PageIndex{13}$.

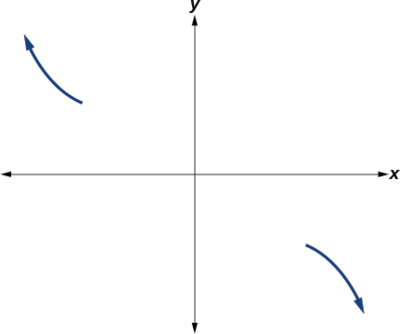
Affichage de la distribution pour le terme principal. — Figure$\PageIndex{13}$ : Affichage de la distribution du terme principal.

Pour l'esquisser, nous considérons que :

En tant$x{\rightarrow}−{\infty}$ que fonction$f(x){\rightarrow}{\infty}$, nous savons que le graphique commence dans le deuxième quadrant et diminue vers l'axe des abscisses.
Comme n'$f(−x)=−2(−x+3)^2(−x–5)$est pas égal à$f(x)$, le graphique n'affiche pas de symétrie.
À$(−3,0)$, le graphe rebondit sur l'axe X, de sorte que la fonction doit commencer à augmenter.
À$(0,90)$, le graphe croise l'axe y à l'intersection Y. Voir la figure$\PageIndex{14}$.

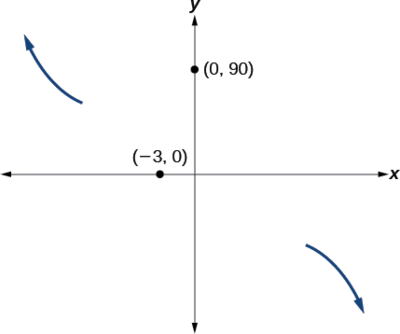
Graphique du comportement final et des interceptions, (-3, 0) et (0, 90), pour la fonction f (x) =-2 (x+3) ^2 (x-5). — Figure$\PageIndex{14}$ : graphique du comportement final et des interceptions,$(-3, 0)$ et$(0, 90)$, pour la fonction$f(x)=-2(x+3)^2(x-5)$.

Quelque part après ce point, le graphe doit rebrousser chemin vers le bas ou commencer à diminuer vers l'axe horizontal, car le graphe passe par l'intersection suivante à$(5,0)$. Voir la figure$\PageIndex{15}$.

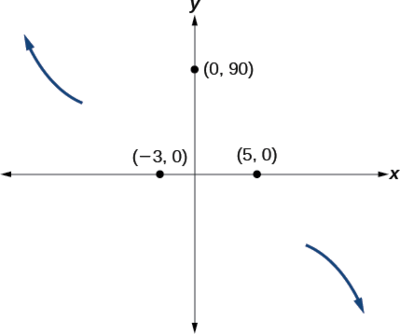
Graphique du comportement final et des interceptions, (-3, 0), (0, 90) et (5, 0), pour la fonction f (x) =-2 (x+3) ^2 (x-5). — Figure$\PageIndex{15}$ : graphique du comportement final et des interceptions$(-3, 0)$,$(0, 90)$ et$(5, 0)$, pour la fonction$f(x)=-2(x+3)^2(x-5)$.

En tant$x{\rightarrow}{\infty}$ que fonction$f(x){\rightarrow}−{\infty}$,

nous savons donc que le graphique continue de diminuer et que nous pouvons arrêter de dessiner le graphique dans le quatrième quadrant.

À l'aide de la technologie, nous pouvons créer le graphe de la fonction polynomiale, illustrée dans la figure$\PageIndex{16}$, et vérifier que le graphe obtenu ressemble à notre esquisse de la figure$\PageIndex{15}$.

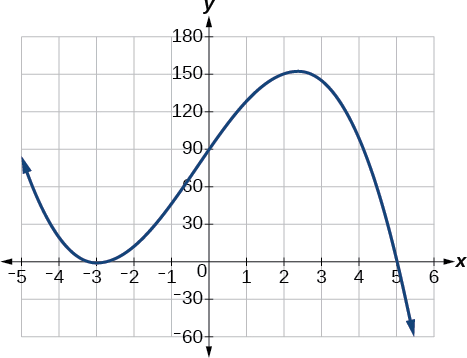
$Le graphe complet de la fonction polynomiale f (x) =−2 (x+3) ^2 (x−5)$
Figure$\PageIndex{16}$ : Le graphe complet de la fonction polynomiale$f(x)=−2(x+3)^2(x−5)$.

Exercice$\PageIndex{8}$

Esquissez un graphique de$f(x)=\dfrac{1}{4}x(x−1)^4(x+3)^3$.

Réponse: $alt$
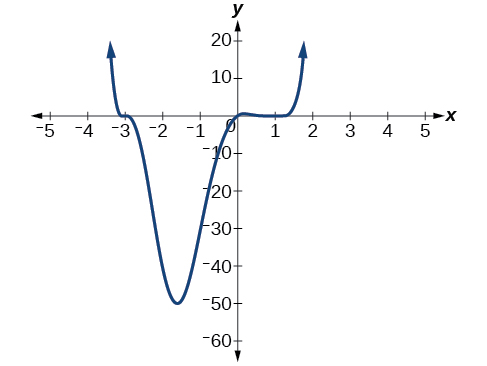
Figure$\PageIndex{17}$ : Graphique de$f(x)=\frac{1}{4}x(x−1)^4(x+3)^3$

Utilisation du théorème des valeurs intermédiaires

Dans certaines situations, nous pouvons connaître deux points sur un graphique, mais pas les zéros. Si ces deux points se trouvent de part et d'autre de l'axe X, nous pouvons confirmer qu'il y a un zéro entre eux. Prenons l'exemple d'une fonction polynomiale$f$ dont le graphe est lisse et continu. Le théorème des valeurs intermédiaires indique que pour deux nombres$a$ et$b$ dans le domaine de$f$, si$a<b$ et$f(a){\neq}f(b)$, alors la fonction$f$ prend toutes les valeurs comprises entre$f(a)$ et$f(b)$. Nous pouvons appliquer ce théorème à un cas particulier qui est utile pour représenter graphiquement des fonctions polynomiales. Si un point du graphe d'une fonction continue$f$ à$x=a$ se trouve au-dessus de l'axe X et qu'un autre point à$x=b$ se trouve en dessous de l'axe X, il doit exister un troisième point entre$x=a$ et$x=b$ où le graphe croise l'axe X. Appelez ce point$(c,f(c))$. Cela signifie que nous sommes assurés qu'il existe une solution$c$ où$f(c)=0$.

En d'autres termes, le théorème des valeurs intermédiaires nous indique que lorsqu'une fonction polynomiale passe d'une valeur négative à une valeur positive, la fonction doit traverser l'axe des abscisses. La figure$\PageIndex{18}$ montre qu'il y a un zéro entre$a$ et$b$.

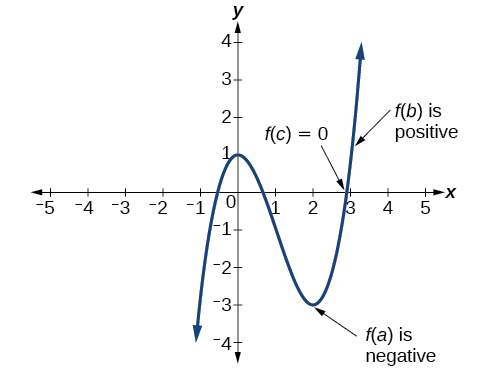
Graphe d'une fonction polynomiale à degrés impairs qui montre un point f (a) négatif, f (b) positif et f (c) égal à 0. — Figure$\PageIndex{18}$ : Utilisation du théorème des valeurs intermédiaires pour montrer qu'il existe un zéro.

Définition : Théorème des valeurs intermédiaires

$f$Soyons une fonction polynomiale. Le théorème des valeurs intermédiaires indique que si$f(a)$ et$f(b)$ ont des signes opposés, il existe au moins une valeur$c$ entre$a$ et$b$ pour laquelle$f(c)=0$.

Exemple$\PageIndex{9}$: Using the Intermediate Value Theorem

Montrez que la fonction$f(x)=x^3−5x^2+3x+6$ possède au moins deux zéros réels entre$x=1$ et$x=4$.

Solution

Pour commencer, évaluez$f(x)$ à partir de valeurs entières$x=1,\;2,\;3,\; \text{and }4$ (Tableau$\PageIndex{2}$).

Tableau$\PageIndex{2}$
$x$	1	2	3	4
$f(x)$	5	0	-3	2

Nous voyons qu'un zéro se produit à$x=2$. De plus, étant donné que$f(4)$ c'$f(3)$est négatif et positif, selon le théorème des valeurs intermédiaires, il doit y avoir au moins un zéro réel entre 3 et 4.

Nous avons montré qu'il y a au moins deux vrais zéros entre$x=1$ et$x=4$.

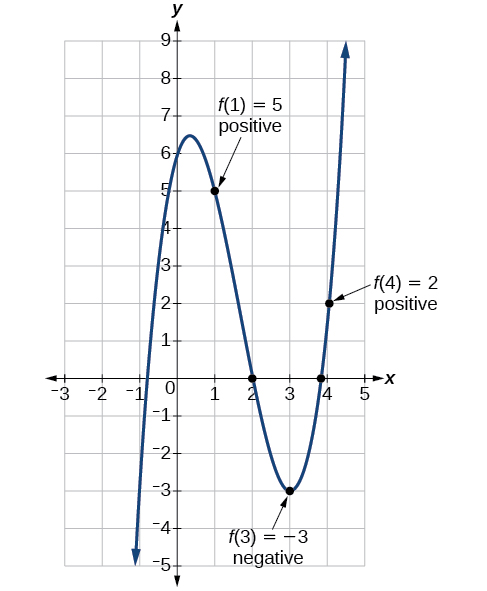
Analyse

Nous pouvons également voir sur le graphique de la fonction de la figure$\PageIndex{19}$ qu'il y a deux zéros réels entre$x=1$ et$x=4$.

Le graphique de f (x) =x^3-5x^2+3x+6 montre, selon le théorème des valeurs intermédiaires, qu'il existe deux zéros puisque f (1) =5 et f (4) =2 sont positifs et f (3) = -3 est négatif. — Chiffre$\PageIndex{19}$.

Exercice$\PageIndex{4}$

Montrez que la fonction$f(x)=7x^5−9x^4−x^2$ possède au moins un vrai zéro compris entre$x=1$ et$x=2$.

Réponse: Parce que$f$ est une fonction polynomiale et qu'elle$f(1)$$f(2)$ est négative et positive, il y a au moins un zéro réel entre$x=1$ et$x=2$.

Écrire des formules pour des fonctions polynomiales

Maintenant que nous savons comment trouver les zéros des fonctions polynomiales, nous pouvons les utiliser pour écrire des formules basées sur des graphes. Comme une fonction polynomiale écrite sous forme factorielle aura une intersection X où chaque facteur est égal à zéro, nous pouvons former une fonction qui passera par un ensemble d'interceptions X en introduisant un ensemble correspondant de facteurs.

Remarque : Forme factorielle des polynômes

Si un polynôme du degré le plus bas$p$ possède des interceptions horizontales à$x=x_1,x_2,…,x_n$, alors le polynôme peut être écrit sous la forme factorielle :$f(x)=a(x−x_1)^{p_1}(x−x_2)^{p_2}⋯(x−x_n)^{p_n}$ où les puissances$p_i$ de chaque facteur peuvent être déterminées par le comportement du graphe à l'intersection correspondante et par le facteur d'étirement$a$ peut être déterminé en fonction d'une valeur de la fonction autre que l'intersection X.

$alt$ À partir du graphe d'une fonction polynomiale, écrivez une formule pour la fonction.

Identifiez les points d'intersection X du graphe pour trouver les facteurs du polynôme.
Examinez le comportement du graphe aux points d'intersection X pour déterminer la multiplicité de chaque facteur.
Détermine le polynôme du moindre degré contenant tous les facteurs trouvés à l'étape précédente.
Utilisez n'importe quel autre point du graphique (l'intersection Y peut être la plus simple) pour déterminer le facteur d'étirement.

Exemple$\PageIndex{10}$: Writing a Formula for a Polynomial Function from the Graph

Écrivez une formule pour la fonction polynomiale illustrée à la figure$\PageIndex{20}$.

Graphique d'un polynôme positif à degrés pairs avec des zéros à x=-3, 2, 5 et y=-2. — Chiffre$\PageIndex{20}$.

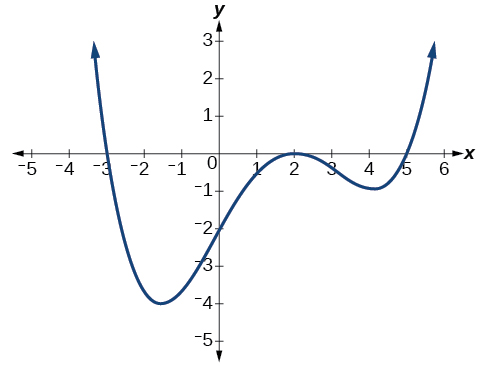
Solution

Ce graphique comporte trois interceptions X :$x=−3,\;2,\text{ and }5$. L'intersection y est située$(0,2)$ à .At$x=−3$ et$ x=5$ le graphe passe par l'axe de manière linéaire, ce qui suggère que les facteurs correspondants du polynôme seront linéaires. À$x=2$, le graphe rebondit à l'intersection, ce qui suggère que le facteur correspondant du polynôme sera le deuxième degré (quadratique). Ensemble, cela nous donne

\[f(x)=a(x+3)(x−2)^2(x−5)\]

Pour déterminer le facteur d'étirement, nous utilisons un autre point du graphique. Nous utiliserons l'intersection$(0,–2)$ Y pour résoudre$a$.

\[\begin{align*} f(0)&=a(0+3)(0−2)^2(0−5) \\ −2&=a(0+3)(0−2)^2(0−5) \\ −2&=−60a \\ a&=\dfrac{1}{30} \end{align*}\]

Le polynôme représenté par un graphe semble représenter la fonction$f(x)=\dfrac{1}{30}(x+3)(x−2)^2(x−5)$.

Exercice$\PageIndex{5}$

Sur la base du graphique illustré à la figure$\PageIndex{21}$, écrivez une formule pour la fonction illustrée.

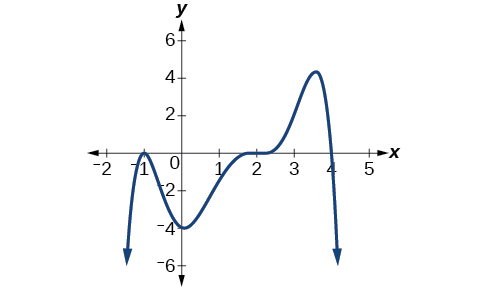
Graphique d'un polynôme pair négatif avec des zéros à x=-1, 2, 4 et y=-4. — Chiffre$\PageIndex{21}$.

Réponse: $f(x)=−\frac{1}{8}(x−2)^3(x+1)^2(x−4)$

Utilisation d'Extrema local et global

Avec les quadratiques, nous avons pu trouver algébriquement la valeur maximale ou minimale de la fonction en trouvant le sommet. Pour les polynômes généraux, il n'est pas possible de trouver ces points de retournement sans techniques plus avancées issues du calcul. Même dans ce cas, trouver où se produisent les extrêmes peut s'avérer difficile sur le plan algébrique. Pour l'instant, nous allons estimer les emplacements des points de retournement à l'aide de la technologie pour générer un graphique.

Chaque point tournant représente un minimum ou un maximum local. Parfois, un point tournant est le point le plus haut ou le plus bas de l'ensemble du graphique. Dans ces cas, nous disons que le point tournant est un maximum global ou un minimum global. Ces valeurs sont également appelées valeurs maximales et minimales absolues de la fonction.

Remarque : Extrema local et global

Un maximum local ou un minimum local à$x=a$ (parfois appelé maximum ou minimum relatif, respectivement) est la sortie au point le plus haut ou le plus bas du graphique dans un intervalle ouvert autour de$x=a$ .Si une fonction a un maximum local à$a$, alors$f(a){\geq}f(x)$ pour tous $x$dans un intervalle ouvert autour de$x=a$. Si une fonction a un minimum local à$a$, alors$f(a){\leq}f(x)$ pour tous$x$ dans un intervalle ouvert autour de$x=a$.

Un maximum global ou un minimum global est la sortie au point le plus haut ou le plus bas de la fonction. Si une fonction a un maximum global à$a$, alors$f(a){\geq}f(x)$ pour tous$x$. Si une fonction a un minimum global à$a$, alors$f(a){\leq}f(x)$ pour tous$x$.

Nous pouvons voir la différence entre les extrêmes locaux et globaux sur la figure$\PageIndex{22}$.

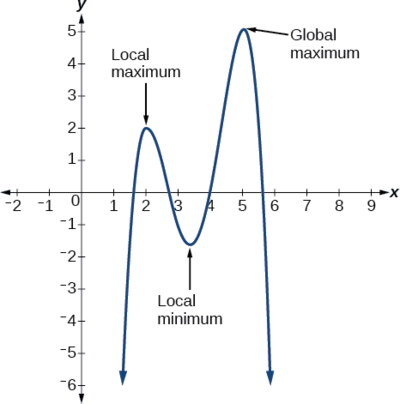
Graphe d'un polynôme à degrés pairs qui indique le maximum et le minimum locaux et le maximum global. — Figure$\PageIndex{22}$ : Graphique d'un polynôme à degrés pairs qui indique le maximum et le minimum locaux et le maximum global.

$alt$ Toutes les fonctions polynomiales ont-elles un minimum ou un maximum global ?

Non. Seules les fonctions polynomiales de degré pair ont un minimum ou un maximum global. Par exemple, n'$f(x)=x$a ni maximum ni minimum global.

Exemple$\PageIndex{11}$: Using Local Extrema to Solve Applications

Une boîte à couvercle ouvert doit être construite en découpant des carrés à chaque coin d'une feuille de plastique de 14 cm sur 20 cm, puis en repliant les côtés. Déterminez la taille des carrés à découper pour maximiser le volume délimité par la boîte.

Solution

Nous allons commencer ce problème en dessinant une image comme celle de la figure$\PageIndex{23}$, en étiquetant la largeur des carrés découpés avec une variable,$w$.

Figure$\PageIndex{23}$ : Schéma d'un rectangle avec quatre carrés aux angles.

Notez qu'une fois qu'un carré a été découpé à chaque extrémité, il laisse un rectangle de$a(14−2w)$$(20−2w)$ cm sur cm pour la base de la boîte, et la boîte aura une hauteur de$w$ cm. Cela donne le volume

\[\begin{align*} V(w)&=(20−2w)(14−2w)w \\ &=280w−68w^2+4w^3 \end{align*}\]

Remarquez, puisque les facteurs sont$20–2w$$14–2w$, et$w$, les trois zéros sont$10, \,7,$ et$0,) respectively. Because a height of \(0$ cm n'est pas raisonnable, nous considérons les seuls zéros$10$ et$7.$ le côté le plus court est$14$ et nous coupons deux carrés, donc les valeurs$w$ peuvent prendre supérieur à zéro ou inférieur à$7.$ Cela signifie que nous allons restreindre le domaine de cette fonction à$0<w<7$ .En utilisant la technologie pour esquisser le graphe de$V(w)$ ce domaine raisonnable, nous obtenons un graphique comme celui de la Figure$\PageIndex{24}$. Nous pouvons utiliser ce graphique pour estimer la valeur maximale du volume, en nous limitant aux valeurs raisonnables pour$w$ ce problème, c'est-à-dire des valeurs comprises entre 0 et 7.

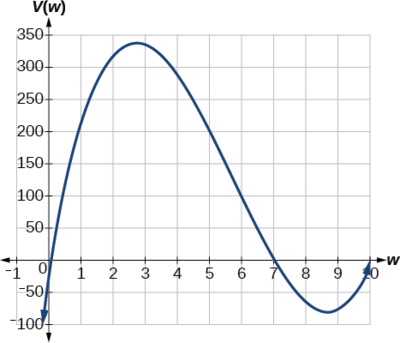
Graphe de V (w) = (20-2w) (14-2w) w où l'axe x est marqué w et l'axe y est étiqueté V (w). — Figure$\PageIndex{24}$ : Graphique de$V(w)=(20-2w)(14-2w)w$

À partir de ce graphique, nous nous concentrons uniquement sur la partie du domaine raisonnable,$[0, 7]$. Nous pouvons estimer la valeur maximale à environ 340 cm cubes, ce qui se produit lorsque les carrés mesurent environ 2,75 cm de chaque côté. Pour améliorer cette estimation, nous pouvons utiliser les fonctionnalités avancées de notre technologie, si elles sont disponibles, ou simplement modifier notre fenêtre pour zoomer sur notre graphique afin de produire la figure$\PageIndex{25}$.

Graphe de V (w) = (20-2w) (14-2w) w où l'axe x est marqué w et l'axe y est étiqueté V (w) sur le domaine [2.4, 3]. — Figure$\PageIndex{25}$ : Graphique de$V(w)=(20-2w)(14-2w)w$.

À partir de cette vue agrandie, nous pouvons affiner notre estimation du volume maximal à environ 339 cm cubes, lorsque les carrés mesurent environ 2,7 cm de chaque côté.

Exercice$\PageIndex{1}$

Utilisez la technologie pour déterminer les valeurs maximale et minimale de l'intervalle$[−1,4]$ de la fonction$f(x)=−0.2(x−2)^3(x+1)^2(x−4)$.

Réponse: Le minimum se produit approximativement au point$(0,−6.5)$
et le maximum se produit approximativement au point$(3.5,7)$.

Concepts clés

Les fonctions polynomiales de degré 2 ou plus sont des fonctions lisses et continues.
Pour trouver les zéros d'une fonction polynomiale, si elle peut être factorisée, factorisez la fonction et définissez chaque facteur sur zéro.
Une autre façon de trouver les points d'intersection X d'une fonction polynomiale consiste à représenter graphiquement la fonction et à identifier les points auxquels le graphe croise l'axe des abscisses.
La multiplicité d'un zéro détermine le comportement du graphe aux points d'intersection X.
Le graphe d'un polynôme traversera l'axe horizontal à zéro avec une multiplicité impaire.
Le graphe d'un polynôme touchera l'axe horizontal à zéro avec une multiplicité uniforme.
Le comportement final d'une fonction polynomiale dépend du terme principal.
Le graphe d'une fonction polynomiale change de direction à ses points de retournement.
Une fonction polynomiale de degré$n$ a tout au plus des points$n−1$ tournants.
Pour représenter graphiquement des fonctions polynomiales, trouvez les zéros et leurs multiplicités, déterminez le comportement final et assurez-vous que le graphe final comporte au maximum de points de$n−1$ retournement.
La représentation graphique d'une fonction polynomiale permet d'estimer les extrêmes locaux et globaux.
Le théorème des valeurs intermédiaires nous indique que si$f(a)$ et$f(b)$ ont des signes opposés, il existe au moins une valeur$c$ entre$a$ et$b$ pour laquelle$f(c)=0$.

Lexique

point de retournement
maximal global le plus élevé sur un graphique ;$f(a)$ où$f(a){\geq}f(x)$ pour tous$x$.

point de retournement minimum global le
plus bas sur un graphique ;$f(a)$ où$f(a){\leq}f(x)$ pour tous$x$.

Théorème des valeurs intermédiaires
pour deux nombres$a$ et$b$ dans le domaine de$f$, si$a<b$ et$f(a){\neq}f(b)$, alors la fonction f prend toutes les valeurs comprises entre$f(a)$ et$f(b)$ ; en particulier, lorsqu'une fonction polynomiale passe d'une valeur négative à une valeur positive, la fonction doit traverser l'axe X

multiplicité
le nombre de fois qu'un facteur donné apparaît sous la forme factorielle de l'équation d'un polynôme ; si un polynôme contient un facteur de la forme$(x−h)^p$,$x=h$ est un zéro de multiplicité$p$.

Tableau\(\PageIndex{2}\)
\(x\)	1	2	3	4
\(f(x)\)	5	0	-3	2