5.2 : Fonctions de puissance et fonctions polynomiales

Last updated
Save as PDF

Page ID: 195551

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Identifiez les fonctions d'alimentation.
Identifiez le comportement final des fonctions d'alimentation.
Identifiez les fonctions polynomiales.
Identifiez le degré et le coefficient principal des fonctions polynomiales.

Supposons qu'une certaine espèce d'oiseau prospère sur une petite île. Sa population au cours des dernières années est indiquée dans le tableau$\PageIndex{1}$.

Tableau$\PageIndex{1}$
Année	2009	2010	2011	2012	2013
Population d'oiseaux	800	897	992	1 083	1 169

La population peut être estimée à l'aide de la fonction$P(t)=−0.3t^3+97t+800$, où$P(t)$ représente la population d'oiseaux sur l'île des$t$ années après 2009. Nous pouvons utiliser ce modèle pour estimer la population maximale d'oiseaux et le moment où elle se produira. Nous pouvons également utiliser ce modèle pour prédire quand la population d'oiseaux disparaîtra de l'île. Dans cette section, nous examinerons les fonctions que nous pouvons utiliser pour estimer et prévoir ces types de changements.

Trois oiseaux sur une falaise avec le soleil levant en arrière-plan. — Figure$\PageIndex{1}$ : (crédit : Jason Bay, Flickr)

Identification des fonctions d'alimentation

Afin de mieux comprendre le problème des oiseaux, nous devons comprendre un type de fonction spécifique. Une fonction de puissance est une fonction avec un seul terme qui est le produit d'un nombre réel, d'un coefficient et d'une variable portée à un nombre réel fixe. (Un nombre qui multiplie une variable élevée jusqu'à un exposant est connu sous le nom de coefficient.)

Par exemple, considérez les fonctions de surface ou de volume. La fonction de l'aire d'un cercle avec un rayon$r$ est

\[A(r)={\pi}r^2 \nonumber\]

et la fonction du volume d'une sphère avec un rayon$r$ est

\[V(r)=\dfrac{4}{3}{\pi}r^3 \nonumber\]

Ces deux fonctions sont des exemples de fonctions de puissance car elles consistent en un coefficient,${\pi}$ ou$\dfrac{4}{3}{\pi}$, multiplié par une variable$r$ portée à une puissance.

Définition : Fonction d'alimentation

Une fonction de puissance est une fonction qui peut être représentée dans le formulaire

\[f(x)=kx^p \label{power}\]

où$k$ et$p$ sont des nombres réels, et$k$ est connu sous le nom de coefficient.

Q&R : Est$f(x)=2^x$ a power function?

Non. Une fonction de puissance contient une base variable portée à une puissance fixe (équation \ ref {power}). Cette fonction a une base constante portée à une puissance variable. C'est ce qu'on appelle une fonction exponentielle, et non une fonction de puissance. Cette fonction sera abordée plus tard.

Exemple$\PageIndex{1}$: Identifying Power Functions

Parmi les fonctions suivantes, lesquelles sont des fonctions d'alimentation ?

\[\begin{align*} f(x)&=1 &\text{Constant function} \\f(x)&=x &\text{Identify function} \\f(x)&=x^2 &\text{Quadratic function} \\ f(x)&=x^3 &\text{Cubic function} \\ f(x)&=\dfrac{1}{x} &\text{Reciprocal function} \\f(x)&=\dfrac{1}{x^2} &\text{Reciprocal squared function} \\ f(x)&=\sqrt{x} &\text{Square root function} \\ f(x)&=\sqrt[3]{x} &\text{Cube root function} \end{align*}\]

Solution

Toutes les fonctions répertoriées sont des fonctions d'alimentation.

Les fonctions de constante et d'identité sont des fonctions de puissance car elles peuvent être écrites$f(x)=x^1$ respectivement au fur$f(x)=x^0$ et à mesure.

Les fonctions quadratique et cubique sont des fonctions de puissance avec des puissances entières$f(x)=x^2$ et$f(x)=x^3$.

Les fonctions quadratiques réciproques et réciproques sont des fonctions de puissance avec des puissances entières négatives car elles peuvent être écrites sous la forme$f(x)=x^{−1}$ et$f(x)=x^{−2}$.

Les fonctions de racine carrée et cubique sont des fonctions de puissance avec des puissances fractionnaires car elles peuvent être écrites sous la forme$f(x)=x^{1/2}$ ou$f(x)=x^{1/3}$.

Exercice$\PageIndex{1}$

Quelles fonctions sont des fonctions de puissance ?

$f(x)=2x^2⋅4x^3$
$g(x)=−x^5+5x^3−4x$
$h(x)=\frac{2x^5−1}{3x^2+4}$

Réponse: $f(x)$est une fonction d'alimentation car elle peut être écrite sous la forme$f(x)=8x^5$. Les autres fonctions ne sont pas des fonctions d'alimentation.

Identification du comportement final des fonctions d'alimentation

La figure$\PageIndex{2}$ montre les graphes de$f(x)=x^2$,$g(x)=x^4$ et et$h(x)=x^6$, qui sont toutes des fonctions de puissance avec des puissances entières paires. Notez que ces graphes ont des formes similaires, très similaires à celles de la fonction quadratique de la boîte à outils. Cependant, à mesure que la puissance augmente, les graphes s'aplatissent légèrement près de l'origine et s'éloignent de plus en plus de l'origine.

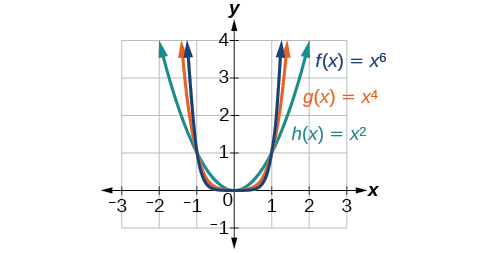
Graphe de trois fonctions, h (x) =x^2 en vert, g (x) =x^4 en orange et f (x) =x^6 en bleu. — Figure$\PageIndex{2}$ : Fonctions à puissance uniforme

Pour décrire le comportement à mesure que les nombres deviennent de plus en plus grands, nous utilisons l'idée de l'infini. Nous utilisons le symbole de$\infty$ l'infini positif et$−\infty$ de l'infini négatif. Lorsque nous disons que « x approche de l'infini », ce qui peut être écrit symboliquement$x{\rightarrow}\infty$, nous décrivons un comportement ; nous disons qu'il$x$ augmente sans limite.

Avec la fonction de puissance égale, lorsque l'entrée augmente ou diminue sans limite, les valeurs de sortie deviennent de très grands nombres positifs. De manière équivalente, nous pourrions décrire ce comportement en disant qu'à mesure que l'infini se$x$ rapproche de l'infini positif ou négatif, les$f(x)$ valeurs augmentent sans limite. Sous forme symbolique, nous pourrions écrire

\[\text{as } x{\rightarrow}{\pm}{\infty}, \;f(x){\rightarrow}{\infty} \nonumber\]

La figure$\PageIndex{3}$ montre les graphes de$f(x)=x^3$$g(x)=x^5$, et$h(x)=x^7$, qui sont toutes des fonctions de puissance avec des puissances impaires et entières. Notez que ces graphiques ressemblent à la fonction cubique de la boîte à outils. Encore une fois, à mesure que la puissance augmente, les graphes s'aplatissent près de l'origine et s'éloignent de plus en plus de l'origine.

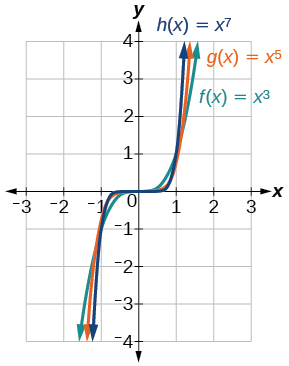
Graphe de trois fonctions, f (x) =x^3 en vert, g (x) =x^5 en orange et h (x) =x^7 en bleu. — Figure$\PageIndex{3}$ : fonction Odd-Power

Ces exemples montrent que les fonctions de la forme$f(x)=x^n$ révèlent une symétrie d'une sorte ou d'une autre. Tout d'abord, dans la figure$f(x)=x^n$,$\PageIndex{2}$$n$ nous voyons que même les fonctions de la forme sont symétriques par rapport à$y$ l'axe. Sur la figure,$\PageIndex{3}$ nous voyons que les fonctions impaires de la forme$f(x)=x^n$,$n$ impaires, sont symétriques par rapport à l'origine.

Car ces fonctions de puissance étranges, lorsqu'elles se$x$ rapprochent de l'infini négatif,$f(x)$ diminuent sans limite. À mesure$x$ que l'infini est positif,$f(x)$ augmente sans limite. Sous forme symbolique, nous écrivons

\[\begin{align*} &\text{as }x{\rightarrow}-{\infty},\;f(x){\rightarrow}-{\infty} \\ &\text{as }x{\rightarrow}{\infty},\;f(x){\rightarrow}{\infty} \end{align*}\]

Le comportement du graphe d'une fonction lorsque les valeurs en entrée deviennent très petites$(x{\rightarrow}−{\infty})$ et très grandes$x{\rightarrow}{\infty}$ est appelé comportement final de la fonction. Nous pouvons utiliser des mots ou des symboles pour décrire le comportement final.

La figure$\PageIndex{4}$ montre le comportement final des fonctions de puissance sous la forme$f(x)=kx^n$ où$n$ est un entier non négatif en fonction de la puissance et de la constante.

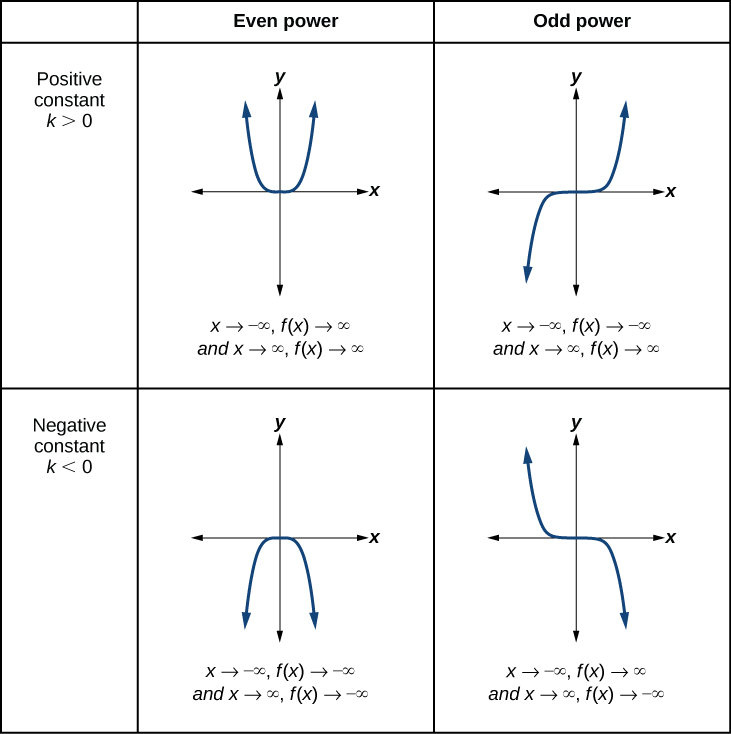
Mode d'emploi : étant donné une fonction de puissance$f(x)=kx^n$ where $n$ is a non-negative integer, identify the end behavior.

Déterminez si la puissance est paire ou impaire.
Déterminez si la constante est positive ou négative.
Utilisez Figure$\PageIndex{4}$ pour identifier le comportement final.

Exemple$\PageIndex{2}$: Identifying the End Behavior of a Power Function

Décrivez le comportement final du graphe de$f(x)=x^8$.

Solution

Le coefficient est de 1 (positif) et l'exposant de la fonction de puissance est de 8 (nombre pair). À mesure que l'infini se$x$ rapproche, la sortie (valeur de$f(x)$) augmente sans limite. Nous écrivons$x→∞,$$f(x)→∞.$ alors que$x$ As approche de l'infini négatif, la sortie augmente sans limite. Sous forme symbolique, car$x→−∞,$$f(x)→∞.$ nous pouvons représenter graphiquement la fonction comme indiqué sur la figure$\PageIndex{5}$.

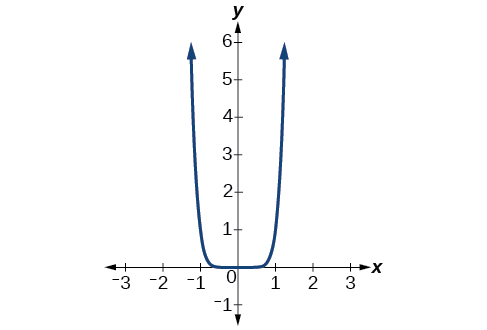
Graphe de f (x) =x^8 — Figure$\PageIndex{5}$ : Graphique de$f(x)=x^8$.

Exemple$\PageIndex{3}$: Identifying the End Behavior of a Power Function.

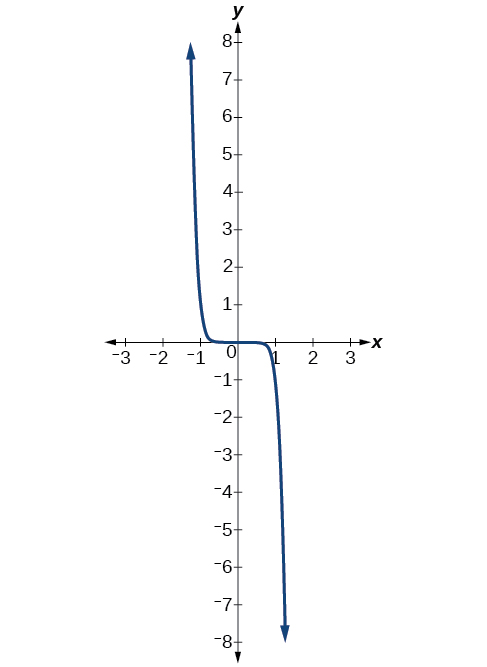
Décrivez le comportement final du graphe de$f(x)=−x^9$.

Solution

L'exposant de la fonction de puissance est 9 (un nombre impair). Comme le coefficient est —1 (négatif), le graphe est le reflet autour de l'$x$axe -du graphe de$f(x)=x^9$. La figure$\PageIndex{6}$ montre qu'à mesure que l'on$x$ approche de l'infini, la sortie diminue sans limite. Lorsque l'$x$infini est proche de l'infini négatif, la sortie augmente sans limite. Sous forme symbolique, nous écririons

\[\begin{align*} \text{as }x{\rightarrow}-{\infty},\;f(x){\rightarrow}{\infty} \\ \text{as }x{\rightarrow}{\infty},\;f(x){\rightarrow}-{\infty} \end{align*}\]

Graphe de f (x) =-x^9 — Figure$\PageIndex{6}$ : Graphique de$f(x)=-x^9$.

Analyse

Nous pouvons vérifier notre travail en utilisant la fonction de tableau d'un utilitaire graphique.

Tableau$\PageIndex{2}$
$x$	$f(x)$
\ (x \) » style="vertical-align:middle ; « >-10	\ (f (x) \) » style="vertical-align:middle ; « >1 000 000 000
\ (x \) » style="vertical-align:middle ; « >-5	\ (f (x) \) » style="vertical-align:middle ; « >1 953 125
\ (x \) » style="vertical-align:middle ; « >0	\ (f (x) \) » style="vertical-align:middle ; « >0
\ (x \) » style="vertical-align:middle ; « >5	\ (f (x) \) » style="vertical-align:middle ; « >-1 953 125
\ (x \) » style="vertical-align:middle ; « >10	\ (f (x) \) » style="vertical-align:middle ; « >-1 000 000 000

Nous pouvons voir dans le tableau$\PageIndex{2}$ que, lorsque nous substituons de très petites valeurs à$x$, la sortie est très grande, et lorsque nous substituons de très grandes valeurs à$x$, la sortie est très petite (ce qui signifie qu'il s'agit d'une très grande valeur négative).

Exercice$\PageIndex{2}$

Décrivez avec des mots et des symboles le comportement final de$f(x)=−5x^4$.

Réponse: À l'$x$approche de l'infini positif ou négatif,$f(x)$ diminue sans limite : comme$x{\rightarrow}{\pm}{\infty}$, à$f(x){\rightarrow}−{\infty}$ cause du coefficient négatif.

Identification des fonctions polynomiales

Un oléoduc éclate dans le golfe du Mexique, provoquant une nappe de pétrole de forme à peu près circulaire. La nappe a actuellement un rayon de 24 miles, mais ce rayon augmente de 13 miles chaque semaine. Nous voulons écrire une formule pour la zone couverte par la nappe de pétrole en combinant deux fonctions. Le rayon$r$ du déversement dépend du nombre de semaines$w$ écoulées. Cette relation est linéaire.

\[r(w)=24+8w \nonumber\]

Nous pouvons combiner cela avec la formule de l'aire A d'un cercle.

\[A(r)={\pi}r^2 \nonumber\]

La composition de ces fonctions donne une formule pour la zone en termes de semaines.

\[ \begin{align*} A(w)&=A(r(w)) \\ &=A(24+8w) \\ & ={\pi}(24+8w)^2 \end{align*}\]

La multiplication donne la formule.

\[A(w)=576{\pi}+384{\pi}w+64{\pi}w^2 \nonumber\]

Cette formule est un exemple de fonction polynomiale. Une fonction polynomiale est constituée de zéro ou de la somme d'un nombre fini de termes non nuls, dont chacun est le produit d'un nombre, appelé coefficient du terme, et d'une variable portée à une puissance entière non négative.

Définition : Fonctions polynomiales

$n$Soit un entier non négatif. Une fonction polynomiale est une fonction qui peut être écrite sous la forme

\[f(x)=a_nx^n+...+a_2x^2+a_1x+a_0 \label{poly}\]

C'est ce que l'on appelle la forme générale d'une fonction polynomiale. Chacun$a_i$ est un coefficient et peut être n'importe quel nombre réel. Chaque produit$a_ix^i$ est un terme d'une fonction polynomiale.

Exemple$\PageIndex{4}$: Identifying Polynomial Functions

Lesquelles des fonctions suivantes sont des fonctions polynomiales ?

$f(x)=2x^3⋅3x+4$
$g(x)=−x(x^2−4)$
$h(x)=5\sqrt{x}+2$

Solution

Les deux premières fonctions sont des exemples de fonctions polynomiales car elles peuvent être écrites sous la forme d'équation \ ref {poly}, où les puissances sont des entiers non négatifs et les coefficients sont des nombres réels.

$f(x)$peut être écrit comme$f(x)=6x^4+4$.
$g(x)$peut être écrit comme$g(x)=−x^3+4x$.
$h(x)$ne peut pas être écrite sous cette forme et n'est donc pas une fonction polynomiale.

Identification du degré et du coefficient principal d'une fonction polynomiale

En raison de la forme d'une fonction polynomiale, nous pouvons observer une variété infinie dans le nombre de termes et la puissance de la variable. Bien que l'ordre des termes dans la fonction polynomiale ne soit pas important pour effectuer des opérations, nous organisons généralement les termes par ordre de puissance décroissant ou sous une forme générale. Le degré du polynôme est la puissance la plus élevée de la variable qui se trouve dans le polynôme ; il s'agit de la puissance de la première variable si la fonction est sous forme générale. Le terme principal est le terme contenant la puissance la plus élevée de la variable, ou le terme avec le degré le plus élevé. Le coefficient principal est le coefficient du terme principal.

Terminologie des fonctions polynomiales

Nous réorganisons souvent les polynômes de manière à ce que les puissances soient descendantes.

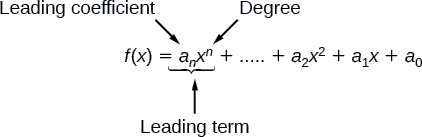
Lorsqu'un polynôme est écrit de cette manière, on dit qu'il est sous forme générale.

Mode d'emploi : À partir d'une fonction polynomiale, identifier le degré et le coefficient directeur

Déterminez la puissance la plus élevée de$x$ pour déterminer la fonction des degrés.
Identifiez le terme contenant la plus grande puissance de$x$ pour trouver le terme principal.
Identifiez le coefficient du terme principal.

Exemple$\PageIndex{5}$: Identifying the Degree and Leading Coefficient of a Polynomial Function

Identifiez le degré, le terme principal et le coefficient principal des fonctions polynomiales suivantes.

$f(x)=3+2x^2−4x^3$

$g(t)=5t^5−2t^3+7t$

$h(p)=6p−p^3−2$

Solution

Pour la fonction$f(x)$, la puissance la plus élevée de$x$ est 3, donc le degré est de 3. Le terme principal est le terme contenant ce diplôme,$−4x^3$. Le coefficient principal est le coefficient de ce terme, −4.

Pour la fonction$g(t)$, la puissance la plus élevée de$t$ est 5, donc le degré est de 5. Le terme principal est le terme contenant ce diplôme,$5t^5$. Le coefficient principal est le coefficient de ce terme, 5.

Pour la fonction$h(p)$, la puissance la plus élevée de$p$ est 3, donc le degré est de 3. Le terme principal est le terme contenant ce degré$−p^3$ ; le coefficient principal est le coefficient de ce terme, −1.

Exercice$\PageIndex{3}$

Identifiez le degré, le terme principal et le coefficient principal du polynôme$f(x)=4x^2−x^6+2x−6$.

Réponse: Le diplôme est$6.$ Le terme principal est$−x^6$. Le coefficient principal est$−1.$

Identification du comportement final des fonctions polynomiales

Connaître le degré d'une fonction polynomiale est utile pour nous aider à prévoir son comportement final. Pour déterminer son comportement final, examinez le terme principal de la fonction polynomiale. Comme la puissance du terme principal est la plus élevée, ce terme augmentera beaucoup plus rapidement que les autres termes lorsqu'il$x$ devient très grand ou très petit, de sorte que son comportement dominera le graphique. Pour tout polynôme, le comportement final du polynôme correspondra au comportement final du terme de plus haut degré (Tableau$\PageIndex{3}$).

Tableau$\PageIndex{3}$
Fonction polynomiale	Terme principal	Graphe de la fonction polynomiale
$f(x)=5x^4+2x^3−x−4$	$5x^4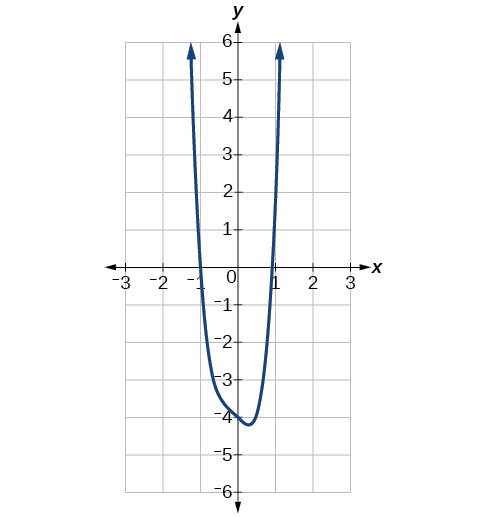$	$Graphique de f (x) =5x^4+2x^3-x-4.$
$f(x)=−2x^6−x^5+3x^4+x^3$	$−2x^6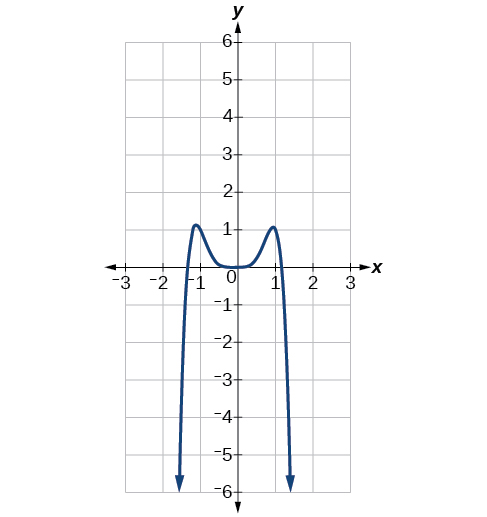$	$Graphique de f (x) =-2x^6-x^5+3x^4+x^3$
$f(x)=3x^5−4x^4+2x^2+1$	$3x^5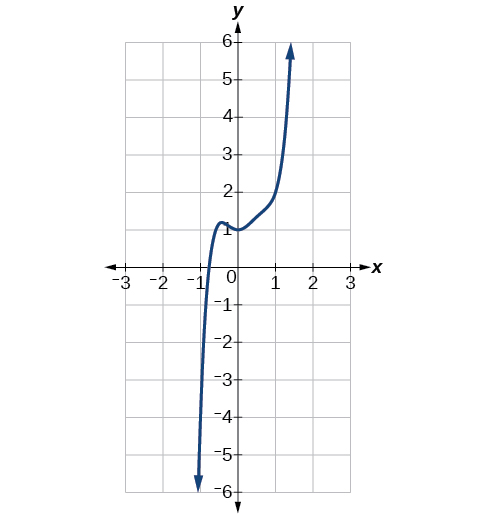$	$Graphique de f (x) =3x^5-4x^4+2x^2+1$
$f(x)=−6x^3+7x^2+3x+1$	$−6x^3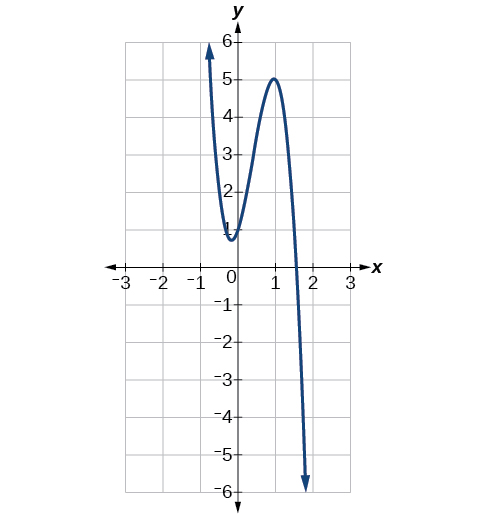$	$Graphique de f (x) =-6x^3+7x^2+3x+1$

Exemple$\PageIndex{6}$: Identifying End Behavior and Degree of a Polynomial Function

Décrivez le comportement final et déterminez un degré possible de la fonction polynomiale dans la figure$\PageIndex{8}$.

Graphe d'un polynôme de degrés impairs. — Chiffre$\PageIndex{8}$.

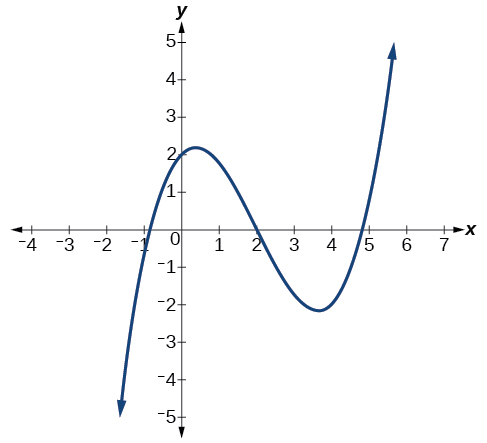
Solution

Lorsque les valeurs en entrée$x$ deviennent très grandes, les valeurs en sortie$f(x)$ augmentent sans limite. Lorsque les valeurs d'entrée$x$ deviennent très petites, les valeurs de sortie$f(x)$ diminuent sans limite. Nous pouvons décrire symboliquement le comportement final en écrivant

\[\text{as } x{\rightarrow}{\infty}, \; f(x){\rightarrow}{\infty} \nonumber\]

\[\text{as } x{\rightarrow}-{\infty}, \; f(x){\rightarrow}-{\infty} \nonumber\]

En d'autres termes, nous pourrions dire que lorsque$x$ les valeurs s'approchent de l'infini, les valeurs des fonctions s'approchent de l'infini et que$x$ les valeurs approchent de l'infini négatif, les valeurs des fonctions se rapprochent de

Nous pouvons dire que ce graphe a la forme d'une fonction de puissance en degrés impairs qui n'a pas été réfléchie, de sorte que le degré du polynôme qui crée ce graphe doit être impair et le coefficient principal doit être positif.

Exercice$\PageIndex{1}$

Décrivez le comportement final et déterminez un degré possible de la fonction polynomiale dans la figure$\PageIndex{9}$.

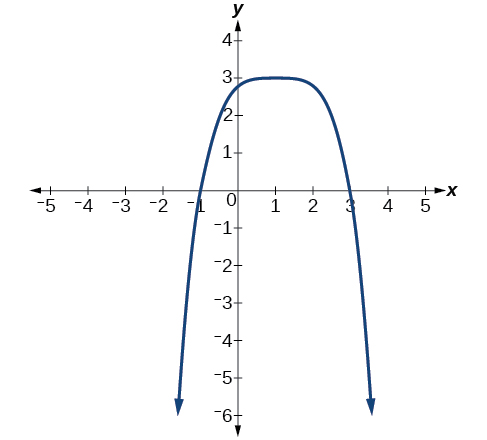
Réponse: $x{\rightarrow}{\infty}$En$f(x){\rightarrow}−{\infty}$ tant que$x{\rightarrow}−{\infty}$,$f(x){\rightarrow}−{\infty}$. Elle a la forme d'une fonction de puissance à degrés pairs avec un coefficient négatif.

Exemple$\PageIndex{7}$: Identifying End Behavior and Degree of a Polynomial Function

Compte tenu de la fonction$f(x)=−3x^2(x−1)(x+4)$, exprimez la fonction sous forme polynomiale sous forme générale et déterminez le terme principal, le degré et le comportement final de la fonction.

Solution

Obtenez la forme générale en développant l'expression donnée pour$f(x)$.

\[\begin{align*} f(x)&=−3x^2(x−1)(x+4) \\ &=−3x^2(x^2+3x−4) \\ &=−3x^4−9x^3+12x^2 \end{align*}\]

La forme générale est$f(x)=−3x^4−9x^3+12x^2$. Le terme principal est$−3x^4$ ; par conséquent, le degré du polynôme est 4. Le degré est pair (4) et le coefficient principal est négatif (—3), donc le comportement final est

\[\text{as }x{\rightarrow}−{\infty}, \; f(x){\rightarrow}−{\infty} \nonumber\]

\[\text{as } x{\rightarrow}{\infty}, \; f(x){\rightarrow}−{\infty} \nonumber\]

Exercice$\PageIndex{7}$

Compte tenu de la fonction$f(x)=0.2(x−2)(x+1)(x−5)$, exprimez la fonction sous forme polynomiale sous forme générale et déterminez le terme principal, le degré et le comportement final de la fonction.

Réponse: Le terme principal est$0.2x^3$ donc un polynôme de degré 3. Lorsque l'on$x$ approche de l'infini positif, il$f(x)$ augmente sans limite ; lorsqu'il$x$ s'approche de l'infini négatif, il$f(x)$ diminue sans limite.

Identification du comportement local des fonctions polynomiales

Outre le comportement final des fonctions polynomiales, nous nous intéressons également à ce qui se passe au « milieu » de la fonction. Nous nous intéressons en particulier aux emplacements où le comportement des graphes change. Un point tournant est un point auquel les valeurs de la fonction passent d'une augmentation à une diminution ou d'une diminution à une augmentation.

Nous sommes également intéressés par les interceptions. Comme pour toutes les fonctions,$y$ -intercept est le point d'intersection du graphe avec l'axe vertical. Le point correspond à la paire de coordonnées dans laquelle la valeur en entrée est nulle. Comme un polynôme est une fonction, une seule valeur de sortie correspond à chaque valeur d'entrée, de sorte qu'il ne peut y avoir qu'une seule$y$ -interception$(0,a_0)$. Les$x$ -intercepts se produisent aux valeurs d'entrée qui correspondent à une valeur de sortie nulle. Il est possible d'avoir plusieurs$x$ -intercept. Voir la figure$\PageIndex{10}$.

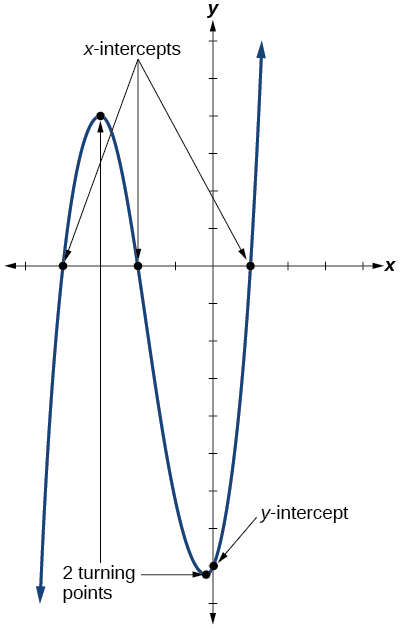
Définition : Interceptions et points de retournement des fonctions polynomiales

Un point tournant d'un graphique est un point auquel le graphe change de direction, passant d'une augmentation à une diminution ou d'une diminution à une augmentation. Le$y$ -intercept est le point auquel la fonction a une valeur d'entrée nulle. Les$x$ -intercepts sont les points auxquels la valeur de sortie est nulle.

$alt$ À partir d'une fonction polynomiale, déterminez les interceptions.

Déterminez l'$y$option -intercept en définissant$x=0$ et en recherchant la valeur de sortie correspondante.
Déterminez les$x$ -intercepts en recherchant les valeurs d'entrée qui donnent une valeur de sortie nulle.

Exemple$\PageIndex{8}$: Determining the Intercepts of a Polynomial Function

À partir de la fonction polynomiale$f(x)=(x−2)(x+1)(x−4)$, écrite sous forme factorielle pour votre commodité, déterminez$x$ les interceptions$y$ - et.

Solution

Le$y$ -intercept se produit lorsque l'entrée est nulle, remplacez donc 0 par$x$.

\[ \begin{align*}f(0)&=(0−2)(0+1)(0−4) \\ &=(−2)(1)(−4) \\ &=8 \end{align*}\]

Le$y$ -intercept est$(0,8)$.

Les$x$ -intercepts se produisent lorsque la sortie est nulle.

\[ 0=(x−2)(x+1)(x−4) \nonumber \]

\[\begin{align*} x−2&=0 & &\text{or} & x+1&=0 & &\text{or} & x−4&=0 \\ x&=2 & &\text{or} & x&=−1 & &\text{or} & x&=4 \end{align*}\]

Les$x$ -intercepts sont$(2,0)$$(–1,0)$, et$(4,0)$.

Nous pouvons voir ces interceptions sur le graphique de la fonction illustrée à la figure$\PageIndex{11}$.

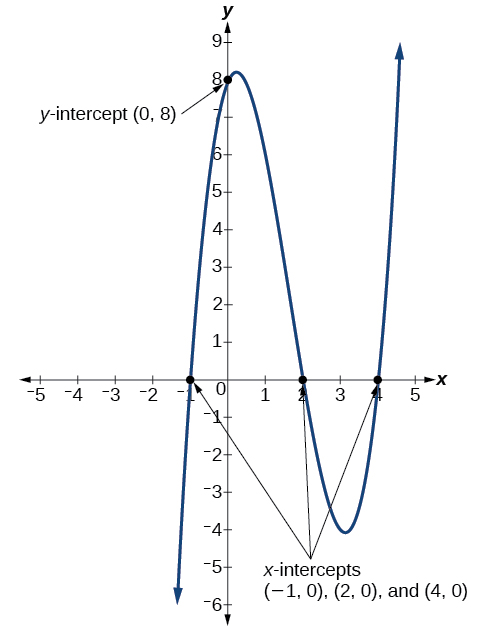
Graphe de f (x) = (x-2) (x+1) (x-4), qui étiquette toutes les interceptions. — Figure$\PageIndex{11}$ : Graphique de$f(x)=(x-2)(x+1)(x-4)$.

Exemple$\PageIndex{9}$: Determining the Intercepts of a Polynomial Function with Factoring

À partir de la fonction polynomiale$f(x)=x^4−4x^2−45$, déterminez les$x$ interceptions$y$ - et -.

Solution

Le$y$ -intercept se produit lorsque l'entrée est nulle.

\[ \begin{align*} f(0) &=(0)^4−4(0)^2−45 \\[4pt] &=−45 \end{align*}\]

Le$y$ -intercept est$(0,−45)$.

Les$x$ -intercepts se produisent lorsque la sortie est nulle. Pour déterminer quand la sortie est nulle, nous devons factoriser le polynôme.

\ [\ begin {align*} f (x) &=x^4−4x^2−45 \ \ &= (x^2−9) (x^2−9) (x^2+5) \ \ &= (x−3) (x^2+5)
\ end {align*} \]

\[0=(x−3)(x+3)(x^2+5) \nonumber\]

\[\begin{align*} x−3&=0 & &\text{or} & x+3&=0 & &\text{or} & x^2+5&=0 \\ x&=3 & &\text{or} & x&=−3 & &\text{or} &\text{(no real solution)} \end{align*}\]

Les$x$ -intercepts sont$(3,0)$ et$(–3,0)$.

Nous pouvons voir ces interceptions sur le graphique de la fonction illustrée à la figure$\PageIndex{12}$. Nous pouvons voir que la fonction est égale$f(x)=f(−x)$.

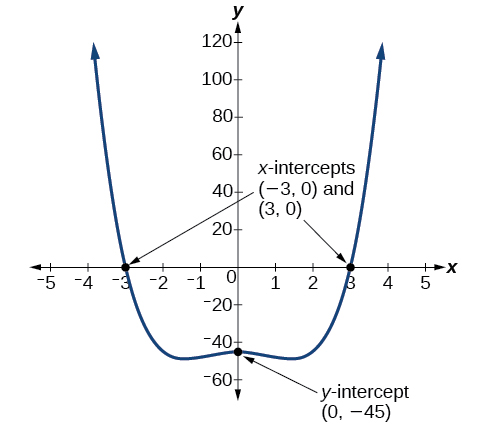
Graphe de f (x) =x^4-4x^2-45, qui étiquette toutes les interceptions à (-3, 0), (3, 0) et (0, -45). — Figure$\PageIndex{12}$ : Graphique de$f(x)=x^4-4x^2-45$.

Exercice$\PageIndex{5}$

$\PageIndex{5}$: À partir de la fonction polynomiale$f(x)=2x^3−6x^2−20x$, déterminez les interceptions$y$ - et$x$ -intercepts.

Solution: $y$-intercepter$(0,0)$ ;$x$ -intercepte$(0,0)$$(–2,0)$, et$(5,0)$

Comparaison de graphes lisses et continus

Le degré d'une fonction polynomiale nous aide à déterminer le nombre de$x$ -intercepts et le nombre de points de retournement. Une fonction polynomiale de$n^\text{th}$ degré est le produit de$n$ facteurs ; elle aura donc tout au plus des$n$ racines ou des zéros, ou des$x$ -intercepts. Le graphe de la fonction polynomiale du degré$n$ doit présenter au plus grand nombre de points de$n–1$ retournement. Cela signifie que le graphe a au plus un point tournant de moins que le degré du polynôme ou un point de moins que le nombre de facteurs.

Le graphique d'une fonction continue ne présente aucune interruption : le graphique peut être dessiné sans lever le stylo du papier. Une courbe lisse est un graphique sans angles vifs. Les points de retournement d'un graphique lisse doivent toujours se produire sur des courbes arrondies. Les graphes des fonctions polynomiales sont à la fois continus et lisses.

Interceptions et points de retournement des polynômes

Un polynôme de degré$n$ aura, tout au plus, des points$n$$x$ d'intersection et des points de$n−1$ retournement.

Exemple$\PageIndex{10}$: Determining the Number of Intercepts and Turning Points of a Polynomial

Sans représenter graphiquement la fonction, déterminez le comportement local de la fonction en déterminant le nombre maximum de$x$ -intercepts et de points de retournement pour$f(x)=−3x^{10}+4x^7−x^4+2x^3$.

Solution

Le polynôme a un degré de 10, il y a donc tout au plus des$n$$x$ interceptions et au plus des points de$n−1$ retournement.

Exercice$\PageIndex{6}$

Sans représenter graphiquement la fonction, déterminez le nombre maximum de$x$ -intercepts et de points de retournement pour$f(x)=108−13x^9−8x^4+14x^{12}+2x^3$

Réponse: Il y a au plus 12$x$ interceptions et au plus 11 points de retournement.

Exemple$\PageIndex{11}$: Drawing Conclusions about a Polynomial Function from the Graph

Que pouvons-nous conclure du polynôme représenté par le graphique de la figure en$\PageIndex{12}$ fonction de ses points d'intersection et de ses points de retournement ?

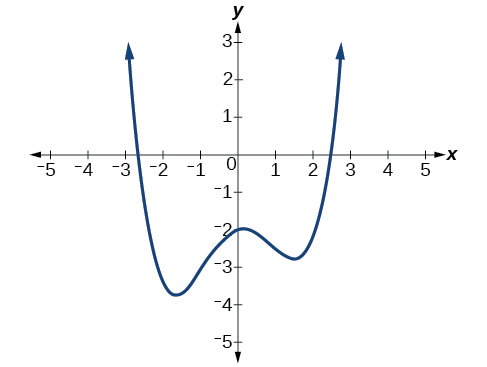
Graphe d'un polynôme de degrés pairs. — Chiffre$\PageIndex{13}$.

Solution

Le comportement final du graphe nous indique qu'il s'agit du graphe d'un polynôme à degrés pairs. Voir la figure$\PageIndex{14}$.

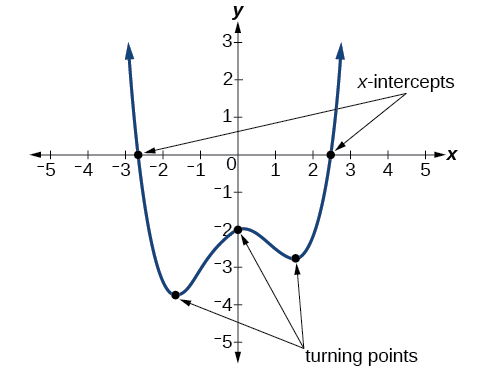
Graphe d'un polynôme à degrés pairs qui indique les points de retournement et les points d'intersection. — Figure$\PageIndex{14}$ : Graphique d'un polynôme de degrés pairs.

Le graphique comporte 2$x$ points d'intersection, suggérant un degré égal ou supérieur à 2, et 3 points de retournement, suggérant un degré égal ou supérieur à 4. Sur cette base, il serait raisonnable de conclure que le degré est égal et d'au moins 4.

Exercice$\PageIndex{7}$

Que pouvons-nous conclure du polynôme représenté par le graphique de la figure en$\PageIndex{15}$ fonction de ses points d'intersection et de ses points de retournement ?

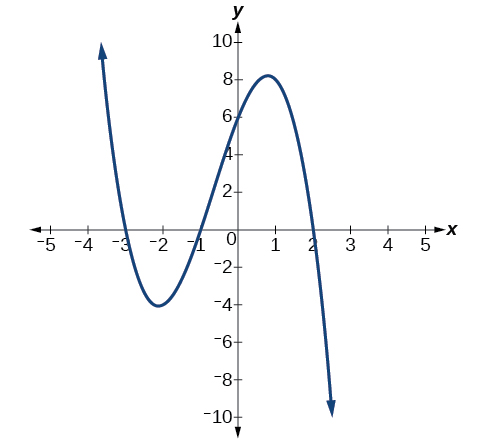
$CNX_Precalc_Figure_03_03_222.jpg$

Chiffre$\PageIndex{15}$.

Réponse: Ajoutez des textes ici. Ne supprimez pas ce texte au préalable.

Solution

Le comportement final indique une fonction polynomiale de degré impair ; il y a 3 points$x$ d'intersection et 2 points de retournement, donc le degré est impair et d'au moins 3. En raison du comportement final, nous savons que le coefficient de plomb doit être négatif.

Exemple$\PageIndex{12}$: Drawing Conclusions about a Polynomial Function from the Factors

$f(x)=−4x(x+3)(x−4)$En fonction de la fonction, déterminez le comportement local.

Solution

Le$y$ -intercept est trouvé en évaluant$f(0)$.

\[\begin{align*} f(0)&=−4(0)(0+3)(0−4) \\ &=0 \end{align*}\]

Le$y$ -intercept est$(0,0)$.

Les$x$ -intercepts sont trouvés en déterminant les zéros de la fonction.

\[\begin{align*} 0&=-4x(x+3)(x-4) \\ x&=0 & &\text{or} & x+3&=0 & &\text{or} & x-4&=0 \\ x&=0 & &\text{or} & x&=−3 & &\text{or} & x&=4 \end{align*}\]

Les$x$ -intercepts sont$(0,0)$$(–3,0)$, et$(4,0)$.

Le degré est de 3, donc le graphique a au plus 2 points de retournement.

Exercice$\PageIndex{8}$

$f(x)=0.2(x−2)(x+1)(x−5)$En fonction de la fonction, déterminez le comportement local.

Réponse: Les$x$ -intercepts sont$(2,0)$, et$(−1,0)$$(5,0)$, le$y$ -intercept est$(0,2)$, et le graphe possède au plus 2 points de retournement.

Équations clés

forme générale d'une fonction polynomiale :$f(x)=a_nx^n+a_{n-1}x^{n-1}...+a_2x^2+a_1x+a_0$

Concepts clés

Une fonction de puissance est une base variable portée à une puissance numérique.
Le comportement d'un graphe lorsque l'entrée diminue sans limite et augmente sans limite est appelé comportement final.
Le comportement final dépend du fait que la puissance soit paire ou impaire.
Une fonction polynomiale est la somme de termes, dont chacun consiste en une fonction de puissance transformée avec une puissance entière positive.
Le degré d'une fonction polynomiale est la puissance la plus élevée de la variable présente dans un polynôme. Le terme contenant la puissance la plus élevée de la variable est appelé terme principal. Le coefficient du terme principal est appelé coefficient principal.
Le comportement final d'une fonction polynomiale est identique à celui de la fonction de puissance représentée par le terme principal de la fonction.
Un polynôme de degré$n$ aura au plus des$n$$x$ interceptions et au plus des points de$n−1$ retournement.

Lexique

coefficient

un nombre réel non nul qui est multiplié par une variable élevée à un exposant (seul le facteur numérique est le coefficient)

fonction continue

une fonction dont le graphique peut être dessiné sans lever le stylo du papier, car il n'y a pas de rupture dans le graphique

diplôme

la puissance la plus élevée de la variable qui apparaît dans un polynôme

comportement final

le comportement du graphe d'une fonction lorsque l'entrée diminue sans limite et augmente sans limite

coefficient principal

le coefficient du terme principal

terme principal

le terme contenant la puissance la plus élevée de la variable

fonction polynomiale

une fonction composée de zéro ou de la somme d'un nombre fini de termes non nuls, dont chacun est le produit d'un nombre, appelé coefficient du terme, et d'une variable portée à une puissance entière non négative.

fonction d'alimentation

une fonction qui peut être représentée sous la forme$f(x)=kx^p$ où$k$ est une constante, la base est une variable et l'exposant est une constante$p$

courbe lisse

un graphique sans angles vifs

terme d'une fonction polynomiale

n'importe$a_ix^i$ laquelle des fonctions polynomiales de la forme$f(x)=a_nx^n+a_{n-1}x^{n-1}...+a_2x^2+a_1x+a_0$

tournant

l'endroit où le graphe d'une fonction change de direction

Fonction polynomiale	Terme principal	Graphe de la fonction polynomiale
\(f(x)=5x^4+2x^3−x−4\)	\(5x^4\)	$Graphique de f (x) =5x^4+2x^3-x-4.$
\(f(x)=−2x^6−x^5+3x^4+x^3\)	\(−2x^6\)	$Graphique de f (x) =-2x^6-x^5+3x^4+x^3$
\(f(x)=3x^5−4x^4+2x^2+1\)	\(3x^5\)	$Graphique de f (x) =3x^5-4x^4+2x^2+1$
\(f(x)=−6x^3+7x^2+3x+1\)	\(−6x^3\)	$Graphique de f (x) =-6x^3+7x^2+3x+1$