4.3 : Ajustement de modèles linéaires aux données

Last updated
Save as PDF

Page ID: 194886

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Dessinez et interprétez des diagrammes de dispersion.
Utilisez un utilitaire graphique pour trouver la ligne la mieux adaptée.
Distinguer les relations linéaires des relations non linéaires.
Ajustez une droite de régression à un ensemble de données et utilisez le modèle linéaire pour effectuer des prédictions.

Un professeur tente d'identifier les tendances des résultats des examens finaux. Sa classe compte un mélange d'étudiants, alors il se demande s'il existe un lien entre l'âge et les résultats des examens finaux. Une façon pour lui d'analyser les notes est de créer un diagramme qui relie l'âge de chaque étudiant à la note obtenue à l'examen. Dans cette section, nous allons examiner l'un de ces diagrammes, connu sous le nom de nuage de points.

Dessiner et interpréter des nuages de points

Un nuage de points est un graphique de points tracés qui peut montrer une relation entre deux ensembles de données. Si la relation provient d'un modèle linéaire, ou d'un modèle presque linéaire, le professeur peut tirer des conclusions en utilisant ses connaissances des fonctions linéaires. La figure$\PageIndex{1}$ montre un exemple de diagramme de dispersion.

Diagramme de dispersion, intitulé « Résultat de l'examen final par rapport à l'âge ». L'axe des abscisses correspond à l'âge et l'axe des ordonnées à la note finale de l'examen. La fourchette d'âge se situe entre 20 et 50 ans, et la fourchette des scores se situe entre les années 50 et 90 — Figure$\PageIndex{1}$ : Diagramme de dispersion des variables relatives à l'âge et au résultat final à l'examen

Notez que ce nuage de points n'indique pas de relation linéaire. Les points ne semblent pas suivre une tendance. En d'autres termes, il ne semble pas y avoir de relation entre l'âge de l'étudiant et la note obtenue à l'examen final.

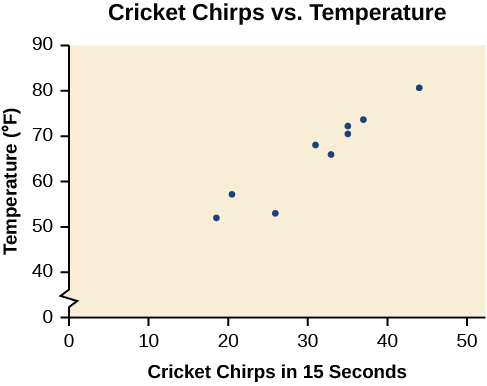
Exemple$\PageIndex{1}$: Using a Scatter Plot to Investigate Cricket Chirps

Le tableau indique le nombre de gazouillis de grillon en 15 secondes, pour différentes températures de l'air, en degrés Fahrenheit [1]. Tracez ces données et déterminez si elles semblent être liées de manière linéaire.

Tableau$\PageIndex{1}$
gazouillis	44	35	20,4	33	31	35	18,5	37	26
Température	80,5	70,5	57	66	68	72	52	73,5	53

Solution

Le traçage de ces données, comme le montre la figure,$\PageIndex{2}$ suggère qu'il peut y avoir une tendance. L'évolution des données montre que le nombre de gazouillis augmente à mesure que la température augmente. La tendance semble être à peu près linéaire, mais certainement pas parfaitement.

Diagramme de dispersion, intitulé « Cricket Chirps Vs Air Temperature ». L'axe X représente les gazouillis de cricket en 15 secondes, et l'axe y est la température (F). La régression linéaire est généralement positive. — Figure$\PageIndex{2}$ : La régression linéaire est généralement positive.

Trouver la gamme qui convient le mieux

Une fois que nous avons reconnu la nécessité d'une fonction linéaire pour modéliser ces données, la question de suivi naturelle est « qu'est-ce que cette fonction linéaire ? » Une façon d'approximer notre fonction linéaire est d'esquisser la ligne qui semble le mieux correspondre aux données. Ensuite, nous pouvons étendre la ligne jusqu'à ce que nous puissions vérifier l'intersection Y. Nous pouvons approximer la pente de la ligne en l'étendant jusqu'à ce que nous puissions estimer la$\frac{\text{rise}}{\text{run}}$.

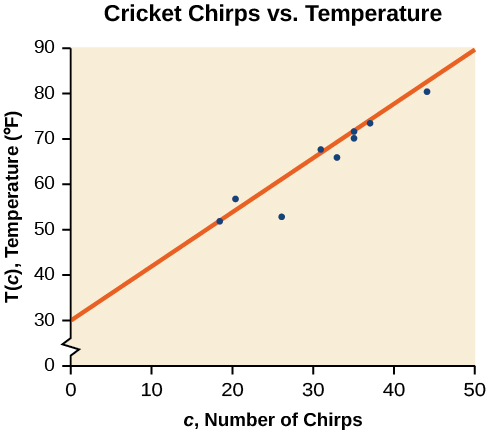
Exemple$\PageIndex{2}$: Finding a Line of Best Fit

Trouvez une fonction linéaire qui correspond aux données du tableau$\PageIndex{1}$ en « regardant » une ligne qui semble correspondre.

Solution

Sur un graphique, on pourrait essayer d'esquisser une ligne.

En utilisant les points de départ et d'arrivée de notre ligne dessinée à la main,$(0, 30)$ les points et$(50, 90)$, ce graphique a une pente de

\[m=\dfrac{60}{50}=1.2\]

et une intersection Y à 30. Cela donne une équation de

\[T(c)=1.2c+30\]

où$c$ est le nombre de gazouillis en 15 secondes et$T(c)$ la température en degrés Fahrenheit. L'équation résultante est représentée sur la figure$\PageIndex{3}$.

Diagramme de dispersion, indiquant la ligne de meilleur ajustement. Il est intitulé « Cricket Chirps Vs Air Temperature ». L'axe des abscisses est « c, Nombre de chirps » et l'axe des Y est « T » (c), Température (F) ». — Figure$\PageIndex{3}$ : Diagramme de dispersion, montrant la ligne de meilleur ajustement.

Analyse

Cette équation linéaire peut ensuite être utilisée pour obtenir des réponses approximatives à diverses questions que nous pourrions nous poser sur la tendance.

Reconnaître l'interpolation ou l'extrapolation

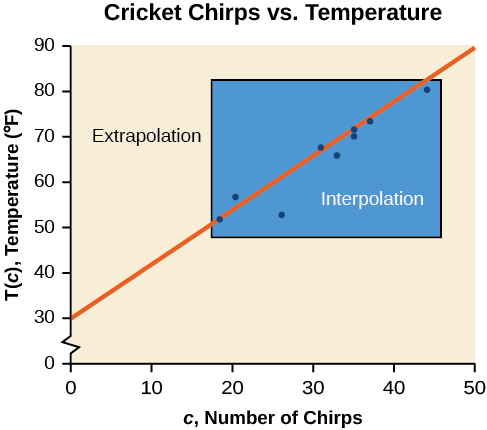
Bien que les données de la plupart des exemples ne correspondent pas parfaitement à la ligne, l'équation est notre meilleure estimation de la façon dont la relation se comportera en dehors des valeurs pour lesquelles nous disposons de données. Nous utilisons un processus appelé interpolation lorsque nous prédisons une valeur à l'intérieur du domaine et de la plage des données. Le processus d'extrapolation est utilisé lorsque nous prédisons une valeur en dehors du domaine et de la plage des données.

La figure$\PageIndex{4}$ compare les deux processus pour les données cricket-chirp traitées dans l'exemple$\PageIndex{2}$. Nous pouvons voir qu'une interpolation se produirait si nous utilisions notre modèle pour prédire la température lorsque les valeurs des chirps se situent entre 18,5 et 44. L'extrapolation se produirait si nous utilisions notre modèle pour prédire la température lorsque les valeurs des chirps sont inférieures à 18,5 ou supérieures à 44.

Il existe une différence entre faire des prédictions à l'intérieur du domaine et de la plage de valeurs pour lesquels nous disposons de données et en dehors de ce domaine et de cette plage. La prédiction d'une valeur en dehors du domaine et de la plage a ses limites. Lorsque notre modèle ne s'applique plus après un certain point, on parle parfois de panne de modèle. Par exemple, la prévision d'une fonction de coût pour une période de deux ans peut impliquer l'examen des données où l'entrée est la période en années et la sortie est le coût. Mais si nous essayons d'extrapoler un coût alors que$x=50$, c'est-à-dire dans 50 ans, le modèle ne s'appliquerait pas parce que nous ne pourrions pas prendre en compte les facteurs dans cinquante ans à l'avenir.

Diagramme de dispersion, indiquant la ligne de meilleur ajustement et l'endroit où se produisent l'interpolation et l'extrapolation. Il est intitulé « Cricket Chirps Vs Air Temperature ». L'axe des abscisses est « c, Nombre de chirps » et l'axe des Y est « T » (c), Température (F) ». — Figure$\PageIndex{4}$ : L'interpolation se produit dans le domaine et la plage des données fournies, tandis que l'extrapolation se produit à l'extérieur.

Interpolation et extrapolation

Différentes méthodes de prévision sont utilisées pour analyser les données.

La méthode d'extrapolation consiste à prédire une valeur en dehors du domaine et/ou de la plage des données.
La panne du modèle se produit au moment où le modèle ne s'applique plus.

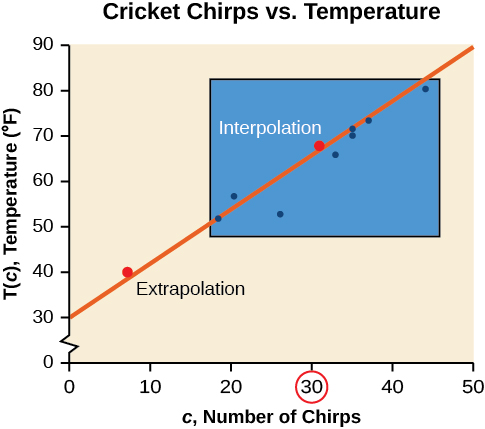
Exemple$\PageIndex{3}$: Understanding Interpolation and Extrapolation

Utilisez les données de cricket du tableau$\PageIndex{1}$ pour répondre aux questions suivantes :

Prédire la température lorsque les grillons chantent 30 fois en 15 secondes serait-il une interpolation ou une extrapolation ? Faites la prédiction et discutez si elle est raisonnable.
Prédire le nombre de gazouillis que les grillons feront à 40 degrés serait-il une interpolation ou une extrapolation ? Faites la prédiction et discutez si elle est raisonnable.

Solution

a. Le nombre de chirps dans les données fournies variait de 18,5 à 44. Une prédiction à 30 chirps par 15 secondes se trouve dans le domaine de nos données, de même que l'interpolation. En utilisant notre modèle :

\[\begin{align} T(30)&=30+1.2(30) \\ &=66 \text{ degrees} \end{align}\]

Sur la base des données dont nous disposons, cette valeur semble raisonnable.
b. Les valeurs de température variaient de 52 à 80,5. Prédire le nombre de gazouillis à 40 degrés est une extrapolation, car 40 se situe en dehors de la plage de nos données. En utilisant notre modèle :

\[\begin{align} 40&=30+1.2c \\ 10&=1.2c \\ c&\approx8.33 \end{align}\]

Nous pouvons comparer les régions d'interpolation et d'extrapolation à l'aide de la figure$\PageIndex{5}$.

Analyse

Notre modèle prédit que les grillons émettraient 8,33 fois en 15 secondes. Bien que cela soit possible, nous n'avons aucune raison de croire que notre modèle est valide en dehors du domaine et de la gamme. En fait, les grillons cessent généralement de gazouiller en dessous de 50 degrés environ.

Exercice$\PageIndex{1}$

Selon les données du Tableau$\PageIndex{1}$, quelle température pouvons-nous prédire si nous comptons 20 gazouillis en 15 secondes ?

Solution

54 °F

Trouver la ligne qui convient le mieux à l'aide d'un utilitaire graphique

Bien que l'observation d'une ligne fonctionne assez bien, il existe des techniques statistiques pour ajuster une ligne aux données qui minimisent les différences entre la ligne et les valeurs des données [2]. L'une de ces techniques est appelée régression par les moindres carrés et peut être calculée par de nombreuses calculatrices graphiques, des tableurs, des logiciels de statistiques et de nombreuses calculatrices Web [3]. La régression par les moindres carrés est un moyen de déterminer la droite qui correspond le mieux aux données, et nous appellerons ici cette méthode « régression linéaire ».

$alt$ À partir des données d'entrée et des sorties correspondantes d'une fonction linéaire, trouvez la droite d'ajustement la mieux adaptée à l'aide de la régression linéaire.

Entrez l'entrée dans la liste 1 (L1).
Entrez la sortie dans la liste 2 (L2).
Dans un utilitaire de création graphique, sélectionnez Régression linéaire (LinReg).

Exemple$\PageIndex{4}$: Finding a Least Squares Regression Line

Trouvez la droite de régression par les moindres carrés à l'aide des données cricket-chirp du tableau$\PageIndex{1}$.

Solution

Entrez l'entrée (chirps) dans la liste 1 (L1).
Entrez la sortie (température) dans la liste 2 (L2). Voir le tableau$\PageIndex{2}$.

Tableau$\PageIndex{2}$
L1	44	35	20,4	33	31	35	18,5	37	26
L2	80,5	70,5	57	66	68	72	52	73,5	53

Dans un utilitaire de création graphique, sélectionnez Régression linéaire (LinReg). En utilisant les données de chirp de cricket antérieures, nous obtenons avec la technologie l'équation suivante :

\[T(c)=30.281+1.143c\]

Analyse

Notez que cette ligne est assez similaire à l'équation que nous avons « regardée » mais qu'elle devrait mieux correspondre aux données. Notez également que l'utilisation de cette équation modifierait notre prédiction de la température lorsque vous entendez 30 gazouillis en 15 secondes, de 66 degrés à :

\[\begin{align} T(30)&=30.281+1.143(30) \\ &=64.571 \\ &\approx 64.6 \text{ degrees} \end{align}\]

Le graphique du nuage de points avec la droite de régression par les moindres carrés est illustré à la figure$\PageIndex{6}$.

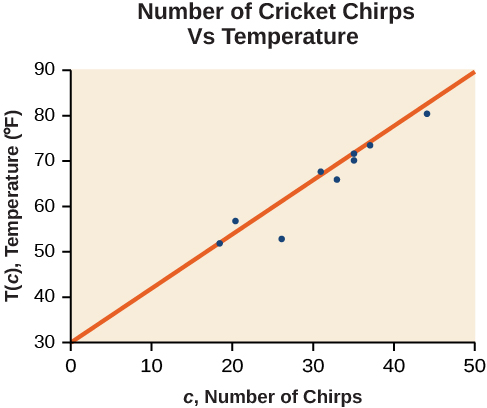
$alt$ Y aura-t-il un cas où deux lignes différentes constitueront la meilleure solution pour les données ?

Non. Il n'existe qu'une seule ligne de coupe optimale.

Distinction entre les modèles linéaires et non linéaires

Comme nous l'avons vu plus haut avec le modèle Cricket-Chirp, certaines données présentent de fortes tendances linéaires, mais d'autres données, comme les résultats des examens finaux tracés par âge, sont clairement non linéaires. La plupart des calculateurs et des logiciels informatiques peuvent également nous fournir le coefficient de corrélation, qui est une mesure du degré d'ajustement de la droite aux données. De nombreuses calculatrices graphiques demandent à l'utilisateur d'activer une sélection « diagnostic activé » pour trouver le coefficient de corrélation, que les mathématiciens appellent$r$. Le coefficient de corrélation permet de se faire une idée facile de la proximité des données par rapport à une ligne.

Nous devons calculer le coefficient de corrélation uniquement pour les données qui suivent un schéma linéaire ou pour déterminer le degré de linéarité d'un ensemble de données. Si les données présentent un schéma non linéaire, le coefficient de corrélation d'une régression linéaire n'a aucun sens. Pour avoir une idée de la relation entre la valeur$r$ et le graphique des données, la figure$\PageIndex{7}$ montre certains grands ensembles de données avec leurs coefficients de corrélation. N'oubliez pas que pour tous les diagrammes, l'axe horizontal représente l'entrée et l'axe vertical montre la sortie.

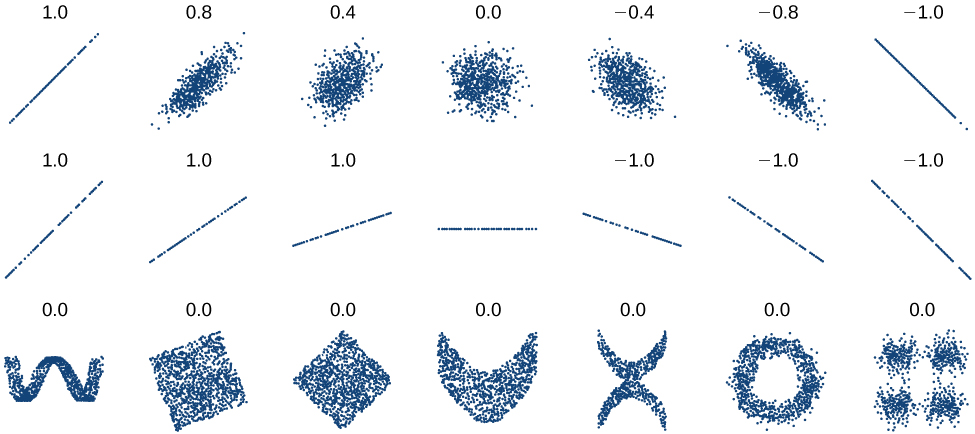
Figure$\PageIndex{7}$ : Données tracées et coefficients de corrélation associés. (crédit : « Denis Boigelot », Wikimedia Commons)

Coefficient de corrélation

Le coefficient de corrélation est une valeur comprise entre -1 et 1.$r$

$r>0$suggère une relation positive (croissante)
$r<0$suggère une relation négative (décroissante)
Plus la valeur est proche de 0, plus les données sont dispersées.
Plus la valeur est proche de 1 ou —1, moins les données sont dispersées.

Exemple$\PageIndex{5}$: Finding a Correlation Coefficient

Calculez le coefficient de corrélation pour les données Cricket-Chirp dans le tableau$\PageIndex{1}$.

Solution

Comme les données semblent suivre un schéma linéaire, nous pouvons utiliser la technologie pour calculer$r$. Entrez les entrées et les sorties correspondantes et sélectionnez la régression linéaire. Le calculateur vous fournira également le coefficient de corrélation,$r=0.9509$. Cette valeur est très proche de 1, ce qui suggère une forte relation linéaire croissante.

Remarque : Pour certaines calculatrices, les diagnostics doivent être activés afin d'obtenir le coefficient de corrélation lors de l'exécution d'une régression linéaire : [2nd] > [0] > [alpha] [x—1], puis faites défiler la page jusqu'à DIAGNOSTICSON.

Prédiction à l'aide d'une droite de régression

Une fois que nous avons déterminé qu'un ensemble de données est linéaire à l'aide du coefficient de corrélation, nous pouvons utiliser la droite de régression pour faire des prévisions. Comme nous l'avons vu plus haut, une droite de régression est la droite la plus proche des données du nuage de points, ce qui signifie qu'une seule de ces droites convient le mieux aux données.

Exemple$\PageIndex{6}$: Using a Regression Line to Make Predictions

La consommation d'essence aux États-Unis n'a cessé d'augmenter. Les données de consommation de 1994 à 2004 sont présentées dans le tableau$\PageIndex{3}$. Déterminez si la tendance est linéaire et, si c'est le cas, trouvez un modèle pour les données. Utilisez le modèle pour prévoir la consommation en 2008.

Tableau$\PageIndex{3}$
Année	94	95	96	97	98	1999	'00	2001	2002	2003	2004
Consommation (milliards de gallons)	113	116	118	119	123	125	126	128	131	133	136

Le nuage de points des données, y compris la droite de régression par les moindres carrés, est illustré à la figure$\PageIndex{8}$.

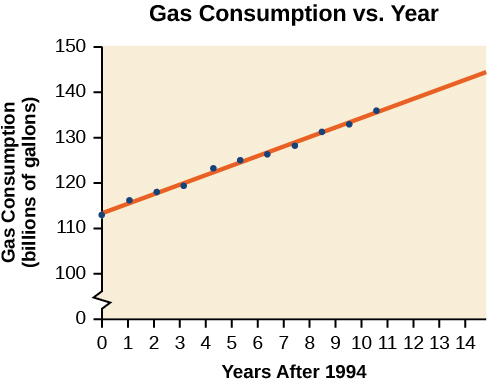
Diagramme de dispersion, indiquant la ligne de meilleur ajustement. Il est intitulé « Consommation de gaz par rapport à l'année ». L'axe X est « Année après 1994 » et l'axe Y est « Consommation de gaz (milliards de gallons) ». — Figure$\PageIndex{8}$ : Diagramme de dispersion, montrant la ligne de meilleur ajustement.

Nous pouvons introduire une nouvelle variable d'entrée$t$, représentant les années écoulées depuis 1994.

L'équation de régression par les moindres carrés est la suivante :

\[C(t)=113.318+2.209t\]

À l'aide de la technologie, le coefficient de corrélation a été calculé à 0,9965, ce qui suggère une très forte tendance linéaire à la hausse.

En s'appuyant sur ces données pour prévoir la consommation en$(t=14)$ 2008,

\[\begin{align} C(14)&=113.318+2.209(14) \\ &=144.244 \end{align}\]

Le modèle prévoit une consommation d'essence de 144,244 milliards de gallons en 2008.

Exercice$\PageIndex{1}$

Utilisez le modèle que nous avons créé à l'aide de la technologie dans$\PageIndex{6}$ Example pour prédire la consommation de gaz en 2011. S'agit-il d'une interpolation ou d'une extrapolation ?

Réponse: 150,871 milliards de gallons ; extrapolation

Concepts clés

Les nuages de points montrent la relation entre deux ensembles de données.
Les nuages de points peuvent représenter des modèles linéaires ou non linéaires.
La ligne la mieux adaptée peut être estimée ou calculée à l'aide d'une calculatrice ou d'un logiciel statistique.
L'interpolation peut être utilisée pour prédire des valeurs à l'intérieur du domaine et de la plage des données, tandis que l'extrapolation peut être utilisée pour prédire des valeurs en dehors du domaine et de la plage des données.
Le coefficient de corrélation,$r$, indique le degré de relation linéaire entre les données.
Une droite de régression correspond le mieux aux données.
La droite de régression par les moindres carrés est obtenue en minimisant les carrés des distances entre les points d'une droite passant par les données et peut être utilisée pour faire des prédictions concernant l'une ou l'autre des variables.