4.2 : Modélisation avec des fonctions linéaires
- Page ID
- 194905
Objectifs d'apprentissage
- Créez des modèles linéaires à partir de descriptions verbales.
- Modélisez un ensemble de données à l'aide d'une fonction linéaire.
Emily est une étudiante qui prévoit de passer un été à Seattle. Elle a économisé 3 500$ pour son voyage et prévoit dépenser 400$ par semaine pour le loyer, la nourriture et les activités. Comment écrire un modèle linéaire pour représenter sa situation ? Que serait l'X-Intercept, et que peut-elle en tirer ? Pour répondre à ces questions et à d'autres questions connexes, nous pouvons créer un modèle à l'aide d'une fonction linéaire. Des modèles tels que celui-ci peuvent être extrêmement utiles pour analyser les relations et faire des prédictions sur la base de ces relations. Dans cette section, nous allons explorer des exemples de modèles de fonctions linéaires.

Identification des étapes pour modéliser et résoudre les problèmes
Lorsque nous modélisons des scénarios avec des fonctions linéaires et résolvons des problèmes impliquant des quantités à taux de variation constant, nous suivons généralement les mêmes stratégies de gestion des problèmes que celles que nous utiliserions pour tout type de fonction. Passons-les brièvement en revue :
Identifiez les quantités changeantes, puis définissez des variables descriptives pour représenter ces quantités. Le cas échéant, esquissez une image ou définissez un système de coordonnées.
Lisez attentivement le problème pour identifier les informations importantes. Recherchez des informations fournissant des valeurs pour les variables ou des valeurs pour des parties du modèle fonctionnel, telles que la pente et la valeur initiale.
Lisez attentivement le problème pour déterminer ce que nous essayons de trouver, d'identifier, de résoudre ou d'interpréter.
Identifiez une voie de solution à partir des informations fournies jusqu'à ce que nous essayons de trouver. Cela implique souvent de vérifier et de suivre les unités, de créer un tableau ou même de trouver une formule pour la fonction utilisée pour modéliser le problème.
Si nécessaire, écrivez une formule pour la fonction.
Résolvez ou évaluez la fonction en utilisant la formule.
Demandez-vous si votre réponse est raisonnable pour la situation donnée et si elle est logique mathématiquement.
Exprimez clairement votre résultat en utilisant les unités appropriées et répondez en phrases complètes si nécessaire.
Création de modèles linéaires
Jetons maintenant un coup d'œil à l'étudiant de Seattle. Dans sa situation, deux quantités changent : le temps et l'argent. Le montant d'argent qu'il lui reste pendant ses vacances dépend de la durée de son séjour. Nous pouvons utiliser ces informations pour définir nos variables, y compris les unités.
- Production :\(M\), argent restant, en dollars
- Entrée :\(t\), heure, en semaines
Ainsi, le montant restant dépend du nombre de semaines :\(M(t)\)
Nous pouvons également identifier la valeur initiale et le taux de variation.
- Valeur initiale : Elle a économisé 3 500$, donc 3 500$ est la valeur initiale pour M.
- Taux de variation : Elle prévoit dépenser 400$ par semaine, donc — 400$ par semaine est le taux de variation, ou pente.
Notez que l'unité de dollars par semaine correspond à l'unité de notre variable de sortie divisée par notre variable d'entrée. De plus, comme la pente est négative, la fonction linéaire est décroissante. Cela devrait avoir du sens car elle dépense de l'argent chaque semaine.
Le taux de variation étant constant, nous pouvons commencer par le modèle linéaire\(M(t)=mt+b\). Ensuite, nous pouvons remplacer l'intersection et la pente fournies.
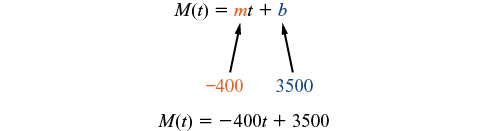
Pour trouver l'intersection X, nous mettons la sortie à zéro et résolvons l'entrée.
\[\begin{align*} 0&=−400t+3500 \\ t&=\dfrac{3500}{400} \\ &=8.75 \end{align*}\]
L'intervalle X est de 8,75 semaines. Comme cela représente la valeur d'entrée lorsque la sortie sera nulle, on pourrait dire qu'Emily n'aura plus d'argent après 8,75 semaines.
Lorsque vous modélisez un scénario réel avec des fonctions, il existe généralement un domaine limité dans lequel ce modèle sera valide ; pratiquement aucune tendance ne se poursuit indéfiniment. Ici, le domaine fait référence au nombre de semaines. Dans ce cas, cela n'a aucun sens de parler de valeurs d'entrée inférieures à zéro. Une valeur d'entrée négative peut faire référence à un certain nombre de semaines avant qu'elle n'économise 3 500$, mais le scénario discuté pose la question une fois qu'elle a économisé 3 500$, car c'est à ce moment que commencent son voyage et ses dépenses subséquentes. Il est également probable que ce modèle ne soit pas valide après l'interception X, à moins qu'Emily utilise une carte de crédit et ne s'endette. Le domaine représente l'ensemble des valeurs d'entrée, donc le domaine raisonnable pour cette fonction est\(0{\leq}t{\leq}8.75\).
Dans l'exemple ci-dessus, nous avons reçu une description écrite de la situation. Nous avons suivi les étapes de modélisation d'un problème pour analyser les informations. Cependant, les informations fournies peuvent ne pas toujours être les mêmes. Parfois, on peut nous fournir une interception. D'autres fois, une valeur de sortie peut nous être fournie. Nous devons être attentifs à analyser les informations qui nous sont fournies et à les utiliser de manière appropriée pour construire un modèle linéaire.
Utiliser une intersection donnée pour créer un modèle
Certains problèmes du monde réel fournissent l'intersection y, qui est la valeur constante ou initiale. Une fois que l'intersection y est connue, l'intersection X peut être calculée. Supposons, par exemple, qu'Hannah envisage de rembourser un prêt sans intérêt auprès de ses parents. Le solde de son prêt est de 1 000$. Elle prévoit payer 250$ par mois jusqu'à ce que son solde soit de 0$. L'intercept Y est le montant initial de sa dette, soit 1 000$. Le taux de variation, ou pente, est de -250 $ par mois. Nous pouvons ensuite utiliser la forme d'interception de pente et les informations fournies pour développer un modèle linéaire.
\[\begin{align*} f(x)&=mx+b \\ &=-250x+1000 \end{align*}\]
Nous pouvons maintenant définir la fonction comme égale à 0 et\(x\) résoudre pour trouver l'intersection X.
\[\begin{align*} 0&=-250+1000 \\ 1000&=250x \\ 4&=x \\ x&=4 \end{align*}\]
Le x-intercept est le nombre de mois qu'il lui faut pour atteindre un solde de 0$. Le X-Intercept dure 4 mois, il faudra donc quatre mois à Hannah pour rembourser son prêt.
Utilisation d'une entrée et d'une sortie données pour créer un modèle
De nombreuses applications du monde réel ne sont pas aussi directes que celles que nous venons d'envisager. Ils nous obligent plutôt à identifier certains aspects d'une fonction linéaire. On peut parfois nous demander d'évaluer le modèle linéaire à une entrée donnée ou de définir l'équation du modèle linéaire égale à une sortie spécifiée.
![]() Dans le cas d'un problème de mots qui inclut deux paires de valeurs d'entrée et de sortie, utilisez la fonction linéaire pour résoudre un problème.
Dans le cas d'un problème de mots qui inclut deux paires de valeurs d'entrée et de sortie, utilisez la fonction linéaire pour résoudre un problème.
- Identifiez les valeurs d'entrée et de sortie.
- Convertissez les données en deux paires de coordonnées.
- Trouve la pente.
- Écrivez le modèle linéaire.
- Utilisez le modèle pour effectuer une prédiction en évaluant la fonction à une valeur x donnée.
- Utilisez le modèle pour identifier une valeur x qui donne une valeur y donnée.
- Répondez à la question posée.
Exemple\(\PageIndex{1}\): Using a Linear Model to Investigate a Town’s Population
La population d'une ville croît de façon linéaire. En 2004, la population était de 6 200 habitants. En 2009, la population était passée à 8 100 habitants. Supposons que cette tendance continue.
- Prédisez la population en 2013.
- Déterminez l'année où la population atteindra 15 000 habitants.
Solution
Les deux quantités changeantes sont la taille de la population et le temps. Bien que nous puissions utiliser la valeur réelle de l'année comme quantité d'entrée, cela tend à conduire à des équations très compliquées car l'intersection y correspondrait à l'année 0, il y a plus de 2000 ans !
Pour rendre le calcul un peu plus agréable, nous définirons notre entrée comme le nombre d'années écoulées depuis 2004 :
- Entrée :\(t\), années depuis 2004
- Résultat :\(P(t)\), la population de la ville
Pour prévoir la population en 2013 (\(t=9\)), nous aurions d'abord besoin d'une équation pour la population. De même, pour déterminer quand la population atteindrait 15 000 habitants, il faudrait résoudre l'entrée qui fournirait une sortie de 15 000 personnes. Pour écrire une équation, nous avons besoin de la valeur initiale et du taux de variation, ou pente.
Pour déterminer le taux de variation, nous utiliserons la variation de la production par variation des entrées.
\[m=\dfrac{\text{change in output}}{\text{change in input}}\]
Le problème nous donne deux paires d'entrées-sorties. En les convertissant pour qu'elles correspondent à nos variables définies, l'année 2004 correspondrait\(t=0\), en donnant le point\((0,6200)\). Notez que grâce à notre choix intelligent de définition de variable, nous nous sommes « donné » l'intersection y de la fonction. L'année 2009 correspondrait à\(t=5\), donnant le point\((5,8100)\).
Les deux paires de coordonnées sont\((0,6200)\) et\((5,8100)\). Rappelons que nous avons rencontré des exemples dans lesquels nous avons reçu deux points plus tôt dans le chapitre. Nous pouvons utiliser ces valeurs pour calculer la pente.
\[\begin{align*} m&=\dfrac{8100-6200}{5-0}\\ &=\dfrac{1900}{5} \\ &=380 \text{ people per year} \end{align*}\]
Nous connaissons déjà l'intersection y de la droite, nous pouvons donc immédiatement écrire l'équation :
\[P(t)=380t+6200\]
Pour prédire la population en 2013, nous évaluons notre fonction à\(t=9\).
\[\begin{align*} P(9)&=380(9)+6,200 \\ &=9,620 \end{align*}\]
Si la tendance se poursuit, notre modèle prévoit une population de 9 620 habitants en 2013.
Pour savoir quand la population atteindra 15 000 habitants, nous pouvons définir\(P(t)=15000\) et résoudre\(t\).
\[\begin{align*} 15000&=380t+6200 \\ 8800&=380t \\ t&{\approx}23.158 \end{align*}\]
Notre modèle prévoit que la population atteindra 15 000 habitants dans un peu plus de 23 ans après 2004, soit vers 2027.
Exercice\(\PageIndex{1A}\)
Une entreprise vend des beignets. Ils assument un coût fixe de 25 000$ pour le loyer, l'assurance et d'autres dépenses. La production de chaque beignet coûte 0,25$.
- Écrivez un modèle linéaire pour représenter le coût C de l'entreprise en fonction du\(x\) nombre de beignets produits.
- Trouvez et interprétez l'intersection Y.
Solution
a.\(C(x)=0.25x+25,000\) b. L'intersection Y est\((0,25,000)\). Si l'entreprise ne produit pas un seul beignet, elle doit quand même payer 25 000$.
Exercice\(\PageIndex{1B}\)
La population d'une ville croît de façon linéaire. En 2008, la population était de 28 200 habitants. En 2012, la population était de 36 800 habitants. Supposons que cette tendance continue.
- Prédisez la population en 2014.
- Déterminez l'année où la population atteindra 54 000 habitants.
Solution
environ 41 100 ans 2020
Utiliser un diagramme pour modéliser un problème
Il est utile pour de nombreuses applications du monde réel de dessiner une image afin de se faire une idée de la façon dont les variables représentant l'entrée et la sortie peuvent être utilisées pour répondre à une question. Pour dessiner le tableau, réfléchissez d'abord à ce que le problème demande. Déterminez ensuite l'entrée et la sortie. Le diagramme doit relier les variables. Souvent, des formes ou des figures géométriques sont dessinées. Les distances sont souvent tracées. Si un triangle droit est esquissé, le théorème de Pythagore relie les côtés. Si un rectangle est dessiné, il est utile d'étiqueter la largeur et la hauteur.
Exemple\(\PageIndex{2}\): Using a Diagram to Model Distance Walked
Anna et Emanuel partent de la même intersection. Anna marche vers l'est à 6,4 km à l'heure tandis qu'Emanuel marche vers le sud à 5 miles par heure. Ils communiquent avec une radio bidirectionnelle d'une portée de 2 miles. Combien de temps après avoir commencé à marcher vont-ils perdre le contact radio ?
Solution
Essentiellement, nous pouvons répondre partiellement à cette question en disant qu'ils ne seront plus en contact radio lorsqu'ils seront séparés de 2 miles, ce qui nous amène à poser une nouvelle question :
« Combien de temps leur faudra-t-il pour être séparés de 3 km ? »
Dans ce problème, nos quantités changeantes dépendent du temps et de la position, mais en fin de compte, nous devons savoir combien de temps il faudra pour qu'elles se trouvent à 2 miles l'une de l'autre. Nous pouvons voir que le temps sera notre variable d'entrée, nous allons donc définir nos variables d'entrée et de sortie.
- Entrée :\(t\), heure en heures.
- Sortie :\(A(t)\), distance en miles et\(E(t)\) distance en miles
Comme il n'est pas évident de définir notre variable de sortie, nous allons commencer par dessiner une image telle que Figure\(\PageIndex{3}\).
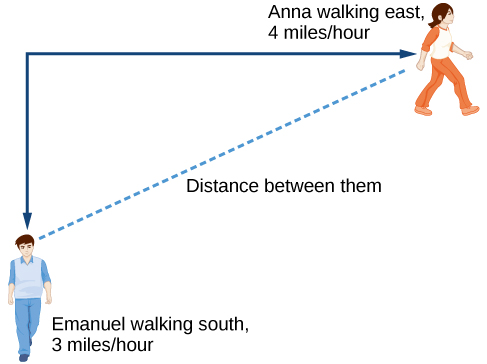
- Valeur initiale : Ils commencent tous les deux à la même intersection, donc quand\(t=0\), la distance parcourue par chaque personne doit également être de 0. Ainsi, la valeur initiale pour chacun est 0.
- Taux de variation : Anna marche 6,4 km à l'heure et Emanuel marche 5 miles par heure, deux taux de variation. La pente pour\(A\) est de 4 et la pente pour\(E\) est de 3.
À l'aide de ces valeurs, nous pouvons écrire des formules pour la distance parcourue par chaque personne.
\[A(t)=4t\]
\[E(t)=3t\]
Pour ce problème, les distances par rapport au point de départ sont importantes. Pour les noter, nous pouvons définir un système de coordonnées, identifiant le « point de départ » à l'intersection où ils ont tous deux commencé. Ensuite, nous pouvons utiliser la variable\(A\), que nous avons introduite ci-dessus, pour représenter la position d'Anna et la définir comme une mesure à partir du point de départ vers l'est. De même, vous pouvez utiliser la variable\(E\), pour représenter la position d'Emanuel, mesurée à partir du point de départ vers le sud. Notez que lors de la définition du système de coordonnées, nous avons spécifié à la fois le point de départ de la mesure et la direction de la mesure.
Nous pouvons ensuite définir une troisième variable\(D\), qui sera la mesure de la distance entre Anna et Emanuel. Comme le montre la figure, il est souvent utile de montrer les variables sur le diagramme\(\PageIndex{4}\).
Rappelez-vous que nous devons savoir combien de temps il faut pour\(D\) que la distance entre eux soit égale à 2 miles. Notez que pour une entrée donnée\(t\), les sorties\(A(t)\)\(E(t)\), et\(D(t)\) représentent des distances.
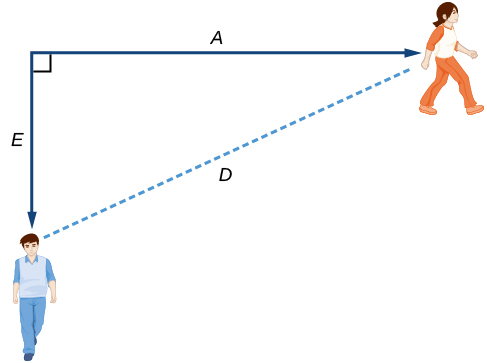
En utilisant le théorème de Pythagore, on obtient :
\[\begin{align*} d(t)^2&=A(t)^2+E(t)^2 \\ &=(4t)^2+(3t)^2 \\ &=16t^2+9t^2 \\ &=25t^2 \\ D(t)&=\pm\sqrt{25t^2} &\text{Solve for $D(t)$ using the square root} \\ &= \pm 5|t| \end{align*}\]
Dans ce scénario, nous ne prenons en compte que des valeurs positives de\(t\), de sorte que notre distance\(D(t)\) sera toujours positive. Nous pouvons simplifier cette réponse à\(D(t)=5t\). Cela signifie que la distance entre Anna et Emanuel est également une fonction linéaire. Comme D est une fonction linéaire, nous pouvons maintenant répondre à la question de savoir quand la distance entre elles atteindra 2 miles. Nous allons définir la sortie\(D(t)=2\) et résoudre pour\(t\).
\[\begin{align*} D(t)&=2 \\ 5t&=2 \\ t&=\dfrac{2}{5}=0.4 \end{align*}\]
Ils ne seront plus en contact radio en 0,4 heure, soit 24 minutes.
![]() Dois-je dessiner des diagrammes lorsque je reçois des informations basées sur une forme géométrique ?
Dois-je dessiner des diagrammes lorsque je reçois des informations basées sur une forme géométrique ?
Oui. Esquissez la figure et étiquetez les quantités et les inconnues sur le croquis.
Exemple\(\PageIndex{3}\): Using a Diagram to Model Distance between Cities
Une route droite mène de la ville de Westborough à Agritown à 30 miles à l'est et à 16 km au nord. À mi-chemin de cette route, elle rejoint une deuxième route, perpendiculaire à la première, menant à la ville d'Eastborough. Si la ville d'Eastborough est située à 20 miles directement à l'est de la ville de Westborough, à quelle distance se trouve le carrefour routier de Westborough ?
Solution
Il pourrait être utile de brosser un tableau de la situation. Voir la figure\(\PageIndex{5}\). Il serait alors utile d'introduire un système de coordonnées. Bien que nous puissions placer l'origine n'importe où, la placer à Westborough semble pratique. Cela place Agritown aux coordonnées\((30, 10)\), et Eastborough à\((20,0)\).
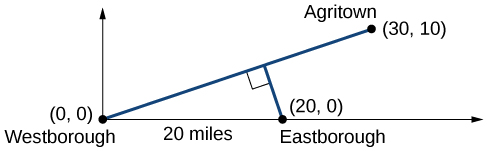
En utilisant ce point et l'origine, nous pouvons trouver la pente de la ligne allant de Westborough à Agritown :
\[m=\dfrac{10-0}{30-0}=\dfrac{1}{3}\]
L'équation de la route de Westborough à Agritown serait
\[W(x)=\dfrac{1}{3}x\]
À partir de là, nous pouvons déterminer que la route perpendiculaire à Eastborough aura une pente\(m=–3\). Comme la ville d'Eastborough est au point\((20, 0)\), nous pouvons trouver l'équation suivante :
\[\begin{align*} E(x)&=−3x+b \\ 0&=−3(20)+b &\text{Substitute in $(20, 0)$} \\ b&=60 \\ E(x)&=−3x+60 \end{align*}\]
Nous pouvons maintenant trouver les coordonnées de la jonction des routes en trouvant l'intersection de ces lignes. Les mettre sur un pied d'égalité
\[\begin{align*} \dfrac{1}{3}x&=−3x+60 \\ \dfrac{10}{3}x&=60 \\ 10x&=180 \\ x&=18 &\text{Substituting this back into $W(x)$} \\ y&=W(18) \\ &= \dfrac{1}{3}(18) \\&=6 \end{align*}\]
Les routes se croisent à cet endroit\((18,6)\). À l'aide de la formule de distance, nous pouvons maintenant déterminer la distance entre Westborough et la jonction.
\[\begin{align*} \text{distance}&=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \\ &=\sqrt{(18-0)^2+(6-0)^2} \\ &\approx 18.743 \text{miles} \end{align*}\]
Analyse
Une bonne utilisation des modèles linéaires est de tirer parti du fait que les graphes de ces fonctions sont des lignes. Cela signifie que les applications du monde réel traitant de cartes ont besoin de fonctions linéaires pour modéliser les distances entre les points de référence.
Exercice\(\PageIndex{2}\)
Une route droite mène de la ville de Timpson à Ashburn à 100 km à l'est et 20 km au nord. À mi-chemin de la route, elle rejoint une deuxième route, perpendiculaire à la première, menant à la ville de Garrison. Si la ville de Garrison est située à 35 km à l'est de la ville de Timpson, à quelle distance se trouve le carrefour routier de Timpson ?
Solution
21,15 milles
Systèmes de construction de modèles linéaires
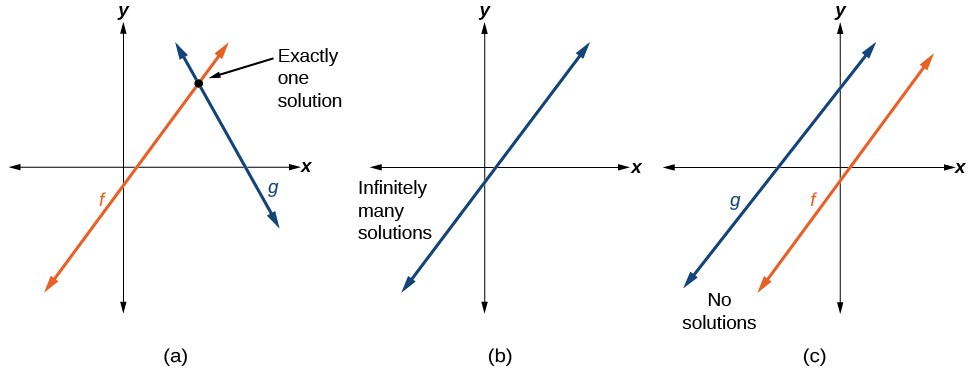
Des situations réelles comprenant deux fonctions linéaires ou plus peuvent être modélisées à l'aide d'un système d'équations linéaires. N'oubliez pas que lorsque vous résolvez un système d'équations linéaires, nous recherchons les points communs entre les deux lignes. En général, trois types de réponses sont possibles, comme le montre la figure\(\PageIndex{6}\).
![]() Dans une situation qui représente un système d'équations linéaires, écrivez le système d'équations et identifiez la solution.
Dans une situation qui représente un système d'équations linéaires, écrivez le système d'équations et identifiez la solution.
- Identifiez l'entrée et la sortie de chaque modèle linéaire.
- Identifiez la pente et l'intersection y de chaque modèle linéaire.
- Trouvez la solution en mettant les deux fonctions linéaires égales à une autre et en\(x\) recherchant ou en trouvant le point d'intersection sur un graphique.
Exemple\(\PageIndex{4}\): Building a System of Linear Models to Choose a Truck Rental Company
Jamal a le choix entre deux sociétés de location de camions. La première, Keep on Trucking, Inc., facture des frais initiaux de 20$, puis 59 cents le mile [1]. Le second, Move It Your Way, facture des frais initiaux de 16$, puis 63 cents le mile. Quand est-ce que Keep on Trucking, Inc. sera le meilleur choix pour Jamal ?
Solution
Les deux facteurs importants de ce problème sont le coût et le nombre de kilomètres parcourus. Comme nous avons deux entreprises à considérer, nous allons définir deux fonctions.
- Entrée :\(d\), distance parcourue en miles
- Extrants :\(K(d):\) coût, en dollars, de la location auprès de Keep on Trucking
\(M(d):\)coût, en dollars, de la location auprès de Move It Your Way
- Valeur initiale : frais initiaux :\(K(0)=20\) et\(M(0)=16\)
- Taux de variation :\(K(d)=\dfrac{$0.59}{\text{mile}}\) et\(P(d)=\dfrac{$0.63}{\text{mile}}\)
Une fonction linéaire est de la forme\(f(x)=mx+b\). En utilisant les taux de variation et les charges initiales, nous pouvons écrire les équations
\[K(d)=0.59d+20 \nonumber\]
\[M(d)=0.63d+16 \nonumber\]
À l'aide de ces équations, nous pouvons déterminer quand Keep on Trucking, Inc. sera le meilleur choix. Comme nous n'avons qu'à prendre cette décision, ce sont les coûts, nous cherchons à savoir quand Keep on Trucking, Inc. coûtera moins cher, ou quand\(K(d)<M(d)\). La voie de solution nous amènera à trouver les équations des deux fonctions, à trouver l'intersection, puis à voir où la\(K(d)\) fonction est la plus petite.
Ces graphiques sont esquissés dans la figure\(\PageIndex{7}\), avec\(K(d)\) en bleu.
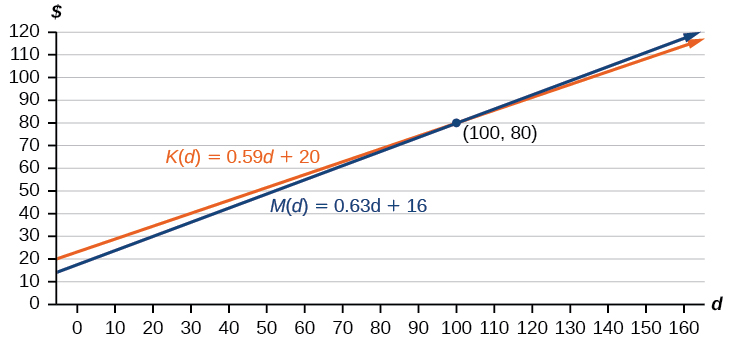
Pour trouver l'intersection, nous mettons les équations égales et résolvons :
\[\begin{align*} K(d)&=M(d) \\ 0.59d+20&=0.63d+16 \\ 4&=0.04d \\ 100&=d \\ d&=100 \end{align*}\]
Cela nous indique que le coût pour les deux compagnies sera le même si 100 miles sont parcourus. Soit en regardant le graphique, soit en constatant que la croissance\(K(d)\) est plus lente, nous pouvons conclure que Keep on Trucking, Inc. sera le prix le moins cher lorsque plus de 100 miles seront parcourus, c'est-à-dire\(d>100\).
Concepts clés
- Nous pouvons utiliser les mêmes stratégies de résolution de problèmes que celles que nous utiliserions pour n'importe quel type de fonction.
- Lorsque vous modélisez et résolvez un problème, identifiez les variables et recherchez des valeurs clés, notamment la pente et l'intersection Y.
- Dessinez un diagramme, le cas échéant.
- Vérifiez le caractère raisonnable de la réponse.
- Des modèles linéaires peuvent être construits en identifiant ou en calculant la pente et en utilisant l'intersection Y.
- L'intersection X peut être trouvée en utilisant le paramètre\(y=0\), qui définit l'expression comme étant\(mx+b\) égale à 0.
- Le point d'intersection d'un système d'équations linéaires est le point où les valeurs x et y sont identiques.
- Un graphique du système peut être utilisé pour identifier les points où une ligne tombe en dessous (ou au-dessus) de l'autre ligne.
Notes
1 Taux obtenus le 2 août 2010 sur www.budgettruck.com et http://www.uhaul.com/


