3.7 : Fonctions inverses
- Page ID
- 195444
Objectifs d'apprentissage
- Vérifiez les fonctions inverses.
- Déterminez le domaine et la plage d'une fonction inverse, et limitez le domaine d'une fonction pour la rendre univoque.
- Trouvez ou évaluez l'inverse d'une fonction.
- Utilisez le graphe d'une fonction biunivoque pour représenter graphiquement sa fonction inverse sur les mêmes axes.
Une pompe à chaleur réversible est un système de climatisation composé d'un climatiseur et d'un chauffage réunis en un seul appareil. Fonctionnant dans un sens, il pompe la chaleur d'une maison pour la rafraîchir. Fonctionnant en sens inverse, il pompe de la chaleur dans le bâtiment depuis l'extérieur, même par temps frais, pour fournir du chauffage. En tant que chauffage, une pompe à chaleur est plusieurs fois plus efficace que le chauffage par résistance électrique classique.
Si certaines machines physiques peuvent fonctionner dans deux directions, on peut se demander si certaines des fonctions « machines » que nous avons étudiées peuvent également fonctionner à rebours. La figure\(\PageIndex{1}\) fournit une représentation visuelle de cette question. Dans cette section, nous examinerons la nature inverse des fonctions.
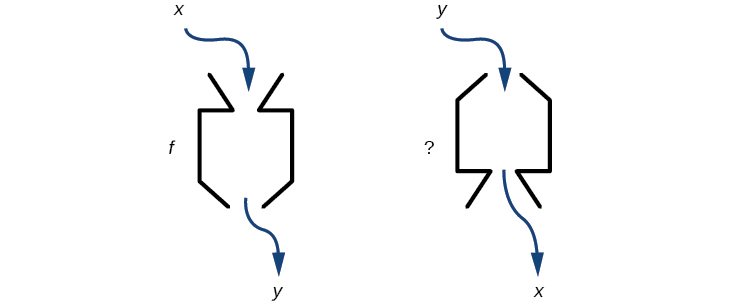
Figure\(\PageIndex{1}\) : Une fonction « machine » peut-elle fonctionner en sens inverse ?
Vérifier que deux fonctions sont des fonctions inverses
Supposons qu'un créateur de mode se rendant à Milan pour un défilé de mode veuille savoir quelle sera la température. Il ne connaît pas l'échelle Celsius. Pour avoir une idée de la relation entre les mesures de température, il demande à son assistante, Betty, de convertir 75 degrés Fahrenheit en degrés Celsius. Elle trouve la formule
\[C=\dfrac{5}{9}(F−32)\]
et remplace 75\(F\) pour calculer
\[\dfrac{5}{9}(75−32)\approx24^{\circ}\]
Sachant qu'une température confortable de 75 degrés Fahrenheit équivaut à environ 24 degrés Celsius, il envoie à son assistante les prévisions météorologiques de la semaine de Figure\(\PageIndex{2}\) for Milan, et lui demande de convertir toutes les températures en degrés Fahrenheit.

Dans un premier temps, Betty envisage d'utiliser la formule qu'elle a déjà trouvée pour effectuer les conversions. Après tout, elle connaît son algèbre et peut facilement résoudre l'équation\(F\) après avoir substitué une valeur à\(C\). Par exemple, pour convertir 26 degrés Celsius, elle pourrait écrire
\[\begin{align} 26&=\dfrac{5}{9}(F-32) \\ 26⋅\dfrac{9}{5}&=F−32 \\ F&=26⋅\dfrac{9}{5}+32\approx79\end{align}\]
Après avoir envisagé cette option pendant un moment, elle se rend compte que la résolution de l'équation pour chacune des températures sera extrêmement fastidieuse. Elle se rend compte que l'évaluation étant plus facile que la résolution, il serait beaucoup plus pratique d'avoir une formule différente, une formule qui prend la température Celsius et produit la température Fahrenheit.
La formule recherchée par Betty correspond à l'idée d'une fonction inverse, c'est-à-dire une fonction pour laquelle l'entrée de la fonction d'origine devient la sortie de la fonction inverse et la sortie de la fonction d'origine devient l'entrée de la fonction inverse.
Pour une fonction donnée\(f(x)\), nous représentons son inverse sous\(f^{−1}(x)\) la forme «\(f\) inverse de »\(x\). Le −1 augmenté fait partie de la notation. Ce n'est pas un exposant ; cela n'implique pas une puissance de -1. En d'autres termes, cela\(f^{−1}(x)\) ne veut pas dire\(\frac{1}{f(x)}\) parce que\(\frac{1}{f(x)}\) c'est l'inverse\(f\) et non l'inverse.
La notation « semblable à un exposant » provient d'une analogie entre la composition des fonctions et la multiplication : tout comme\(a^{−1}a=1\) (1 est l'élément d'identité pour la multiplication) pour tout nombre non nul\(a\), est\(f^{−1}{\circ}f\) égal à la fonction d'identité, c'est-à-dire
\[(f^{−1}{\circ}f)(x)=f^{−1}(f(x))=f^{−1}(y)=x\]
Cela vaut pour tous\(x\) dans le domaine de\(f\). De manière informelle, cela signifie que les fonctions inverses « s'annulent » mutuellement. Cependant, tout comme zéro n'a pas d'inverse, certaines fonctions n'ont pas d'inverse.
Étant donné une fonction\(f(x)\), nous pouvons vérifier si une autre fonction\(g(x)\) est l'inverse\(f(x)\) en vérifiant si l'une\(g(f(x))=x\) ou l'autre\(f(g(x))=x\) est vraie. Nous pouvons tester l'équation la plus pratique à utiliser, car elles sont logiquement équivalentes (c'est-à-dire que si l'une est vraie, l'autre l'est également).
Par exemple,\(y=4x\) et\(y=\frac{1}{4}x\) sont des fonctions inverses.
\[(f^{−1}{\circ}f)(x)=f^{-1}(4x)=\dfrac{1}{4}(4x)=x\]
et
\[(f{\circ}f^{−1})(x)=f\Big(\dfrac{1}{4}x\Big)=4\Big(\dfrac{1}{4}x\Big)=x\]
Quelques paires de coordonnées du graphe de la fonction\(y=4x\) sont\((−2, −8)\)\((0, 0)\), et\((2, 8)\). Quelques paires de coordonnées du graphe de la fonction\(y=\frac{1}{4}x\) sont\((−8, −2)\)\((0, 0)\), et\((8, 2)\). Si nous échangeons l'entrée et la sortie de chaque paire de coordonnées d'une fonction, les paires de coordonnées échangées apparaîtront sur le graphe de la fonction inverse.
Définition : Fonction inverse
Pour toute fonction biunivoque\(f(x)=y\), une fonction\(f^{−1}(x)\) est une fonction inverse de\(f\) if\(f^{−1}(y)=x\). Cela peut également s'écrire comme\(f^{−1}(f(x))=x\) pour tous\(x\) dans le domaine de\(f\). Il s'ensuit également que\(f(f^{−1}(x))=x\) pour tous\(x\), le domaine de\(f^{−1}\) if\(f^{−1}\) est l'inverse de\(f\).
La notation\(f^{−1}\) est lue «\(f\) inverse ». Comme toute autre fonction, nous pouvons utiliser n'importe quel nom de variable comme entrée. Nous écrivons donc souvent\(f^{−1}(x)\), ce que nous lisons comme « l'\(f\)inverse de »\(x\).\(f^{−1}\) Gardez à l'esprit que
\[f^{−1}(x)\neq\dfrac{1}{f(x)}\]
et toutes les fonctions n'ont pas d'inverses.
Exemple\(\PageIndex{1}\): Identifying an Inverse Function for a Given Input-Output Pair
S'il s'agit d'une fonction\(f(2)=4\) biunivoque particulière\(f(5)=12\), quelles sont les valeurs d'entrée et de sortie correspondantes pour la fonction inverse ?
Solution
La fonction inverse inverse les quantités d'entrée et de sortie, donc si
\[f(2)=4, \text{ then } f^{-1}(4)=2 ;\\ f(5)=12, \text{ then }f^{-1}(12)=5\].
Sinon, si nous voulons nommer la fonction inverse\(g\), alors\(g(4)=2\) et\(g(12)=5\).
Analyse
Notez que si nous affichons les paires de coordonnées sous forme de tableau, l'entrée et la sortie sont clairement inversées. Voir le tableau\(\PageIndex{1}\).
| \((x,f(x))\) | \((x,g(x))\) |
|---|---|
| \ (x, f (x)) \) » style="vertical-align:middle ; text-align:center ; « >\((2,4)\) | \ (x, g (x)) \) » style="vertical-align:middle ; text-align:center ; « >\((4,2)\) |
| \ (x, f (x)) \) » style="vertical-align:middle ; text-align:center ; « >\((5,12)\) | \ (x, g (x)) \) » style="vertical-align:middle ; text-align:center ; « >\((12,5)\) |
Exercice\(\PageIndex{1}\)
Dans ces conditions\(h^{-1}(6)=2\), quelles sont les valeurs d'entrée et de sortie correspondantes de la fonction d'origine\(h\) ?
- Réponse
-
\(h(2)=6\)
Mode d'emploi : deux fonctions étant données\(f(x)\) and \(g(x)\), test whether the functions are inverses of each other.
- Déterminez si\(f(g(x))=x\) ou\(g(f(x))=x\).
- Si les deux affirmations sont vraies, alors\(g=f^{-1}\) et\(f=g^{-1}\). Si l'une ou l'autre des affirmations est fausse, les deux sont fausses, et\(g{\neq}f^{-1}\) et\(f{\neq}g^{-1}\).
Exemple\(\PageIndex{2}\): Testing Inverse Relationships Algebraically
Si\(f(x)=\frac{1}{x+2}\) et\(g(x)=\frac{1}{x}−2\), est-ce\(g=f^{-1}\) ?
Solution
\[\begin{align} g(f(x))&=\dfrac{1}{(\frac{1}{x+2})−2} \\ &=x+2−2 \\&=x \end{align}\]
donc
\[g=f^{-1} \text{ and } f=g^{-1}\]
Cela suffit pour répondre oui à la question, mais nous pouvons également vérifier l'autre formule.
\[\begin{align} f(g(x))&=\dfrac{1}{\frac{1}{x}-2+2} \\ &= \dfrac{1}{\frac{1}{x}} \\ &=x \end{align}\]
Analyse
Notez que les opérations inverses sont dans l'ordre inverse des opérations de la fonction d'origine.
Exercice\(\PageIndex{2}\)
Si\(f(x)=x^3−4\) et\(g(x)=\sqrt[3]{x+4}\), est-ce\(g=f^{-1}\) ?
- Réponse
-
Oui
Exemple\(\PageIndex{3}\): Determining Inverse Relationships for Power Functions
Si\(f(x)=x^3\) (la fonction cube) et\(g(x)=\frac{1}{3}x\), est-ce que\(g=f^{-1}\) ?
Solution
\[f(g(x))=\dfrac{x^3}{27}{\neq}x\]
Non, les fonctions ne sont pas inverses.
Analyse
L'inverse correct du cube est, bien entendu, la racine du cube\(\sqrt[3]{x}=x^{\frac{1}{3}}\), c'est-à-dire que le tiers est un exposant et non un multiplicateur.
Exercice\(\PageIndex{3}\)
Si\(f(x)=(x−1)^3\) et\(g(x)=\sqrt[3]{x}+1\), est-ce\(g=f^{-1}\) ?
- Réponse
-
Oui
Trouver un domaine et une plage de fonctions inverses
Les sorties de la fonction\(f\) sont les entrées de\(f^{-1}\), de sorte que la plage de\(f\) est également le domaine de\(f^{-1}\). De même, étant donné que les entrées à\(f\) sont les sorties de\(f^{-1}\), le domaine de\(f\) est la plage de\(f^{-1}\). Nous pouvons visualiser la situation comme dans la figure\(\PageIndex{3}\).
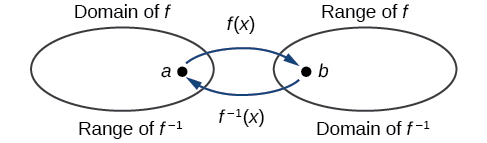
Figure\(\PageIndex{3}\) : Domaine et plage d'une fonction et son inverse.
Lorsqu'une fonction n'a pas de fonction inverse, il est possible de créer une nouvelle fonction où cette nouvelle fonction sur un domaine limité possède une fonction inverse. Par exemple, l'inverse de\(f(x)=\sqrt{x}\) est\(f^{-1}(x)=x^2\), car un carré « annule » une racine carrée ; mais le carré n'est que l'inverse de la racine carrée du domaine\(\left[0,\infty\right)\), puisqu'il s'agit de la plage de\(f(x)=\sqrt{x}\).
Nous pouvons examiner ce problème de l'autre côté, en commençant par la fonction carrée (boîte à outils quadratique)\(f(x)=x^2\). Si nous voulons construire une inverse de cette fonction, nous rencontrons un problème, car pour chaque sortie donnée de la fonction quadratique, il y a deux entrées correspondantes (sauf lorsque l'entrée est 0). Par exemple, la sortie 9 de la fonction quadratique correspond aux entrées 3 et -3. Mais une sortie d'une fonction est une entrée vers son inverse ; si cette entrée inverse correspond à plus d'une sortie inverse (entrée de la fonction d'origine), alors « l'inverse » n'est pas du tout une fonction ! En d'autres termes, la fonction quadratique n'est pas une fonction biunivoque ; elle échoue au test de la ligne horizontale, elle n'a donc pas de fonction inverse. Pour qu'une fonction ait un inverse, il doit s'agir d'une fonction biunivoque.
Dans de nombreux cas, si une fonction n'est pas biunivoque, nous pouvons toujours la restreindre à une partie de son domaine sur laquelle elle est biunivoque. Par exemple, nous pouvons créer une version restreinte de la fonction carrée\(f(x)=x^2\) avec sa plage limitée à\(\left[0,\infty\right)\), qui est une fonction biunivoque (elle passe le test de la ligne horizontale) et qui a un inverse (la fonction racine carrée).
Si cette\(f(x)=(x−1)^2\) option est activée\([1,∞)\), la fonction inverse l'est\(f^{-1}(x)=\sqrt{x}+1\).
- Le domaine de\(f\) = range of\(f^{-1} = \left[1,\infty\right)\).
- Le domaine de\(f^{-1}\) = range of\(f = \left[0,\infty\right)\).
![]() Est-il possible qu'une fonction ait plus d'un inverse ?
Est-il possible qu'une fonction ait plus d'un inverse ?
Non. Si deux fonctions supposées différentes, disons\(g\) et h, répondent toutes deux à la définition d'être inversées d'une autre fonction\(f\), alors vous pouvez le prouver\(g=h\). Nous venons de voir que certaines fonctions n'ont des inverses que si l'on restreint le domaine de la fonction d'origine. Dans ces cas, il peut y avoir plusieurs manières de restreindre le domaine, ce qui entraîne différents inverses. Cependant, sur n'importe quel domaine, la fonction d'origine n'a toujours qu'un seul inverse unique.
Remarque : Domaine et plage de fonctions inverses
La plage d'une fonction\(f(x)\) est le domaine de la fonction inverse\(f^{-1}(x)\).
Le domaine de\(f(x)\) est la gamme de\(f^{-1}(x)\).
Mode d'emploi : À partir d'une fonction, trouvez le domaine et la plage de son inverse.
- Si la fonction est biunivoque, écrivez la plage de la fonction d'origine comme domaine de l'inverse et écrivez le domaine de la fonction d'origine comme plage de l'inverse.
- Si le domaine de la fonction d'origine doit être restreint pour la rendre biunivoque, alors ce domaine restreint devient la plage de la fonction inverse.
Exemple\(\PageIndex{4}\): Finding the Inverses of Toolkit Functions
Identifiez les fonctions de la boîte à outils autres que la fonction quadratique qui ne sont pas biunivoque et trouvez un domaine restreint dans lequel chaque fonction est individuelle, le cas échéant. Les fonctions de la boîte à outils sont examinées dans le tableau\(\PageIndex{2}\). Nous limitons le domaine de telle sorte que la fonction assume toutes les valeurs y exactement une fois.
| Constante | Identité | Quadratique | Cubique | réciproque |
|---|---|---|---|---|
| \(f(x)=c\) | \(f(x)=x\) | \(f(x)=x^2\) | \(f(x)=x^3\) | \(f(x)=\frac{1}{x}\) |
| Carré réciproque | Racine cubique | Racine carrée | Valeur absolue | |
| \(f(x)=\frac{1}{x^2}\) | \(f(x)=\sqrt[3]{x}\) | \(f(x)=\sqrt{x}\) | \(f(x)=|x|\) |
Solution
La fonction constante n'est pas biunivoque et il n'existe aucun domaine (à l'exception d'un point unique) sur lequel elle pourrait être biunivoque, de sorte que la fonction constante n'a pas d'inverse significatif.
La fonction de valeur absolue peut être limitée au domaine\(\left[0,\infty\right)\), où elle est égale à la fonction d'identité.
La fonction quadratique réciproque peut être limitée au domaine\((0,\infty)\).
Analyse
Nous pouvons voir que ces fonctions (si elles ne sont pas limitées) ne sont pas individuelles en regardant leurs graphiques, illustrés dans la figure\(\PageIndex{4}\). Ils échoueraient tous les deux au test de la ligne horizontale. Toutefois, si une fonction est limitée à un certain domaine de sorte qu'elle passe le test de la ligne horizontale, elle peut avoir un inverse dans ce domaine restreint.
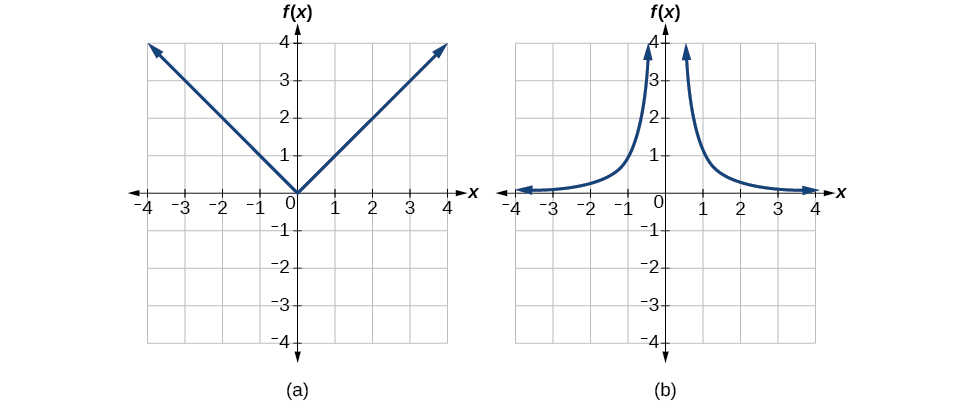
Figure\(\PageIndex{4}\) : (a) Valeur absolue (b) Carré réciproque
![]() \(\PageIndex{4}\): Le domaine de la fonction\(f\) est\((1,\infty)\) et la plage de fonctions\(f\) est\((−\infty,−2)\). Déterminez le domaine et la plage de la fonction inverse.
\(\PageIndex{4}\): Le domaine de la fonction\(f\) est\((1,\infty)\) et la plage de fonctions\(f\) est\((−\infty,−2)\). Déterminez le domaine et la plage de la fonction inverse.
Solution
Le domaine de la fonction\(f^{-1}\) est\((−\infty,−2)\) et la gamme de fonctions\(f^{-1}\) est\((1,\infty)\).
Recherche et évaluation de fonctions inverses
Une fois que nous avons une fonction biunivoque, nous pouvons évaluer son inverse à des entrées de fonction inverse spécifiques ou construire une représentation complète de la fonction inverse dans de nombreux cas.
Inverser les fonctions tabulaires
Supposons que nous souhaitions trouver l'inverse d'une fonction représentée sous forme de tableau. N'oubliez pas que le domaine d'une fonction est la plage de l'inverse et que la plage de la fonction est le domaine de l'inverse. Nous devons donc échanger le domaine et la plage.
Chaque ligne (ou colonne) d'entrées devient la ligne (ou colonne) de sorties pour la fonction inverse. De même, chaque ligne (ou colonne) de sorties devient la ligne (ou colonne) d'entrées pour la fonction inverse.
Exemple\(\PageIndex{5}\): Interpreting the Inverse of a Tabular Function
Une fonction\(f(t)\) est donnée dans le tableau\(\PageIndex{3}\), indiquant la distance en miles parcourue par une voiture en\(t\) minutes. Trouvez et interprétez\(f^{-1}(70)\)
| \(t\)(minutes) | 30 | 50 | 70 | 90 |
|---|---|---|---|---|
| \(f(t)\)(milles) | 20 | 40 | 60 | 70 |
La fonction inverse prend une sortie de\(f\) et renvoie une entrée pour\(f\). Ainsi, dans l'expression\(f^{-1}(70)\), 70 est une valeur de sortie de la fonction d'origine, représentant 70 miles. L'inverse renverra l'entrée correspondante de la fonction d'origine\(f\), soit 90 minutes, donc\(f^{-1}(70)=90\). L'interprétation de cela est que, pour parcourir 70 miles, il a fallu 90 minutes.
Sinon, rappelez-vous que la définition de l'inverse était la suivante : si\(f(a)=b\), alors\(f^{-1}(b)=a\). Selon cette définition, si on nous donne\(f^{-1}(70)=a\), alors nous recherchons une valeur\(a\) telle que\(f(a)=70\). Dans ce cas, nous cherchons un\(t\) tel qui\(f(t)=70\), c'est quand\(t=90\).
Exercice\(\PageIndex{5}\)
À l'aide de Table\(\PageIndex{4}\), recherchez et interprétez (\(f(60)\)a) et (b)\(f^{-1}(60)\).
| \(t\)(minutes) | 30 | 50 | 60 | 70 | 90 |
|---|---|---|---|---|---|
| \(f(t)\)(milles) | 20 | 40 | 50 | 60 | 70 |
- Réponse
-
\(f(60)=50\). En 60 minutes, 50 miles sont parcourus.
\(f^{-1}(60)=70\). Pour parcourir 60 miles, il faudra 70 minutes.
Évaluation de l'inverse d'une fonction, à partir d'un graphe de la fonction d'origine
Nous avons vu dans Fonctions et notation des fonctions que le domaine d'une fonction peut être lu en observant l'étendue horizontale de son graphe. Nous trouvons le domaine de la fonction inverse en observant l'étendue verticale du graphe de la fonction d'origine, car cela correspond à l'étendue horizontale de la fonction inverse. De même, nous trouvons la plage de la fonction inverse en observant l'étendue horizontale du graphe de la fonction d'origine, car il s'agit de l'étendue verticale de la fonction inverse. Si nous voulons évaluer une fonction inverse, nous trouvons son entrée dans son domaine, qui correspond à tout ou partie de l'axe vertical du graphe de la fonction d'origine.
![]() À partir du graphe d'une fonction, évaluez son inverse à des points spécifiques.
À partir du graphe d'une fonction, évaluez son inverse à des points spécifiques.
- Trouvez l'entrée souhaitée sur l'axe y du graphe donné.
- Lisez la sortie de la fonction inverse à partir de l'axe X du graphe donné.
Exemple\(\PageIndex{6}\): Evaluating a Function and Its Inverse from a Graph at Specific Points
Une fonction\(g(x)\) est donnée dans la figure\(\PageIndex{5}\). Trouvez\(g(3)\) et\(g^{-1}(3)\).
.
Solution
Pour évaluer\(g(3)\), nous trouvons 3 sur l'axe des abscisses et trouvons la valeur de sortie correspondante sur l'axe des y. \((3,1)\)Ce point nous le dit\(g(3)=1\).
Pour évaluer\(g^{-1}(3)\), rappelons que par définition,\(g^{-1}(3)\) on entend la valeur de\(x\) pour laquelle\(g(x)=3\). En recherchant la valeur de sortie 3 sur l'axe vertical, nous trouvons le point\((5,3)\) sur le graphique, ce qui signifie\(g(5)=3\), par définition,\(g^{-1}(3)=5.\) voir Figure\(\PageIndex{6}\).
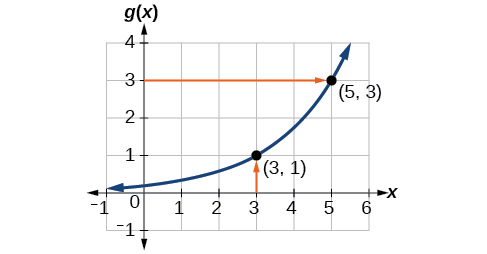
Exercice\(\PageIndex{6}\)
À l'aide du graphique de la figure\(\PageIndex{6}\), (a) trouvez\(g^{-1}(1)\) et (b) estimez\(g^{-1}(4)\).
- Répondez à une
-
3
- Réponse b
-
5.6
Trouver les inverses des fonctions représentées par des formules
Parfois, nous aurons besoin de connaître une fonction inverse pour tous les éléments de son domaine, pas seulement quelques-uns. Si la fonction d'origine est donnée sous forme de formule, par exemple\(y\) en fonction de\(x\), nous pouvons souvent trouver la fonction inverse en résolvant pour obtenir\(x\) en fonction de\(y\).
Procédure : à partir d'une fonction représentée par une formule, trouvez l'inverse.
- Assurez-vous qu'\(f\)il s'agit d'une fonction individuelle.
- Résolvez pour\(x\)
- Échange\(x\) et\(y\).
Exemple\(\PageIndex{7}\): Inverting the Fahrenheit-to-Celsius Function
Trouvez une formule pour la fonction inverse qui donne la température Fahrenheit en fonction de la température Celsius.
\[C=\dfrac{5}{9}(F−32)\]
Solution
\[\begin{align} C&=\frac{5}{9}(F-32) \\ C{\cdot}\frac{9}{5}&=F−32 \\ F&=\frac{9}{5}C+32\end{align}\]
En résolvant en général, nous avons découvert la fonction inverse. Si\[C=h(F)=\dfrac{5}{9}(F−32)\],
alors
\[F=h^{-1}(C)=\dfrac{9}{5}C+32.\]
Dans ce cas, nous avons introduit une fonction\(h\) pour représenter la conversion car les variables d'entrée et de sortie sont descriptives et l'écriture\(C^{-1}\) peut prêter à confusion.
Exercice\(\PageIndex{7}\)
Résolvez\(x\) en termes de\(y\) données\(y=\frac{1}{3}(x−5)\)
- Réponse
-
\(x=3y+5\)
Exemple\(\PageIndex{8}\): Solving to Find an Inverse Function
Détermine l'inverse de la fonction\(f(x)=\frac{2}{x−3}+4\).
Solution
\[\begin{align} y&=\dfrac{2}{x−3+4} &\text{Set up an equation.} \\ y−4&=\dfrac{2}{x−3} &\text{Subtract 4 from both sides.} \\ x−3&=\dfrac{2}{y−4} &\text{Multiply both sides by x−3 and divide by y−4.} \\ x&=\dfrac{2}{y−4}+3 &\text{Add 3 to both sides.} \end{align}\]
Donc\(f^{-1}(y)=\frac{2}{y−4}+3\) ou\(f^{-1}(x)=\frac{2}{x−4}+3\).
Analyse
Le domaine et la plage de\(f\) excluent les valeurs 3 et 4, respectivement. \(f\)et\(f^{-1}\) sont égaux à deux points mais ne sont pas la même fonction, comme nous pouvons le voir en créant Table\(\PageIndex{5}\).
| \(x\) | 1 | 2 | 5 | \(f^{-1}(y)\) |
|---|---|---|---|---|
| \(f(x)\) | 3 | 2 | 5 | \(y\) |
Exemple\(\PageIndex{9}\): Solving to Find an Inverse with Radicals
Détermine l'inverse de la fonction\(f(x)=2+\sqrt{x−4}\).
Solution
\[ \begin{align} y&=2+\sqrt{x-4} \\ (y-2)^2&=x-4 \\ x&=(y-2)^2+4 \end{align}\]
Donc\(f^{-1}(x)=(x−2)^2+4\).
Le domaine de\(f\) est\(\left[4,\infty\right)\). Notez que la plage de\(f\) est\(\left[2,\infty\right)\), ce qui signifie que le domaine de la fonction inverse\(f^{-1}\) est également\(\left[2,\infty\right)\)
Analyse
La formule que nous avons trouvée\(f^{-1}(x)\) semble être valable pour tout ce qui est réel\(x\). Cependant,\(f^{-1}\) lui-même doit avoir un inverse (à savoir\(f\)), nous devons donc restreindre le domaine de\(f^{-1}\)\(\left[2,\infty\right)\) à afin de créer\(f^{-1}\) une fonction biunivoque. Ce domaine de\(f^{-1}\) correspond exactement à la gamme de\(f\).
Exercice\(\PageIndex{8}\)
Quel est l'inverse de la fonction\(f(x)=2-\sqrt{x}\) ? Indiquez les domaines de la fonction et de la fonction inverse.
- Réponse
-
\(f^{-1}(x)=(2−x)^2\); domaine de\(f\) :\(\left[0,\infty\right)\) ; domaine de\(f^{-1}\) :\(\left(−\infty,2\right]\)
Trouver des fonctions inverses et leurs graphes
Maintenant que nous pouvons trouver l'inverse d'une fonction, nous allons explorer les graphes des fonctions et leurs inverses. Revenons à la fonction quadratique\(f(x)=x^2\) limitée au domaine\(\left[0,\infty\right)\), sur laquelle cette fonction est biunivoque, et représentons-la comme dans la Figure\(\PageIndex{7}\).
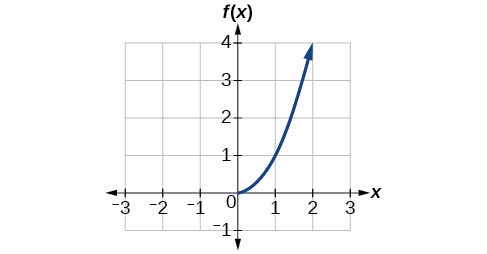
Figure\(\PageIndex{7}\) : Fonction quadratique avec domaine restreint à\([0, \infty)\).
Restreindre le domaine à\(\left[0,\infty\right)\) rendre la fonction une à une (elle passera évidemment le test de la ligne horizontale), donc elle a un inverse sur ce domaine restreint.
Nous savons déjà que l'inverse de la fonction quadratique de la boîte à outils est la fonction racine carrée, c'est-à-dire\(f^{-1}(x)=\sqrt{x}\). Que se passe-t-il si nous dessinons les deux axes\(f\) et\(f^{-1}\) sur le même ensemble d'axes, en utilisant l'axe X comme entrée pour les deux axes\(f\) et\(f^{-1}\) ?
Nous remarquons une relation distincte : le graphique de\(f^{-1}(x)\) est le graphique du\(f(x)\) reflet autour de la diagonale\(y=x\), que nous appellerons la ligne d'identité, illustrée sur la figure\(\PageIndex{8}\).
\ (f (x) \) et\(f^(-1)(x)\). « src= » https://math.libretexts.org/@api/dek..._01_07_009.jpg « fileid="1026" />.
Figure\(\PageIndex{8}\) : Fonctions carrées et racines carrées sur le domaine non négatif
Cette relation sera observée pour toutes les fonctions biunivoque, car elle est le résultat de la fonction et de ses entrées et sorties d'échange inverse. Cela revient à alterner les rôles des axes vertical et horizontal.
Exemple\(\PageIndex{10}\): Finding the Inverse of a Function Using Reflection about the Identity Line
À partir du graphique de\(f(x)\) la figure\(\PageIndex{9}\), esquissez un graphique de\(f^{-1}(x)\).
Il s'agit d'une fonction biunivoque, nous serons donc en mesure d'esquisser une inverse. Notez que le graphique présenté a un domaine apparent\((0,\infty)\) et une plage de\((−\infty,\infty)\), de sorte que l'inverse aura un domaine\((−\infty,\infty)\) et une plage de\((0,\infty)\).
Si nous réfléchissons ce graphique sur la ligne\(y=x\), le point se\((1,0)\) reflète vers\((0,1)\) et le point se\((4,2)\) reflète vers\((2,4)\). L'esquisse de l'inverse sur les mêmes axes que le graphique d'origine donne la figure\(\PageIndex{10}\).
Exercice\(\PageIndex{1}\)
Dessinez des graphes des fonctions\(f\) et\(f^{-1}\) à partir de l'exemple\(\PageIndex{8}\).
- Réponse
-
\ (f (x) \) et\(f^(-1)(x)\). » src= » https://math.libretexts.org/@api/dek..._01_07_012.jpg « fileid="1029" />
Figure\(\PageIndex{11}\) : Graphique de\(f(x)\) et\(f^(-1)(x)\).
![]() Y a-t-il une fonction égale à son propre inverse ?
Y a-t-il une fonction égale à son propre inverse ?
Oui. Si\(f=f^{-1}\), alors\(f(f(x))=x\), nous pouvons penser à plusieurs fonctions qui ont cette propriété. La fonction d'identité
fait, et la fonction réciproque aussi, parce que
\[\dfrac{1}{\frac{1}{x}}=x\]
Toute fonction\(f(x)=c−x\), où\(c\) est une constante, est également égale à son propre inverse.
Concepts clés
- Si\(g(x)\) est l'inverse de\(f(x)\), alors\(g(f(x))=f(g(x))=x\).
- Chacune des fonctions de la boîte à outils possède un inverse.
- Pour qu'une fonction ait une inverse, elle doit être biunivoque (passer le test de la ligne horizontale).
- Une fonction qui n'est pas univoque sur l'ensemble de son domaine peut l'être sur une partie de son domaine.
- Pour une fonction tabulaire, échangez les lignes d'entrée et de sortie pour obtenir l'inverse.
- L'inverse d'une fonction peut être déterminé à des points spécifiques de son graphe.
- Pour trouver l'inverse d'une formule, résolvez l'équation\(y=f(x)\) de\(x\) en fonction de\(y\). Ensuite, échangez les étiquettes\(x\) et\(y\).
- Le graphe d'une fonction inverse est le reflet du graphe de la fonction d'origine sur la ligne\(y=x\).


