3.4 : Composition des fonctions

Objectifs d'apprentissage

• Combinez des fonctions à l'aide d'opérations algébriques.
• Créez une nouvelle fonction par composition de fonctions.
• Évaluez les fonctions composites.
• Trouvez le domaine d'une fonction composite.
• Décomposez une fonction composite en fonctions constitutives.

Supposons que nous souhaitions calculer le coût du chauffage d'une maison un jour donné de l'année. Le coût du chauffage d'une maison dépendra de la température quotidienne moyenne et, à son tour, la température quotidienne moyenne dépend du jour de l'année. Remarquez comment nous venons de définir deux relations : le coût dépend de la température, et la température dépend du jour.

À l'aide de variables descriptives, nous pouvons noter ces deux fonctions. La fonction\(C(T)\) indique le coût\(C\) du chauffage d'une maison pour une température quotidienne moyenne donnée en\(T\) degrés Celsius. La fonction\(T(d)\) donne la température quotidienne moyenne le jour d de l'année. Pour un jour donné,\(Cost=C(T(d))\) cela signifie que le coût dépend de la température, qui dépend à son tour du jour de l'année. Ainsi, nous pouvons évaluer la fonction de coût à la température\(T(d)\). Par exemple, nous pourrions\(T(5)\) effectuer une évaluation pour déterminer la température quotidienne moyenne le 5 de l'année. Ensuite, nous pourrions évaluer la fonction de coût à cette température. Nous écririons\(C(T(5))\).

Figure\(\PageIndex{1}\) : Explication de\(C(T(5))\), qui est le coût de la température et\(T(5)\) la température au jour 5.

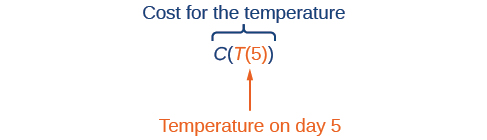
En combinant ces deux relations en une seule fonction, nous avons réalisé la composition des fonctions, qui est l'objet de cette section.

Combinaison de fonctions à l'aide d'opérations algébriques

La composition des fonctions n'est qu'un moyen de combiner des fonctions existantes. Une autre méthode consiste à effectuer les opérations algébriques habituelles sur des fonctions, telles que l'addition, la soustraction, la multiplication et la division. Pour ce faire, nous effectuons les opérations avec les sorties de la fonction, en définissant le résultat comme la sortie de notre nouvelle fonction.

Supposons que nous devions ajouter deux colonnes de chiffres qui représentent les revenus annuels distincts d'un mari et d'une femme sur une période donnée, le résultat étant le revenu total de leur ménage. Nous voulons le faire pour chaque année, en ajoutant uniquement les revenus de cette année, puis en collectant toutes les données dans une nouvelle colonne. Si\(w(y)\) c'est le revenu de la femme et\(h(y)\) le revenu du mari pour l'année\(y\), et que nous\(T\) voulons représenter le revenu total, alors nous pouvons définir une nouvelle fonction.

\[T(y)=h(y)+w(y) \nonumber\]

Si cela est vrai pour chaque année, alors nous pouvons nous concentrer sur la relation entre les fonctions sans référence à une année et écrire

\[T=h+w \nonumber\]

Tout comme pour cette somme de deux fonctions, nous pouvons définir des fonctions de différence, de produit et de ratio pour n'importe quelle paire de fonctions qui ont les mêmes types d'entrées (pas nécessairement des nombres) et également les mêmes types de sorties (qui doivent être des nombres pour que les opérations habituelles d'algèbre puissent s'appliquer à elles, et qui doit également avoir les mêmes unités ou aucune unité lorsque nous ajoutons et soustrayons). De cette façon, nous pouvons penser à ajouter, soustraire, multiplier et diviser des fonctions.

Pour deux fonctions\(f(x)\) et\(g(x)\) avec des sorties en nombre réel, nous définissons de nouvelles fonctions\(f+g\)\(f−g\)\(fg\),, et\(\frac{f}{g}\) par les relations.

\[ \begin{align*} (f+g)(x) &=f(x)+g(x) \\[4pt] (f−g)(x) &=f(x)−g(x) \\[4pt] (fg)(x)&=f(x)g(x) \\[4pt] \left(\dfrac{f}{g}\right)(x) &=\dfrac{f(x)}{g(x)} \end{align*}\]

Exemple\(\PageIndex{1}\): Performing Algebraic Operations on Functions

Trouvez et simplifiez les fonctions\((g−f)(x)\) et\(\left(\dfrac{g}{f}\right)(x)\), étant donné\(f(x)=x−1\) et\(g(x)=x^2−1\). Sont-elles la même fonction ?

Solution

Commencez par écrire la forme générale, puis remplacez-la par les fonctions données.

\[\begin{align*} (g−f)(x) &= g(x)−f(x) \\[4pt] (g−f)(x) &=x^2−1−(x−1) \\[4pt] &=x^2−x \\[4pt] &=x(x−1) \end{align*}\]

\[\begin{align*} \left(\dfrac{g}{f}\right)(x)&=g(x)f(x) \\[4pt] \left(\dfrac{g}{f}\right)(x)&=\dfrac{x^2−1}{x−1} \\[4pt] &=\dfrac{(x+1)(x−1)}{x−1} \\[4pt]&=x+1 \end{align*}\]

Non, les fonctions ne sont pas les mêmes.

Remarque : Pour\(\left(\dfrac{g}{f}\right)(x)\), la condition\(x\neq1\) est nécessaire car quand\(x=1\), le dénominateur est égal à 0, ce qui rend la fonction indéfinie.

Exercice\(\PageIndex{1}\)

Trouvez et simplifiez les fonctions\((fg)(x)\) et\((f−g)(x)\).

\[f(x)=x−1 \nonumber\]

et

\[g(x)=x^2−1 \nonumber\]

Sont-elles la même fonction ?

Réponse

\((fg)(x)=f(x)g(x)=(x−1)(x2−1)=x^3−x^2−x+1 \\[4pt] (f−g)(x)=f(x)−g(x)=(x−1)−(x^2−1)=x−x^2\)

Non, les fonctions ne sont pas les mêmes.

Création d'une fonction par composition de fonctions

L'exécution d'opérations algébriques sur des fonctions les combine en une nouvelle fonction, mais nous pouvons également créer des fonctions en composant des fonctions. Lorsque nous avons voulu calculer un coût de chauffage à partir d'un jour de l'année, nous avons créé une nouvelle fonction qui prend un jour comme entrée et produit un coût comme sortie. Le processus qui consiste à combiner des fonctions de telle sorte que la sortie d'une fonction devienne l'entrée d'une autre est connu sous le nom de composition de fonctions. La fonction résultante est connue sous le nom de fonction composite. Nous représentons cette combinaison par la notation suivante :

\[f{\circ}g(x)=f(g(x))\]

Nous lisons le côté gauche comme «\(f\) composé par\(g\) at\(x\) » et le côté droit comme «\(f\)\(g\) de »\(x\). Les deux côtés de l'équation ont la même signification mathématique et sont égaux. Le symbole du cercle ouvert\(\circ\) est appelé opérateur de composition. Nous utilisons cet opérateur principalement lorsque nous souhaitons mettre l'accent sur la relation entre les fonctions elles-mêmes sans faire référence à une valeur d'entrée particulière. La composition est une opération binaire qui prend deux fonctions et forme une nouvelle fonction, tout comme l'addition ou la multiplication prend deux nombres et donne un nouveau nombre. Cependant, il est important de ne pas confondre composition des fonctions et multiplication car, comme nous l'avons appris plus haut, dans la plupart des cas\(f(g(x)){\neq}f(x)g(x)\).

Il est également important de comprendre l'ordre des opérations lors de l'évaluation d'une fonction composite. Nous suivons la convention habituelle avec les parenthèses en commençant par les parenthèses les plus intérieures, puis en travaillant vers l'extérieur. Dans l'équation ci-dessus, la fonction\(g\) prend l'entrée en\(x\) premier et produit une sortie\(g(x)\). Ensuite, la fonction\(f\) prend\(g(x)\) comme entrée et produit une sortie\(f(g(x))\).

Figure\(\PageIndex{2}\) : Explication de la fonction composite.

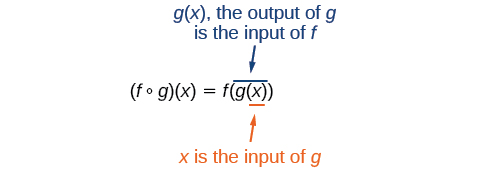
En général,\(f{\circ}g\) et\(g{\circ}f\) sont des fonctions différentes. En d'autres termes, dans de nombreux cas\(f(g(x)){\neq}g(f(x))\) pour tous\(x\). Nous verrons également que parfois deux fonctions ne peuvent être composées que dans un ordre précis.

Par exemple, si\(f(x)=x^2\) et\(g(x)=x+2\), alors

\[\begin{align*} f(g(x))&= f(x+2) \\[4pt]&=(x+2)^2 \\[4pt] &=x^2+4x+4 \end{align*}\]

mais

\[\begin{align*} g(f(x))&= g(x^2) \\[4pt]&=x^2+2 \end{align*}\]

Ces expressions ne sont pas égales pour toutes les valeurs de x, de sorte que les deux fonctions ne sont pas égales. Peu importe que les expressions soient égales pour la valeur d'entrée unique\(x=−\frac{1}{2}\).

Notez que la plage de la fonction interne (la première fonction à évaluer) doit se situer dans le domaine de la fonction externe. De manière moins formelle, la composition doit avoir du sens en termes d'entrées et de sorties.

Composition des fonctions

Lorsque la sortie d'une fonction est utilisée comme entrée d'une autre, nous appelons l'ensemble de l'opération une composition de fonctions. Pour toutes les entrées\(x\)\(f\) et fonctions\(g\), cette action définit une fonction composite, que nous écrivons comme\(f{\circ}g\) telle que

\[(f{\circ}g)(x)=f(g(x))\]

Le domaine de la fonction composite\(f{\circ}g\) est tout\(x\) ce qui\(x\) se trouve dans le domaine de\(g\) et\(g(x)\) se trouve dans le domaine de\(f\).

Il est important de se rendre compte que le produit des fonctions n'\(fg\)est pas le même que la composition de la fonction\(f(g(x))\), car, en général,\(f(x)g(x){\neq}f(g(x))\).

Exemple\(\PageIndex{2}\): Determining whether Composition of Functions is Commutative

À l'aide des fonctions fournies, recherchez\(f(g(x))\) et\(g(f(x))\). Déterminez si la composition des fonctions est commutative.

\[f(x)=2x+1 \;\;\;\; g(x)=3−x \nonumber\]

Solution

Commençons par le remplacer\(g(x)\) par\(f(x)\).

\[\begin{align*} f(g(x))&= 2(3−x)+1 \\[4pt] &=6−2x+1 \\[4pt] &=7−2x \end{align*}\]

Maintenant, nous pouvons\(f(x)\) le remplacer par\(g(x)\).

\[\begin{align*} g(f(x))&= 3−(2x+1) \\[4pt]&=3−2x−1 \\[4pt] &=2-2x \end{align*}\]

Nous constatons que\(g(f(x)){\neq}f(g(x))\) le fonctionnement de la composition des fonctions n'est donc pas commutatif.

Exemple\(\PageIndex{3}\): Interpreting Composite Functions

La fonction\(c(s)\) indique le nombre de calories brûlées en effectuant\(s\) des redressements assis et\(s(t)\) indique le nombre de redressements assis qu'une personne peut effectuer en\(t\) quelques minutes. Interpréter\(c(s(3))\).

Solution

L'expression intérieure de la composition est\(s(3)\). Parce que l'entrée de la\(s\) fonction -est le temps,\(t=3\) représente 3 minutes et\(s(3)\) correspond au nombre de redressements assis terminés en 3 minutes.

L'utilisation\(s(3)\) comme entrée de la fonction nous\(c(s)\) donne le nombre de calories brûlées pendant le nombre de redressements assis pouvant être effectués en 3 minutes, ou simplement le nombre de calories brûlées en 3 minutes (en faisant des redressements assis).

Exemple\(\PageIndex{4}\): Investigating the Order of Function Composition

Supposons qu'il\(f(x)\) donne des kilomètres qui peuvent être parcourus en\(x\) quelques heures et\(g(y)\) indique les gallons d'essence utilisés pour parcourir des\(y\) kilomètres. Laquelle de ces expressions est significative :\(f(g(y))\) ou\(g(f(x))\) ?

Solution

La fonction\(y=f(x)\) est une fonction dont la sortie est le nombre de miles parcourus correspondant au nombre d'heures parcourues.

\[\text{number of miles } =f (\text{number of hours}) \nonumber\]

La fonction\(g(y)\) est une fonction dont la sortie est le nombre de gallons utilisés correspondant au nombre de miles parcourus. Cela signifie :

\[\text{number of gallons } =g(\text{number of miles}) \nonumber\]

L'expression\(g(y)\) prend des miles en entrée et un nombre de gallons en sortie. La fonction\(f(x)\) nécessite un certain nombre d'heures en entrée. Essayer de saisir un nombre de gallons n'a aucun sens. L'expression\(f(g(y))\) n'a aucun sens.

L'expression\(f(x)\) prend des heures en entrée et un nombre de kilomètres parcourus en sortie. La fonction\(g(y)\) nécessite un nombre de miles en entrée. Il est logique d'utiliser\(f(x)\) (miles parcourus) comme valeur d'entrée pour\(g(y)\), où les gallons d'essence dépendent des kilomètres parcourus. L'expression\(g(f(x))\) est logique et donnera le nombre de gallons d'essence utilisés\(g\), en parcourant un certain nombre de kilomètres\(f(x)\), en\(x\) heures.

Question/Réponse

Y a-t-il des situations où\(f(g(y))\) et\(g(f(x))\) seraient à la fois des expressions significatives ou utiles ?

Oui Pour de nombreuses fonctions purement mathématiques, les deux compositions ont du sens, même si elles produisent généralement de nouvelles fonctions différentes. Dans les problèmes du monde réel, les fonctions dont les entrées et les sorties ont les mêmes unités peuvent également donner des compositions significatives dans les deux ordres

Exercice\(\PageIndex{2}\)

La force gravitationnelle sur une planète\(r\) éloignée du soleil est donnée par la fonction\(G(r)\). L'accélération d'une planète soumise à une force quelconque\(F\) est donnée par la fonction\(a(F)\). Formez une composition significative de ces deux fonctions et expliquez ce que cela signifie.

Réponse

Une force gravitationnelle est toujours une force, donc\(a(G(r))\) cela a du sens en tant qu'accélération d'une planète\(r\) éloignée du Soleil (due à la gravité), mais\(G(a(F))\) cela n'a aucun sens.

Évaluation des fonctions composites

Une fois que nous avons composé une nouvelle fonction à partir de deux fonctions existantes, nous devons être en mesure de l'évaluer pour toutes les entrées de son domaine. Pour ce faire, nous utiliserons des entrées numériques spécifiques pour les fonctions exprimées sous forme de tableaux, de graphiques et de formules et avec des variables comme entrées de fonctions exprimées sous forme de formules. Dans chaque cas, nous évaluons la fonction interne à l'aide de l'entrée de départ, puis nous utilisons la sortie de la fonction interne comme entrée pour la fonction externe.

Évaluation de fonctions composites à l'aide de

Lorsque nous travaillons avec des fonctions présentées sous forme de tableaux, nous lisons les valeurs d'entrée et de sortie à partir des entrées de la table et travaillons toujours de l'intérieur vers l'extérieur. Nous évaluons d'abord la fonction interne, puis utilisons la sortie de la fonction interne comme entrée de la fonction externe.

Exemple\(\PageIndex{5}\): Using a Table to Evaluate a Composite Function

À l'aide de Tableau\(\PageIndex{1}\), évaluez\(f(g(3))\) et\(g(f(3))\).

Tableau\(\PageIndex{1}\)

\(x\)	\(f(x)\)	\(g(x)\)
\ (x \) » style="vertical-align:middle ; text-align:center ; » class="lt-math-1296">1	\ (f (x) \) » style="vertical-align:middle ; text-align:center ; » class="lt-math-1296">6	\ (g (x) \) » style="vertical-align:middle ; text-align:center ; » class="lt-math-1296">3
\ (x \) » style="vertical-align:middle ; text-align:center ; » class="lt-math-1296">2	\ (f (x) \) » style="vertical-align:middle ; text-align:center ; » class="lt-math-1296">8	\ (g (x) \) » style="vertical-align:middle ; text-align:center ; » class="lt-math-1296">5
\ (x \) » style="vertical-align:middle ; text-align:center ; » class="lt-math-1296">3	\ (f (x) \) » style="vertical-align:middle ; text-align:center ; » class="lt-math-1296">3	\ (g (x) \) » style="vertical-align:middle ; text-align:center ; » class="lt-math-1296">2
\ (x \) » style="vertical-align:middle ; text-align:center ; » class="lt-math-1296">4	\ (f (x) \) » style="vertical-align:middle ; text-align:center ; » class="lt-math-1296">1	\ (g (x) \) » style="vertical-align:middle ; text-align:center ; » class="lt-math-1296">7

Solution

Pour évaluer\(f(g(3))\), on part de l'intérieur avec la valeur d'entrée 3. Nous évaluons ensuite l'expression interne à\(g(3)\) l'aide de la table qui définit la fonction\(g: g(3)=2\). Nous pouvons ensuite utiliser ce résultat comme entrée de la fonction\(f\), il\(g(3)\) est donc remplacé par 2 et nous obtenons\(f(2)\). Ensuite, en utilisant la table qui définit la fonction\(f\), nous trouvons cela\(f(2)=8\).

\[g(3)=2 \nonumber\]

\[f(g(3))=f(2)=8 \nonumber\]

Pour évaluer\(g(f(3))\), nous évaluons d'abord l'expression interne à\(f(3)\) l'aide du premier tableau :\(f(3)=3\). Ensuite, en utilisant le tableau pour\(g\), nous pouvons évaluer

\[g(f(3))=g(3)=2 \nonumber\]

Le tableau\(\PageIndex{2}\) présente les fonctions composites\(f{\circ}g\) et\(g{\circ}f\) sous forme de tableaux.

Tableau\(\PageIndex{2}\)

\(x\)	\(g(x)\)	\(f(g(x))\)	\(f(x)\)	\(g(f(x))\)
\ (x \) » style="vertical-align:middle ; text-align:center ; » class="lt-math-1296">3	\ (g (x) \) » style="vertical-align:middle ; text-align:center ; » class="lt-math-1296">2	\ (f (g (x)) \) » style="vertical-align:middle ; text-align:center ; » class="lt-math-1296">8	\ (f (x) \) » style="vertical-align:middle ; text-align:center ; » class="lt-math-1296">3	\ (g (f (x)) \) » style="vertical-align:middle ; text-align:center ; » class="lt-math-1296">2

Exercice\(\PageIndex{3}\)

À l'aide de Tableau\(\PageIndex{1}\), évaluez\(f(g(1))\) et\(g(f(4))\).

Réponse

\(f(g(1))=f(3)=3\)et\(g(f(4))=g(1)=3\)

Évaluation de fonctions composites à l'aide de

Lorsque des fonctions individuelles nous sont présentées sous forme de graphes, la procédure d'évaluation des fonctions composites est similaire à celle que nous utilisons pour évaluer des tables. Nous lisons les valeurs d'entrée et de sortie, mais cette fois, à partir des axes x et y des graphes.

Comment...

À partir d'une fonction composite et de graphes de ses fonctions individuelles, évaluez-la à l'aide des informations fournies par les graphiques.

1. Localisez l'entrée donnée de la fonction interne sur l'axe X de son graphe.
2. Lisez la sortie de la fonction interne à partir de l'axe y de son graphe.
3. Localisez la sortie de la fonction interne sur l'axe X du graphe de la fonction externe.
4. Lisez la sortie de la fonction externe à partir de l'axe y de son graphe. Il s'agit de la sortie de la fonction composite.

Exemple\(\PageIndex{6}\): Using a Graph to Evaluate a Composite Function

À l'aide de Figure\(\PageIndex{3}\), évaluez\(f(g(1))\)

Figure\(\PageIndex{3}\) : Deux graphiques représentant une parabole positive et une parabole négative.

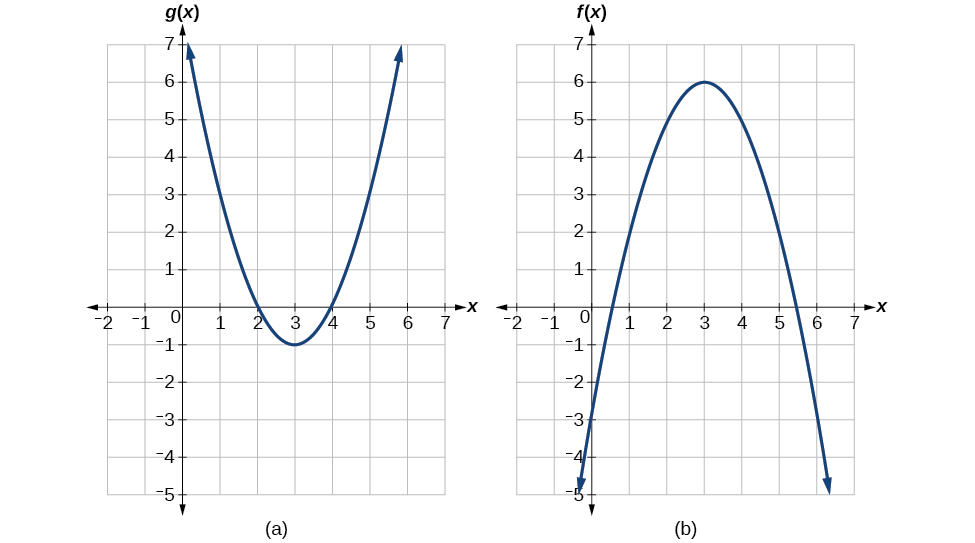
Solution

Pour évaluer\(f(g(1))\), nous commençons par l'évaluation interne. Voir la figure\(\PageIndex{4}\).

Figure\(\PageIndex{4}\) : Deux graphiques représentant une parabole positive\(g(x)\) et une parabole négative\(f(x)\). Les points suivants sont tracés :\(g(1)=3\) et\(f(3)=6\).

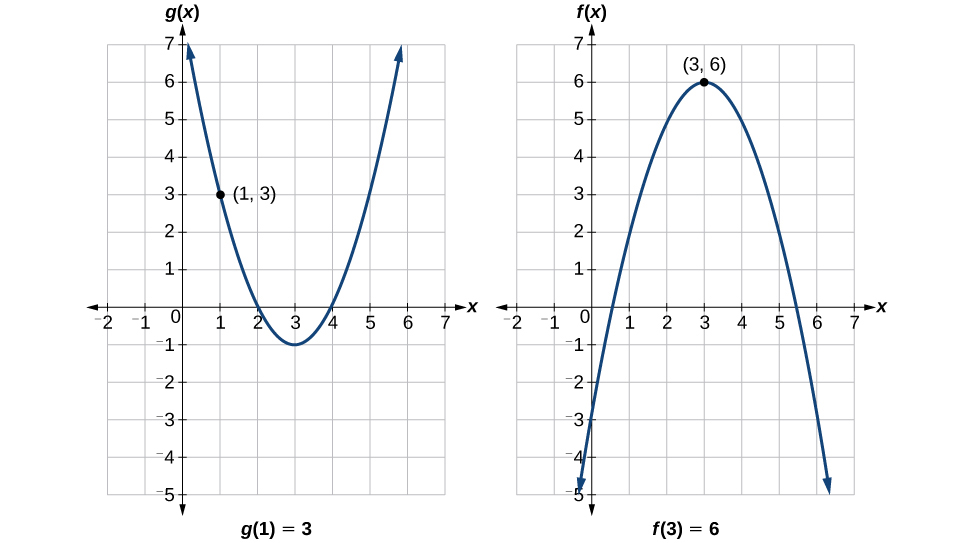
Nous évaluons\(g(1)\) à l'aide du graphe de\(g(x)\), en trouvant l'entrée de 1 sur l'axe des abscisses et en trouvant la valeur de sortie du graphique à cette entrée. Ici,\(g(1)=3\). Nous utilisons cette valeur comme entrée de la fonction\(f\).

\[f(g(1))=f(3) \nonumber\]

Nous pouvons ensuite évaluer la fonction composite en examinant le graphe de\(f(x)\), en trouvant l'entrée de 3 sur l'axe des abscisses et en lisant la valeur de sortie du graphe à cette entrée. Ici\(f(3)=6\), donc\(f(g(1))=6\).

Analyse

La figure\(\PageIndex{5}\) montre comment marquer les graphiques avec des flèches pour tracer le chemin entre la valeur d'entrée et la valeur de sortie.

Figure\(\PageIndex{5}\) : Deux graphiques représentant une parabole positive et une parabole négative.

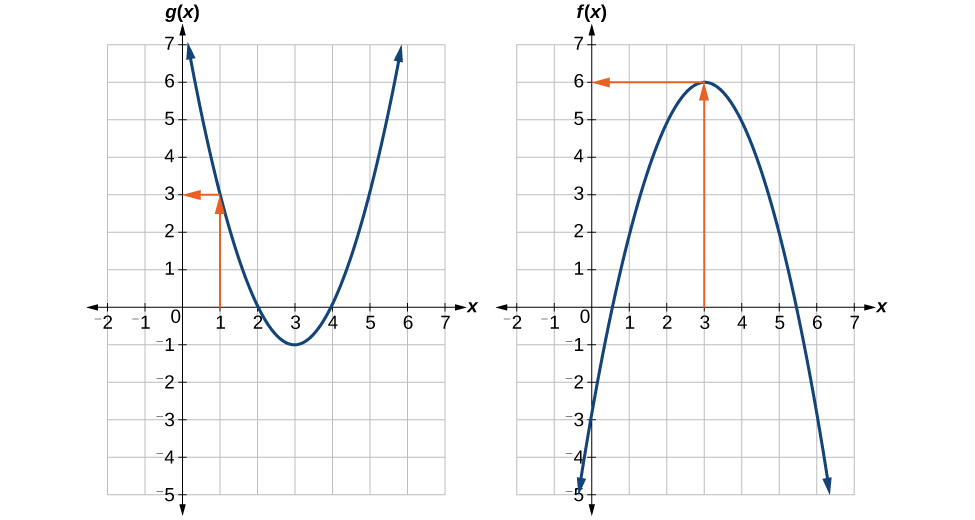
Exercice\(\PageIndex{4}\)

À l'aide de Figure\(\PageIndex{3}\), évaluez\(g(f(2))\)

Réponse

\(g(f(2))=g(5)=3\)

Évaluation de fonctions composites à l'aide de

Lors de l'évaluation d'une fonction composite dans laquelle nous avons créé ou reçu des formules, la règle qui consiste à travailler de l'intérieur vers l'extérieur reste la même. La valeur d'entrée de la fonction externe sera la sortie de la fonction interne, qui peut être une valeur numérique, un nom de variable ou une expression plus complexe.

Bien que nous puissions composer les fonctions pour chaque valeur d'entrée individuelle, il est parfois utile de trouver une formule unique qui calculera le résultat d'une composition\(f(g(x))\). Pour ce faire, nous allons élargir notre idée de l'évaluation des fonctions. Rappelez-vous que, lorsque nous évaluons une fonction telle que\(f(t)=t^2−t\), nous substituons la valeur entre parenthèses dans la formule partout où nous voyons la variable d'entrée.

Comment...

À partir d'une formule pour une fonction composite, évaluez la fonction.

1. Évaluez la fonction interne à l'aide de la valeur d'entrée ou de la variable fournie.
2. Utilisez la sortie résultante comme entrée de la fonction externe.

Exemple\(\PageIndex{7}\): Evaluating a Composition of Functions Expressed as Formulas with a Numerical Input

Donné\(f(t)=t^2−t\) et\(h(x)=3x+2\), évaluez\(f(h(1))\).

Solution

Comme l'expression interne est\(h(1)\), nous commençons par évaluer\(h(x)\) à 1.

\[ \begin{align*} h(1)=3(1)+2 \\[4pt] h(1)&=5 \end{align*} \]

Ensuite\(f(h(1))=f(5)\), nous évaluons\(f(t)\) à une entrée de 5.

\[ \begin{align*} f(h(1)) &=f(5) \\[5pt] f(h(1))&=5^2−5 \\[5pt] f(h(1))&=20 \end{align*} \]

Analyse

La manière dont les variables\(t\) d'entrée\(x\) ont été appelées dans ce problème ne fait aucune différence, car nous les avons évaluées pour des valeurs numériques spécifiques.

Exercice\(\PageIndex{5}\)

Donné\(f(t)=t^2−t\) et\(h(x)=3x+2\), évaluez

a.\(h(f(2))\)
b.\(h(f(−2))\)

Répondez à

8

Réponse b

20

Trouver le domaine d'une fonction composite

Comme nous l'avons vu précédemment, le domaine d'une fonction composite telle que\(f{\circ}g\) dépend du domaine\(g\) et du domaine de\(f\). Il est important de savoir quand nous pouvons appliquer une fonction composite et quand nous ne le pouvons pas, c'est-à-dire connaître le domaine d'une fonction telle que\(f{\circ}g\). Supposons que nous connaissions les domaines des fonctions\(f\) et\(g\) séparément. Si nous écrivons la fonction composite pour une entrée\(x\) sous la forme\(f(g(x))\), nous pouvons voir immédiatement qu'elle\(x\) doit appartenir au domaine de g pour que l'expression soit significative, sinon nous ne pouvons pas terminer l'évaluation de la fonction interne. Cependant, nous voyons également qu'\(g(x)\)il doit appartenir au domaine de\(f\), sinon l'évaluation de la deuxième fonction\(f(g(x))\) ne peut pas être terminée et l'expression n'est toujours pas définie. Ainsi, le domaine de\(f{\circ}g\) comprend uniquement les entrées du domaine de\(g\) qui produisent des sorties\(g\) appartenant au domaine de\(f\). Notez que le domaine de\(f\) composé avec\(g\) est l'ensemble de tous\(x\) ceux qui\(x\) se trouvent dans le domaine de\(g\) et g (x) \) appartient au domaine de\(f\).

Définition : Domaine d'une fonction composite

Le domaine d'une fonction composite\(f(g(x))\) est l'ensemble des entrées\(x\) dans le domaine de\(g\) pour lesquelles\(g(x)\) se trouve dans le domaine de\(f\).

Comment...

En fonction de la composition d'une fonction\(f(g(x))\), déterminez son domaine.

1. Trouvez le domaine de\(g\).
2. Trouvez le domaine de\(f\).
3. Recherchez les entrées\(x\) dans le domaine de\(g\) pour lesquelles\(g(x)\) se trouve dans le domaine de\(f\). C'est-à-dire, excluez les entrées\(x\) du domaine de\(g\) pour lesquelles ne\(g(x)\) se trouve pas dans le domaine de\(f\). L'ensemble obtenu est le domaine de\(f{\circ}g\).

Exemple\(\PageIndex{8A}\): Finding the Domain of a Composite Function

Trouvez le domaine de

\[(f∘g)(x) \text{ where } f(x)=\dfrac{5}{x−1} \text{ and } g(x)=\dfrac{4}{3x−2} \nonumber\]

Solution

Le domaine de\(g(x)\) se compose de tous les nombres réels sauf\(x=\frac{2}{3}\), car cette valeur d'entrée nous obligerait à diviser par 0. De même, le domaine de\(f\) comprend tous les nombres réels sauf 1. Nous devons donc exclure du domaine de\(g(x)\) cette valeur\(x\) pour laquelle\(g(x)=1\).

\[\begin{align*} \dfrac{4}{3x-2}&= 1 \\[4pt] 4 &=3x-2 \\[4pt] 6&=3x \\[4pt] x&= 2 \end{align*}\]

Le domaine de\(f{\circ}g\) est donc l'ensemble de tous les nombres réels sauf\(\frac{2}{3}\) et\(2\). Cela signifie que

\[x{\neq} \dfrac{2}{3} \text{ or } x\neq2 \nonumber\]

Nous pouvons l'écrire en notation par intervalles comme

\[\left(−\infty,\dfrac{2}{3}\right)\cup \left(\dfrac{2}{3},2 \right)\cup \left(2,\infty \right) \nonumber\]

Exemple\(\PageIndex{8B}\): Finding the Domain of a Composite Function Involving Radicals

Trouvez le domaine de

\[(f{\circ}g)(x) \text{ where } f(x)=\sqrt{x+2} \text{ and } g(x)=\sqrt{3−x} \nonumber\]

Solution

Parce que nous ne pouvons pas prendre la racine carrée d'un nombre négatif, le domaine de\(g\) est\(\left(−\infty,3\right]\). Nous vérifions maintenant le domaine de la fonction composite

\[(f{\circ}g)(x)=\sqrt{\sqrt{3−x}+2} \nonumber\]

Car\((f∘g)(x)=\sqrt{ \sqrt{3−x}+2},\sqrt{3−x}+2≥0,\) puisque le radical d'une racine carrée doit être positif. Puisque les racines carrées sont positives\(\sqrt{3−x}≥0\), ou,\(3−x≥0,\) ce qui donne un domaine de\((-∞,3]\).

Analyse

Cet exemple montre que la connaissance de la gamme de fonctions (en particulier de la fonction interne) peut également être utile pour trouver le domaine d'une fonction composite. Cela montre également que le domaine de\(f{\circ}g\) peut contenir des valeurs qui ne font pas partie du domaine de\(f\), bien qu'elles doivent appartenir au domaine de\(g\).

Exercice\(\PageIndex{6}\)

Trouvez le domaine de

\[(f{\circ}g)(x) \text{ where } f(x)=\dfrac{1}{x−2} \text{ and } g(x)=\sqrt{x+4} \nonumber\]

Réponse

\([−4,0)∪(0,∞)\)

Décomposer une fonction composite en ses fonctions constitutives

Dans certains cas, il est nécessaire de décomposer une fonction compliquée. En d'autres termes, nous pouvons l'écrire comme une composition de deux fonctions plus simples. Il peut y avoir plusieurs manières de décomposer une fonction composite, nous pouvons donc choisir la décomposition qui semble la plus appropriée.

Exemple\(\PageIndex{9}\): Decomposing a Function

Ecrivez\(f(x)=\sqrt{5−x^2}\) comme la composition de deux fonctions.

Solution

Nous recherchons deux fonctions\(h\),\(g\) et donc\(f(x)=g(h(x))\). Pour ce faire, nous recherchons une fonction à l'intérieur d'une fonction dans la formule pour\(f(x)\). Comme possibilité, nous pouvons remarquer que l'expression\(5−x^2\) se trouve à l'intérieur de la racine carrée. Nous pourrions ensuite décomposer la fonction comme

\[h(x)=5−x^2 \text{ and } g(x)=\sqrt{x} \nonumber\]

Nous pouvons vérifier notre réponse en recomposant les fonctions.

\[g(h(x))=g(5−x^2)=\sqrt{5−x^2} \nonumber\]

Exercice\(\PageIndex{7}\)

Ecrivez\(f(x)=\dfrac{4}{3−\sqrt{4+x^2}}\) comme la composition de deux fonctions.

Réponse

Réponses possibles :

\(g(x)=\sqrt{4+x^2}\)

\(h(x)=\dfrac{4}{3−x}\)

\(f=h{\circ}g\)

Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur les fonctions composites.

• Fonctions composites (http://openstaxcollege.org/l/compfunction)
• Application de notation des fonctions composites (http://openstaxcollege.org/l/compfuncnot)
• Fonctions composites utilisant des graphes (http://openstaxcollege.org/l/compfuncgraph)
• Décomposer les fonctions (http://openstaxcollege.org/l/decompfunction)
• Valeurs des fonctions composites (http://openstaxcollege.org/l/compfuncvalue)

Équation clé

• Fonction composite\((f{\circ}g)(x)=f(g(x))\)

Concepts clés

• Nous pouvons effectuer des opérations algébriques sur des fonctions. Voir l'exemple.
• Lorsque des fonctions sont combinées, la sortie de la première fonction (interne) devient l'entrée de la seconde fonction (externe).
• La fonction produite par la combinaison de deux fonctions est une fonction composite. Voir Exemple et Exemple.
• L'ordre de composition des fonctions doit être pris en compte lors de l'interprétation de la signification des fonctions composites. Voir l'exemple.
• Une fonction composite peut être évaluée en évaluant la fonction interne à l'aide de la valeur d'entrée donnée, puis en évaluant la fonction externe en prenant comme entrée la sortie de la fonction interne.
• Une fonction composite peut être évaluée à partir d'un tableau. Voir l'exemple.
• Une fonction composite peut être évaluée à partir d'un graphique. Voir l'exemple.
• Une fonction composite peut être évaluée à partir d'une formule. Voir l'exemple.
• Le domaine d'une fonction composite comprend les entrées du domaine de la fonction interne qui correspondent aux sorties de la fonction interne qui se trouvent dans le domaine de la fonction externe. Voir Exemple et Exemple.
• Tout comme les fonctions peuvent être combinées pour former une fonction composite, les fonctions composites peuvent être décomposées en fonctions plus simples.
• Les fonctions peuvent souvent être décomposées de plusieurs manières. Voir l'exemple.

Lexique

fonction composite

la nouvelle fonction formée par la composition des fonctions, lorsque la sortie d'une fonction est utilisée comme entrée d'une autre