3.3 : Taux de changement et comportement des graphes

Objectifs d'apprentissage

• Détermine le taux de variation moyen d'une fonction.
• Utilisez un graphique pour déterminer où une fonction est croissante, décroissante ou constante.
• Utilisez un graphique pour localiser les maxima locaux et les minima locaux.
• Utilisez un graphique pour localiser le maximum absolu et le minimum absolu.

Les coûts de l'essence ont connu de fortes fluctuations au cours des dernières décennies. Le tableau\(\PageIndex{1}\) indique le coût moyen, en dollars, d'un gallon d'essence pour les années 2005 à 2012. Le coût de l'essence peut être considéré en fonction de l'année.

Tableau\(\PageIndex{1}\)

\(y\)	2005	2006	2007	2008	2009	2010	2011	2012
\(C(y)\)	2.31	2,62	2,84	3,30	2,41	2,84	3,58	3,68

Si nous nous intéressions uniquement à l'évolution du prix de l'essence entre 2005 et 2012, nous pourrions calculer que le coût par gallon est passé de 2,31$ à 3,68$, soit une augmentation de 1,37$. Bien que cela soit intéressant, il serait peut-être plus utile de voir dans quelle mesure le prix a changé par an. Dans cette section, nous étudierons les modifications de ce type.

Déterminer le taux de variation moyen d'une fonction

La variation de prix par an est un taux de variation car elle décrit la façon dont une quantité de production change par rapport à la variation de la quantité d'entrée. Nous pouvons constater que le prix de l'essence indiqué dans le tableau\(\PageIndex{1}\) n'a pas varié de la même manière chaque année, de sorte que le taux de variation n'était pas constant. Si nous n'utilisons que les données de début et de fin, nous trouverions le taux de variation moyen sur la période spécifiée. Pour déterminer le taux de variation moyen, nous divisons la variation de la valeur de sortie par la variation de la valeur d'entrée.

\[\begin{align*} \text{Average rate of change}&=\dfrac{\text{Change in output}}{\text{Change in input}} \\[4pt] &=\dfrac{\Delta y}{\Delta x}\\[4pt] &=\dfrac{y_2-y_1}{x_2-x_1}\\[4pt] &=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}\end{align*} \label{1.3.1}\]

La lettre grecque\(\Delta\) (delta) signifie le changement d'une quantité ; nous lisons le rapport comme « delta-\(y\) sur delta-\(x\) » ou « la variation\(y\) divisée par la variation de »\(x\). Parfois, nous écrivons à la\(\Delta f\) place de\(\Delta y\), ce qui représente toujours la modification de la valeur de sortie de la fonction résultant d'une modification de sa valeur d'entrée. Cela ne signifie pas que nous transformons la fonction en une autre.

Dans notre exemple, le prix de l'essence a augmenté de 1,37$ entre 2005 et 2012. Sur une période de 7 ans, le taux de variation moyen était de

\[\dfrac{\Delta y}{\Delta x}=\dfrac{$1.37}{7 \text{years}}\approx \text{0.196 dollars per year.} \label{1.3.2}\]

En moyenne, le prix de l'essence a augmenté d'environ 19,6 cents par année. Parmi les autres exemples de taux de variation, citons :

• Une population de rats augmentant de 40 rats par semaine
• Une voiture parcourant 68 miles par heure (la distance parcourue change de 110 miles chaque heure au fil du temps)
• Une voiture parcourant 27 miles par gallon (la distance parcourue change de 27 miles pour chaque gallon)
• Le courant traversant un circuit électrique augmentant de 0,125 ampère pour chaque volt de tension accrue
• Le montant d'argent sur un compte universitaire diminuant de 4 000 dollars par trimestre

Définition : Taux de variation

Un taux de variation décrit la façon dont une quantité de sortie change par rapport à la variation de la quantité d'entrée. Les unités d'un taux de variation sont des « unités de sortie par unités d'entrée ».

Le taux de variation moyen entre deux valeurs d'entrée est la variation totale des valeurs de fonction (valeurs de sortie) divisée par la variation des valeurs d'entrée.

\[\dfrac{\Delta y}{\Delta x}=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}\]

Comment...

Étant donné la valeur d'une fonction à différents points, calculez le taux de variation moyen d'une fonction pour l'intervalle entre deux valeurs\(x_1\) et\(x_2\).

1. Calculez la différence\(y_2−y_1=\Delta y\).
2. Calculez la différence\(x_2−x_1=\Delta x\).
3. Trouve le ratio\(\dfrac{\Delta y}{\Delta x}\).

Exemple\(\PageIndex{1}\): Computing an Average Rate of Change

À l'aide des données du tableau\(\PageIndex{1}\), déterminez le taux de variation moyen du prix de l'essence entre 2007 et 2009.

Solution

En 2007, le prix de l'essence était de 2,84$. En 2009, le coût était de 2,41$. Le taux de variation moyen est

\[\begin{align*} \dfrac{\Delta y}{\Delta x}&=\dfrac{y_2−y_1}{x_2−x_1} \\[4pt] &=\dfrac{$2.41−$2.84}{2009−2007} \\[4pt] &=\dfrac{−$0.43}{2 \text{ years}} \\[4pt] &=−$0.22 \text{ per year} \end{align*}\]

Analyse

Notez qu'une diminution est exprimée par un changement négatif ou une « augmentation négative ». Un taux de variation est négatif lorsque la sortie diminue lorsque l'entrée augmente ou lorsque la sortie augmente lorsque l'entrée diminue.

Exercice\(\PageIndex{1}\)

À l'aide des données du tableau\(\PageIndex{1}\), déterminez le taux de variation moyen entre 2005 et 2010.

Solution

\(\dfrac{$2.84−$2.315}{5 \text{ years}} =\dfrac{$0.535}{5 \text{ years}} =$0.106 \text{per year.}\)

Exemple\(\PageIndex{2}\): Computing Average Rate of Change from a Graph

À l'aide de la fonction\(g(t)\) illustrée dans la figure\(\PageIndex{1}\), déterminez le taux de variation moyen de l'intervalle\([−1,2]\).

Figure\(\PageIndex{1}\) : Graphique d'une parabole.

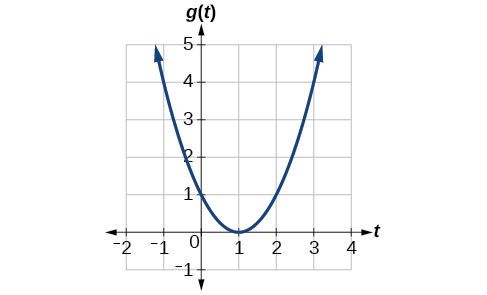
Solution

À\(t=−1\), la figure\(\PageIndex{2}\) le montre\(g(−1)=4\). À\(t=2\), le graphique le montre\(g(2)=1\).

Figure\(\PageIndex{2}\) : Graphique d'une parabole avec une droite partant des points (-1, 4) et (2, 1) pour montrer les variations pour g (t) et t.

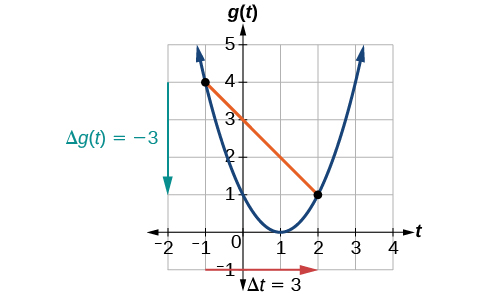
Le changement horizontal\(\Delta t=3\) est indiqué par la flèche rouge et le changement vertical\(\Delta g(t)=−3\) est indiqué par la flèche turquoise. La sortie change de —3 tandis que l'entrée change de 3, ce qui donne un taux de variation moyen de

\[\dfrac{1−4}{2−(−1)}=\dfrac{−3}{3}=−1\]

Analyse

Notez que l'ordre que nous choisissons est très important. Si, par exemple, nous utilisons\(\dfrac{y_2−y_1}{x_1−x_2}\), nous n'obtiendrons pas la bonne réponse. Décidez quel point sera 1 et quel point sera 2, et gardez les coordonnées fixes comme\((x_1,y_1)\) et\((x_2,y_2)\).

Exemple\(\PageIndex{3}\): Computing Average Rate of Change from a Table

Après être allée chercher un ami qui habite à 16 km, Anna enregistre la distance qu'elle a parcourue par rapport à la maison au fil du temps Les valeurs sont présentées dans le tableau\(\PageIndex{2}\). Trouvez sa vitesse moyenne sur les 6 premières heures.

Tableau\(\PageIndex{2}\)

\(t\)(heures)	0	1	2	3	4	5	6	7
\(D(t)\)(milles)	10	55	90	153	214	240	292	300

Solution

Ici, la vitesse moyenne est le taux de variation moyen. Elle a parcouru 292 miles en 6 heures, pour une vitesse moyenne de

\[\begin{align*}\dfrac{292−10}{6−0}&=\dfrac{282}{6}\\[4pt] &= 47\end{align*}\]

La vitesse moyenne est d'environ 77 miles par heure.

Analyse

Comme la vitesse n'est pas constante, la vitesse moyenne dépend de l'intervalle choisi. Pour l'intervalle\([2,3]\), la vitesse moyenne est de 100 km/h.

Exemple\(\PageIndex{4}\): Computing Average Rate of Change for a Function Expressed as a Formula

Calculez le taux de variation moyen de\(f(x)=x^2−\frac{1}{x}\) sur l'intervalle\([2, 4]\).

Solution

Nous pouvons commencer par calculer les valeurs des fonctions à chaque extrémité de l'intervalle.

\[\begin{align*}f(2)&=2^2−\frac{1}{2} f(4)&=4^2−\frac{1}{4} \\[4pt] &=4−\frac{1}{2} &=16−\frac{1}{4} \\[4pt] &=72 &=\frac{63}{4}\end{align*}\]

Nous calculons maintenant le taux de variation moyen.

\[\begin{align*}\text{Average rate of change} &=\dfrac{f(4)−f(2)}{4−2} \\[4pt] &=\dfrac{\frac{63}{4}-\frac{7}{2}}{4-2} \\[4pt] &=\dfrac{\frac{49}{4}}{2} \\[4pt] &= \dfrac{49}{8}\end{align*}\]

Exercice\(\PageIndex{2}\)

Détermine le taux de variation moyen\(f(x)=x−2\sqrt{x}\) de l'intervalle\([1, 9]\).

Solution

\(\frac{1}{2}\)

Exemple\(\PageIndex{5}\): Finding the Average Rate of Change of a Force

La force électrostatique\(F\), mesurée en newtons, entre deux particules chargées peut être liée à la distance entre les particules\(d\), en centimètres, par la formule\(F(d)=\frac{2}{d^2}\). Déterminez le taux moyen de variation de force si la distance entre les particules passe de 2 cm à 6 cm.

Solution

Nous calculons le taux de variation moyen\(F(d)=\dfrac{2}{d^2}\) de l'intervalle\([2,6]\).

\[\begin{align*}\text{Average rate of change }&=\dfrac{F(6)−F(2)}{6−2} \\[4pt] &=\dfrac{\frac{2}{6^2}-\frac{2}{2^2}}{6-2} & \text{Simplify} \\[4pt] &=\dfrac{\frac{2}{36}-\frac{2}{4}}{4} \\[4pt] &=\dfrac{-\frac{16}{36}}{4} & \text{Combine numerator terms.} \\[4pt] &=−\dfrac{1}{9} & \text{Simplify}\end{align*}\]

Le taux de variation moyen est de\(−\frac{1}{9}\) newtons par centimètre.

Exemple\(\PageIndex{6}\): Finding an Average Rate of Change as an Expression

Détermine le taux de variation moyen\(g(t)=t^2+3t+1\) de l'intervalle\([0, a]\). La réponse sera une expression impliquant\(a\).

Solution

Nous utilisons la formule du taux de variation moyen.

\(\begin{align*}\text{Average rate of change} &=\dfrac{g(a)−g(0)}{a−0} & \text{Evaluate.} \\[4pt] &=\dfrac{(a^2+3a+1)−(0^2+3(0)+1)}{a−0} & \text{Simplify.} \\[4pt] &=\dfrac{a^2+3a+1−1}{a} & \text{Simplify and factor.}\\[4pt] &= \dfrac{a(a+3)}{a} & \text{Divide by the common factor a.}\\[4pt] &= a+3 \end{align*}\)

Ce résultat nous indique le taux de variation moyen en termes de point intermédiaire\(t=0\) et de tout autre point\(t=a\). Par exemple, sur l'intervalle\([0,5]\), le taux de variation moyen serait de\(5+3=8\).

Exercice\(\PageIndex{3}\)

Détermine le taux de variation moyen\(f(x)=x^2+2x−8\) de l'intervalle\([5, a]\).

Solution

\(a+7\)

Utilisation d'un graphique pour déterminer où une fonction augmente, diminue ou est constante

Dans le cadre de l'exploration de la façon dont les fonctions changent, nous pouvons identifier les intervalles au cours desquels la fonction change de manière spécifique. Nous disons qu'une fonction augmente sur un intervalle si les valeurs de la fonction augmentent au fur et à mesure que les valeurs d'entrée augmentent au cours de cet intervalle. De même, une fonction décroît sur un intervalle si les valeurs de la fonction diminuent à mesure que les valeurs en entrée augmentent au cours de cet intervalle. Le taux de variation moyen d'une fonction croissante est positif et le taux de variation moyen d'une fonction décroissante est négatif. La figure\(\PageIndex{3}\) montre des exemples d'intervalles croissants et décroissants sur une fonction.

Figure\(\PageIndex{3}\) : La fonction\(f(x)=x^3−12x\) augmente au fur\((−\infty, −2)\cup (2,\infty)\) et à mesure qu'elle diminue\((−2, 2)\).

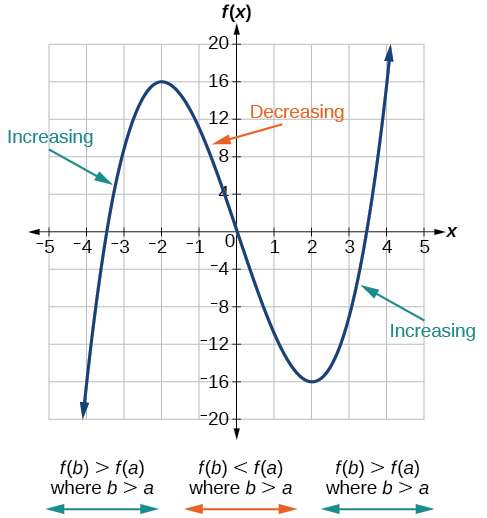
Alors que certaines fonctions augmentent (ou diminuent) sur l'ensemble de leur domaine, de nombreuses autres ne le sont pas. Une valeur de l'entrée où une fonction passe d'une fonction croissante à une valeur décroissante (lorsque nous allons de gauche à droite, c'est-à-dire lorsque la variable d'entrée augmente) est appelée maximum local. Si une fonction en possède plusieurs, on dit qu'elle a des maxima locaux. De même, une valeur de l'entrée où une fonction passe d'une fonction décroissante à une augmentation à mesure que la variable d'entrée augmente est appelée minimum local. La forme plurielle est « minima locaux ». Ensemble, les maxima et minima locaux sont appelés extrêmes locaux, ou valeurs extrêmes locales, de la fonction. (La forme singulière est « extremum ».) Souvent, le terme local est remplacé par le terme relatif. Dans ce texte, nous utiliserons le terme local.

Il est clair qu'une fonction n'augmente ni ne diminue sur un intervalle où elle est constante. De plus, une fonction n'augmente ni ne diminue à des degrés extrêmes. Notez que nous devons parler d'extrema local, car un extremum local donné tel que défini ici n'est pas nécessairement le maximum le plus élevé ou le minimum le plus bas dans l'ensemble du domaine de la fonction.

Pour la fonction dont le graphique est illustré sur la figure\(\PageIndex{4}\), le maximum local est 16 et il se produit à\(x=−2\). Le minimum local est de −16 et il se produit à\(x=2\).

Figure\(\PageIndex{4}\) : Graphique d'un polynôme qui montre les intervalles croissants et décroissants et le maximum.maximum local

Pour localiser les maxima et minima locaux à partir d'un graphique, nous devons observer le graphique afin de déterminer où le graphe atteint ses points les plus élevés et les plus bas, respectivement, dans un intervalle ouvert. Comme le sommet d'une montagne russe, le graphique d'une fonction est plus élevé à un maximum local qu'aux points voisins des deux côtés. Le graphique sera également plus bas au minimum local qu'aux points voisins. La figure\(\PageIndex{5}\) illustre ces idées pour un maximum local.

Figure\(\PageIndex{5}\) : Définition d'un maximum local

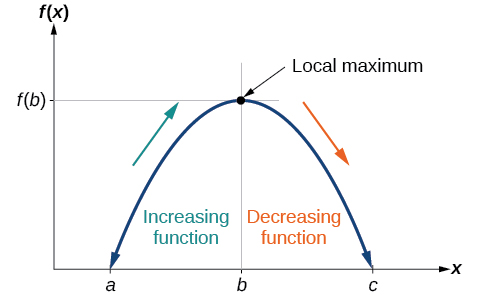
Ces observations nous amènent à définir formellement les extrêmes locaux.

Minimums locaux et maxima locaux

• Une fonction\(f\) est une fonction croissante sur un intervalle ouvert si\(f(b)>f(a)\) pour chaque\(a\),\(b\) intervalle où\(b>a\).
• Une fonction\(f\) est une fonction décroissante sur un intervalle ouvert si\(f(b)<f(a)\) pour chaque\(a\),\(b\) intervalle où\(b>a\).

Une fonction\(f\) possède un maximum local à un point\(b\) d'un intervalle ouvert\((a,c)\) s'il\(f(b)\) est supérieur ou égal à\(f(x)\) pour chaque point\(x\) (\(x\)n'est pas égal\(b\)) de l'intervalle. De même,\(f\) possède un minimum local à un point où\(b\)\((a,c)\) il\(f(b)\) est inférieur ou égal à\(f(x)\) pour chaque\(x\) (\(x\)n'est pas égal\(b\)) dans l'intervalle.

Exemple\(\PageIndex{7}\) Finding Increasing and Decreasing Intervals on a Graph

\(p(t)\)À partir de la fonction de la figure\(\PageIndex{6}\), identifiez les intervalles sur lesquels la fonction semble augmenter.

Figure\(\PageIndex{6}\) : Graphique d'un polynôme.

Solution

Nous voyons que la fonction n'est constante sur aucun intervalle. La fonction augmente lorsqu'elle s'incline vers le haut lorsque nous nous déplaçons vers la droite et diminue lorsqu'elle s'incline vers le bas lorsque nous nous déplaçons vers la droite. La fonction semble augmenter de\(t=1\) à\(t=3\) et de\(t=4\) nouveau.

En notation par intervalles, nous dirions que la fonction semble augmenter en fonction de l'intervalle\((1,3)\) et de l'intervalle\((4,\infty)\).

Analyse

Notez dans cet exemple que nous avons utilisé des intervalles ouverts (intervalles qui n'incluent pas les points de terminaison), car la fonction n'augmente ni ne diminue à\(t=1\)\(t=3\), et\(t=4\). Ces points sont les extrêmes locaux (deux minima et un maximum).

Exemple\(\PageIndex{8}\): Finding Local Extrema from a Graph

Tracez la fonction\(f(x)=\frac{2}{x}+\frac{x}{3}\). Utilisez ensuite le graphique pour estimer les extrêmes locaux de la fonction et pour déterminer les intervalles sur lesquels la fonction augmente.

Solution

En utilisant la technologie, nous constatons que le graphique de la fonction ressemble à celui de la Figure\(\PageIndex{7}\). Il semble qu'il y ait un point bas, ou minimum local, entre\(x=2\) et\(x=3\), et un point haut de l'image miroir, ou maximum local, quelque part entre\(x=−3\) et\(x=−2\)

.

Figure\(\PageIndex{7}\) : Graphique d'une fonction réciproque.

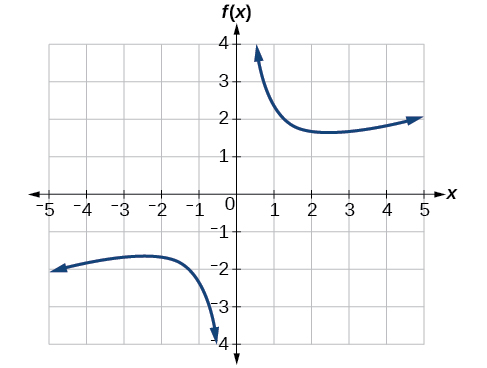Analyse

La plupart des calculateurs graphiques et des utilitaires de création graphique peuvent estimer l'emplacement des maxima et des minima. La figure\(\PageIndex{8}\) fournit des images d'écran provenant de deux technologies différentes, montrant l'estimation du maximum et du minimum locaux.

Figure\(\PageIndex{8}\) : Graphique de la fonction réciproque sur une calculatrice graphique.

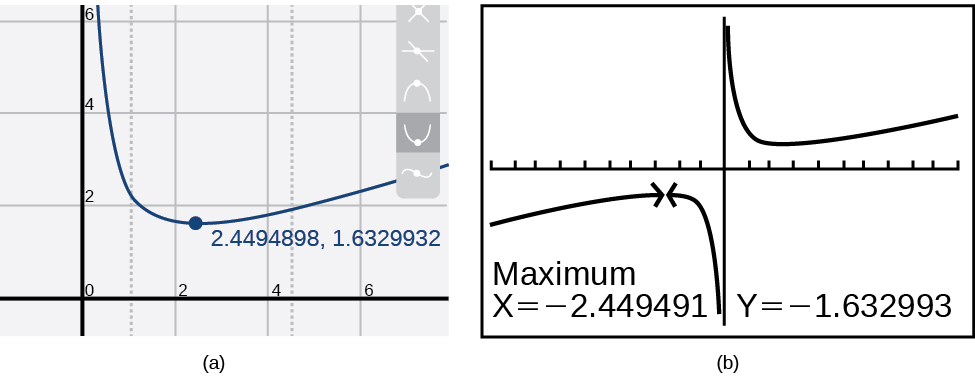
Sur la base de ces estimations, la fonction augmente sur l'intervalle\((−\infty,−2.449)\) et\((2.449,\infty)\). Notez que, bien que nous nous attendions à ce que les extrêmes soient symétriques, les deux technologies différentes ne s'accordent que jusqu'à quatre décimales en raison des algorithmes d'approximation différents utilisés par chacune d'entre elles. (L'emplacement exact des extrêmes se trouve à\(\pm\sqrt{6}\), mais pour le déterminer, il faut faire un calcul.)

Exercice\(\PageIndex{8}\)

Tracez la fonction\(f(x)=x^3−6x^2−15x+20\) pour estimer les extrêmes locaux de la fonction. Utilisez-les pour déterminer les intervalles selon lesquels la fonction augmente et diminue.

Solution

Le maximum local semble se produire à\((−1,28)\), et le minimum local se produit à\((5,−80)\). La fonction augmente\((−\infty,−1)\cup(5,\infty)\) et diminue au fur et à mesure\((−1,5)\).

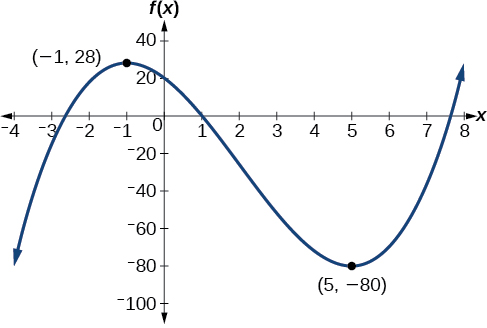
Graphe d'un polynôme avec un maximum local à (-1, 28) et un minimum local à (5, -80).

Exemple\(\PageIndex{9}\): Finding Local Maxima and Minima from a Graph

Pour la fonction f dont le graphique est illustré sur la figure\(\PageIndex{9}\), trouvez tous les maxima et minima locaux.

Figure\(\PageIndex{9}\) : Graphique d'un polynôme.

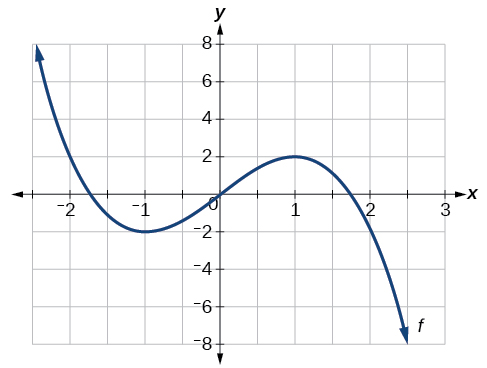
Solution

Observez le graphique de\(f\). Le graphe atteint un maximum local à\(x=1\) parce qu'il s'agit du point le plus élevé d'un intervalle ouvert autour\(x=1\) de. Le maximum local est la coordonnée y à\(x=1\), qui est 2.

Le graphique atteint un minimum local à\(x=−1\) parce qu'il s'agit du point le plus bas d'un intervalle ouvert autour de\(x=−1\). Le minimum local est la coordonnée y à\(x=−1\), qui est de −2.

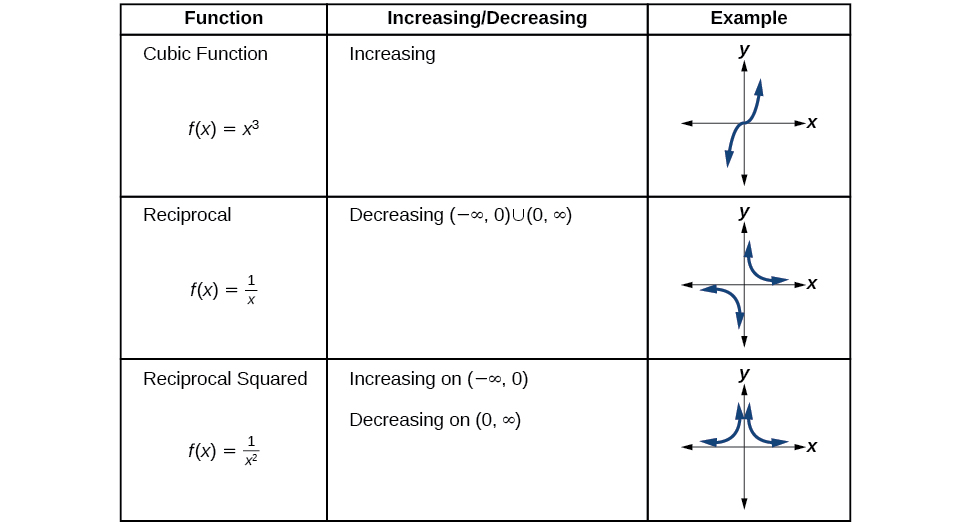
Analyse des fonctions de la boîte à outils pour augmenter ou diminuer les intervalles

Nous allons maintenant revenir aux fonctions de notre boîte à outils et discuter de leur comportement graphique dans Figure\(\PageIndex{10}\)\(\PageIndex{11}\), Figure et Figure\(\PageIndex{12}\).

Figurine\(\PageIndex{10}\)

.

Figurine\(\PageIndex{11}\)

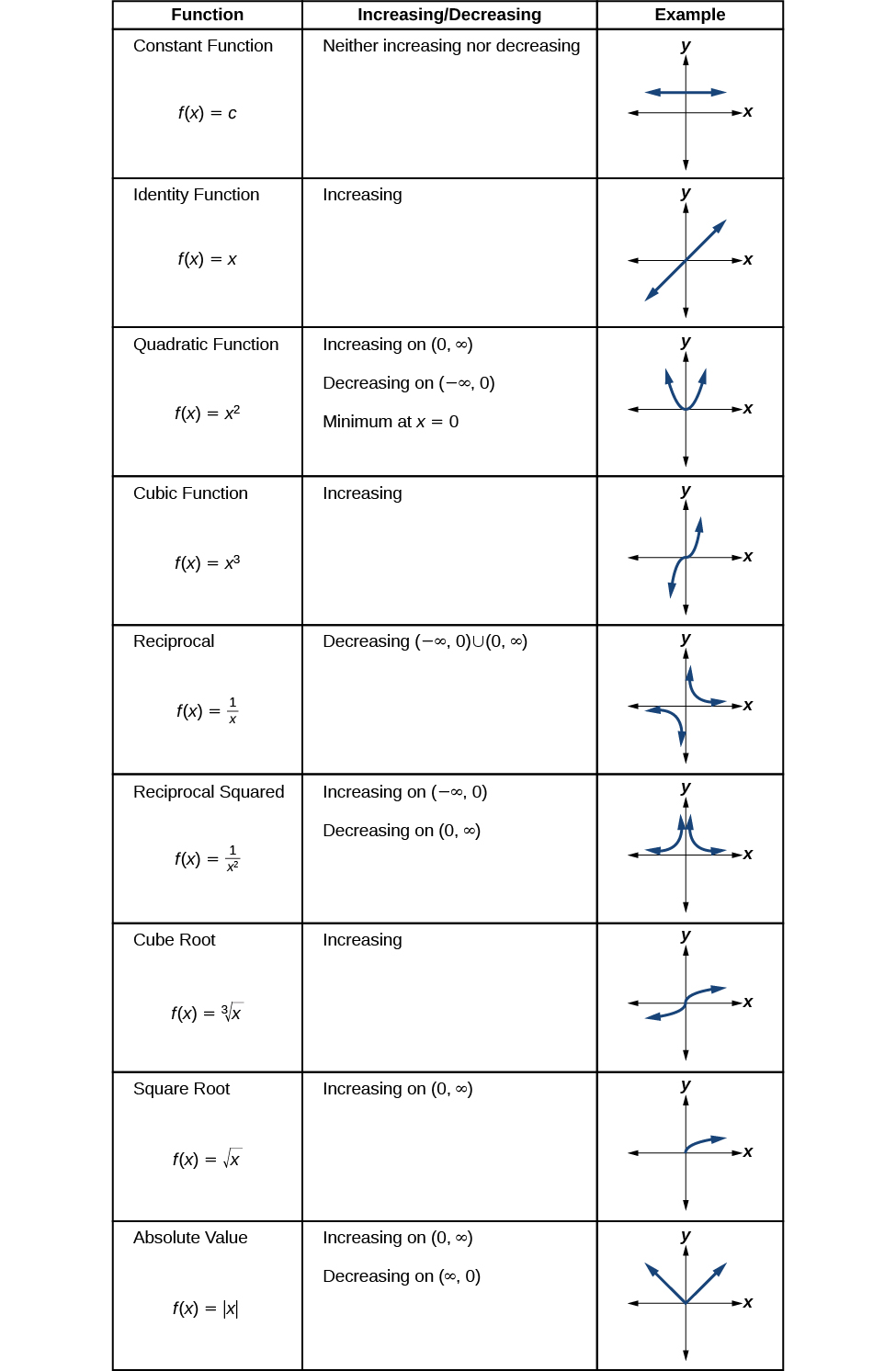
Figurine\(\PageIndex{12}\)

Utiliser un graphique pour localiser le maximum absolu et le minimum absolu

Il existe une différence entre la localisation des points les plus élevés et les plus bas d'un graphe dans une région située autour d'un intervalle ouvert (localement) et la localisation des points les plus élevés et les plus bas sur le graphique pour l'ensemble du domaine. Les coordonnées y (sortie) aux points le plus haut et le plus bas sont appelées maximum absolu et minimum absolu, respectivement. Pour localiser les maxima et les minima absolus à partir d'un graphique, nous devons observer le graphe afin de déterminer où le graphe atteint ses points les plus élevés et les plus bas dans le domaine de la fonction (Figure\(\PageIndex{13}\)).

Figure\(\PageIndex{13}\) : Graphique d'un segment d'une parabole avec un minimum absolu à (0, -2) et un maximum absolu à (2, 2).

Toutes les fonctions n'ont pas de valeur maximale ou minimale absolue. La fonction de boîte à outils\(f(x)=x^3\) est l'une de ces fonctions.

Maxima et minima absolus

• Le maximum absolu de\(f\) at\(x=c\) est\(f(c)\) où\(f(c)≥f(x)\) pour tous\(x\) dans le domaine de\(f\).
• Le minimum absolu de\(f\) at\(x=d\) est\(f(d)\) où\(f(d)≤f(x)\) pour tous\(x\) dans le domaine de\(f\).

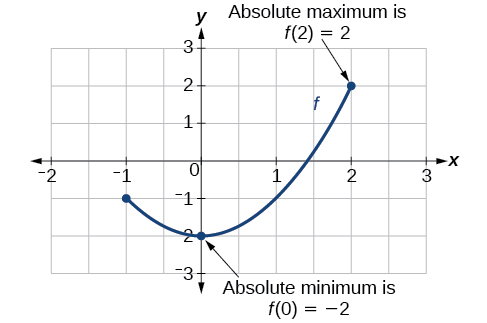
Exemple\(\PageIndex{10}\): Finding Absolute Maxima and Minima from a Graph

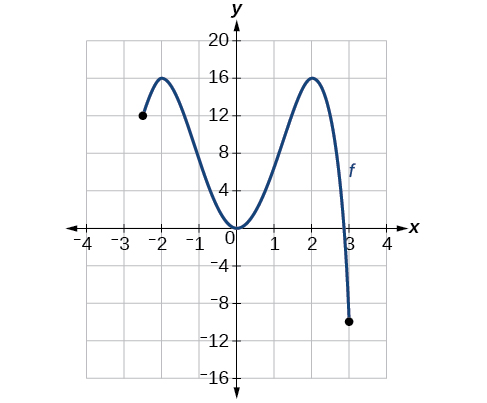
Pour la fonction f illustrée à la figure\(\PageIndex{14}\), trouvez tous les maxima et minima absolus.

Figure\(\PageIndex{14}\) : Graphique d'un polynôme.

Solution

Observez le graphique de\(f\). Le graphe atteint un maximum absolu à deux emplacements\(x=−2\) et, dans la mesure où\(x=2\), à ces emplacements, le graphe atteint son point le plus élevé dans le domaine de la fonction. Le maximum absolu est la coordonnée y à\(x=−2\) et\(x=2\), qui est 16.

Le graphe atteint un minimum absolu à x=3, car il s'agit du point le plus bas du domaine du graphe de la fonction. Le minimum absolu est la coordonnée y à x=3, soit −10.

Équations clés

• Taux de variation moyen :\(\dfrac{\Delta y}{\Delta x}=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}\)

Concepts clés

• Un taux de variation relie un changement d'une quantité de sortie à un changement d'une quantité d'entrée. Le taux de variation moyen est déterminé en utilisant uniquement les données de début et de fin. Voir l'exemple.
• Les points d'identification qui marquent l'intervalle sur un graphique peuvent être utilisés pour déterminer le taux de variation moyen. Voir l'exemple.
• La comparaison de paires de valeurs d'entrée et de sortie dans un tableau peut également être utilisée pour déterminer le taux de variation moyen. Voir l'exemple.
• Un taux de variation moyen peut également être calculé en déterminant les valeurs des fonctions aux extrémités d'un intervalle décrit par une formule. Voir Exemple et Exemple.
• Le taux de variation moyen peut parfois être déterminé sous forme d'expression. Voir l'exemple.
• Une fonction augmente lorsque son taux de variation est positif et décroît lorsque son taux de variation est négatif. Voir l'exemple.
• Un maximum local est celui où une fonction passe d'une fonction croissante à une valeur décroissante et possède une valeur de sortie plus grande (plus positive ou moins négative) que les valeurs de sortie des valeurs d'entrée voisines.
• Un minimum local correspond à l'endroit où la fonction passe d'une fonction décroissante à une valeur croissante (à mesure que l'entrée augmente) et possède une valeur de sortie plus petite (plus négative ou moins positive) que les valeurs de sortie des valeurs d'entrée voisines.
• Les minima et maxima sont également appelés extrema.
• Nous pouvons trouver les extrêmes locaux à partir d'un graphique. Voir Exemple et Exemple.
• Les points les plus élevés et les plus bas d'un graphique indiquent les maxima et les minima. Voir l'exemple.