2.6 : Autres types d'équations
- Page ID
- 195212
- Résoudre des équations impliquant des exposants rationnels
- Résolvez des équations par factorisation.
- Résoudre des équations radicales
- Résolvez des équations de valeurs
- Résolvez d'autres types d'équations.
Nous avons résolu des équations linéaires, des équations rationnelles et des équations quadratiques en utilisant plusieurs méthodes. Cependant, il existe de nombreux autres types d'équations, et nous en étudierons quelques autres dans cette section. Nous examinerons des équations impliquant des exposants rationnels, des équations polynomiales, des équations radicales, des équations de valeur absolue, des équations sous forme quadratique et certaines équations rationnelles pouvant être transformées en quadratiques. La résolution de n'importe quelle équation utilise toutefois les mêmes règles algébriques de base. Nous apprendrons de nouvelles techniques applicables à certaines équations, mais l'algèbre ne changera jamais.
Résolution d'équations impliquant des exposants rationnels
Les exposants rationnels sont des exposants qui sont des fractions, où le numérateur est une puissance et le dénominateur est une racine. Par exemple,\({16}^{\tfrac{1}{2}}\) c'est une autre façon d'écrire\(\sqrt{16}\) ;\(8^{\tfrac{1}{3}}\) c'est une autre façon d'écrire\(\sqrt[3]{8}\). La capacité de travailler avec des exposants rationnels est une compétence utile, car elle est très applicable en calcul.
Nous pouvons résoudre des équations dans lesquelles une variable est élevée à un exposant rationnel en élevant les deux côtés de l'équation à l'inverse de l'exposant. Si nous élevons l'équation à l'inverse de l'exposant, c'est parce que nous voulons éliminer l'exposant sur le terme variable, et un nombre multiplié par ses égaux réciproques\(1\). Par exemple,
\[\dfrac{2}{3}\left (\dfrac{3}{2} \right )=1 \nonumber\]
\[3\left (\dfrac{1}{3} \right )=1, \nonumber\]
et ainsi de suite.
Un exposant rationnel indique une puissance dans le numérateur et une racine dans le dénominateur. Il existe plusieurs manières d'écrire une expression, une variable ou un nombre avec un exposant rationnel :
\[a^{\tfrac{m}{n}}={\left (a^{\tfrac{1}{n}} \right )}^m={a^m}^{\tfrac{1}{n}}=\sqrt[n]{a^m}={(\sqrt[n]{a})}^m\]
Évaluer\(8^{\tfrac{2}{3}}\)
Solution
Que l'on prenne la racine en premier ou le pouvoir en premier dépend du nombre. Il est facile de trouver la racine cubique de\(8\), donc réécrivez\(8^{\tfrac{2}{3}}\) comme\({\left (8^{\tfrac{1}{3}} \right )}^2\).
\[\begin{align*} {\left (8^{\tfrac{1}{3}} \right )}^2&= {(2)}^2\\ &= 4 \end{align*}\]
Évaluer\({64}^{-\tfrac{1}{3}}\)
- Réponse
-
\(\dfrac{1}{4}\)
Résolvez l'équation dans laquelle une variable est élevée à un exposant rationnel :\(x^{\tfrac{5}{4}} = 32\).
Solution
La façon de supprimer l'exposant sur\(x\) consiste à élever les deux côtés de l'équation à une puissance qui est l'inverse de\(\dfrac{5}{4}\), qui est\(\dfrac{4}{5}\).
\[\begin{align*} x^{\tfrac{5}{4}}&= 32\\ {\left(x^{\tfrac{5}{4}}\right)}^{\tfrac{4}{5}}&= {\left(32\right)}^{\tfrac{4}{5}}\\ x&= (2)^4\\ &= 16 \end{align*}\]
Résolvez l'équation\(x^{\tfrac{3}{2}} = 125\).
- Réponse
-
\(25\)
Résoudre\(3x^{\tfrac{3}{4}} = x^{\tfrac{1}{2}}\).
Solution
Cette équation implique des exposants rationnels ainsi que la factorisation des exposants rationnels. Faisons cela étape par étape. Tout d'abord, placez les termes variables d'un côté du signe égal et définissez l'équation sur zéro.
\[\begin{align*} 3x^{\tfrac{3}{4}}-\left(x^{\tfrac{1}{2}}\right)&= x^{\tfrac{1}{2}}-\left(x^{\tfrac{1}{2}}\right)\\ 3x^{\tfrac{3}{4}}-x^{\tfrac{1}{2}}&= 0 \end{align*}\]
Maintenant, il semble que nous devrions prendre en compte le côté gauche, mais que devons-nous prendre en compte ? Nous pouvons toujours factoriser le terme avec l'exposant le plus faible. Réécrivez\(x^{\tfrac{1}{2}}\) en tant que\(x^{\tfrac{2}{4}}\). Ensuite, éliminez\(x^{\tfrac{2}{4}}\) les deux termes sur la gauche.
\[\begin{align*} 3x^{\tfrac{3}{4}}-x^{\tfrac{1}{2}}&= 0\\ x^{\tfrac{2}{4}}\left (3x^{\tfrac{1}{4}}-1 \right )&= 0 \end{align*}\]
D'où\(x^{\tfrac{1}{4}}\) viennent-ils ? N'oubliez pas que lorsque nous multiplions deux nombres avec la même base, nous ajoutons les exposants. Par conséquent, si nous multiplions à\(x^{\tfrac{2}{4}}\) nouveau en utilisant la propriété distributive, nous obtenons l'expression que nous avions avant la factorisation, ce qui devrait se produire. Nous avons besoin d'un exposant tel que lorsqu'il est ajouté à des\(\dfrac{2}{4}\) valeurs égales\(\dfrac{3}{4}\). Ainsi, l'exposant entre parenthèses est\(\dfrac{1}{4}\).\(x\)
Continuons. Nous avons maintenant deux facteurs et pouvons utiliser le théorème du facteur zéro.
\ [\ begin {align*}
x^ {\ tfrac {2} {4}} \ gauche (3x^ {\ tfrac {1} {4}} -1 \ droite) &= 0 \ \ x^ {\ tfrac {2} {4}} &= 0 \ \
x&= 0 \ \ 3x^ {\ tfrac {1} {4}}
-1&= 0 \ \
x&= 0 \ 3x^ {\ tfrac {1} {4}} -1&= 0 \ \ x&= 0 \
3x^ {\ tfrac {1} {4}}
3x^ {\ tfrac {1} {4}} &= 1 \ x^ {\ tfrac {1} {4}} &= \ dfrac {1} {3}, \ quad \ text {Divisez les deux côtés par 3.} \ \
{\ left (x^ {\ tfrac {1} {4}} \ right)} ^4&= {\ left (\ dfrac {1} {3} \ right)} ^4, \ qquad \ text {Élevez les deux côtés jusqu'à la réciproque de} \ dfrac {1} {1} {4} \ \
x&= \ dfrac {1} {81}
\ end {align*} {1}]
Les deux solutions sont\(0\) et\(\dfrac{1}{81}\).
Résoudre :\({\left(x+5\right)}^{\tfrac{3}{2}}=8\).
- Réponse
-
\(-1\)
Résolution d'équations par factorisation
Nous avons utilisé la factorisation pour résoudre des équations quadratiques, mais il s'agit d'une technique que nous pouvons utiliser avec de nombreux types d'équations polynomiales, qui sont des équations contenant une chaîne de termes comprenant des coefficients numériques et des variables. Lorsque nous sommes confrontés à une équation contenant des polynômes de degré supérieur à\(2\), nous pouvons souvent les résoudre par factorisation.
Un polynôme de degré\(n\) est une expression du type
\[a_nx^n+a_{n−1}x^{n−1}+⋅⋅⋅+a_2x^2+a_1x+a_0\]
où\(n\) is a positive integer and \(a_n ,…, a_0\) are real numbers and \(a_n≠0\).
Si le polynôme est égal à zéro, on obtient une équation polynomiale. Le nombre total de solutions (réelles et complexes) d'une équation polynomiale est égal à l'exposant le plus élevé\(n\).
Résolvez le polynôme en factorisant :\(5x^4 = 80x^2\).
Solution
Tout d'abord, définissez l'équation à zéro. Tenez ensuite compte de ce qui est commun aux deux termes, le GCF.
\[\begin{align*} 5x^4-80x^2&= 0\\ 5x^2(x^2-16)&= 0 \end{align*}\]
Notez que nous avons la différence des carrés dans le facteur\(x^2−16\), que nous continuerons à factoriser et à obtenir deux solutions. Le premier terme,\(5x^2\), génère techniquement deux solutions comme l'exposant\(2\), mais il s'agit de la même solution.
\[\begin{align*} 5x^2&= 0\\ x&=0\\ x^2-16&= 0\\ (x+4)(x-4)&= 0\\ x&= 4\\ x&= -4 \end{align*}\]
Les solutions sont\(0\) (solution double)\(4\), et\(−4\).
Analyse
Nous pouvons voir les solutions sur le graphique de la figure\(\PageIndex{1}\). Les coordonnées X des points où le graphique croise l'\(x\)axe -sont les solutions, c'est-à-dire\(x\) les interceptions. Vous remarquerez sur le graphique qu'à la solution\(0\), le graphe touche\(x\) l'axe -et rebondit. Il ne traverse pas l'\(x\)axe. C'est typique des solutions doubles.
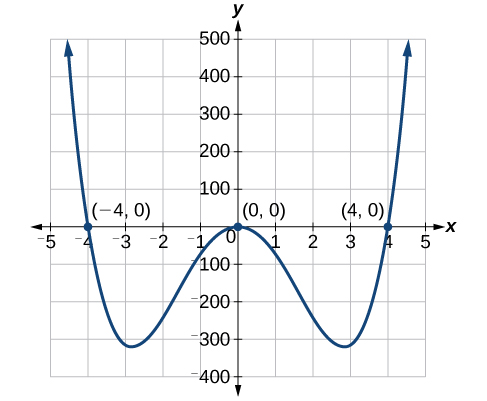
Résolvez en affacturant :\(12x^4 = 3x^2\).
- Réponse
-
\(x=0, x=12, x=−12\)
Résolvez un polynôme en regroupant :\(x^3+x^2−9x−9=0\).
Solution
Ce polynôme est composé de\(4\) termes, que nous pouvons résoudre par regroupement. Les procédures de regroupement nécessitent de factoriser les deux premiers termes, puis de factoriser les deux derniers termes. Si les facteurs entre parenthèses sont identiques, nous pouvons poursuivre le processus et le résoudre, à moins qu'une factorisation supplémentaire ne soit suggérée.
\[\begin{align*} x^3+x^2-9x-9&= 0\\ x^2(x+1)-9(x+1)&= 0\\ (x^2-9)(x+1)&= 0 \end{align*}\]
Le processus de regroupement s'arrête là, car nous pouvons factoriser\(x^2−9\) en utilisant la formule de différence de carrés.
\[\begin{align*} (x^2-9)(x+1)&= 0\\ (x-3)(x+3)(x+1)&= 0\\ x&= 3\\ x&= -3\\ x&= -1 \end{align*}\]
Les solutions sont\(3\)\(−3\), et\(−1\). Notez que l'exposant le plus élevé est\(3\) et nous avons obtenu\(3\) des solutions. Nous pouvons voir les solutions, les interceptions en X, sur le graphique de la figure\(\PageIndex{2}\).
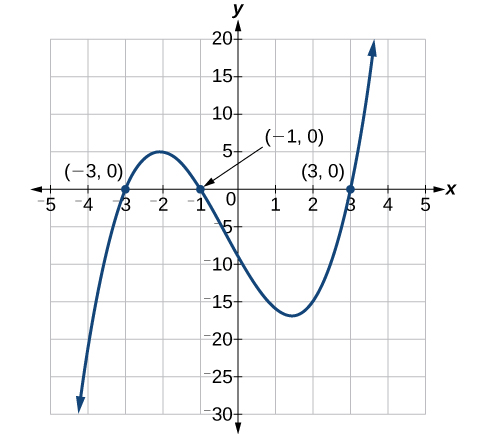
Analyse
Nous avons cherché à résoudre des équations quadratiques en factorisant lorsque le coefficient principal est\(1\). Lorsque le coefficient principal ne l'est pas\(1\), nous avons résolu par regroupement. Le regroupement nécessite quatre termes, que nous avons obtenus en divisant le terme linéaire des équations quadratiques. Nous pouvons également utiliser le regroupement pour certains polynômes de degré supérieur à\(2\), comme nous l'avons vu ici, puisqu'il y avait déjà quatre termes.
Résoudre des équations
Les équations radicales sont des équations qui contiennent des variables dans le radical (expression sous un symbole radical), telles que
\[\sqrt{3x+18}=x \nonumber\]
\[\sqrt{x+3}=x-3 \nonumber\]
\[\sqrt{x+5}-\sqrt{x-3}=2 \nonumber\]
Les équations radicales peuvent comporter un ou plusieurs termes radicaux et sont résolues en éliminant chaque radical, un à la fois. Nous devons être prudents lorsque nous résolvons des équations radicales, car il n'est pas rare de trouver des solutions superflues, des racines qui ne sont pas, en fait, des solutions à l'équation. Ces solutions ne sont pas dues à une erreur dans la méthode de résolution, mais résultent du processus qui consiste à élever les deux côtés d'une équation à une puissance. Cependant, vérifier chaque réponse de l'équation d'origine confirmera les vraies solutions.
Une équation contenant des termes avec une variable dans le radical est appelée équation radicale.
- Isolez l'expression radicale d'un côté du signe égal. Mettez tous les termes restants de l'autre côté.
- Si le radical est une racine carrée, mettez les deux côtés de l'équation au carré. S'il s'agit d'une racine cubique, augmentez les deux côtés de l'équation à la troisième puissance. En d'autres termes, pour un\(n^{th}\) radical radical, portez les deux camps au\(n^{th}\) pouvoir. Cela permet d'éliminer le symbole radical.
- Résolvez l'équation restante.
- S'il reste un terme radical, répétez les étapes 1 à 2.
- Confirmez les solutions en les remplaçant dans l'équation d'origine.
Résoudre\(\sqrt{15−2x}=x\).
Solution
Le radical est déjà isolé sur le côté gauche du côté égal, alors procédez au carré des deux côtés.
\[\begin{align*} \sqrt{15-2x}&= x\\ {\left (\sqrt{15-2x} \right )}^2&= {(x)}^2\\ 15-2x&= x^2 \end{align*}\]
Nous voyons que l'équation restante est quadratique. Réglez-le à zéro et résolvez.
\[\begin{align*} 0&= x^2+2x-15\\ 0&= (x+5)(x-3)\\ x&= -5\\ x&= 3 \end{align*}\]
Les solutions proposées sont\(−5\) et\(3\). Revoyons chaque solution dans l'équation d'origine. Tout d'abord, vérifiez\(x=−5\).
\[\begin{align*} \sqrt{15-2x}&= x\\ \sqrt{15-2(-5)}&=-5\\ \sqrt{25}&= -5\\ 5&\neq -5 \end{align*}\]
Il s'agit d'une solution superflue. Bien qu'aucune erreur n'ait été commise lors de la résolution de l'équation, nous avons trouvé une solution qui ne satisfait pas l'équation initiale.
Vérifiez\(x=3\).
\[\begin{align*} \sqrt{15-2x}&= x\\ \sqrt{15-2(3)}&= 3\\ \sqrt{9}&= 3\\ 3&= 3 \end{align*}\]
La solution est\(3\).
Résolvez l'équation radicale :\(\sqrt{x+3}=3x-1\)
- Réponse
-
\(x=1\), solution étrangère\(x=−\dfrac{2}{9}\)
Résoudre\(\sqrt{2x+3}+\sqrt{x-2}=4\)
Solution
Comme cette équation contient deux radicaux, on isole un radical, on l'élimine, puis on isole le second radical.
\[\sqrt{2x+3}+\sqrt{x-2}=4 \nonumber\]
\[\begin{align*} \sqrt{2x+3}&= 4-\sqrt{x-2} \qquad \text{Subtract } \sqrt{x-2} \text{ from both sides}\\ {\left (\sqrt{2x+3} \right )}^2&= {\left (4-\sqrt{x-2} \right )}^2\qquad \text{Square both sides} \end{align*}\]
Utilisez la formule carrée parfaite pour élargir le côté droit :\({(a−b)}^2=a^2−2ab+b^2\).
\[\begin{align*} 2x+3&= {(4)}^2-2(4)\sqrt{x-2}+{(\sqrt{x-2})}^2\\ 2x+3&= 16-8\sqrt{x-2}+(x-2)\\ 2x+3&= 14+x-8\sqrt{x-2} \qquad \text{Combine like terms}\\ x-11&= -8\sqrt{x-2} \qquad \text{Isolate the second radical}\\ {(x-11)}^2&= {(-8\sqrt{x-2})}^2 \qquad \text{Square both sides}\\ x^2-22x+121&= 64(x-2) \end{align*}\]
Maintenant que les deux radicaux ont été éliminés, réglez le quadratique à zéro et résolvez.
\[\begin{align*} x^2-22x+121&= 64x-128\\ x^2-86x+249&= 0\\ (x-3)(x-83)&= 0\\ x&= 3\\ x&= 83 \end{align*}\]
Les solutions proposées sont\(3\) et\(83\). Vérifiez chaque solution dans l'équation d'origine.
\[\begin{align*} \sqrt{2x+3}+\sqrt{x-2}&= 4\\ \sqrt{2x+3}&= 4-\sqrt{x-2}\\ \sqrt{2(3)+3}&= 4-\sqrt{(3)-2}\\ \sqrt{9}&= 4-\sqrt{1}\\ 3&= 3 \end{align*}\]
Une solution est\(3\).
Vérifiez\(x=83\).
\[\begin{align*} \sqrt{2x+3}+\sqrt{x-2}&= 4\\ \sqrt{2x+3}&= 4-\sqrt{x-2}\\ \sqrt{2(83)+3}&= 4-\sqrt{(83)-2}\\ \sqrt{169}&= 4-\sqrt{81}\\ 13&\neq -5 \end{align*}\]
La seule solution est\(3\). Nous voyons qu'il\(x=83\) s'agit d'une solution superflue.
Résolvez l'équation avec deux radicaux :\(\sqrt{3x+7}+\sqrt{x+2}=1\)
- Réponse
-
\(x=−2\), solution étrangère\(x=−1\)
Résolution d'une équation de valeur absolue
Ensuite, nous allons apprendre comment résoudre une équation de valeur absolue. Pour résoudre une équation telle que\(|2x−6|=8\), nous remarquons que la valeur absolue sera égale à\(8\) si la quantité à l'intérieur des barres de valeurs absolues est\(8\) ou\(−8\). Cela conduit à deux équations différentes que nous pouvons résoudre indépendamment.
\[\begin{align*} 2x-6&= 8\\ 2x&= 14\\ x&= 7 \end{align*}\]
OU
\[\begin{align*} 2x-6&= -8\\ 2x&= -2\\ x&= -1 \end{align*}\]
Il est utile de savoir comment résoudre des problèmes impliquant des fonctions de valeurs absolues. Par exemple, nous pouvons avoir besoin d'identifier des nombres ou des points sur une ligne situés à une distance spécifiée d'un point de référence donné.
La valeur absolue de\(x\) est écrite sous la forme\(|x|\). Il possède les propriétés suivantes :
Si\(x≥0\), alors\(|x|=x\). Si\(x<0\), alors\(x=−x\).
Pour les nombres réels\(A\) et\(B\), une équation de la forme\(|A|=B\), avec\(B≥0\), aura des solutions quand\(A=B\) ou\(A=−B\). Si\(B<0\), l'équation n'\(|A|=B\)a pas de solution.
Une équation de valeur absolue dans le formulaire\(|ax+b|=c\) possède les propriétés suivantes :
- Si\(c<0\), n'\(|ax+b|=c\)a pas de solution.
- Si\(c=0\),\(|ax+b|=c\) a une solution.
- Si\(c>0\),\(|ax+b|=c\) a deux solutions.
À partir d'une équation de valeur absolue, résolvez-la.
- Isolez l'expression de valeur absolue d'un côté du signe égal.
- Si\(c>0\), écrivez et résolvez deux équations :\(ax+b=c\) et\(ax+b=−c\).
Résolvez les équations de valeur absolue suivantes :
- \(|6x+4|=8\)
- \(|3x+4|=−9\)
- \(|3x−5|−4=6\)
- \(|−5x+10|=0\)
Solution
- \(|6x+4|=8\)
Écrivez deux équations et résolvez chacune :
\[\begin{align*} 6x+4&= 8\\ 6x&= 4\\ x&= \dfrac{2}{3} \end{align*}\]
OU
\[\begin{align*} 6x+4&= -8\\ 6x&= -12\\ x&= -2 \end{align*}\]
Les deux solutions sont\(\dfrac{2}{3}\) et\(−2\).
- \(|3x+4|=−9\)
Il n'y a pas de solution car une valeur absolue ne peut pas être négative.
- \(|3x−5|−4=6\)
Isolez l'expression de la valeur absolue, puis écrivez deux équations.
\[\begin{align*} |3x-5|-4&= 6\\ |3x-5|&= 10\\ 3x-5&= 10\\ 3x&= 15\\ x&= 5 \end{align*}\]
OU
\[\begin{align*} 3x-5&= -10\\ 3x=-5\\ x=\dfrac{5}{3} \end{align*}\]
Il existe deux solutions :\(5\), et\(-\dfrac{5}{3}\).
- \(|−5x+10|=0\)
L'équation est fixée à zéro, nous ne devons donc écrire qu'une seule équation.
\[\begin{align*} -5x+10&= 0\\ -5x&= -10\\ x&= 2 \end{align*}\]
Il existe une solution : \ (2 \).
Résolvez l'équation de la valeur absolue :\(|1−4x|+8=13\).
- Réponse
-
\(x=−1, x=\dfrac{3}{2}\)
Résolution d'autres types d'équations
Il existe de nombreux autres types d'équations en plus de celles dont nous avons parlé jusqu'à présent. Nous en verrons d'autres tout au long du texte. Ici, nous allons discuter des équations qui sont sous forme quadratique et des équations rationnelles qui aboutissent à une forme quadratique.
Résolution d'équations sous forme quadratique
Les équations sous forme quadratique sont des équations à trois termes. Le premier terme a un pouvoir autre que\(2\). Le terme moyen possède un exposant qui est la moitié de l'exposant du terme principal. Le troisième terme est une constante. Nous pouvons résoudre des équations sous cette forme comme si elles étaient quadratiques. Quelques exemples de ces équations incluent\(x^4−5x^2+4=0\)\(x^6+7x^3−8=0\), et\(x^{\tfrac{2}{3}} +4x^{\tfrac{1}{3}}+2=0\). Dans chacun d'eux, le fait de doubler l'exposant du terme moyen équivaut à l'exposant du terme principal. Nous pouvons résoudre ces équations en remplaçant le moyen terme par une variable.
Si l'exposant du terme moyen est la moitié de l'exposant du terme principal, nous avons une équation sous forme quadratique, que nous pouvons résoudre comme s'il s'agissait d'une équation quadratique. Nous substituons une variable au moyen terme pour résoudre des équations sous forme quadratique.
- Identifiez l'exposant sur le terme principal et déterminez s'il est le double de l'exposant sur le terme moyen.
- Si tel est le cas, remplacez par une variable\(u\), par exemple, la partie variable du terme moyen.
- Réécrivez l'équation pour qu'elle prenne la forme standard d'un quadratique.
- Résolvez en utilisant l'une des méthodes habituelles pour résoudre un quadratique.
- Remplacez la variable de substitution par le terme d'origine.
- Résolvez l'équation restante.
Résolvez cette équation du quatrième degré :\(3x^4−2x^2−1=0\).
Solution
Cette équation répond au critère principal, à savoir que la puissance sur le terme principal est le double de la puissance sur le moyen terme. Ensuite, nous allons remplacer le terme variable au milieu. Laissez\(u =x^2\). Réécrivez l'équation dans\(u\).
\[3u^2−2u−1=0 \nonumber\]
Maintenant, résolvez le quadratique.
\[\begin{align*} 3u^2-2u-1&= 0\\ (3u+1)(u-1)&= 0 \end{align*}\]
Résolvez chaque facteur et remplacez le terme original pour\(u\).
\[\begin{align*} 3u+1&= 0\\ 3u&= -1\\ u&= -\dfrac{1}{3}\\ x^2&= -\dfrac{1}{3}\\ x&= \pm i\sqrt{\dfrac{1}{3}}\\ u-1&= 0\\ u&= 1\\ x^2&= 1\\ x&= \pm 1 \end{align*}\]
Les solutions sont\(x=±i\sqrt{\dfrac{1}{3}}\) et\(x=±1\)
Résoudre en utilisant la substitution :\(x^4−8x^2−9=0\).
- Réponse
-
\(x=−3,3,−i,i\)
Résolvez l'équation sous forme quadratique :\({(x+2)}^2+11(x+2)−12=0\).
Solution
Cette équation contient un binôme à la place de la variable unique. La tendance est d'élargir ce qui est présenté. Cependant, le fait de reconnaître qu'il répond aux critères d'une forme quadratique fait toute la différence dans le processus de résolution. Tout d'abord, faites une substitution, laissez\(u =x+2\). Réécrivez ensuite l'équation dans\(u\).
\[\begin{align*} u^2+11u-12&= 0\\ (u+12)(u-1)&= 0 \end{align*}\]
Résolvez en utilisant la propriété de facteur zéro, puis\(u\) remplacez-la par l'expression d'origine.
\[\begin{align*} u+12&= 0\\ u&= -12\\ x+2&= -12\\ x&= -14 \end{align*}\]
Le deuxième facteur se traduit par
\[\begin{align*} u-1&= 0\\ u&= 1\\ x+2&= 1\\ x&= -1 \end{align*}\]
Nous avons deux solutions :\(−14\), et\(−1\).
Résoudre :\({(x−5)}^2−4(x−5)−21=0\).
- Réponse
-
\(x=2,x=12\)
Résolution d'équations rationnelles aboutissant à un quadratique
Auparavant, nous avons résolu des équations rationnelles. Parfois, la résolution d'une équation rationnelle aboutit à une équation quadratique. Lorsque cela se produit, nous poursuivons la solution en simplifiant l'équation quadratique par l'une des méthodes que nous avons vues. Il se peut qu'il n'y ait pas de solution.
Résolvez l'équation rationnelle suivante :\(\dfrac{-4x}{x-1}+\dfrac{4}{x+1}=\dfrac{-8}{x^2-1}\)
Solution
Nous voulons que tous les dénominateurs soient pris en compte pour trouver l'écran LCD. Deux des dénominateurs ne peuvent pas être davantage pris en compte. Toutefois,\(x^2−1=(x+1)(x−1)\). Ensuite, l'écran LCD est\((x+1)(x−1)\). Ensuite, nous multiplions l'équation complète par l'écran LCD.
\ [\ begin {align*} (x+1) (x-1) \ left (\ dfrac {-4x} {x-1} + \ dfrac {4} {x+1} \ right) &= \ left (\ dfrac {-8}} {x^2-1} \ right) (x+1) (x-1) \ \ -4x (x+1) +4 (x-1) &= -8 \ \ -4x^2-4x+4x-4&= -8 \ \ -4x^2+4&= 0 \ \
-4 (x^2-1) &= 0 \ \ -4 (x+1) (x+1) (x-1) &= 0 \ \ x&= -1 \ \ x&= 1 \ end {align*} \]
Dans ce cas, l'une ou l'autre des solutions produit un zéro dans le dénominateur de l'équation d'origine. Il n'y a donc pas de solution.
Résoudre\(\dfrac{3x+2}{x-2}+\dfrac{1}{x}=\dfrac{-2}{x^2-2x}\)
- Réponse
-
\(x=−1, x= 0\)n'est pas une solution.
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires avec différents types d'équations.
- Équation rationnelle sans solution
- Résolution d'équations avec des exposants rationnels en utilisant des puissances
- Résolution d'équations radicales, partie 1 de 2
- Résolution d'équations radicales, partie 2 de 2
Concepts clés
- Les exposants rationnels peuvent être réécrits de différentes manières en fonction de ce qui convient le mieux au problème. Pour la résoudre, les deux côtés de l'équation sont élevés à une puissance qui rendra l'exposant de la variable égal à\(1\). Voir Exemple, Exemple et Exemple.
- La factorisation s'étend aux polynômes d'ordre supérieur lorsqu'elle implique de factoriser le GCF ou de factoriser par regroupement. Voir Exemple et Exemple.
- Nous pouvons résoudre des équations radicales en isolant le radical et en élevant les deux côtés de l'équation à une puissance correspondant à l'indice. Voir Exemple et Exemple.
- Pour résoudre des équations de valeur absolue, nous devons écrire deux équations, l'une pour la valeur positive et l'autre pour la valeur négative. Voir l'exemple.
- Les équations sous forme quadratique sont faciles à repérer, car l'exposant du premier terme est le double de l'exposant du deuxième terme et le troisième terme est une constante. Nous pouvons également voir un binôme à la place de la variable unique. Nous utilisons la substitution pour résoudre. Voir Exemple et Exemple.
- La résolution d'une équation rationnelle peut également mener à une équation quadratique ou à une équation sous forme quadratique. Voir l'exemple.


