2.5 : Équations quadratiques
- Page ID
- 195093
- Résolvez des équations quadratiques par factorisation.
- Résolvez des équations quadratiques par la propriété de la racine carrée.
- Résolvez des équations quadratiques en complétant le carré.
- Résolvez des équations quadratiques à l'aide de la formule quadratique.
L'écran d'ordinateur de gauche sur la figure\(\PageIndex{1}\) est un modèle en\(23.6\) pouces et celui de droite est un modèle en\(27\) pouces. Proportionnellement, les moniteurs semblent très similaires. Si l'espace est limité et que nous souhaitons le plus grand écran possible, comment décider lequel choisir ? Dans cette section, nous allons apprendre à résoudre de tels problèmes en utilisant quatre méthodes différentes.

Résolution d'équations quadratiques par factorisation
Une équation contenant un polynôme du second degré est appelée équation quadratique. Par exemple, les équations telles que\(2x^2 +3x−1=0\) et\(x^2−4= 0\) sont des équations quadratiques. Ils sont utilisés de nombreuses manières dans les domaines de l'ingénierie, de l'architecture, de la finance, des sciences biologiques et, bien sûr, des mathématiques.
La méthode la plus simple pour résoudre une équation quadratique est souvent la factorisation. La factorisation consiste à trouver des expressions qui peuvent être multipliées ensemble pour obtenir l'expression d'un côté de l'équation.
Si une équation quadratique peut être factorisée, elle est écrite comme un produit de termes linéaires. La résolution par factorisation dépend de la propriété de produit zéro, qui indique si\(a⋅b=0\), alors\(a = 0\) ou\(b =0\), où a et b sont des nombres réels ou des expressions algébriques. En d'autres termes, si le produit de deux nombres ou de deux expressions est égal à zéro, alors l'un des nombres ou l'une des expressions doit être égal à zéro, car zéro multiplié par quelque chose est égal à zéro.
La multiplication des facteurs permet d'étendre l'équation à une chaîne de termes séparés par des signes plus ou moins. Ainsi, en ce sens, l'opération de multiplication annule l'opération de factorisation. Par exemple, développez l'expression factorielle\((x−2)(x+3)\) en multipliant les deux facteurs ensemble.
\[\begin{align*} (x-2)(x+3)&= x^2+3x-2x-6\\ &= x^2+x-6\\ \end{align*}\]
Le produit est une expression quadratique. Fixé égal à zéro,\(x^2+x−6= 0\) est une équation quadratique. Si nous devions factoriser l'équation, nous retrouverions les facteurs que nous avons multipliés.
Le processus de factorisation d'une équation quadratique dépend du coefficient principal, qu'il s'agisse d'un entier\(1\) ou d'un autre. Nous examinerons les deux situations ; mais d'abord, nous voulons confirmer que l'équation est écrite sous forme standard\(ax^2+bx+c=0\), où\(a\)\(b\), et\(c\) sont des nombres réels, et\(a≠0\). L'équation\(x^2 +x−6= 0\) se présente sous forme standard.
Nous pouvons utiliser la propriété du produit zéro pour résoudre des équations quadratiques dans lesquelles nous devons d'abord factoriser le plus grand facteur commun (GCF), et pour des équations qui ont également des formules de factorisation spéciales, telles que la différence des carrés, que nous verrons plus loin dans cette section.
La propriété « zéro produit » indique
Si\(a⋅b=0\), alors\(a=0\) ou\(b=0\),
où\(a\) et\(b\) sont des nombres réels ou des expressions algébriques.
Une équation quadratique est une équation contenant un polynôme du second degré ; par exemple
\[ax^2+bx+c=0\]
où\(a\)\(b\), et\(c\) sont des nombres réels, et si\(a≠0\), c'est sous forme standard.
Résolution de questions quadratiques avec un coefficient principal de\(1\)
Dans l'équation quadratique\(x^2 +x−6=0\), le coefficient principal, ou coefficient de\(x^2\), est\(1\). Nous avons une méthode pour factoriser les équations quadratiques sous cette forme.
- Trouve deux nombres dont le produit est égal\(c\) et dont la somme est égale\(b\).
- Utilisez ces nombres pour écrire deux facteurs de la forme\((x+k)\) ou\((x−k)\), où k est l'un des nombres trouvés à l'étape 1. Utilisez les chiffres tels qu'ils sont. En d'autres termes, si les deux nombres sont\(1\) et\(−2\), les facteurs le sont\((x+1)(x−2)\).
- Résolvez en utilisant la propriété zero-product en définissant chaque facteur égal à zéro et en résolvant la variable.
Factoriez et résolvez l'équation :\(x^2+x−6=0\).
Solution
Pour factoriser\(x^2 +x−6=0\), nous recherchons deux nombres dont le produit est égal\(−6\) et dont la somme est égale\(1\). Commencez par examiner les facteurs possibles de\(−6\).
\[1⋅(−6) \nonumber \]
\[(−6)⋅1 \nonumber \]
\[2⋅(−3) \nonumber \]
\[3⋅(−2) \nonumber \]
La dernière paire s'\(3⋅(−2)\)additionne à\(1\), donc voici les nombres. Notez qu'une seule paire de chiffres fonctionnera. Ensuite, écrivez les facteurs.
\[(x−2)(x+3)=0 \nonumber \]
Pour résoudre cette équation, nous utilisons la propriété de produit zéro. Définissez chaque facteur égal à zéro et résolvez.
\[\begin{align*} (x-2)(x+3)&= 0\\ (x-2)&= 0\\ x&= 2\\ (x+3)&= 0\\ x&= -3 \end{align*}\]
Les deux solutions sont\(2\) et\(−3\). Nous pouvons voir comment les solutions se rapportent au graphique de la figure\(\PageIndex{2}\). Les solutions sont les interceptions X de\(x^2 +x−6=0\).
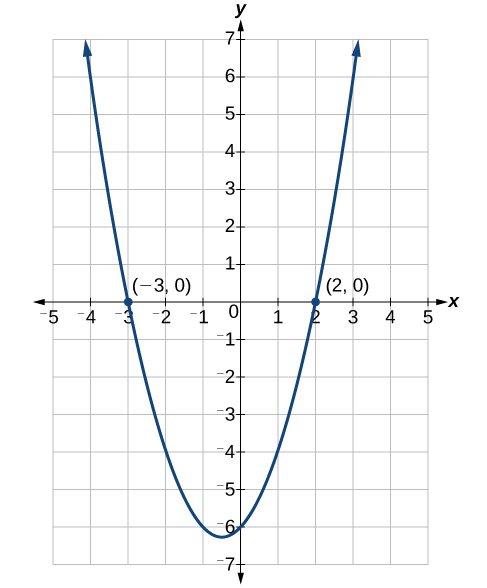
Factoriez et résolvez l'équation quadratique :\(x^2−5x−6=0\).
- Réponse
-
\((x−6)(x+1)=0\),\(x=6\),\(x=−1\)
Résolvez l'équation quadratique en factorisant :\(x^2+8x+15=0\).
Solution
Trouve deux nombres dont le produit est égal\(15\) et dont la somme est égale\(8\). Énumérez les facteurs de\(15\).
\[1⋅15 \nonumber \]
\[3⋅5 \nonumber \]
\[(−1)⋅(−15) \nonumber \]
\[(−3)⋅(−5) \nonumber \]
Les nombres qui s'ajoutent à\(8\) sont\(3\) et\(5\). Ensuite, écrivez les facteurs, définissez chaque facteur sur zéro et résolvez.
\[\begin{align*} (x+3)(x+5)&= 0\\ (x+3)&= 0\\ x&= -3\\ (x+5)&= 0\\ x&= -5 \end{align*}\]
Les solutions sont\(−3\) et\(−5\).
Résolvez l'équation quadratique en factorisant :\(x^2−4x−21=0\).
- Réponse
-
\((x−7)(x+3)=0\),\(x=7\),\(x=−3\)
Résolvez l'équation de différence de carrés à l'aide de la propriété de produit zéro :\(x^2−9=0\).
Solution
Reconnaissant que l'équation représente la différence des carrés, nous pouvons écrire les deux facteurs en prenant la racine carrée de chaque terme, en utilisant un signe moins comme opérateur dans un facteur et un signe plus comme opérateur dans l'autre. Résolvez en utilisant la propriété de facteur zéro.
\[\begin{align*} x^2-9&= 0\\ (x-3)(x+3)&= 0\\ x-3&= 0\\ x&= 3\\ (x+3)&= 0\\ x&= -3 \end{align*}\]
Les solutions sont\(3\) et\(−3\).
Résolvez en affacturant :\(x^2−25=0\).
- Réponse
-
\((x+5)(x−5)=0, x=−5, x=5\)
Factorisation et résolution d'une équation quadratique d'ordre supérieur
Lorsque le coefficient principal ne l'est pas\(1\), nous factorisons une équation quadratique en utilisant la méthode appelée regroupement, qui nécessite quatre termes.
Avec l'équation sous forme standard, passons en revue les procédures de regroupement
- Avec le quadratique sous forme standard\(ax^2+bx+c=0\), multipliez\(a⋅c\).
- Trouve deux nombres dont le produit est égal à ac et dont la somme est égale à\(b\).
- Réécrivez l'équation en remplaçant le\(bx\) terme par deux termes en utilisant les nombres trouvés à l'étape\(1\) comme coefficients de\(x\).
- Facturez les deux premiers termes, puis factorisez les deux derniers termes. Les expressions entre parenthèses doivent être exactement les mêmes pour utiliser le regroupement.
- Éliminez l'expression entre parenthèses.
- Définissez les expressions égales à zéro et résolvez la variable.
Utilisez le regroupement pour factoriser et résoudre l'équation quadratique :\(4x^2+15x+9=0\).
Solution
Multipliez d'abord\(ac:4(9)=36\). Énumérez ensuite les facteurs de\(36\).
\[1⋅36 \nonumber\]
\[2⋅18 \nonumber\]
\[3⋅12 \nonumber\]
\[4⋅9 \nonumber\]
\[6⋅6 \nonumber\]
La seule paire de facteurs qui se résume à\(15\) est\(3+12\). Réécrivez l'équation en remplaçant le terme b\(15x\), par deux termes en utilisant\(3\) et\(12\) comme coefficients de\(x\). Facturez les deux premiers termes, puis factorisez les deux derniers termes.
\[\begin{align*} 4x^2+3x+12x+9&= 0\\ x(4x+3)+3(4x+3)&= 0\\ (4x+3)(x+3)&= 0 \qquad \text{Solve using the zero-product property}\\ (4x+3)&= 3\\ x&= -\dfrac{3}{4}\\ (x+3)&= 0\\ x&= -3 \end{align*}\]
Les solutions sont\(−\dfrac{3}{4}\), et\(−3\). Voir la figure\(\PageIndex{3}\).
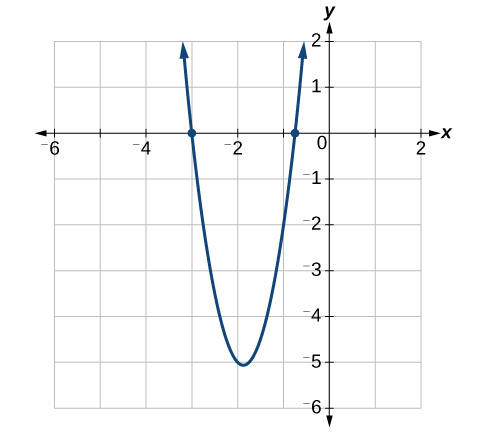
Résolvez en utilisant la factorisation en regroupant :\(12x^2+11x+2=0\).
- Réponse
-
\((3x+2)(4x+1)=0\),\(x=−\dfrac{2}{3}\),\(x=−\dfrac{1}{4}\)
Résolvez l'équation en factorisant :\(−3x^3−5x^2−2x=0\).
Solution
Cette équation ne ressemble pas à une équation quadratique, comme l'est\(3\) la puissance la plus élevée\(2\). N'oubliez pas que la première chose que nous voulons faire pour résoudre une équation est de factoriser le GCF, s'il en existe un. Et c'est le cas ici. Nous pouvons prendre\(−x\) en compte tous les termes, puis procéder au regroupement.
\ [\ begin {align*}
-3x^3-5x^2-2x&= 0 \ \
-x (3x^2+5x+2) &= 0 \ \
-x (3x^2+3x+2x+2) &= 0 \ qquad \ text {Utilisez le regroupement sur l'expression entre parenthèses} \ \
-x [3x (x+1) +2 (x+1)] &= 0 \
--x x (3x+2) (x+1) &= 0 \ \
\ text {Maintenant, nous utilisons la propriété « zéro produit ». Notez que nous avons trois facteurs.} \ \
-x&= 0 \ \
x&= 0 \ \
3x+2&= 0 \ \
x&= - \ dfrac {2} {3} \ \
x+1&= 0 \ \
x&= -1
\ end {align*} \]
Les solutions sont\(0\)\(−\dfrac{2}{3}\), et\(−1\).
Résolvez en affacturant :\(x^3+11x^2+10x=0\).
- Réponse
-
\(x=0, x=−10, x=−1\)
Utilisation de la propriété Square Root
Lorsqu'il n'y a pas de terme linéaire dans l'équation, une autre méthode pour résoudre une équation quadratique consiste à utiliser la propriété de racine carrée, dans laquelle nous isolons le\(x^2\) terme et prenons la racine carrée du nombre situé de l'autre côté du signe égal. Gardez à l'esprit que nous pouvons parfois avoir à manipuler l'équation pour isoler le\(x^2\) terme afin que la propriété de la racine carrée puisse être utilisée.
Avec le\(x^2\) terme isolé, la propriété de racine carrée indique que :
où\(k\) est un nombre réel différent de zéro.
- Isolez le\(x^2\) terme d'un côté du signe égal.
- Prenez la racine carrée des deux côtés de l'équation, en plaçant un\(±\) signe avant l'expression sur le côté opposé au terme carré.
- Simplifiez les chiffres sur le côté avec le\(±\) signe.
Résolvez le quadratique en utilisant la propriété de racine carrée :\(x^2=8\).
Solution
Prenez la racine carrée des deux côtés, puis simplifiez le radical. N'oubliez pas d'utiliser un\(±\) signe avant le symbole radical.
\[\begin{align*} x^2&= 8\\ x&= \pm \sqrt{8}\\ &= \pm 2\sqrt{2} \end{align*}\]
Les solutions sont les suivantes\(2\sqrt{2}\) :\(-2\sqrt{2}\)
Résolvez l'équation quadratique :\(4x^2+1=7\).
Solution
Tout d'abord, isolez le\(x^2\) terme. Prenez ensuite la racine carrée des deux côtés.
\[\begin{align*} 4x^2+1&= 7\\ 4x^2&= 6\\ x^2&= \dfrac{6}{4}\\ x&= \pm \dfrac{\sqrt{6}}{2} \end{align*}\]
Les solutions sont\(\dfrac{\sqrt{6}}{2}\), et\(-\dfrac{\sqrt{6}}{2}\).
Résolvez l'équation quadratique en utilisant la propriété de racine carrée :\(3{(x−4)}^2=15\).
- Réponse
-
\(x=4±\sqrt{5}\)
Compléter le carré
Toutes les équations quadratiques ne peuvent pas être factorisées ou résolues dans leur forme d'origine à l'aide de la propriété de racine carrée. Dans ces cas, nous pouvons utiliser une méthode pour résoudre une équation quadratique appelée complétion du carré. En utilisant cette méthode, nous ajoutons ou soustrayons des termes des deux côtés de l'équation jusqu'à obtenir un trinôme carré parfait sur un côté du signe égal. Nous appliquons ensuite la propriété de racine carrée. Pour compléter le carré, le coefficient principal,\(a\), doit être égal\(1\). Si ce n'est pas le cas, divisez l'ensemble de l'équation par\(a\). Ensuite, nous pouvons utiliser les procédures suivantes pour résoudre une équation quadratique en complétant le carré.
Nous utiliserons l'exemple\(x^2+4x+1=0\) pour illustrer chaque étape.
Étant donné une équation quadratique qui ne peut pas être prise en compte, et avec\(a=1\), first add or subtract the constant term to the right sign of the equal sign.
\ [\ begin {align*}
x^2+4x+1&= 0 \ \
x^2+4x&= -1 \ qquad \ text {Multipliez le terme b} \ text {par} \ dfrac {1} {2} \ text {et mettez-le au carré.} \ \
\ dfrac {1} {2} (4) &= 2 \ \
2^2&= 4 \ qquad \ text {Add} \ left ({\ dfrac {1} {2}} \ right) ^2 \ text {des deux côtés du signe égal et simplifiez le côté droit. Nous avons} \ \
x^2+4x+4&= -1+4 \ \
x^2+4x+4&= 3 \ qquad \ text {Le côté gauche de l'équation peut désormais être considéré comme un carré parfait.} \ \
{(x+2)} ^2&=3 \ \
\ sqrt {{(x+2)} ^2} &= \ pm \ sqrt {3} \ qquad \ text {Utilisez la propriété de racine carrée et résolvez.} \ \
\ sqrt {{(x+2)} ^2} &= \ pm \ sqrt {3} \ \
x+2&= \ pm \ sqrt {3} \ \
x&= -2 \ pm \ sqrt {3}
\ end {align*} \]
Les solutions sont\(−2+\sqrt{3}\), et\(−2−\sqrt{3}\).
Résolvez l'équation quadratique en complétant le carré :\(x^2−3x−5=0\).
Solution
Déplacez d'abord le terme constant vers la droite du signe égal.
\ [\ begin {align*}
x^2-3x&= 5 \ qquad \ text {Ensuite, prenez} \ dfrac {1} {2} \ text {du terme b et mettez-le au carré.} \ \
\ dfrac {1} {2} (-3) &= - \ dfrac {3} {2} \ \ {\ left (- \ dfrac
{3} {2} \ right)} ^2= \ dfrac {9} {4} \ \ x^2-3x+ {\ left (- \ dfrac {3} {2} \ right)}
^2&= 5x^2-3x+ {\ left (- \ dfrac {3} {2} \ right)} ^2&= 5x^3x+ {\ left (- \ dfrac {3} {\ left (- \ dfrac {3} {2} \ right)} ^2 \ qquad \ text {Ajoutez le résultat des deux côtés du signe égal.} \ \
x^2-3x+ \ dfrac {9} {4} &= 5+ \ dfrac {9} {4} \ \
\ text {Considérez le côté gauche comme un carré parfait et simplifiez le côté droit.} \ \
{\ left (x- \ dfrac {3} {2} \ right)} ^2&= \ dfrac {29} {4} \ \
(x- \ dfrac {3} {2}) &= \ pm \ dfrac {\ sqrt {29}} {2} \ qquad \ text {Utilisez la propriété de racine carrée et résolvez.} \ \
x&= \ dfrac {3} {2} \ pm \ dfrac {\ sqrt {29}} {2} \ \
\ end {align*} \]
Les solutions sont\(\dfrac{3}{2}+\dfrac{\sqrt{29}}{2}\), et\(\dfrac{3}{2}-\dfrac{\sqrt{29}}{2}\)
Résolvez en complétant le carré :\(x^2−6x=13\).
- Réponse
-
\(x=3±\sqrt{22}\)
Utilisation de la formule quadratique
La quatrième méthode pour résoudre une équation quadratique consiste à utiliser la formule quadratique, une formule qui résoudra toutes les équations quadratiques. Bien que la formule quadratique fonctionne sur n'importe quelle équation quadratique sous forme standard, il est facile de faire des erreurs en substituant les valeurs dans la formule. Faites très attention lors de la substitution et utilisez des parenthèses lorsque vous insérez un nombre négatif.
Nous pouvons obtenir la formule quadratique en complétant le carré. Nous supposerons que le coefficient principal est positif ; s'il est négatif, nous pouvons multiplier l'équation par\(−1\) et obtenir un a. Étant donné\(ax^2+bx+c=0, a≠0\), nous allons compléter le carré comme suit :
Déplacez d'abord le terme constant vers la droite du signe égal :
\[ax^2+bx=−c \nonumber \]
Comme nous voulons que le coefficient principal soit égal\(1\), divisez par\(a\) :
\[x^2+\dfrac{b}{a}x=−\dfrac{c}{a} \nonumber \]
Ensuite, trouvez\(\dfrac{1}{2}\) le terme moyen et ajoutez-le\({(\dfrac{1}{2}\dfrac{b}{a})}^2=\dfrac{b^2}{4a^2}\) des deux côtés du signe égal :
\[x^2+\dfrac{b}{a}x+\dfrac{b^2}{4a^2}=\dfrac{b^2}{4a^2}-\dfrac{c}{a} \nonumber \]
Ensuite, écrivez le côté gauche comme un carré parfait. Trouvez le dénominateur commun du côté droit et écrivez-le sous la forme d'une fraction unique :
\[{(x+\dfrac{b}{2a})}^2=\dfrac{b^2-4ac}{4a^2} \nonumber \]
Maintenant, utilisez la propriété de racine carrée, qui donne
\[x+\dfrac{b}{2a}=±\sqrt{\dfrac{b^2-4ac}{4a^2}} \nonumber \]
\[x+\dfrac{b}{2a}=\dfrac{±\sqrt{b^2-4ac}}{2a} \nonumber \]
Enfin, ajoutez\(-\dfrac{b}{2a}\) les deux côtés de l'équation et combinez les termes du côté droit. Ainsi,
\[x=\dfrac{-b±\sqrt{b^2-4ac}}{2a} \nonumber \]
Écrite sous forme standard\(ax^2+bx+c=0\), n'importe quelle équation quadratique peut être résolue à l'aide de la formule quadratique :
\[x=\dfrac{-b±\sqrt{b^2-4ac}}{2a}\]où\(a\)\(b\), et\(c\) sont des nombres réels et\(a≠0\).
Étant donné une équation quadratique, résolvez-la à l'aide de la formule quadratique
- Assurez-vous que l'équation est sous forme standard :\(ax^2+bx+c=0\).
- Prenez note des valeurs des coefficients et du terme constant,\(a\),\(b\), et\(c\).
- Remplacez soigneusement les valeurs indiquées à l'étape 2 dans l'équation. Pour éviter des erreurs inutiles, placez des parenthèses autour de chaque nombre saisi dans la formule.
- Calculez et résolvez.
Résolvez l'équation quadratique :\(x^2+5x+1=0\).
Solution
Identifiez les coefficients :\(a=1,b=5,c=1\). Utilisez ensuite la formule quadratique.
\[\begin{align*} x&= \dfrac{-(5) \pm \sqrt{(5)^2-4(1)(1)}}{2(1)}\\ &= \dfrac{-5 \pm \sqrt{25-4}}{2}\\ &= \dfrac{-5 \pm \sqrt{21}}{2} \end{align*}\]
Utilisez la formule quadratique pour résoudre\(x^2+x+2=0\).
Solution
Tout d'abord, nous identifions les coefficients :\(a=1\)\(b=1\),, et\(c=2\).
Substituez ces valeurs dans la formule quadratique.
\[\begin{align*} x&= \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}\\ &= \dfrac{-(1) \pm \sqrt{(1)^2-4(1)(2)}}{2(1)}\\ &= \dfrac{-1 \pm \sqrt{1-8}}{2}\\ &= \dfrac{-1 \pm \sqrt{-7}}{2}\\ &= \dfrac{-1 \pm i\sqrt{7}}{2} \end{align*}\]
Résolvez l'équation quadratique à l'aide de la formule quadratique :\(9x^2+3x−2=0\).
- Réponse
-
\(x=-\dfrac{2}{3},x=\dfrac{1}{3}\)
Le discriminant
La formule quadratique génère non seulement les solutions d'une équation quadratique, mais elle nous renseigne sur la nature des solutions lorsque nous considérons le discriminant, ou l'expression sous le radical\(b^2−4ac\). Le discriminant nous indique si les solutions sont des nombres réels ou des nombres complexes, et combien de solutions de chaque type sont attendues. Le\(\PageIndex{1}\) tableau met en relation la valeur du discriminant aux solutions d'une équation quadratique.
| Valeur du discriminant | Résultats |
|---|---|
| \(b^2−4ac=0\) | Une solution rationnelle (solution double) |
| \(b^2−4ac>0\), carré parfait | Deux solutions rationnelles |
| \(b^2−4ac>0\), ce n'est pas un carré parfait | Deux solutions irrationnelles |
| \(b^2−4ac<0\) | Deux solutions complexes |
Car\(ax^2+bx+c=0\), où\(a\)\(b\), et\(c\) sont des nombres réels, le discriminant est l'expression sous le radical dans la formule quadratique :\(b^2−4ac\). Il nous indique si les solutions sont des nombres réels ou des nombres complexes et combien de solutions de chaque type sont attendues.
Utilisez le discriminant pour déterminer la nature des solutions aux équations quadratiques suivantes :
- \(x^2+4x+4=0\)
- \(8x^2+14x+3=0\)
- \(3x^2−5x−2=0\)
- \(3x^2−10x+15=0\)
Solution
Calculez le discriminant\(b^2−4ac\) pour chaque équation et indiquez le type de solution attendu.
un.
\(x^2+4x+4=0\)
\(b^2-4ac={(4)}^2-4(1)(4)=0\)Il y aura une double solution rationnelle.
b.
\(8x^2+14x+3=0\)
\(b^2-4ac={(14)}^2-4(8)(3)=100\)Comme\(100\) c'est le cas pour un carré parfait, il y aura deux solutions rationnelles.
c.
\(3x^2−5x−2=0\)
\(b^2-4ac={(-5)}^2-4(3)(-2)=49\)Comme\(49\) c'est le cas pour un carré parfait, il y aura deux solutions rationnelles.
d.
\(3x^2−10x+15=0\)
\(b^2-4ac={(-10)}^2-4(3)(15)=-80\)Il y aura deux solutions complexes.
Utilisation du théorème de Pythagore
L'une des formules les plus connues en mathématiques est le théorème de Pythagore. Il est basé sur un triangle droit et indique la relation entre les longueurs des côtés comme\(a^2+b^2=c^2\), où\(a\) et\(b\) se réfère aux jambes d'un triangle droit adjacent à l'\(90°\)angle, et\(c\) fait référence à l'hypoténuse. Il a des utilisations incommensurables en architecture, en ingénierie, en sciences, en géométrie, en trigonométrie et en algèbre, ainsi que dans des applications quotidiennes.
Nous utilisons le théorème de Pythagore pour déterminer la longueur d'un côté d'un triangle lorsque nous avons la longueur des deux autres. Comme chacun des termes est quadratique dans le théorème, lorsque nous résolvons pour un côté d'un triangle, nous avons une équation quadratique. Nous pouvons utiliser les méthodes de résolution d'équations quadratiques que nous avons apprises dans cette section pour résoudre le côté manquant.
Le théorème de Pythagore est donné comme
\[a^2+b^2=c^2\]
où\(a\) et\(b\) se réfèrent aux jambes d'un triangle droit adjacent à l'\(90°\)angle, et\(c\) fait référence à l'hypoténuse, comme indiqué dans.
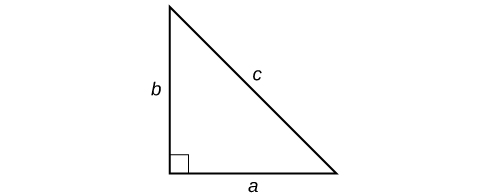
Déterminez la longueur du côté manquant du triangle droit dans la figure\(\PageIndex{5}\).
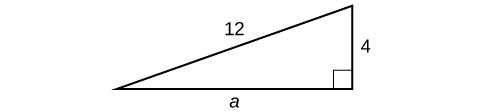
Solution
Comme nous avons des mesures pour le côté\(b\) et l'hypoténuse, le côté manquant l'est\(a\).
\[\begin{align*} a^2+b^2&= c^2\\ a^2+{(4)}^2&= {(12)}^2\\ a^2+16&= 144\\ a^2&= 128\\ a&= \sqrt{128}\\ &= 8\sqrt{2} \end{align*}\]
Utilisez le théorème de Pythagore pour résoudre le problème du triangle droit : la jambe a mesure 4 unités, la jambe b mesure 3 unités. Détermine la longueur de l'hypoténuse.
- Réponse
-
\(5\)unités
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur les équations quadratiques.
- Résolution d'équations quadratiques par factorisation
- La propriété « zéro produit »
- Compléter le carré
- Formule quadratique avec deux solutions rationnelles
- Longueur de la jambe d'un triangle droit
Équations clés
| formule quadratique | \(x=\dfrac{−b±\sqrt{b^2-4ac}}{2a}\) |
Concepts clés
- De nombreuses équations quadratiques peuvent être résolues par factorisation lorsque l'équation a un coefficient principal de\(1\) ou si l'équation est une différence de carrés. La propriété de facteur zéro est ensuite utilisée pour trouver des solutions. Voir Exemple, Exemple et Exemple.
- De nombreuses équations quadratiques avec un coefficient principal autre que celui\(1\) peuvent être résolues par factorisation à l'aide de la méthode de regroupement. Voir Exemple et Exemple.
- Une autre méthode pour résoudre les quadratiques est la propriété de la racine carrée. La variable est au carré. Nous isolons le terme carré et prenons la racine carrée des deux côtés de l'équation. La solution produira une solution positive et une solution négative. Voir Exemple et Exemple.
- Compléter le carré est une méthode qui permet de résoudre des équations quadratiques lorsque l'équation ne peut pas être factorisée. Voir l'exemple.
- Une méthode très fiable pour résoudre des équations quadratiques est la formule quadratique, basée sur les coefficients et le terme constant de l'équation. Voir l'exemple.
- Le discriminant est utilisé pour indiquer la nature des racines que l'équation quadratique produira : réelles ou complexes, rationnelles ou irrationnelles, et combien de racines chacune d'entre elles. Voir l'exemple.
- Le théorème de Pythagore, l'un des plus célèbres théorèmes de l'histoire, est utilisé pour résoudre les problèmes du triangle droit et a des applications dans de nombreux domaines. Pour déterminer la longueur d'un côté d'un triangle droit, il faut résoudre une équation quadratique. Voir l'exemple.


