1.5 : Factorisation des polynômes
- Page ID
- 195295
Dans cette section, les étudiants vont :
- Facteur le plus grand facteur commun d'un polynôme.
- Facteur un trinôme.
- Facteur par regroupement.
- Optez pour un trinôme carré parfait.
- Facturez une différence de carrés.
- Facturez la somme et la différence des cubes.
- Expressions factorielles utilisant des exposants fractionnaires ou négatifs.
Imaginez que nous essayions de trouver la superficie d'une pelouse afin de déterminer la quantité de semences de gazon à acheter. La pelouse est la partie verte de la figure\(\PageIndex{1}\).
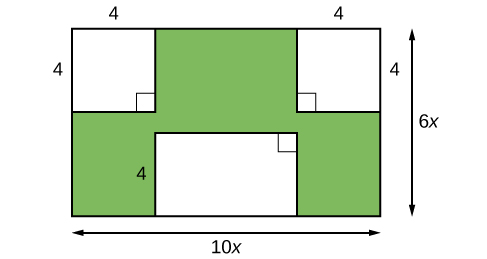
L'aire de la région entière peut être déterminée à l'aide de la formule de l'aire d'un rectangle.
\[\begin{align*} A &= lw\\ &= 10x\times6x\\ &= 60x^2\; units^2 \end{align*}\]
Les surfaces des parties qui ne nécessitent pas de semences de gazon doivent être soustraites de la superficie de la région entière. Les deux régions carrées ont chacune une superficie de\(A =s^2=4^2= 16\; units^2\). L'autre région rectangulaire possède un côté de longueur\(10x−8\) et un côté de longueur\(4\), ce qui donne une surface de
\[A =lw=4(10x−8)=40x−32\; \text{units}^2. \nonumber\]
Ainsi, la région qui doit être soustraite a une superficie de
\[2(16)+40x−32= 40x\; \text{units}^2. \nonumber\]
La superficie de la région qui a besoin de semences de gazon est déterminée par soustraction\(60x^2−40x\; \text{units}^2\). Cette zone peut également être exprimée sous forme factorielle comme\(20x (3x−2)\; \text{units}^2\). Nous pouvons confirmer qu'il s'agit d'une expression équivalente en la multipliant.
De nombreuses expressions polynomiales peuvent être écrites sous des formes plus simples par factorisation. Dans cette section, nous allons examiner diverses méthodes qui peuvent être utilisées pour factoriser les expressions polynomiales.
Factorisation du plus grand facteur commun d'un polynôme
Lorsque nous étudions des fractions, nous apprenons que le plus grand facteur commun (GCF) de deux nombres est le plus grand nombre qui se divise uniformément en deux nombres. Par exemple,\(4\) le GCF de\(16\) et\(20\) parce que c'est le plus grand nombre qui se divise uniformément en deux\(16\) et\(20\) Le FBC des polynômes fonctionne de la même manière :\(4x\) est le GCF de\(16x\) et\(20x^2\) parce que c'est le plus grand polynôme qui se divise uniformément à la fois\(16x\) et\(20x^2\).
Lors de la factorisation d'une expression polynomiale, notre première étape doit être de vérifier la présence d'un GCF. Recherchez le GCF des coefficients, puis le GCF des variables.
Le plus grand facteur commun (GCF) des polynômes est le plus grand polynôme qui se divise uniformément en polynômes.
- Identifiez le GCF des coefficients.
- Identifiez le GCF des variables.
- Combinez pour trouver le GCF de l'expression.
- Déterminez par quoi le GCF doit être multiplié pour obtenir chaque terme de l'expression.
- Écrivez l'expression factorielle comme le produit du GCF et de la somme des termes par lesquels nous devons multiplier.
Facteur\(6x^3y^3 +45x^2y^2+21xy\).
Solution
Déterminez d'abord le GCF de l'expression. Le GCF de\(6\)\(45\), et\(21\) est\(3\). Le GCF de\(x^3\)\(x^2\), et\(x\) est\(x\). (Notez que le GCF d'un ensemble d'expressions du formulaire\(x^n\) sera toujours l'exposant du degré le plus bas.) Et le GCF de\(y^3\)\(y^2\), et\(y\) est\(y\). Combinez-les pour trouver le GCF du polynôme,\(3xy\).
Ensuite, déterminez par quoi le GCF doit être multiplié pour obtenir chaque terme du polynôme. Nous constatons que
- \(3xy(2x^2y^2)=6x^3y^3\),
- \(3xy(15xy)=45x^2y^2\), et
- \(3xy(7)=21xy\).
Enfin, écrivez l'expression factorielle comme le produit du GCF et de la somme des termes par lesquels nous avons dû multiplier.
\[(3xy)(2x^2y^2+15xy+7) \nonumber\]
Analyse
Après affacturage, nous pouvons vérifier notre travail en multipliant. Utilisez la propriété distributive pour confirmer que
\[(3xy)(2x^2y^2+15xy+7)=6x^3y^3+45x^2y^2+21xy \nonumber\]
\(x(b^2−a)+6(b^2−a)\)Tenez compte en retirant le GCF.
- Réponse
-
\((b^2−a)(x+6)\)
Factorisation d'un trinôme avec le coefficient principal 1
Bien que nous devions toujours commencer par rechercher un GCF, extraire le GCF n'est pas le seul moyen de factoriser les expressions polynomiales. Le polynôme\(x^2+5x+6\) a un GCF de\(1\), mais il peut être écrit comme le produit des facteurs\((x+2)\) et\((x+3)\).
Les trinômes de la forme\(x^2+bx+c\) peuvent être factorisés en trouvant deux nombres avec un produit de\(c\) et une somme de\(b\). Le trinôme\(x^2+10x+16\), par exemple, peut être factorisé à l'aide des nombres\(2\) et\(8\) parce que le produit de ces nombres est\(16\) et leur somme est\(10\). Le trinôme peut être réécrit comme le produit de\((x+2)\) et\((x+8)\).
Un trinôme du formulaire\(x^2+bx+c\) peut être écrit sous forme\((x+p)(x+q)\) factorielle comme où\(pq=c\) et\(p+q=b\).
Non. Certains polynômes ne peuvent pas être pris en compte. Ces polynômes sont considérés comme premiers.
- Énumérer les facteurs de\(c\).
- Trouvez\(p\) et\(q\), une paire de facteurs\(c\) avec une somme de\(b\).
- Écrivez l'expression factorisée\((x+p)(x+q)\).
Facteur\(x^2+2x−15\).
Solution
Nous avons un trinôme avec un coefficient principal\(1\)\(b=2\), et\(c=−15\). Nous devons trouver deux nombres avec un produit\(−15\) et une somme de\(2\). Dans le tableau\(\PageIndex{1}\), nous listons les facteurs jusqu'à ce que nous trouvions une paire avec la somme souhaitée.
| Facteurs de −15 | Somme des facteurs |
|---|---|
| 1, −15 | −14 |
| −1,15 | 14 |
| 3, −5 | −2 |
| −3,5 |
Maintenant que nous avons identifié\(p\) et\(q\) comme\(−3\) et\(5\), écrivez le formulaire factorisé comme\((x−3)(x+5)\).
Analyse
Nous pouvons vérifier notre travail en multipliant. Utilisez FOIL pour le confirmer\((x−3)(x+5)=x^2+2x−15\).
Non. La multiplication étant commutative, l'ordre des facteurs n'a pas d'importance.
Facteur\(x^2−7x+6\).
- Réponse
-
\((x−6)(x−1)\)
Affacturage par regroupement
Les trinômes dont les coefficients principaux sont autres que ceux qui\(1\) sont légèrement plus compliqués à factoriser. Pour ces trinômes, nous pouvons factoriser par regroupement en divisant le terme x en la somme de deux termes, en factorisant chaque partie de l'expression séparément, puis en factorisant le GCF de l'expression entière. Le trinôme\(2x^2+5x+3\) peut être réécrit en\((2x+3)(x+1)\) utilisant ce processus. Nous commençons par réécrire l'expression d'origine au fur\(2x^2+2x+3x+3\) et à mesure, puis nous factorisons chaque partie de l'expression pour obtenir\(2x(x+1)+3(x+1)\). Nous extrayons ensuite le GCF de\((x+1)\) pour trouver l'expression factorisée.
Pour factoriser un trinôme dans la forme\(ax^2+bx+c\) par regroupement, nous trouvons deux nombres avec un produit\(ac\) et une somme de\(b\). Nous utilisons ces nombres pour diviser le\(x\) terme en la somme de deux termes et factoriser chaque partie de l'expression séparément, puis soustraire le GCF de l'expression entière.
- Énumérer les facteurs de\(ac\).
- Trouvez\(p\) et\(q\), une paire de facteurs\(ac\) avec une somme de\(b\).
- Réécrivez l'expression d'origine en tant que\(ax^2+px+qx+c\).
- Retirez le GCF de\(ax^2+px\).
- Retirez le GCF de\(qx+c\).
- Tenez compte du GCF de l'expression.
Facteur\(5x^2+7x−6\) par regroupement.
Solution
Nous avons un trinôme avec\(a=5\)\(b=7\), et\(c=−6\). Tout d'abord, déterminez\(ac=−30\). Nous devons trouver deux nombres avec un produit\(−30\) et une somme de\(7\). Dans le tableau ci-dessous, nous listons les facteurs jusqu'à ce que nous trouvions une paire avec la somme souhaitée.
| Facteurs de −30 | Somme des facteurs |
|---|---|
| 1, −30 | −29 |
| −1,30 | 29 |
| 2, −15 | −13 |
| −2,15 | 13 |
| 3, −10 | −7 |
| −3,10 | 7 |
Donc\(p=−3\) et\(q=10\).
\(5x^2−3x+10x−6\)Réécrivez l'expression d'origine en tant que\(ax^2+px+qx+c\).
\(x(5x−3)+2(5x−3)\)Tenez compte du GCF de chaque pièce
\((5x−3)(x+2)\)Tenez compte du GCF de l'expression.
Analyse
Nous pouvons vérifier notre travail en multipliant. Utilisez FOIL pour le confirmer\((5x−3)(x+2)=5x^2+7x−6\).
Facteur :
- \(2x^2+9x+9\)
- \(6x^2+x−1\)
- Répondez à
-
\((2x+3)(x+3)\)
- Réponse b
-
\((3x-1)(2x+1)\)
Factorisation d'un trinôme carré parfait
Un trinôme carré parfait est un trinôme qui peut être écrit comme le carré d'un binôme. Rappelons que lorsqu'un binôme est mis au carré, le résultat est le carré du premier terme ajouté au double du produit des deux termes et du carré du dernier terme.
\[a^2+2ab+b^2={(a+b)}^2\]
et
\[a^2-2ab+b^2={(a-b)}^2\]
Nous pouvons utiliser cette équation pour factoriser n'importe quel trinôme carré parfait.
Un trinôme carré parfait peut s'écrire comme le carré d'un binôme :
\[a^2+2ab+b^2=(a+b)^2\]
- Confirmez que le premier et le dernier terme sont des carrés parfaits.
- Confirmez que le moyen terme est le double du produit de\(ab\).
- Écrivez le formulaire factoriel sous la forme\({(a+b)}^2\).
Facteur\(25x^2+20x+4\).
Solution
Remarquez que\(25x^2\) et ce\(4\) sont des carrés parfaits car\(25x^2={(5x)}^2\) et\(4=2^2\). Vérifiez ensuite si le moyen terme est le double du produit de\(5x\) et\(2\). Le moyen terme est, en effet, le double du produit :\(2(5x)(2)=20x\). Par conséquent, le trinôme est un trinôme carré parfait et peut être écrit sous la forme\({(5x+2)}^2\).
Facteur\(49x^2−14x+1\).
- Réponse
-
\({(7x−1)}^2\)
Factorisation d'une différence de carrés
Une différence de carrés est un carré parfait soustrait d'un carré parfait. Rappelez-vous qu'une différence de carrés peut être réécrite sous forme de facteurs contenant les mêmes termes mais des signes opposés, car les termes du milieu s'annulent lorsque les deux facteurs sont multipliés.
\[a^2−b^2=(a+b)(a−b)\]
Nous pouvons utiliser cette équation pour factoriser les différences entre les carrés.
Une différence de carrés peut être réécrite sous la forme de deux facteurs contenant les mêmes termes mais des signes opposés.
\[a^2−b^2=(a+b)(a−b)\]
- Confirmez que le premier et le dernier terme sont des carrés parfaits.
- Écrivez le formulaire factoriel sous la forme\((a+b)(a−b)\).
Facteur\(9x^2−25\).
Solution
Remarquez que\(9x^2\) et ce\(25\) sont des carrés parfaits car\(9x^2={(3x)}^2\) et\(25=5^2\). Le polynôme représente une différence de carrés et peut être réécrit comme\((3x+5)(3x−5)\).
Facteur\(81y^2−100\).
- Réponse
-
\((9y+10)(9y−10)\)
Non. La somme des carrés ne peut pas être factorisée.
Factorisation de la somme et de la différence des cubes
Nous allons maintenant examiner deux nouveaux produits spéciaux : la somme et la différence des cubes. Bien que la somme des carrés ne puisse pas être factorisée, la somme des cubes peut être factorisée dans un binôme et un trinôme.
\[a^3+b^3=(a+b)(a^2−ab+b^2)\]
De même, la somme des cubes peut être prise en compte dans un binôme et un trinôme, mais avec des signes différents.
\[a^3−b^3=(a−b)(a^2+ab+b^2)\]
Nous pouvons utiliser l'acronyme SOAP pour mémoriser les signes lors de la factorisation de la somme ou de la différence de cubes. La première lettre de chaque mot se rapporte aux signes : Même opposé, toujours positif. Prenons l'exemple suivant, par exemple.
\[x^3−2^3=(x−2)(x^2+2x+4)\]
Le signe des 2 premiers est le même que le signe entre\(x^3−2^3\). Le signe du\(2x\) terme est opposé au signe entre\(x^3−2^3\). Et le signe du dernier mandat est toujours positif.\(4\)
Nous pouvons factoriser la somme de deux cubes comme
\[a^3+b^3=(a+b)(a^2−ab+b^2)\]Nous pouvons prendre en compte la différence entre deux cubes comme suit :
\[a^3−b^3=(a−b)(a^2+ab+b^2)\]
- Vérifiez que le premier et le dernier terme sont des cubes,\(a^3+b^3\) ou\(a^3−b^3\).
- Pour obtenir une somme de cubes, écrivez la forme factorielle sous la forme\((a+b)(a^2−ab+b^2)\). Pour une différence de cubes, écrivez la forme factorielle sous la forme\((a−b)(a^2+ab+b^2)\).
Facteur\(x^3+512\).
Solution
Remarquez cela\(x^3\) et ce\(512\) sont des cubes parce que\(8^3=512\). Réécrivez la somme des cubes comme suit\((x+8)(x^2−8x+64)\) :
Analyse
Après avoir écrit la somme des cubes de cette façon, nous pourrions penser que nous devrions vérifier si la partie trinomiale peut être davantage prise en compte. Cependant, la partie trinomiale ne peut pas être prise en compte, nous n'avons donc pas besoin de vérifier.
Facteur la somme des cubes :\(216a^3+b^3\).
- Réponse
-
\((6a+b)(36a^2−6ab+b^2)\)
Facteur\(8x^3−125\).
Solution
Remarquez que\(8x^3\) et ce\(125\) sont des cubes parce que\(8x^3={(2x)}^3\) et\(125=5^3\). Écrivez la différence des cubes comme suit\((2x−5)(4x^2+10x+25)\) :
Analyse
Tout comme pour la somme des cubes, nous ne serons pas en mesure de factoriser davantage la partie trinomiale.
Tenez compte de la différence entre les cubes :\(1000x^3−1\)
- Réponse
-
\((10x−1)(100x^2+10x+1)\)
Factorisation d'expressions avec des exposants fractionnaires ou négatifs
Les expressions avec des exposants fractionnaires ou négatifs peuvent être factorisées en extrayant un GCF. Recherchez la variable ou l'exposant commun à chaque terme de l'expression et extrayez cette variable ou cet exposant porté à la puissance la plus faible. Ces expressions suivent les mêmes règles de factorisation que celles utilisant des exposants entiers. Par exemple,\(2x^{\tfrac{1}{4}}+5x^{\tfrac{3}{4}}\) peut être pris en compte en retirant\(x^{\tfrac{1}{4}}\) et en étant réécrit comme\(x^{\tfrac{1}{4}}(2+5x^{\tfrac{1}{2}})\).
Facteur\(3x{(x+2)}^{-\tfrac{1}{3}}+4{(x+2)}^{\tfrac{2}{3}}\).
Solution
Facturez le terme dont la valeur de l'exposant est la plus faible. Dans ce cas, ce serait le cas\({(x+2)}^{-\tfrac{1}{3}}\).
\[\begin{align*} &(x+2)^{-\tfrac{1}{3}}(3x+4(x+2))\qquad \text{Factor out the GCF }\\ &(x+2)^{-\tfrac{1}{3}}(3x+4x+8)\qquad \text{Simplify } \\ &(x+2)^{-\tfrac{1}{3}}(7x+8) \end{align*}\]
Facteur\(2{(5a−1)}^{\tfrac{3}{4}}+7a{(5a−1)}^{−\tfrac{1}{4}}\).
- Réponse
-
\({(5a−1)}^{−\tfrac{1}{4}}(17a−2)\)
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur la factorisation des polynômes.
2. Facteur : trinômes lorsque a est égal à 1
Équations clés
| différence de carrés | \(a^2−b^2=(a+b)(a−b)\) |
| trinôme carré parfait | \(a^2+2ab+b^2=(a+b)^2\) |
| somme de cubes | \(a^3+b^3=(a+b)(a^2−ab+b^2)\) |
| différence de cubes | \(a^3−b^3=(a−b)(a^2+ab+b^2)\) |
- Le plus grand facteur commun, ou GCF, peut être factorisé à partir d'un polynôme. La vérification d'un GCF devrait être la première étape de tout problème d'affacturage. Voir l'exemple.
- Les trinômes dont le coefficient principal est 1 peuvent être factorisés en trouvant des nombres dont le produit est le troisième terme et la somme du deuxième terme. Voir l'exemple.
- Les trinômes peuvent être factorisés à l'aide d'un processus appelé affacturage par regroupement. Voir l'exemple.
- Les trinômes carrés parfaits et la différence des carrés sont des produits spéciaux qui peuvent être factorisés à l'aide d'équations. Voir Exemple et Exemple.
- La somme des cubes et la différence entre les cubes peuvent être factoriées à l'aide d'équations. Voir Exemple et Exemple.
- Les polynômes contenant des exposants fractionnaires et négatifs peuvent être factorisés en extrayant un GCF. Voir l'exemple.


