1.4 : Polynômes
- Page ID
- 195323
Dans cette section, les étudiants vont :
- Identifiez le degré et le coefficient principal des polynômes.
- Additionnez et soustrayez des polynômes.
- Multipliez les polynômes.
- Utilisez FOIL pour multiplier les binômes.
- Réaliser des opérations avec une polynomie
- ls contient plusieurs variables.
Earl construit une niche dont la façade a la forme d'un carré surmonté d'un triangle. Il y aura une porte rectangulaire par laquelle le chien pourra entrer et sortir de la maison. Earl veut trouver la zone de la façade de la niche afin de pouvoir acheter la bonne quantité de peinture. À l'aide des mesures de la façade de la maison, illustrées dans la figure\(\PageIndex{1}\), nous pouvons créer une expression qui combine plusieurs termes variables, ce qui nous permet de résoudre ce problème et d'autres problèmes similaires.
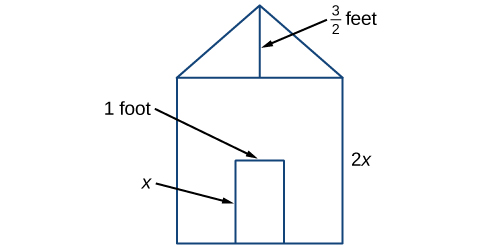
- Trouvez d'abord la superficie du carré en pieds carrés.
\[\begin{align*} A &= s^2\\ &= {(2x)}^2\\ &= 4x^2 \end{align*}\]
- Trouvez ensuite l'aire du triangle en pieds carrés.
\[\begin{align*} A &= \dfrac{1}{2}bh\\ &= \dfrac{1}{2}(2x)\left (\dfrac{3}{2} \right )\\ &= \dfrac{3}{2}x \end{align*}\]
- Ensuite, trouvez la surface de la porte rectangulaire en pieds carrés.
\[\begin{align*} A &= lw\\ &= x\times1\\ &= x \end{align*}\]
La surface de l'avant de la niche peut être trouvée en additionnant les aires du carré et du triangle, puis en soustrayant la surface du rectangle. Lorsque nous faisons cela, nous obtenons
\(4x^2+\dfrac{3}{2}x-x\)\(ft^2\)
ou
\(4x^2+\dfrac{1}{2}x\)\(ft^2\)
Dans cette section, nous examinerons des expressions telles que celle-ci, qui combinent plusieurs termes variables.
Identification du degré et du coefficient principal des polynômes
La formule qui vient d'être trouvée est un exemple de polynôme, qui est une somme ou une différence de termes, chacun étant constitué d'une variable portée à une puissance entière non négative. Un nombre multiplié par une variable portée à un exposant, tel que\(384\pi\), est appelé coefficient. Les coefficients peuvent être positifs, négatifs ou nuls et peuvent être des nombres entiers, des décimales ou des fractions. Chaque produit\(a_ix^i\), par exemple\(384\pi w\), est un terme d'un polynôme. Si un terme ne contient pas de variable, il est appelé constante.
Un polynôme contenant un seul terme, tel que\(5x^4\), est appelé monomial. Un polynôme contenant deux termes, tels que\(2x−9\), est appelé binôme. Un polynôme contenant trois termes, tels que\(−3x^2+8x−7\), est appelé trinôme.
Nous pouvons déterminer le degré d'un polynôme en identifiant la puissance la plus élevée de la variable qui se trouve dans le polynôme. Le terme ayant obtenu le diplôme le plus élevé est appelé terme principal car il est généralement écrit en premier. Le coefficient du terme principal est appelé coefficient principal. Lorsqu'un polynôme est écrit de telle sorte que les puissances descendent, on dit qu'il est sous forme standard.
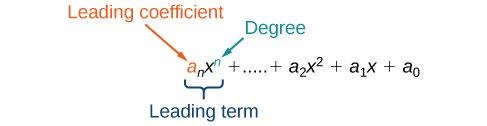
Un polynôme est une expression qui peut être écrite sous la forme
Chaque nombre réel ai est appelé coefficient. Le nombre\(a_0\) qui n'est pas multiplié par une variable est appelé constant. Chaque produit\(a_ix^i\) est un terme d'un polynôme. La puissance la plus élevée de la variable qui apparaît dans le polynôme est appelée degré d'un polynôme. Le terme principal est le terme ayant la puissance la plus élevée, et son coefficient est appelé coefficient principal.
- Trouvez la puissance la plus élevée de x pour déterminer le degré.
- Identifiez le terme contenant la plus grande puissance de x pour trouver le terme principal.
- Identifiez le coefficient du terme principal.
Pour les polynômes suivants, identifiez le degré, le terme principal et le coefficient principal.
- \(3+2x^2−4x^3\)
- \(5t^5−2t^3+7t\)
- \(6p−p^3−2\)
Solution
- La plus grande puissance de l'\(x\)est\(3\), donc le diplôme l'est\(3\). Le terme principal est le terme contenant ce diplôme,\(−4x^3\). Le coefficient principal est le coefficient de ce terme,\(−4\).
- La plus grande puissance de l'\(t\)est\(5\), donc le diplôme l'est\(5\). Le terme principal est le terme contenant ce diplôme,\(5t^5\). Le coefficient principal est le coefficient de ce terme,\(5\).
- La plus grande puissance de l'\(p\)est\(3\), donc le diplôme l'est\(3\). Le terme principal est le terme contenant ce degré,\(−p^3\), Le coefficient principal est le coefficient de ce terme, -1.
Identifiez le degré, le terme principal et le coefficient principal du polynôme\(4x^2−x^6+2x−6\).
- Réponse
-
Le degré est\(6\), le terme principal est\(−x^6\) et le coefficient principal est\(−1\).
Ajouter et soustraire des polynômes
Nous pouvons ajouter et soustraire des polynômes en combinant des termes similaires, c'est-à-dire des termes qui contiennent les mêmes variables élevées aux mêmes exposants. Par exemple,\(5x^2\) et\(−2x^2\) sont des termes similaires et peuvent être ajoutés pour obtenir\(3x^2\), mais\(3x\) et ne\(3x^2\) sont pas des termes similaires, et ne peuvent donc pas être ajoutés.
- Combinez les mêmes termes.
- Simplifiez et rédigez sous forme standard.
Trouve la somme.
\((12x^2+9x−21)+(4x^3+8x^2−5x+20)\)
Solution
\[\begin{align*} &4x^3+(12x^2+8x^2)+(9x-5x)+(-21+20)\qquad \text{Combine like terms} \\ &4x^3+20x^2+4x-1\qquad \qquad \qquad \qquad \qquad \qquad \; \; \; \text{Simplify} \end{align*}\]
Analyse
Nous pouvons vérifier nos réponses à ces types de problèmes à l'aide d'une calculatrice graphique. Pour vérifier, tracez le problème tel qu'il est indiqué avec la réponse simplifiée. Les deux graphiques doivent être équivalents. Veillez à utiliser la même fenêtre pour comparer les graphiques. L'utilisation de fenêtres différentes peut rendre les expressions équivalentes alors qu'elles ne le sont pas.
Trouve la somme.
\((2x^3+5x^2−x+1)+(2x^2−3x−4)\)
- Réponse
-
\(2x^3+7x^2−4x−3\)
Trouve la différence.
\((7x^4−x^2+6x+1)−(5x^3−2x^2+3x+2)\)
Solution
\(7x^4−5x^3+(−x^2+2x^2)+(6x−3x)+(1−2)\)Combinez des termes similaires
\(7x^4−5x^3+x^2+3x−1\)SIMPLIFIER
Analyse
Notez que trouver la différence entre deux polynômes revient à ajouter l'opposé du second polynôme au premier.
Trouve la différence.
\((−7x^3−7x^2+6x−2)−(4x^3−6x^2−x+7)\)
- Réponse
-
\(−11x^3−x^2+7x−9\)
Multiplier des polynômes
Multiplier des polynômes est un peu plus difficile que d'ajouter et de soustraire des polynômes. Nous devons utiliser la propriété distributive pour multiplier chaque terme du premier polynôme par chaque terme du second polynôme. Nous combinons ensuite les mêmes termes. Nous pouvons également utiliser un raccourci appelé méthode FOIL lors de la multiplication de binômes. Certains produits spéciaux suivent des modèles que nous pouvons mémoriser et utiliser au lieu de multiplier les polynômes manuellement à chaque fois. Nous examinerons différentes manières de multiplier les polynômes.
Multiplier des polynômes à l'aide de la propriété distributive
Pour multiplier un nombre par un polynôme, nous utilisons la propriété distributive. Le nombre doit être réparti entre chaque terme du polynôme. Nous pouvons distribuer\(2\) l'entrée\(2(x+7)\) pour obtenir l'expression équivalente\(2x+14\). Lors de la multiplication de polynômes, la propriété distributive nous permet de multiplier chaque terme du premier polynôme par chaque terme du second. Nous additionnons ensuite les produits et combinons les termes similaires pour simplifier.
- Multipliez chaque terme du premier polynôme par chaque terme du second.
- Combinez les mêmes termes.
- Simplifiez.
Trouvez le produit.
\((2x+1)(3x^2−x+4)\)
Solution
\[\begin{align*} &2x(3x^2-x+4)+1(3x^2-x+4)\qquad \text{ Use the distributive property }\\ &(6x^3-2x^2+8x)+(3x^2-x+4)\qquad \text{ Multiply }\\ &6x^3+(-2x^2+3x^2)+(8x-x)+4\qquad \text{ Combine like terms } \\ &6x^3+x^2+7x+4\qquad \text{ Simplify } \end{align*}\]
Analyse
Nous pouvons utiliser un tableau pour suivre notre travail, comme indiqué dans le tableau\(\PageIndex{1}\). Écrivez un polynôme sur le dessus et l'autre sur le côté. Pour chaque case du tableau, multipliez le terme de cette ligne par le terme de cette colonne. Ajoutez ensuite tous les termes, combinez les termes similaires et simplifiez.
| \(3x^2\) | \(−x\) | \(+4\) | |
| \(2x\) | \(6x^3\) | \(−2x^2\) | \(8x\) |
| \(+1\) | \(3x^2\) | \(−x\) | \(4\) |
Trouvez le produit.
\((3x+2)(x^3−4x^2+7)\)
- Réponse
-
\(3x^4−10x^3−8x^2+21x+14\)
Utiliser FOIL pour multiplier des binômes
Un raccourci appelé FOIL est parfois utilisé pour trouver le produit de deux binômes. Il s'appelle FOIL parce que nous multiplions les premiers termes, les termes extérieurs, les termes intérieurs, puis les derniers termes de chaque binôme.

La méthode FOIL est issue de la propriété distributive. Nous multiplions simplement chaque terme du premier binôme par chaque terme du second binôme, puis nous combinons des termes similaires.
À partir de deux binômes, utilisez FOIL pour simplifier l'expression.
- Multipliez les termes extérieurs des binômes.
- Multipliez les derniers termes de chaque binôme.
- Combinez des termes similaires et simplifiez.
Utilisez FOIL pour trouver le produit.
\((2x−10)(3x+3) \nonumber\)
Solution
Trouvez le produit des premiers termes.

Trouvez le produit des termes extérieurs.

Trouvez le produit des termes internes.

Trouvez le produit des derniers termes.

\[\begin{align*} &6x^2+6x-54x-54\qquad \text{Add the products}\\ &6x^2+(6x-54x)-54\qquad \text{Combine like terms} \\ &6x^2-48x-54\qquad \qquad \qquad \text{Simplify} \end{align*}\]
Utilisez FOIL pour trouver le produit.
\((x+7)(3x−5)\)
- Réponse
-
\(3x^2+16x−35\)
Trinômes carrés parfaits
Certains produits binomiaux ont des formes spéciales. Lorsqu'un binôme est mis au carré, le résultat est appelé trinôme carré parfait. Nous pouvons trouver le carré en multipliant le binôme par lui-même. Cependant, chacun de ces trinômes carrés parfaits prend une forme particulière, et la mémorisation de cette forme rend la mise au carré des binômes beaucoup plus facile et plus rapide. Examinons quelques trinômes carrés parfaits pour nous familiariser avec la forme.
\({(x+5)}^2=x^2+10x+25\)
\({(x-3)}^2=x^2-6x+9\)
Remarquez que le premier terme de chaque trinôme est le carré du premier terme du binôme et que, de même, le dernier terme de chaque trinôme est le carré du dernier terme du binôme. Le moyen terme est le double du produit des deux termes. Enfin, nous voyons que le premier signe du trinôme est le même que le signe du binôme.
Lorsqu'un binôme est mis au carré, le résultat est le premier terme au carré ajouté pour doubler le produit des deux termes et du dernier terme au carré.
\[{(x+a)}^2=(x+a)(x+a)=x^2+2ax+a^2\]
- Mettre au carré le premier terme du binôme.
- Mettre au carré le dernier terme du binôme.
- Pour le terme moyen du trinôme, doublez le produit des deux termes.
- Ajoutez et simplifiez.
Élargir\((3x−8)^2\).
Solution
Commencez par mettre le premier terme et le dernier terme au carré. Pour le terme moyen du trinôme, doublez le produit des deux termes.
\[\begin{align*} &{(3x)}^2-2(3x)(8)+{(-8)}^2 \\ &9x^2-48x+64\qquad \qquad \; \; \; \; \text{Simplify} \end{align*}\]
Élargir\({(4x−1)}^2\).
- Réponse
-
\(16x^2−8x+1\)
Différence de carrés
Un autre produit spécial est appelé différence de carrés, qui se produit lorsque nous multiplions un binôme par un autre binôme avec les mêmes termes mais le signe opposé. Voyons ce qui se passe lorsque nous multiplions à\((x+1)(x−1)\) l'aide de la méthode FOIL.
\[\begin{align*} (x+1)(x-1) &= x^2-x+x-1\\ &= x^2-1 \end{align*}\]
Le terme moyen disparaît, ce qui entraîne une différence de carrés. Tout comme nous l'avons fait pour les carrés parfaits, examinons quelques exemples.
\((x+5)(x-5)=x^2-25\)
\((x+11)(x-11)=x^2-121\)
\((2x+3)(2x-3)=4x^2-9\)
Comme le signe change dans le second binôme, les termes extérieur et intérieur s'annulent mutuellement, et il ne nous reste plus que le carré du premier terme moins le carré du dernier terme.
Existe-t-il un formulaire spécial pour la somme des carrés ?
Non La différence de carrés se produit parce que les signes opposés des binômes font disparaître les termes intermédiaires. Il n'existe pas deux binômes qui se multiplient pour obtenir une somme de carrés.
Lorsqu'un binôme est multiplié par un binôme contenant les mêmes termes séparés par le signe opposé, le résultat est le carré du premier terme moins le carré du dernier terme.
\[(a+b)(a−b)=a^2−b^2\]
- Mettre au carré le premier terme des binômes.
- Mettre au carré le dernier terme des binômes.
- Soustrayez le carré du dernier terme du carré du premier terme.
Multipliez\((9x+4)(9x−4)\).
Solution
Quadrillez le premier terme pour obtenir\({(9x)}^2=81x^2\). Qualifiez le dernier terme pour l'obtenir\(4^2=16\). Soustrayez le carré du dernier terme du carré du premier terme pour obtenir le produit de\(81x^2−16\).
Multipliez\((2x+7)(2x−7)\).
- Réponse
-
\(4x^2−49\)
Exécution d'opérations avec des polynômes de plusieurs variables
Nous avons examiné des polynômes contenant une seule variable. Cependant, un polynôme peut contenir plusieurs variables. Les mêmes règles s'appliquent lorsque vous travaillez avec des polynômes contenant plusieurs variables. Prenons un exemple :
\[\begin{align*} &(a+2b)(4a-b-c) a(4a-b-c)+2b(4a-b-c)\qquad \text{ Use the distributive property }\\ &4a^2-ab-ac+8ab-2b^2-2bc\qquad \qquad\qquad\qquad\qquad \text{ Multiply }\\ &4a^2+(-ab+8ab)-ac-2b^2-2bc\qquad \qquad\qquad\qquad \; \text{ Combine like terms } \\ &4a^2+7ab-ac-2bc-2b^2\qquad \qquad \qquad \qquad \qquad \qquad\text{ Simplify } \end{align*}\]
Multipliez\((x+4)(3x−2y+5)\).
Solution
\[\begin{align*} &x(3x-2y+5)+4(3x-2y+5)\qquad \text{ Use the distributive property }\\ &3x^2-2xy+5x+12x-8y+20\qquad \text{ Multiply }\\ &3x^2-2xy+(5x+12x)-8y+20\qquad \text{ Combine like terms } \\ &3x^2-2xy+17x-8y+20\qquad \qquad\text{ Simplify } \end{align*}\]
Multipliez\((3x−1)(2x+7y−9)\).
- Réponse
-
\(6x^2+21xy−29x−7y+9\)
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner avec les polynômes.
Équations clés
| trinôme carré parfait | \({(x+a)}^2=(x+a)(x+a)=x^2+2ax+a^2\) |
| différence de carrés | \((a+b)(a−b)=a^2−b^2\) |
Concepts clés
- Un polynôme est une somme de termes composés chacun d'une variable portée à une puissance entière non négative. Le degré est la puissance la plus élevée de la variable qui apparaît dans le polynôme. Le terme principal est le terme contenant le degré le plus élevé, et le coefficient principal est le coefficient de ce terme. Voir l'exemple.
- Nous pouvons ajouter et soustraire des polynômes en combinant des termes similaires. Voir Exemple et Exemple.
- Pour multiplier des polynômes, utilisez la propriété distributive pour multiplier chaque terme du premier polynôme par chaque terme du second. Ajoutez ensuite les produits. Voir l'exemple.
- FOIL (First, Outer, Inner, Last) est un raccourci qui peut être utilisé pour multiplier des binômes. Voir l'exemple.
- Les trinômes carrés parfaits et la différence de carrés sont des produits spéciaux. Voir Exemple et Exemple.
- Suivez les mêmes règles pour travailler avec des polynômes contenant plusieurs variables. Voir l'exemple.


