5.6 : Représentation graphique des systèmes d'inégalités linéaires
- Page ID
- 194488
À la fin de cette section, vous serez en mesure de :
- Déterminer si une paire ordonnée est la solution d'un système d'inégalités linéaires
- Résolvez un système d'inégalités linéaires en graphiant
- Résoudre des applications de systèmes d'inégalités
Avant de commencer, répondez à ce questionnaire de préparation.
- Diagramme x>2 sur une ligne numérique.
Si vous avez oublié ce problème, passez en revue l'exercice 2.7.1. - Résolvez l'inégalité 2a<5a+12.
Si vous avez oublié ce problème, passez en revue l'exercice 2.7.22. - Déterminez si la paire commandée\((3,\frac{1}{2})\) constitue une solution pour le système\(\left\{\begin{array}{l}{x+2 y=4} \\ {y=6 x}\end{array}\right.\).
Si vous avez oublié ce problème, passez en revue l'exercice 5.1.1.
Déterminer si une paire ordonnée est la solution d'un système d'inégalités linéaires
La définition d'un système d'inégalités linéaires est très similaire à la définition d'un système d'équations linéaires.
Deux inégalités linéaires ou plus regroupées forment un système d'inégalités linéaires.
Un système d'inégalités linéaires ressemble à un système d'équations linéaires, mais il comporte des inégalités au lieu d'équations. Un système de deux inégalités linéaires est illustré ci-dessous.
\[\left\{\begin{array}{l}{x+4 y \geq 10} \\ {3 x-2 y<12}\end{array}\right.\]
Pour résoudre un système d'inégalités linéaires, nous trouverons les valeurs des variables qui sont des solutions aux deux inégalités. Nous résolvons le système en utilisant les graphes de chaque inégalité et montrons la solution sous forme de graphique. Nous trouverons la région sur le plan qui contient toutes les paires ordonnées (x, y) (x, y) qui confirment les deux inégalités.
Les solutions d'un système d'inégalités linéaires sont les valeurs des variables qui rendent toutes les inégalités vraies.
La solution d'un système d'inégalités linéaires est présentée sous la forme d'une région ombrée dans le système de coordonnées x-y qui inclut tous les points dont les paires ordonnées confirment les inégalités.
Pour déterminer si une paire ordonnée est une solution à un système de deux inégalités, nous substituons les valeurs des variables dans chaque inégalité. Si la paire ordonnée confirme les deux inégalités, c'est une solution pour le système.
Déterminez si la paire commandée constitue une solution pour le système. \(\left\{\begin{array}{l}{x+4 y \geq 10} \\ {3 x-2 y<12}\end{array}\right.\)
- (−2, 4)
- (3,1)
- Réponse
-
1. La paire ordonnée (−2, 4) est-elle une solution ?

La paire ordonnée (−2, 4) a confirmé les deux inégalités. (−2, 4) est donc une solution à ce système.
2. La paire commandée (3,1) est-elle une solution ?

La paire ordonnée (3,1) a rendu une inégalité vraie, mais l'autre fausse. Par conséquent, (3,1) n'est pas une solution à ce système.
Déterminez si la paire commandée constitue une solution pour le système. \(\left\{\begin{array}{l}{x-5 y>10} \\ {2 x+3 y>-2}\end{array}\right.\)
- (3, -1)
- (6, -3)
- Réponse
-
- non
- oui
Déterminez si la paire commandée constitue une solution pour le système. \(\left\{\begin{array}{l}{y>4 x-2} \\ {4 x-y<20}\end{array}\right.\)
- (2,1)
- (4, -1)
- Réponse
-
- non
- non
Résolvez un système d'inégalités linéaires en graphiant
La solution à une inégalité linéaire unique est la région d'un côté de la ligne de démarcation qui contient tous les points qui rendent l'inégalité vraie. La solution à un système de deux inégalités linéaires est une région qui contient les solutions aux deux inégalités. Pour trouver cette région, nous allons représenter graphiquement chaque inégalité séparément, puis localiser la région où elles sont toutes deux vraies. La solution est toujours présentée sous forme de graphique.
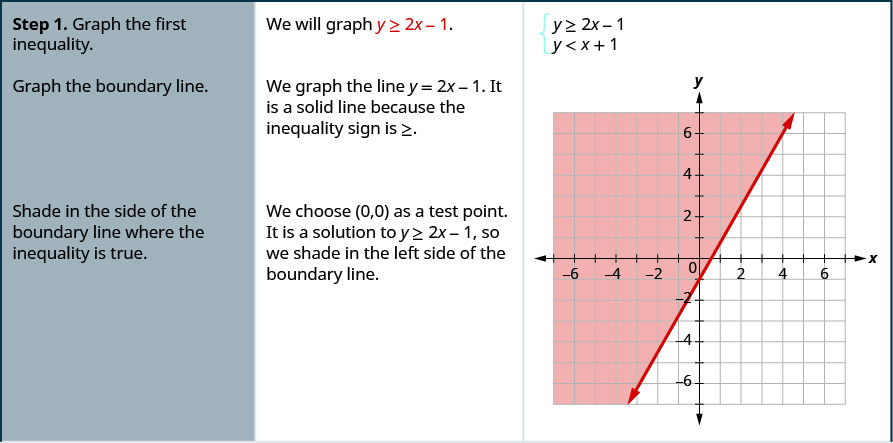
Résolvez le système en dessinant un graphique. \(\left\{\begin{array}{l}{y \geq 2 x-1} \\ {y<x+1}\end{array}\right.\)
- Réponse
-


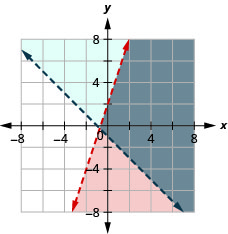
Résolvez le système en dessinant un graphique. \(\left\{\begin{array}{l}{y<3 x+2} \\ {y>-x-1}\end{array}\right.\)
- Réponse
-
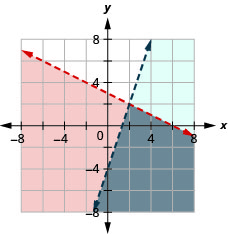
Résolvez le système en dessinant un graphique. \(\left\{\begin{array}{l}{y<-\frac{1}{2} x+3} \\ {y<3 x-4}\end{array}\right.\)
- Réponse
-
- Tracez la première inégalité.
- Tracez la ligne de limite.
- De l'ombre sur le côté de la ligne de démarcation où l'inégalité est vraie.
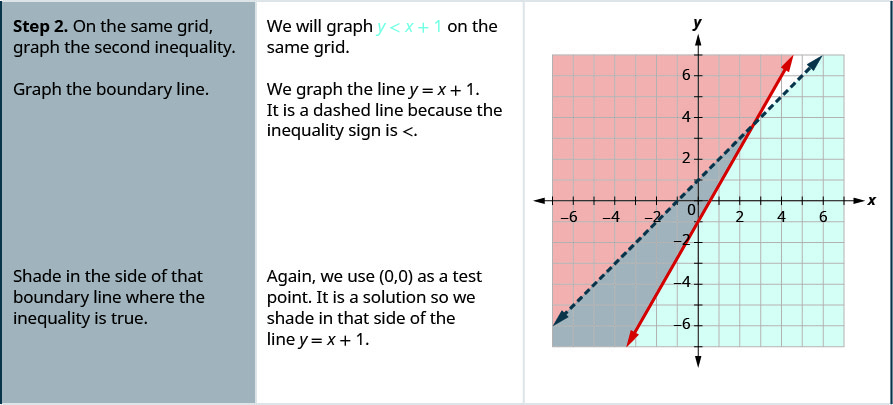
- Sur la même grille, tracez la deuxième inégalité.
- Tracez la ligne de limite.
- De l'ombre sur le côté de cette ligne de démarcation où l'inégalité est vraie.
- La solution est la zone où les ombres se chevauchent.
- Vérifiez en choisissant un point de test.
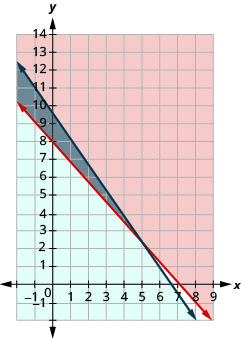
Résolvez le système en dessinant un graphique. \(\left\{\begin{array}{l}{x-y>3} \\ {y<-\frac{1}{5} x+4}\end{array}\right.\)
- Réponse
-
Tracez x − y > 3, en représentant graphiquement x − y = 3 et en
testant un point.
Les points d'intersection sont x = 3 et y = −3 et la
ligne de démarcation sera pointillée.
Test (0, 0). Cela rend l'inégalité fausse. Donc,
ombrez le côté qui ne contient pas (0, 0) de rouge.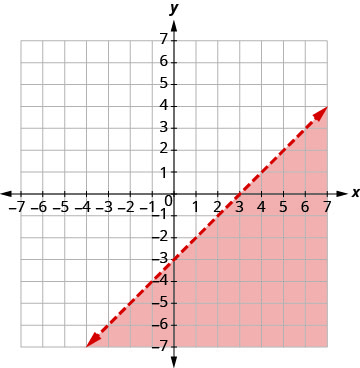
Le point d'intersection des deux lignes n'est pas inclus car les deux lignes de démarcation étaient pointillées. La solution est la zone ombrée deux fois, qui est la zone ombrée la plus foncée.Tracez y<−15x+4 en traçant y=−15x+4
en utilisant la pente m=−15 et y −intercept
b = 4. La ligne de démarcation sera pointillée.
Test (0, 0). Cela rend l'inégalité vraie, alors ombrez le côté qui contient (0, 0) du bleu.
Choisissez un point de test dans la solution et vérifiez qu'il s'agit d'une solution aux deux inégalités.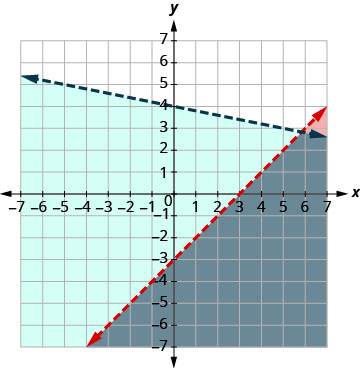
Résolvez le système en dessinant un graphique. \(\left\{\begin{array}{l}{x+y \leq 2} \\ {y \geq \frac{2}{3} x-1}\end{array}\right.\)
- Réponse
-
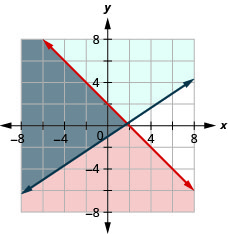
Résolvez le système en dessinant un graphique. \(\left\{\begin{array}{l}{3 x-2 y \leq 6} \\ {y>-\frac{1}{4} x+5}\end{array}\right.\)
- Réponse
-
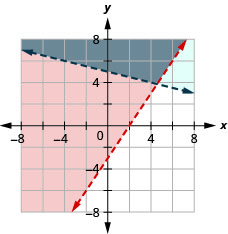
Résolvez le système en dessinant un graphique. \(\left\{\begin{array}{l}{x-2 y<5} \\ {y>-4}\end{array}\right.\)
- Réponse
-
Diagramme x−2y<5, en traçant x−2y=5 et en testant un point.
Les points d'intersection sont x = 5 et y = −2,5 et la ligne de démarcation sera pointillée.
Test (0, 0). Cela confirme l'inégalité. Donc, ombrez le côté
qui contient (0, 0) de rouge.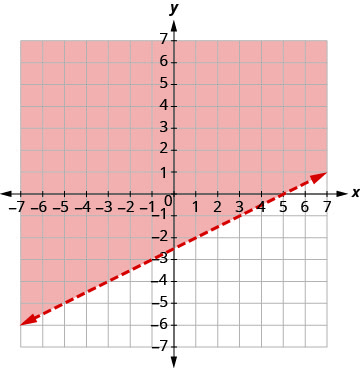
Tracez y > −4, en traçant y = −4 et en reconnaissant qu'il s'agit d'une ligne
horizontale passant par y = −4. La ligne de démarcation sera pointillée.
Test (0, 0). Cela confirme l'inégalité. Donc, ombrez (bleu)
le côté qui contient (0, 0) du bleu.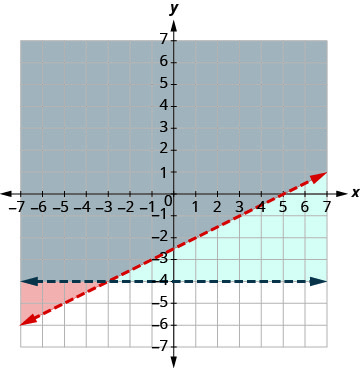
Le point (0, 0) se trouve dans la solution et nous avons déjà trouvé qu'il s'agissait d'une solution à chaque inégalité. Le point d'intersection des deux lignes n'est pas inclus car les deux lignes de démarcation étaient pointillées.
La solution est la zone ombrée deux fois, qui est la zone ombrée la plus foncée.
Résolvez le système en dessinant un graphique. \(\left\{\begin{array}{l}{y \geq 3 x-2} \\ {y<-1}\end{array}\right.\)
- Réponse
-
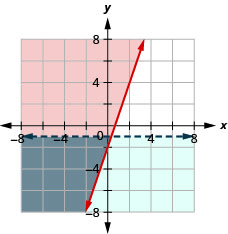
Résolvez le système en dessinant un graphique. \(\left\{\begin{array}{l}{x>-4} \\ {x-2 y \leq-4}\end{array}\right.\)
- Réponse
-
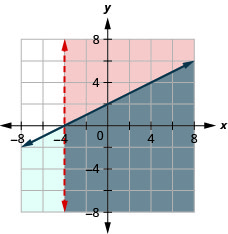
Les systèmes d'inégalités linéaires où les lignes de démarcation sont parallèles n'ont peut-être pas de solution. Nous allons voir cela dans Example\(\PageIndex{13}\).
Résolvez le système en dessinant un graphique. \(\left\{\begin{array}{l}{4 x+3 y \geq 12} \\ {y<-\frac{4}{3} x+1}\end{array}\right.\)
- Réponse
-
\(4x+3y\geq 12\)Tracez, en traçant 4x+3y=12 et en testant un point.
Les points d'intersection sont x = 3 et y = 4 et la ligne de démarcation sera pleine.
Test (0, 0). Cela rend l'inégalité fausse. Donc,
ombrez le côté qui ne contient pas (0, 0) de rouge.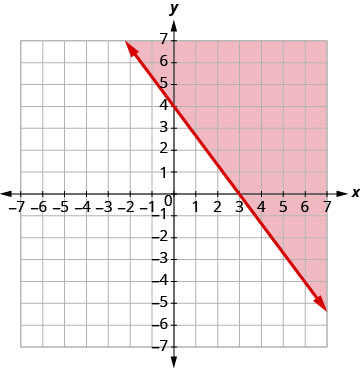
Il n'y a aucun point dans les deux zones ombrées, de sorte que le système n'a pas de solution. Ce système n'a pas de solution.Tracez un graphique\(y<−\frac{4}{3}x+1\)\(y=−\frac{4}{3}x+1\) à l'aide de la
pente\(m = \frac{4}{3}\) et de l'intersection y b = 1. La ligne de démarcation sera pointillée.
Test (0, 0). Cela confirme l'inégalité. Donc,
ombrez le côté qui contient (0, 0) du bleu.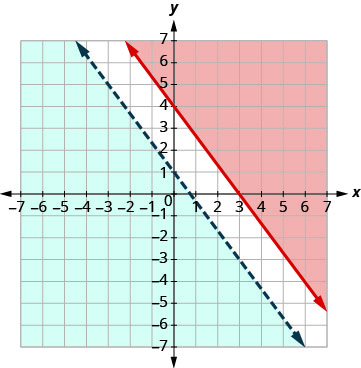
Résolvez le système en dessinant un graphique. \(\left\{\begin{array}{l}{3 x-2 y \leq 12} \\ {y \geq \frac{3}{2} x+1}\end{array}\right.\)
- Réponse
-
aucune solution
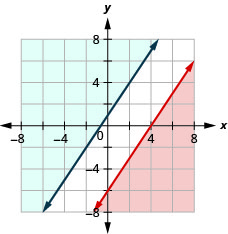
Résolvez le système en dessinant un graphique. \(\left\{\begin{array}{l}{x+3 y>8} \\ {y<-\frac{1}{3} x-2}\end{array}\right.\)
- Réponse
-
aucune solution
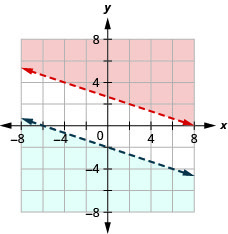
Résolvez le système en dessinant un graphique. \(\left\{\begin{array}{l}{y>\frac{1}{2} x-4} \\ {x-2 y<-4}\end{array}\right.\)
- Réponse
-
\(y>\frac{1}{2}x−4\)Tracez un graphique\(y=\frac{1}{2}x−4\)
à l'aide de la pente\(m=\frac{1}{2}\) et de l'intersection
b = −4. La ligne de démarcation sera pointillée.
Test (0, 0). Cela confirme l'inégalité. Donc,
ombrez le côté qui contient (0, 0) de rouge.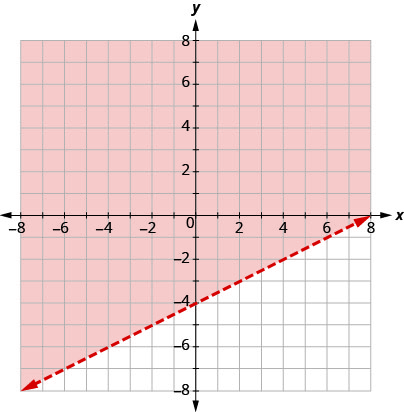
Tracez x−2y<−4x−2y<−4 en traçant x−2y=−4x−2y=−4 et en testant un point.
Les points d'intersection sont x = −4 et y = 2 et la
ligne de démarcation sera pointillée.
Choisissez un point de test dans la solution et vérifiez
qu'il s'agit d'une solution aux deux inégalités.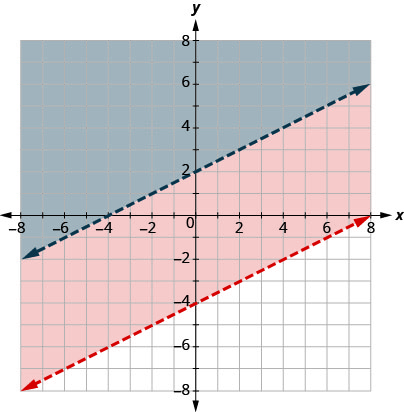
Aucun point sur les lignes de démarcation n'est inclus dans la solution car les deux lignes sont pointillées.
La solution est la région qui est ombrée deux fois, qui est également la solution à x−2y<−4.
Résolvez le système en dessinant un graphique. \(\left\{\begin{array}{l}{y \geq 3 x+1} \\ {-3 x+y \geq-4}\end{array}\right.\)
- Réponse
-
\(y \geq 3 x+1\)
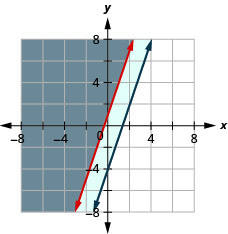
Résolvez le système en dessinant un graphique. \(\left\{\begin{array}{l}{y \leq-\frac{1}{4} x+2} \\ {x+4 y \leq 4}\end{array}\right.\)
- Réponse
-
\(x+4 y \leq 4\)

Résoudre les applications des systèmes d'inégalités
La première chose à faire pour résoudre les applications des systèmes d'inégalités est de traduire chaque condition en inégalité. Ensuite, nous graphiquons le système comme nous l'avons fait ci-dessus pour voir la région qui contient les solutions. De nombreuses situations ne seront réalistes que si les deux variables sont positives, de sorte que leurs graphiques n'afficheront que le quadrant I.
Christy vend ses photos sur un stand lors d'une foire de rue. Au début de la journée, elle souhaite avoir au moins 25 photos à exposer sur son stand. Chaque petite photo qu'elle expose lui coûte 4$ et chaque grande photo lui coûte 10$. Elle ne veut pas dépenser plus de 200$ en photos à exposer.
- Écrivez un système d'inégalités pour modéliser cette situation.
- Tracez le système.
- Pourrait-elle afficher 15 petites et 5 grandes photos ?
- Pourrait-elle afficher 3 grandes et 22 petites photos ?
- Réponse
-
1. Soit x le nombre de petites photos.
y= le nombre de grandes photos
Pour trouver le système d'inégalités, traduisez les informations.
\(\begin{array}{c}{\text { She wants to have at least } 25 \text { photos. }} \\ {\text { The number of small plus the number of large should be at least } 25 .} \\ {x+y \geq 25} \\ {\$ 4 \text { for each small and } \$ 10 \text { for each large must be no more than } \$ 200} \\ {4 x+10 y \leq 200}\end{array}\)
Nous avons notre système d'inégalités. \(\left\{\begin{array}{l}{x+y \geq 25} \\ {4 x+10 y \leq 200}\end{array}\right.\)2.
Pour représenter\(x+y\geq 25\) graphiquement, tracez x + y = 25 sous la forme d'une ligne continue.
Choisissez (0, 0) comme point de test. Comme cela ne signifie pas que l'inégalité
est vraie, ombrez le côté qui n'inclut pas le point (0, 0) en rouge.
Pour représenter\(4x+10y\leq 200\) graphiquement, tracez 4 x + 10 y = 200 sous la forme d'une ligne continue.
Choisissez (0, 0) comme point de test. Comme cela ne confirme pas l'inégalité,
ombrez le côté qui inclut le point (0, 0) en bleu.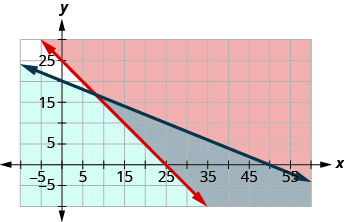
La solution du système est la zone du graphique qui est ombrée deux fois et qui est donc ombrée plus foncée.3. Pour déterminer si 10 petites et 20 grandes photos peuvent fonctionner, nous voyons si le point (10, 20) se trouve dans la zone de solution. Ça ne l'est pas. Christy n'a pas voulu afficher 10 petites photos et 20 grandes photos.
4. Pour déterminer si 20 petites photos et 10 grandes photos peuvent fonctionner, nous voyons si le point (20, 10) se trouve dans la zone de solution. Ça l'est. Christy pourrait choisir d'exposer 20 petites photos et 10 grandes photos.
Notez que nous pourrions également tester les solutions possibles en substituant les valeurs dans chaque inégalité.
Une remorque peut transporter un poids maximum de 160 livres et un volume maximal de 15 pieds cubes. Un four à micro-ondes pèse 30 livres et a un volume de 2 pieds cubes, tandis qu'une imprimante pèse 20 livres et dispose de 3 pieds cubes d'espace.
- Écrivez un système d'inégalités pour modéliser cette situation.
- Tracez le système.
- Est-ce que 4 micro-ondes et 2 imprimantes peuvent être transportés sur cette remorque ?
- Est-ce que 7 micro-ondes et 3 imprimantes peuvent être transportés sur cette remorque ?
- Réponse
-
- \(\left\{\begin{array}{l}{30 m+20 p \leq 160} \\ {2 m+3 p \leq 15}\end{array}\right.\)
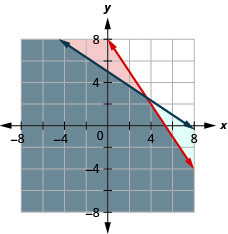
3. oui
4. Non
Mary doit acheter des feuilles de réponses et des crayons pour un test standardisé qui sera donné aux juniors de son lycée. Le nombre de feuilles de réponses nécessaires est supérieur d'au moins 5 au nombre de crayons. Les crayons coûtent 2$ et les feuilles de réponses coûtent 1$. Le budget de Mary pour ces fournitures permet un coût maximum de 400$.
- Écrivez un système d'inégalités pour modéliser cette situation.
- Tracez le système.
- Mary pourrait-elle acheter 100 crayons et 100 feuilles de réponses ?
- Mary pourrait-elle acheter 150 crayons et 150 feuilles de réponses ?
- Réponse
-
- \(\left\{\begin{array}{l}{a \geq p+5} \\ {a+2 p \leq 400}\end{array}\right.\)
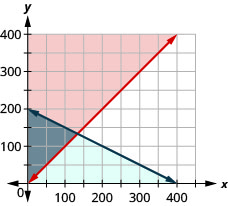
3. Non
4. Non
Omar doit manger au moins 800 calories avant de se rendre à l'entraînement de son équipe. Il ne veut que des hamburgers et des biscuits, et il ne veut pas dépenser plus de 5 dollars. Au restaurant de hamburgers près de son université, chaque hamburger contient 240 calories et coûte 1,40$. Chaque biscuit contient 160 calories et coûte 0,50$.
- Écrivez un système d'inégalités pour modéliser cette situation.
- Tracez le système.
- Pourrait-il manger 1 biscuit et 3 hamburgers ?
- Pourrait-il manger 4 biscuits et 2 hamburgers ?
- Réponse
-
Soit h = le nombre de hamburgers.
c= le nombre de cookies
Pour trouver le système d'inégalités, traduisez les informations.
Les calories provenant des hamburgers à 240 calories chacun, plus les calories des biscuits à 160 calories chacun doivent être supérieures à 800.\[240 h+160 c \geq 800\]
Le montant dépensé pour les hamburgers à 1,40$ chacun, plus le montant dépensé en biscuits à 0,50$ chacun ne doit pas dépasser 5$.
\[1.40 h+0.50 c \leq 5\]
\(\text { We have our system of inequalities. } \quad \left\{\begin{array}{l}{240 h+160 c \geq 800} \\ {1.40 h+0.50 c \leq 5}\end{array}\right.\)
2.
Pour représenter\(240h+160c\geq 800\) graphiquement le graphique 240h+160c=800 sous la forme d'une ligne continue.
Choisissez (0, 0) comme point de test. Cela ne signifie pas que l'inégalité est vraie.
Donc, ombrez (rouge) le côté qui n'inclut pas le point (0, 0).
Pour représenter graphiquement\(1.40 h+0.50 c \leq 5\), tracez 1,40h+0,50c=5 en trait plein.
Choisissez (0,0) comme point de test. Cela confirme l'inégalité. Donc,
ombrez (en bleu) le côté qui inclut le point.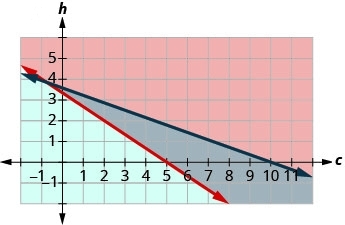
La solution du système est la zone du graphique qui est ombrée deux fois et qui est donc ombrée plus foncée.
3. Pour déterminer si 1 biscuit et 3 hamburgers répondent aux critères d'Omar, nous voyons si le point (1, 3) se trouve dans la zone de solution. Ça ne l'est pas.
4. Pour déterminer si 4 biscuits et 2 hamburgers répondent aux critères d'Omar, nous voyons si le point (4, 2) se trouve dans la zone de solution. Ça l'est. Il pourrait choisir de manger 4 biscuits et 2 hamburgers.Nous pourrions également tester les solutions possibles en substituant les valeurs dans chaque inégalité.
La tension a besoin de consommer au moins 1 000 calories supplémentaires par jour pour se préparer à courir un marathon. Il n'a que 25$ à dépenser pour les aliments supplémentaires dont il a besoin et il les dépensera pour des beignets de 0,75$ contenant 360 calories chacun et 2 dollars pour des boissons énergisantes contenant 110 calories.
- Rédigez un système d'inégalités qui modélise cette situation.
- Tracez le système.
- Peut-il acheter 8 beignets et 4 boissons énergisantes ?
- Peut-il acheter 1 beignet et 3 boissons énergisantes ?
- Réponse
-
- \(\left\{\begin{array}{l}{0.75 d+2 e \leq 25} \\ {360 d+110 e \geq 1000}\end{array}\right.\)
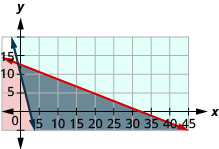
3. oui
4. Non
Le médecin de Philip lui dit qu'il devrait ajouter au moins 1 000 calories supplémentaires par jour à son alimentation habituelle. Philip veut acheter des barres protéinées qui coûtent 1,80$ chacune et contiennent 140 calories et du jus qui coûte 1,25$ par bouteille et contient 125 calories. Il ne veut pas dépenser plus de 12 dollars.
- Rédigez un système d'inégalités qui modélise cette situation.
- Tracez le système.
- Peut-il acheter 3 barres protéinées et 5 bouteilles de jus de fruits ?
- Peut-il acheter 5 barres protéinées et 3 bouteilles de jus ?
- Réponse
-
- \(\left\{\begin{array}{l}{140 p+125 j \geq 1000} \\ {1.80 p+1.25 j \leq 12}\end{array}\right.\)
3. oui
4. Non
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur les systèmes de représentation graphique des inégalités linéaires.
- Système graphique des inégalités
- Systèmes d'inégalités
- Résolution de systèmes d'inégalités linéaires par représentation graphique
Concepts clés
- Pour résoudre un système d'inégalités linéaires à l'aide d'un graphique
- Tracez la première inégalité.
- Tracez la ligne de limite.
- De l'ombre sur le côté de la ligne de démarcation où l'inégalité est vraie.
- Sur la même grille, tracez la deuxième inégalité.
- Tracez la ligne de limite.
- De l'ombre sur le côté de cette ligne de démarcation où l'inégalité est vraie.
- La solution est la zone où les ombres se chevauchent.
- Vérifiez en choisissant un point de test.
- Tracez la première inégalité.
Lexique
- système d'inégalités linéaires
- Deux inégalités linéaires ou plus regroupées forment un système d'inégalités linéaires.


