5.3 : Résoudre des systèmes d'équations par élimination
- Page ID
- 194474
À la fin de cette section, vous serez en mesure de :
- Résoudre un système d'équations par élimination
- Résoudre les applications de systèmes d'équations par élimination
- Choisissez la méthode la plus pratique pour résoudre un système d'équations linéaires
Avant de commencer, répondez à ce questionnaire de préparation.
- Simplifiez −5 (6−3a).
Si vous avez oublié ce problème, passez en revue l'exercice 1.10.43. - Résolvez l'équation\(\frac{1}{3}x+\frac{5}{8}=\frac{31}{24}\).
Si vous avez oublié ce problème, passez en revue l'exercice 2.5.1.
Nous avons résolu des systèmes d'équations linéaires par graphes et par substitution. La représentation graphique fonctionne bien lorsque les coefficients variables sont faibles et que la solution comporte des valeurs entières. La substitution fonctionne bien lorsque nous pouvons facilement résoudre une équation pour l'une des variables sans avoir trop de fractions dans l'expression résultante.
La troisième méthode de résolution de systèmes d'équations linéaires s'appelle la méthode d'élimination. Lorsque nous avons résolu un système par substitution, nous avons commencé avec deux équations et deux variables et nous l'avons réduit à une équation avec une variable. C'est ce que nous ferons également avec la méthode d'élimination, mais nous aurons une autre façon d'y parvenir.
Résoudre un système d'équations par élimination
La méthode d'élimination est basée sur la propriété d'addition d'égalité. La propriété d'addition de l'égalité indique que lorsque vous ajoutez la même quantité des deux côtés d'une équation, vous obtenez toujours l'égalité. Nous allons étendre la propriété d'addition de l'égalité pour indiquer que lorsque vous ajoutez des quantités égales des deux côtés d'une équation, les résultats sont égaux.
Pour toutes les expressions a, b, c et d,
\[\begin{array}{lc} \text{ if } & a=b \\ \text { and } & c=d \\ \text { then } &a+c =b+d \end{array}\]
Pour résoudre un système d'équations par élimination, nous commençons par les deux équations sous forme standard. Ensuite, nous décidons quelle variable sera la plus facile à éliminer. Comment décidons-nous ? Nous voulons que les coefficients d'une variable soient opposés, afin de pouvoir additionner les équations et éliminer cette variable.
Remarquez comment cela fonctionne lorsque nous ajoutons ces deux équations :
\[\begin{array}{l} 3x+y=5 \\ \underline{2x-y=0} \\ 5x\quad\quad=5\end{array}\]
Les y s'additionnent à zéro et nous avons une équation avec une variable.
Essayons-en un autre :
\[\left\{\begin{array}{l}{x+4 y=2} \\ {2 x+5 y=-2}\end{array}\right.\]
Cette fois, nous ne voyons pas de variable qui puisse être immédiatement éliminée si nous ajoutons les équations.
Mais si nous multiplions la première équation par −2, nous rendrons les coefficients de x opposés. Nous devons multiplier chaque terme des deux côtés de l'équation par −2.
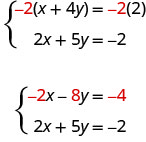
Nous voyons maintenant que les coefficients des termes x sont opposés, donc x sera éliminé lorsque nous ajouterons ces deux équations.
Ajoutez les équations vous-même. Le résultat doit être −3 y = −6. Et cela semble facile à résoudre, n'est-ce pas ? Voici à quoi cela ressemblerait.
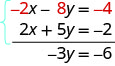
Nous allons en faire une de plus :
\[\left\{\begin{array}{l}{4 x-3 y=10} \\ {3 x+5 y=-7}\end{array}\right.\]
Il ne semble pas que nous puissions obtenir des coefficients d'une variable opposés en multipliant l'une des équations par une constante, à moins d'utiliser des fractions. Au lieu de cela, nous devrons multiplier les deux équations par une constante.
Nous pouvons faire en sorte que les coefficients de x soient opposés si nous multiplions la première équation par 3 et la seconde par −4, donc nous obtenons 12 x et −12 x.
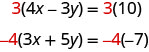
Cela nous donne ces deux nouvelles équations :
\[\left\{\begin{aligned} 12 x-9 y &=30 \\-12 x-20 y &=28 \end{aligned}\right.\]
Lorsque nous ajoutons ces équations,
\[\[\left\{\begin{array}{r}{12 x-9 y=30} \\ {\underline{-12 x-20 y=28}} \\\end{array}\right.\\\quad\qquad {-29 y=58}\]\]
les x sont éliminés et nous avons juste −29 y = 58.
Une fois que nous obtenons une équation avec une seule variable, nous la résolvons. Ensuite, nous remplaçons cette valeur dans l'une des équations d'origine pour résoudre la variable restante. Et, comme toujours, nous vérifions notre réponse pour nous assurer qu'elle est une solution aux deux équations d'origine.
Nous allons maintenant voir comment utiliser l'élimination pour résoudre le même système d'équations que nous avons résolu par graphe et par substitution.
Résolvez le système par élimination. \(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)
- Réponse
-







Résolvez le système par élimination. \(\left\{\begin{array}{l}{3 x+y=5} \\ {2 x-3 y=7}\end{array}\right.\)
- Réponse
-
(2, -1)
Résolvez le système par élimination. \(\left\{\begin{array}{l}{4 x+y=-5} \\ {-2 x-2 y=-2}\end{array}\right.\)
- Réponse
-
(−2,3)
Les étapes sont répertoriées ci-dessous pour faciliter la consultation.
- Écrivez les deux équations sous forme standard. Si certains coefficients sont des fractions, supprimez-les.
- Faites en sorte que les coefficients d'une variable soient opposés.
- Déterminez quelle variable vous allez éliminer.
- Multipliez l'une des équations ou les deux de manière à ce que les coefficients de cette variable soient opposés.
- Ajoutez les équations résultant de l'étape 2 pour éliminer une variable.
- Résolvez pour la variable restante.
- Remplacez la solution de l'étape 4 par l'une des équations d'origine. Résolvez ensuite pour l'autre variable.
- Écrivez la solution sous forme de paire ordonnée.
- Vérifiez que la paire ordonnée est une solution aux deux équations d'origine.
Nous allons d'abord faire un exemple où nous pouvons éliminer une variable immédiatement.
Résolvez le système par élimination. \(\left\{\begin{array}{l}{x+y=10} \\ {x-y=12}\end{array}\right.\)
- Réponse
-

Les deux équations sont présentées sous forme standard. Les coefficients de y sont déjà opposés. Ajoutez les deux équations pour éliminer y.
L'équation qui en résulte ne comporte qu'une seule variable, x.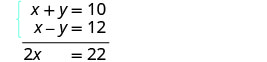
Résolvez pour x, la variable restante.
Remplacez x = 11 dans l'une des équations d'origine.

Résolvez pour l'autre variable, y. 
Écrivez la solution sous forme de paire ordonnée. La paire ordonnée est (11, -1). Vérifiez que la paire ordonnée est une solution
aux deux équations d'origine.
\(\begin{array}{rllrll} x+y &=&10 &x-y&=&12\\ 11+(-1) &\stackrel{?}{=}&10 & 11-(-1) &\stackrel{?}{=}&12\\ 10 &=&10 \checkmark & 12 &=&12 \checkmark \end{array}\)La solution est (11, -1).
Résolvez le système par élimination. \(\left\{\begin{array}{l}{2 x+y=5} \\ {x-y=4}\end{array}\right.\)
- Réponse
-
(3, -1)
Résolvez le système par élimination. \(\left\{\begin{array}{l}{x+y=3} \\ {-2 x-y=-1}\end{array}\right.\)
- Réponse
-
(−2,5)
Dans l'exercice\(\PageIndex{7}\), nous serons en mesure de rendre les coefficients d'une variable opposés en multipliant une équation par une constante.
Résolvez le système par élimination. \(\left\{\begin{array}{l}{3 x-2 y=-2} \\ {5 x-6 y=10}\end{array}\right.\)
- Réponse
-

Les deux équations sont présentées sous forme standard. Aucun des coefficients n'est opposé. Nous pouvons rendre les coefficients de y opposés en multipliant
la première équation par −3.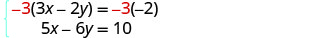
Simplifiez. 
Ajoutez les deux équations pour éliminer y. 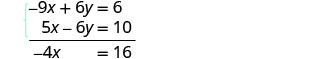
Résolvez pour la variable restante, x.
Remplacez x = −4 dans l'une des équations d'origine.

Résolvez pour y. 


Écrivez la solution sous forme de paire ordonnée. La paire ordonnée est (−4, −5). Vérifiez que la paire ordonnée est une solution aux
deux équations d'origine.
\(\begin{array}{rllrll} 3x-2y &=&-2 &5x-6y&=&10\\ 3(-4)-2(-5) &\stackrel{?}{=}&-2 & 5(-4)-6(-5) &\stackrel{?}{=}&10\\ -12+10&\stackrel{?}{=}&-2 &-20+30&\stackrel{?}{=}&10\\-2 &=&-2 \checkmark & 10 &=&10 \checkmark \end{array}\)La solution est (−4, −5).
Résolvez le système par élimination. \(\left\{\begin{array}{l}{4 x-3 y=1} \\ {5 x-9 y=-4}\end{array}\right.\)
- Réponse
-
(1,1)
Résolvez le système par élimination. \(\left\{\begin{array}{l}{3 x+2 y=2} \\ {6 x+5 y=8}\end{array}\right.\)
- Réponse
-
(−2,4)
Nous allons maintenant faire un exemple où nous devons multiplier les deux équations par des constantes afin de rendre les coefficients d'une variable opposés.
Résolvez le système par élimination. \(\left\{\begin{array}{l}{4 x-3 y=9} \\ {7 x+2 y=-6}\end{array}\right.\)
- Réponse
-
Dans cet exemple, nous ne pouvons pas multiplier une seule équation par n'importe quelle constante pour obtenir des coefficients opposés. Nous allons donc multiplier stratégiquement les deux équations par une constante pour obtenir les contraires.

Les deux équations sont présentées sous forme standard. Pour obtenir
les coefficients opposés de y, nous allons multiplier la première équation par 2
et la deuxième équation par 3.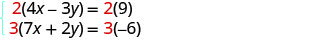
Simplifiez. 
Ajoutez les deux équations pour éliminer y. 
Résolvez pour x.
Remplacez x = 0 dans l'une des équations d'origine.

Résolvez pour y. 

Écrivez la solution sous la forme d'une paire ordonnée. La paire ordonnée est (0, −3). Vérifiez que la paire ordonnée est une solution aux
deux équations d'origine.
\(\begin{array}{rllrll} 4x-3y &=&9 &7x+2y&=&-6\\ 4(0)-3(-3) &\stackrel{?}{=}&9 & 7(0)+2(-3) &\stackrel{?}{=}&-6\\9 &=&9 \checkmark & -6 &=&-6 \checkmark \end{array}\)La solution est (0, -3).
Résolvez le système par élimination. \(\left\{\begin{array}{l}{3 x-4 y=-9} \\ {5 x+3 y=14}\end{array}\right.\)
- Réponse
-
(1,3)
Résolvez le système par élimination. \(\left\{\begin{array}{l}{7 x+8 y=4} \\ {3 x-5 y=27}\end{array}\right.\)
- Réponse
-
(4, −3)
Lorsque le système d'équations contient des fractions, nous allons d'abord effacer les fractions en multipliant chaque équation par son écran LCD.
Résolvez le système par élimination. \(\left\{\begin{array}{l}{x+\frac{1}{2} y=6} \\ {\frac{3}{2} x+\frac{2}{3} y=\frac{17}{2}}\end{array}\right.\)
- Réponse
-
Dans cet exemple, les deux équations comportent des fractions. Notre première étape sera de multiplier chaque équation par son écran LCD pour effacer les fractions.
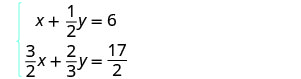
Pour effacer les fractions, multipliez chaque équation par son écran LCD. 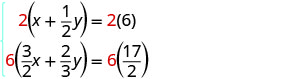
Simplifiez. 
Nous sommes maintenant prêts à éliminer l'une des variables. Notez que
les deux équations sont sous forme standard.On peut éliminer y multipliant l'équation supérieure par −4. 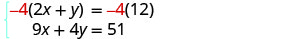
Simplifiez et ajoutez.
Remplacez x = 3 dans l'une des équations d'origine.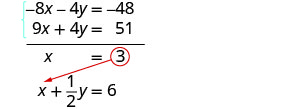
Résolvez pour y. 


Écrivez la solution sous la forme d'une paire ordonnée. La paire commandée est (3, 6). Vérifiez que la paire ordonnée est une solution
aux deux équations d'origine.
\(\begin{array}{rllrll} x+\frac{1}{2}y &=&6 &\frac{3}{2}x+\frac{2}{3}y&=&\frac{17}{2}\\ 3+\frac{1}{2}(6) &\stackrel{?}{=}&6 &\frac{3}{2}(3) + \frac{2}{3}(6)&\stackrel{?}{=}&\frac{17}{2}\\ 3 + 3 &\stackrel{?}{=}&6 & \frac{9}{2 }+4 &\stackrel{?}{=} & \frac{17}{2}\\ 6 &=&6 \checkmark & \frac{9}{2} + \frac{8}{2} &\stackrel{?}{=} & \frac{17}{2}\\ && & \frac{17}{2} &=&\frac{17}{2} \checkmark \end{array}\)La solution est (3, 6).
Résolvez le système par élimination. \(\left\{\begin{array}{l}{\frac{1}{3} x-\frac{1}{2} y=1} \\ {\frac{3}{4} x-y=\frac{5}{2}}\end{array}\right.\)
- Réponse
-
(6,2)
Résolvez le système par élimination. \(\left\{\begin{array}{l}{x+\frac{3}{5} y=-\frac{1}{5}} \\ {-\frac{1}{2} x-\frac{2}{3} y=\frac{5}{6}}\end{array}\right.\)
- Réponse
-
(1, −2)
Dans Solving Systems of Equations by Graphing, nous avons vu que tous les systèmes d'équations linéaires n'ont pas une seule paire ordonnée comme solution. Lorsque les deux équations étaient vraiment identiques, il y avait une infinité de solutions. Nous avons appelé cela un système cohérent. Lorsque les deux équations décrivaient des lignes parallèles, il n'y avait pas de solution. Nous avons dit que c'était un système incohérent.
Résolvez le système par élimination. \(\left\{\begin{array}{l}{3 x+4 y=12} \\ {y=3-\frac{3}{4} x}\end{array}\right.\)
- Réponse
-
\(\begin{array} {ll} & \left\{\begin{aligned} 3 x+4 y &=12 \\ y &=3-\frac{3}{4} x \end{aligned}\right. \\\\\text{Write the second equation in standard form.} & \left\{\begin{array}{l}{3 x+4 y=12} \\ {\frac{3}{4} x+y=3}\end{array}\right.\\ \\ \text{Clear the fractions by multiplying thesecond equation by 4.} & \left\{\begin{aligned} 3 x+4 y &=12 \\ 4\left(\frac{3}{4} x+y\right) &=4(3) \end{aligned}\right. \\\\ \text{Simplify.} & \left\{\begin{array}{l}{3 x+4 y=12} \\ {3 x+4 y=12}\end{array}\right.\\\\ \text{To eliminate a variable, we multiply thesecond equation by −1.} & \left\{\begin{array}{c}{3 x+4 y=12} \\ \underline{-3 x-4 y=-12} \end{array}\right.\\ &\qquad\qquad\quad 0=0 \\ \text{Simplify and add.} \end{array}\)
C'est une affirmation vraie. Les équations sont cohérentes mais dépendantes. Leurs graphiques seraient sur la même ligne. Le système propose une infinité de solutions.
Après avoir effacé les fractions de la deuxième équation, avez-vous remarqué que les deux équations étaient identiques ? Cela signifie que nous avons des lignes coïncidentes.
Résolvez le système par élimination. \(\left\{\begin{array}{l}{5 x-3 y=15} \\ {y=-5+\frac{5}{3} x}\end{array}\right.\)
- Réponse
-
une infinité de solutions
Résolvez le système par élimination. \(\left\{\begin{array}{l}{x+2 y=6} \\ {y=-\frac{1}{2} x+3}\end{array}\right.\)
- Réponse
-
une infinité de solutions
Résolvez le système par élimination. \(\left\{\begin{array}{l}{-6 x+15 y=10} \\ {2 x-5 y=-5}\end{array}\right.\)
- Réponse
-
\(\begin{array} {ll} \text{The equations are in standard form.}& \left\{\begin{aligned}-6 x+15 y &=10 \\ 2 x-5 y &=-5 \end{aligned}\right. \\\\ \text{Multiply the second equation by 3 to eliminate a variable.} & \left\{\begin{array}{l}{-6 x+15 y=10} \\ {3(2 x-5 y)=3(-5)}\end{array}\right. \\\\ \text{Simplify and add.} & \left\{\begin{aligned}{-6 x+15 y =10} \\ \underline{6 x-15 y =-15} \end{aligned}\right. \\ & \qquad \qquad \quad0\neq 5 \end{array}\)
Cette déclaration est fausse. Les équations étant incohérentes, leurs graphes seraient des lignes parallèles.
Le système n'a pas de solution.
Résolvez le système par élimination. \(\left\{\begin{array}{l}{-3 x+2 y=8} \\ {9 x-6 y=13}\end{array}\right.\)
- Réponse
-
aucune solution
Résolvez le système par élimination. \(\left\{\begin{array}{l}{7 x-3 y=-2} \\ {-14 x+6 y=8}\end{array}\right.\)
- Réponse
-
aucune solution
Résoudre les applications de systèmes d'équations par élimination
Certains problèmes d'applications se traduisent directement en équations sous forme standard, nous utiliserons donc la méthode d'élimination pour les résoudre. Comme auparavant, nous utilisons notre stratégie de résolution de problèmes pour nous aider à rester concentrés et organisés.
La somme de deux nombres est 39. Leur différence est de 9. Trouve les numéros.
- Réponse
-
\(\begin{array} {ll} \textbf{Step 1. Read}\text{ the problem}& \\ \textbf{Step 2. Identify} \text{ what we are looking for.} & \text{We are looking for two numbers.} \\\textbf{Step 3. Name} \text{ what we are looking for.} & \text{Let n = the first number.} \\ & \text{ m = the second number} \\\textbf{Step 4. Translate} \text{ into a system of equations.}& \\ & \text{The sum of two numbers is 39.} \\ & n+m=39\\ & \text{Their difference is 9.} \\ & n−m=9 \\ \\ \text{The system is:} & \left\{\begin{array}{l}{n+m=39} \\ {n-m=9}\end{array}\right. \\\\ \textbf{Step 5. Solve} \text{ the system of equations. } & \\ \text{To solve the system of equations, use} \\ \text{elimination. The equations are in standard} \\ \text{form and the coefficients of m are} & \\ \text{opposites. Add.} & \left\{\begin{array}{l}{n+m=39} \\ \underline{n-m=9}\end{array}\right. \\ &\quad 2n\qquad=48 \\ \\\text{Solve for n.} & n=24 \\ \\ \text{Substitute n=24 into one of the original} &n+m=39 \\ \text{equations and solve form.} & 24+m=39 \\ & m=15 \\ \textbf{Step 6. Check}\text{ the answer.} & \text{Since 24+15=39 and 24−15=9, the answers check.}\\ \textbf{Step 7. Answer} \text{ the question.} & \text{The numbers are 24 and 15.} \end{array}\)
La somme de deux nombres est 42. Leur différence est de 8. Trouve les numéros.
- Réponse
-
Les chiffres sont 25 et 17.
La somme de deux nombres est de −15. Leur différence est de −35. Trouve les numéros.
- Réponse
-
Les nombres sont −25 et 10.
Joe s'arrête tous les jours dans un restaurant de hamburgers sur le chemin du travail. Lundi, il a pris une commande de frites moyennes et deux petits sodas, qui contenaient un total de 620 calories. Mardi, il a pris deux commandes de frites moyennes et un petit soda, pour un total de 820 calories. Combien de calories y a-t-il dans une commande de frites moyennes ? Combien de calories dans un petit soda ?
- Réponse
-
Étape 1. Lisez le problème. Étape 2. Identifiez ce que nous recherchons. Nous recherchons le nombre de
calories dans une commande de frites moyennes
et dans un petit soda.Étape 3. Nommez ce que nous recherchons. Soit f le nombre de calories dans
1 ordre de frites moyennes.
s = le nombre de calories dans
1 petit soda.Étape 4. Traduisez en un système d'équations : une frite moyenne et deux petits sodas contenaient un
total de 620 calories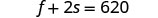
deux frites de taille moyenne et un petit soda contenaient un
total de 820 calories.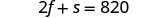
Notre système est le suivant : 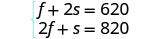
Étape 5. Résolvez le système d'équations.
Pour résoudre le système d'équations, utilisez
l'élimination. Les équations sont présentées sous
forme standard. Pour obtenir les coefficients opposés de f,
multipliez l'équation supérieure par −2.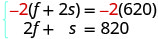
Simplifiez et ajoutez. 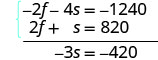
Résolvez pour nous. 
Remplacez s = 140 dans l'une des
équations d'origine, puis résolvez pour f.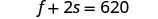
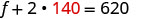
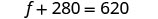
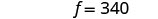
Étape 6. Vérifiez la réponse. Vérifiez que ces chiffres ont un sens
dans le problème et qu'ils constituent
des solutions aux deux équations.
Nous vous en laissons le soin !Étape 7. Réponds à la question. Le petit soda contient 140 calories et
les frites 340 calories.
Malik s'arrête à l'épicerie pour acheter un sac de couches et 2 canettes de lait maternisé. Il dépense au total 37$. La semaine suivante, il s'arrête et achète 2 sacs de couches et 5 canettes de lait maternisé pour un total de 87$. Combien coûte un sac de couches ? Combien coûte une boîte de lait maternisé ?
- Réponse
-
Le sac de couches coûte 11$ et la boîte de lait maternisé coûte 13$.
Pour obtenir sa consommation quotidienne de fruits pour la journée, Sasha mange une banane et 8 fraises le mercredi pour un nombre de calories de 145. Le mercredi suivant, elle mange deux bananes et 5 fraises pour un total de 235 calories pour le fruit. Combien de calories y a-t-il dans une banane ? Combien de calories contient une fraise ?
- Réponse
-
Il y a 105 calories dans une banane et 5 calories dans une fraise.
Choisissez la méthode la plus pratique pour résoudre un système d'équations linéaires
Lorsque vous devrez résoudre un système d'équations linéaires dans un cours de mathématiques ultérieur, on ne vous dira généralement pas quelle méthode utiliser. Vous devrez prendre cette décision vous-même. Vous devez donc choisir la méthode la plus simple à utiliser et qui minimise les risques d'erreur.

Pour chaque système d'équations linéaires, décidez s'il serait plus pratique de le résoudre par substitution ou par élimination. Expliquez votre réponse.
- \(\left\{\begin{array}{l}{3 x+8 y=40} \\ {7 x-4 y=-32}\end{array}\right.\)
- \(\left\{\begin{array}{l}{5 x+6 y=12} \\ {y=\frac{2}{3} x-1}\end{array}\right.\)
- Réponse
-
1. \(\left\{\begin{array}{l}{3 x+8 y=40} \\ {7 x-4 y=-32}\end{array}\right.\)
Comme les deux équations se présentent sous une forme standard, l'élimination sera plus pratique.
2. \(\left\{\begin{array}{l}{5 x+6 y=12} \\ {y=\frac{2}{3} x-1}\end{array}\right.\)
Comme une équation est déjà résolue pour y, l'utilisation de la substitution sera plus pratique.
Pour chaque système d'équations linéaires, décidez s'il serait plus pratique de le résoudre par substitution ou par élimination. Expliquez votre réponse.
- \(\left\{\begin{array}{l}{4 x-5 y=-32} \\ {3 x+2 y=-1}\end{array}\right.\)
- \(\left\{\begin{array}{l}{x=2 y-1} \\ {3 x-5 y=-7}\end{array}\right.\)
- Réponse
-
- Comme les deux équations se présentent sous une forme standard, l'élimination sera plus pratique.
- Comme une équation est déjà résolue pour xx, l'utilisation de la substitution sera plus pratique.
Pour chaque système d'équations linéaires, décidez s'il serait plus pratique de le résoudre par substitution ou par élimination. Expliquez votre réponse.
- \(\left\{\begin{array}{l}{y=2 x-1} \\ {3 x-4 y=-6}\end{array}\right.\)
- \(\left\{\begin{array}{l}{6 x-2 y=12} \\ {3 x+7 y=-13}\end{array}\right.\)
- Réponse
-
- Comme une équation est déjà résolue pour yy, l'utilisation de la substitution sera la plus pratique ;
- Comme les deux équations se présentent sous une forme standard, l'élimination sera plus pratique.
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à résoudre des systèmes d'équations linéaires par élimination.
- Systèmes pédagogiques de résolution vidéo d'équations par élimination
- Résolution de vidéos pédagogiques par élimination
- Systèmes de résolution vidéo pédagogique par élimination
Concepts clés
- Pour résoudre un système d'équations par élimination
- Écrivez les deux équations sous forme standard. Si certains coefficients sont des fractions, supprimez-les.
- Faites en sorte que les coefficients d'une variable soient opposés.
- Déterminez quelle variable vous allez éliminer.
- Multipliez l'une des équations ou les deux de manière à ce que les coefficients de cette variable soient opposés.
- Ajoutez les équations résultant de l'étape 2 pour éliminer une variable.
- Résolvez pour la variable restante.
- Remplacez la solution de l'étape 4 par l'une des équations d'origine. Résolvez ensuite pour l'autre variable.
- Écrivez la solution sous la forme d'une paire ordonnée.
- Vérifiez que la paire ordonnée est une solution aux deux équations d'origine.


