5.2 : Résoudre des systèmes d'équations par substitution
- Page ID
- 194462
À la fin de cette section, vous serez en mesure de :
- Résoudre un système d'équations par substitution
- Résoudre des applications de systèmes d'équations par substitution
Avant de commencer, répondez à ce questionnaire de préparation.
- Simplifiez −5 (3−x).
Si vous avez oublié ce problème, passez en revue l'exercice 1.10.43. - Simplifiez 4−2 (n+5).
Si vous avez oublié ce problème, passez en revue l'exercice 1.10.41. - Résolvez pour y. 8y−8=32−2y
Si vous avez oublié ce problème, passez en revue l'exercice 2.3.22. - Résolvez pour x. 3x−9y=−3
Si vous avez oublié ce problème, passez en revue l'exercice 2.6.22.
La résolution de systèmes d'équations linéaires à l'aide de graphiques est un bon moyen de visualiser les types de solutions qui peuvent en résulter. Cependant, dans de nombreux cas, la résolution graphique d'un système n'est pas pratique ou imprécise. Si les graphes s'étendent au-delà de la petite grille avec x et y compris entre −10 et 10, la représentation graphique des lignes peut s'avérer fastidieuse. Et si les solutions du système ne sont pas des nombres entiers, il peut être difficile de lire leurs valeurs avec précision à partir d'un graphique.
Dans cette section, nous allons résoudre des systèmes d'équations linéaires par la méthode de substitution.
Résoudre un système d'équations par substitution
Nous utiliserons le même système que celui que nous avons utilisé en premier pour la création de graphiques.
\(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)
Nous allons d'abord résoudre l'une des équations pour x ou y. Nous pouvons choisir l'une ou l'autre des équations et résoudre l'une ou l'autre variable, mais nous essaierons de faire un choix qui facilitera le travail.
Ensuite, nous substituons cette expression dans l'autre équation. Le résultat est une équation avec une seule variable, et nous savons comment les résoudre !
Après avoir trouvé la valeur d'une variable, nous la remplacerons dans l'une des équations d'origine et la résoudrons pour l'autre variable. Enfin, nous vérifions notre solution et nous nous assurons qu'elle rend les deux équations vraies.
Nous allons maintenant compléter toutes ces étapes dans Exercice\(\PageIndex{1}\).
Résolvez le système par substitution. \(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)
- Réponse
-






Résolvez le système par substitution. \(\left\{\begin{array}{l}{-2 x+y=-11} \\ {x+3 y=9}\end{array}\right.\)
- Réponse
-
(6,1)
Résolvez le système par substitution. \(\left\{\begin{array}{l}{x+3 y=10} \\ {4 x+y=18}\end{array}\right.\)
- Réponse
-
(4,2)
- Résolvez l'une des équations pour chaque variable.
- Remplacez l'expression de l'étape 1 dans l'autre équation.
- Résolvez l'équation résultante.
- Remplacez la solution de l'étape 3 dans l'une des équations d'origine pour trouver l'autre variable.
- Écrivez la solution sous la forme d'une paire ordonnée.
- Vérifiez que la paire ordonnée est une solution aux deux équations d'origine.
Si l'une des équations du système est donnée sous forme pente-intersection, l'étape 1 est déjà terminée ! Nous verrons cela dans Exercice\(\PageIndex{4}\).
Résolvez le système par substitution. \(\left\{\begin{array}{l}{x+y=-1} \\ {y=x+5}\end{array}\right.\)
- Réponse
-
La deuxième équation est déjà résolue pour y. Nous allons remplacer l'expression par y dans la première équation.
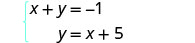
La deuxième équation est déjà résolue pour y.
Nous allons la remplacer dans la première équation.Remplacez le y par x + 5. 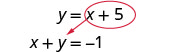
Résolvez l'équation résultante pour x. 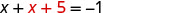
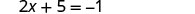
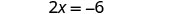
Remplacez x = −3 par y = x + 5 pour trouver y. 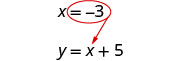
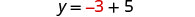
La paire ordonnée est (−3, 2). 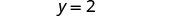
Vérifiez la paire ordonnée dans les deux équations :
\(\begin{array} {rllrll} x+y &=&-1 & y&=&x+5\\-3+2 &\stackrel{?}{=}&-1 &2& \stackrel{?}{=} & -3 + 5\\-1 &=&-1\checkmark &2 &=&2\checkmark \end{array}\)La solution est (−3, 2).
Résolvez le système par substitution. \(\left\{\begin{array}{l}{x+y=6} \\ {y=3 x-2}\end{array}\right.\)
- Réponse
-
(2,4)
Résolvez le système par substitution. \(\left\{\begin{array}{l}{2 x-y=1} \\ {y=-3 x-6}\end{array}\right.\)
- Réponse
-
(−1, −3)
Si les équations sont données sous forme standard, nous devrons commencer par résoudre l'une des variables. Dans l'exemple suivant, nous allons résoudre la première équation pour y.
Résolvez le système par substitution. \(\left\{\begin{array}{l}{3 x+y=5} \\ {2 x+4 y=-10}\end{array}\right.\)
- Réponse
-
Nous devons résoudre une équation pour une variable. Nous remplacerons ensuite cette expression dans l'autre équation.
Résolvez pour y.
Substituez dans l'autre équation.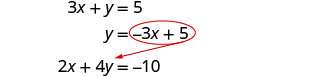
Remplacez le y par −3 x + 5. 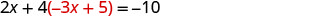
Résolvez l'équation résultante pour x. 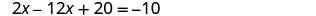
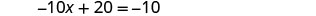
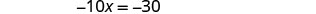
Remplacez x = 3 par 3 x + y = 5 pour trouver y. 


La paire ordonnée est (3, −4). 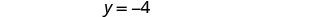
Vérifiez la paire ordonnée dans les deux équations :
\(\begin{array} {rllrll} 3x+y &=&5 & 2x+4y&=&-10\\3\cdot3+(-4) &\stackrel{?}{=}&5 &2\cdot3 + 4(-4)& \stackrel{?}{=} & -10\\9-4&\stackrel{?}{=}&5 &6-16& \stackrel{?}{=} & -10\\5 &=&5\checkmark &-10&=&-10\checkmark \end{array}\)La solution est (3, -4).
Résolvez le système par substitution. \(\left\{\begin{array}{l}{4 x+y=2} \\ {3 x+2 y=-1}\end{array}\right.\)
- Réponse
-
(1, −2)
Résolvez le système par substitution. \(\left\{\begin{array}{l}{-x+y=4} \\ {4 x-y=2}\end{array}\right.\)
- Réponse
-
(2,6)
Dans l'exercice,\(\PageIndex{7}\) il était plus facile de résoudre y dans la première équation car son coefficient était de 1. Dans l'exercice,\(\PageIndex{10}\) il sera plus facile de résoudre x.
Résolvez le système par substitution. \(\left\{\begin{array}{l}{x-2 y=-2} \\ {3 x+2 y=34}\end{array}\right.\)
- Réponse
-
Nous allons résoudre la première équation pour xx, puis substituer l'expression dans la deuxième équation.

Résolvez pour x.
Substituez dans l'autre équation.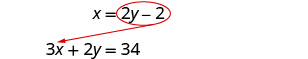
Remplacez le x par 2 y − 2. 
Résolvez l'équation résultante pour y. 
Remplacez y = 5 par x − 2 y = −2 pour trouver x.

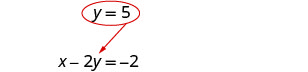



La paire commandée est (8, 5). Vérifiez la paire ordonnée dans les deux équations :
\(\begin{array} {rllrll} x-2y &=&-2 & 3x+2y&=&34\\8-2\cdot 5 &\stackrel{?}{=}&-2 &3\cdot8 + 2\cdot5& \stackrel{?}{=} & 34\\8-10&\stackrel{?}{=}&-2 &24+10& \stackrel{?}{=} & 34\\-2 &=&-2\checkmark &34&=&34\checkmark \end{array}\)La solution est (8, 5).
Résolvez le système par substitution. \(\left\{\begin{array}{l}{x-5 y=13} \\ {4 x-3 y=1}\end{array}\right.\)
- Réponse
-
(−2, −3)
Résolvez le système par substitution. \(\left\{\begin{array}{l}{x-6 y=-6} \\ {2 x-4 y=4}\end{array}\right.\)
- Réponse
-
(6,2)
Lorsque les deux équations sont déjà résolues pour la même variable, il est facile de les remplacer !
Résolvez le système par substitution. \(\left\{\begin{array}{l}{y=-2 x+5} \\ {y=\frac{1}{2} x}\end{array}\right.\)
- Réponse
-
Puisque les deux équations sont résolues pour y, nous pouvons les remplacer l'une par l'autre.
Remplacez\(\frac{1}{2}x\) y dans la première équation. 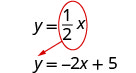
Remplacez le y par\(\frac{1}{2}x\) 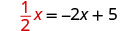
Résolvez l'équation résultante. Commencez
par effacer la fraction.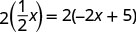
Résolvez pour x. 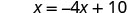
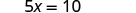
Remplacez x = 2 par\(y = \frac{1}{2}x\) pour trouver y. 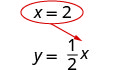
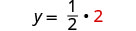
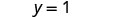
La paire commandée est (2,1). Vérifiez la paire ordonnée dans les deux équations :
\(\begin{array} {rllrll} y &=&\frac{1}{2}x & y&=&-2x+5\\1 &\stackrel{?}{=}&\frac{1}{2}\cdot2 &1& \stackrel{?}{=} & -2\cdot2+5\\1 &=&1\checkmark &1 &=&-4+5\\ &&&1&=&1\checkmark \end{array}\)La solution est (2,1).
Résolvez le système par substitution. \(\left\{\begin{array}{l}{y=3 x-16} \\ {y=\frac{1}{3} x}\end{array}\right.\)
- Réponse
-
(6,2)
Résolvez le système par substitution. \(\left\{\begin{array}{l}{y=-x+10} \\ {y=\frac{1}{4} x}\end{array}\right.\)
- Réponse
-
(8,2)
Soyez très prudent avec les signes de l'exemple suivant.
Résolvez le système par substitution. \(\left\{\begin{array}{l}{4 x+2 y=4} \\ {6 x-y=8}\end{array}\right.\)
- Réponse
-
Nous devons résoudre une équation pour une variable. Nous allons résoudre la première équation pour y.

Résolvez la première équation pour y. 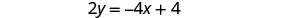
Dans la deuxième équation, remplacez y par −2 x + 2. 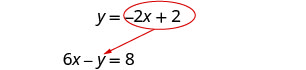
Remplacez le y par −2 x + 2. 
Résolvez l'équation pour x. 


\(x = \frac{5}{4}\)Remplacez par 4 x + 2 y = 4 pour trouver y.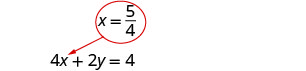



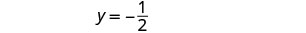
La paire commandée est\((\frac{5}{4},−\frac{1}{2})\). Vérifiez la paire ordonnée dans les deux équations.
\(\begin{array} {rllrll} 4x+2y &=&4& 6x-y&=&8\\4(\frac{5}{4}) +2(-\frac{1}{2})&\stackrel{?}{=}&4 &6(\frac{5}{4}) - (-\frac{1}{2})& \stackrel{?}{=} & 8\\5-1&\stackrel{?}{=}&4 &\frac{15}{4} - (-\frac{1}{2}) &\stackrel{?}{=} & 8\\4 &=&4\checkmark &\frac{16}{2} &\stackrel{?}{=}&8\\ &&&8&=&8\checkmark \end{array}\)La solution est (54, -12).
Résolvez le système par substitution. \(\left\{\begin{array}{l}{x-4 y=-4} \\ {-3 x+4 y=0}\end{array}\right.\)
- Réponse
-
\((2,\frac{3}{2})\)
Résolvez le système par substitution. \(\left\{\begin{array}{l}{4 x-y=0} \\ {2 x-3 y=5}\end{array}\right.\)
- Réponse
-
\((−\frac{1}{2},−2)\)
Dans l'exemple, il faudra un peu plus de travail pour résoudre une équation pour x ou y.
Résolvez le système par substitution. \(\left\{\begin{array}{l}{4 x-3 y=6} \\ {15 y-20 x=-30}\end{array}\right.\)
- Réponse
-
Nous devons résoudre une équation pour une variable. Nous allons résoudre la première équation pour x.
Puisque 0 = 0 est une déclaration vraie, le système est cohérent. Les équations sont dépendantes. Les graphes de ces deux équations donneraient la même droite. Le système propose une infinité de solutions.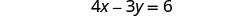
Résolvez la première équation pour x. 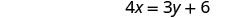
Remplacez\(\frac{3}{4} y+\frac{3}{2}\) x dans la deuxième équation. 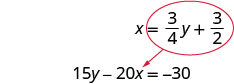
Remplacez le x par\(\frac{3}{4} y+\frac{3}{2}\) 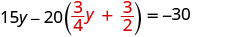
Résolvez pour y. 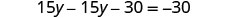
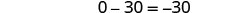

Résolvez le système par substitution. \(\left\{\begin{array}{l}{2 x-3 y=12} \\ {-12 y+8 x=48}\end{array}\right.\)
- Réponse
-
une infinité de solutions
Résolvez le système par substitution. \(\left\{\begin{array}{l}{5 x+2 y=12} \\ {-4 y-10 x=-24}\end{array}\right.\)
- Réponse
-
une infinité de solutions
Revenez aux équations de l'exercice\(\PageIndex{22}\). Y a-t-il un moyen de reconnaître qu'il s'agit de la même lignée ?
Voyons ce qui se passe dans l'exemple suivant.
Résolvez le système par substitution. \(\left\{\begin{array}{l}{5 x-2 y=-10} \\ {y=\frac{5}{2} x}\end{array}\right.\)
- Réponse
-
La deuxième équation est déjà résolue pour y, nous pouvons donc remplacer y dans la première équation.
Puisque 0 = −10 est une fausse déclaration, les équations sont incohérentes. Les graphes des deux équations seraient des lignes parallèles. Le système ne propose aucune solution.Remplacez x par y dans la première équation. 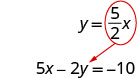
Remplacez le y par\(\frac{5}{2}x\). 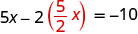
Résolvez pour x. 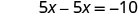

Résolvez le système par substitution. \(\left\{\begin{array}{l}{3 x+2 y=9} \\ {y=-\frac{3}{2} x+1}\end{array}\right.\)
- Réponse
-
aucune solution
Résolvez le système par substitution. \(\left\{\begin{array}{l}{5 x-3 y=2} \\ {y=\frac{5}{3} x-4}\end{array}\right.\)
- Réponse
-
aucune solution
Résoudre les applications de systèmes d'équations par substitution
Nous allons copier ici la stratégie de résolution de problèmes que nous avons utilisée dans la section Résolution de systèmes d'équations par représentation graphique pour résoudre des systèmes d'équations. Maintenant que nous savons comment résoudre des systèmes par substitution, c'est ce que nous allons faire à l'étape 5.
- Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris.
- Identifiez ce que nous recherchons.
- Nommez ce que nous recherchons. Choisissez des variables pour représenter ces quantités.
- Traduisez en un système d'équations.
- Résolvez le système d'équations en utilisant de bonnes techniques d'algèbre.
- Vérifiez la réponse au problème et assurez-vous qu'elle est logique.
- Répondez à la question par une phrase complète.
Certaines personnes trouvent qu'il est plus facile de configurer des problèmes de mots avec deux variables que de les configurer avec une seule variable. Le choix des noms de variables est plus facile lorsque vous n'avez qu'à écrire deux lettres. Réfléchissez à cela dans l'exemple suivant : comment l'auriez-vous fait avec une seule variable ?
La somme de deux nombres est égale à zéro. Un chiffre est neuf de moins que l'autre. Trouve les numéros.
- Réponse
-
Étape 1 Lisez le problème. Étape 2 Identifiez ce que nous recherchons. Nous recherchons deux chiffres. Étape 3. Nommez ce que nous recherchons. Soit n = le premier nombre
Soit m = le deuxième nombreÉtape 4. Traduisez en un système d'équations. La somme de deux nombres est égale à zéro. 
Un chiffre est neuf de moins que l'autre. 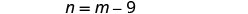
Le système est le suivant : 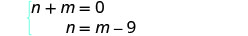
Étape 5. Résolvez le système d'
équations. Nous utiliserons la substitution
puisque la deuxième équation est résolue
pour n.Dans la première équation, remplacez m − 9 par n. 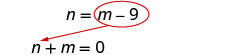
Résolvez pour moi. 


Substituez\(m=\frac{9}{2}\) dans la deuxième équation,
puis résolvez pour n.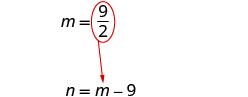
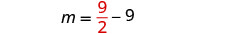
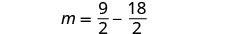
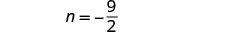
Étape 6. Vérifiez la réponse au problème. Ces chiffres ont-ils un sens dans
le problème ? Nous vous en remettons à vous !Étape 7. Réponds à la question. Les chiffres sont\(\frac{9}{2}\) et\(-\frac{9}{2}\).
La somme de deux nombres est de 10. Un chiffre est inférieur de 4 à l'autre. Trouve les numéros.
- Réponse
-
Les chiffres sont 3 et 7.
La somme de deux nombres est de −6. Un chiffre est inférieur de 10 à l'autre. Trouve les numéros.
- Réponse
-
Les nombres sont 2 et −8.
Dans l'exercice\(\PageIndex{28}\), nous utiliserons la formule pour le périmètre d'un rectangle, P = 2 L + 2 W.
Ajoutez le texte des exercices ici.
- Réponse
-
Étape 1 Lisez le problème. 
Étape 2 Identifiez ce que vous recherchez. Nous recherchons la longueur et la largeur. Étape 3 Nommez ce que nous recherchons. Soit L = la longueur
W = la largeurÉtape 4. Traduisez en un système d'équations. Le périmètre d'un rectangle est de 88. 2 L+2 W = P
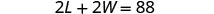
La longueur est cinq fois plus que deux fois la largeur. 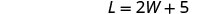
Le système est le suivant : 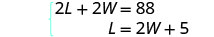
Étape 5. Résolvez le système d'équations.
Nous utiliserons la substitution puisque la deuxième
équation est résolue pour L.
Dans la première équation, remplacez 2 W + 5 par L.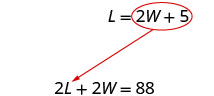
Résolvez pour W. 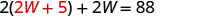
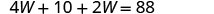
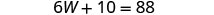
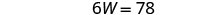
Remplacez W = 13 dans la deuxième
équation, puis résolvez pour L.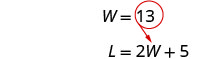
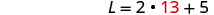
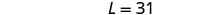
Étape 6 Vérifiez la réponse au problème. Un rectangle d'une longueur 31 et d'une largeur de
13 a-t-il un périmètre de 88 ? Oui.Étape 7 Répondez à l'équation. La longueur est de 31 et la largeur de 13.
Le périmètre d'un rectangle est de 40. La longueur est supérieure de 4 % à la largeur. Détermine la longueur et la largeur du rectangle.
- Réponse
-
La longueur est de 12 et la largeur de 8.
Le périmètre d'un rectangle est de 58. La longueur est 5 fois plus que trois fois la largeur. Détermine la longueur et la largeur du rectangle.
- Réponse
-
La longueur est de 23 et la largeur de 6.
Pour l'exercice,\(\PageIndex{31}\) nous devons nous rappeler que la somme des mesures des angles d'un triangle est de 180 degrés et qu'un triangle droit a un angle de 90 degrés.
La mesure de l'un des petits angles d'un triangle droit est dix fois plus que trois fois la mesure de l'autre petit angle. Trouvez les mesures des deux angles.
- Réponse
-
Nous allons dessiner et étiqueter une figure.
Étape 1 Lisez le problème. 
Étape 2 Identifiez ce que vous recherchez. Nous recherchons les mesures des angles. Étape 3 Nommez ce que nous recherchons. Soit a = la mesure du 1 er angle
b = la mesure du 2 ème angleÉtape 4. Traduisez en un système d'équations. La mesure de l'un des petits angles
d'un triangle droit est dix fois plus que trois
fois la mesure de l'autre petit angle.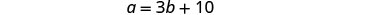
La somme des mesures des angles d'
un triangle est de 180.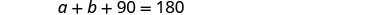
Le système est le suivant : 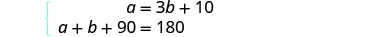
Étape 5. Résolvez le système d'équations.
Nous utiliserons la substitution puisque la première
équation est résolue pour a.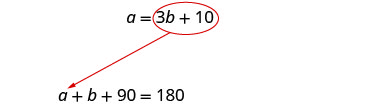
Dans la
deuxième équation, remplacez a par 3 b + 10.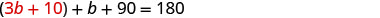
Résolvez pour b. 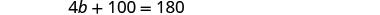


Substituez b = 20 dans la première
équation, puis résolvez pour a.

Étape 6 Vérifiez la réponse au problème. Nous vous en remettons à vous ! Étape 7 Réponds à la question. Les mesures des petits angles sont de
20 et 70.
La mesure de l'un des petits angles d'un triangle droit est 2 fois plus que 3 fois la mesure de l'autre petit angle. Détermine la mesure des deux angles.
- Réponse
-
La mesure des angles est de 22 degrés et 68 degrés.
La mesure de l'un des petits angles d'un triangle droit est inférieure de 18 à deux fois la mesure de l'autre petit angle. Détermine la mesure des deux angles.
- Réponse
-
La mesure des angles est de 36 degrés et 54 degrés.
Heather s'est vu offrir deux options pour son salaire en tant qu'entraîneuse au gymnase. L'option A lui verserait 25 000$ plus 15$ pour chaque séance de formation. L'option B lui verserait 10 000$ plus 40$ pour chaque séance de formation. Combien de sessions de formation rendraient les options salariales égales ?
- Réponse
-
Étape 1 Lisez le problème. Étape 2 Identifiez ce que vous recherchez. Nous recherchons le nombre de sessions de formation
qui permettraient d'obtenir un salaire égal.Étape 3 Nommez ce que nous recherchons. Soit le salaire d'Heather.
n= le nombre de séances d'entraînementÉtape 4. Traduisez en un système d'équations. L'option A lui verserait 25 000$ plus 15$
pour chaque séance de formation.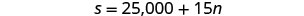
L'option B lui verserait 10 000$ plus 40$
pour chaque séance de formation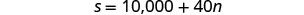
Le système est le suivant : 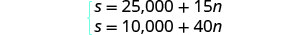
Étape 5. Résolvez le système d'équations.
Nous utiliserons la substitution.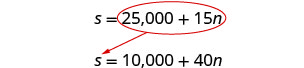
Remplacez 25 000 + 15 n par s dans la deuxième équation. 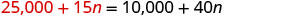
Résolvez pour n. 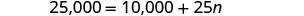
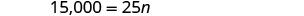

Étape 6 Vérifiez la réponse. 600 sessions de formation par an sont-elles raisonnables ?
Les deux options sont-elles égales lorsque n = 600 ?Étape 7 Réponds à la question. Les options salariales seraient égales pour 600 sessions de formation.
Géraldine s'est vu proposer des postes par deux compagnies d'assurance. La première entreprise verse un salaire de 12 000$ plus une commission de 100$ pour chaque police vendue. Le second verse un salaire de 20 000$ plus une commission de 50$ pour chaque police vendue. Combien de polices devraient être vendues pour que le salaire total soit le même ?
- Réponse
-
Il faudrait vendre 160 polices pour que le salaire total soit le même.
Kenneth vend actuellement des costumes pour l'entreprise A à un salaire de 22 000$ plus une commission de 10$ pour chaque costume vendu. La société B lui offre un poste avec un salaire de 28 000$ plus une commission de 4$ pour chaque costume vendu. Combien de costumes Kenneth devrait-il vendre pour que les options soient égales ?
- Réponse
-
Kenneth aurait besoin de vendre 1 000 costumes.
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à résoudre des systèmes d'équations par substitution.
Concepts clés
- Résoudre un système d'équations par substitution
- Résolvez l'une des équations pour chaque variable.
- Remplacez l'expression de l'étape 1 dans l'autre équation.
- Résolvez l'équation résultante.
- Remplacez la solution de l'étape 3 dans l'une des équations d'origine pour trouver l'autre variable.
- Écrivez la solution sous la forme d'une paire ordonnée.
- Vérifiez que la paire ordonnée est une solution aux deux équations d'origine.


