Skip to main content
Global

5.1 : Résoudre des systèmes d'équations en les représentant graphiquement

  1. Last updated
  2. Save as PDF
  • Page ID
    194514

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Déterminer si une paire ordonnée est la solution d'un système d'équations
    • Résolvez un système d'équations linéaires en traçant un graphique
    • Déterminer le nombre de solutions d'un système linéaire
    • Résolvez des applications de systèmes d'équations en graphiant
    Remarque

    Avant de commencer, répondez à ce questionnaire de préparation.

    1. Pour l'équation\(y=\frac{2}{3}x−4\)
      ⓐ est-ce que (6,0) est une solution ? ⓑ est (−3, −2) une solution ?
      Si vous avez oublié ce problème, passez en revue l'exercice 2.1.1.
    2. Détermine la pente et l'intersection y de la droite 3x−y=12.
      Si vous avez oublié ce problème, passez en revue l'exercice 4.5.7.
    3. Détermine les interceptions x et y de la ligne 2x−3y=12.
      Si vous avez oublié ce problème, passez en revue l'exercice 4.3.7.

    Déterminer si une paire ordonnée est la solution d'un système d'équations

    Dans la section sur la résolution d'équations et d'inégalités linéaires, nous avons appris à résoudre des équations linéaires avec une variable. N'oubliez pas que la solution d'une équation est une valeur de la variable qui produit une déclaration vraie lorsqu'elle est substituée dans l'équation. Nous allons maintenant travailler avec des systèmes d'équations linéaires, c'est-à-dire deux équations linéaires ou plus regroupées.

    Définition : SYSTÈME D'ÉQUATIONS LINÉAIRES

    Lorsque deux équations linéaires ou plus sont regroupées, elles forment un système d'équations linéaires.

    Nous concentrerons nos travaux ici sur des systèmes de deux équations linéaires dans deux inconnues. Plus tard, vous pouvez résoudre de plus grands systèmes d'équations.

    Un exemple de système de deux équations linéaires est présenté ci-dessous. Nous utilisons une accolade pour montrer que les deux équations sont regroupées pour former un système d'équations.

    \[\begin{cases}{2 x+y=7} \\ {x-2 y=6}\end{cases}\]

    Une équation linéaire à deux variables, comme 2 x + y = 7, possède un nombre infini de solutions. Son graphique est une ligne. N'oubliez pas que chaque point de la ligne est une solution à l'équation et que chaque solution à l'équation est un point sur la ligne.

    Pour résoudre un système de deux équations linéaires, nous voulons trouver les valeurs des variables qui sont des solutions aux deux équations. En d'autres termes, nous recherchons les paires ordonnées (x, y) qui rendent les deux équations vraies. C'est ce que l'on appelle les solutions à un système d'équations.

    Définition : SOLUTIONS D'UN SYSTÈME D'ÉQUATIONS

    Les solutions d'un système d'équations sont les valeurs des variables qui rendent toutes les équations vraies. La solution d'un système de deux équations linéaires est représentée par une paire ordonnée (x, y).

    Pour déterminer si une paire ordonnée est une solution à un système de deux équations, nous substituons les valeurs des variables dans chaque équation. Si la paire ordonnée rend les deux équations vraies, c'est une solution pour le système.

    Considérons le système ci-dessous :

    \[\begin{cases}{3x−y=7} \\ {x−2y=4}\end{cases}\]

    La paire ordonnée (2, -1) est-elle une solution ?

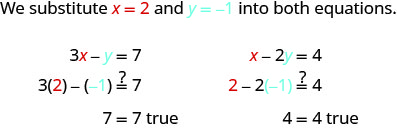
    Cette figure commence par une phrase : « Nous substituons x =2 et y = -1 dans les deux équations. » La première équation montre que 3x moins y est égal à 7. Ensuite, 3 fois 2 moins un négatif, entre parenthèses, équivaut à 7. Alors 7 est égal à 7, c'est vrai. La deuxième équation indique que x moins 2y est égal à 4. Ensuite, 2 moins 2 fois moins un négatif entre parenthèses équivaut à 4. Alors 4 = 4 est vrai.

    La paire ordonnée (2, -1) a confirmé la véracité des deux équations. (2, -1) est donc une solution à ce système.

    Essayons une autre paire commandée. La paire commandée (3, 2) est-elle une solution ?

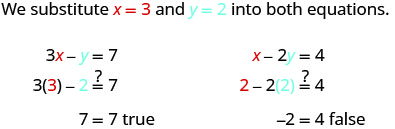
    Cette figure commence par la phrase « Nous substituons x égal à 3 et y est égal à 2 dans les deux équations ». La première équation se lit comme suit : 3 fois x moins 7 est égal à 7. Ensuite, 3 fois 3 moins 2 égale 7. Alors 7 = 7 est vrai. La deuxième équation indique que x moins 2y est égal à 4. Les n fois 2 moins 2 fois 2 = 4. Donc, moins 2 = 4 est faux.

    La paire ordonnée (3, 2) a rendu une équation vraie, mais a rendu l'autre équation fausse. Comme il ne s'agit pas d'une solution aux deux équations, il ne s'agit pas d'une solution à ce système.

    Exercice\(\PageIndex{1}\)

    Déterminez si la paire commandée est une solution pour le système :\(\begin{cases}{x−y=−1} \\ {2x−y=−5}\end{cases}\)

    1. (−2, −1)
    2. (−4, −3)
    Réponse

    1.
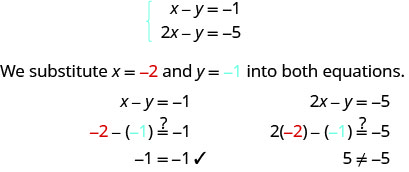
    Cette figure montre deux équations entre crochets. Le premier est x moins y = moins 1. La seconde est 2 fois x moins y égale moins 5. La phrase suivante : « Nous substituons x = moins 2 et y = 1 dans les deux équations ». La première équation montre la substitution et révèle que moins 1 = négatif 1. La deuxième équation montre la substitution et révèle que 5 ne sont pas égaux à -5. Sous la première équation se trouve la phrase « (négatif 2, négatif 1) ne rend pas les deux équations vraies ». Sous la deuxième équation se trouve la phrase « (négatif 2, négatif 1) n'est pas une solution ».
    (−2, −1) ne rend pas les deux équations vraies. (−2, −1) n'est pas une solution.

    2.
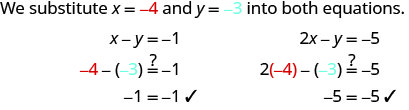
    Cette figure commence par la phrase « Nous substituons x = -4 et y = -3 dans les deux équations ». La première équation répertoriée montre x — y = -1. Alors -4 - (-3) = -1. Alors -1 = -1. La deuxième équation répertoriée montre 2x — y = -5. Puis 2 fois (-4) — (-3) = -5. Alors -5 = -5. Sous la première équation se trouve la phrase « (-4, -3) rend les deux équations vraies ». Sous la deuxième équation se trouve la phrase « (-4, -3) est une solution ».
    (−4, −3) ne rend pas les deux équations vraies. (−4, −3) est une solution.

    Exercice\(\PageIndex{2}\)

    Déterminez si la paire commandée est une solution pour le système :\(\begin{cases}{3x+y=0} \\ {x+2y=−5}\end{cases}\)

    1. (1, −3)
    2. (0,0)
    Réponse
    1. oui
    2. non
    Exercice\(\PageIndex{3}\)

    Déterminez si la paire commandée est une solution pour le système :\(\begin{cases}{x−3y=−8} \\ {−3x−y=4}\end{cases}\)

    1. (2, −2)
    2. (−2,2)
    Réponse
    1. non
    2. oui

    Résolvez un système d'équations linéaires en traçant un graphique

    Dans ce chapitre, nous utiliserons trois méthodes pour résoudre un système d'équations linéaires. La première méthode que nous utiliserons est la création graphique. Le graphique d'une équation linéaire est une droite. Chaque point de la ligne est une solution à l'équation. Pour un système de deux équations, nous allons représenter graphiquement deux droites. Ensuite, nous pouvons voir tous les points qui sont des solutions à chaque équation. Et, en découvrant ce que les lignes ont en commun, nous trouverons la solution au système.

    La plupart des équations linéaires d'une variable ont une solution, mais nous avons vu que certaines équations, appelées contradictions, n'ont pas de solution et que pour d'autres équations, appelées identités, tous les nombres sont des solutions. De même, lorsque nous résolvons un système de deux équations linéaires représentées par un graphe de deux lignes dans le même plan, il existe trois cas possibles, comme le montre la figure\(\PageIndex{1}\) :

    Cette figure montre trois plans de coordonnées x y. Le premier plan montre deux lignes qui se croisent en un point. Sous le graphique, il est écrit : « Les lignes se croisent. Les lignes qui se croisent ont un point commun. Il existe une solution à ce système. » Le deuxième plan de coordonnées x y montre deux lignes parallèles. Sous le graphique, il est écrit : « Les lignes sont parallèles. Les lignes parallèles n'ont aucun point commun. Il n'y a pas de solution à ce système. » Le troisième plan de coordonnées x y montre une ligne. Sous le graphique, il est écrit : « Les deux équations donnent la même droite. Comme nous n'avons qu'une seule ligne, il existe une infinité de solutions. »
    Figurine\(\PageIndex{1}\)

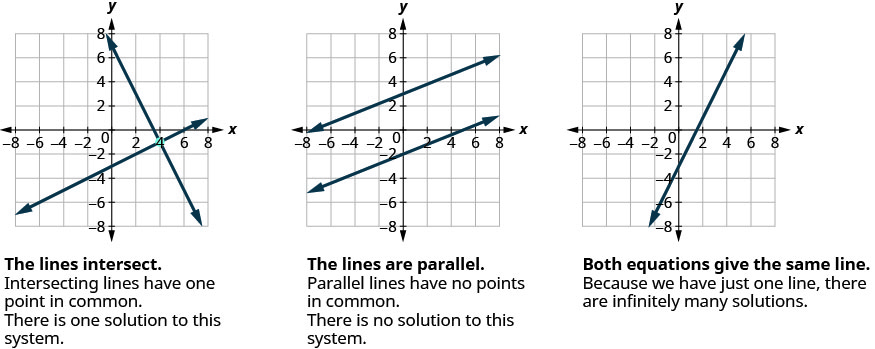
    Pour le premier exemple de résolution d'un système d'équations linéaires dans cette section et dans les deux sections suivantes, nous allons résoudre le même système de deux équations linéaires. Mais nous utiliserons une méthode différente dans chaque section. Après avoir vu la troisième méthode, vous déciderez quelle est la méthode la plus pratique pour résoudre ce système.

    Exercice\(\PageIndex{4}\): How to Solve a System of Linear Equations by Graphing

    Résolvez le système en représentant graphiquement :\(\begin{cases}{2x+y=7} \\ {x−2y=6}\end{cases}\)

    Réponse

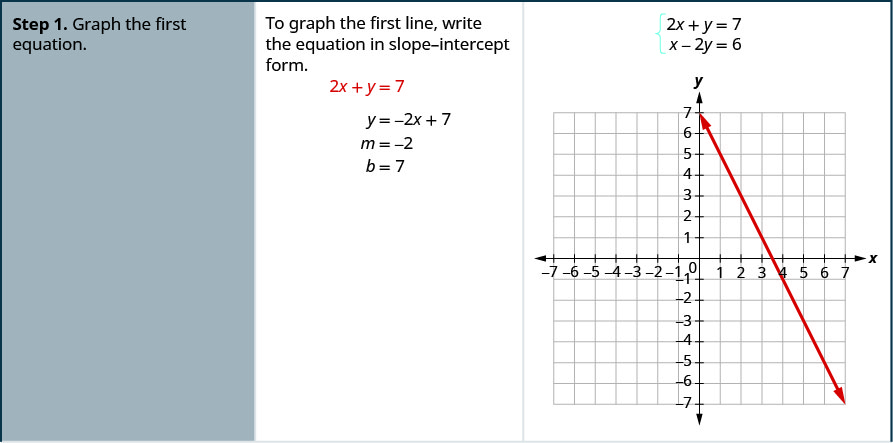
    Ce tableau comporte quatre lignes et trois colonnes. La première colonne fait office de colonne d'en-tête. La première rangée se lit comme suit : « Étape 1. Tracez la première équation. » Ensuite, on peut lire : « Pour tracer la première ligne, écrivez l'équation sous forme d'intersection de pente ». L'équation se lit comme suit : 2x + y = 7 et devient y = -2x + 7 où m = -2 et b = 7. Ensuite, il montre un graphique des équations 2x + y = 7. 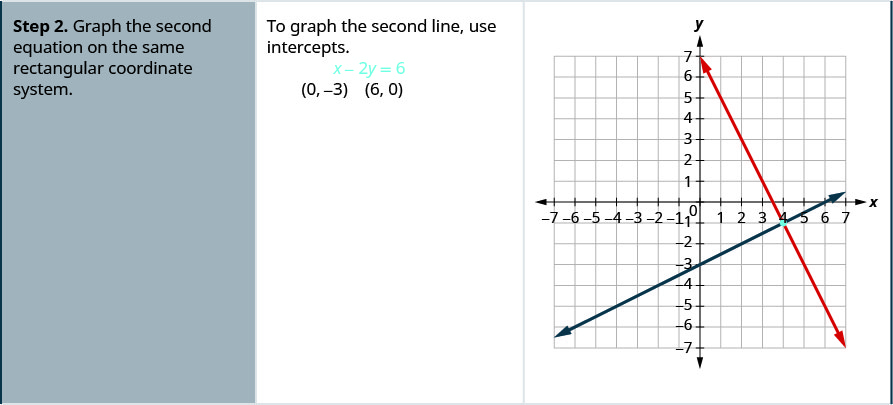L'équation x — 2y = 6 est également répertoriée.La deuxième rangée se lit comme suit : « Étape 2. Tracez la deuxième équation sur le même système de coordonnées rectangulaires. » Ensuite, il est écrit : « Pour tracer la deuxième ligne, utilisez des interceptions. » Elle est suivie de l'équation x — 2y = 6 et des paires ordonnées (0, -3) et (6, 0). La dernière colonne de cette ligne montre un graphique des deux équations.La troisième rangée se lit comme suit : « Étape 3. Déterminez si les lignes se croisent, sont parallèles ou forment la même ligne. » Puis « Regardez le graphique des lignes ». Enfin, on peut lire : « Les lignes se croisent ».La quatrième rangée se lit comme suit : « Étape 4. Identifiez la solution du système. Si les lignes se croisent, identifiez le point d'intersection. Vérifiez qu'il s'agit d'une solution aux deux équations. C'est la solution au système. Si les lignes sont parallèles, le système n'a pas de solution. Si les lignes sont identiques, le système propose une infinité de solutions. » Ensuite, on peut lire : « Puisque les lignes se croisent, trouvez le point d'intersection. Vérifiez le point dans les deux équations. » Enfin, on peut lire : « Les lignes se croisent en (4, -1). Il utilise ensuite la substitution pour montrer que « La solution est (4, -1) ».

    Exercice\(\PageIndex{5}\)

    Résolvez chaque système en représentant graphiquement :\(\begin{cases}{x−3y=−3} \\ {x+y=5}\end{cases}\)

    Réponse

    (3,2)

    Exercice\(\PageIndex{6}\)

    Résolvez chaque système en représentant graphiquement :\(\begin{cases}{−x+y=1} \\ {3x+2y=12}\end{cases}\)

    Réponse

    (2,3)

    Les étapes à suivre pour résoudre un système d'équations linéaires par représentation graphique sont présentées ci-dessous.

    RÉSOUDRE UN SYSTÈME D'ÉQUATIONS LINÉAIRES PAR REPRÉSENTATION GRAPHIQUE.
    1. Tracez la première équation.
    2. Tracez la deuxième équation sur le même système de coordonnées rectangulaires.
    3. Déterminez si les lignes se croisent, sont parallèles ou constituent la même ligne.
    4. Identifiez la solution du système.
      • Si les lignes se croisent, identifiez le point d'intersection. Vérifiez qu'il s'agit d'une solution aux deux équations. C'est la solution au système.
      • Si les lignes sont parallèles, le système n'a pas de solution.
      • Si les lignes sont identiques, le système dispose d'un nombre infini de solutions.
    Exercice\(\PageIndex{7}\)

    Résolvez le système en représentant graphiquement :\(\begin{cases}{y=2x+1} \\ {y=4x−1}\end{cases}\)

    Réponse

    Les deux équations de ce système sont présentées sous forme d'intersection de pente, nous utiliserons donc leurs pentes et leurs interceptions y pour les représenter graphiquement. \(\begin{cases}{y=2x+1} \\ {y=4x−1}\end{cases}\)

    Détermine la pente et l'intersection y de la
    première équation.    		 .
    Détermine la pente et l'intersection y de la
    première équation.    		 .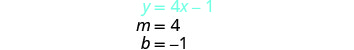
    Tracez les deux lignes.  
    Déterminez le point d'intersection. Les lignes se croisent en (1, 3).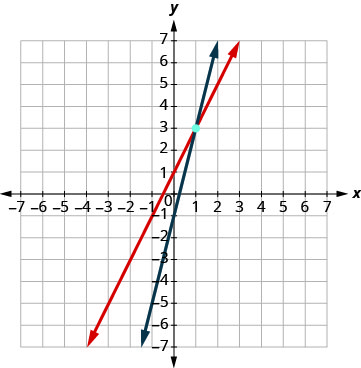
      .
    Vérifiez la solution dans les deux équations. \(\begin{array}{l}{y=2 x+1} & {y = 4x - 1}\\{3\stackrel{?}{=}2 \cdot 1+1} &{3\stackrel{?}{=}4 \cdot 1-1} \\ {3=3 \checkmark}&{3=3 \checkmark} \end{array}\)
      La solution est (1, 3).
    Exercice\(\PageIndex{8}\)

    Résolvez le système en représentant graphiquement :\(\begin{cases}{y=2x+2} \\ {y=-x−4}\end{cases}\)

    Réponse

    (−2, −2)

    Exercice\(\PageIndex{9}\)

    Résolvez le système en représentant graphiquement :\(\begin{cases}{y=3x+3} \\ {y=-x+7}\end{cases}\)

    Réponse

    (1,6)

    Les deux équations de l'exercice\(\PageIndex{7}\) ont été données sous forme de pente et d'intersection. Cela nous a permis de tracer rapidement les lignes. Dans l'exemple suivant, nous allons d'abord réécrire les équations sous forme pente-intersection.

    Exercice\(\PageIndex{10}\)

    Résolvez le système en représentant graphiquement :\(\begin{cases}{3x+y=−1} \\ {2x+y=0}\end{cases}\)

    Réponse

    Nous allons résoudre ces deux équations pour yy afin de pouvoir facilement les représenter graphiquement en utilisant leurs pentes et leurs interceptions y. \(\begin{cases}{3x+y=−1} \\ {2x+y=0}\end{cases}\)

    Résolvez la première équation pour y.


    Trouvez la pente et l'intersection y.


    Résolvez la deuxième équation pour y.


    Trouvez la pente et l'intersection y.    		 \(\begin{aligned} 3 x+y &=-1 \\ y &=-3 x-1 \\ m &=-3 \\ b &=-1 \\ 2 x+y &=0 \\ y &=-2 x \\ b &=0 \end{aligned}\)
    Tracez les lignes. .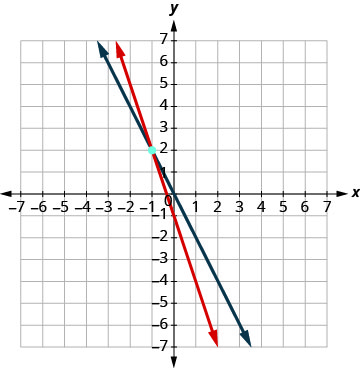
    Déterminez le point d'intersection. Les lignes se croisent en (−1, 2).
    Vérifiez la solution dans les deux équations. \(\begin{array}{rllrll}{3x+y}&{=}&{-1} & {2x +y}&{=}&{0}\\{3(-1)+ 2}&{\stackrel{?}{=}}&{-1} &{2(-1)+2}&{\stackrel{?}{=}}&{0} \\ {-1}&{=}&{-1 \checkmark}&{0}&{=}&{0 \checkmark} \end{array}\)
      La solution est (-1, 2).
    Exercice\(\PageIndex{11}\)

    Résolvez chaque système en représentant graphiquement :\(\begin{cases}{−x+y=1} \\ {2x+y=10}\end{cases}\)

    Réponse

    (3,4)

    Exercice\(\PageIndex{12}\)

    Résolvez chaque système en représentant graphiquement :\(\begin{cases}{ 2x+y=6} \\ {x+y=1}\end{cases}\)

    Réponse

    (5, −4)

    Habituellement, lorsque les équations sont données sous forme standard, le moyen le plus pratique de les représenter graphiquement est d'utiliser les interceptions. Nous allons le faire dans Exercice\(\PageIndex{13}\).

    Exercice\(\PageIndex{13}\)

    Résolvez le système en représentant graphiquement :\(\begin{cases}{x+y=2} \\ {x−y=4}\end{cases}\)

    Réponse

    Nous trouverons les interceptions x et y des deux équations et les utiliserons pour tracer les lignes.

      .  
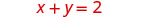
    Pour trouver les interceptions, soit x = 0 et résolvez
    pour y, puis laissez y = 0 et résolvez pour x.    		 \(\begin{aligned} x+y &=2 \quad x+y=2 \\ 0+y &=2 \quad x+0=2 \\ y &=2 \quad x=2 \end{aligned}\) .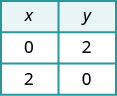
      .  
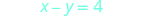
    Pour trouver les interceptions, soit
    x = 0 puis y = 0.    		 \ begin {array} {rlr} {x-y} et {=4} et {x-y} et {= 4} \ \ {0-y} et {=4} et {x-0} et {=4} \ \ {-y} et {=4} & {x} et {=4} \ \ {y} et {=-4} \ end {tableau}
    .
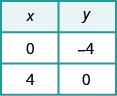
    Tracez la ligne. 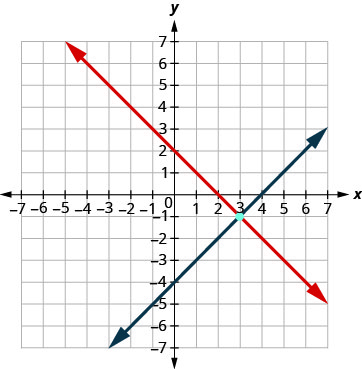Ce graphique montre l'intersection de deux lignes au point (3, -1) sur un plan de coordonnées x y.  
    Déterminez le point d'intersection. Les lignes se croisent en (3, -1).  
    Vérifiez la solution dans les deux équations.

    \(\begin{array}{rllrll}{x+y}&{=}&{2} & {x-y}&{=}&{4}\\{3+(-1)}&{\stackrel{?}{=}}&{2} &{3 - (-1)}&{\stackrel{?}{=}}&{4} \\ {2}&{=}&{2 \checkmark}&{4}&{=}&{4 \checkmark} \end{array}\)

    La solution est (3, -1).
    Exercice\(\PageIndex{14}\)

    Résolvez chaque système en représentant graphiquement :\(\begin{cases}{x+y=6} \\ {x−y=2}\end{cases}\)

    Réponse

    (4,2)

    Exercice\(\PageIndex{15}\)

    Résolvez chaque système en représentant graphiquement :\(\begin{cases}{x+y=2} \\ {x−y=-8}\end{cases}\)

    Réponse

    (5, −3)

    Vous souvenez-vous comment représenter graphiquement une équation linéaire avec une seule variable ? Il s'agira d'une ligne verticale ou horizontale.

    Exercice\(\PageIndex{16}\)

    Résolvez le système en représentant graphiquement :\(\begin{cases}{y=6} \\ {2x+3y=12}\end{cases}\)

    Réponse
      .
    Nous savons que la première équation représente une
    droite horizontale dont l'intersection y est égale à 6.    		 .
    La deuxième équation est représentée graphiquement de manière plus pratique à
    l'aide d'interceptions.    		 .
    Pour trouver les interceptions, soit x = 0, puis y = 0. .
    Tracez les lignes. .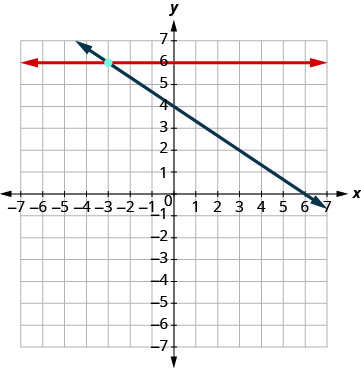
    Déterminez le point d'intersection. Les lignes se croisent en (−3, 6).
    Vérifiez la solution des deux équations. \(\begin{array}{rllrll}{y}&{=}&{6} & {2x+3y}&{=}&{12}\\{6}&{\stackrel{?}{=}}&{6} &{2(-3) + 3(6)}&{\stackrel{?}{=}}&{12} \\ {6}&{=}&{6 \checkmark} &{-6+18}&{\stackrel{?}{=}}&{12} \\ {}&{}&{}&{12}&{=}&{12 \checkmark} \end{array}\)
      La solution est (−3, 6).
    Exercice\(\PageIndex{17}\)

    Résolvez chaque système en représentant graphiquement :\(\begin{cases}{y=−1} \\ {x+3y=6}\end{cases}\)

    Réponse

    (9, −1)

    Exercice\(\PageIndex{18}\)

    Résolvez chaque système en représentant graphiquement :\(\begin{cases}{x=4} \\ {3x−2y=24}\end{cases}\)

    Réponse

    (4, −6)

    Jusqu'à présent, dans tous les systèmes d'équations linéaires, les lignes se croisaient et la solution était un point. Dans les deux exemples suivants, nous allons examiner un système d'équations qui n'a pas de solution et un système d'équations qui possède un nombre infini de solutions.

    Exercice\(\PageIndex{19}\)

    Résolvez le système en représentant graphiquement :\(\begin{cases}{y=\frac{1}{2}x−3} \\ {x−2y=4}\end{cases}\)

    Réponse
      .
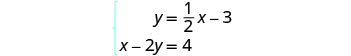
    Pour représenter graphiquement la première équation, nous
    utiliserons sa pente et son intersection y.    		 .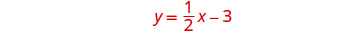
      .
      .
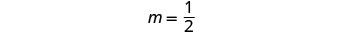
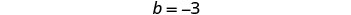
    Pour représenter graphiquement la deuxième équation,
    nous utiliserons les interceptions.    		 .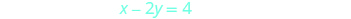
      .
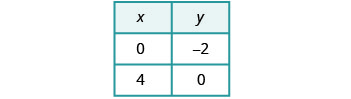
    Tracez les lignes. .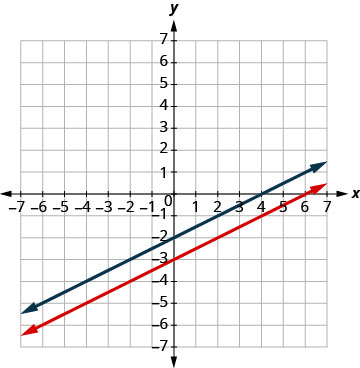
    Déterminez le point d'intersection. Les lignes sont parallèles.
      Comme aucun point ne se trouve sur les deux lignes, aucune paire ordonnée ne rend
    les deux équations vraies. Il n'existe pas de solution à
    ce système.
    Exercice\(\PageIndex{20}\)

    Résolvez chaque système en représentant graphiquement :\(\begin{cases}{y=-\frac{1}{4}x+2} \\ {x+4y=-8}\end{cases}\)

    Réponse

    aucune solution

    Exercice\(\PageIndex{21}\)

    Résolvez chaque système en représentant graphiquement :\(\begin{cases}{y=3x−1} \\ {6x−2y=6}\end{cases}\)

    Réponse

    aucune solution

    Exercice\(\PageIndex{22}\)

    Résolvez le système en représentant graphiquement :\(\begin{cases}{y=2x−3} \\ {−6x+3y=−9}\end{cases}\)

    Réponse
      .
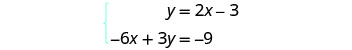
    Détermine la pente et l'intersection y de la
    première équation.    		 .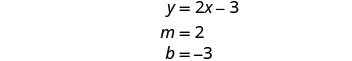
    Trouvez les points d'intersection de la deuxième équation. .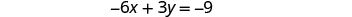
      .
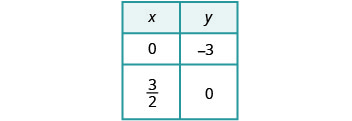
    Tracez les lignes. .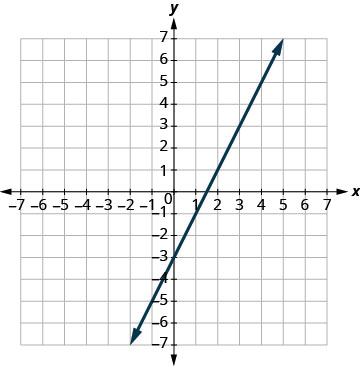
    Déterminez le point d'intersection. Les lignes sont les mêmes !
      Comme chaque point de la ligne rend les deux équations
    vraies, il existe une infinité de paires ordonnées qui rendent
    les deux équations vraies.
      Il existe une infinité de solutions à ce système.
    Exercice\(\PageIndex{23}\)

    Résolvez chaque système en représentant graphiquement :\(\begin{cases}{y=−3x−6} \\ {6x+2y=−12}\end{cases}\)

    Réponse

    une infinité de solutions

    Exercice\(\PageIndex{24}\)

    Résolvez chaque système en représentant graphiquement :\(\begin{cases}{y=\frac{1}{2}x−4} \\ {2x−4y=16}\end{cases}\)

    Réponse

    une infinité de solutions

    Si vous écrivez la deuxième équation de l'exercice\(\PageIndex{22}\) sous forme d'intersection de pente, vous reconnaîtrez peut-être que les équations ont la même pente et la même intersection y.

    Lorsque nous avons représenté graphiquement la deuxième ligne dans le dernier exemple, nous l'avons dessinée juste au-dessus de la première ligne. Nous disons que les deux lignes coïncident. Les droites coïncidentes ont la même pente et la même intersection y.

    LIGNES CONCORDANTES

    Les droites coïncidentes ont la même pente et la même intersection y.

    Déterminer le nombre de solutions d'un système linéaire

    Il y aura des moments où nous voudrons savoir combien de solutions il y aura à un système d'équations linéaires, mais il se peut que nous n'ayons pas vraiment à trouver la solution. Il sera utile de le déterminer sans créer de graphique.

    Nous avons vu que deux lignes d'un même plan doivent se croiser ou être parallèles. Les systèmes d'équations utilisés dans\(\PageIndex{4}\) Exercice à Exercice comportaient\(\PageIndex{16}\) tous deux lignes croisées. Chaque système avait une solution.

    Un système avec des lignes parallèles, comme Exercise\(\PageIndex{19}\), n'a pas de solution. Que s'est-il passé pendant l'exercice\(\PageIndex{22}\) ? Les équations ayant des lignes coïncidentes, le système avait une infinité de solutions.

    Nous organiserons ces résultats dans la figure\(\PageIndex{2}\) ci-dessous :

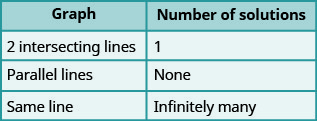
    Ce tableau comporte deux colonnes et quatre rangées. La première ligne indique que chaque colonne est « Graphique » et « Nombre de solutions ». Sous « Graphe », vous trouverez « 2 lignes croisées », « Lignes parallèles » et « Même ligne ». Sous « Nombre de solutions », vous trouverez « 1 », « Aucune » et « Infiniment nombreuses ».
    Figurine\(\PageIndex{2}\)

    Les lignes parallèles ont la même pente mais des intersections y différentes. Ainsi, si nous écrivons les deux équations dans un système d'équations linéaires sous forme de pente et d'intersection, nous pouvons voir combien de solutions il y aura sans graphique ! Regardez le système que nous avons résolu dans Exercice\(\PageIndex{19}\).

    \(\begin{array} {cc} & \begin{cases}{y=\frac{1}{2}x−3} \\ {x−2y=4}\end{cases}\\ \text{The first line is in slope–intercept form.} &\text { If we solve the second equation for } y, \text { we get } \\ &x-2 y =4 \\ y = \frac{1}{2}x -3& x-2 y =-x+4 \\ &y =\frac{1}{2} x-2 \\ m=\frac{1}{2}, b=-3&m=\frac{1}{2}, b=-2 \end{array}\)

    Les deux lignes ont la même pente mais des intersections y différentes. Ce sont des lignes parallèles.

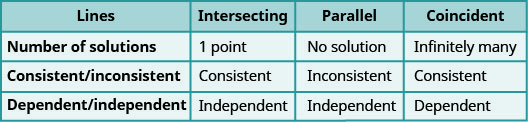
    La figure\(\PageIndex{3}\) montre comment déterminer le nombre de solutions d'un système linéaire en examinant les pentes et les points d'intersection.

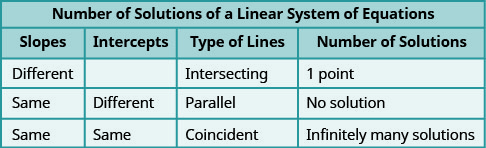
    Ce tableau s'intitule « Nombre de solutions d'un système linéaire d'équations ». Il y a quatre colonnes. Les colonnes sont intitulées « Pentes », « Interceptions », « Type de lignes », « Nombre de solutions ». Sous « Pistes », vous trouverez « Différent », « Identique » et « Identique ». Sous « Intercepts », la première cellule est vide, puis les mots « Différent » et « Identique » apparaissent. Sous « Types de lignes » se trouvent les mots « intersection », « parallèle » et « coïncidente ». Sous « Nombre de solutions », vous trouverez « 1 point », « Aucune solution » et « Une infinité de solutions ».
    Figurine\(\PageIndex{3}\)

    Regardons encore une fois nos équations de l'exercice\(\PageIndex{19}\) qui nous ont donné des lignes parallèles.

    \ [\ begin {cas} {y= \ frac {1} {2} x−3} \ \ {x−2y=4} \ end {cas} \)]

    Lorsque les deux lignes étaient en forme d'interception en pente, nous avions :

    \[y=\frac{1}{2} x-3 \quad y=\frac{1}{2} x-2\]

    Reconnaissez-vous qu'il est impossible d'avoir une seule paire ordonnée (x, y) qui soit une solution à ces deux équations ?

    Nous appelons un système d'équations comme celui-ci un système incohérent. Il n'y a pas de solution.

    Un système d'équations comportant au moins une solution est appelé système cohérent.

    SYSTÈMES COHÉRENTS ET INCOHÉRENTS

    Un système d'équations cohérent est un système d'équations comportant au moins une solution.

    Un système d'équations incohérent est un système d'équations sans solution.

    Nous classons également les équations dans un système d'équations en les qualifiant d'indépendantes ou de dépendantes. Si deux équations sont des équations indépendantes, elles ont chacune leur propre ensemble de solutions. Les lignes qui se croisent et les lignes parallèles sont indépendantes.

    Si deux équations sont dépendantes, toutes les solutions d'une équation sont également des solutions de l'autre équation. Lorsque nous tracons deux équations dépendantes, nous obtenons des droites coïncidentes.

    ÉQUATIONS INDÉPENDANTES ET DÉPENDANTES

    Deux équations sont indépendantes si elles ont des solutions différentes.

    Deux équations sont dépendantes si toutes les solutions d'une équation sont également des solutions de l'autre équation.

    Résumons cela en examinant les graphiques des trois types de systèmes. Voir Figure\(\PageIndex{4}\) et Figure\(\PageIndex{5}\).

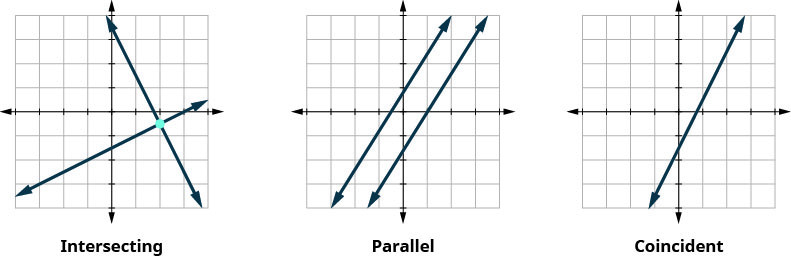
    Cette figure montre trois plans de coordonnées x y sur une ligne horizontale. La première montre deux lignes qui se croisent. La seconde montre deux lignes parallèles. La troisième montre deux lignes coïncidentes.
    Figurine\(\PageIndex{4}\)
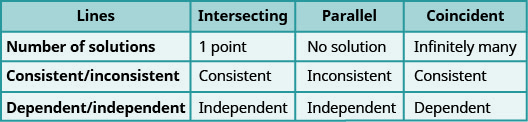
    Ce tableau comporte quatre colonnes et quatre lignes. Les colonnes sont intitulées « Lignes », « Intersection », « Parallèle » et « Coïncidente ». Dans la première rangée, sous la colonne intitulée « Lignes », on peut lire « Nombre de solutions ». Une lecture transversale nous indique qu'une ligne qui se croise contient 1 point, qu'une ligne parallèle n'apporte aucune solution et qu'une ligne coïncidente contient une infinité de solutions. Une ligne cohérente/incohérente a des lignes cohérentes si elles se croisent, des lignes incohérentes si elles sont parallèles et cohérentes si les lignes coïncident. Enfin, les lignes dépendantes et indépendantes sont considérées comme indépendantes si les lignes se croisent, elles le sont également si les lignes sont parallèles et elles sont dépendantes si les lignes coïncident.
    Figurine\(\PageIndex{5}\)
    Exercice\(\PageIndex{25}\)

    Sans créer de graphique, déterminez le nombre de solutions puis classez le système d'équations :\(\begin{cases}{y=3x−1} \\ {6x−2y=12}\end{cases}\)

    Réponse

    \(\begin{array}{lrrl} \text{We will compare the slopes and intercepts} & \begin{cases}{y=3x−1} \\ {6x−2y=12}\end{cases} \\ \text{of the two lines.} \\ \text{The first equation is already in} \\ \text{slope-intercept form.} \\ & {y = 3x - 1}\\ \text{Write the second equation in} \\ \text{slope–intercept form.} \\ & 6x-2y &=&12 \\ & -2y &=& -6x - 12 \\ &\frac{-2y}{-2} &=& \frac{-6x + 12}{-2}\\ &y&=&3x-6\\\\ \text{Find the slope and intercept of each line.} & y = 3x-1 & y=3x-6 \\ &m = 3 & m = 3 \\&b=-1 &b=-6 \\ \text{Since the slopes are the same andy-intercepts} \\ \text{are different, the lines are parallel.}\end{array}\)

    Un système d'équations dont les graphes sont des lignes parallèles n'a pas de solution et est incohérent et indépendant.

    Exercice\(\PageIndex{26}\)

    Sans créer de graphique, déterminez le nombre de solutions, puis classez le système d'équations.

    \(\begin{cases}{y=−2x−4} \\ {4x+2y=9}\end{cases}\)

    Réponse

    pas de solution, incohérent, indépendant

    Exercice\(\PageIndex{27}\)

    Sans créer de graphique, déterminez le nombre de solutions, puis classez le système d'équations.

    \(\begin{cases}{y=\frac{1}{3}x−5} \\ {x-3y=6}\end{cases}\)

    Réponse

    pas de solution, incohérent, indépendant

    Exercice\(\PageIndex{28}\)

    Sans créer de graphique, déterminez le nombre de solutions puis classez le système d'équations :\(\begin{cases}{2x+y=−3} \\ {x−5y=5}\end{cases}\)

    Réponse

    \(\begin{array}{lrrlrl} \text{We will compare the slopes and intercepts} & \begin{cases}{2x+y=-3} \\ {x−5y=5}\end{cases} \\ \text{of the two lines.} \\ \text{Write the second equation in} \\ \text{slope–intercept form.} \\ &2x+y&=&-3 & x−5y&=&5\\ & y &=& -2x -3 & -5y &=&-x+5 \\ &&&&\frac{-5y}{-5} &=& \frac{-x + 5}{-5}\\ &&&&y&=&\frac{1}{5}x-1\\\\ \text{Find the slope and intercept of each line.} & y &=& -2x-3 & y&=&\frac{1}{5}x-1 \\ &m &=& -2 & m &=& \frac{1}{5} \\&b&=&-3 &b&=&-1 \\ \text{Since the slopes are the same andy-intercepts} \\ \text{are different, the lines are parallel.}\end{array}\)

    Un système d'équations dont les graphes se croisent n'a qu'une solution et est cohérent et indépendant.

    Exercice\(\PageIndex{29}\)

    Sans créer de graphique, déterminez le nombre de solutions, puis classez le système d'équations.

    \(\begin{cases}{3x+2y=2} \\ {2x+y=1}\end{cases}\)

    Réponse

    une solution, cohérente et indépendante

    Exercice\(\PageIndex{30}\)

    Sans créer de graphique, déterminez le nombre de solutions, puis classez le système d'équations.

    \(\begin{cases}{x+4y=12} \\ {−x+y=3}\end{cases}\)

    Réponse

    une solution, cohérente et indépendante

    Exercice\(\PageIndex{31}\)

    Sans créer de graphique, déterminez le nombre de solutions, puis classez le système d'équations. \(\begin{cases}{3x−2y=4} \\ {y=\frac{3}{2}x−2}\end{cases}\)

    Réponse

    \(\begin{array}{lrrlrl} \text{We will compare the slopes and intercepts of the two lines.}& \begin{cases}{3x−2y} &=&{4} \\ {y}&=&{\frac{3}{2}x−2}\end{cases} \\ \text{Write the second equation in} \\ \text{slope–intercept form.} \\ &3x-2y&=&4 \\ & -2y &=& -3x +4 \\ &\frac{-2y}{-2} &=& \frac{-3x + 4}{-2}\\ &y&=&\frac{3}{2}x-2\\\\ \text{Find the slope and intercept of each line.} &y&=&\frac{3}{2}x-2\\ \text{Since the equations are the same, they have the same slope} \\ \text{and samey-intercept and so the lines are coincident.}\end{array}\)

    Un système d'équations dont les graphes sont des lignes coïncidentes possède une infinité de solutions et est cohérent et dépendant.

    Exercice\(\PageIndex{32}\)

    Sans créer de graphique, déterminez le nombre de solutions, puis classez le système d'équations.

    \(\begin{cases}{4x−5y=20} \\ {y=\frac{4}{5}x−4}\end{cases}\)

    Réponse

    infiniment de solutions, cohérentes, dépendantes

    Exercice\(\PageIndex{33}\)

    Sans créer de graphique, déterminez le nombre de solutions, puis classez le système d'équations.

    \(\begin{cases}{ −2x−4y=8} \\ {y=−\frac{1}{2}x−2}\end{cases}\)

    Réponse

    infiniment de solutions, cohérentes, dépendantes

    Résolvez des applications de systèmes d'équations en graphiant

    Nous utiliserons la même stratégie de résolution de problèmes que celle utilisée dans les modèles mathématiques pour configurer et résoudre des applications de systèmes d'équations linéaires. Nous allons modifier légèrement la stratégie ici pour l'adapter aux systèmes d'équations.

    UTILISEZ UNE STRATÉGIE DE RÉSOLUTION DE PROBLÈMES POUR LES SYSTÈMES D'ÉQUATIONS LINÉAIRES.
    1. Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris.
    2. Déterminez ce que nous recherchons.
    3. Nommez ce que nous recherchons. Choisissez des variables pour représenter ces quantités.
    4. Traduisez en un système d'équations.
    5. Résolvez le système d'équations en utilisant de bonnes techniques d'algèbre.
    6. Vérifiez la réponse au problème et assurez-vous qu'elle est logique.
    7. Répondez à la question par une phrase complète.

    C'est à l'étape 5 que nous utiliserons la méthode présentée dans cette section. Nous allons représenter graphiquement les équations et trouver la solution.

    Exercice\(\PageIndex{34}\)

    Sondra prépare 10 pintes de punch à partir de jus de fruits et de soda. Le nombre de pintes de jus de fruits est 4 fois supérieur au nombre de pintes de club soda. De combien de litres de jus de fruits et de combien de litres de soda Sondra a-t-elle besoin ?

    Réponse

    Étape 1 Lisez le problème.

    Étape 2 Identifiez ce que nous recherchons.

    Nous recherchons le nombre de pintes de jus de fruits et le nombre de pintes de soda dont Sondra aura besoin.

    Étape 3. Nommez ce que nous recherchons. Choisissez des variables pour représenter ces quantités.

    Soit f = nombre de pintes de jus de fruits.
    c= nombre de pintes de soda

    Étape 4. Traduisez en un système d'équations.

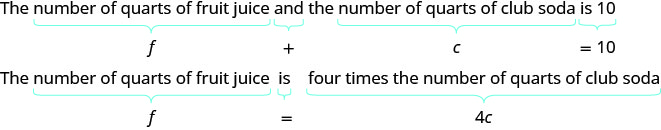
    Cette figure montre des phrases converties en équations. La première phrase se lit comme suit : « Le nombre de pintes de jus de fruits et le nombre de pintes de club soda sont de 10. « Nombre de pintes de jus de fruits » contient une parenthèse frisée sous la phrase et un « f » centré sous la parenthèse. Le « Et » contient également un crochet bouclé en dessous et un signe plus centré en dessous. « Nombre de pintes de club soda » contient une parenthèse frisée avec la variable « c » en dessous. Enfin, l'expression « est 10 » contient un crochet bouclé. En dessous, cela se lit comme suit : 10. La deuxième phrase se lit comme suit : « Le nombre de pintes de jus de fruits est quatre fois supérieur au nombre de pintes de club soda ». Cette phrase est configurée de la même manière en ce que chaque phrase contient un crochet bouclé en dessous. La variable « f » représente « Le nombre de pintes de jus de fruits ». Un signe égal représente « est » et « 4c » représente quatre fois le nombre de pintes de club soda. »

    Nous avons maintenant le système. \(\begin{cases}{ f+c=10} \\ {f=4c}\end{cases}\)

    Étape 5. Résolvez le système d'équations en utilisant de bonnes techniques d'algèbre.

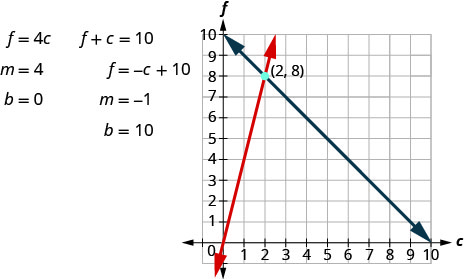
    Cette figure montre deux équations et leur graphique. La première équation est f = 4c où b = 4 et b = 0. La deuxième équation est f + c = 10. f = négatif c +10 où b = négatif 1 et b = 10. Le plan de coordonnées x y montre un graphique de ces deux lignes qui se croisent en (2, 8).

    Le point d'intersection (2, 8) est la solution. Cela signifie que Sondra a besoin de 2 pintes de club soda et de 8 pintes de jus de fruits.

    Étape 6. Vérifiez la réponse au problème et assurez-vous qu'elle est logique.

    Est-ce que cela a un sens dans le problème ?

    Oui, le nombre de pintes de jus de fruits, 8, c'est 4 fois le nombre de pintes de club soda, 2.

    Oui, 10 pintes de punch, c'est 8 pintes de jus de fruits plus 2 pintes de soda.

    Étape 7. Répondez à la question par une phrase complète.

    Sondra a besoin de 8 pintes de jus de fruits et de 2 pintes de soda.

    Exercice\(\PageIndex{35}\)

    Manny prépare 12 pintes de jus d'orange à partir de concentré et d'eau. Le nombre de pintes d'eau est 3 fois supérieur au nombre de pintes de concentré. De combien de litres de concentré et de combien de litres d'eau Manny a-t-il besoin ?

    Réponse

    Manny a besoin de 3 pintes de jus concentré et de 9 pintes d'eau.

    Exercice\(\PageIndex{36}\)

    Alisha prépare une boisson au café de 18 onces à base de café infusé et de lait. Le nombre d'onces de café infusé est 5 fois supérieur au nombre d'onces de lait. De combien d'onces de café et de combien d'onces de lait Alisha a-t-elle besoin ?

    Réponse

    Alisha a besoin de 15 onces de café et 3 onces de lait.

    Remarque

    Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à résoudre des systèmes d'équations à l'aide de graphiques.

    Concepts clés

    • Pour résoudre un système d'équations linéaires en traçant un graphique
      1. Tracez la première équation.
      2. Tracez la deuxième équation sur le même système de coordonnées rectangulaires.
      3. Déterminez si les lignes se croisent, sont parallèles ou constituent la même ligne.
      4. Identifiez la solution du système.
        Si les lignes se croisent, identifiez le point d'intersection. Vérifiez qu'il s'agit d'une solution aux deux équations. C'est la solution au système.
        Si les lignes sont parallèles, le système n'a pas de solution.
        Si les lignes sont identiques, le système dispose d'un nombre infini de solutions.
      5. Vérifiez la solution dans les deux équations.
    • Déterminer le nombre de solutions à partir du graphique d'un système linéaire
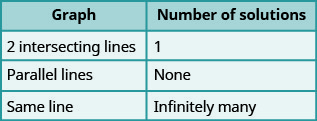
      Ce tableau comporte deux colonnes et quatre rangées. La première ligne indique que chaque colonne est « Graphique » et « Nombre de solutions ». Sous « Graphe », vous trouverez « 2 lignes croisées », « Lignes parallèles » et « Même ligne ». Sous « Nombre de solutions », vous trouverez « 1 », « Aucune » et « Infiniment nombreuses ».
    • Déterminez le nombre de solutions d'un système linéaire en examinant les pentes et les points d'intersection
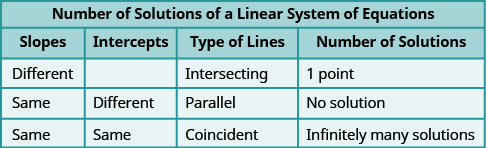
      Ce tableau s'intitule « Nombre de solutions d'un système linéaire d'équations ». Il y a quatre colonnes. Les colonnes sont intitulées « Pentes », « Interceptions », « Type de lignes », « Nombre de solutions ». Sous « Pistes », vous trouverez « Différent », « Identique » et « Identique ». Sous « Intercepts », la première cellule est vide, puis les mots « Différent » et « Identique » apparaissent. Sous « Types de lignes » se trouvent les mots « intersection », « parallèle » et « coïncidente ». Sous « Nombre de solutions », vous trouverez « 1 point », « Aucune solution » et « Une infinité de solutions ».
    • Déterminez le nombre de solutions et comment classer un système d'équations
      Ce tableau comporte quatre colonnes et quatre lignes. Les colonnes sont intitulées « Lignes », « Intersection », « Parallèle » et « Coïncidente ». Dans la première rangée, sous la colonne intitulée « Lignes », on peut lire « Nombre de solutions ». Une lecture transversale nous indique qu'une ligne qui se croise contient 1 point, qu'une ligne parallèle n'apporte aucune solution et qu'une ligne coïncidente contient une infinité de solutions. Une ligne cohérente/incohérente a des lignes cohérentes si elles se croisent, des lignes incohérentes si elles sont parallèles et cohérentes si les lignes coïncident. Enfin, les lignes dépendantes et indépendantes sont considérées comme indépendantes si les lignes se croisent, elles le sont également si les lignes sont parallèles et elles sont dépendantes si les lignes coïncident.
    • Stratégie de résolution de problèmes pour les systèmes d'équations linéaires
      1. Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris.
      2. Déterminez ce que nous recherchons.
      3. Nommez ce que nous recherchons. Choisissez des variables pour représenter ces quantités.
      4. Traduisez en un système d'équations.
      5. Résolvez le système d'équations en utilisant de bonnes techniques d'algèbre.
      6. Vérifiez la réponse au problème et assurez-vous qu'elle est logique.
      7. Répondez à la question par une phrase complète.

    Lexique

    lignes coïncidentes
    Les lignes coïncidentes sont des lignes qui ont la même pente et la même intersection y.
    système cohérent
    Un système d'équations cohérent est un système d'équations comportant au moins une solution.
    équations dépendantes
    Deux équations sont dépendantes si toutes les solutions d'une équation sont également des solutions de l'autre équation.
    système incohérent
    Un système d'équations incohérent est un système d'équations sans solution.
    équations indépendantes
    Deux équations sont indépendantes si elles ont des solutions différentes.
    solutions d'un système d'équations
    Les solutions d'un système d'équations sont les valeurs des variables qui rendent toutes les équations vraies. La solution d'un système de deux équations linéaires est représentée par une paire ordonnée (x, y).
    système d'équations linéaires
    Lorsque deux équations linéaires ou plus sont regroupées, elles forment un système d'équations linéaires.