2.4 : Utiliser une stratégie générale pour résoudre des équations linéaires

Last updated
Save as PDF

Page ID: 194683

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

Résoudre des équations en utilisant une stratégie générale
Classer les équations

Remarque

Avant de commencer, répondez à ce questionnaire de préparation.

Simplifiez :$−(a−4)$.
Si vous avez oublié ce problème, passez en revue l'exercice 1.10.46
Multipliez :$\frac{3}{2}(12x+20)$
si vous avez oublié ce problème, passez en revue l'exercice 1.10.34.
Simplifier :$5−2(n+1)$
si vous avez oublié ce problème, passez en revue l'exercice 1.10.49.
Multipliez :$3(7y+9)$
si vous avez oublié ce problème, passez en revue l'exercice 1.10.34.
Multipliez :$(2.5)(6.4)$
si vous avez oublié ce problème, passez en revue l'exercice 1.8.19.

Résoudre des équations en utilisant la stratégie générale

Jusqu'à présent, nous avons traité de la résolution d'une forme spécifique d'équation linéaire. Il est temps maintenant de définir une stratégie globale qui peut être utilisée pour résoudre n'importe quelle équation linéaire. Certaines équations que nous résolvons ne nécessiteront pas toutes ces étapes pour être résolues, mais beaucoup le feront.

Commencer par simplifier chaque côté de l'équation facilite les étapes restantes.

Exercice$\PageIndex{1}$: How to Solve Linear Equations Using the General Strategy

Résoudre :$-6(x + 3) = 24$.

Réponse: $Cette figure est un tableau composé de trois colonnes et de cinq lignes. La première colonne est une colonne d'en-tête qui contient les noms et les numéros de chaque étape. La deuxième colonne contient d'autres instructions écrites. La troisième colonne contient des données mathématiques. Dans la rangée supérieure du tableau, la première cellule de gauche se lit comme suit : « Étape 1. Simplifiez chaque côté de l'équation autant que possible. » Le texte de la deuxième cellule se lit comme suit : « Utilisez la propriété distributive. Notez que chaque côté de l'équation est simplifié autant que possible. » La troisième cellule contient l'équation négative 6 fois x plus 3, où x plus 3 est entre parenthèses, est égal à 24. En dessous se trouve la même équation avec le 6 négatif réparti entre parenthèses : moins 6 x moins 18 équivaut à 24.$ $Étape 2. Recueillez tous les termes variables d'un côté de l'équation. Ici, il n'y a plus rien à faire, puisqu'il n'y a qu'un seul x sur le côté gauche.$ $Dans la troisième rangée du tableau, la première cellule indique : « Étape 3. Recueillez les termes constants de l'autre côté de l'équation. Dans la deuxième cellule, les instructions disent : « Pour obtenir des constantes uniquement sur la droite, ajoutez 18 de chaque côté. Simplifiez. » La troisième cellule contient la même équation, 18 étant ajoutée des deux côtés : moins 6 x moins 18 plus 18 équivaut à 24 plus 18. En dessous se trouve l'équation négative 6x égale 42.$ $Étape 4. Établissez le coefficient de x un. Ici, on divise les deux côtés par -6 et on simplifie !$ $Dans la cinquième rangée du tableau, la première cellule indique : « Étape 5. Vérifiez la solution. » Dans la deuxième cellule, les instructions indiquent : « Soit x égal à moins 7. Simplifiez. Multipliez. » Dans la troisième cellule, il y a l'instruction : « Vérifier », et à droite se trouve à nouveau l'équation d'origine : moins 6 fois x plus 3, avec x plus 3 entre parenthèses, égal à 24. Ci-dessous se trouve la même équation avec moins 7 substitué par x : moins 6 fois moins 7 plus 3, avec moins 7 plus 3 entre parenthèses, peut être égal à 24. En dessous se trouve l'équation négative 6 fois moins 4 peut être égale à 24. En dessous se trouve l'équation 24 égale 24, avec une coche à côté.$

Exercice$\PageIndex{2}$

Résoudre :$5(x + 3)=35$

Réponse: $x = 4$

Exercice$\PageIndex{3}$

Résoudre :$6(y - 4) = -18$

Réponse: $y = 1$

STRATÉGIE GÉNÉRALE POUR RÉSOUDRE DES ÉQUATIONS LINÉAIRES.

Simplifiez chaque côté de l'équation autant que possible.
Utilisez la propriété distributive pour supprimer les parenthèses.
Combinez les mêmes termes.
Collectez tous les termes variables d'un côté de l'équation.
Utilisez la propriété d'addition ou de soustraction de l'égalité.
Recueillez tous les termes constants de l'autre côté de l'équation.
Utilisez la propriété d'addition ou de soustraction de l'égalité.
Rendre le coefficient du terme variable égal à 1.
Utilisez la propriété de multiplication ou de division de l'égalité.
Indiquez la solution de l'équation.
Vérifiez la solution. Remplacez la solution dans l'équation d'origine pour vous assurer que le résultat est vrai.

Exercice$\PageIndex{4}$

Résoudre :$-(y + 9) = 8$

Réponse

		$.$
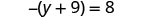
Simplifiez chaque côté de l'équation autant que possible en distribuant.		$.$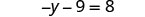
Le seul terme y se trouve sur le côté gauche, donc tous les termes variables se trouvent sur le côté gauche de l'équation.
Ajoutez 9 des deux côtés pour obtenir tous les termes constants sur le côté droit de l'équation.		$.$
Simplifiez.		$.$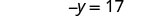
Réécrivez −y en −1y.		$.$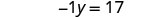
Rendre le coefficient du terme variable égal à 1 en divisant les deux côtés par −1.		$.$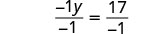
Simplifiez.		$.$
Vérifiez :	$.$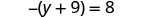
Soit y=−17.	$.$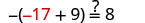
	$.$
	$.$

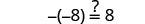
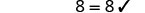
Exercice$\PageIndex{5}$

Résoudre :$-(y + 8) = -2$

Réponse: $y = -6$

Exercice$\PageIndex{6}$

Résoudre :$-(z + 4) = -12$

Réponse: $z = 8$

Exercice$\PageIndex{7}$

Résoudre :$5(a - 3) + 5 = -10$

Réponse

		$.$
Simplifiez chaque côté de l'équation autant que possible.
Distribuez.		$.$
Combinez les mêmes termes.		$.$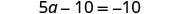
Le seul terme se trouve sur le côté gauche, de sorte que tous les termes variables se trouvent d'un côté de l'équation.
Ajoutez 10 des deux côtés pour obtenir tous les termes constants de l'autre côté de l'équation.		$.$
Simplifiez.		$.$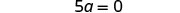
Faites en sorte que le coefficient du terme variable soit égal à 11 en divisant les deux côtés par 55.		$.$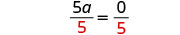
Simplifiez.		$.$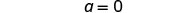
Vérifiez :	$.$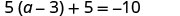
Soit a=0.	$.$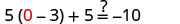
	$.$
	$.$
	$.$

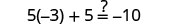
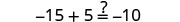
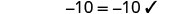
Exercice$\PageIndex{8}$

Résoudre :$2(m - 4) + 3 = -1$

Réponse: $m = 2$

Exercice$\PageIndex{9}$

Résoudre :$7(n - 3) - 8 = -15$

Réponse: $n = 2$

Exercice$\PageIndex{10}$

Résoudre :$\frac{2}{3}(6m - 3) = 8 - m$

Réponse

		$.$
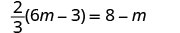
Distribuez.		$.$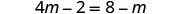
Ajoutez m pour obtenir les variables uniquement à gauche.		$.$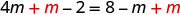
Simplifiez.		$.$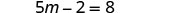
Ajoutez 2 pour obtenir des constantes uniquement sur la droite.		$.$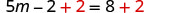
Simplifiez.		$.$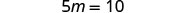
Divisez par 5.		$.$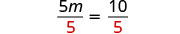
Simplifiez.		$.$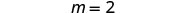
Vérifiez :	$.$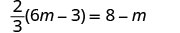
Soit m=2.	$.$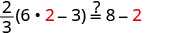
	$.$
	$.$
	$.$

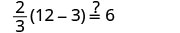
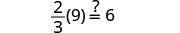
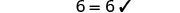
Exercice$\PageIndex{11}$

Résoudre :$\frac{1}{3}(6u + 3) = 7 - u$

Réponse: $u = 2$

Exercice$\PageIndex{12}$

Résoudre :$\frac{2}{3}(9x - 12) = 8 + 2x$

Réponse: $x = 4$

Exercice$\PageIndex{13}$

Résoudre :$8 - 2(3y + 5) = 0$

Réponse

	$.$
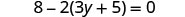
Simplifier : utilisez la propriété distributive.	$.$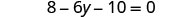
Combinez les mêmes termes.	$.$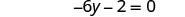
Ajoutez 2 des deux côtés pour collecter les constantes sur la droite.	$.$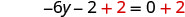
Simplifiez.	$.$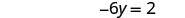
Divisez les deux côtés par −6−6.	$.$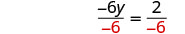
Simplifiez.	$.$
Vérifiez : Soit y=−13. $.$

Exercice$\PageIndex{14}$

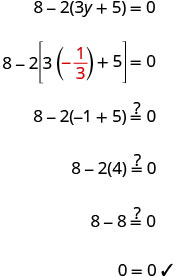
Résoudre :$12 - 3(4j + 3) = -17$

Réponse: $j = \frac{5}{3}$

Exercice$\PageIndex{15}$

Résoudre :$-6 - 8(k - 2) = -10$

Réponse: $k = \frac{5}{2}$

Exercice$\PageIndex{16}$

Résoudre :$4(x - 1)-2=5(2x+3)+6$

Réponse

		$.$
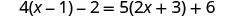
Distribuez.		$.$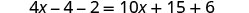
Combinez les mêmes termes.		$.$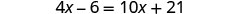
Soustrayez 4x pour obtenir les variables uniquement sur le côté droit depuis$10>4$.		$.$
Simplifiez.		$.$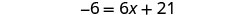
Soustrayez 21 pour obtenir les constantes sur la gauche.		$.$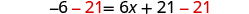
Simplifiez.		$.$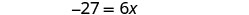
Divisez par 6.		$.$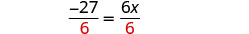
Simplifiez.		$.$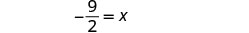
Vérifiez :	$.$
Laissez$x=-\frac{9}{2}$.	$.$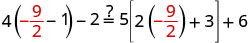
	$.$
	$.$
	$.$
	$.$

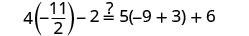
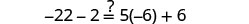
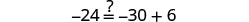
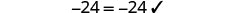
Exercice$\PageIndex{17}$

Résoudre :$6(p-3)-7=5(4p+3)-12$

Réponse: $p = -2$

Exercice$\PageIndex{18}$

Résoudre :$8(q +1)-5=3(2q-4)-1$

Réponse: $q = -8$

Exercice$\PageIndex{19}$

Résoudre :$10[3 - 8(2s-5)] = 15(40 - 5s)$

Réponse

		$.$
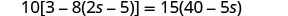
Simplifiez d'abord à partir des parenthèses les plus intérieures.		$.$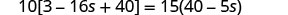
Combinez des termes similaires entre crochets.		$.$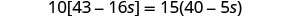
Distribuez.		$.$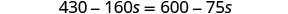
Ajoutez 160 pour placer les s vers la droite.		$.$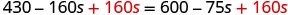
Simplifiez.		$.$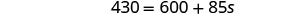
Soustrayez 600 pour obtenir les constantes vers la gauche.		$.$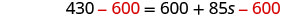
Simplifiez.		$.$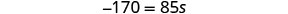
Diviser.		$.$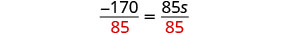
Simplifiez.		$.$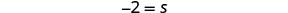
Vérifiez :	$.$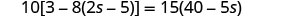
Substitut s=−2.	$.$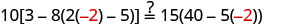
	$.$
	$.$
	$.$
	$.$
	$.$

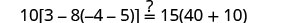
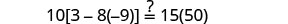
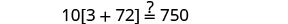
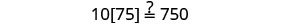
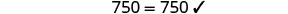
Exercice$\PageIndex{20}$

Résoudre :$6[4−2(7y−1)]=8(13−8y)$.

Réponse: $y = -\frac{17}{5}$

Exercice$\PageIndex{21}$

Résoudre :$12[1−5(4z−1)]=3(24+11z)$.

Réponse: $z = 0$

Exercice$\PageIndex{22}$

Résoudre :$0.36(100n+5)=0.6(30n+15)$.

Réponse

		$.$
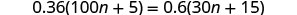
Distribuez.		$.$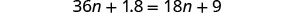
Soustrayez 18n pour obtenir les variables vers la gauche.		$.$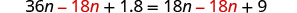
Simplifiez.		$.$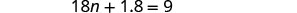
Soustrayez 1,8 pour obtenir les constantes vers la droite.		$.$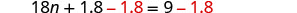
Simplifiez.		$.$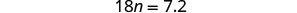
Diviser.		$.$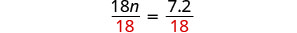
Simplifiez.		$.$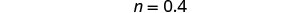
Vérifiez :	$.$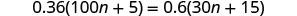
Soit n = 0,4.	$.$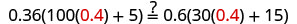
	$.$
	$.$
	$.$

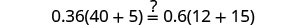
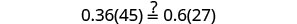
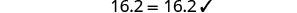
Exercice$\PageIndex{23}$

Résoudre :$0.55(100n+8)=0.6(85n+14)$.

Réponse: $n = 1$

Exercice$\PageIndex{24}$

Résoudre :$0.15(40m−120)=0.5(60m+12)$.

Réponse: $m = -1$

Classer les équations

Considérez l'équation que nous avons résolue au début de la dernière section, 7x+8=−13. La solution que nous avons trouvée était x=−3. Cela signifie que l'équation 7x+8=−13 est vraie lorsque nous remplaçons la variable, x, par la valeur −3. Nous l'avons montré en vérifiant la solution x=−3 et en évaluant 7x+8=−13 pour x=−3.

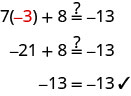
$Cette figure montre pourquoi nous pouvons dire que l'équation 7x plus 8 est égale à moins 13 est vraie lorsque la variable x est remplacée par la valeur négative 3. La première ligne montre l'équation où moins 3 est remplacé par x : 7 fois moins 3 plus 8 peuvent être égaux à moins 13. En dessous se trouve l'équation : moins 21 plus 8 peut être égal à moins 13. En dessous se trouve l'équation : moins 13 est égale à moins 13, avec une coche à côté.$

Si nous évaluons 7x+8 pour une valeur différente de x, le côté gauche ne sera pas −13.

L'équation 7x+8=−13 est vraie lorsque nous remplaçons la variable, x, par la valeur −3, mais pas vraie lorsque nous remplaçons x par une autre valeur. La véracité ou non de l'équation 7x+8=−13 dépend de la valeur de la variable. De telles équations sont appelées équations conditionnelles.

Toutes les équations que nous avons résolues jusqu'à présent sont des équations conditionnelles.

ÉQUATION CONDITIONNELLE

Une équation vraie pour une ou plusieurs valeurs de la variable et fausse pour toutes les autres valeurs de la variable est une équation conditionnelle.

Considérons maintenant l'équation 2y+6=2 (y+3). Reconnaissez-vous que le côté gauche et le côté droit sont équivalents ? Voyons ce qui se passe lorsque nous résolvons pour y.

	$.$
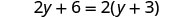Distribuez.	$.$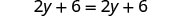
Soustrayez 2y pour mettre les Y de côté.	$.$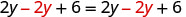
Simplifiez : il n'y a plus de Y !	$.$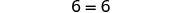

Mais 6=6 est vrai.

Cela signifie que l'équation 2y+6=2 (y+3) est vraie pour toute valeur de y. Nous disons que la solution à l'équation se trouve dans tous les nombres réels. Une équation qui est vraie pour n'importe quelle valeur de la variable comme celle-ci est appelée identité.

IDENTITÉ

Une équation qui est vraie pour n'importe quelle valeur de la variable est appelée identité.

La solution d'une identité réside dans les vrais nombres.

Que se passe-t-il lorsque nous résolvons l'équation 5z=5z−1 ?

	$.$
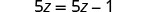Soustrayez 5z pour obtenir la constante seule sur la droite.	$.$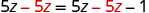
Simplifiez : les Z ont disparu !	$.$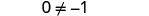

Mais$0\neq −1$.

La résolution de l'équation 5z=5z−1 a conduit à la fausse déclaration 0=−1. L'équation 5z=5z−1 ne sera vraie pour aucune valeur de z. Elle n'a pas de solution. Une équation qui n'a pas de solution ou qui est fausse pour toutes les valeurs de la variable est appelée contradiction.

CONTRACTION

Une équation qui est fausse pour toutes les valeurs de la variable est appelée contradiction.

Une contradiction n'a pas de solution.

Exercice$\PageIndex{25}$

Classifiez l'équation comme une équation conditionnelle, une identité ou une contradiction. Indiquez ensuite la solution.

$6(2n−1)+3=2n−8+5(2n+1)$

Réponse

$.$
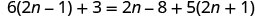
Distribuez.	$.$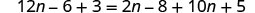
Combinez les mêmes termes.	$.$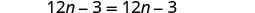
Soustrayez 12n pour mettre les nn de côté.	$.$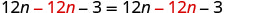
Simplifiez.	$.$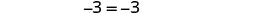
C'est une affirmation vraie.	L'équation est une identité. La solution, ce sont tous des nombres réels.

Exercice$\PageIndex{26}$

Classifiez l'équation en tant qu'équation conditionnelle, identité ou contradiction, puis énoncez la solution :

$4+9(3x−7)=−42x−13+23(3x−2)$

Réponse: identité ; tous les nombres réels

Exercice$\PageIndex{27}$

Classifiez l'équation en tant qu'équation conditionnelle, identité ou contradiction, puis énoncez la solution :

$8(1−3x)+15(2x+7)=2(x+50)+4(x+3)+1$

Réponse: identité ; tous les nombres réels

Exercice$\PageIndex{28}$

Classifiez-la comme une équation conditionnelle, une identité ou une contradiction. Indiquez ensuite la solution.

$10+4(p−5)=0$

Réponse

	$.$
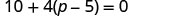
Distribuez.	$.$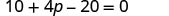
Combinez les mêmes termes.	$.$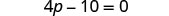
Ajoutez-en 10 des deux côtés.	$.$
Simplifiez.	$.$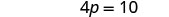
Diviser.	$.$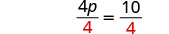
Simplifiez.	$.$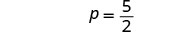
L'équation est vraie quand$p = frac{5}{2}$.	Il s'agit d'une équation conditionnelle. La solution est$p = frac{5}{2}$.

Exercice$\PageIndex{29}$

Classifiez l'équation en tant qu'équation conditionnelle, identité ou contradiction, puis énoncez la solution :$11(q+3)−5=19$

Réponse: équation conditionnelle ; \ (q = \ frac {9} {11} \

Exercice$\PageIndex{30}$

Classifiez l'équation en tant qu'équation conditionnelle, identité ou contradiction, puis énoncez la solution :$6+14(k−8)=95$

Réponse: équation conditionnelle ;$k = \frac{193}{14}$

Exercice$\PageIndex{31}$

Classifiez l'équation comme une équation conditionnelle, une identité ou une contradiction. Indiquez ensuite la solution.

$5m+3(9+3m)=2(7m−11)$

Réponse

	$.$
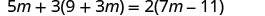
Distribuez.	$.$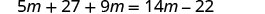
Combinez les mêmes termes.	$.$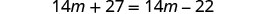
Soustrayez 14 m des deux côtés.	$.$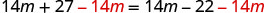
Simplifiez.	$.$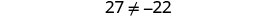
Mais$27\neq −22$.	L'équation est contradictoire. Il n'y a pas de solution.

Exercice$\PageIndex{32}$

Classifiez l'équation en tant qu'équation conditionnelle, identité ou contradiction, puis énoncez la solution :

$12c+5(5+3c)=3(9c−4)$

Réponse: contradiction ; pas de solution

Exercice$\PageIndex{33}$

Classifiez l'équation en tant qu'équation conditionnelle, identité ou contradiction, puis énoncez la solution :

$4(7d+18)=13(3d−2)−11d$

Réponse: contradiction ; pas de solution

Type d'équation	Que se passe-t-il lorsque vous le résolvez ?	Solution
Équation conditionnelle	Vrai pour une ou plusieurs valeurs des variables et faux pour toutes les autres valeurs	Une ou plusieurs valeurs
Identité	Vrai pour n'importe quelle valeur de la variable	Tous les nombres réels
Contro	Faux pour toutes les valeurs de la variable	Aucune solution

Concepts clés

Stratégie générale pour résoudre des équations linéaires
1. Simplifiez chaque côté de l'équation autant que possible.
  Utilisez la propriété distributive pour supprimer les parenthèses.
  Combinez les mêmes termes.
2. Collectez tous les termes variables d'un côté de l'équation.
  Utilisez la propriété d'addition ou de soustraction de l'égalité.
3. Recueillez tous les termes constants de l'autre côté de l'équation.
  Utilisez la propriété d'addition ou de soustraction de l'égalité.
4. Rendre le coefficient du terme variable égal à 1.
  Utilisez la propriété de multiplication ou de division de l'égalité.
  Indiquez la solution de l'équation.
5. Vérifiez la solution.
  Remplacez la solution dans l'équation d'origine.

Exercice\(\PageIndex{1}\): How to Solve Linear Equations Using the General Strategy

Exercice\(\PageIndex{2}\)

Exercice\(\PageIndex{3}\)

STRATÉGIE GÉNÉRALE POUR RÉSOUDRE DES ÉQUATIONS LINÉAIRES.

Exercice\(\PageIndex{4}\)

Exercice\(\PageIndex{5}\)

Exercice\(\PageIndex{6}\)

Exercice\(\PageIndex{7}\)

Exercice\(\PageIndex{8}\)

Exercice\(\PageIndex{9}\)

Exercice\(\PageIndex{10}\)

Exercice\(\PageIndex{11}\)

Exercice\(\PageIndex{12}\)

Exercice\(\PageIndex{13}\)

Exercice\(\PageIndex{14}\)

Exercice\(\PageIndex{15}\)

Exercice\(\PageIndex{16}\)

Exercice\(\PageIndex{17}\)

Exercice\(\PageIndex{18}\)

Exercice\(\PageIndex{19}\)

Exercice\(\PageIndex{20}\)

Exercice\(\PageIndex{21}\)

Exercice\(\PageIndex{22}\)

Exercice\(\PageIndex{23}\)

Exercice\(\PageIndex{24}\)

ÉQUATION CONDITIONNELLE

IDENTITÉ

CONTRACTION

Exercice\(\PageIndex{25}\)

Exercice\(\PageIndex{26}\)

Exercice\(\PageIndex{27}\)

Exercice\(\PageIndex{28}\)

Exercice\(\PageIndex{29}\)

Exercice\(\PageIndex{30}\)

Exercice\(\PageIndex{31}\)

Exercice\(\PageIndex{32}\)

Exercice\(\PageIndex{33}\)