17.4 : L'équation de Nernst
- Page ID
- 193913
- Associez les potentiels cellulaires aux changements d'énergie libre
- Utilisez l'équation de Nernst pour déterminer les potentiels cellulaires dans des conditions non standard
- Effectuer des calculs impliquant la conversion entre les potentiels des cellules, les variations d'énergie libre et les constantes d'équilibre
Nous allons maintenant étendre l'électrochimie en déterminant la relation entre\(E^\circ_\ce{cell}\) et les grandeurs thermodynamiques telles que Δ G° (énergie libre de Gibbs) et K (la constante d'équilibre). Dans les cellules galvaniques, l'énergie chimique est convertie en énergie électrique, qui peut fonctionner. Le travail électrique est le produit de la charge transférée multipliée par la différence de potentiel (tension) :
\[\mathrm{electrical\: work=volts \times (charge\: in\: coulombs)=J} \nonumber \]
La charge sur 1 mole d'électrons est donnée par la constante de Faraday (F)
\[ \begin{align*} F &=\dfrac{6.022 \times 10^{23}\:e^-}{mol} \times \dfrac{1.602 \times 10^{−19}\:C}{e^-} \\[4pt] &=9.648 \times 10^4\:\dfrac{C}{mol} \\[4pt] &=9.648 \times 10^4\:\dfrac{J}{V⋅mol} \end{align*} \nonumber \]
Par conséquent
\[\mathrm{total\: charge=(number\: of\: moles\: of\: e^-)} \times F=nF \nonumber \]
Dans cette équation,\(n\) est le nombre de moles d'électrons nécessaires à la réaction d'oxydoréduction équilibrée. Le potentiel de la cellule mesuré est le potentiel maximum que la cellule peut produire et est lié au travail électrique (w ele) par
\[E_\ce{cell}=\dfrac{−w_\ce{ele}}{nF}\hspace{40px}\ce{or}\hspace{40px}w_\ce{ele}=−nFE_\ce{cell} \nonumber \]
Le signe négatif indique que le travail électrique est effectué par le système (la cellule galvanique) sur l'environnement. Dans un chapitre précédent, l'énergie libre était définie comme l'énergie disponible pour travailler. En particulier, la variation de l'énergie libre a été définie en termes de travail maximum (\(w_{max}\)), qui, pour les systèmes électrochimiques, est\(w_{ele}\).
\[\begin{align*} ΔG&=w_\ce{max}=w_\ce{ele} \\[4pt] &=−nFE_\ce{cell} \end{align*} \nonumber \]
Nous pouvons vérifier que les signes sont corrects lorsque nous nous rendons compte que ce\(n\)\(F\) sont des constantes positives et que les cellules galvaniques, qui ont un potentiel cellulaire positif, impliquent des réactions spontanées. Ainsi, les réactions spontanées, qui l'ont fait\(ΔG < 0\), doivent avoir\(E_{cell} > 0\). Si tous les réactifs et produits sont dans leur état standard, cela devient
\[ΔG°=−nFE^\circ_\ce{cell} \nonumber \]
Cela permet de relier les potentiels cellulaires standard aux constantes d'équilibre, puisque
\[ΔG°=−RT\ln K \nonumber \]
\[−nFE^\circ_\ce{cell}=−RT\ln K \nonumber \]
ou
\[ E^\circ_\ce{cell}=\dfrac{RT}{nF}\ln K \nonumber \]
La plupart du temps, les réactions électrochimiques se déroulent à température standard (298,15 K). La collecte de termes à cette température donne
\[\begin{align*} E^\circ_\ce{cell}&=\dfrac{RT}{nF}\:\ln K \\[4pt] &=\dfrac{\left(8.314\:\dfrac{\ce{J}}{\textrm{K⋅mol}}\right)(298.15\:K)}{n \times 96,485\: \textrm{C/V⋅mol}}\:\ln K \\[4pt] &=\dfrac{\mathrm{0.0257\: V}}{n}\:\ln K \end{align*} \nonumber \]
où\(n\) est le nombre de moles d'électrons. Le logarithme des équations impliquant des potentiels cellulaires est souvent exprimé à l'aide de logarithmes en base 10 (c'est-à-dire\(\log_{10}\) ou simplement\(\log\)), qui modifient la constante par un facteur de 2,303 :
\[E^\circ_\ce{cell}=\dfrac{\mathrm{0.0592\: V}}{n}\:\log K \nonumber \]
Ainsi, si Δ G°, K ou\(E^\circ_\ce{cell}\) est connu ou peut être calculé, les deux autres grandeurs peuvent être facilement déterminées. Les relations sont illustrées graphiquement dans la figure\(\PageIndex{1}\).
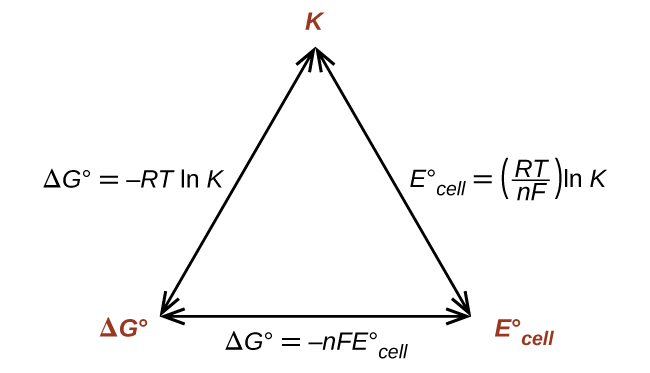
En fonction de l'une quelconque des quantités, les deux autres peuvent être calculées.
Quels sont le changement d'énergie libre et la constante d'équilibre standard de Gibbs pour la réaction suivante à 25 °C ?
\[\ce{2Ag+}(aq)+\ce{Fe}(s)⇌\ce{2Ag}(s)+\ce{Fe^2+}(aq) \nonumber \]
Solution de sol
La réaction implique une réaction d'oxydoréduction, de sorte que le potentiel cellulaire standard peut être calculé à l'aide des données du tableau P1.
\ [\ begin {align*}
& \ textrm {anode (oxydation) :} \ ce {Fe} (s) ⟶ \ ce {Fe^2+} (aq) + \ ce {2e-} \ hspace {40px} E^ \ circ_ {\ ce {Fe^2+/Fe}} = \ mathrm {−0,447 \ : V} \ nonnumber \ \
& \ textrm cathode (réduction) :} 2 \ fois (\ ce {Ag+} (aq) + \ ce {e-} ⟶ \ ce {Ag} (s)) \ hspace {40px} E^ \ circ_ {\ ce {Ag+/Ag}} = \ mathrm {0,7996 \ : V} \ nonumber \ \
&E^ \ circ_ \ ce {cellule} =E^ \ circ_ \ ce {cathode} −E^ \ circ_ \ ce {anode} =E^ \ circ_ {\ ce {Ag+/Ag}} −E^ \ circ_ {\ ce {Fe^2+/Fe}} = \ mathrm {+1,247 \ : V} \ non number
\ end {align*} \ nonnumber \]
N'oubliez pas que le potentiel de la cellule pour la cathode n'est pas multiplié par deux lors de la détermination du potentiel de cellule standard. Avec n = 2, la constante d'équilibre est alors
\[E^\circ_\ce{cell}=\dfrac{\mathrm{0.0592\: V}}{n}\:\log K \nonumber \]
\[\begin{align*} K&=10^{n \times E^\circ_\ce{cell}/\mathrm{0.0592\: V}} \\[4pt] &=10^{2 \times \mathrm{1.247\: V/0.0592\: V}} \\[4pt] &=10^{42.128} \\[4pt] &=1.3 \times 10^{42}\end{align*} \nonumber \]
L'énergie libre standard est alors
\[ΔG°=−nFE^\circ_\ce{cell} \nonumber \]
\[ΔG°=\mathrm{−2 \times 96,485\:\dfrac{J}{\textrm{V⋅mol}} \times 1.247\: V=−240.6\:\dfrac{kJ}{mol}} \nonumber \]
Vérifiez votre réponse : Un potentiel cellulaire standard positif signifie une réaction spontanée. Le changement d'énergie libre standard doit donc être négatif et une constante d'équilibre doit être supérieure à 1.
Quelle est la variation d'énergie libre standard de Gibbs et la constante d'équilibre pour la réaction suivante à température ambiante ? La réaction est-elle spontanée ?
\[\ce{Sn}(s)+\ce{2Cu^2+}(aq)⇌\ce{Sn^2+}(aq)+\ce{2Cu+}(aq) \nonumber \]
- Réponse
-
Spontané ; n = 2\(E^\circ_\ce{cell}=\mathrm{+0.291\: V}\) ;\(ΔG°=\mathrm{−56.2\:\dfrac{kJ}{mol}}\) ; ;\(K = 6.8 \times 10^9\).
Maintenant que le lien entre l'énergie libre et les potentiels cellulaires a été établi, des concentrations non standard s'ensuivent. Rappelons que
\[ΔG=ΔG°+RT\ln Q \nonumber \]
où\(Q\) est le quotient de réaction (voir le chapitre sur les fondamentaux de l'équilibre). Conversion en potentiels cellulaires :
\[−nFE_\ce{cell}=−nFE^\circ_\ce{cell}+RT\ln Q \label{nernst1A} \]
ou
\[E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{RT}{nF}\:\ln Q \label{nernst1B} \]
L'équation \ ref {Nernst1b} est l'équation de Nernst généralisée applicable à n'importe quelle température. Cependant, il peut être simplifié pour les réactions se produisant à 25 °C (298,15 K) en le réécrivant comme
\[E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{\mathrm{0.0257\: V}}{n}\:\ln Q \label{nernst2A} \]
ou
\[ E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{\mathrm{0.0592\: V}}{n}\log_{10} Q \label{nernst2B} \]
Si la température n'est pas de 298,15 K, il est nécessaire de recalculer le potentiel à l'aide de l'équation \ ref {Nernst1b}. L'équation de Nernst permet de calculer le potentiel cellulaire dans des conditions non standard. Cet ajustement est nécessaire car les potentiels déterminés dans différentes conditions auront des valeurs différentes.
Envisagez la réaction suivante à température ambiante :
\[\ce{Co}(s)+\ce{Fe^2+}(aq,\:1.94\:M)⟶\ce{Co^2+}(aq,\: 0.15\:M)+\ce{Fe}(s) \nonumber \]
Le processus est-il spontané ?
Solution
Il existe deux manières de résoudre le problème. Si les informations thermodynamiques du tableau T1 étaient disponibles, vous pourriez calculer la variation d'énergie libre. Si le changement d'énergie libre est négatif, le processus est spontané. L'autre approche, que nous utiliserons, nécessite des informations telles que celles données dans le tableau P1. À l'aide de ces données, le potentiel cellulaire peut être déterminé. Si le potentiel cellulaire est positif, le processus est spontané. Collecte d'informations à partir du tableau P1 et du problème,
\ [\ begin {align*}
& \ textrm {Anode (oxydation) :} \ ce {Co} (s) ⟶ \ ce {Co^2+} (aq) + \ ce {2e-} \ hspace {40px} E^ \ circ_ {\ ce {Co^2+/Co}} = \ mathrm {−0,28 \ : V} \ \
& \ textrm {Réduction de la cathode () :} \ ce {Fe^2+} (aq) + \ ce {2e-} ⟶ \ ce {Fe} (s) \ hspace {40px} E^ \ circ_ {\ ce {Fe^2+/Fe}} = \ mathrm {−0,447 \ : V} \ \
&E^ \ circ_ \ ce {cellule} =E^ \ circ_ \ ce {cathode} −E^ \ circ_ \ ce {anode} = \ mathrm {−0,447 \ : V− (−0,28 \ : V) =−0,17 \ : V}
\ end {align*} \ nonnumber \]
Le processus n'est pas spontané dans des conditions standard. En utilisant l'équation de Nernst et les concentrations indiquées dans le problème et\(n = 2\),
\[Q=\ce{\dfrac{[Co^2+]}{[Fe^2+]}}=\dfrac{0.15\:M}{1.94\:M}=0.077 \nonumber \]
Nous pouvons maintenant les insérer dans l'équation de Nernst à température ambiante (Équation \ ref {Nernst2b})
\[\begin{align*} E_\ce{cell} &=E^\circ_\ce{cell}−\dfrac{\mathrm{0.0592\: V}}{n}\:\log Q \\[4pt] &=\mathrm{−0.17\: V−\dfrac{0.0592\: V}{2}\:\log 0.077} \\[4pt] &=\mathrm{−0.17\: V+0.033\: V=−0.14\: V} \end{align*} \nonumber \]
Le processus est (toujours) non spontané.
Quel est le potentiel de la cellule pour la réaction suivante à température ambiante ?
\[\ce{Al}(s)│\ce{Al^3+}(aq,\:0.15\:M)║\ce{Cu^2+}(aq,\:0.025\:M)│\ce{Cu}(s) \nonumber \]
Quelles sont les valeurs de n et de Q pour la réaction globale ? La réaction est-elle spontanée dans ces conditions ?
- Réponse
-
n = 6 ; Q = 1440 ; cellule E = +1,97 V, spontanée.
Enfin, nous examinerons brièvement un type spécial de cellule appelé cellule de concentration. Dans une cellule de concentration, les électrodes sont du même matériau et les demi-cellules ne diffèrent que par leur concentration. Comme l'un des compartiments ou les deux ne sont pas standard, les potentiels des cellules seront inégaux ; il y aura donc une différence de potentiel, qui peut être déterminée à l'aide de l'équation de Nernst.
Quel est le potentiel cellulaire de la cellule de concentration décrite par
\[\ce{Zn}(s)│\ce{Zn^2+}(aq,\: 0.10\:M)║\ce{Zn^2+}(aq,\: 0.50\:M)│\ce{Zn}(s) \nonumber \]
Solution de sol
D'après les informations fournies :
\ [\ begin {align*}
& \ textrm {Anode :} \ ce {Zn} (s) ⟶ \ ce {Zn^2+} (aq, \ : 0,10 \ :M) + \ ce {2e-} \ hspace {40px} E^ \ circ_ \ ce {anode} = \ mathrm {−0,7618 \ : V} \ \
& \ textrm {Cathode :} ce {Zn^2+} (aq, \ : 0,50 \ :M) + \ ce {2e-} ⟶ \ ce {Zn} (s) \ hspace {40px} E^ \ circ_ \ ce {cathode} = \ mathrm {−0,7618 \ : V} \ \
& amp ; \ overline {\ textrm {Globalement :} \ ce {Zn^2+} (aq, \ : 0,50 \ :M) ⟶ \ ce {Zn^2+} (aq, \ : 0,10 \ :M) \ hspace {40px} E^ \ circ_ \ ce {cell} = \ mathrm {0.000 \ : V}}
\ end {align*} \ nonumber \]
Le potentiel standard de la cellule est nul car l'anode et la cathode impliquent la même réaction ; seule la concentration de Zn 2 + change. En remplaçant dans l'équation de Nernst,
\[E_\ce{cell}=\mathrm{0.000\: V−\dfrac{0.0592\: V}{2}\:\log\dfrac{0.10}{0.50}=+0.021\: V} \nonumber \]
et le processus est spontané dans ces conditions.
Vérifiez votre réponse : Dans une cellule de concentration, le potentiel cellulaire standard sera toujours nul. Pour obtenir un potentiel cellulaire positif (processus spontané), le quotient de réaction Q doit être inférieur à 1. Q < 1 dans ce cas, donc le processus est spontané.
Quelle valeur de Q pour la cellule de concentration précédente produirait une tension de 0,10 V ? Si la concentration en ions zinc à la cathode était de 0,50 M, quelle était la concentration à l'anode ?
- Réponse
-
Q = 0,00042 ; [Zn 2 +] cat = 2,1 \ fois 10 −4 M.
Résumé
Le travail électrique (w ele) est le résultat négatif du produit de la charge totale (Q) et du potentiel de la cellule (cellule E). La charge totale peut être calculée comme le nombre de moles d'électrons (n) multiplié par la constante de Faraday (F = 96 485 C/mol e −). Le travail électrique est le travail maximal que le système peut produire et est donc égal à la variation de l'énergie libre. Ainsi, tout ce qui peut être fait avec ou pour un changement d'énergie libre peut également être fait avec ou avec un potentiel cellulaire. L'équation de Nernst relie le potentiel cellulaire dans des conditions non standard au logarithme du quotient de réaction. Les cellules de concentration exploitent cette relation et produisent un potentiel cellulaire positif en utilisant des demi-cellules qui ne diffèrent que par la concentration de leurs solutés.
Équations clés
- \(E^\circ_\ce{cell}=\dfrac{RT}{nF}\:\ln K\)
- \(E^\circ_\ce{cell}=\dfrac{\mathrm{0.0257\: V}}{n}\:\ln K=\dfrac{\mathrm{0.0592\: V}}{n}\:\log K \hspace{40px} \mathrm{(at\: 298.15\:\mathit{K})}\)
- \(E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{RT}{nF}\:\ln Q \hspace{40px} \textrm{(Nernst equation)}\)
- \(E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{\mathit{0.0257\: V}}{n}\:\ln Q=E^\circ_\ce{cell}−\dfrac{\mathrm{0.0592\: V}}{n}\:\log Q \hspace{40px} \mathrm{(at\: 298.15\:\mathit{K})}\)
- Δ G = − Cellule NFe
- \(ΔG^∘=−nFE^\circ_\ce{cell}\)
- \(w_\ce{ele}=w_\ce{max}=−nFE_\ce{cell}\)
Lexique
- cellule de concentration
- cellule galvanique dans laquelle les deux demi-cellules sont identiques à l'exception de la concentration des solutés ; spontanée lorsque la réaction globale est la dilution du soluté
- travaux électriques (w ele)
- négatif de la charge totale multiplié par le potentiel de la cellule ; égal à w max pour le système, donc égal à la variation d'énergie libre (Δ G)
- Constante de Faraday (F)
- charge sur 1 mol d'électrons ; F = 96 485 C/mol e -
- équation de Nernst
- équation qui relie le logarithme du quotient de réaction (Q) à des potentiels cellulaires non standard ; peut être utilisée pour relier les constantes d'équilibre aux potentiels cellulaires standard


