Skip to main content
Global

17.3 : Potentiels de réduction standard

  1. Last updated
  2. Save as PDF
  • Page ID
    193911

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage
    • Déterminer les potentiels cellulaires standard pour les réactions d'oxydoréduction
    • Utiliser des potentiels de réduction standard pour déterminer le meilleur agent oxydant ou réducteur parmi plusieurs choix possibles

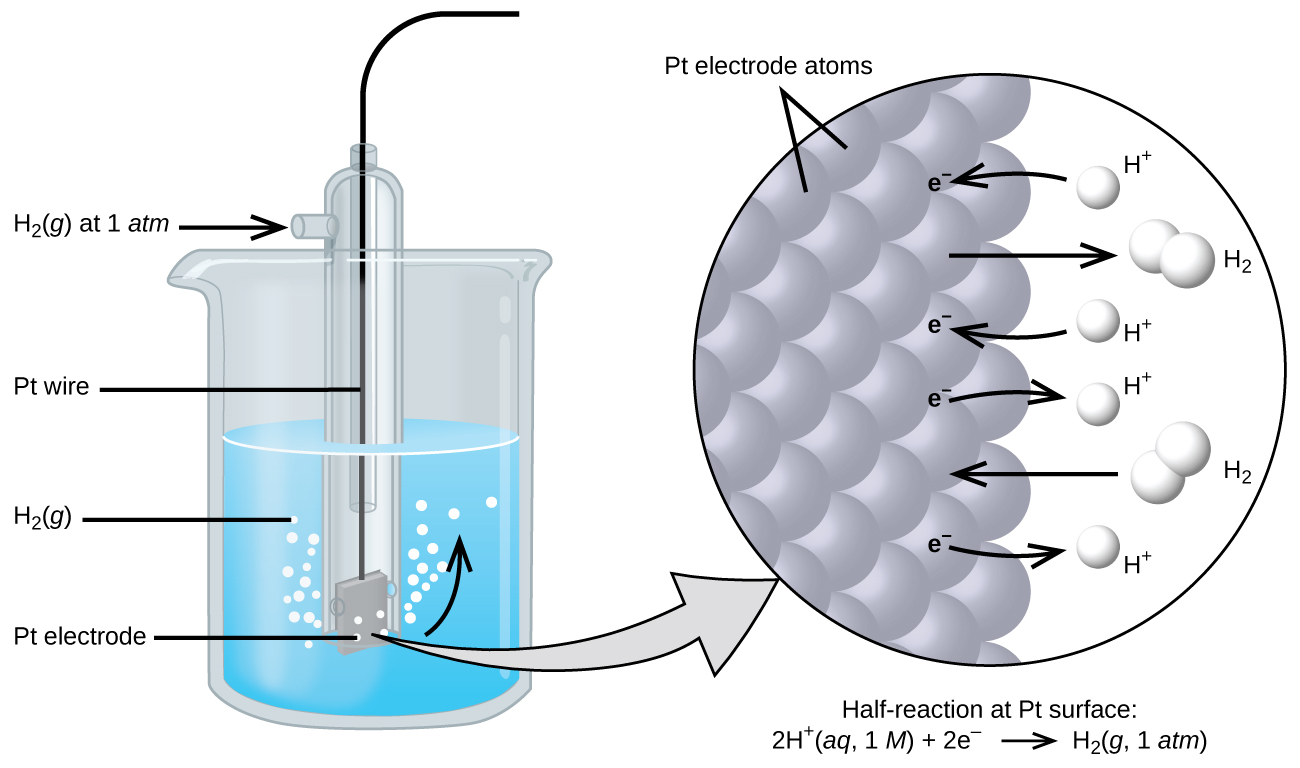
    Le potentiel de la cellule résulte de la différence des potentiels électriques de chaque électrode. Bien qu'il soit impossible de déterminer le potentiel électrique d'une seule électrode, nous pouvons attribuer à une électrode la valeur zéro et l'utiliser ensuite comme référence. L'électrode choisie comme zéro est illustrée sur la Figure 17.4.1 et est appelée électrode à hydrogène standard (SHE). Le SHE se compose de 1 atm d'hydrogène gazeux barboté dans une solution de HCl 1 M, généralement à température ambiante. Le platine, chimiquement inerte, est utilisé comme électrode. La demi-réaction de réduction choisie comme référence est

    \[\ce{2H+}(aq,\: 1\:M)+\ce{2e-}⇌\ce{H2}(g,\:1\: \ce{atm}) \hspace{20px} E°=\mathrm{0\: V} \nonumber \]

    E° est le potentiel de réduction standard. L'exposant «° » sur le E indique les conditions standard (1 bar ou 1 atm pour les gaz, 1 M pour les solutés). La tension est définie comme nulle pour toutes les températures.

    alt
    Figure\(\PageIndex{1}\) : De l'hydrogène gazeux à 1 atm est fait barboter dans une solution de HCl 1 M. Le platine, inerte à l'action du HCl 1 M, est utilisé comme électrode. Les électrons à la surface de l'électrode se combinent avec le H + en solution pour produire de l'hydrogène gazeux.

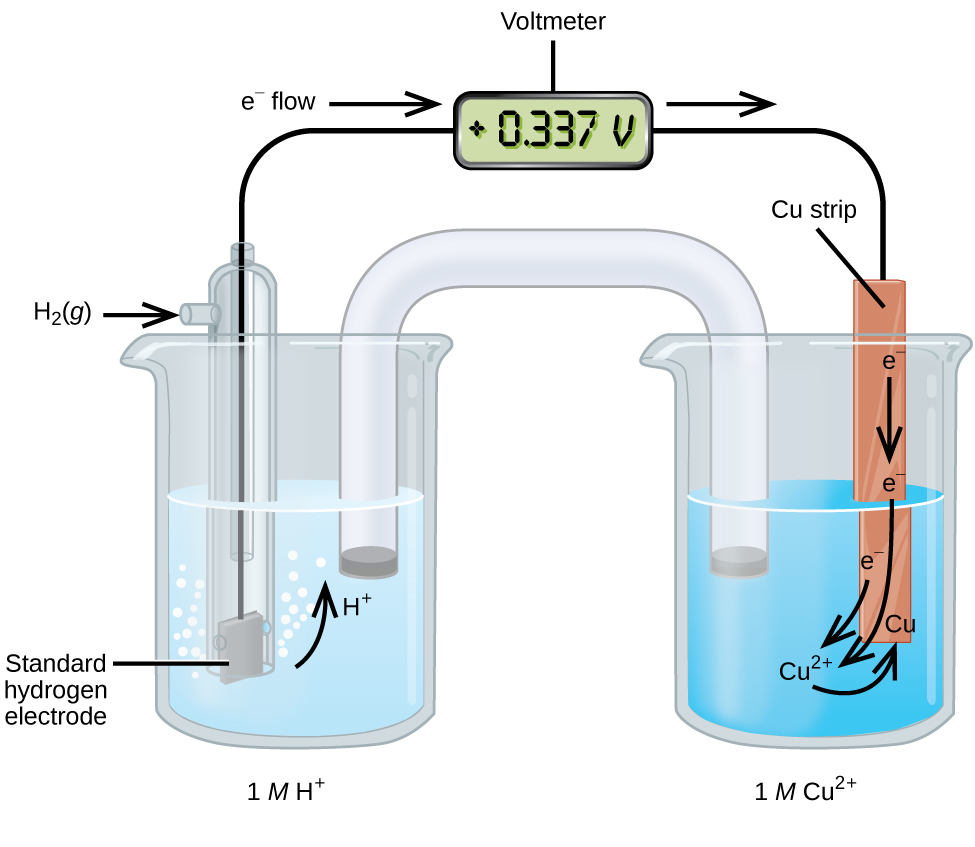
    Une cellule galvanique composée d'une demi-cellule SHE et d'une demi-cellule Cu 2 + /Cu peut être utilisée pour déterminer le potentiel de réduction standard pour le Cu 2 + (Figure\(\PageIndex{2}\)). En notation cellulaire, la réaction est

    \[\ce{Pt}(s)│\ce{H2}(g,\:1\: \ce{atm})│\ce{H+}(aq,\:1\:M)║\ce{Cu^2+}(aq,\:1\:M)│\ce{Cu}(s) \nonumber \]

    Les électrons circulent de l'anode à la cathode. Les réactions, qui sont réversibles, sont

    \ [\ begin {align*}
    & \ textrm {Anode (oxydation) :} \ ce {H2} (g) ⟶ \ ce {2H+} (aq) + \ ce {2e-} \ \
    & \ textrm {Cathode (réduction) :} \ ce {Cu^2+} (aq) + \ ce {2e-} ⟶ \ ce {Cu} (s) \ \
    & \ overline {\ textrm {Globalement :} \ ce {Cu^2+} (aq) + \ ce {H2} (g) ⟶ \ ce {2H+} (aq) + \ ce {Cu} (s)}
     \ end {align* } \ aucun numéro \]

    Le potentiel de réduction standard peut être déterminé en soustrayant le potentiel de réduction standard pour la réaction se produisant à l'anode du potentiel de réduction standard pour la réaction se produisant à la cathode. Le signe moins est nécessaire car l'oxydation est l'inverse de la réduction.

    \[E^\circ_\ce{cell}=E^\circ_\ce{cathode}−E^\circ_\ce{anode} \nonumber \]

    \[\mathrm{+0.34\: V}=E^\circ_{\ce{Cu^2+/Cu}}−E^\circ_{\ce{H+/H2}}=E^\circ_{\ce{Cu^2+/Cu}}−0=E^\circ_{\ce{Cu^2+/Cu}} \nonumber \]

    alt
    Figure\(\PageIndex{2}\) : Une cellule galvanique peut être utilisée pour déterminer le potentiel de réduction standard du Cu 2 +.

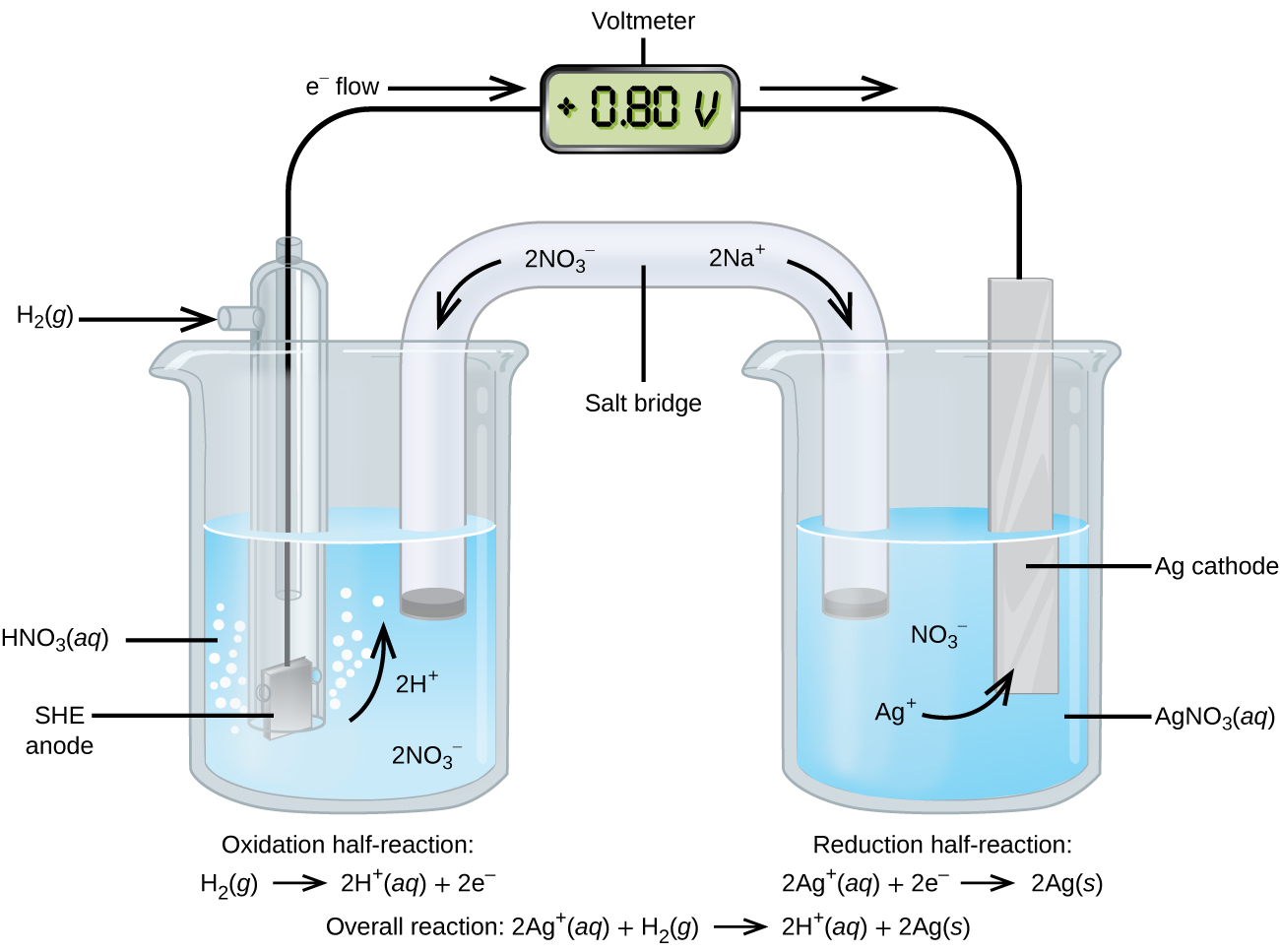
    En utilisant le SHE comme référence, d'autres potentiels de réduction standard peuvent être déterminés. Considérez la cellule illustrée dans la figure\(\PageIndex{2}\), où

    \[\ce{Pt}(s)│\ce{H2}(g,\:1\: \ce{atm})│\ce{H+}(aq,\: 1\:M)║\ce{Ag+}(aq,\: 1\:M)│\ce{Ag}(s) \nonumber \]

    Les électrons circulent de gauche à droite, et les réactions sont

    \ [\ begin {align*}
    & \ textrm {anode (oxydation) :} \ ce {H2} (g) ⟶ \ ce {2H+} (aq) + \ ce {2e-} \ \
    & \ textrm {cathode (réduction) :} \ ce {2Ag+} (aq) + \ ce {2e-} ⟶ \ ce {2Ag} (s) \ \
    & \ overline \ textrm {globalement :} \ ce {2Ag+} (aq) + \ ce {H2} (g) ⟶ \ ce {2H+} (aq) + \ ce {2Ag} (s)}
     \ end {align*} \ aucun numéro \]

    Le potentiel de réduction standard peut être déterminé en soustrayant le potentiel de réduction standard pour la réaction se produisant à l'anode du potentiel de réduction standard pour la réaction se produisant à la cathode. Le signe moins est nécessaire car l'oxydation est l'inverse de la réduction.

    \[E^\circ_\ce{cell}=E^\circ_\ce{cathode}−E^\circ_\ce{anode} \nonumber \]

    \[\mathrm{+0.80\: V}=E^\circ_{\ce{Ag+/Ag}}−E^\circ_{\ce{H+/H2}}=E^\circ_{\ce{Ag+/Ag}}−0=E^\circ_{\ce{Ag+/Ag}} \nonumber \]

    Il est important de noter que le potentiel n'est pas doublé pour la réaction cathodique.

    Le SHE est assez dangereux et rarement utilisé en laboratoire. Son principal intérêt est qu'il a établi le zéro pour les potentiels de réduction standard. Une fois déterminés, les potentiels de réduction standard peuvent être utilisés pour déterminer le potentiel cellulaire standard\(E^\circ_\ce{cell}\), pour n'importe quelle cellule. Par exemple, pour la cellule suivante :

    \[\ce{Cu}(s)│\ce{Cu^2+}(aq,\:1\:M)║\ce{Ag+}(aq,\:1\:M)│\ce{Ag}(s) \nonumber \]

    \ [\ begin {align*}
    & \ textrm {anode (oxydation) :} \ ce {Cu} (s) ⟶ \ ce {Cu^2+} (aq) + \ ce {2e-} \ \
    & \ textrm {cathode (réduction) :} \ ce {2Ag+} (aq) + \ ce {2e-} ⟶ \ ce {2Ag} (s) \ \
    & \ overline {\ textrm {globalement :} \ ce {Cu} (s) + \ ce {2Ag+} (aq) ⟶ \ ce {Cu^2+} (aq) + \ ce {2Ag} (s)}
     \ end { align*} \ nonnumber \]

    \[E^\circ_\ce{cell}=E^\circ_\ce{cathode}−E^\circ_\ce{anode}=E^\circ_{\ce{Ag+/Ag}}−E^\circ_{\ce{Cu^2+/Cu}}=\mathrm{0.80\: V−0.34\: V=0.46\: V} \nonumber \]

    Encore une fois, notez que lors du calcul\(E^\circ_\ce{cell}\), les potentiels de réduction standard restent toujours les mêmes, même lorsqu'une demi-réaction est multipliée par un facteur. Les potentiels de réduction standard pour certaines réactions de réduction sont présentés dans le tableau\(\PageIndex{1}\). Une liste plus complète est fournie dans les tableaux P1 ou P2.

    alt
    Figure\(\PageIndex{3}\) : Une cellule galvanique peut être utilisée pour déterminer le potentiel de réduction standard de l'Ag +. Le SHE sur la gauche est l'anode et un potentiel de réduction standard de zéro lui est attribué.
    Tableau\(\PageIndex{1}\) : Potentiels de réduction standard sélectionnés à 25 °C
    Demi-réaction E° (V)
    \(\ce{F2}(g)+\ce{2e-}⟶\ce{2F-}(aq)\) +2 866
    \(\ce{PbO2}(s)+\ce{SO4^2-}(aq)+\ce{4H+}(aq)+\ce{2e-}⟶\ce{PbSO4}(s)+\ce{2H2O}(l)\) +1,69
    \(\ce{MnO4-}(aq)+\ce{8H+}(aq)+\ce{5e-}⟶\ce{Mn^2+}(aq)+\ce{4H2O}(l)\) +1,507
    \(\ce{Au^3+}(aq)+\ce{3e-}⟶\ce{Au}(s)\) +1 498
    \(\ce{Cl2}(g)+\ce{2e-}⟶\ce{2Cl-}(aq)\) +1 35827
    \(\ce{O2}(g)+\ce{4H+}(aq)+\ce{4e-}⟶\ce{2H2O}(l)\) +1,229
    \(\ce{Pt^2+}(aq)+\ce{2e-}⟶\ce{Pt}(s)\) +1,20
    \(\ce{Br2}(aq)+\ce{2e-}⟶\ce{2Br-}(aq)\) +1,0873
    \(\ce{Ag+}(aq)+\ce{e-}⟶\ce{Ag}(s)\) +0,7996
    \(\ce{Hg2^2+}(aq)+\ce{2e-}⟶\ce{2Hg}(l)\) +0,7973
    \(\ce{Fe^3+}(aq)+\ce{e-}⟶\ce{Fe^2+}(aq)\) +0,771
    \(\ce{MnO4-}(aq)+\ce{2H2O}(l)+\ce{3e-}⟶\ce{MnO2}(s)+\ce{4OH-}(aq)\) +0,558
    \(\ce{I2}(s)+\ce{2e-}⟶\ce{2I-}(aq)\) +0,5355
    \(\ce{NiO2}(s)+\ce{2H2O}(l)+\ce{2e-}⟶\ce{Ni(OH)2}(s)+\ce{2OH-}(aq)\) +0,49
    \(\ce{Cu^2+}(aq)+\ce{2e-}⟶\ce{Cu}(s)\) +0,34
    \(\ce{Hg2Cl2}(s)+\ce{2e-}⟶\ce{2Hg}(l)+\ce{2Cl-}(aq)\) +0,26808
    \(\ce{AgCl}(s)+\ce{e-}⟶\ce{Ag}(s)+\ce{Cl-}(aq)\) +0,22233
    \(\ce{Sn^4+}(aq)+\ce{2e-}⟶\ce{Sn^2+}(aq)\) +0,151
    \(\ce{2H+}(aq)+\ce{2e-}⟶\ce{H2}(g)\) 0,00
    \(\ce{Pb^2+}(aq)+\ce{2e-}⟶\ce{Pb}(s)\) −0,1262
    \(\ce{Sn^2+}(aq)+\ce{2e-}⟶\ce{Sn}(s)\) −0,1375
    \(\ce{Ni^2+}(aq)+\ce{2e-}⟶\ce{Ni}(s)\) −0,257
    \(\ce{Co^2+}(aq)+\ce{2e-}⟶\ce{Co}(s)\) −0,28
    \(\ce{PbSO4}(s)+\ce{2e-}⟶\ce{Pb}(s)+\ce{SO4^2-}(aq)\) −0,3505
    \(\ce{Cd^2+}(aq)+\ce{2e-}⟶\ce{Cd}(s)\) −0,4030
    \(\ce{Fe^2+}(aq)+\ce{2e-}⟶\ce{Fe}(s)\) −0,447
    \(\ce{Cr^3+}(aq)+\ce{3e-}⟶\ce{Cr}(s)\) −0,744
    \(\ce{Mn^2+}(aq)+\ce{2e-}⟶\ce{Mn}(s)\) −1,185
    \(\ce{Zn(OH)2}(s)+\ce{2e-}⟶\ce{Zn}(s)+\ce{2OH-}(aq)\) −1 245
    \(\ce{Zn^2+}(aq)+\ce{2e-}⟶\ce{Zn}(s)\) −0,7618
    \(\ce{Al^3+}(aq)+\ce{3e-}⟶\ce{Al}(s)\) −1,662
    \(\ce{Mg^2+}(aq)+\ce{2e-}⟶\ce{Mg}(s)\) −2,372
    \(\ce{Na+}(aq)+\ce{e-}⟶\ce{Na}(s)\) −2,71
    \(\ce{Ca^2+}(aq)+\ce{2e-}⟶\ce{Ca}(s)\) −2,868
    \(\ce{Ba^2+}(aq)+\ce{2e-}⟶\ce{Ba}(s)\) −2,912
    \(\ce{K+}(aq)+\ce{e-}⟶\ce{K}(s)\) −2,931
    \(\ce{Li+}(aq)+\ce{e-}⟶\ce{Li}(s)\) −3,04

    Des tableaux comme celui-ci permettent de déterminer le potentiel cellulaire standard pour de nombreuses réactions d'oxydoréduction.

    Exemple\(\PageIndex{1}\): Cell Potentials from Standard Reduction Potentials

    Quel est le potentiel de cellule standard pour une cellule galvanique composée de demi-cellules Au 3 + /Au et Ni 2 + /Ni ? Identifier les agents oxydants et réducteurs.

    Solution

    À l'aide du tableau\(\PageIndex{1}\), les réactions impliquées dans la cellule galvanique, toutes deux écrites sous forme de réductions, sont

    \[\ce{Au^3+}(aq)+\ce{3e-}⟶\ce{Au}(s) \hspace{20px} E^\circ_{\ce{Au^3+/Au}}=\mathrm{+1.498\: V} \nonumber \]

    \[\ce{Ni^2+}(aq)+\ce{2e-}⟶\ce{Ni}(s) \hspace{20px} E^\circ_{\ce{Ni^2+/Ni}}=\mathrm{−0.257\: V} \nonumber \]

    Les cellules galvaniques ont des potentiels cellulaires positifs et toutes les réactions de réduction sont réversibles. La réaction à l'anode sera la demi-réaction avec le potentiel de réduction standard le plus faible ou le plus négatif. En inversant la réaction à l'anode (pour montrer l'oxydation) mais pas son potentiel de réduction standard, on obtient :

    \ [\ begin {align*}
    & \ textrm {Anode (oxydation) :} \ ce {Ni} (s) ⟶ \ ce {Ni^2+} (aq) + \ ce {2e-} \ hspace {20e} E^ \ circ_ \ ce {anode} =E^ \ circ_ {\ ce {Ni^2+/Ni}} = \ mathrm {−0,257 \ ce {Ni^2+/Ni}} = \ mathrm {−0,257 \ ce \ : V} \ \
    & \ textrm {Cathode (réduction) :} \ ce {Au^3+} (aq) + \ ce {3e-} ⟶ \ ce {Au} (s) \ hspace {1080p} E^ \ circ_ \ ce {cathode} =E^ \ circ_ {\ ce {Au ^3+/ Au}} = \ mathrm {+1.498 \ : V}
     \ end {align*} \ nonnumber \]

    Le facteur le moins courant est six, donc la réaction globale est

    \(\ce{3Ni}(s)+\ce{2Au^3+}(aq)⟶\ce{3Ni^2+}(aq)+\ce{2Au}(s)\)

    Les potentiels de réduction ne sont pas mis à l'échelle par les coefficients stœchiométriques lors du calcul du potentiel de la cellule, et les potentiels de réduction standard non modifiés doivent être utilisés.

    \[E^\circ_\ce{cell}=E^\circ_\ce{cathode}−E^\circ_\ce{anode}=\mathrm{1.498\: V−(−0.257\: V)=1.755\: V} \nonumber \]

    À partir des demi-réactions, le Ni est oxydé, c'est donc l'agent réducteur, et l'Au 3 + est réduit, donc c'est l'agent oxydant.

    Exercice\(\PageIndex{1}\)

    Une cellule galvanique se compose d'une électrode de Mg dans une solution de 1 M de Mg (NO 3) 2 et d'une électrode d'Ag dans une solution de 1 M d'AgNO 3. Calculez le potentiel cellulaire standard à 25 °C.

    Réponse

    \[\ce{Mg}(s)+\ce{2Ag+}(aq)⟶\ce{Mg^2+}(aq)+\ce{2Ag}(s) \hspace{20px} E^\circ_\ce{cell}=\mathrm{0.7996\: V−(−2.372\: V)=3.172\: V} \nonumber \]

    Résumé

    L'attribution du potentiel de l'électrode à hydrogène standard (SHE) à zéro volt permet de déterminer des potentiels de réduction standard, E°, pour les demi-réactions dans les cellules électrochimiques. Comme leur nom l'indique, les potentiels de réduction standard utilisent des états standard (1 bar ou 1 atm pour les gaz ; 1 M pour les solutés, souvent à 298,15 K) et sont écrits sous forme de réductions (où les électrons apparaissent sur le côté gauche de l'équation). Les réactions de réduction étant réversibles, les potentiels standard des cellules peuvent être calculés en soustrayant le potentiel de réduction standard pour la réaction à l'anode de la réduction standard pour la réaction à la cathode. Lors du calcul du potentiel cellulaire standard, les potentiels de réduction standard ne sont pas mis à l'échelle par les coefficients stœchiométriques de l'équation globale équilibrée.

    Équations clés

    • \(E^\circ_\ce{cell}=E^\circ_\ce{cathode}−E^\circ_\ce{anode}\)

    Lexique

    potentiel cellulaire standard\( (E^\circ_\ce{cell})\)
    le potentiel de la cellule lorsque tous les réactifs et produits sont dans leur état standard (1 bar ou 1 atm pour les gaz ; 1 M pour les solutés), généralement à 298,15 K ; peut être calculé en soustrayant le potentiel de réduction standard pour la demi-réaction à l'anode du potentiel de réduction standard pour la demi-réaction à l'anode du potentiel de réduction standard pour la demi-réaction à l'anode réaction se produisant à la cathode
    électrode à hydrogène standard (SHE)
    l'électrode consiste en un gaz d'hydrogène faisant barboter de l'acide chlorhydrique sur une électrode inerte en platine dont la réduction dans des conditions standard se voit attribuer une valeur de 0 V ; point de référence pour les potentiels de réduction standard
    potentiel de réduction standard (E°)
    la valeur de la réduction dans des conditions standard (1 bar ou 1 atm pour les gaz ; 1 M pour les solutés), généralement à 298,15 K ; valeurs tabulées utilisées pour calculer les potentiels cellulaires standard