16.4 : Gibbs Energy
- Page ID
- 193885
- Définissez l'énergie libre de Gibbs et décrivez sa relation avec la spontanéité
- Calculer la variation d'énergie libre standard pour un procédé en utilisant les énergies libres standard de formation de ses réactifs et de ses produits
- Calculer la variation d'énergie libre standard pour un procédé en utilisant les senthalpies de formation et les entropies de ses réactifs et de ses produits
- Expliquer comment la température affecte la spontanéité de certains processus
- Reliez les variations d'énergie libre standard aux constantes d'équilibre
L'un des défis liés à l'utilisation de la deuxième loi de la thermodynamique pour déterminer si une réaction chimique est spontanée est que nous devons déterminer le changement d'entropie pour le système et le changement d'entropie pour l'environnement. Un deuxième défi lorsque l'on travaille sur une réaction chimique est que nous devons prendre en compte le mélange des substances, un problème qui ne se pose pas lors de l'observation du changement de phase d'une substance pure. Une approche alternative impliquant une nouvelle propriété thermodynamique définie uniquement en termes de propriétés du système a été introduite à la fin du XIXe siècle par le mathématicien américain Josiah Willard Gibbs. Cette nouvelle propriété est appelée énergie libre de Gibbs (\(G\)) (ou simplement énergie libre), et elle est définie en termes d'enthalpie et d'entropie d'un système comme suit :
\[G=H−TS \nonumber \]
L'énergie libre est une fonction d'état et, à température et pression constantes, la variation standard de l'énergie libre (ΔG°) peut être exprimée comme suit :
\[ΔG^º_\ce{sys}=ΔH^º_\ce{sys}−TΔS^º_\ce{sys} \nonumber \]
(Par souci de simplicité, l'indice « sys » sera désormais omis.) Nous pouvons comprendre la relation entre cette propriété du système et la spontanéité d'un processus en rappelant l'expression de la deuxième loi dérivée précédemment :
\[ΔS_\ce{univ}=ΔS+\dfrac{q_\ce{surr}}{T} \nonumber \]
La première loi l'exige\(q_{surr} = −q_{sys}\), et sous une pression constante\(q_{sys} = ΔH\), et cette expression peut donc être réécrite comme suit :
\[ΔS_\ce{univ}=ΔS−\dfrac{ΔH}{T} \nonumber \]
ΔH est le changement d'enthalpie du système. En multipliant les deux côtés de cette équation par −T et en réorganisant cette équation, on obtient ce qui suit :
\[−TΔS_\ce{univ}=ΔH−TΔS \nonumber \]
La comparaison de cette équation à la précédente pour le changement d'énergie libre montre la relation suivante :
\[ΔG=−TΔS_\ce{univ} \label{6} \]
Le changement d'énergie libre est donc un indicateur fiable de la spontanéité d'un processus, étant directement lié à l'indicateur de spontanéité précédemment identifié\(ΔS_{univ}\). \(\PageIndex{1}\)Le tableau résume la relation entre la spontanéité d'un processus et les signes arithmétiques de ces indicateurs.
| \(ΔS_{univ} > 0\) | Δ G < 0 | se déplace spontanément vers l'avant, comme indiqué, pour atteindre l'équilibre |
| \(ΔS_{univ} < 0\) | Δ G > 0 |
non spontané vers l'avant, tel qu'il est écrit, mais se déplace spontanément dans la direction inverse, comme indiqué, pour atteindre l'équilibre |
| \(ΔS_{univ} = 0\) | Δ G = 0 | réversible (à l'équilibre) |
Calcul de la variation d'énergie libre
L'énergie libre est une fonction de l'état, de sorte que sa valeur dépend uniquement des conditions des états initial et final du système qui ont subi certaines modifications. Une approche pratique et courante pour le calcul des variations d'énergie libre liées aux changements physiques et aux réactions chimiques consiste à utiliser des compilations largement disponibles de données thermodynamiques d'état standard. Une méthode implique l'utilisation d'enthalpies et d'entropies standard pour calculer les changements d'énergie libre standard selon la relation suivante, comme le montre l'exemple\(\PageIndex{1}\).
\[ ΔG°=ΔH°−TΔS° \label{7} \]
Il est important de comprendre que pour les changements de phase, il vous\(\Delta G^º\) indique si le changement de phase est spontané ou non ; est-ce qu'il se produira ou non. Pour les réactions chimiques,\(\Delta G^º\) indique l'ampleur de la réaction. En d'autres termes,\(\Delta G^º\) une réaction vous indique la quantité de produit qui sera présente à l'équilibre. Une réaction avec\(\Delta G^º\) < 0 est considérée comme favorisée par le produit à l'équilibre ; il y aura plus de produits que de réactifs lorsque la réaction atteindra l'équilibre. Une réaction avec\(\Delta G^º\) > 0 est considérée comme favorisée par le réactif à l'équilibre ; il y aura plus de réactifs que de produits lorsque la réaction atteindra l'équilibre.
Utilisez les données d'enthalpie et d'entropie standard des tableaux T1 ou T2 pour calculer la variation d'énergie libre standard pour la vaporisation de l'eau à température ambiante (298 K). Que révèle la valeur calculée pour ΔG° sur la spontanéité de ce changement physique pour une substance pure ?
Solution
Le processus qui nous intéresse est le suivant :
\[\ce{H2O}(l)⟶\ce{H2O}(g) \label{\(\PageIndex{8}\)} \]
La variation standard de l'énergie libre peut être calculée à l'aide de l'équation suivante :
\[ΔG^\circ_{298}=ΔH°−TΔS° \label{\(\PageIndex{9}\)} \]
À partir des tableaux T1 ou T2, voici les données :
| Substance | \(ΔH^\circ_\ce{f}\ce{(kJ/mol)}\) | \(S^\circ_{298}\textrm{(J/K⋅mol)}\) |
|---|---|---|
| H 2 O (l) | \ (ΔH^ \ circ_ \ ce {f} \ ce {(kJ/mol)} \) » style="text-align:center ; « >−286,83 | \ (S^ \ circ_ {298} \ textrm {(J/k⋅mol)} \) » style="text-align:center ; « >70,0 |
| H 2 O (g) | \ (ΔH^ \ circ_ \ ce {f} \ ce {(kJ/mol)} \) » style="text-align:center ; « >−241,82 | \ (S^ \ circ_ {298} \ textrm {(J/k⋅mol)} \) » style="text-align:center ; « >188,8 |
Combinaison à 298 K :
\[\begin{align*} ΔH°&=ΔH^\circ_{298}=ΔH^\circ_\ce{f}(\ce{H2O}(g))−ΔH^\circ_\ce{f}(\ce{H2O}(l)) \\[4pt] &=[−241.82\: kJ−(−285.83)]\:kJ/mol \\[4pt] &=44.01\: kJ/mol \\[4pt] ΔS° &=ΔS^\circ_{298}=S^\circ_{298}(\ce{H2O}(g))−S^\circ_{298}(\ce{H2O}(l)) \\[4pt] &=188.8\:J/mol⋅K−70.0\:J/K \\[4pt] &=118.8\:J/mol⋅K \end{align*} \nonumber \]
puis utilisez l'équation \ ref {7} :
\[ΔG°=ΔH°−TΔS° \nonumber \]
Convertir le tout en kJ et combiner à 298 K :
\[\begin{align*}ΔG^\circ_{298} &=ΔH°−TΔS° \\[4pt] &=44.01\: kJ/mol−(298\: K×118.8\:J/mol⋅K)×\dfrac{1\: kJ}{1000\: J} \end{align*} \nonumber \]
\[\mathrm{44.01\: kJ/mol−35.4\: kJ/mol=8.6\: kJ/mol} \nonumber \]
À 298 K (25 °C)\(ΔG^\circ_{298}>0\), l'ébullition est donc non spontanée (non spontanée) à 298 K.
Utilisez les données d'enthalpie et d'entropie standard des tableaux T1 ou T2 pour calculer la variation d'énergie libre standard pour la réaction présentée ici (298 K). Que révèle la valeur calculée pour ΔG° sur l'ampleur de cette réaction à 298 K ?
\[\ce{C2H6}(g)⟶\ce{H2}(g)+\ce{C2H4}(g) \nonumber \]
- Réponse
-
\(ΔG^\circ_{298}=\mathrm{102.0\: kJ/mol}\); la réaction est favorisée par le réactif à l'équilibre à 25 °C. Il y aura\(\ce{C2H6}(g)\) plus que\(\ce{H2}(g)\) et\(\ce{C2H4}(g) \) à l'équilibre
Les changements d'énergie libre peuvent également utiliser l'énergie libre standard de formation\( (ΔG^\circ_\ce{f})\), pour chacun des réactifs et produits impliqués dans la réaction. L'énergie libre standard de formation est le changement d'énergie libre qui accompagne la formation d'une mole d'une substance à partir de ses éléments dans leurs états standard. Semblable aux enthalpies de formation standard, elle\( (ΔG^\circ_\ce{f})\) est par définition nulle pour les substances élémentaires dans des conditions d'état standard. L'approche utilisée pour calculer le changement d'énergie libre pour une réaction à l'aide de cette approche est la même que celle démontrée précédemment pour les variations d'enthalpie et d'entropie. Pour la réaction
\[m\ce{A}+n\ce{B}⟶x\ce{C}+y\ce{D}, \nonumber \]
la variation d'énergie libre standard à température ambiante peut être calculée comme
\[ \begin{align} ΔG^\circ_{298}&=ΔG° \\[4pt] &=∑νΔG^\circ_{298}(\ce{products})−∑νΔG^\circ_{298}(\ce{reactants})\\[4pt] &=[xΔG^\circ_\ce{f}(\ce{C})+yΔG^\circ_\ce{f}(\ce{D})]−[mΔG^\circ_\ce{f}(\ce{A})+nΔG^\circ_\ce{f}(\ce{B})]. \end{align} \nonumber \]
Prenons l'exemple de la décomposition de l'oxyde jaune de mercure (II).
\[\ce{HgO}(s,\,\ce{yellow})⟶\ce{Hg}(l)+ \ce{ 1/2 O2(g)} \nonumber \]
Calculez la variation d'énergie libre standard à température ambiante\(ΔG^\circ_{298}\), en utilisant :
- énergies libres de formation standard et
- enthalpies de formation standard et entropies standard.
Les résultats indiquent-ils que la réaction est favorisée par le produit ou par le réactif à l'équilibre ?
Solution
Les données requises sont disponibles dans les tableaux T1 ou T2 et sont présentées ici.
| Composé | \(ΔG^\circ_\ce{f}\:\mathrm{(kJ/mol)}\) | \(ΔH^\circ_\ce{f}\:\mathrm{(kJ/mol)}\) | \(S^\circ_{298}\:\textrm{(J/K⋅mol)}\) |
|---|---|---|---|
| Go (s, jaune) | \ (ΔG^ \ circ_ \ ce {f} \ : \ mathrm {(kJ/mol)} \) » style="text-align:center ; « >−58,43 | \ (ΔH^ \ circ_ \ ce {f} \ : \ mathrm {(kJ/mol)} \) » style="text-align:center ; « >−90,46 | \ (S^ \ circ_ {298} \ : \ textrm {(J/k⋅mol)} \) » style="text-align:center ; « >71,13 |
| Hg (l) | \ (ΔG^ \ circ_ \ ce {f} \ : \ mathrm {(kJ/mol)} \) » style="text-align:center ; « >0 | \ (ΔH^ \ circ_ \ ce {f} \ : \ mathrm {(kJ/mol)} \) » style="text-align:center ; « >0 | \ (S^ \ circ_ {298} \ : \ textrm {(J/k⋅mol)} \) » style="text-align:center ; « >75,9 |
| O 2 (g) | \ (ΔG^ \ circ_ \ ce {f} \ : \ mathrm {(kJ/mol)} \) » style="text-align:center ; « >0 | \ (ΔH^ \ circ_ \ ce {f} \ : \ mathrm {(kJ/mol)} \) » style="text-align:center ; « >0 | \ (S^ \ circ_ {298} \ : \ textrm {(J/k⋅mol)} \) » style="text-align:center ; « >205,2 |
(a) Utilisation des énergies libres de formation :
\[ \begin{align*} ΔG^\circ_{298}&=∑νGS^\circ_{298}(\ce{products})−∑νΔG^\circ_{298}(\ce{reactants}) \\[4pt] &=\left[1ΔG^\circ_{298}\ce{Hg}(l)+\dfrac{1}{2}ΔG^\circ_{298}\ce{O2}(g)\right]−1ΔG^\circ_{298}\ce{HgO}(s,\,\ce{yellow}) \\[4pt] & \mathrm{=\left[1\:mol(0\: kJ/mol)+\dfrac{1}{2}mol(0\: kJ/mol)\right]−1\: mol(−58.43\: kJ/mol)=58.43\: kJ/mol} \end{align*} \nonumber \]
(b) Utilisation des enthalpies et des entropies de formation :
\[\begin{align*}ΔH^\circ_{298}&=∑νΔH^\circ_{298}(\ce{products})−∑νΔH^\circ_{298}(\ce{reactants}) \\[4pt] &=\left[1ΔH^\circ_{298}\ce{Hg}(l)+\dfrac{1}{2}ΔH^\circ_{298}\ce{O2}(g)\right]−1ΔH^\circ_{298}\ce{HgO}(s,\,\ce{yellow}) \\[4pt] &\mathrm{=[1\: mol(0\: kJ/mol)+\dfrac{1}{2}mol(0\: kJ/mol)]−1\: mol(−90.46\: kJ/mol)=90.46\: kJ/mol} \\[4pt] ΔS^\circ_{298} &=∑νΔS^\circ_{298}(\ce{products})−∑νΔS^\circ_{298}(\ce{reactants}) \\[4pt] &=\left[1ΔS^\circ_{298}\ce{Hg}(l)+\dfrac{1}{2}ΔS^\circ_{298}\ce{O2}(g)\right]−1ΔS^\circ_{298}\ce{HgO}(s,\,\ce{yellow}) \\[4pt] & \mathrm{=\left[1\: mol(75.9\: J/mol\: K)+\dfrac{1}{2}mol(205.2\: J/mol\: K)\right]−1\: mol(71.13\: J/mol\: K)=107.4\: J/mol\: K} \end{align*} \nonumber \]
alors nous pouvons utiliser directement l'équation \ ref7} :
\[\begin{align*}ΔG°&=ΔH°−TΔS°\\[4pt] &=\mathrm{90.46\: kJ−298.15\: K×107.4\: J/K⋅mol×\dfrac{1\: kJ}{1000\: J}} \\[4pt] &=\mathrm{(90.46−32.01)\:kJ/mol=58.45\: kJ/mol} \end{align*} \nonumber \]
Les deux méthodes de calcul de la variation standard de l'énergie libre à 25 °C donnent la même valeur numérique (jusqu'à trois chiffres significatifs), et toutes deux prédisent que le processus est favorisé par les réactifs à l'équilibre à température ambiante.
Calculez ΔG° en utilisant (a) les énergies libres de formation et (b) les enthalpies de formation et les entropies (tableaux T1 ou T2). Les résultats indiquent-ils que la réaction est favorisée par le produit ou par le réactif à l'équilibre à 25 °C ?
\[\ce{C2H4}(g)⟶\ce{H2}(g)+\ce{C2H2}(g) \nonumber \]
- Réponse
-
141,5 kJ/mol, réactif préféré à l'équilibre
Dépendance de la spontanéité en fonction de la température et de l'ampleur
Comme cela a déjà été démontré dans la section de ce chapitre sur l'entropie, la spontanéité d'un processus peut dépendre de la température du système. Les transitions de phase, par exemple, se feront spontanément dans un sens ou dans l'autre en fonction de la température de la substance en question. De la même manière, mais pas de la même manière, certaines réactions chimiques peuvent passer d'une réaction favorable au produit à l'équilibre à une réaction à une réaction à l'équilibre, en fonction de la température.
La valeur numérique de\(\Delta G^º\) dépend toujours de la température. Dans cette section, nous déterminons si le signe de\(\Delta G^º\) dépend ou non de la température.
Pour illustrer ce concept, l'équation reliant le changement d'énergie libre aux variations d'enthalpie et d'entropie du processus est considérée :
\[ ΔG^º=ΔH^º−TΔS^º \nonumber \]
L'ampleur d'un processus, telle que reflétée par le signe arithmétique de sa variation standard d'énergie libre, est ensuite déterminée par les signes des variations d'enthalpie et d'entropie et, dans certains cas, par la température absolue. Puisque T est la température absolue (Kelvin), elle ne peut avoir que des valeurs positives. Quatre possibilités existent donc en ce qui concerne les signes des changements d'enthalpie et d'entropie :
- Δ H º et Δ S º sont tous deux positifs. Cette condition décrit un processus endothermique impliquant une augmentation de l'entropie du système. Dans ce cas, Δ G º sera négatif si l'amplitude du terme T Δ S º est supérieure à Δ H º. Si le terme T Δ S º est inférieur à Δ H º, le changement d'énergie libre sera positif. Un tel procédé est favorisé par le produit à l'équilibre à des températures élevées et par le réactif à l'équilibre à basses températures.
- Δ H º et Δ S º sont tous deux négatifs. Cette condition décrit un processus exothermique qui implique une diminution de l'entropie du système. Dans ce cas, Δ G º sera négatif si l'amplitude du terme T Δ S º est inférieure à Δ H º. Si la magnitude du terme T Δ S º est supérieure à Δ H º, le changement d'énergie libre sera positif. Un tel procédé est favorisé par le produit à l'équilibre à basse température et par le réactif à l'équilibre à des températures élevées.
- Δ H º est positif et Δ S º est négatif. Cette condition décrit un processus endothermique qui implique une diminution de l'entropie du système. Dans ce cas, Δ G º sera positif quelle que soit la température. Un tel procédé est favorisé par les réactifs à l'équilibre à toutes les températures.
- Δ H º est négatif et Δ S º est positif. Cette condition décrit un processus exothermique qui implique une augmentation de l'entropie du système. Dans ce cas, Δ G º sera négatif quelle que soit la température. Un tel procédé est privilégié par le produit à l'équilibre à toutes les températures.
Ces quatre scénarios sont résumés dans le tableau\(\PageIndex{1}\)
|
Signe de\(\Delta H^o\) |
Signe de\(\Delta S^o\) |
Signe de\(\Delta G^o\) |
Dépendance thermique de\(\Delta G^o\) |
|---|---|---|---|
| \ (\ Delta H^O \) « >- | \ (\ Delta S^o \) « >+ | \ (\ Delta G^o \) « >- | \ (\ Delta G^O \) « >Le signe de\(\Delta G^o\) ne dépend pas de la température. La réaction est favorisée par le produit à l'équilibre à toutes les températures. |
| \ (\ Delta H^o \) « >+ | \ (\ Delta S^o \) « >- | \ (\ Delta G^o \) « >+ | \ (\ Delta G^O \) « >Le signe de\(\Delta G^o\) ne dépend pas de la température. La réaction est favorisée par les réactifs à l'équilibre à toutes les températures. |
| \ (\ Delta H^O \) « >- | \ (\ Delta S^o \) « >- | \ (\ Delta G^o \) « >- ou + | \ (\ Delta G^o \) « >Le signe\(\Delta G^o\) de dépend de la température. La réaction sera favorisée par le produit à l'équilibre à des températures plus basses. |
| \ (\ Delta H^o \) « >+ | \ (\ Delta S^o \) « >+ | \ (\ Delta G^o \) « >- ou + | \ (\ Delta G^o \) « >
Le signe de\(\Delta G^o\) la dose dépend de la température. La réaction sera favorisée par le produit à l'équilibre à des températures plus basses. |
La combustion incomplète du carbone est décrite par l'équation suivante :
\[\ce{2C}(s)+\ce{O2}(g)⟶\ce{2CO}(g) \nonumber \]
Le signe\(\Delta G^º\) de ce processus dépend-il de la température ?
Solution
Les processus de combustion sont exothermiques (\(ΔH^º < 0\)). Cette réaction particulière implique une augmentation de l'entropie due à l'augmentation concomitante de la quantité d'espèces gazeuses (gain net d'une mole de gaz\(ΔS^º > 0\)). La réaction est donc favorisée par le produit à l'équilibre (\(ΔG^º < 0\)) à toutes les températures.
Les chauffe-mains chimiques populaires génèrent de la chaleur par oxydation du fer à l'air :
\[\ce{4Fe}(s)+\ce{3O2}(g)⟶\ce{2Fe2O3}(s) \nonumber \]
Le signe\(\Delta G^o\) de ce processus dépend-il de la température ?
- Réponse
-
Δ H º et Δ S º sont tous deux négatifs ; la réaction est favorisée par le produit à l'équilibre à basse température.
Lors de l'examen des conclusions tirées concernant la dépendance à la température du signe de Δ G º, il est important de garder à l'esprit la signification des termes « haut » et « bas ». Comme ces termes sont des adjectifs, les températures en question sont considérées comme élevées ou basses par rapport à une température de référence. Un processus qui est favorisé par le réactif à l'équilibre à une température mais par le produit à l'équilibre à une autre température subira nécessairement un changement d' « étendue » (comme en témoigne son Δ G º) à mesure que la température varie. Ceci est clairement illustré par une présentation graphique de l'équation du changement d'énergie libre, dans laquelle Δ G º est tracé sur l'axe des y contre T sur l'axe des x :
\[ΔG^º=ΔH^º−TΔS^º \nonumber \]
\[y=b+mx \nonumber \]
Un tel diagramme est illustré sur la figure\(\PageIndex{2}\). Un processus dont les variations d'enthalpie et d'entropie sont du même signe arithmétique présentera une dépendance à la température pour le signe de Δ G º, comme le montrent les deux lignes jaunes du graphique. Chaque ligne passe d'un domaine de spontanéité (Δ G º positif ou négatif) à l'autre à une température caractéristique du processus en question. Cette température est représentée par l'intersection x de la droite, c'est-à-dire la valeur de T pour laquelle Δ G º est nul :
\[ΔG^º=0=ΔH^º−TΔS^º \nonumber \]
\[T=\dfrac{ΔH^º}{ΔS^º} \nonumber \]
Ainsi, le fait de dire qu'un procédé est préféré au produit à l'équilibre à des températures « élevées » ou « basses » signifie que la température est supérieure ou inférieure, respectivement, à la température à laquelle Δ G º pour le processus est nul.
Dans cette discussion, nous avons utilisé deux descriptions différentes pour la signification du signe de Δ G º. Vous devez connaître la signification de chaque description.
a) Étendue de la réaction : Cette description est utilisée pour prédire le rapport entre les concentrations du produit et du réactif à l'équilibre. Dans cette description, nous utilisons le terme thermodynamique Δ G º pour nous donner les mêmes informations que la constante d'équilibre, K. Lorsque Δ G º < 0, K > 1, et la réaction sera favorisée par le produit à l'équilibre. Lorsque Δ G º > 0, K< 1, et que la réaction est favorisée par le réactif à l'équilibre. Lorsque Δ G º = 0, K = 1, et la réaction contiendra des quantités à peu près égales de produits et de réactifs à l'équilibre. Dans tous les cas, la réaction formera un mélange de produits et de réactifs à l'équilibre. Nous utilisons le signe et l'amplitude de Δ G º pour nous indiquer la quantité de produit qui sera produite si l'on laisse la réaction atteindre l'équilibre.
b) Spontanéité : Cette description est beaucoup plus compliquée car elle implique deux interprétations différentes de la façon dont se produit une réaction à l'état standard. L'une des interprétations implique le processus hypothétique selon lequel la réaction passe du point de départ des réactifs purs au point final de produits purs, toutes les substances étant isolées dans leurs propres récipients dans des conditions d'état standard. Dans la seconde interprétation, plus réaliste, la réaction commence avec tous les réactifs et tous les produits dans leur état standard dans un seul récipient. Nous laissons ensuite ce mélange spécifique réagir en quantité infinitésimale afin d'obtenir un taux de variation de l'énergie libre par rapport à l'étendue de la réaction lorsque tous les réactifs et produits sont mélangés et (essentiellement) dans leurs états standard. Bien que chaque interprétation décrit un scénario de réaction différent, la valeur de la différence d'énergie libre et la valeur du taux de variation de l'énergie libre sont les mêmes valeurs. Si Δ G º < 0, nous disons que la réaction est spontanée, ce qui signifie que la réaction se déroulerait vers l'avant, comme indiqué, pour former des produits purs dans leur état standard. Si Δ G º > 0, nous disons que la réaction n'est pas spontanée, ce qui signifie que la réaction se déroulera dans le sens inverse, comme indiqué, pour former des réactifs purs dans leur état standard. Si Δ G º = 0, nous disons que ni les réactifs ni les produits ne sont favorisés pour se former.
Un traitement détaillé de la signification de ΔGº se trouve dans l'article « Free Energy versus Extent of Reaction » de Richard S. Treptow, Journal of Chemical Education, 1996, volume 73 (1), 51-54.
Tel que défini dans le chapitre sur les liquides et les solides, le point d'ébullition d'un liquide est la température à laquelle ses phases solide et liquide sont en équilibre (c'est-à-dire lorsque la vaporisation et la condensation se produisent à des vitesses égales). Utilisez les informations des tableaux T1 ou T2 pour estimer le point d'ébullition de l'eau.
Solution
Le processus qui nous intéresse est le changement de phase suivant :
Lorsque ce processus est à l'équilibre, Δ G = 0, donc ce qui suit est vrai :
\[0=ΔH°−TΔS°\hspace{40px}\ce{or}\hspace{40px}T=\dfrac{ΔH°}{ΔS°} \nonumber \]
En utilisant les données thermodynamiques standard des tableaux T1 ou T2,
\ [\ begin {align*}
ΔH°&=ΔH^ \ circ_ \ ce {f} (\ ce {H2O} (g)) −ΔH^ \ circ_ \ ce {f} (\ ce {H2O} (l)) \ nonnumber \ \
&= \ mathrm {−241,82 \ : kJ/mol− (−285,83 \ : kJ/mol) =44,4 01 \ : kJ/mol} \ nonnumber
\ end {align*} \ nonnumber \]
\ [\ begin {align*}
ΔS°&=ΔS^ \ circ_ {298} (\ ce {H2O} (g)) −ΔS^ \ circ_ {298} (\ ce {H2O} (l)) \ nonnumber \ \
&= \ mathrm {188,8 \ : J/k⋅mol−70,0 \ : J/k⋅mol=118,8 \ : J/k⋅mol=118,8 \ : J/k⋅mol−70,0 \ : J/k⋅mol=118,8 \ : J/k⋅mol=118,8 \ : J/k⋅ K⋅mol}
\ nonnumber \ end {align*} \ nonnumber \]
\[T=\dfrac{ΔH°}{ΔS°}=\mathrm{\dfrac{44.01×10^3\:J/mol}{118.8\:J/K⋅mol}=370.5\:K=97.3\:°C} \nonumber \]
La valeur acceptée pour le point d'ébullition normal de l'eau est de 373,2 K (100,0 °C), ce calcul est donc en accord raisonnable. Il convient de noter que les valeurs des données sur les changements d'enthalpie et d'entropie utilisées ont été dérivées des données standard à 298 K (tableaux T1 ou T2.). Si vous le souhaitez, vous pouvez obtenir des résultats plus précis en utilisant les variations d'enthalpie et d'entropie déterminées au point d'ébullition réel (ou du moins plus près).
Utilisez les informations des tableaux T1 ou T2 pour estimer le point d'ébullition du CS 2.
- Réponse
-
313 K (valeur acceptée 319 K).
Énergie libre et équilibre
Le changement d'énergie libre d'un processus peut être considéré comme une mesure de sa force motrice. Une valeur négative pour Δ G représente une force motrice finie pour le processus vers l'avant, tandis qu'une valeur positive représente une force motrice pour le processus dans le sens inverse. Lorsque Δ G est nul, les forces motrices en marche avant et en marche arrière sont égales, de sorte que le processus se déroule dans les deux sens à la même vitesse (le système est en équilibre).
Dans le chapitre sur l'équilibre, le quotient de réaction, Q, a été introduit comme mesure pratique de l'état d'un système d'équilibre. Rappelez-vous que Q est la valeur numérique de l'expression d'action de masse du système et que vous pouvez utiliser sa valeur pour identifier la direction dans laquelle une réaction se déroulera afin d'atteindre l'équilibre. Lorsque Q est inférieur à la constante d'équilibre K, la réaction se poursuit vers l'avant jusqu'à ce que l'équilibre soit atteint et que Q = K. Inversement, si Q > K, le processus se déroulera dans le sens inverse jusqu'à ce que l'équilibre soit atteint.
Le changement d'énergie libre pour un processus se déroulant avec des réactifs et des produits présents dans des conditions non standard, Δ G, est lié au changement d'énergie libre standard, Δ G°, selon cette équation :
\[ΔG=ΔG°+RT\ln Q \label{eq10A} \]
R est la constante du gaz (8,314 J/K mol), T est le kelvin ou la température absolue et Q est le quotient de réaction. Nous pouvons utiliser cette équation pour prédire la spontanéité d'un processus dans n'importe quel ensemble de conditions, comme illustré dans l'exemple\(\PageIndex{1}\).
Quel est le changement d'énergie libre pour le processus présenté ici dans les conditions spécifiées ?
T = 25 °C\(P_{\ce{N2}}=\mathrm{0.870\: atm}\),\(P_{\ce{H2}}=\mathrm{0.250\: atm}\), et\(P_{\ce{NH3}}=\mathrm{12.9\: atm}\)
\[\ce{2NH3}(g)⟶\ce{3H2}(g)+\ce{N2}(g) \hspace{20px} ΔG°=\mathrm{33.0\: kJ/mol} \nonumber \]
Une solution
L'équation \ ref {EQ10a} relie le changement d'énergie libre au changement d'énergie libre standard et au quotient de réaction et peut être utilisée directement :
\[\begin{align*} ΔG&=ΔG°+RT\ln Q \\[4pt] &=\mathrm{33.0\:\dfrac{kJ}{mol}+\left(8.314\:\dfrac{J}{mol\: K}×298\: K×\ln\dfrac{(0.250^3)×0.870}{12.9^2}\right)}\\[4pt] &=\mathrm{9680\:\dfrac{J}{mol}\:or\: 9.68\: kJ/mol} \end{align*} \nonumber \]
La valeur calculée pour Δ G étant positive, la réaction n'est pas spontanée dans ces conditions. La réaction se déroulera dans le sens inverse pour atteindre l'équilibre.
Calculez le changement d'énergie libre pour cette même réaction à 875 °C dans un mélange de 5,00 L contenant 0,100 mol de chaque gaz. La réaction est-elle spontanée dans ces conditions ?
- Réponse
-
Δ G = −47 kJ ; oui, la réaction se déroule vers l'avant, comme indiqué, pour atteindre l'équilibre.
Pour un système à l'équilibre, Q = K et Δ G = 0, et l'équation \ ref {EQ10a} peut être écrite comme
\[ \underbrace{0=ΔG°+RT\ln K}_{\text{at equilibrium}} \nonumber \]
\[ΔG°=−RT\ln K \label{eq4A} \]
ou bien
\[K=e^{−\frac{ΔG°}{RT}} \label{eq4B} \]
Cette forme d'équation fournit un lien utile entre ces deux propriétés thermodynamiques essentielles, et elle peut être utilisée pour dériver des constantes d'équilibre à partir des variations d'énergie libre standard et vice versa. Les relations entre les variations standard d'énergie libre et les constantes d'équilibre sont résumées dans le tableau\(\PageIndex{1}\).
| K | ΔG° | Commentaires |
|---|---|---|
| < 1 | > 0 | Les réactifs sont plus abondants à l'équilibre. |
| = 1 | = 0 | Les réactifs et les produits sont également abondants à l'équilibre. |
| > 1 | < 0 | Les produits sont plus abondants à l'équilibre. |
Étant donné que les énergies libres standard de formation d'Ag + (aq), de Cl − (aq) et d'AgCl (s) sont de 77,1 kJ/mol, −131,2 kJ/mol et −109,8 kJ/mol, respectivement, calculez le produit de solubilité, K sp, pour AgCl.
Solution
La réaction intéressante est la suivante :
\[\ce{AgCl}(s)⇌\ce{Ag+}(aq)+\ce{Cl-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Ag+][Cl- ]} \nonumber \]
Le changement d'énergie libre standard pour cette réaction est d'abord calculé à l'aide des énergies libres standard de formation de ses réactifs et de ses produits :
\[ \begin{align*} ΔG° =ΔG^\circ_{298} &=[ΔG^\circ_\ce{f}(\ce{Ag+}(aq))+ΔG^\circ_\ce{f}(\ce{Cl-}(aq))]−[ΔG^\circ_\ce{f}(\ce{AgCl}(s))] \\[4pt] &=[77.1\: kJ/mol−131.2\: kJ/mol]−[−109.8\: kJ/mol] \\[4pt] &=55.7\: kJ/mol \end{align*} \nonumber \]
La constante d'équilibre de la réaction peut ensuite être dérivée de son changement d'énergie libre standard via l'équation \ ref {eQ4b} :
\[\begin{align*} K_\ce{sp}&=e^{−\dfrac{ΔG°}{RT}}=\exp\left(−\dfrac{ΔG°}{RT}\right) \\[4pt] &=\mathrm{\exp\left(−\dfrac{55.7×10^3\:J/mol}{8.314\:J/mol⋅K×298.15\:K}\right)}\\&=\mathrm{\exp(−22.470)=e^{−22.470}=1.74×10^{−10}} \end{align*} \nonumber \]
Utiliser les données thermodynamiques fournies dans les tableaux T1 ou T2 pour calculer la constante d'équilibre pour la dissociation du tétroxyde d'azote à 25 °C.
\[\ce{NO}_{2(g)} \rightleftharpoons \ce{N_2O}_{4(g)} \nonumber \]
- Réponse
-
K = 6,9
Pour mieux illustrer la relation entre ces deux concepts thermodynamiques essentiels, considérez l'observation selon laquelle les réactions se déroulent spontanément dans une direction qui établit finalement un équilibre. Comme on peut le montrer en traçant la variation de l'énergie libre en fonction de l'ampleur de la réaction (par exemple, comme le reflète la valeur de Q), l'équilibre est établi lorsque l'énergie libre du système est minimisée (Figure\(\PageIndex{3}\)). Si un système est présent avec des réactifs et des produits présents en quantités non équilibrées (Q ↓ K), la réaction se déroulera spontanément dans la direction nécessaire pour établir l'équilibre.
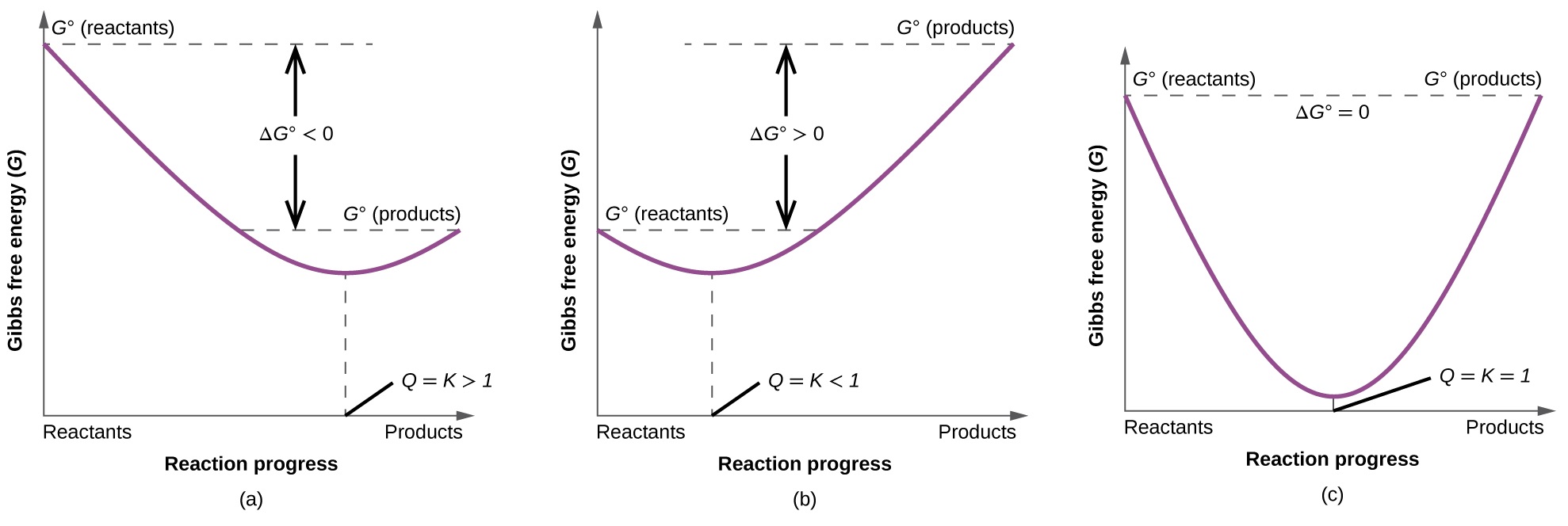
Résumé
L'énergie libre de Gibbs (G) est une fonction d'état définie en fonction des quantités du système uniquement et peut être utilisée pour prédire la spontanéité d'un processus. Une valeur négative pour Δ G indique que le processus se poursuivra vers l'avant pour atteindre l'équilibre ; une valeur Δ G positive indique que le processus se poursuivra dans la direction inverse pour atteindre l'équilibre ; et une Δ G de zéro indique que le système est à équilibre. Une valeur négative pour Δ G º signifie que la réaction est favorisée par le produit à l'équilibre. Une valeur positive pour Δ G º signifie que la réaction est favorisée par le réactif à l'équilibre. Si Δ G º est égal à 0 (ce qui est rare), la réaction contient des quantités à peu près égales de réactifs et de produits à l'équilibre. Un certain nombre d'approches pour le calcul des variations d'énergie libre sont possibles.
Équations clés
- Δ G = Δ H − T Δ S
- Δ G = Δ G° + RT sur Q
- Δ G° = − RT en K
Lexique
- Changement d'énergie sans Gibbs (G)
- propriété thermodynamique définie en termes d'enthalpie et d'entropie du système ; tous les processus spontanés impliquent une diminution de G
- changement d'énergie libre standard (Δ G°)
- variation de l'énergie libre pour un processus se déroulant dans des conditions standard (pression de 1 bar pour les gaz, concentration de 1 M pour les solutions)
- énergie libre de formation standard\( (ΔG^\circ_\ce{f})\)
- modification de l'énergie libre accompagnant la formation d'une mole de substance à partir de ses éléments à l'état standard


