16.2 : Entropie

Objectifs d'apprentissage

• Définir l'entropie
• Expliquer la relation entre l'entropie et le nombre de microétats
• Prédire le signe du changement d'entropie pour les processus chimiques et physiques

En 1824, à l'âge de 28 ans, Nicolas Léonard Sadi Carnot (Figure\(\PageIndex{2}\)) a publié les résultats d'une étude approfondie concernant l'efficacité des moteurs thermiques à vapeur. Dans une revue ultérieure des résultats de Carnot, Rudolf Clausius a introduit une nouvelle propriété thermodynamique qui relie le flux de chaleur spontané accompagnant un processus à la température à laquelle le processus se déroule. Cette nouvelle propriété a été exprimée comme le rapport entre la chaleur réversible (q _rev) et la température en kelvins (T). Le terme processus réversible fait référence à un processus qui se déroule à une vitesse si lente qu'il est toujours à l'équilibre et que sa direction peut être modifiée (il peut être « inversé ») par un changement infinitésimal, c'est une condition. Notez que l'idée d'un processus réversible est un formalisme nécessaire pour soutenir le développement de divers concepts thermodynamiques ; aucun processus réel n'est vraiment réversible, il est plutôt classé comme irréversible.

Figure\(\PageIndex{1}\) : (a) Les recherches de Nicholas Léonard Sadi Carnot sur les machines à vapeur et (b) l'étude ultérieure de ces résultats par Rudolf Clausius ont conduit à des découvertes révolutionnaires sur les processus de flux de chaleur spontanés.

Comme les autres propriétés thermodynamiques, cette nouvelle quantité est une fonction d'état, et son changement dépend donc uniquement des états initial et final d'un système. En 1865, Clausius a nommé cette propriété entropie (S) et a défini sa modification pour tout processus comme suit :

\[ΔS=\dfrac{q_\ce{rev}}{T} \label{Eq1} \]

Le changement d'entropie pour un processus réel et irréversible est alors égal à celui du processus réversible théorique qui implique les mêmes états initial et final.

Entropie et microétats

À la suite des travaux de Carnot et Clausius, Ludwig Boltzmann a développé un modèle statistique à l'échelle moléculaire qui reliait l'entropie d'un système au nombre de microétats possibles pour le système. Un microétat (\(\Omega\))est une configuration spécifique des emplacements et des énergies des atomes ou des molécules) qui constituent un système tel que le suivant :

\[S=k \ln \Omega \label{Eq2} \]

Ici, k est la constante de Boltzmann et a pour valeur\(1.38 \times 10^{−23}\, J/K\).

Comme pour les autres fonctions d'état, le changement d'entropie d'un processus correspond à la différence entre ses valeurs finales (S _f) et initiales (S _i) :

\[\begin{align} ΔS &=S_\ce{f}−S_\ce{i} \nonumber \\[4pt] &=k \ln \Omega_\ce{f} − k \ln \Omega_\ce{i} \nonumber \\[4pt] &=k \ln\dfrac{\Omega_\ce{f}}{\Omega_\ce{i}} \label{Eq2a} \end{align} \]

Pour les processus impliquant une augmentation du nombre de microétats du système\(\Omega_f > \Omega_i\), l'entropie du système augmente,\(ΔS > 0\). Inversement, les processus qui réduisent le nombre de microétats dans le système entraînent\(\Omega_f < \Omega_i\) une diminution de l'entropie du système,\(ΔS < 0\). Cette interprétation de l'entropie à l'échelle moléculaire fournit un lien avec la probabilité qu'un processus se produise, comme illustré dans les paragraphes suivants.

Figure\(\PageIndex{2}\) : Les seize microétats associés à la mise en place de quatre particules dans deux cases sont illustrés. Les microétats sont collectés selon cinq distributions — (a), (b), (c), (d) et (e) — en fonction du nombre de particules dans chaque boîte.

Cinq rangées de diagrammes qui ressemblent à des dominos sont affichées et étiquetées a, b, c, d et e. La rangée a contient un « domino » qui comporte quatre points sur le côté gauche, rouge, vert, bleu et jaune dans le sens des aiguilles d'une montre à partir du coin supérieur gauche, et aucun point sur la droite. La rangée b comporte quatre « dominos », chacun avec trois points à gauche et un point à droite. La première montre un « domino » avec du vert, du jaune et du bleu à gauche et du rouge à droite. Le deuxième « domino » a du jaune, du bleu et du rouge à gauche et du vert à droite. Le troisième « domino » est rouge, vert et jaune à gauche et bleu à droite, tandis que le quatrième est rouge, vert et bleu à gauche et jaune à droite. La rangée c comporte six « dominos », chacun avec deux points de chaque côté. Le premier a un rouge et un vert à gauche et un bleu et un jaune à droite. Le second a un rouge et un bleu à gauche et un vert et jaune à droite tandis que le troisième a un jaune et un rouge à gauche et un vert et bleu à droite. Le quatrième a un vert et un bleu à gauche et un rouge et un jaune à droite. Le cinquième a un vert et un jaune sur la gauche et un rouge et un bleu sur la droite. Le sixième a un bleu et un jaune à gauche et un vert et un rouge à droite. La rangée d comporte quatre « dominos », chacun avec un point à gauche et trois à droite. Le premier « domino » est rouge à gauche et bleu, vert et jaune à droite. Le second a un vert sur la gauche et un rouge, un jaune et un bleu sur la droite. Le troisième a un bleu à gauche et un rouge, un vert et un jaune à droite. Le quatrième a un jaune à gauche et un rouge, vert et bleu à droite. La rangée e comporte 1 « domino » sans points sur la gauche et quatre points sur la droite qui sont rouges, verts, bleus et jaunes.

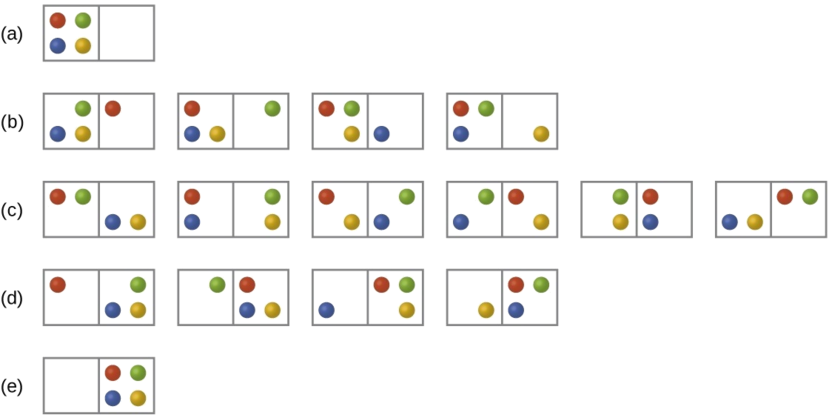
Prenons le cas général d'un système composé de N particules réparties dans n boîtes. Le nombre de microétats possibles pour un tel système est ^{n N.} Par exemple, la distribution de quatre particules dans deux boîtes donnera 2 ⁴ = 16 microétats différents, comme illustré à la figure\(\PageIndex{2}\). Les microétats présentant des arrangements de particules équivalents (sans tenir compte de l'identité individuelle des particules) sont regroupés et sont appelés distributions (parfois appelées macroétats ou configurations). La probabilité qu'un système existe avec ses composants dans une distribution donnée est proportionnelle au nombre de microétats au sein de cette distribution. Comme l'entropie augmente de façon logarithmique avec le nombre de microétats, la distribution la plus probable est donc celle de l'entropie la plus importante.

Pour ce système, la configuration la plus probable est l'un des six microétats associés à la distribution (c) où les particules sont réparties uniformément entre les boîtes, c'est-à-dire une configuration de deux particules dans chaque boîte. La probabilité de trouver le système dans cette configuration est

 

\[\dfrac{6}{16} = \dfrac{3}{8} \nonumber \]

La configuration la moins probable du système est celle dans laquelle les quatre particules se trouvent dans une seule boîte, correspondant aux distributions (a) et (e), chacune avec une probabilité de

\[\dfrac{1}{16} \nonumber \]

La probabilité de trouver toutes les particules dans une seule case (case de gauche ou de droite) est alors

\[\left(\dfrac{1}{16}+\dfrac{1}{16}\right)=\dfrac{2}{16} = \dfrac{1}{8} \nonumber \]

 

À mesure que vous ajoutez de nouvelles particules au système, le nombre de microétats possibles augmente de façon exponentielle (2 ^N). Un système macroscopique (de la taille d'un laboratoire) serait généralement composé de moles de particules (N ~ 10 ²³), et le nombre correspondant de microétats serait incroyablement énorme. Cependant, quel que soit le nombre de particules dans le système, les distributions dans lesquelles un nombre à peu près égal de particules se trouvent dans chaque boîte sont toujours les configurations les plus probables.

La distribution la plus probable est donc celle qui présente la plus grande entropie.

La description précédente d'un gaz idéal se dilatant dans le vide est un exemple macroscopique de ce modèle de particules dans une boîte. Pour ce système, il est confirmé que la distribution la plus probable est celle dans laquelle la matière est dispersée ou répartie le plus uniformément entre les deux flacons. Le processus spontané par lequel le gaz contenu initialement dans un flacon se dilate pour remplir les deux flacons de manière égale entraîne donc une augmentation de l'entropie pour le système.

Figure\(\PageIndex{3}\) : Ceci montre un modèle de microétats décrivant le flux de chaleur d'un objet chaud vers un objet froid. (a) Avant que le flux de chaleur ne se produise, l'objet composé des particules A et B contient les deux unités d'énergie et est représenté par une distribution de trois microétats. (b) Si le flux de chaleur entraîne une dispersion uniforme de l'énergie (une unité d'énergie transférée), il en résulte une distribution de quatre microétats. (c) Si les deux unités d'énergie sont transférées, la distribution résultante comporte trois microétats.

Trois rangées étiquetées a, b et c sont affichées et chacune contient des rectangles à deux côtés, le côté gauche étant étiqueté « A » et « B » et le côté droit étant étiqueté « C » et « D ». La rangée a comporte trois rectangles, le premier comportant un point au-dessus et en dessous de la lettre A, le second un point au-dessus des lettres A et B, et le troisième un point au-dessus et en dessous de la lettre B. La ligne b comporte quatre rectangles ; la première un point au-dessus de A et C, la seconde un point au-dessus de A et D, la troisième un point au-dessus de B et C et le quatrième a un point au-dessus de B et D. La rangée c comporte trois rectangles ; la première a un point au-dessus et en dessous de la lettre C, la seconde un point au-dessus de C et D et la troisième un point au-dessus et en dessous de la lettre D.

Une approche similaire peut être utilisée pour décrire le flux de chaleur spontané. Prenons l'exemple d'un système composé de deux objets contenant chacun deux particules et deux unités d'énergie (représentées par « * ») sur la figure\(\PageIndex{3}\). L'objet chaud est composé de particules A et B et contient initialement les deux unités d'énergie. L'objet froid est composé de particules C et D, qui n'ont initialement aucune unité énergétique. La distribution (a) montre les trois microétats possibles pour l'état initial du système, les deux unités d'énergie étant contenues dans l'objet chaud. Si l'une des deux unités d'énergie est transférée, le résultat est une distribution (b) composée de quatre microétats. Si les deux unités d'énergie sont transférées, le résultat est une distribution (c) composée de trois microétats. Nous pouvons donc décrire ce système par un total de dix microétats. La probabilité que la chaleur ne circule pas lorsque les deux objets sont mis en contact, c'est-à-dire que le système reste dans la distribution (a), est de\(\frac{3}{10}\). Le flux de chaleur est plus susceptible de produire l'une des deux autres distributions, la probabilité combinée étant\(\frac{7}{10}\). Le résultat le plus probable est que le flux de chaleur produit la dispersion uniforme de l'énergie représentée par la distribution (b), la probabilité de cette configuration étant\(\frac{4}{10}\). Comme pour l'exemple précédent de dispersion de matière, l'extrapolation de ce traitement à des collections macroscopiques de particules augmente considérablement la probabilité d'une distribution uniforme par rapport aux autres distributions. Cela confirme l'observation courante selon laquelle la mise en contact d'objets chauds et froids entraîne un flux de chaleur spontané qui, en fin de compte, égalise la température des objets. Et, encore une fois, ce processus spontané se caractérise également par une augmentation de l'entropie du système.

Exemple\(\PageIndex{1}\): Determination of ΔS

Considérez le système présenté ici. Quel est le changement d'entropie pour un processus qui convertit le système de la distribution (a) à (c) ?

 

Un diagramme montre un rectangle à deux côtés avec quatre points, rouge, vert, jaune et bleu écrits sur le côté gauche. Une flèche orientée vers la droite mène à six autres rectangles à deux côtés, chacun comportant deux points sur les côtés gauche et droit. Le premier rectangle comporte un point rouge et vert à gauche et un point bleu et jaune à droite, tandis que le second montre un point rouge et bleu à gauche et un vert et jaune à droite. Le troisième rectangle comporte un point rouge et jaune à gauche et un point bleu et vert à droite, tandis que le quatrième montre un point vert et bleu à gauche et un rouge et jaune à droite. Le cinquième rectangle comporte un point jaune et vert à gauche et un point bleu et rouge à droite, tandis que le sixième montre un point jaune et bleu à gauche et un vert et rouge à droite.

Solution

Nous sommes intéressés par le changement suivant :

Le nombre initial de microétats est de un, les six derniers :

\[\begin{align} ΔS &=k \ln\dfrac{\Omega_\ce{c}}{\Omega_\ce{a}} \nonumber \\[4pt] &= 1.38×10^{−23}\:J/K × \ln\dfrac{6}{1} \nonumber \\[4pt] &= 2.47×10^{−23}\:J/K \nonumber \end{align} \nonumber \]

Le signe de ce résultat est conforme aux attentes ; comme il y a plus de microétats possibles pour l'état final que pour l'état initial, le changement d'entropie devrait être positif.

Exercice\(\PageIndex{1}\)

Considérez le système illustré à la figure\(\PageIndex{3}\). Quel est le changement d'entropie pour le processus où toute l'énergie est transférée de l'objet chaud (AB) à l'objet froid (CD) ?

Réponse

0 KG/KG

Prédiction du signe du Δ S

Les relations entre l'entropie, les microétats et la dispersion de la matière/de l'énergie décrites précédemment nous permettent de faire des généralisations concernant les entropies relatives des substances et de prédire le signe de changements d'entropie pour les processus chimiques et physiques. Considérez les changements de phase illustrés dans la figure\(\PageIndex{4}\). Dans la phase solide, les atomes ou les molécules sont limités à des positions presque fixes les uns par rapport aux autres et ne sont capables que de légères oscillations autour de ces positions. Les emplacements des particules constitutives du système étant essentiellement fixes, le nombre de microétats est relativement faible. Dans la phase liquide, les atomes ou les molécules sont libres de se déplacer les uns sur les autres, bien qu'ils restent relativement proches les uns des autres. Cette liberté de mouvement accrue entraîne une plus grande variation des emplacements possibles des particules, de sorte que le nombre de microétats est proportionnellement supérieur à celui du solide. Par conséquent, S _liquide > S _solide et le processus de conversion d'une substance de solide en liquide (fusion) se caractérisent par une augmentation de l'entropie, Δ S > 0. Selon la même logique, le processus réciproque (congélation) présente une diminution de l'entropie, Δ S < 0.

Figure\(\PageIndex{4}\) : L'entropie d'une substance augmente (ΔS > 0) lorsqu'elle passe d'un solide relativement ordonné à un liquide moins ordonné, puis à un gaz encore moins ordonné. L'entropie diminue (ΔS < 0) lorsque la substance passe d'un gaz à un liquide, puis à un solide.

Trois flacons bouchés sont représentés par des flèches orientées vers la droite et vers la gauche entre chacun ; le premier est étiqueté ci-dessus comme « delta S supérieur à 0 » et ci-dessous comme « delta S inférieur à 0 », tandis que le second est étiqueté au-dessus comme « delta S supérieur à 0 » et ci-dessous comme « delta S inférieur à 0 ». Une longue flèche orientée vers la droite est dessinée au-dessus de tous les flacons et est intitulée « Augmenter l'entropie ». Le flacon de gauche contient vingt-sept particules disposées en cube au fond du flacon et porte l'étiquette « Solide cristallin » ci-dessous. Le flacon central contient vingt-sept particules dispersées de façon aléatoire au fond du flacon et est étiqueté « Liquide » ci-dessous. La fiole droite contient vingt-sept particules dispersées à l'intérieur de la fiole et se déplaçant rapidement. Elle est étiquetée « Gaz » ci-dessous.

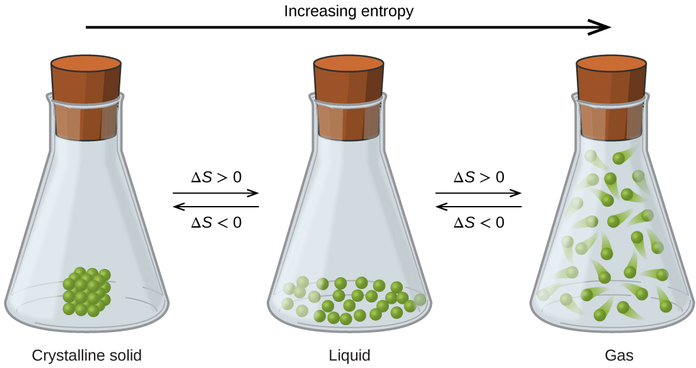
Considérons maintenant la phase vapeur ou gazeuse. Les atomes ou les molécules occupent un volume beaucoup plus important que dans la phase liquide ; par conséquent, chaque atome ou molécule peut être trouvé à beaucoup plus d'endroits que dans la phase liquide (ou solide). Par conséquent, pour toute substance, S _gaz > S _liquide > S _solide, et les processus de vaporisation et de sublimation impliquent également une augmentation de l'entropie, Δ S > 0. De même, les transitions de phase réciproques, condensation et dépôt, impliquent des diminutions de l'entropie, Δ S < 0.

Selon la théorie cinétique et moléculaire, la température d'une substance est proportionnelle à l'énergie cinétique moyenne de ses particules. L'augmentation de la température d'une substance entraînera des vibrations plus importantes des particules dans les solides et des translations plus rapides des particules dans les liquides et les gaz. À des températures plus élevées, la distribution des énergies cinétiques entre les atomes ou les molécules de la substance est également plus large (plus dispersée) qu'à des températures plus basses. Ainsi, l'entropie de toute substance augmente avec la température (Figure\(\PageIndex{5}\)).

Figure\(\PageIndex{5}\) : L'entropie augmente à mesure que la température d'une substance augmente, ce qui correspond à une plus grande dispersion des énergies cinétiques. Lorsqu'une substance fond ou se vaporise, elle subit une augmentation significative de son entropie.

Deux graphiques sont présentés. L'axe Y du graphique de gauche est intitulé « Fraction de molécules », tandis que l'axe X est étiqueté « Vitesse, v (m/s) » et possède des valeurs comprises entre 0 et 1 500 le long de l'axe avec des incréments de 500. Quatre lignes sont tracées sur ce graphique. Le premier, étiqueté « 100 K », culmine à environ 200 m/s tandis que le second, étiqueté « 200 K », culmine à près de 300 m/s et se situe légèrement plus bas sur l'axe y que le premier. La troisième ligne, intitulée « 500 K », culmine à environ 550 m/s et est plus basse que les deux premières sur l'axe Y. La quatrième ligne, intitulée « 1 000 K », culmine à environ 750 m/s et est la plus basse des quatre sur l'axe Y. Chaque ligne s'élargit de plus en plus. Le deuxième graphique comporte un axe y intitulé « Entropie, S », avec une flèche orientée vers le haut et un axe x intitulé « Température (K) » et une flèche orientée vers la droite. Le graphique comporte trois colonnes équidistantes en arrière-plan, intitulées « Solide », « Liquide » et « Gaz », de gauche à droite. Une ligne s'étend légèrement vers le haut à travers la première colonne dans une direction légèrement ascendante, puis remonte tout droit dans la transition entre les deux premières colonnes. Il progresse ensuite légèrement vers le haut à travers la deuxième colonne, puis remonte considérablement entre les deuxième et troisième colonnes, puis continue légèrement vers le haut une fois de plus. La première région verticale de cette ligne est étiquetée « Fusion » et la seconde, « Ébullition ».

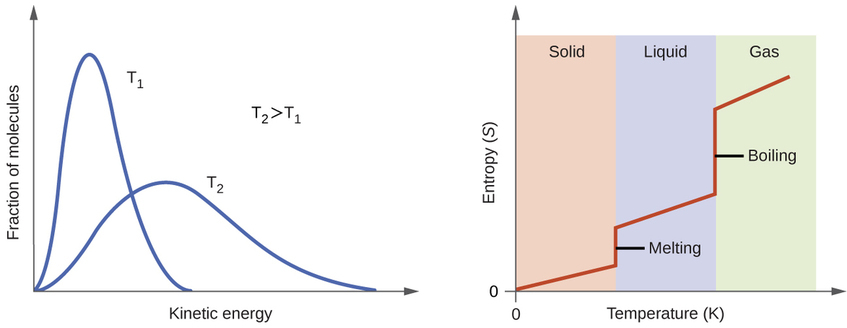
L'entropie d'une substance est influencée par la structure des particules (atomes ou molécules) qui la composent. En ce qui concerne les substances atomiques, les atomes les plus lourds possèdent une plus grande entropie à une température donnée que les atomes plus légers, ce qui est une conséquence de la relation entre la masse d'une particule et l'espacement des niveaux d'énergie translationnelle quantifiés (sujet qui dépasse le cadre de notre traitement). Pour les molécules, un plus grand nombre d'atomes (quelle que soit leur masse) augmente la façon dont les molécules peuvent vibrer et donc le nombre de microétats possibles et l'entropie du système.

Enfin, les variations des types de particules affectent l'entropie d'un système. Par rapport à une substance pure, dans laquelle toutes les particules sont identiques, l'entropie d'un mélange de deux ou plusieurs types de particules différents est plus grande. Cela est dû aux orientations et interactions supplémentaires qui sont possibles dans un système composé de composants non identiques. Par exemple, lorsqu'un solide se dissout dans un liquide, les particules du solide bénéficient à la fois d'une plus grande liberté de mouvement et d'interactions supplémentaires avec les particules de solvant. Cela correspond à une dispersion plus uniforme de la matière et de l'énergie et à un plus grand nombre de microétats. Le processus de dissolution implique donc une augmentation de l'entropie, Δ S > 0.

La prise en compte des divers facteurs qui influent sur l'entropie nous permet de prédire en connaissance de cause le signe du Δ S pour divers processus chimiques et physiques, comme illustré dans l'exemple.

Exemple\(\PageIndex{2}\): Predicting the Sign of ∆S

Prédisez le signe du changement d'entropie pour les processus suivants. Indiquez la raison de chacune de vos prédictions.

1. Une mole d'eau liquide à température ambiante,\(⟶\) une mole d'eau liquide à 50 °C
2. \(\ce{Ag+}(aq)+\ce{Cl-}(aq)⟶\ce{AgCl}(s)\)
3. \(\ce{C6H6}(l)+\dfrac{15}{2}\ce{O2}(g)⟶\ce{6CO2}(g)+\ce{3H2O}(l)\)
4. \(\ce{NH3}(s)⟶\ce{NH3}(l)\)

Une solution

1. positif, la température augmente
2. négatif, réduction du nombre d'ions (particules) dans la solution, diminution de la dispersion de la matière
3. diminution nette négative de la quantité d'espèces gazeuses
4. positif, transition de phase du solide au liquide, augmentation nette de la dispersion de la matière

Exercice\(\PageIndex{2}\)

Prédisez le signe du changement d'enthalpie pour les processus suivants. Donnez une raison à votre prédiction.

1. \(\ce{NaNO3}(s)⟶\ce{Na+}(aq)+\ce{NO3-}(aq)\)
2. la congélation de l'eau liquide
3. \(\ce{CO2}(s)⟶\ce{CO2}(g)\)
4. \(\ce{CaCO}(s)⟶\ce{CaO}(s)+\ce{CO2}(g)\)

Répondez à une

Positif ; le solide se dissout pour donner une augmentation des ions mobiles en solution.

Réponse b

Négatif ; Le liquide devient un solide plus ordonné.

Réponse c

Positif ; le solide relativement ordonné devient un gaz

Réponse d

Positif ; il y a une production nette d'une mole de gaz.

Résumé

L'entropie (\(S\)) est une fonction d'état qui peut être liée au nombre de microétats d'un système (le nombre de manières dont le système peut être organisé) et au rapport entre la chaleur réversible et la température en kelvins. Elle peut être interprétée comme une mesure de la dispersion ou de la distribution de matière et/ou d'énergie dans un système, et elle est souvent décrite comme représentant le « désordre » du système. Pour une substance donnée,\(S_{solid} < S_{liquid} \ll S_{gas}\) dans un état physique donné et à une température donnée, l'entropie est généralement plus grande pour les atomes plus lourds ou les molécules plus complexes. L'entropie augmente lorsqu'un système est chauffé et lorsque des solutions se forment. À l'aide de ces directives, le signe de changements d'entropie pour certaines réactions chimiques peut être prédit de manière fiable.

Équations clés

• \(ΔS=\dfrac{q_\ce{rev}}{T}\)
• S = k sur W
• \(ΔS=k\ln\dfrac{W_\ce{f}}{W_\ce{i}}\)

Lexique

entropie (S)

fonction d'état qui est une mesure de la dispersion de la matière et/ou de l'énergie au sein d'un système, déterminée par le nombre de microétats du système souvent décrits comme une mesure du désordre du système

microétat (W)

configuration ou disposition possibles de la matière et de l'énergie au sein d'un système

processus réversible

processus qui se déroule si lentement qu'il est capable de changer de direction en réponse à un changement infinitésimal des conditions ; construction hypothétique qui ne peut être approximée que par des processus réels supprimée