Skip to main content
Global

14.7 : Titrages acido-basiques

  1. Last updated
  2. Save as PDF
  • Page ID
    194088

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage
    • Interpréter les courbes de titrage pour les systèmes acido-basiques forts et faibles
    • Calculez le pH de l'échantillon aux étapes importantes d'un titrage
    • Expliquer la fonction des indicateurs acido-basiques

    Comme indiqué dans le chapitre sur la stœchiométrie des réactions chimiques, les titrages peuvent être utilisés pour analyser quantitativement les solutions en fonction de leurs concentrations en acide ou en base. Dans cette section, nous allons explorer les variations des concentrations des espèces acides et basiques présentes dans une solution au cours du processus de titrage.

    Courbes de titrage

    Auparavant, lorsque nous avons étudié les réactions acide-base en solution, nous nous sommes concentrés uniquement sur le point où l'acide et la base étaient stoechiométriquement équivalents. Aucune considération n'a été accordée au pH de la solution avant, pendant ou après la neutralisation.

    Exemple\(\PageIndex{1}\): Calculating pH for Titration Solutions: Strong Acid/Strong Base

    Un titrage est effectué pour 25,00 ml de HCl (acide fort) à 0,100 M avec 0,100 M de NaOH à base forte. La courbe de titrage est illustrée à la figure\(\PageIndex{1}\). Calculez le pH à ces volumes de solution de base ajoutée :

    1. 0,00 ml
    2. 12,50 ml
    3. 25,00 ml
    4. 37,50 ml
    Solution

    Comme le HCl est un acide fort, on peut supposer que tout se dissocie. La concentration initiale en H 3 O + est de\(\ce{[H3O+]_0}=0.100\:M\). Lorsque la solution de base est ajoutée, elle se dissocie également complètement, fournissant des ions OH −. Les ions H 3 O + et OH − se neutralisent mutuellement, de sorte qu'il ne reste que ceux des deux qui étaient en excès, et leur concentration détermine le pH. Ainsi, la solution est initialement acide (pH < 7), mais finalement tous les ions hydronium présents dans l'acide d'origine sont neutralisés et la solution devient neutre. Au fur et à mesure que de la base est ajoutée, la solution devient basique.

    La quantité initiale totale des ions hydronium est de :

    \[\mathrm{n(H^+)_0=[H_3O^+]_0×0.02500\: L=0.002500\: mol} \nonumber \]

    Une fois que X ml de la solution de base à 0,100 M sont ajoutés, le nombre de moles des ions OH − introduits est de :

    \[\mathrm{n(OH^-)_0=0.100\:\mathit{M}×X\: mL×\left(\dfrac{1\: L}{1000\: mL}\right)} \nonumber \]

    Le volume total devient :

    \[V=\mathrm{(25.00\: mL+X\: mL)\left(\dfrac{1\: L}{1000\: mL}\right)} \nonumber \]

    Le nombre de moles de H 3 O + devient :

    \[\mathrm{n(H^+)=n(H^+)_0-n(OH^-)_0=0.002500\: mol-0.100\:\mathit{M}×X\: mL×\left(\dfrac{1\: L}{1000\: mL}\right)} \nonumber \]

    La concentration de H 3 O + est :

    \[\mathrm{[H_3O^+]=\dfrac{n(H^+)}{V}=\dfrac{0.002500\: mol-0.100\:\mathit{M}×X\: mL×\left(\dfrac{1\: L}{1000\: mL}\right)}{(25.00\: mL+X\: mL)\left(\dfrac{1\: L}{1000\: mL}\right)}} \nonumber \]

    \[\mathrm{=\dfrac{0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)-0.100\:\mathit{M}×X\: mL}{25.00\: mL+X\: mL}} \nonumber \]

    avec la définition de\(\mathrm{pH}\) :

    \[\mathrm{pH=−\log([H_3O^+])} \label{phdef} \]

    Les calculs précédents fonctionnent si\(\mathrm{n(H^+)_0-n(OH^-)_0>0}\) et donc n (H +) > 0. Lorsque\(\mathrm{n(H^+)_0=n(OH^-)_0}\) les ions H 3 O + de l'acide et les ions OH - de la base se neutralisent mutuellement. À ce stade, les seuls ions hydronium restants sont ceux issus de l'auto-ionisation de l'eau, et aucune particule OH − ne permet de les neutraliser. Par conséquent, dans ce cas :

    \[\ce{[H3O+]}=\ce{[OH- ]},\:\ce{[H3O+]}=K_\ce{w}=1.0\times 10^{-14};\:\ce{[H3O+]}=1.0\times 10^{-7} \nonumber \]

    \[\mathrm{pH=-log(1.0\times 10^{-7})=7.00} \nonumber \]

    Enfin\(\mathrm{n(OH^-)_0>n(H^+)_0}\), lorsqu'il n'y a pas assez d'ions H 3 O + pour neutraliser tous les ions OH −, et au lieu de cela\(\mathrm{n(H^+)=n(H^+)_0-n(OH^-)_0}\), nous calculons :\(\mathrm{n(OH^-)=n(OH^-)_0-n(H^+)_0}\)

    Dans ce cas :

    \[\mathrm{[OH^-]=\dfrac{n(OH^-)}{\mathit{V}}=\dfrac{0.100\:\mathit{M}×X\: mL×\left(\dfrac{1\: L}{1000\: mL}\right)-0.002500\: mol}{(25.00\: mL+X\: mL)\left(\dfrac{1\: L}{1000\: mL}\right)}} \nonumber \]

    \[\mathrm{=\dfrac{0.100\:\mathit{M}×X\: mL-0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)}{25.00\: mL+X\: mL}} \nonumber \]

    puis en utilisant la définition de\(pOH\) et sa relation avec les solutions aqueuses\(pH\) à température ambiante (Équation \ ref {phdef}) :

    \[\begin{align} pH &=14-pOH \nonumber \\&=14+\log([OH^-]) \nonumber\end{align} \nonumber \]

    Examinons maintenant les quatre cas spécifiques présentés dans ce problème :

    (a) X = 0 ml

    \[\mathrm{[H_3O^+]=\dfrac{n(H^+)}{\mathit{V}}=\dfrac{0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)}{25.00\: mL}=0.1\:\mathit{M}} \nonumber \]

    puis en utilisant la définition de\(pH\) (Équation \ ref {phdef}) :

    \[\begin{align} pH &= −\log(0.100) \nonumber \\ &= 1.000 \nonumber\end{align} \nonumber \]

    (b) X = 12,50 ml

    \[\mathrm{[H_3O^+]=\dfrac{n(H^+)}{\mathit{V}}=\dfrac{0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)-0.100\:\mathit{M}×12.50\: mL}{25.00\: mL+12.50\: mL}=0.0333\:\mathit{M}} \nonumber \]

    puis en utilisant la définition de\(pH\) (Équation \ ref {phdef}) :

    \[ \begin{align} pH &= −\log(0.0333) \nonumber \\ &= 1.477 \nonumber\end{align} \nonumber \]

    (c) X = 25,00 ml

    Les volumes et les concentrations des solutions acides et basiques étant les mêmes :

    \[\mathrm{n(H^+)_0=n(OH^-)_0} \nonumber \]

    et

    \[pH = 7.000 \nonumber \]

    comme décrit précédemment.

    (d) X = 37,50 ml

    Dans ce cas :

    \[\mathrm{n(OH^-)_0>n(H^+)_0} \nonumber \]

    \[\mathrm{[OH^-]=\dfrac{n(OH^-)}{\mathit{V}}=\dfrac{0.100\:\mathit{M}×35.70\: mL-0.002500\: mol×\left(\dfrac{1000\: mL}{1\: L}\right)}{25.00\: mL+37.50\: mL}=0.0200\:\mathit{M}} \nonumber \]

    puis en utilisant la définition de\(pH\) (Équation \ ref {phdef}) :

    \[ \begin{align}[pH = 14 − pOH \nonumber\\ &= 14 + \log([OH^{−}]) \nonumber \\ &= 14 + \log(0.0200) \nonumber \\ &= 12.30 \nonumber \end{align} \nonumber \]

    Exercice\(\PageIndex{1}\)

    Calculer le pH pour le titrage acide fort/base forte entre 50,0 ml de 0,100 M de HNO 3 (aq) et 0,200 M de NaOH (titrant) aux volumes de base ajoutés indiqués :

    1. 0,00 ml,
    2. 15,0 ml,
    3. 25,0 ml, et
    4. 40,0 ml.
    Répondez à une

    0,00 : 1 000

    Réponse b

    15,0 : 1 5111

    Réponse c

    25,0 : 7e. Ne supprimez pas ce texte au préalable.

    Réponse d

    40,0 : 12 523

    Dans l'exemple\(\PageIndex{1}\), nous avons calculé le pH à quatre points lors d'un titrage. Le tableau\(\PageIndex{1}\) montre une séquence détaillée des changements du pH d'un acide fort et d'un acide faible lors d'un titrage avec du NaOH.

    Tableau\(\PageIndex{1}\) : Valeurs de pH dans les titrages d'un acide fort à base forte et d'un acide faible à base forte
    Volume de 0,100 M de NaOH ajouté (mL) Moles de NaOH ajoutées Valeurs de pH 0,100 M HCl 1 Valeurs de pH 0,100 M\(CH_3CO_2H\) 2
    0,0 0,0 1,00 \ (CH_3CO_2H \) 2" style="text-align:center ; « >2,87
    5,0 0,00050 1,18 \ (CH_3CO_2H \) 2" style="text-align:center ; « >4,14
    10,0 0,00100 1,37 \ (CH_3CO_2H \) 2" style="text-align:center » ; « >4,57
    15,0 0,00150 1,60 \ (CH_3CO_2H \) 2" style="text-align:center ; « >4,92
    20,0 0,00200 1,95 \ (CH_3CO_2H \) 2" style="text-align:center ; « >5,35
    22,0 0,00220 2,20 \ (CH_3CO_2H \) 2" style="text-align:center » ; « >5,61
    24,0 0,00240 2,69 \ (CH_3CO_2H \) 2" style="text-align:center » ; « >6,13
    24,5 0,00245 3,00 \ (CH_3CO_2H \) 2" style="text-align:center » ; « >6,44
    24,9 0,00249 3,70 \ (CH_3CO_2H \) 2" style="text-align:center ; « >7,14
    25,0 0,00250 7,00 \ (CH_3CO_2H \) 2" style="text-align:center » ; « >8,72
    25.1 0,00251 10h30 \ (CH_3CO_2H \) 2" style="text-align:center ; « >10h30
    25,5 0,00255 11h00 \ (CH_3CO_2H \) 2" style="text-align:center ; « >11,00
    26,0 0,00260 11,29 \ (CH_3CO_2H \) 2" style="text-align:center ; « >11,29
    28,0 0,00280 11,75 \ (CH_3CO_2H \) 2" style="text-align:center » ; « >11,75
    30,0 0,00300 11,96 \ (CH_3CO_2H \) 2" style="text-align:center » ; « >11,96
    35,0 0,00350 12,22 \ (CH_3CO_2H \) 2" style="text-align:center » ; « >12,22
    40,0 0,00400 12,36 \ (CH_3CO_2H \) 2" style="text-align:center » ; « >12,36
    45,0 0,00450 12,46 \ (CH_3CO_2H \) 2" style="text-align:center » ; « >12,46
    50,0 0,00500 12,52 \ (CH_3CO_2H \) 2" style="text-align:center » ; « >12,52
    \ (CH_3CO_2H \) 2" style="text-align:center ; « >
    1. Titrage de 25,00 ml de HCl 0,100 M (0,00250 mol de HCI) avec 0,100 M de NaOH.
    2. Titrage de 25,00 ml de 0,100 M de CH 3 CO 2 H (0,00250 mol de CH 3 CO 2 H) avec 0,100 M de NaOH.

    Les réactions acide-base les plus simples sont celles d'un acide fort avec une base forte. Le tableau\(\PageIndex{1}\) montre les données pour le titrage d'un échantillon de 25,0 ml d'acide chlorhydrique à 0,100 M avec de l'hydroxyde de sodium à 0,100 M. Les valeurs du pH mesurées après des ajouts successifs de petites quantités de NaOH sont répertoriées dans la première colonne de ce tableau et sont représentées graphiquement sur la figure\(\PageIndex{1}\), sous une forme appelée courbe de titrage. Le pH augmente lentement au début, augmente rapidement dans la partie médiane de la courbe, puis augmente lentement à nouveau. Le point d'inflexion (situé au milieu de la partie verticale de la courbe) est le point d'équivalence pour le titrage. Il indique quand des quantités équivalentes d'acide et de base sont présentes. Pour le titrage d'un acide fort avec une base forte, le point d'équivalence se situe à un pH de 7,00 et les points de la courbe de titrage peuvent être calculés par stœchiométrie en solution (tableau\(\PageIndex{1}\) et figure\(\PageIndex{1}\)).

    Figure\(\PageIndex{1}\) : (a) La courbe de titrage pour le titrage de 25,00 ml de HCl 0,100 M (acide fort) avec 0,100 M de NaOH (base forte) a un point d'équivalence de 7,00 pH. (b) La courbe de titrage pour le titrage de 25,00 ml de 0,100 M CH 3 CO 2 H (acide faible) avec 0,100 M de NaOH (base forte) a un point d'équivalence de 8,72 pH.
    Deux graphiques sont présentés. Le premier graphique de gauche s'intitule « Titrage de l'acide faible ». L'axe horizontal est intitulé « Volume de 0,100 M N par O H ajouté (m L) ». Des marquages et des quadrillages verticaux sont fournis toutes les 5 unités, de 0 à 50. L'axe vertical est étiqueté « p H » et est marqué toutes les 1 unités à partir de 0 et jusqu'à 14. Une courbe rouge est tracée sur le graphique qui augmente régulièrement depuis le point (0, 3) jusqu'à environ (20, 5,5), après quoi le graphique présente une section verticale allant de (25, 7) à (25, 11). Le graphique se stabilise ensuite jusqu'à une valeur d'environ 12,5, d'environ 40 m L à 50 m L. Le point médian du segment vertical de la courbe est intitulé « Point d'équivalence p H, 8,72 ». Le deuxième graphique de droite s'intitule « Titrage de l'acide fort ». L'axe horizontal est intitulé « Volume de 0,100 M N par O H ajouté (m L) ». Des marquages et des quadrillages verticaux sont fournis toutes les 5 unités, de 0 à 50. L'axe vertical est étiqueté « p H » et est marqué toutes les 1 unités à partir de 0 jusqu'à 14. Une courbe rouge est tracée sur le graphique qui augmente progressivement depuis le point (0, 1) jusqu'à environ (22,5, 2,2), après quoi le graphique présente une section verticale allant de (25, 4) à presque (25, 11). Le graphique se stabilise ensuite jusqu'à une valeur d'environ 12,4, d'environ 40 m L à 50 m L. Le point médian du segment vertical de la courbe est intitulé « Point d'équivalence p H, 7,00 ».

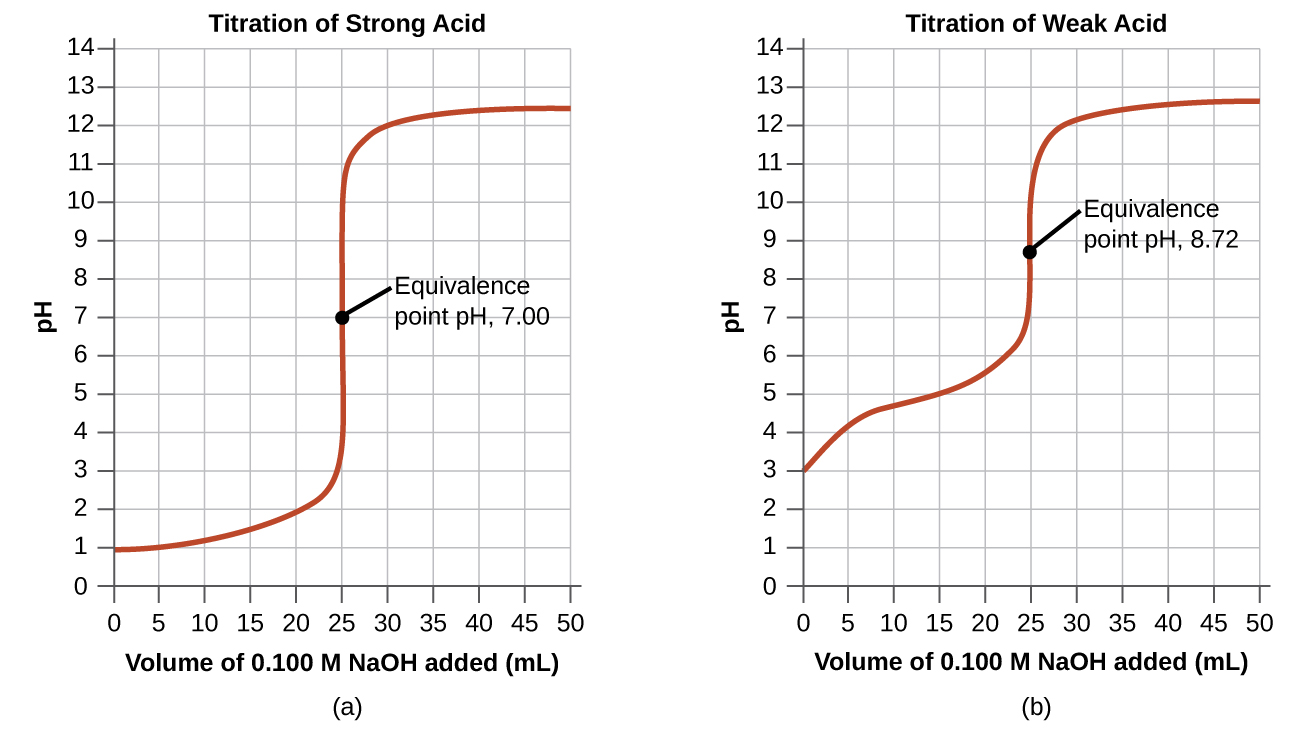
    Le titrage d'un acide faible avec une base forte (ou d'une base faible avec un acide fort) est un peu plus compliqué que celui qui vient d'être discuté, mais il suit les mêmes principes généraux. Examinons le titrage de 25,0 ml d'acide acétique 0,100 M (un acide faible) avec 0,100 M d'hydroxyde de sodium et comparons la courbe de titrage à celle de l'acide fort. Le tableau\(\PageIndex{1}\) indique les valeurs de pH pendant le titrage, la figure\(\PageIndex{1b}\) montre la courbe de titrage.

    Bien que le volume initial et la molarité des acides soient identiques, il existe des différences importantes entre les deux courbes de titrage. La courbe de titrage pour l'acide faible commence à une valeur plus élevée (moins acide) et maintient des valeurs de pH plus élevées jusqu'au point d'équivalence. En effet, l'acide acétique est un acide faible, qui n'est que partiellement ionisé. Le pH au point d'équivalence est également plus élevé (8,72 au lieu de 7,00) en raison de l'hydrolyse de l'acétate, une base faible qui augmente le pH :

    \[\ce{CH3CO2-}(aq)+\ce{H2O}(l)⇌\ce{CH3CO2H}(l)+\ce{OH-}(aq) \nonumber \]

    Après le point d'équivalence, les deux courbes sont identiques car le pH dépend de l'excès d'ion hydroxyde dans les deux cas.

    Exemple\(\PageIndex{2}\): Titration of a Weak Acid with a Strong Base

    La courbe de titrage illustrée à la figure\(\PageIndex{1b}\) correspond au titrage de 25,00 ml de 0,100 M de CH 3 CO 2 H avec 0,100 M de NaOH. La réaction peut être représentée comme suit :

    \[\ce{CH3CO2H + OH- ⟶ CH3CO2- + H2O} \nonumber \]

    1. Quel est le pH initial avant qu'une quantité quelconque de la solution de NaOH ne soit ajoutée ? K a = 1,8 × 10 −5 pour le CH 3 CO 2 H.
    2. Déterminez le pH après avoir ajouté 25,00 ml de solution de NaOH.
    3. Déterminez le pH après l'ajout de 12,50 ml de solution de NaOH.
    4. Déterminez le pH après avoir ajouté 37,50 ml de solution de NaOH.
    Solution

    (a) En supposant que la quantité dissociée est faible par rapport à 0,100 M, nous trouvons que :

    \[K_\ce{a}=\ce{\dfrac{[H3O+][CH3CO2- ]}{[CH3CO2H]}}≈\ce{\dfrac{[H3O+]^2}{[CH3CO2H]_0}} \nonumber \]

    et

    \[\ce{[H3O+]}=\sqrt{K_\ce{a}×\ce{[CH3CO2H]}}=\sqrt{1.8\times 10^{-5}×0.100}=1.3\times 10^{-3} \nonumber \]

    \[\mathrm{pH=-\log(1.3\times 10^{-3})=2.87} \nonumber \]

    (b) Après l'ajout de 25,00 ml de NaOH, le nombre de moles de NaOH et de CH 3 CO 2 H est égal car les quantités de solutions et leurs concentrations sont les mêmes. Tout le CH 3 CO 2 H a été converti en\(\ce{CH3CO2-}\). La concentration de l'\(\ce{CH3CO2-}\)ion est de :

    \[\mathrm{\dfrac{0.00250\: mol}{0.0500\: L}=0.0500\: \ce{MCH3CO2-}} \nonumber \]

    L'équilibre sur lequel il faut se concentrer maintenant est l'équilibre de basicité pour\(\ce{CH3CO2-}\) :

    \[\ce{CH3CO2-}(aq)+\ce{H2O}(l)⇌\ce{CH3CO2H}(aq)+\ce{OH-}(aq) \nonumber \]

    nous devons donc déterminer K b pour la base en utilisant la constante du produit ionique pour l'eau :

    \[K_\ce{b}=\ce{\dfrac{[CH3CO2H][OH- ]}{[CH3CO2- ]}} \nonumber \]

    \[K_\ce{a}=\ce{\dfrac{[CH3CO2- ][H+]}{[CH3CO2H]}},\textrm{ so }\ce{\dfrac{[CH3CO2H]}{[CH3CO2- ]}}=\dfrac{\ce{[H+]}}{K_\ce{a}}. \nonumber \]

    Puisque K w = [H +] [OH −] :

    \[\begin{align} K_\ce{b} &=\dfrac{\ce{[H+][OH- ]}}{K_\ce{a}} \\ &=\dfrac{K_\ce{w}}{K_\ce{a}} \\ &=\dfrac{1.0\times 10^{-14}}{1.8\times 10^{-5}} \\ &=5.6\times 10^{-10} \end{align} \nonumber \]

    Dénotons la concentration de chacun des produits de cette réaction, CH 3 CO 2 H et OH -, par x. En supposant que x est petit par rapport à 0,0500 M\(K_\ce{b}=\dfrac{x^2}{0.0500\:M}\), puis :

    \[x=\ce{[OH- ]}=5.3\times 10^{−6} \nonumber \]

    \[\ce{pOH}=-\log(5.3\times 10^{-6})=5.28 \nonumber \]

    \[\ce{pH}=14.00−5.28=8.72 \nonumber \]

    Notez que le pH au point d'équivalence de ce titrage est significativement supérieur à 7.

    (c) Dans (a), 25,00 ml de solution de NaOH ont été ajoutés, ce qui a permis de transformer pratiquement tout le CH 3 CO 2 H en\(\ce{CH3CO2-}\). Dans ce cas, seuls 12,50 ml de la solution de base ont été introduits, de sorte que seule la moitié de tout le CH 3 CO 2 H est convertie en\(\ce{CH3CO2-}\). Le nombre initial total de moles de CH 3 CO 2 H est de 0,02500L × 0,100 M = 0,00250 mol. Ainsi, après addition du NaOH, le nombre de moles de CH 3 CO 2 H et\(\ce{CH3CO2-}\) est à peu près égal à\(\mathrm{\dfrac{0.00250\: mol}{2}=0.00125\: mol}\), et leur les concentrations sont les mêmes.

    Comme la quantité de base ajoutée est inférieure à la quantité initiale d'acide, le point d'équivalence n'a pas été atteint, la solution reste un tampon, et nous pouvons utiliser l'équation de Henderson-Hasselbalch :

    \(\ce{pH}=\ce p K_\ce{a}+\log\ce{\dfrac{[Base]}{[Acid]}}=-\log(\mathit{K}_\ce{a})+\log\ce{\dfrac{[CH3CO2- ]}{[CH3CO2H]}}=-\log(1.8\times 10^{-5})+\log(1)\)

    (car les concentrations de\(\ce{CH3CO2-}\) et de CH 3 CO 2 H sont les mêmes)

    Ainsi :

    \[\ce{pH}=−\log(1.8\times 10^{−5})=4.74 \nonumber \]

    (le pH = le p K a à mi-parcours lors d'un titrage d'un acide faible)

    (d) Une fois 37,50 ml de NaOH ajoutés, la quantité de NaOH est de 0,03750 L × 0,100 M = 0,003750 mol de NaOH. Comme le point d'équivalence est dépassé, l'excès d'ions hydroxyde rendra la solution basique, et nous pouvons à nouveau utiliser des calculs stœchiométriques pour déterminer le pH :

    \(\mathrm{[OH^-]=\dfrac{(0.003750\: mol−0.00250\: mol)}{0.06250\: L}}=2.00\times 10^{−2}\:M\)

    Donc :

    \(\mathrm{pOH=−\log(2.00\times 10^{−2})=1.70,\: and\: pH=14.00−1.70=12.30}\)

    Notez que ce résultat est le même que pour l'exemple de titrage entre acides forts et bases fortes fourni, car la quantité de base forte ajoutée fait passer la solution au-delà du point d'équivalence.

    Exercice\(\PageIndex{2}\)

    Calculer le pH pour le titrage à base faible/base forte entre 50,0 ml de 0,100 M de HCOOH (aq) (acide formique) et 0,200 M de NaOH (titrant) aux volumes de base ajoutés indiqués :

    1. 0,00 ml,
    2. 15,0 ml,
    3. 25,0 ml, et
    4. 30,0 ml.
    Répondez à une

    0,00 ml : 2,37

    Réponse b

    15,0 ml : 3,92

    Réponse c

    25,00 ml : 8,29

    Réponse d

    30,0 ml : 12 097

    Indicateurs acido-basiques

    Certaines substances organiques changent de couleur en solution diluée lorsque la concentration en ions hydronium atteint une certaine valeur. Par exemple, la phénolphtaléine est une substance incolore présente dans toute solution aqueuse dont la concentration en ions hydronium est supérieure à 5,0 × 10 −9 M (pH < 8,3). Dans les solutions plus basiques où la concentration en ions hydronium est inférieure à 5,0 × 10 −9 M (pH > 8,3), elle est rouge ou rose. Des substances telles que la phénolphtaléine, qui peuvent être utilisées pour déterminer le pH d'une solution, sont appelées indicateurs acido-basiques. Les indicateurs acido-basiques sont soit des acides organiques faibles, soit des bases organiques faibles.

    L'équilibre dans une solution de l'indicateur acide-base méthylorange, un acide faible, peut être représenté par une équation dans laquelle nous utilisons\(\ce{HIn}\) comme représentation simple de la molécule complexe d'orange méthylique :

    \[\underbrace{\ce{HIn (aq)}}_{\ce{red}}+\ce{H2O (l)}⇌\ce{H3O^{+} (aq)}+\underbrace{\ce{In^{-} (aq)}}_{\ce{yellow}} \nonumber \]

    \[K_\ce{a}=\ce{\dfrac{[H3O+][In- ]}{[HIn]}}=4.0\times 10^{−4} \nonumber \]

    L'anion de l'orange méthylique est jaune et la forme non ionisée est rouge.\(\ce{In^{-}}\)\(\ce{HIn}\) Lorsque nous ajoutons de l'acide à une solution d'orange méthylique, l'augmentation de la concentration en ions hydronium déplace l'équilibre vers la forme rouge non ionisée, conformément au principe de Le Chatelier. Si on ajoute de la base, on déplace l'équilibre vers la forme jaune. Ce comportement est tout à fait analogue à l'action des buffers.

    La couleur d'un indicateur est le résultat visible du rapport des concentrations des deux espèces In − et\(\ce{HIn}\). Si la majeure partie de l'indicateur (généralement environ 60 à 90 % ou plus) est présente sous forme de\(\ce{In^{-}}\), alors nous voyons la couleur de l'\(\ce{In^{-}}\)ion, qui serait jaune pour l'orange méthyle. Si la plus grande partie est présente sous forme\(\ce{HIn}\), alors nous voyons la couleur de la\(\ce{HIn}\) molécule : rouge pour l'orange méthyle. Pour le méthyl orange, on peut réarranger l'équation de K a et écrire :

    \[\mathrm{\dfrac{[In^-]}{[HIn]}=\dfrac{[substance\: with\: yellow\: color]}{[substance\: with\: red\: color]}=\dfrac{\mathit{K}_a}{[H_3O^+]}} \label{ABeq2} \]

    L'équation \ ref {ABeQ2} nous montre comment le ratio de\(\ce{\dfrac{[In- ]}{[HIn]}}\) varie en fonction de la concentration en ion hydronium. L'expression ci-dessus décrivant l'équilibre de l'indicateur peut être réorganisée :

    \[ \begin{align} \dfrac{[H_3O^+]}{\mathit{K}_a} &=\dfrac{[HIn]}{[In^- ]} \\[8pt] \log\left(\dfrac{[H_3O^+]}{\mathit{K}_a}\right) &= \log\left(\dfrac{[HIn]}{[In^- ]}\right) \\[8pt] \log([H_3O^+])-\log(\mathit{K}_a) &=-\log\left(\dfrac{[In^-]}{[HIn]}\right) \\[8pt] -pH+p\mathit{K}_a & =-\log\left(\dfrac{[In^-]}{[HIn]}\right) \\[8pt] pH &=p\mathit{K}_a+\log\left(\dfrac{[In^-]}{[HIn]}\right) \end {align} \nonumber \]

    ou en termes généraux

    \[pH=p\mathit{K}_a+\log\left(\dfrac{[base]}{[acid]}\right) \label{HHeq} \]

    L'équation \ ref {HHeq} est identique à l'équation de Henderson-Hasselbalch, qui peut être utilisée pour décrire l'équilibre des indicateurs.

    Lorsque [H 3 O +] a la même valeur numérique que K a, le rapport entre [In −] et [HiN] est égal à 1, ce qui signifie que 50 % de l'indicateur est présent sous forme rouge (HiN) et 50 % sous forme ionique jaune (In -), et la solution apparaît de couleur orange. Lorsque la concentration en ions hydronium augmente jusqu'à 8 × 10 −4 M (pH de 3,1), la solution devient rouge. Aucun changement de couleur n'est visible en cas d'augmentation supplémentaire de la concentration en ions hydronium (diminution du pH). À une concentration en ions hydronium de 4 × 10 −5 M (pH de 4,4), la majeure partie de l'indicateur se présente sous forme ionique jaune, et une nouvelle diminution de la concentration en ions hydronium (augmentation du pH) ne produit pas de changement de couleur visible. La plage de pH comprise entre 3,1 (rouge) et 4,4 (jaune) est l'intervalle de changement de couleur de l'orange méthyle ; le changement de couleur prononcé se produit entre ces valeurs de pH.

    Il existe de nombreux indicateurs acido-basiques qui couvrent une large gamme de valeurs de pH et peuvent être utilisés pour déterminer le pH approximatif d'une solution inconnue par un processus d'élimination. Les indicateurs universels et le papier de pH contiennent un mélange d'indicateurs et présentent différentes couleurs à différents pH. La figure\(\PageIndex{2}\) présente plusieurs indicateurs, leurs couleurs et leurs intervalles de changement de couleur.

    alt
    Figure\(\PageIndex{2}\) : Ce graphique illustre les plages de changement de couleur pour plusieurs indicateurs acido-basiques.

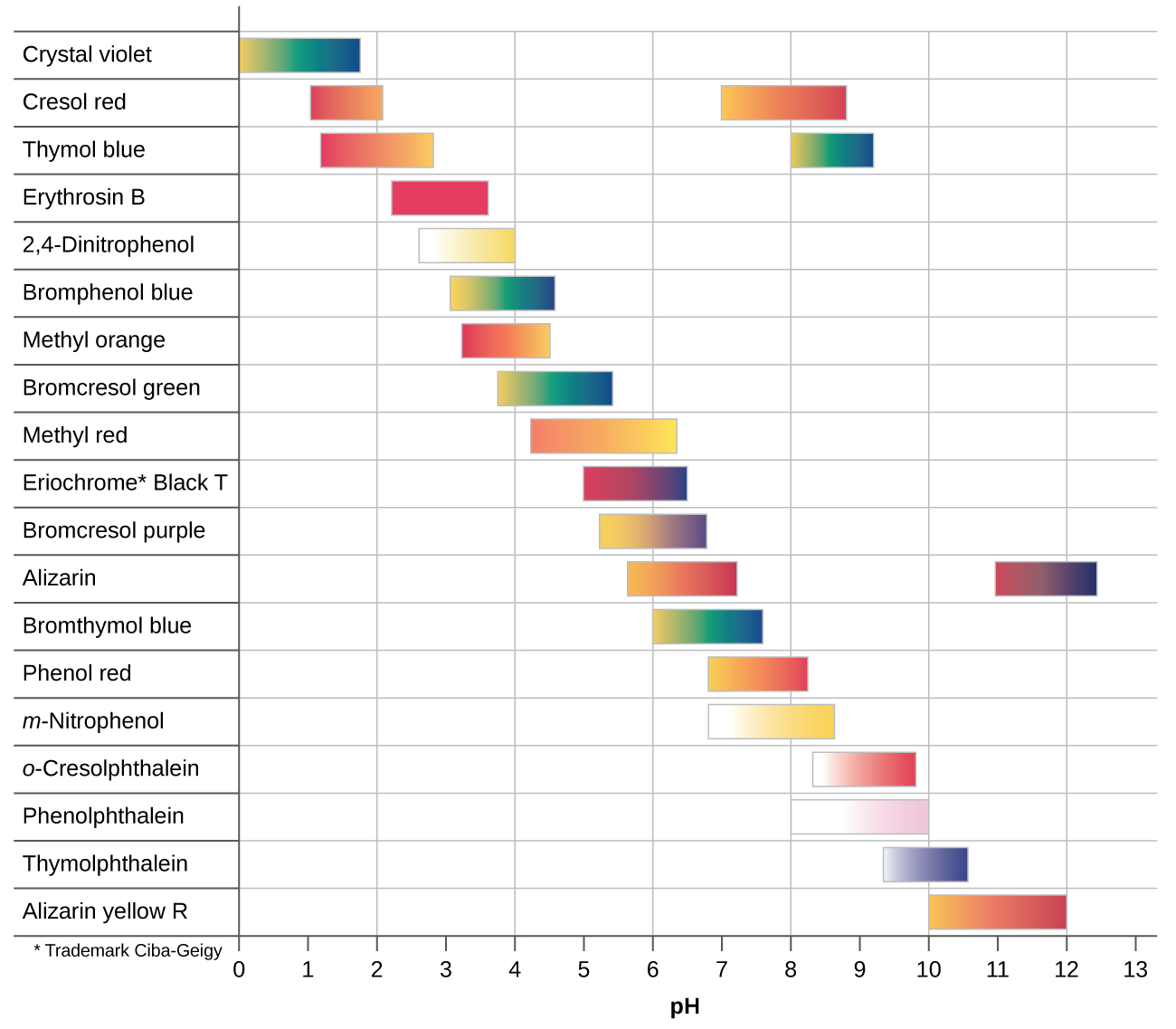
    Les courbes de titrage nous aident à choisir un indicateur qui fournira un changement de couleur net au point d'équivalence. Le meilleur choix serait un indicateur dont l'intervalle de changement de couleur est compris entre parenthèses par le pH au point d'équivalence du titrage.

    Les intervalles de changement de couleur de trois indicateurs sont illustrés sur la figure\(\PageIndex{3}\). Les points d'équivalence du titrage de l'acide fort et de l'acide faible se situent dans l'intervalle de changement de couleur de la phénolphtaléine. Nous pouvons l'utiliser pour les titrages d'acide fort avec base forte ou d'acide faible avec base forte.

    Figure\(\PageIndex{3}\) : Le graphique montre une courbe de titrage pour le titrage de 25,00 ml de 0,100 M CH 3 CO 2 H (acide faible) avec 0,100 M de NaOH (base forte) et la courbe de titrage pour le titrage de HCl (acide fort) avec du NaOH (base forte). Les plages de pH pour le changement de couleur de la phénolphtaléine, du tournesol et de l'orange méthyle sont indiquées par les zones ombrées.
    Un graphique intitulé « Titrage de l'acide faible » est présenté. L'axe horizontal est intitulé « Volume de 0,100 M N par O H ajouté (m L) » et commence à 0 avec des marques toutes les 5 unités jusqu'à 50. L'axe vertical est étiqueté « p H » et commence à 0 et augmente d'unités individuelles jusqu'à 14. Une courbe rouge est dessinée sur le graphique. La courbe commence à (0, 3) et passe par les points (5, 4.1), (10, 4,7), (15, 5), (20, 5,5) et (22,5, 6), après quoi elle augmente rapidement pour former une section verticale centrée sur le point (25, 8.7). L'augmentation rapide de la courbe se stabilise alors et la courbe passe par les points (30, 12), (35, 12,4), (40, 12,5), (45, 12,6) et (50, 12,6). Un rectangle brun s'étend horizontalement sur le graphique et couvre un pH compris entre 3 et 4,2. À droite, ce rectangle est étiqueté « Plage de pH pour l'orange méthylique ». Un rectangle bleu s'étend horizontalement sur le graphique et couvre un pH compris entre 4,6 et 8. À droite, ce rectangle est intitulé « Gamme Litmus p H ». Un rectangle violet s'étend horizontalement sur le graphique et couvre un pH compris entre 8,4 et 10. À droite, ce rectangle est intitulé « Gamme de phénolphtaléines p H ». Le point médian du segment vertical de la courbe est intitulé « Point d'équivalence p H, 8,72 ».

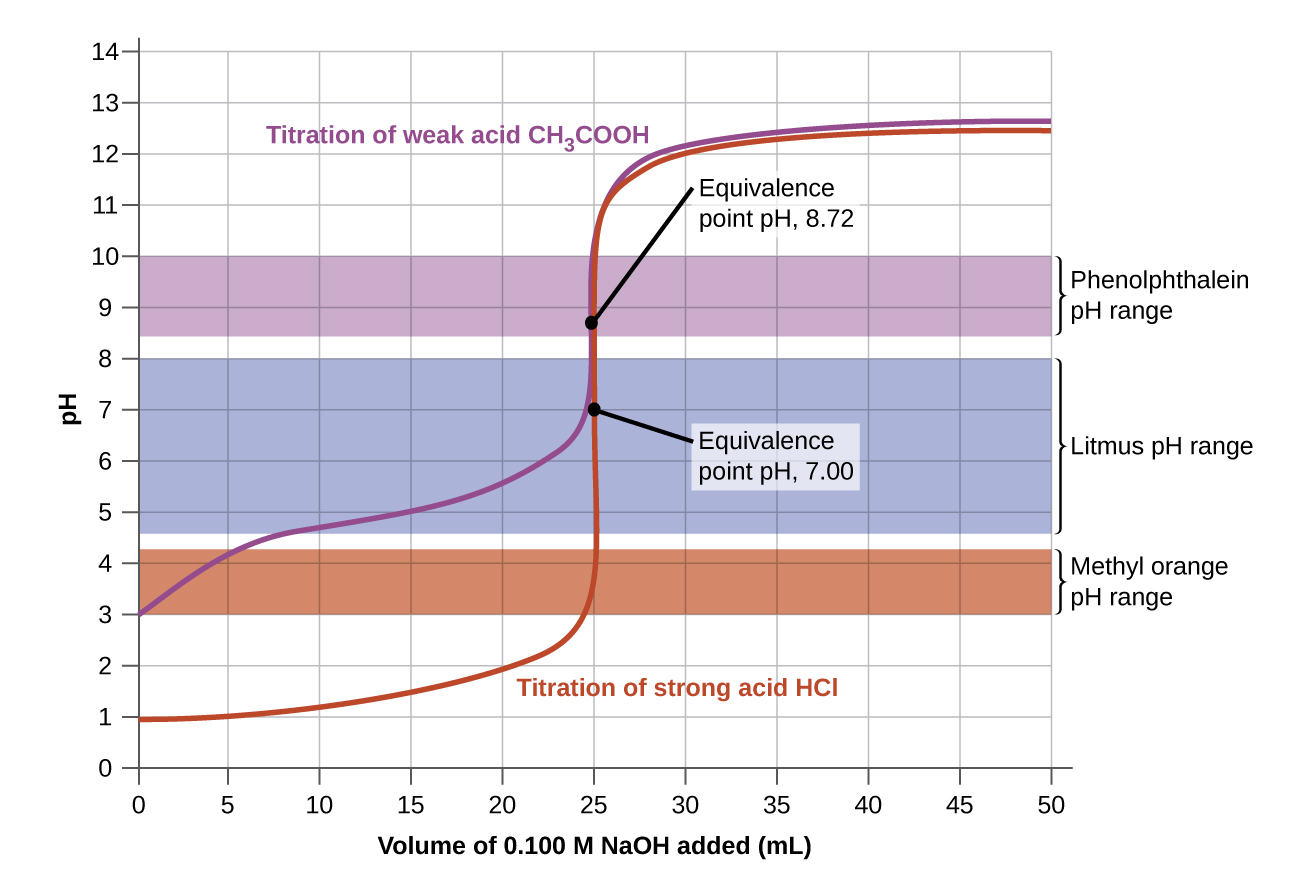
    Le litmus est un indicateur approprié pour le titrage du HCl car son changement de couleur entre crochets le point d'équivalence. Cependant, nous ne devons pas utiliser de tournesol pour le titrage du CH 3 CO 2 H, car le pH se situe dans l'intervalle de changement de couleur du tournesol lorsque seulement 12 ml de NaOH ont été ajoutés, et il ne quitte pas cette plage avant l'ajout de 25 ml. Le changement de couleur serait très progressif, se produisant lors de l'ajout de 13 ml de NaOH, rendant le tournesol inutile comme indicateur du point d'équivalence.

    Nous pourrions utiliser de l'orange méthylique pour le titrage du HCl, mais cela ne donnerait pas de résultats très précis : (1) Il complète son changement de couleur légèrement avant que le point d'équivalence ne soit atteint (mais très proche de celui-ci, donc ce n'est pas trop grave) ; (2) il change de couleur, comme le\(\PageIndex{2}\) montre la figure, lors de l'ajout de près de 0,5 ml de NaOH, dont le changement de couleur n'est pas aussi marqué que celui du tournesol ou de la phénolphtaléine ; et (3) il passe du jaune à l'orange puis au rouge, ce qui rend la détection d'un paramètre précis beaucoup plus difficile que le changement incolore à rose de la phénolphtaléine. La figure\(\PageIndex{2}\) montre que l'orange méthylique serait totalement inutile en tant qu'indicateur pour le titrage du CH 3 CO 2 H. Son changement de couleur commence après l'ajout d'environ 1 ml de NaOH et se termine lorsqu'environ 8 ml ont été ajoutés. Le changement de couleur est terminé bien avant que le point d'équivalence (qui se produit lorsque 25,0 ml de NaOH ont été ajoutés) ne soit atteint et ne fournit donc aucune indication du point d'équivalence.

    Nous basons notre choix d'indicateur sur un pH calculé, le pH au point d'équivalence. Au point d'équivalence, des quantités équimolaires d'acide et de base ont été mélangées, et le calcul devient celui du pH d'une solution du sel résultant du titrage.

    Résumé

    Une courbe de titrage est un graphique qui relie la variation du pH d'une solution acide ou basique au volume de titrant ajouté. Les caractéristiques de la courbe de titrage dépendent des solutions spécifiques à titrer. Le pH de la solution au point d'équivalence peut être supérieur, égal ou inférieur à 7,00. Le choix d'un indicateur pour un titrage donné dépend du pH attendu au point d'équivalence du titrage et de la plage de changement de couleur de l'indicateur.

    Lexique

    indicateur acido-basique
    acide ou base organique dont la couleur change en fonction du pH de la solution dans laquelle il se trouve
    intervalle de changement de couleur
    plage de pH sur laquelle se produit le changement de couleur d'un indicateur
    courbe de titrage
    diagramme du pH d'une solution d'acide ou de base en fonction du volume de base ou d'acide ajouté lors d'un titrage