14.6 : Tampons
- Page ID
- 194098
- Décrire la composition et la fonction des tampons acides-bases
- Calculer le pH d'un tampon avant et après l'ajout d'acide ou de base
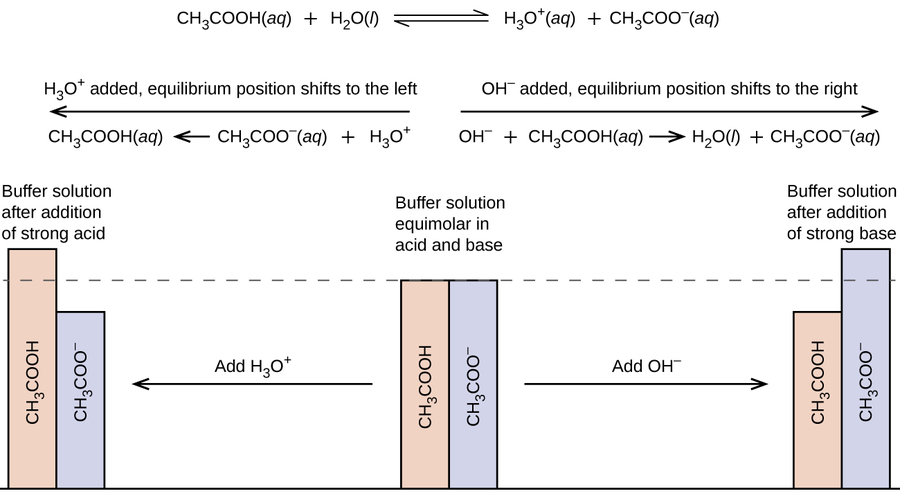
Un mélange d'un acide faible et de sa base conjuguée (ou un mélange d'une base faible et de son acide conjugué) est appelé solution tampon, ou tampon. Les solutions tampons résistent à une modification du pH lorsque de petites quantités d'un acide fort ou d'une base forte sont ajoutées (Figure\(\PageIndex{1}\)). Une solution d'acide acétique (\(\ce{CH3COOH}\)et d'acétate de sodium\(\ce{CH3COONa}\)) est un exemple de tampon composé d'un acide faible et de son sel. Un exemple de tampon composé d'une base faible et de son sel est une solution d'ammoniac (\(\ce{NH3(aq)}\)) et de chlorure d'ammonium (\(\ce{NH4Cl(aq)}\)).

Comment fonctionnent les buffers
Un mélange d'acide acétique et d'acétate de sodium est acide car le K a de l'acide acétique est supérieur au K b de son acétate de base conjugué. C'est un tampon car il contient à la fois l'acide faible et son sel. Il agit donc pour maintenir la concentration en ions hydronium (et le pH) presque constants par l'ajout d'une petite quantité d'un acide fort ou d'une base forte. Si nous ajoutons une base telle que l'hydroxyde de sodium, les ions hydroxyde réagissent avec les quelques ions hydronium présents. Ensuite, une plus grande partie de l'acide acétique réagit avec l'eau, rétablissant la concentration en ions hydronium presque à sa valeur initiale :
\[\ce{CH3CO2H}(aq)+\ce{H2O}(l)⟶\ce{H3O+}(aq)+\ce{CH3CO2-}(aq) \nonumber \]
Le pH change très peu. Si nous ajoutons un acide tel que l'acide chlorhydrique, la plupart des ions hydronium de l'acide chlorhydrique se combinent avec des ions acétate, formant des molécules d'acide acétique :
\[\ce{H3O+}(aq)+\ce{CH3CO2-}(aq)⟶\ce{CH3CO2H}(aq)+\ce{H2O}(l) \nonumber \]
Ainsi, la concentration de l'ion hydronium n'augmente que très peu et le pH reste pratiquement inchangé (Figure\(\PageIndex{2}\)).
Un mélange d'ammoniac et de chlorure d'ammonium est basique car le K b pour l'ammoniac est supérieur au K a pour l'ion ammonium. C'est un tampon car il contient également le sel de la base faible. Si nous ajoutons une base (ions hydroxyde), les ions ammonium du tampon réagissent avec les ions hydroxyde pour former de l'ammoniac et de l'eau et réduire la concentration en ions hydroxyde presque à sa valeur initiale :
\[\ce{NH4+}(aq)+\ce{OH-}(aq)⟶\ce{NH3}(aq)+\ce{H2O}(l) \nonumber \]
Si nous ajoutons un acide (ions hydronium), les molécules d'ammoniac du mélange tampon réagissent avec les ions hydronium pour former des ions ammonium et réduire la concentration en ions hydronium presque à sa valeur initiale :
\[\ce{H3O+}(aq)+\ce{NH3}(aq)⟶\ce{NH4+}(aq)+\ce{H2O}(l) \nonumber \]
Les trois parties de l'exemple suivant illustrent le changement de pH qui accompagne l'ajout de base à une solution tamponnée d'un acide faible et à une solution non tamponnée d'un acide fort.
Les tampons en acétate sont utilisés dans les études biochimiques des enzymes et d'autres composants chimiques des cellules afin de prévenir les changements de pH susceptibles de modifier l'activité biochimique de ces composés.
- Calculez le pH d'un tampon d'acétate qui est un mélange de 0,10 M d'acide acétique et de 0,10 M d'acétate de sodium.
- Calculez le pH après avoir ajouté 1,0 ml de NaOH 0,10 M à 100 ml de ce tampon, pour obtenir une solution d'un volume de 101 ml.
Solution
- Calculez le pH d'un tampon d'acétate qui est un mélange de 0,10 M d'acide acétique et de 0,10 M d'acétate de sodium.
Pour déterminer le pH de la solution tampon, nous utilisons un calcul d'équilibre typique (comme illustré dans les exemples précédents) :

- Déterminez la direction du changement. L'équilibre dans un mélange de H 3 O + et de CH 3 CO 2 H est le suivant :\(\ce{CH3CO2-}\)
\[\ce{CH3CO2H}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{CH3CO2-}(aq) \nonumber \]
La constante d'équilibre pour le CH 3 CO 2 H n'est pas donnée, nous la recherchons donc dans le Tableau E1 : K a = 1,8 × 10 −5. Avec [CH 3 CO 2 H]\(\ce{[CH3CO2- ]}\) = 0,10 M et [H 3 O +] = ~0 M, la réaction se déplace vers la droite pour former H 3 O +.
- Déterminez les concentrations x et d'équilibre. Voici un tableau des variations et des concentrations :
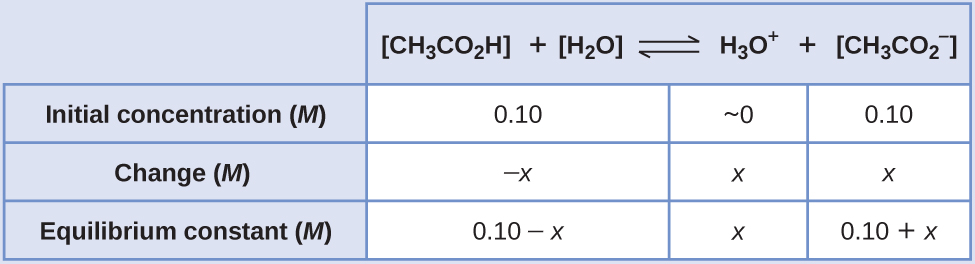
- Déterminez la direction du changement. L'équilibre dans un mélange de H 3 O + et de CH 3 CO 2 H est le suivant :\(\ce{CH3CO2-}\)
- Résolvez pour x et les concentrations d'équilibre. Nous trouvons :
\[x=1.8×10^{−5}\:M \nonumber \]
- et
\[\ce{[H3O+]}=0+x=1.8×10^{−5}\:M \nonumber \]
Ainsi :\[\mathrm{pH=−log[H_3O^+]=−log(1.8×10^{−5})} \nonumber \]
\[=4.74 \nonumber \]
4. Vérifiez le travail. Si nous calculons toutes les concentrations d'équilibre calculées, nous trouvons que la valeur d'équilibre du coefficient de réaction, Q = K a.
(b) Calculer le pH après avoir ajouté 1,0 ml de NaOH 0,10 M à 100 ml de ce tampon, pour obtenir une solution d'un volume de 101 ml.
Tout d'abord, nous calculons les concentrations d'un mélange intermédiaire résultant de la réaction complète entre l'acide contenu dans le tampon et la base ajoutée. Ensuite, nous déterminons les concentrations du mélange au nouvel équilibre :
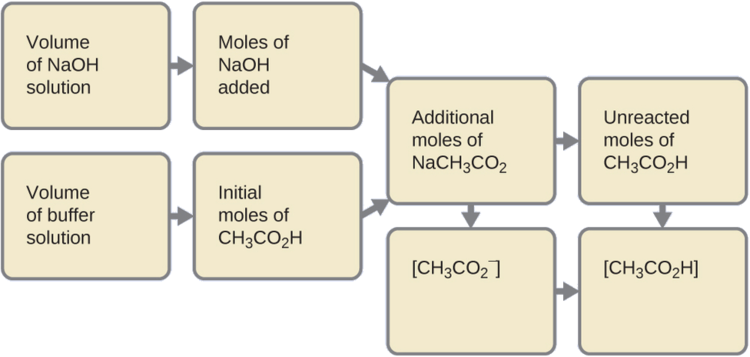
- Déterminez les moles de NaOH. Un millilitre (0,0010 L) de NaOH 0,10 M contient :
\[\mathrm{0.0010\cancel{L}×\left(\dfrac{0.10\:mol\: NaOH}{1\cancel{L}}\right)=1.0×10^{−4}\:mol\: NaOH} \nonumber \]
- Déterminer les moles de CH 2 CO 2 H. Avant la réaction, 0,100 L de la solution tampon contient :
\[\mathrm{0.100\cancel{L}×\left(\dfrac{0.100\:mol\:CH_3CO_2H}{1\cancel{L}}\right)=1.00×10^{−2}\:mol\:CH_3CO_2H} \nonumber \]
- Déterminer la quantité de NaCH 3 CO 2 produite. Le 1,0 × 10 -4 mol de NaOH neutralise 1,0 × 10 -4 mol de CH 3 CO 2 H, laissant :
\[\mathrm{(1.0×10^{−2})−(0.01×10^{−2})=0.99×10^{−2}\:mol\:CH_3CO_2H} \nonumber \]
et produisant 1,0 × 10 -4 mol de NaCH 3 CO 2. Cela fait un total de :
[\ mathrm {(1,0 × 10^ {−2}) + (0,01 × 10^ {−2}) =1,01 × 10^ {−2} \ :mol \ :nach_3co_2} \ nonnumber \]
4. Déterminez la molarité des produits. Après réaction, le CH 3 CO 2 H et le NaCH 3 CO 2 sont contenus dans 101 ml de la solution intermédiaire, donc :
\[\ce{[CH3CO2H]}=\mathrm{\dfrac{9.9×10^{−3}\:mol}{0.101\:L}}=0.098\:M \nonumber \]
\[\ce{[NaCH3CO2]}=\mathrm{\dfrac{1.01×10^{−2}\:mol}{0.101\:L}}=0.100\:M \nonumber \]
Nous calculons maintenant le pH une fois que la solution intermédiaire, qui est de 0,098 M dans le CH 3 CO 2 H et de 0,100 M dans le NaCH 3 CO 2, est arrivée à l'équilibre. Le calcul est très similaire à celui de la partie (a) de cet exemple :

Cette série de calculs donne un pH = 4,75. Ainsi, l'ajout de la base modifie à peine le pH de la solution.
(c) À des fins de comparaison, calculez le pH après avoir ajouté 1,0 ml de NaOH 0,10 M à 100 ml d'une solution non tamponnée ayant un pH de 4,74 (une solution de HCl 1,8 × 10 −5 - M). Le volume de la solution finale est de 101 ml.
Solution
Cette solution 1,8 × 10 −5 - M de HCl a la même concentration en ions hydronium que la solution 0,10- M de tampon acide acétique et acétate de sodium décrite dans la partie (a) de cet exemple. La solution contient :
\(\mathrm{0.100\:L×\left(\dfrac{1.8×10^{−5}\:mol\: HCl}{1\:L}\right)=1.8×10^{−6}\:mol\: HCl} \)
Comme indiqué dans la partie (b), 1 ml de NaOH 0,10 M contient 1,0 × 10 -4 mol de NaOH. Lorsque les solutions de NaOH et de HCl sont mélangées, le HCl est le réactif limitant de la réaction. Tout le HCl réagit, et la quantité de NaOH restante est de :
\( (1.0×10^{−4})−(1.8×10^{−6})=9.8×10^{−5}\:M \)
La concentration de NaOH est de :
\(\dfrac{9.8×10^{−5}\:M\:\ce{NaOH}}{0.101\:\ce{L}}=9.7×10^{−4}\:M \)
Le PoH de cette solution est le suivant :
\(\mathrm{pOH=−log[OH^- ]=−log(9.7×10^{−4})=3.01} \)Le pH est de :
\(\mathrm{pH=14.00−pOH=10.99} \)
Le pH passe de 4,74 à 10,99 dans cette solution non tamponnée. Cela se compare au changement de 4,74 à 4,75 qui s'est produit lorsque la même quantité de NaOH a été ajoutée à la solution tamponnée décrite dans la partie (b).
Montrez que l'ajout de 1,0 ml de HCl 0,10 M fait passer le pH de 100 ml d'une solution de HCl 1,8 × 10 -5 M de 4,74 à 3,00.
- Réponse
-
pH initial de 1,8 × 10 −5 M HCl ; pH = −log [H 3 O +] = −log [1,8 × 10 −5] = 4,74
Moles de H 3 O + ajoutées par addition de 1,0 ml de HCl 0,10 M : 0,10 moles/L × 0,0010 L = 1,0 × 10 -4 moles ; pH final après addition de 1,0 ml de HCl 0,10 M :
\[\mathrm{pH=−log[H_3O^+]=−log\left(\dfrac{total\: moles\:H_3O^+}{total\: volume}\right)=−log\left(\dfrac{1.0×10^{−4}\:mol+1.8×10^{−6}\:mol}{101\:mL\left(\dfrac{1\:L}{1000\:mL}\right)}\right)=3.00} \nonumber \]
Capacité du tampon
Les solutions tampons n'ont pas une capacité illimitée à maintenir un pH relativement constant (Figure\(\PageIndex{3}\)). Si nous ajoutons une telle quantité de base à un tampon que l'acide faible est épuisé, aucune action tampon supplémentaire sur la base n'est possible. D'un autre côté, si nous ajoutons un excès d'acide, la base faible serait épuisée et aucune action tampon supplémentaire ne serait possible à l'égard d'un acide supplémentaire. En fait, il n'est même pas nécessaire d'épuiser tout l'acide ou la base d'un tampon pour le submerger ; son effet tampon diminuera rapidement à mesure qu'un composant donné approche de l'épuisement.

Figure\(\PageIndex{3}\) : La couleur de l'indicateur (orange méthyle) montre qu'une petite quantité d'acide ajoutée à une solution tamponnée de pH 8 (bécher à gauche) n'a que peu d'effet sur le système tamponné (bécher du milieu). Cependant, une grande quantité d'acide épuise la capacité tampon de la solution et le pH change radicalement (bécher à droite). (crédit : modification de l'œuvre de Mark Ott) La capacité tampon est la quantité d'acide ou de base qui peut être ajoutée à un volume donné d'une solution tampon avant que le pH ne change de manière significative, généralement d'une unité. La capacité tampon dépend des quantités d'acide faible et de sa base conjuguée présentes dans un mélange tampon. Par exemple, 1 L d'une solution qui contient 1,0 M dans l'acide acétique et 1,0 M dans l'acétate de sodium a une capacité tampon supérieure à 1 L d'une solution de 0,10 M dans l'acide acétique et de 0,10 M dans l'acétate de sodium, même si les deux solutions ont le même pH. La première solution a une plus grande capacité tampon car elle contient plus d'acide acétique et d'ions acétate.
Sélection de mélanges de tampons appropriés
Il existe deux règles de base utiles pour sélectionner les mélanges tampons :
- Un bon mélange tampon doit avoir des concentrations à peu près égales de ses deux composants. Une solution tampon perd généralement son utilité lorsqu'un composant de la paire de tampons est inférieur à environ 10 % de l'autre. La figure\(\PageIndex{4}\) montre un tampon ionique d'acide acétique et d'acétate lorsque la base est ajoutée. Le pH initial est de 4,74. Un changement de 1 unité de pH se produit lorsque la concentration en acide acétique est réduite à 11 % de la concentration en ions acétate.
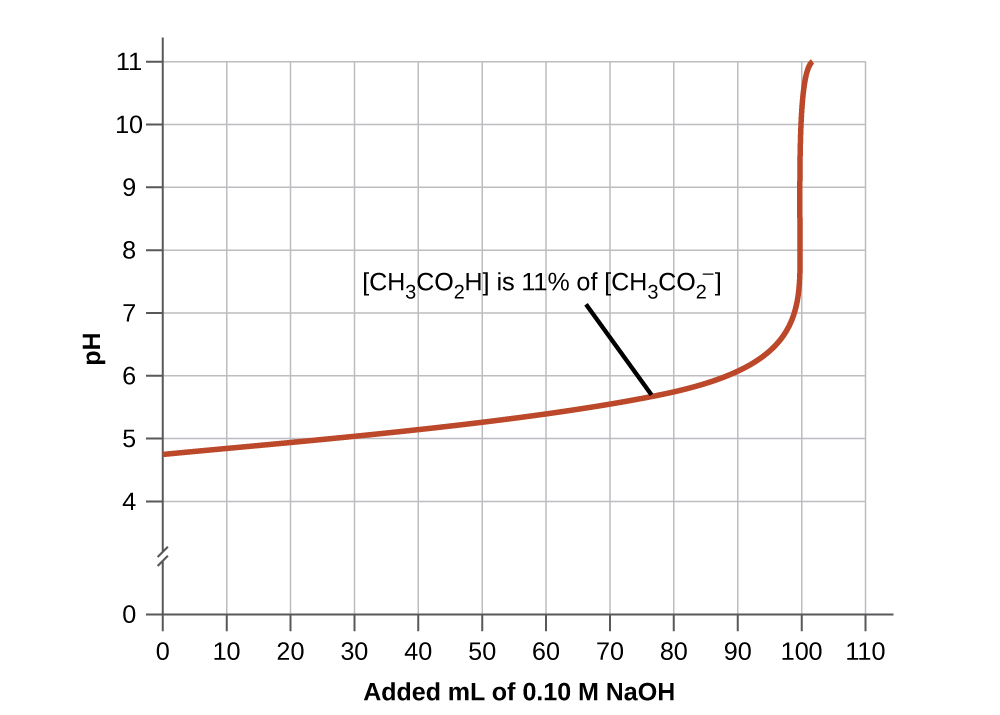
Figure\(\PageIndex{4}\) : Le graphique, une illustration de l'action tampon, montre l'évolution du pH lorsqu'une quantité croissante d'une solution de NaOH de 0,10 M est ajoutée à 100 ml d'une solution tampon dans laquelle, initialement,\([\ce{CH3CO2H}] = 0.10\: M\) et\(\ce{[CH3CO2^{-}]}=0.10\:M\).
- Les acides faibles et leurs sels sont meilleurs comme tampons pour les pH inférieurs à 7 ; les bases faibles et leurs sels sont meilleurs comme tampons pour les pH supérieurs à 7.
Le sang est un exemple important de solution tamponnée, les principaux acides et ions responsables de l'action tampon étant l'acide carbonique, H 2 CO 3, et l'ion bicarbonate\(\ce{HCO3-}\). Lorsqu'un excès d'ions hydrogène pénètre dans la circulation sanguine, il est éliminé principalement par la réaction :
\[\ce{H3O+}(aq)+\ce{HCO3-}(aq)⟶\ce{H2CO3}(aq)+\ce{H2O}(l) \nonumber \]
Lorsqu'un excès d'ion hydroxyde est présent, il est éliminé par la réaction :
\[\ce{OH-}(aq)+\ce{H2CO3}(aq)⟶\ce{HCO3-}(aq)+\ce{H2O}(l) \nonumber \]
Le pH du sang humain reste donc très proche de 7,35, c'est-à-dire légèrement basique. Les variations sont généralement inférieures à 0,1 unité de pH. Une modification de 0,4 unité de pH est susceptible d'être fatale.
L'approximation de Henderson-Hasselbalch
L'expression de la constante d'ionisation pour une solution d'un acide faible peut s'écrire comme suit :
\[K_\ce{a}=\ce{\dfrac{[H3O+][A- ]}{[HA]}} \nonumber \]
En réarrangeant pour résoudre [H 3 O +], on obtient :
\[\ce{[H3O+]}=K_\ce{a}×\ce{\dfrac{[HA]}{[A- ]}} \nonumber \]
En utilisant le logarithme négatif des deux côtés de cette équation, nous arrivons à :
\[\mathrm{−log[H_3O^+]=−log\mathit{K}_a − log\dfrac{[HA]}{[A^- ]}} \nonumber \]
qui peut être écrit comme
\[\mathrm{pH=p\mathit{K}_a+log\dfrac{[A^- ]}{[HA]}} \nonumber \]
où p K a est le négatif du logarithme commun de la constante d'ionisation de l'acide faible (p K a = −log K a). Cette équation met en relation le pH, la constante d'ionisation d'un acide faible et les concentrations de l'acide faible et de son sel dans une solution tamponnée. Les scientifiques utilisent souvent cette expression, appelée approximation de Henderson-Hasselbalch, pour calculer le pH des solutions tampons. Il est important de noter que l'hypothèse « x est petit » doit être valide pour utiliser cette équation.
Lawrence Joseph Henderson (1878-1942) était un médecin, biochimiste et physiologiste américain, pour ne citer que quelques-unes de ses nombreuses activités. Il a obtenu un diplôme de médecine à Harvard et a ensuite passé 2 ans à étudier à Strasbourg, alors dans une partie de l'Allemagne, avant de revenir occuper un poste de maître de conférences à Harvard. Il est finalement devenu professeur à Harvard et y a travaillé toute sa vie. Il a découvert que l'équilibre acido-basique du sang humain est régulé par un système tampon formé par le dioxyde de carbone dissous dans le sang. Il a écrit une équation en 1908 pour décrire le système tampon acide carbonique-carbonate dans le sang. Henderson possédait de vastes connaissances ; outre ses importantes recherches sur la physiologie du sang, il a également écrit sur les adaptations des organismes et leur adaptation à leur environnement, sur la sociologie et sur l'enseignement universitaire. Il a également fondé le laboratoire de fatigue de la Harvard Business School, qui a examiné la physiologie humaine en mettant l'accent sur le travail dans l'industrie, l'exercice et la nutrition.
En 1916, Karl Albert Hasselbalch (1874-1962), médecin et chimiste danois, a partagé la paternité d'un article avec Christian Bohr en 1904 qui décrivait l'effet Bohr, qui montrait que la capacité de l'hémoglobine dans le sang à se lier à l'oxygène était inversement liée à l'acidité du sang et la concentration de dioxyde de carbone. L'échelle de pH a été introduite en 1909 par un autre Danois, Sørensen, et en 1912, Hasselbalch a publié des mesures du pH du sang. En 1916, Hasselbalch a exprimé l'équation de Henderson en termes logarithmiques, conformément à l'échelle logarithmique du pH, et c'est ainsi que l'équation de Henderson-Hasselbalch est née.
Le pH normal du sang humain est d'environ 7,4. Le système tampon carbonaté dans le sang utilise la réaction d'équilibre suivante :
\[\ce{CO2}(g)+\ce{2H2O}(l)⇌\ce{H2CO3}(aq)⇌\ce{HCO3-}(aq)+\ce{H3O+}(aq) \nonumber \]
La concentration en acide carbonique, H 2 CO 3, est d'environ 0,0012 M, et la concentration en ion hydrogénocarbonate est d'environ 0,024 M.\(\ce{HCO3-}\) À l'aide de l'équation de Henderson-Hasselbalch et du p K a de l'acide carbonique à la température corporelle, nous pouvons calculer le pH du sang :
\[\mathrm{pH=p\mathit{K}_a+\log\dfrac{[base]}{[acid]}=6.1+\log\dfrac{0.024}{0.0012}=7.4} \nonumber \]
Le fait que la concentration de H 2 CO 3 soit nettement inférieure à celle de l'\(\ce{HCO3-}\)ion peut sembler inhabituel, mais ce déséquilibre est dû au fait que la plupart des sous-produits de notre métabolisme qui pénètrent dans notre circulation sanguine sont acides. Par conséquent, il doit y avoir une plus grande proportion de base que d'acide, afin que la capacité du tampon ne soit pas dépassée.
L'acide lactique est produit dans nos muscles lorsque nous faisons de l'exercice. Lorsque l'acide lactique pénètre dans la circulation sanguine, il est neutralisé par l'\(\ce{HCO3-}\)ion, produisant du H 2 CO 3. Une enzyme accélère ensuite la décomposition de l'excès d'acide carbonique en dioxyde de carbone et en eau, qui peuvent être éliminés par la respiration. En effet, en plus des effets régulateurs du système tampon des carbonates sur le pH du sang, l'organisme utilise la respiration pour réguler le pH sanguin. Si le pH du sang baisse trop fortement, une augmentation de la respiration élimine le CO 2 du sang par les poumons, provoquant ainsi la réaction d'équilibre, de telle sorte que [H 3 O +] est abaissé. Si le sang est trop alcalin, une diminution du rythme respiratoire augmente la concentration de CO 2 dans le sang, ce qui entraîne la réaction d'équilibre dans l'autre sens, augmente [H +] et rétablit un pH approprié.
Résumé
Une solution contenant un mélange d'un acide et de sa base conjuguée, ou d'une base et de son acide conjugué, est appelée solution tampon. Contrairement à une solution acide, basique ou saline, la concentration en ions hydronium d'une solution tampon ne change pas beaucoup lorsqu'une petite quantité d'acide ou de base est ajoutée à la solution tampon. La base (ou l'acide) du tampon réagit avec l'acide (ou la base) ajouté.
Équations clés
- p K a = −log K a
- p K b = −log K b
- \(\mathrm{pH=p\mathit{K}_a+\log\dfrac{[A^- ]}{[HA]}}\)
Lexique
- capacité du tampon
- quantité d'acide ou de base qui peut être ajoutée au volume d'une solution tampon avant que son pH ne change de manière significative (généralement d'une unité de pH)
- tampon
- mélange d'un acide faible ou d'une base faible et du sel de son conjugué ; le pH d'un tampon résiste au changement lorsque de petites quantités d'acide ou de base sont ajoutées
- Équation de Henderson-Hasselbalch
- équation utilisée pour calculer le pH des solutions tampons
- Déterminez les moles de NaOH. Un millilitre (0,0010 L) de NaOH 0,10 M contient :


