Skip to main content
Global

14.5 : Acides polyprotiques

  1. Last updated
  2. Save as PDF
  • Page ID
    194107

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage
    • Étendre les concepts d'équilibre précédemment introduits aux acides et aux bases qui peuvent donner ou accepter plus d'un proton

    Nous pouvons classer les acides en fonction du nombre de protons par molécule qu'ils peuvent abandonner lors d'une réaction. Les acides tels que\(\ce{HCl}\)\(\ce{HNO3}\), et\(\ce{HCN}\) qui contiennent un atome d'hydrogène ionisable dans chaque molécule sont appelés acides monoprotiques. Leurs réactions avec l'eau sont les suivantes :

    \[\ce{HCl}(aq)+\ce{H2O}(l)⟶\ce{H3O+}(aq)+\ce{Cl-}(aq) \nonumber \]

    \[\ce{HNO3}(aq)+\ce{H2O}(l)⟶\ce{H3O+}(aq)+\ce{NO3-}(aq) \nonumber \]

    \[\ce{HCN}(aq)+\ce{H2O}(l)⟶\ce{H3O+}(aq)+\ce{CN-}(aq) \nonumber \]

    Même s'il contient quatre atomes d'hydrogène\(\ce{CH3CO2H}\), l'acide acétique est également monoprotique car seul l'atome d'hydrogène du groupe carboxyle (\(\ce{-COOH}\)) réagit avec les bases :

     

    Cette image contient deux réactions d'équilibre. La première montre un atome de C lié à trois atomes H et à un autre atome de C. Le second atome C est doublement lié à un atome O et forme également une liaison simple avec un autre atome O. Le second atome O est lié à un atome H. Il y a un signe plus et ensuite la formule moléculaire H indice 2 O. Une flèche d'équilibre suit l'indice H 2 O. À droite de la flèche se trouve l'indice H 3 O, signe positif. Il y a un signe plus. La structure finale montre un atome de C lié aux trois atomes H et à un autre atome de C. Ce second atome de C est lié deux fois à un atome O et simple à un autre atome O. L'ensemble de la structure est entre crochets et un signe négatif en exposant apparaît à l'extérieur des crochets. La deuxième réaction montre l'indice C H 3 C O O H (a q) plus l'indice H 2 O (l), la flèche d'équilibre H, l'indice H 3 O (a q) plus l'indice C H 3 C O O O, le signe négatif (a q).

    De même, les bases monoprotiques sont des bases qui accepteront un seul proton.

    Acides diprotiques

    Les acides diprotiques contiennent deux atomes d'hydrogène ionisables par molécule ; l'ionisation de ces acides se fait en deux étapes. La première ionisation a toujours lieu dans une plus grande mesure que la seconde ionisation. Par exemple, l'acide sulfurique, un acide fort, s'ionise comme suit :

    • La première ionisation est

    \[ \ce{H2SO4}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{HSO4-}(aq) \nonumber \]

    avec\(K_{\ce a1} > 10^2;\: {complete\: dissociation}\).

    • La deuxième ionisation est

    \[ \ce{HSO4-}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{SO4^{2−}}(aq) \nonumber \]

    avec\( K_{\ce a2}=1.2×10^{−2}\).

    Ce processus d'ionisation par étapes se produit pour tous les acides polyprotiques. Lorsque nous fabriquons une solution d'acide diprotique faible, nous obtenons une solution contenant un mélange d'acides. L'acide\(\ce{H2CO3}\) carbonique est un exemple d'acide diprotique faible. La première ionisation de l'acide carbonique produit des ions hydronium et des ions bicarbonate en petites quantités.

    • Première ionisation

    \[\ce{H2CO3}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{HCO3-}(aq) \nonumber \]

    avec

    \[K_{\ce{H2CO3}}=\ce{\dfrac{[H3O+][HCO3- ]}{[H2CO3]}}=4.3×10^{−7} \nonumber \]

    L'ion bicarbonate peut également agir comme un acide. Il ionise et forme des ions hydronium et des ions carbonate en quantités encore plus petites.

    • Deuxième ionisation

    \[\ce{HCO3-}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{CO3^2-}(aq) \nonumber \]

    avec

    \[ K_{\ce{HCO3-}}=\ce{\dfrac{[H3O+][CO3^2- ]}{[HCO3- ]}}=4.7×10^{−11} \nonumber \]

    \(K_{\ce{H2CO3}}\)est plus grand que\(K_{\ce{HCO3-}}\) d'un facteur 10 4, de sorte que H 2 CO 3 est le principal producteur d'ions hydronium dans la solution. Cela signifie qu'une petite partie de la substance\(\ce{HCO3-}\) formée par l'ionisation de H 2 CO 3 s'ionise pour donner des ions hydronium (et des ions carbonate), et que les concentrations de H 3 O +\(\ce{HCO3-}\) sont pratiquement égales dans une solution aqueuse pure de H 2 CO 3.

    Si la première constante d'ionisation d'un acide diprotique faible est supérieure à la seconde d'un facteur d'au moins 20, il convient de traiter la première ionisation séparément et de calculer les concentrations qui en résultent avant de calculer les concentrations d'espèces résultant d'une ionisation ultérieure. Cela peut considérablement simplifier notre travail, car nous pouvons déterminer la concentration de H 3 O + et de la base conjuguée à partir de la première ionisation, puis déterminer la concentration de la base conjuguée de la deuxième ionisation dans une solution dont les concentrations sont déterminées par la première ionisation.

    Exemple\(\PageIndex{1}\): Ionization of a Diprotic Acid

    Lorsque nous achetons de l'eau gazeuse (eau gazeuse), nous achetons une solution de dioxyde de carbone dans de l'eau. La solution est acide car le CO 2 réagit avec l'eau pour former de l'acide carbonique, H 2 CO 3. Que sont\(\ce{[H3O+]}\)\(\ce{[HCO3- ]}\), et\(\ce{[CO3^2- ]}\) dans une solution saturée de CO 2 avec une valeur initiale [H 2 CO 3] = 0,033 M ?

    \[\ce{H2CO3}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{HCO3-}(aq) \hspace{20px} K_{\ce a1}=4.3×10^{−7} \label{step1} \tag{equilibrium step 1} \]

    \[\ce{HCO3-}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{CO3^2-}(aq) \hspace{20px} K_{\ce a2}=4.7×10^{−11} \label{step2} \tag{equilibrium step 2} \]

    Solution

    Comme l'indiquent les constantes d'ionisation, le H 2 CO 3 est un acide beaucoup plus fort que\(\ce{HCO3-}\) le principal producteur d'ions hydronium en solution.\(\ce{H2CO3}\) La solution de ce problème comporte donc deux volets :

    1. En utilisant les quatre étapes habituelles, nous déterminons la concentration de H 3 O +\(\ce{HCO3-}\) produite par ionisation de H 2 CO 3.
    2. Ensuite, nous déterminons la concentration de\(\ce{CO3^2-}\) dans une solution avec la concentration de H 3 O + et\(\ce{HCO3-}\) déterminée en (1).

    Pour résumer :

     

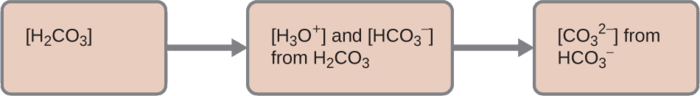
    Quatre rectangles bruns sont représentés, reliés par des flèches pointant vers la droite. Le premier est intitulé « crochet gauche H indice 2 C O indice 3 crochet droit ». Le second est intitulé « crochet gauche H indice 3 O exposant plus crochet droit et crochet gauche H C O indice 3 exposant négatif crochet droit de l'indice H 2 C O indice 3 exposant négatif crochet droit de l'indice H 2 C O indice 3 ». Le troisième est intitulé « crochet gauche C O indice 3 exposant 2 parenthèse droite négative de H C O indice 3 exposant négatif ».

    1. Première ionisation : Déterminez les concentrations de\(\ce{H3O+}\) et\(\ce{HCO3-}\).

    Comme \ ref {step1} est beaucoup\(K_{a1}=4.3×10^{−7}\) plus grand que\(K_{a2}=4.7×10^{−11}\) pour \ ref {step2}, nous pouvons ignorer en toute sécurité la deuxième étape d'ionisation et nous concentrer uniquement sur la première étape (mais y répondre dans la partie suivante du problème).

    \[\ce{H2CO3}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{HCO3-}(aq) \hspace{20px} K_{\ce a1}=4.3×10^{−7} \nonumber \]

    En ce qui concerne l'ionisation de tout autre acide faible :

     

    Quatre rectangles bruns sont représentés, reliés par des flèches pointant vers la droite. Le premier est intitulé « Déterminer la direction du changement ». La seconde est intitulée « Déterminer x et les concentrations d'équilibre ». Le troisième est intitulé « Résolvez pour x et les concentrations d'équilibre ». Le quatrième est intitulé « Vérifiez les calculs ».

    Un tableau abrégé des variations et des concentrations indique :

    Tableau abrégé des variations et des concentrations
    Table ICE \(\ce{H2CO3}(aq)\) \(\ce{H2O}(l)\) \( \ce{H3O+}(aq) \) \(\ce{HCO3-}(aq)\)
    Dans l'original (M) \ (\ ce {H2CO3} (aq) \) » style="text-align:center ; « >\(0.033 \:M\) \ (\ ce {H2O} (l) \) » style="text-align:center ; « >- \ (\ ce {H3O+} (aq) \) » style="text-align:center ; « >\(0\) \ (\ ce {HCO3-} (aq) \) » style="text-align:center ; « >\(0\)
    Changement de courant continu (M) \ (\ ce {H2CO3} (aq) \) » style="text-align:center ; « >\(- x\) \ (\ ce {H2O} (l) \) » style="text-align:center ; « >- \ (\ ce {H3O+} (aq) \) » style="text-align:center ; « >\(+x\) \ (\ ce {HCO3-} (aq) \) » style="text-align:center ; « >\(+x\)
    Équilibre E (M) \ (\ ce {H2CO3} (aq) \) » style="text-align:center ; « >\(0.033 \:M - x\) \ (\ ce {H2O} (l) \) » style="text-align:center ; « >- \ (\ ce {H3O+} (aq) \) » style="text-align:center ; « >\(x\) \ (\ ce {HCO3-} (aq) \) » style="text-align:center ; « >\( x\)

    En substituant les concentrations d'équilibre à la constante d'équilibre, on obtient :

    \[K_{\ce{H2CO3}}=\ce{\dfrac{[H3O+][HCO3- ]}{[H2CO3]}}=\dfrac{(x)(x)}{0.033−x}=4.3×10^{−7} \nonumber \]

    La résolution de l'équation précédente en utilisant nos hypothèses standard donne :

    \[x=1.2×10^{−4} \nonumber \]

    Ainsi :

    \[\ce{[H2CO3]}=0.033\:M \nonumber \]

    \[\ce{[H3O+]}=\ce{[HCO3- ]}=1.2×10^{−4}\:M \nonumber \]

    2. Deuxième ionisation : Déterminez la concentration de \(CO_3^{2-}\)dans une solution à l'équilibre.

    Puisque le \ ref {step1} est beaucoup\(K_a\) plus grand que \ ref {step2}, nous pouvons calculer les conditions d'équilibre à partir de la première partie de l'exemple comme conditions initiales pour une table ICER pour le \ ref {step2} :

    \[\ce{HCO3-}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{CO3^2-}(aq) \nonumber \]

    Tableau ICER pour le \ ref {step2} :
    Table ICE \(\ce{HCO3-}(aq)\) \(\ce{H2O}(l)\) \( \ce{H3O+}(aq) \) \(\ce{CO3^2-}(aq)\)
    Dans l'original (M) \ (\ ce {HCO3-} (aq) \) » style="text-align:center ; « >\(1.2×10^{−4}\:M\) \ (\ ce {H2O} (l) \) » style="text-align:center ; « >- \ (\ ce {H3O+} (aq) \) » style="text-align:center ; « >\(1.2×10^{−4}\:M\) \ (\ ce {CO3^2-} (aq) \) » style="text-align:center ; « >\(0\)
    Changement de courant continu (M) \ (\ ce {HCO3-} (aq) \) » style="text-align:center ; « >\(- y\) \ (\ ce {H2O} (l) \) » style="text-align:center ; « >- \ (\ ce {H3O+} (aq) \) » style="text-align:center ; « >\(+y\) \ (\ ce {CO3^2-} (aq) \) » style="text-align:center ; « >\(+y\)
    Équilibre E (M) \ (\ ce {HCO3-} (aq) \) » style="text-align:center ; « >\(1.2×10^{−4}\:M - y\) \ (\ ce {H2O} (l) \) » style="text-align:center ; « >- \ (\ ce {H3O+} (aq) \) » style="text-align:center ; « >\(1.2×10^{−4}\:M + y\) \ (\ ce {CO3^2-} (aq) \) » style="text-align:center ; « >\( y\)

    \[ \begin{align*} K_{\ce{HCO3-}}&=\ce{\dfrac{[H3O+][CO3^2- ]}{[HCO3- ]}} \\[4pt] &=\dfrac{(1.2×10^{−4}\:M + y) (y)}{(1.2×10^{−4}\:M - y)} \end{align*} \nonumber \]

    Pour éviter de résoudre une équation quadratique, nous pouvons supposer\(y \ll 1.2×10^{−4}\:M \) que

    \[K_{\ce{HCO3-}} = 4.7×10^{−11} \approx \dfrac{(1.2×10^{−4}\:M ) (y)}{(1.2×10^{−4}\:M)} \nonumber \]

    Réorganisation pour résoudre\(y\)

    \[y \approx \dfrac{ (4.7×10^{−11})(1.2×10^{−4}\:M )}{ 1.2×10^{−4}\:M} \nonumber \]

    \[[\ce{CO3^2-}]=y \approx 4.7×10^{−11} \nonumber \]

    Pour résumer :

    Dans la partie 1 de cet exemple, nous avons constaté que la solution\(\ce{H2CO3}\) dans une solution de 0,033- M s'ionise légèrement et à l'équilibre\([\ce{H2CO3}] = 0.033\, M\)\([\ce{H3O^{+}}] = 1.2 × 10^{−4}\), et\(\ce{[HCO3- ]}=1.2×10^{−4}\:M\). Dans la deuxième partie, nous avons déterminé que\(\ce{[CO3^2- ]}=5.6×10^{−11}\:M\).

    Exercice\(\PageIndex{2}\): Hydrogen Sulfide

    La concentration de\(H_2S\) dans une solution aqueuse saturée à température ambiante est d'environ 0,1 M. Calculez\(\ce{[H3O+]}\)\(\ce{[HS^{−}]}\), et\(\ce{[S^{2−}]}\) dans la solution :

    \[\ce{H2S}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{HS-}(aq) \hspace{20px} K_{\ce a1}=8.9×10^{−8} \nonumber \]

    \[\ce{HS-}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{S^2-}(aq) \hspace{20px} K_{\ce a2}=1.0×10^{−19} \nonumber \]

    Réponse

    \([\ce{H2S}] = 0.1 M\),\(\ce{[H3O+]} = [HS^{−}] = 0.0001\, M\),\([S^{2−}] = 1 × 10^{−19}\, M\)

    Nous notons que la concentration de l'ion sulfure est la même que celle de K a2. Cela est dû au fait que chaque dissociation ultérieure se produit dans une moindre mesure (à mesure que l'acide s'affaiblit).

    Acides triprotiques

    Un acide triprotique est un acide qui possède trois protons dissociables qui subissent une ionisation par étapes : l'acide phosphorique en est un exemple typique :

    • La première ionisation est

    \[\ce{H3PO4}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{H2PO4-}(aq) \nonumber \]

    avec\(K_{\ce a1}=7.5×10^{−3} \).

    • La deuxième ionisation est

    \[\ce{H2PO4-}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{HPO4^2-}(aq) \nonumber \]

    avec\( K_{\ce a2}=6.2×10^{−8} \).

    • La troisième ionisation est

    \[\ce{HPO4^2-}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{PO4^3-}(aq) \nonumber \]

    avec\( K_{\ce a3}=4.2×10^{−13} \).

    Comme pour les acides diprotiques, les différences dans les constantes d'ionisation de ces réactions nous indiquent qu'à chaque étape successive, le degré d'ionisation est significativement plus faible. Il s'agit d'une caractéristique générale des acides polyprotiques et les constantes d'ionisation successives diffèrent souvent d'un facteur d'environ 10 5 à 10 6. Cet ensemble de trois réactions de dissociation peut sembler compliquer le calcul des concentrations d'équilibre dans une solution de H 3 PO 4. Cependant, comme les constantes d'ionisation successives diffèrent d'un facteur de 10 5 à 10 6, les calculs peuvent être décomposés en une série de parties similaires à celles des acides diprotiques.

    Les bases polyprotiques peuvent accepter plus d'un ion hydrogène en solution. L'ion carbonate est un exemple de base diprotique, puisqu'il peut accepter jusqu'à deux protons. Les solutions de carbonates de métaux alcalins sont assez alcalines, en raison des réactions :

    \[\ce{H2O}(l)+\ce{CO3^2-}(aq)⇌\ce{HCO3-}(aq)+\ce{OH-}(aq) \nonumber \]

    et

    \[\ce{H2O}(l)+\ce{HCO3-}(aq)⇌\ce{H2CO3}(aq)+\ce{OH-}(aq) \nonumber \]

    Résumé

    Un acide qui contient plus d'un proton ionisable est un acide polyprotique. Les protons de ces acides s'ionisent par étapes. Les différences dans les constantes d'ionisation acide pour les ionisations successives des protons dans un acide polyprotique varient généralement d'environ cinq ordres de grandeur. Tant que la différence entre les valeurs successives de K a de l'acide est supérieure à environ un facteur 20, il convient de décomposer les calculs des concentrations des ions en solution en une série d'étapes.

    Lexique

    acide diprotique
    acide contenant deux atomes d'hydrogène ionisables par molécule. Un acide diprotique s'ionise en deux étapes
    base diprotique
    base capable d'accepter deux protons. Les protons sont acceptés en deux étapes
    acide monoprotique
    acide contenant un atome d'hydrogène ionisable par molécule
    ionisation par étapes
    processus dans lequel un acide est ionisé en perdant des protons de manière séquentielle
    acide triprotique
    acide contenant trois atomes d'hydrogène ionisables par molécule ; l'ionisation des acides triprotiques se fait en trois étapes