14.3 : Formats relatifs des acides et des bases
- Page ID
- 194078
- Évaluer les forces relatives des acides et des bases en fonction de leurs constantes d'ionisation
- Rationaliser les tendances de la résistance acide-base en fonction de la structure moléculaire
- Effectuer des calculs d'équilibre pour les systèmes acide-base faibles
Nous pouvons classer les forces des acides en fonction de leur degré d'ionisation en solution aqueuse. La réaction d'un acide avec l'eau est donnée par l'expression générale :
\[\ce{HA}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{A-}(aq) \nonumber \]
L'eau est la base qui réagit avec l'acide\(\ce{HA}\),\(\ce{A^{−}}\) est la base conjuguée de l'acide\(\ce{HA}\) et l'ion hydronium est l'acide conjugué de l'eau. Un acide fort produit 100 % (ou presque) de\(\ce{H3O+}\) et\(\ce{A^{−}}\) lorsque l'acide s'ionise dans l'eau ; la figure\(\PageIndex{1}\) répertorie plusieurs acides forts. Un acide faible donne de petites quantités\(\ce{H3O+}\) de sable\(\ce{A^{−}}\).
| Six acides forts | Six bases solides | ||
|---|---|---|---|
| \(\ce{HClO4}\) | acide perchlorique | \(\ce{LiOH}\) | hydroxyde de lithium |
| \(\ce{HCl}\) | acide chlorhydrique | \(\ce{NaOH}\) | hydroxyde de sodium |
| \(\ce{HBr}\) | acide bromhydrique | \(\ce{KOH}\) | hydroxyde de potassium |
| \(\ce{HI}\) | acide iodhydrique | \(\ce{Ca(OH)2}\) | hydroxyde de calcium |
| \(\ce{HNO3}\) | acide nitrique | \(\ce{Sr(OH)2}\) | hydroxyde de strontium |
| \(\ce{H2SO4}\) | acide sulfurique | \(\ce{Ba(OH)2}\) | hydroxyde de barium |
Les forces relatives des acides peuvent être déterminées en mesurant leurs constantes d'équilibre dans des solutions aqueuses. Dans des solutions de même concentration, les acides plus forts s'ionisent dans une plus grande mesure et produisent donc des concentrations d'ions hydronium plus élevées que les acides plus faibles. La constante d'équilibre d'un acide est appelée constante d'ionisation acide, K a. Pour la réaction d'un acide\(\ce{HA}\) :
\[\ce{HA}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{A-}(aq) \nonumber \]
nous écrivons l'équation de la constante d'ionisation comme suit :
\[K_\ce{a}=\ce{\dfrac{[H3O+][A- ]}{[HA]}} \nonumber \]
où les concentrations sont celles à l'équilibre. Comme indiqué dans la section sur les constantes d'équilibre, bien que l'eau soit un réactif dans la réaction, elle est également le solvant. Son activité a donc une valeur de 1, ce qui ne change pas la valeur de\(K_a\).
C'est une erreur courante de prétendre que la concentration molaire du solvant est d'une manière ou d'une autre impliquée dans la loi d'équilibre. Cette erreur est le résultat d'une mauvaise compréhension de la thermodynamique des solutions. Par exemple, on prétend souvent que K a = K eq [H 2 O] pour les solutions aqueuses. Cette équation est incorrecte car il s'agit d'une interprétation erronée de l'équation correcte K a = K eq (\(\textit{a}_{H_2O}\)). Parce que\(\textit{a}_{H_2O}\) = 1 pour une solution diluée, K a = K eq (1), ou K a = K eq.
Plus la valeur\(K_a\) d'un acide est grande, plus la concentration de\(\ce{H3O+}\) et\(\ce{A^{−}}\) par rapport à la concentration de l'acide non ionisé est importante,\(\ce{HA}\). Ainsi, un acide plus fort a une constante d'ionisation plus grande qu'un acide plus faible. Les constantes d'ionisation augmentent à mesure que la force des acides augmente.
Les données suivantes sur les constantes d'ionisation des acides indiquent l'ordre de résistance de l'acide :\(\ce{CH3CO2H} < \ce{HNO2} < \ce{HSO4-}\)
\[ \begin{aligned} \ce{CH3CO2H}(aq) + \ce{H2O}(l) &⇌\ce{H3O+}(aq)+\ce{CH3CO2-}(aq) \quad &K_\ce{a}=1.8×10^{−5} \\[4pt] \ce{HNO2}(aq)+\ce{H2O}(l) &⇌\ce{H3O+}(aq)+\ce{NO2-}(aq) &K_\ce{a}=4.6×10^{-4} \\[4pt] \ce{HSO4-}(aq)+\ce{H2O}(l) &⇌\ce{H3O+}(aq)+\ce{SO4^2-}(aq) & K_\ce{a}=1.2×10^{−2} \end{aligned} \nonumber \]
Une autre mesure de la force d'un acide est son pourcentage d'ionisation. Le pourcentage d'ionisation d'un acide faible est le rapport entre la concentration de l'acide ionisé et la concentration initiale en acide, multiplié par 100 :
\[\% \:\ce{ionization}=\ce{\dfrac{[H3O+]_{eq}}{[HA]_0}}×100\% \label{PercentIon} \]
Comme le rapport inclut la concentration initiale, le pourcentage d'ionisation d'une solution d'un acide faible donné varie en fonction de la concentration initiale de l'acide et diminue en fait avec l'augmentation de la concentration d'acide.
Calculer le pourcentage d'ionisation d'une solution d'acide nitreux (un acide faible) à 0,125- M, avec un pH de 2,09.
Solution
Le pourcentage d'ionisation d'un acide est de :
\[\ce{\dfrac{[H3O+]_{eq}}{[HNO2]_0}}×100 \nonumber \]
L'équation chimique pour la dissociation de l'acide nitreux est la suivante :
\[\ce{HNO2}(aq)+\ce{H2O}(l)⇌\ce{NO2-}(aq)+\ce{H3O+}(aq). \nonumber \]
Depuis\(10^{−pH} = \ce{[H3O+]}\), nous trouvons que\(10^{−2.09} = 8.1 \times 10^{−3}\, M\), de sorte que le pourcentage d'ionisation (équation \ ref {percEntion}) est :
\[\dfrac{8.1×10^{−3}}{0.125}×100=6.5\% \nonumber \]
N'oubliez pas que le logarithme 2,09 indique une concentration en ions hydronium avec seulement deux chiffres significatifs.
Calculer le pourcentage d'ionisation d'une solution d'acide acétique à 0,10 M avec un pH de 2,89.
- Réponse
-
1,3 % ionisé
Nous pouvons classer les forces des bases en fonction de leur tendance à former des ions hydroxyde en solution aqueuse. La réaction d'une base de Brønsted-Lowry avec l'eau est donnée par :
\[\ce{B}(aq)+\ce{H2O}(l)⇌\ce{HB+}(aq)+\ce{OH-}(aq) \nonumber \]
L'eau est l'acide qui réagit avec la base,\(\ce{HB^{+}}\) est l'acide conjugué de la base\(\ce{B}\) et l'ion hydroxyde est la base conjuguée de l'eau. Une base forte produit 100 % (ou presque) de OH − et de HB+ lorsqu'elle réagit avec l'eau ; la figure\(\PageIndex{1}\) répertorie plusieurs bases fortes. Une base faible produit une faible proportion d'ions hydroxyde. Les hydroxydes ioniques solubles tels que le NaOH sont considérés comme des bases fortes car ils se dissocient complètement lorsqu'ils sont dissous dans l'eau.
Comme nous l'avons fait pour les acides, nous pouvons mesurer les forces relatives des bases en mesurant leur constante d'ionisation des bases (K b) dans des solutions aqueuses. Dans des solutions de même concentration, les bases plus fortes s'ionisent dans une plus grande mesure et produisent donc des concentrations d'ions hydroxyde plus élevées que les bases plus faibles. Une base plus forte a une constante d'ionisation plus grande qu'une base plus faible. Pour la réaction d'une base,\(\ce{B}\)
\[\ce{B}(aq)+\ce{H2O}(l)⇌\ce{HB+}(aq)+\ce{OH-}(aq), \nonumber \]
nous écrivons l'équation de la constante d'ionisation comme suit :
\[K_\ce{b}=\ce{\dfrac{[HB+][OH- ]}{[B]}} \nonumber \]
où les concentrations sont celles à l'équilibre. Encore une fois, nous ne voyons pas l'eau dans l'équation car l'eau est le solvant et a une activité de 1. Les réactions chimiques et les constantes d'ionisation des trois bases présentées sont les suivantes :
\[ \begin{aligned} \ce{NO2-}(aq)+\ce{H2O}(l) &⇌\ce{HNO2}(aq)+\ce{OH-}(aq) \quad &K_\ce{b}=2.17×10^{−11} \\[4pt] \ce{CH3CO2-}(aq)+\ce{H2O}(l) &⇌\ce{CH3CO2H}(aq)+\ce{OH-}(aq) &K_\ce{b}=5.6×10^{−10} \\[4pt] \ce{NH3}(aq)+\ce{H2O}(l) &⇌\ce{NH4+}(aq)+\ce{OH-}(aq) &K_\ce{b}=1.8×10^{−5} \end{aligned} \nonumber \]
Un tableau des constantes d'ionisation des bases faibles figure dans le tableau E2. Comme pour les acides, le pourcentage d'ionisation peut être mesuré pour les solutions basiques, mais il varie en fonction de la constante d'ionisation des bases et de la concentration initiale de la solution.
Considérez les réactions d'ionisation pour une paire acide-base conjuguée\(\ce{HA − A^{−}}\) :
\[\ce{HA}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{A-}(aq) \nonumber \]
avec\(K_\ce{a}=\ce{\dfrac{[H3O+][A- ]}{[HA]}}\).
\[\ce{A-}(aq)+\ce{H2O}(l)⇌\ce{OH-}(aq)+\ce{HA}(aq) \nonumber \]
avec\(K_\ce{b}=\ce{\dfrac{[HA][OH]}{[A- ]}}\).
L'addition de ces deux équations chimiques donne l'équation de l'auto-ionisation de l'eau :
\[\begin{align*} \cancel{\ce{HA}(aq)}+\ce{H2O}(l)+\cancel{\ce{A-}(aq)}+\ce{H2O}(l) &⇌ \ce{H3O+}(aq)+\cancel{\ce{A-}(aq)}+\ce{OH-}(aq)+\cancel{\ce{HA}(aq)} \\[4pt] \ce{2H2O}(l) &⇌\ce{H3O+}(aq)+\ce{OH-}(aq) \end{align*} \nonumber \]
Comme indiqué dans le chapitre précédent sur l'équilibre, l'\(K\)expression d'une équation chimique dérivée de l'addition de deux autres équations ou plus est le produit mathématique des\(K\) expressions des autres équations. En multipliant les expressions d'action de masse et en annulant les termes courants, nous constatons que :
\[K_\ce{a}×K_\ce{b}=\ce{\dfrac{[H3O+][A- ]}{[HA]}×\dfrac{[HA][OH- ]}{[A- ]}}=\ce{[H3O+][OH- ]}=K_\ce{w} \nonumber \]
Par exemple, la constante d'ionisation acide de l'acide acétique (CH 3 COOH) est de 1,8 × 10 −5, et la constante d'ionisation de base de sa base conjuguée, l'ion acétate (\(\ce{CH3COO-}\)), est de 5,6 × 10 −10 −10. Le produit de ces deux constantes est en effet égal à\(K_w\) :
\[K_\ce{a}×K_\ce{b}=(1.8×10^{−5})×(5.6×10^{−10})=1.0×10^{−14}=K_\ce{w} \nonumber \]
La mesure dans laquelle un acide\(\ce{HA}\) donne des protons aux molécules d'eau dépend de la force de la base conjuguée de l'acide.\(\ce{A^{−}}\) \(\ce{A^{−}}\)Il s'agit d'une base solide, tous les protons donnés aux molécules d'eau sont recapturés par\(\ce{A^{−}}\). Il y en a donc relativement peu\(\ce{A^{−}}\) et\(\ce{H3O+}\) en solution\(\ce{HA}\), et l'acide est faible. C'\(\ce{A^{−}}\)est une base faible, l'eau lie plus fortement les protons et la solution contient principalement\(\ce{A^{−}}\) et\(\ce{H3O^{+}}\) —l'acide est fort. Les acides forts forment des bases conjuguées très faibles et les acides faibles forment des bases conjuguées plus fortes (Figure\(\PageIndex{2}\)).
 « style="largeur : 784 px ; hauteur : 271 px ; » width="784 px » height="271 px » src= »/@api /deki/files/65684/CNX_Chem_14_03_strengths.jpg « >
« style="largeur : 784 px ; hauteur : 271 px ; » width="784 px » height="271 px » src= »/@api /deki/files/65684/CNX_Chem_14_03_strengths.jpg « >
La\(\PageIndex{3}\) figure présente une série d'acides et de bases dans l'ordre des forces décroissantes des acides et des forces croissantes correspondantes des bases. L'acide et la base d'une rangée donnée sont conjugués l'un à l'autre.
Les six premiers acides de la figure\(\PageIndex{3}\) sont les acides forts les plus courants. Ces acides sont complètement dissociés en solution aqueuse. Les bases conjuguées de ces acides sont des bases plus faibles que celles de l'eau. Lorsque l'un de ces acides se dissout dans l'eau, ses protons sont complètement transférés dans l'eau, la base la plus résistante.
Les acides qui se trouvent entre l'ion hydronium et l'eau sur la figure\(\PageIndex{3}\) forment des bases conjuguées qui peuvent entrer en compétition avec l'eau pour la possession d'un proton. Les ions hydronium et les molécules d'acide non ionisé sont présents en équilibre dans une solution de l'un de ces acides. Les composés qui sont des acides plus faibles que l'eau (ceux qui se trouvent sous l'eau dans la colonne d'acides) de la figure ne\(\PageIndex{3}\) présentent aucun comportement acide observable lorsqu'ils sont dissous dans l'eau. Leurs bases conjuguées sont plus fortes que l'ion hydroxyde, et si une base conjuguée se formait, elle réagirait avec l'eau pour reformer l'acide.
 « style="largeur : 798 px ; hauteur : 715 px ; » width="798 px » height="715px » src= »/@api /deki/files/65685/CNX_Chem_14_03_Corresp.jpg « >
« style="largeur : 798 px ; hauteur : 715 px ; » width="798 px » height="715px » src= »/@api /deki/files/65685/CNX_Chem_14_03_Corresp.jpg « >
La mesure dans laquelle une base forme des ions hydroxyde en solution aqueuse dépend de la force de la base par rapport à celle de l'ion hydroxyde, comme indiqué dans la dernière colonne de la figure\(\PageIndex{3}\). Une base forte, telle que l'une de celles situées sous l'ion hydroxyde, accepte les protons de l'eau pour produire 100 % de l'acide conjugué et de l'ion hydroxyde. Les bases situées entre l'eau et l'ion hydroxyde acceptent les protons de l'eau, mais il en résulte un mélange de l'ion hydroxyde et de la base. Les bases plus faibles que l'eau (celles qui se trouvent au-dessus de l'eau dans la colonne de bases) ne présentent aucun comportement basique observable en solution aqueuse.
Utilisez le\(K_b\) pour l'ion nitrite\(\ce{NO2-}\),,\(K_a\) pour calculer l'acide conjugué.
Solution
K b pour\(\ce{NO2-}\) est donné dans cette section sous la forme 2,17 × 10 −11. L'acide conjugué de\(\ce{NO2-}\) est le HNO 2 ; K a pour le HNO 2 peut être calculé en utilisant la relation :
\[K_\ce{a}×K_\ce{b}=1.0×10^{−14}=K_\ce{w} \nonumber \]
En résolvant K a, on obtient :
\[\begin{align*} K_\ce{a} &=\dfrac{K_\ce{w}}{K_\ce{b}} \\[4pt] &=\dfrac{1.0×10^{−14}}{2.17×10^{−11}} \\[4pt] &=4.6×10^{−4} \end{align*} \nonumber \]
Cette réponse peut être vérifiée en trouvant le K a pour le HNO 2 dans le tableau E1.
Nous pouvons déterminer les forces acides relatives de\(\ce{NH4+}\) et\(\ce{HCN}\) en comparant leurs constantes d'ionisation. La constante d'ionisation de\(\ce{HCN}\) est donnée dans le tableau E1 sous la forme 4,9 × 10 −10. La constante d'ionisation de n'\(\ce{NH4+}\)est pas répertoriée, mais la constante d'ionisation de sa base conjuguée\(\ce{NH3}\),, est répertoriée comme 1,8 × 10 −5. Déterminez la constante d'ionisation de\(\ce{NH4+}\), et décidez quel est l'acide le plus fort,\(\ce{HCN}\) ou\(\ce{NH4+}\).
- Réponse
-
\(\ce{NH4+}\)est l'acide légèrement plus fort (K a pour\(\ce{NH4+}\) = 5,6 × 10 −10).
L'ionisation des acides faibles et des bases faibles
De nombreux acides et bases sont faibles, c'est-à-dire qu'ils ne s'ionisent pas complètement en solution aqueuse. Une solution d'un acide faible dans l'eau est un mélange d'acide non ionisé, d'ion hydronium et de la base conjuguée de l'acide, l'acide non ionisé étant présent à la plus forte concentration. Ainsi, un acide faible augmente la concentration en ions hydronium dans une solution aqueuse (mais pas autant que la même quantité d'un acide fort).
L'acide acétique (\(\ce{CH3CO2H}\)) est un acide faible. Lorsque nous ajoutons de l'acide acétique à l'eau, il s'ionise légèrement selon l'équation :
\[\ce{CH3CO2H}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{CH3CO2-}(aq) \nonumber \]
donnant un mélange d'équilibre avec la majeure partie de l'acide présent sous forme non ionisée (moléculaire). Cet équilibre, comme les autres équilibres, est dynamique ; les molécules d'acide acétique donnent des ions hydrogène aux molécules d'eau et forment des ions hydronium et des ions acétate au même rythme que les ions hydronium transmettent des ions hydrogène aux ions acétate pour reformer les molécules d'acide acétique et les molécules d'eau. En mesurant le pH d'une solution aqueuse de concentration connue, nous pouvons déterminer que seule une fraction de l'acide faible est ionisée à tout moment (Figure\(\PageIndex{4}\)). L'acide faible restant est présent sous forme non ionisée.
Pour l'acide acétique, à l'équilibre :
\[K_\ce{a}=\ce{\dfrac{[H3O+][CH3CO2- ]}{[CH3CO2H]}}=1.8 \times 10^{−5} \nonumber \]

| Réaction d'ionisation | K a à 25 °C |
|---|---|
| \(\ce{HSO4- + H2O ⇌ H3O+ + SO4^2-}\) | 1,2 × 10 −2 |
| \(\ce{HF + H2O ⇌ H3O+ + F-}\) | 3,5 × 10 −4 |
| \(\ce{HNO2 + H2O ⇌ H3O+ + NO2-}\) | 4,6 × 10 −4 |
| \(\ce{HNCO + H2O ⇌ H3O+ + NCO-}\) | 2 × 10 −4 |
| \(\ce{HCO2H + H2O ⇌ H3O+ + HCO2-}\) | 1,8 × 10 −4 |
| \(\ce{CH3CO2H + H2O ⇌ H3O+ + CH3CO2-}\) | 1,8 × 10 −5 |
| \(\ce{HCIO + H2O ⇌ H3O+ + CIO-}\) | 2,9 × 10 −8 |
| \(\ce{HBrO + H2O ⇌ H3O+ + BrO-}\) | 2,8 × 10 −9 |
| \(\ce{HCN + H2O ⇌ H3O+ + CN-}\) | 4,9 × 10 −10 |
Le tableau\(\PageIndex{1}\) donne les constantes d'ionisation de plusieurs acides faibles ; des constantes d'ionisation supplémentaires peuvent être trouvées dans le tableau E1.
À l'équilibre, une solution d'une base faible dans l'eau est un mélange de la base non ionisée, de l'acide conjugué de la base faible et de l'ion hydroxyde, la base non ionisée étant présente à la plus forte concentration. Ainsi, une base faible augmente la concentration en ions hydroxyde dans une solution aqueuse (mais pas autant que la même quantité d'une base forte).
Par exemple, une solution de triméthylamine, une base faible, (CH 3) 3 N, dans de l'eau réagit selon l'équation suivante :
\[\ce{(CH3)3N}(aq)+\ce{H2O}(l)⇌\ce{(CH3)3NH+}(aq)+\ce{OH-}(aq) \nonumber \]
On obtient ainsi un mélange d'équilibre avec la majeure partie de la base présente sous forme d'amine non ionisée. Cet équilibre est analogue à celui décrit pour les acides faibles.
Nous pouvons confirmer en mesurant le pH d'une solution aqueuse d'une base faible de concentration connue que seule une fraction de la base réagit avec l'eau (Figure 14.4.5). La base faible restante est présente sous la forme n'ayant pas réagi. La constante d'équilibre pour l'ionisation d'une base faible est appelée constante d'ionisation de la base faible et est égale au quotient de réaction lorsque la réaction est à l'équilibre.\(K_b\) Pour la triméthylamine, à l'équilibre :
\[K_\ce{b}=\ce{\dfrac{[(CH3)3NH+][OH- ]}{[(CH3)3N]}} \nonumber \]
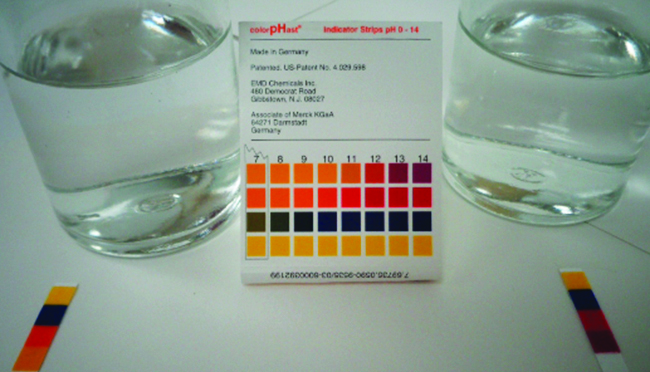
Les constantes d'ionisation de plusieurs bases faibles sont données dans le Tableau 1\(\PageIndex{2}\) et le Tableau E2.
| Réaction d'ionisation | K b à 25 °C |
|---|---|
| \(\ce{(CH3)2NH + H2O ⇌ (CH3)2NH2+ + OH-}\) | 5,9 × 10 −4 |
| \(\ce{CH3NH2 + H2O ⇌ CH3NH3+ + OH-}\) | 4,4 × 10 −4 |
| \(\ce{(CH3)3N + H2O ⇌ (CH3)3NH+ + OH-}\) | 6,3 × 10 −5 |
| \(\ce{NH3 + H2O ⇌ NH4+ + OH-}\) | 1,8 × 10 −5 |
| \(\ce{C6H5NH2 + H2O ⇌ C6N5NH3+ + OH-}\) | 4,3 × 10 −10 |
L'acide acétique est l'ingrédient principal du vinaigre ; c'est pourquoi il a un goût acidulé. À l'équilibre, une solution contient [CH 3 CO 2 H] = 0,0787 M et\(\ce{[H3O+]}=\ce{[CH3CO2- ]}=0.00118\:M\). Quelle est la valeur de\(K_a\) l'acide acétique ?

Solution
On nous demande de calculer une constante d'équilibre à partir des concentrations d'équilibre. À l'équilibre, la valeur de la constante d'équilibre est égale au quotient de réaction pour la réaction :
\[\ce{CH3CO2H}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{CH3CO2-}(aq) \nonumber \]
\[\begin{align*} K_\ce{a} &=\ce{\dfrac{[H3O+][CH3CO2- ]}{[CH3CO2H]}} \\[4pt] &=\dfrac{(0.00118)(0.00118)}{0.0787} \\[4pt] &=1.77×10^{−5} \end{align*} \nonumber \]
Quelle est la constante d'équilibre pour l'ionisation de l'\(\ce{HSO4-}\)ion, l'acide faible utilisé dans certains nettoyants ménagers :
\[\ce{HSO4-}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{SO4^2-}(aq) \nonumber \]
Dans un mélange de NaHSO 4 et de Na 2 SO 4 à l'équilibre,\(\ce{[H3O+]}\) = 0,027 M ;\(\ce{[HSO4- ]}=0.29\:M\) ; et\(\ce{[SO4^2- ]}=0.13\:M\).
- Réponse
-
\(K_a\)pour\(\ce{HSO_4^-}= 1.2 ×\times 10^{−2}\)
La caféine, C 8 H 10 N 4 O 2 est une base faible. Quelle est la valeur de K b pour la caféine si une solution à l'équilibre a [C 8 H 10 N 4 O 2] = 0,050 M,\(\ce{[C8H10N4O2H+]}\) = 5,0 × 10 −3 M et [OH −] = 2,5 × 10 −3 M ?
Solution
À l'équilibre, la valeur de la constante d'équilibre est égale au quotient de réaction pour la réaction :
\[\ce{C8H10N4O2}(aq)+\ce{H2O}(l)⇌\ce{C8H10N4O2H+}(aq)+\ce{OH-}(aq) \nonumber \]
donc
\[K_\ce{b}=\ce{\dfrac{[C8H10N4O2H+][OH- ]}{[C8H10N4O2]}}=\dfrac{(5.0×10^{−3})(2.5×10^{−3})}{0.050}=2.5×10^{−4} \nonumber \]
Quelle est la constante d'équilibre pour l'ionisation de l'\(\ce{HPO4^2-}\)ion, une base faible :
\[\ce{HPO4^2-}(aq)+\ce{H2O}(l)⇌\ce{H2PO4-}(aq)+\ce{OH-}(aq) \nonumber \]
Dans une solution contenant un mélange\(\ce{NaH2PO4}\) et\(\ce{Na2HPO4}\) en équilibre avec :
- \([\ce{OH^{−}}] = 1.3 × 10^{−6} M\)
- \(\ce{[H2PO4^{-}]=0.042\:M}\)et
- \(\ce{[HPO4^{2-}]=0.341\:M}\).
- Réponse
-
K b pour\(\ce{HPO4^2-}=1.6×10^{−7} \)
Le pH d'une solution d'acide nitreux à 0,0516- M est de 2,34.\(\ce{HNO2}\) Qu'est-ce que c'est\(K_a\) ?
\[\ce{HNO2}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{NO2-}(aq) \nonumber \]
Solution
Nous déterminons une constante d'équilibre en commençant par les concentrations initiales de HNO 2 et\(\ce{H3O+}\),\(\ce{NO2-}\) en plus de l'une des concentrations finales, la concentration en ions hydronium à l'équilibre. (N'oubliez pas que le pH est simplement une autre façon d'exprimer la concentration en ions hydronium.)
Nous pouvons résoudre ce problème en suivant les étapes suivantes dans lesquelles x est un changement de concentration d'une espèce dans la réaction :
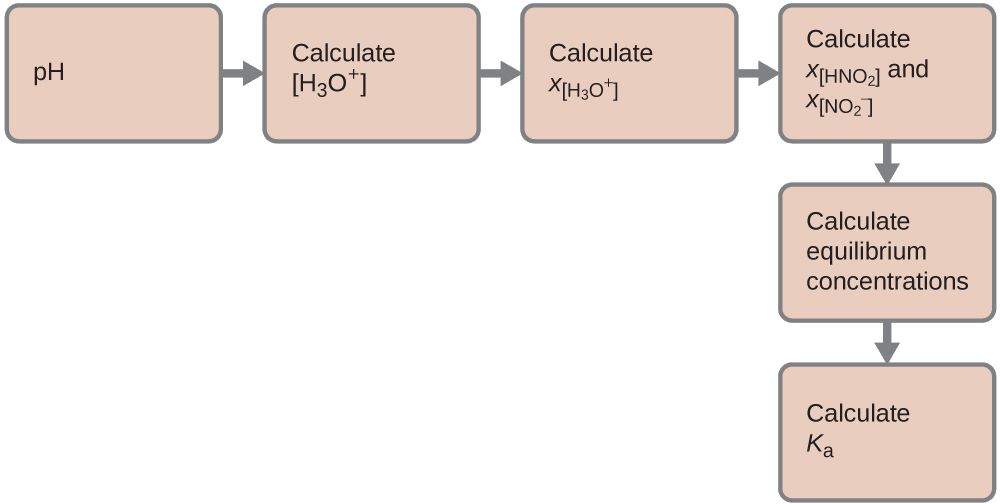
Nous pouvons résumer les différentes concentrations et variations comme indiqué ici. L'eau étant le solvant, elle possède une activité fixe égale à 1. Toute petite quantité d'eau produite ou utilisée pendant la réaction ne modifiera pas le rôle de l'eau en tant que solvant, de sorte que la valeur de son activité reste égale à 1 tout au long de la réaction.
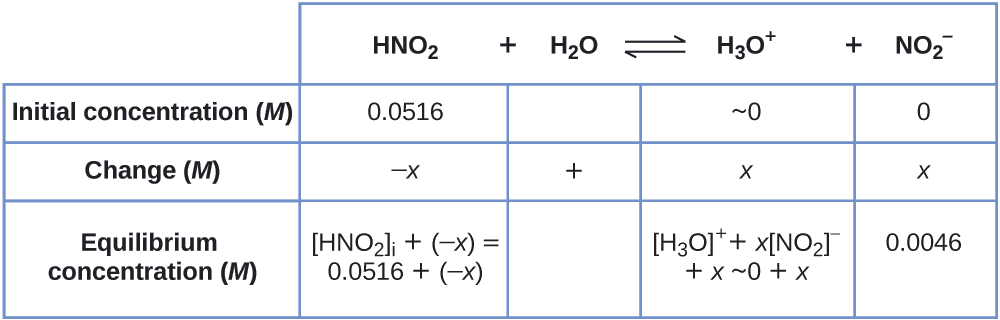
Pour obtenir les différentes valeurs du tableau ICE (Initial, Change, Equilibrium), nous\(\ce{[H3O+]}\) calculons d'abord la concentration d'équilibre de\(\ce{H3O+}\), à partir du pH :
\[\ce{[H3O+]}=10^{−2.34}=0.0046\:M \nonumber \]
Le changement de concentration de\(\ce{H3O+}\)\(x_{\ce{[H3O+]}}\), est la différence entre la concentration d'équilibre de H 3 O +, que nous avons déterminée à partir du pH, et la concentration initiale,\(\mathrm{[H_3O^+]_i}\). La concentration initiale de\(\ce{H3O+}\) est sa concentration dans l'eau pure, qui est tellement inférieure à la concentration finale que nous l'approchons de zéro (~0).
La variation de la concentration de\(\ce{NO2-}\) est égale à la variation de la concentration de\(\ce{[H3O+]}\). Pour chaque mole de\(\ce{H3O+}\) ces formes, 1 mol de\(\ce{NO2-}\) formes. La concentration d'équilibre du HNO 2 est égale à sa concentration initiale augmentée de la variation de sa concentration.
Nous pouvons maintenant remplir le tableau ICE avec les concentrations à l'équilibre, comme indiqué ici :
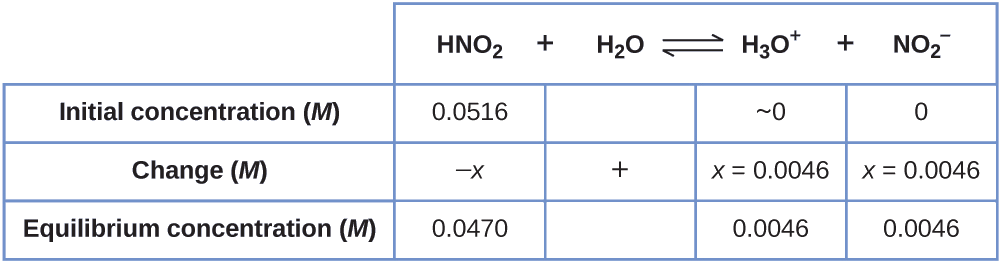
Enfin, nous calculons la valeur de la constante d'équilibre à l'aide des données du tableau :
\[K_\ce{a}=\ce{\dfrac{[H3O+][NO2- ]}{[HNO2]}}=\dfrac{(0.0046)(0.0046)}{(0.0470)}=4.5×10^{−4} \nonumber \]
Le pH d'une solution d'ammoniac domestique, une solution de NH 3 à 0,950- M, est de 11,612. Qu'est-ce que K b pour NH 3.
- Réponse
-
\(K_b = 1.8 × 10^{−5}\)
L'acide formique, HCO 2 H, est l'irritant qui provoque la réaction de l'organisme aux piqûres de fourmis.

Quelle est la concentration d'ion hydronium et le pH dans une solution d'acide formique à 0,534- M ?
\[\ce{HCO2H}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{HCO2-}(aq) \hspace{20px} K_\ce{a}=1.8×10^{−4} \nonumber \]
Soluti sur
1. Déterminez les concentrations x et d'équilibre. L'expression d'équilibre est la suivante :
\[\ce{HCO2H}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{HCO2-}(aq) \nonumber \]
L'eau étant le solvant, elle possède une activité fixe égale à 1. Toute petite quantité d'eau produite ou utilisée pendant la réaction ne modifiera pas le rôle de l'eau en tant que solvant, de sorte que la valeur de son activité reste égale à 1 tout au long de la réaction, de sorte que nous n'avons pas besoin d'en tenir compte lors de l'établissement de la table ICE.
Le tableau indique les concentrations initiales (concentrations avant l'ionisation de l'acide), les variations de concentration et les concentrations d'équilibre suivantes (les données données dans le problème apparaissent en couleur) :
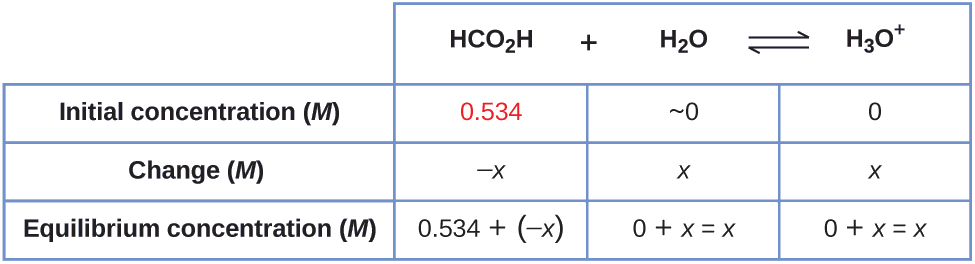
2. Résolvez\(x\) et déterminez les concentrations d'équilibre. À l'équilibre :
\[\begin{align*} K_\ce{a} &=1.8×10^{−4}=\ce{\dfrac{[H3O+][HCO2- ]}{[HCO2H]}} \\[4pt] &=\dfrac{(x)(x)}{0.534−x}=1.8×10^{−4} \end{align*} \nonumber \]
Maintenant, résolvez pour\(x\). Comme la concentration initiale d'acide est raisonnablement élevée et\(K_a\) très faible, nous supposons que cela\(x << 0.534\), ce qui nous permet de simplifier le terme dénominateur en tant que\((0.534 − x) = 0.534\). Cela donne :
\[K_\ce{a}=1.8×10^{−4}=\dfrac{x^{2}}{0.534} \nonumber \]
Résolvez\(x\) comme suit :
\[\begin{align*} x^2 &=0.534×(1.8×10^{−4}) \\[4pt] &=9.6×10^{−5} \\[4pt] x &=\sqrt{9.6×10^{−5}} \\[4pt] &=9.8×10^{−3} \end{align*} \nonumber \]
Pour vérifier l'hypothèse qui\(x\) est faible par rapport à 0,534, nous calculons :
\[\begin{align*} \dfrac{x}{0.534} &=\dfrac{9.8×10^{−3}}{0.534} \\[4pt] &=1.8×10^{−2} \, \textrm{(1.8% of 0.534)} \end{align*} \nonumber \]
\(x\)est inférieur à 5 % de la concentration initiale ; l'hypothèse est valable.
Nous trouvons la concentration d'équilibre en ion hydronium dans cette solution d'acide formique à partir de sa concentration initiale et de la variation de cette concentration, comme indiqué à la dernière ligne du tableau :
\[\begin{align*} \ce{[H3O+]} &=~0+x=0+9.8×10^{−3}\:M. \\[4pt] &=9.8×10^{−3}\:M \end{align*} \nonumber \]
Le pH de la solution peut être déterminé en prenant le logarithme négatif du\(\ce{[H3O+]}\), donc :
\[pH = −\log(9.8×10^{−3})=2.01 \nonumber \]
Seule une petite fraction d'un acide faible s'ionise en solution aqueuse. Quel est le pourcentage d'ionisation de l'acide acétique dans une solution à 0,100 M d'acide acétique, CH 3 CO 2 H ?
\[\ce{CH3CO2H}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{CH3CO2-}(aq) \hspace{20px} K_\ce{a}=1.8×10^{−5} \nonumber \]
- Allusion
-
Déterminez\(\ce{[CH3CO2- ]}\) à l'équilibre.) Rappelons que le pourcentage d'ionisation est la fraction d'acide acétique ionisée × 100, ou\(\ce{\dfrac{[CH3CO2- ]}{[CH3CO2H]_{initial}}}×100\).
- Réponse
-
pourcentage d'ionisation = 1,3 %
L'exemple suivant montre que la concentration des produits produits par ionisation d'une base faible peut être déterminée par la même série d'étapes que celle utilisée avec un acide faible.
Déterminez la concentration d'ion hydroxyde dans une solution à 0,25 M de triméthylamine, une base faible :
\[\ce{(CH3)3N}(aq)+\ce{H2O}(l)⇌\ce{(CH3)3NH+}(aq)+\ce{OH-}(aq) \hspace{20px} K_\ce{b}=6.3×10^{−5} \nonumber \]
Solution Ce problème nécessite de calculer une concentration d'équilibre en déterminant les changements de concentration lorsque l'ionisation d'une base atteint l'équilibre. La solution est abordée de la même manière que celle de l'exemple pour l'ionisation de l'acide formique\(\PageIndex{6}\). Les réactifs et les produits seront différents et les nombres seront différents, mais la logique sera la même :

1. Déterminez les concentrations x et d'équilibre. Le tableau montre les variations et les concentrations :
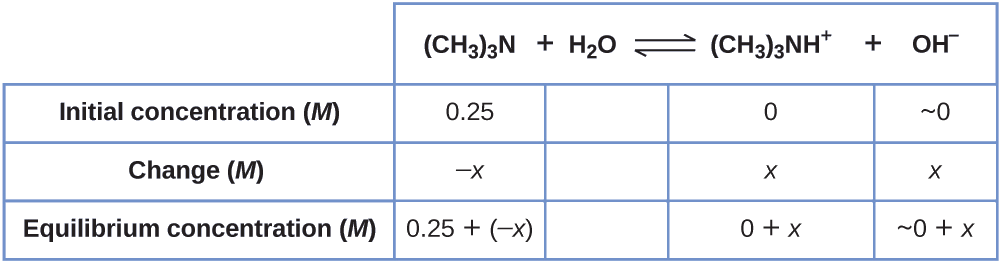
2. Résolvez\(x\) et déterminez les concentrations d'équilibre. À l'équilibre :
\[K_\ce{b}=\ce{\dfrac{[(CH3)3NH+][OH- ]}{[(CH3)3N]}}=\dfrac{(x)(x)}{0.25−x=}6.3×10^{−5} \nonumber \]
Si nous supposons que x est petit par rapport à 0,25, alors nous pouvons remplacer (0,25 − x) dans l'équation précédente par 0,25. La résolution de l'équation simplifiée donne :
\[x=4.0×10^{−3} \nonumber \]
Ce changement est inférieur à 5 % de la concentration initiale (0,25), de sorte que l'hypothèse est justifiée.
Rappelons que, pour ce calcul,\(x\) est égal à la concentration d'équilibre en ion hydroxyde dans la solution (voir tabulation précédente) :
\[\begin{align*} (\ce{[OH- ]}=~0+x=x=4.0×10^{−3}\:M \\[4pt] &=4.0×10^{−3}\:M \end{align*} \nonumber \]
Calculez ensuite le PoH comme suit :
\[\ce{pOH}=−\log(4.3×10^{−3})=2.40 \nonumber \]
En utilisant la relation présentée dans la section précédente de ce chapitre :
\[\mathrm{pH + pOH=p\mathit{K}_w=14.00}\nonumber \]
permet de calculer le pH :
\[\mathrm{pH=14.00−pOH=14.00−2.37=11.60} \nonumber \]
Vérifiez le travail. Une vérification de notre arithmétique le montre\(K_b = 6.3 \times 10^{−5}\).
- Montrez que le calcul de l'étape 2 de cet exemple donne un x de 4,3 × 10 −3 et que le calcul de l'étape 3 indique que K b = 6,3 × 10 −5.
- Détermine la concentration d'ion hydroxyde dans une solution d'ammoniac à 0,0325- M, une base faible avec un K b de 1,76 × 10 −5. Calculez le pourcentage d'ionisation de l'ammoniac, la fraction ionisée × 100, ou\(\ce{\dfrac{[NH4+]}{[NH3]}}×100 \%\)
- Répondez à
-
\(7.56 × 10^{−4}\, M\), 2,33 %
- Réponse b
-
2,33 %
Certains acides et bases faibles s'ionisent à un point tel que l'hypothèse simplificatrice selon laquelle x est faible par rapport à la concentration initiale de l'acide ou de la base n'est pas appropriée. Lorsque nous déterminerons les concentrations d'équilibre dans de tels cas, nous verrons que nous ne pouvons pas négliger le changement de la concentration initiale de l'acide ou de la base et que nous devons résoudre les équations d'équilibre en utilisant l'équation quadratique.
Le bisulfate de sodium, NaHSO 4, est utilisé dans certains nettoyants ménagers car il contient de l'\(\ce{HSO4-}\)ion, un acide faible. Quel est le pH d'une solution à 0,50 M de\(\ce{HSO4-}\) ?
\[\ce{HSO4-}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{SO4^2-}(aq) \hspace{20px} K_\ce{a}=1.2×10^{−2} \nonumber \]
Soluti sur
Nous devons déterminer la concentration d'équilibre de l'ion hydronium résultant de l'ionisation de\(\ce{HSO4-}\) afin de pouvoir l'utiliser\(\ce{[H3O+]}\) pour déterminer le pH. Comme dans les exemples précédents, nous pouvons aborder la solution en suivant les étapes suivantes :

1. Déterminer\(x\) et équilibrer les concentrations. Ce tableau montre les variations et les concentrations :

2. Résolvez pour\(x\) et pour les concentrations.
Au fur et à mesure que nous commencerons à résoudre\(x\), nous constaterons que cela est plus compliqué que dans les exemples précédents. Lorsque nous discutons de ces complications, nous ne devons pas perdre de vue que le but de cette étape est toujours de déterminer la valeur de\(x\).
À l'équilibre :
\[K_\ce{a}=1.2×10^{−2}=\ce{\dfrac{[H3O+][SO4^2- ]}{[HSO4- ]}}=\dfrac{(x)(x)}{0.50−x} \nonumber \]
Si nous supposons que x est petit et approximatif (0,50 − x) égal à 0,50, nous trouvons :
\[x=7.7×10^{−2} \nonumber \]
Lorsque nous vérifions l'hypothèse, nous confirmons :
\[\dfrac{x}{\mathrm{[HSO_4^- ]_i}} \overset{?}{\le} 0.05 \nonumber \]
qui pour ce système est
\[\dfrac{x}{0.50}=\dfrac{7.7×10^{−2}}{0.50}=0.15(15\%) \nonumber \]
La valeur de n'\(x\)est pas inférieure à 5 % de 0,50, donc l'hypothèse n'est pas valide. Nous avons besoin de la formule quadratique pour trouver\(x\).
L'équation :
\[K_\ce{a}=1.2×10^{−2}=\dfrac{(x)(x)}{0.50−x}\nonumber \]
donne
\[6.0×10^{−3}−1.2×10^{−2}x=x^{2+} \nonumber \]
ou
\[x^{2+}+1.2×10^{−2}x−6.0×10^{−3}=0 \nonumber \]
Cette équation peut être résolue à l'aide de la formule quadratique. Pour une équation de la forme
\[ax^{2+} + bx + c=0, \nonumber \]
\(x\)est donné par l'équation quadratique :
\[x=\dfrac{−b±\sqrt{b^{2+}−4ac}}{2a} \nonumber \]
Dans ce problème\(a = 1\),\(b = 1.2 × 10^{−3}\), et\(c = −6.0 × 10^{−3}\).
La résolution de x donne une racine négative (qui ne peut pas être correcte puisque la concentration ne peut pas être négative) et une racine positive :
\[x=7.2×10^{−2} \nonumber \]
Déterminez maintenant la concentration en ions hydronium et le pH :
\[\begin{align*} \ce{[H3O+]} &=~0+x=0+7.2×10^{−2}\:M \\[4pt] &=7.2×10^{−2}\:M \end{align*} \nonumber \]
Le pH de cette solution est de :
\[\mathrm{pH=−log[H_3O^+]=−log7.2×10^{−2}=1.14} \nonumber \]
- Montrez que la formule quadratique donne\(x = 7.2 × 10^{−2}\).
- Calculez le pH dans une solution de caféine à 0,010- M, une base faible :
\[\ce{C8H10N4O2}(aq)+\ce{H2O}(l)⇌\ce{C8H10N4O2H+}(aq)+\ce{OH-}(aq) \hspace{20px} K_\ce{b}=2.5×10^{−4} \nonumber \]
- Allusion
-
Il sera nécessaire de convertir [OH −] en pH\(\ce{[H3O+]}\) ou PoH en pH vers la fin du calcul.
- Réponse
-
pH 11,16
Les forces relatives des acides et des bases forts
Les acides forts, tels que\(\ce{HCl}\)\(\ce{HBr}\), et\(\ce{HI}\), présentent tous la même force dans l'eau. La molécule d'eau est une base tellement forte par rapport aux bases conjuguées Cl −, Br − et I − que l'ionisation de ces acides forts est pratiquement complète dans les solutions aqueuses. Dans les solvants moins basiques que l'eau\(\ce{HCl}\)\(\ce{HBr}\), nous trouvons, et nous\(\ce{HI}\) différons nettement dans leur tendance à céder un proton au solvant. Par exemple, lorsqu'il est dissous dans de l'éthanol (une base plus faible que l'eau), le degré d'ionisation augmente dans l'ordre\(\ce{HCl < HBr < HI}\), et\(\ce{HI}\) il est donc démontré qu'il s'agit du plus fort de ces acides. L'incapacité de discerner les différences de force entre les acides forts dissous dans l'eau est connue sous le nom d'effet nivelant de l'eau.
L'eau exerce également un effet nivelant sur la résistance des bases solides. Par exemple, l'ion oxyde, O 2−, et l'ion amide sont des bases si fortes qu'ils réagissent complètement avec l'eau :\(\ce{NH2-}\)
\[\ce{O^2-}(aq)+\ce{H2O}(l)⟶\ce{OH-}(aq)+\ce{OH-}(aq) \nonumber \]
\[\ce{NH2-}(aq)+\ce{H2O}(l)⟶\ce{NH3}(aq)+\ce{OH-}(aq) \nonumber \]
Ainsi, l'O 2− et\(\ce{NH2-}\) semblent avoir la même résistance basique dans l'eau ; ils donnent tous deux un rendement de 100 % en ions hydroxyde.
En l'absence de tout effet de nivellement, la résistance acide des composés binaires d'hydrogène et de non-métaux (A) augmente à mesure que la force de liaison H-A diminue vers le bas d'un groupe du tableau périodique. Pour le groupe 17, l'ordre d'augmentation de l'acidité est\(\ce{HF < HCl < HBr < HI}\). De même, pour le groupe 16, l'ordre d'augmentation de la résistance acide est H 2 O < H 2 S < H 2 Se < H 2 Te. Sur une ligne du tableau périodique, la force acide des composés binaires d'hydrogène augmente avec l'électronégativité de l'atome non métallique, car la polarité de la liaison H-A augmente. Ainsi, l'ordre d'augmentation de l'acidité (pour l'élimination d'un proton) sur la deuxième rangée est\(\ce{CH4 < NH3 < H2O < HF}\) ; sur la troisième rangée, c'est le\(\ce{SiH4 < PH3 < H2S < HCl}\) cas (voir Figure\(\PageIndex{6}\)).
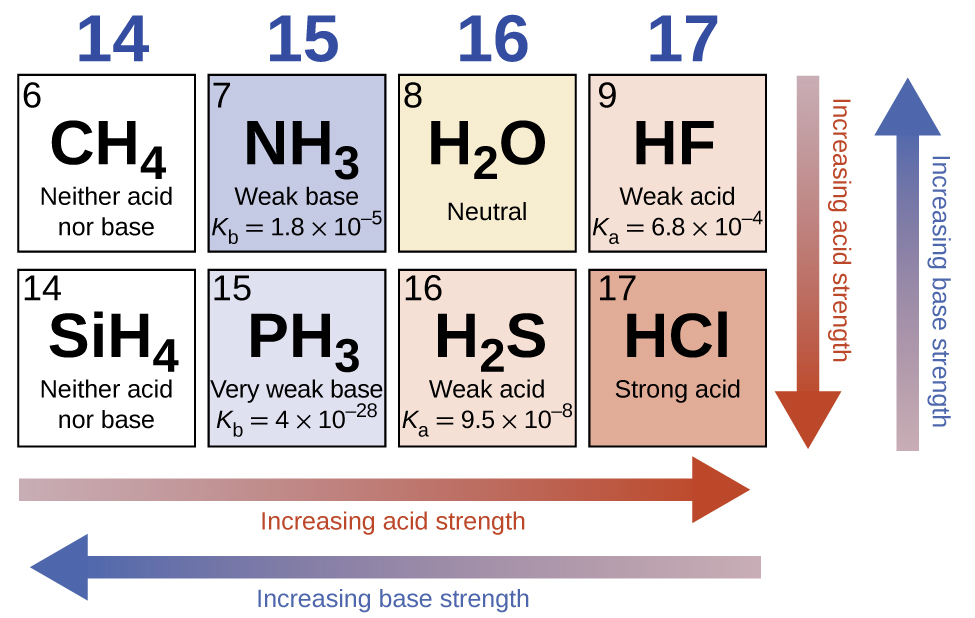
Les composés contenant de l'oxygène et un ou plusieurs groupes hydroxyle (OH) peuvent être acides, basiques ou amphotères, selon la position dans le tableau périodique de l'atome central E, l'atome lié au groupe hydroxyle. Ces composés répondent à la formule générale O n E (OH) m et comprennent l'acide sulfurique\(\ce{O2S(OH)2}\), l'acide sulfureux,\(\ce{OS(OH)2}\) l'acide nitrique, l'acide perchlorique\(\ce{O2NOH}\), l'hydroxyde d'aluminium\(\ce{O3ClOH}\)\(\ce{Al(OH)3}\), l'hydroxyde de calcium et l'hydroxyde de potassium,\(\ce{KOH}\) :\(\ce{Ca(OH)2}\)
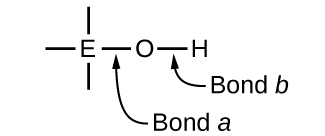
Si l'atome central, E, possède une faible électronégativité, son attraction pour les électrons est faible. L'atome central a peu tendance à former une forte liaison covalente avec l'atome d'oxygène, et la liaison a entre l'élément et l'oxygène est plus facilement rompue que la liaison b entre l'oxygène et l'hydrogène. La liaison a est donc ionique, des ions hydroxyde sont libérés dans la solution et le matériau se comporte comme une base, c'est le cas du Ca (OH) 2 et du KOH. Une électronégativité plus faible est caractéristique des éléments les plus métalliques ; par conséquent, les éléments métalliques forment des hydroxydes ioniques qui sont par définition des composés basiques.
Si, par contre, l'atome E possède une électronégativité relativement élevée, il attire fortement les électrons qu'il partage avec l'atome d'oxygène, faisant de la liaison une liaison relativement fortement covalente. La liaison oxygène-hydrogène, la liaison b, est ainsi affaiblie parce que les électrons se déplacent vers E. La liaison b est polaire et libère facilement des ions hydrogène dans la solution, de sorte que le matériau se comporte comme un acide. Des électronégativités élevées sont caractéristiques des éléments les plus non métalliques. Ainsi, les éléments non métalliques forment des composés covalents contenant des groupes −OH acides appelés oxyacides.
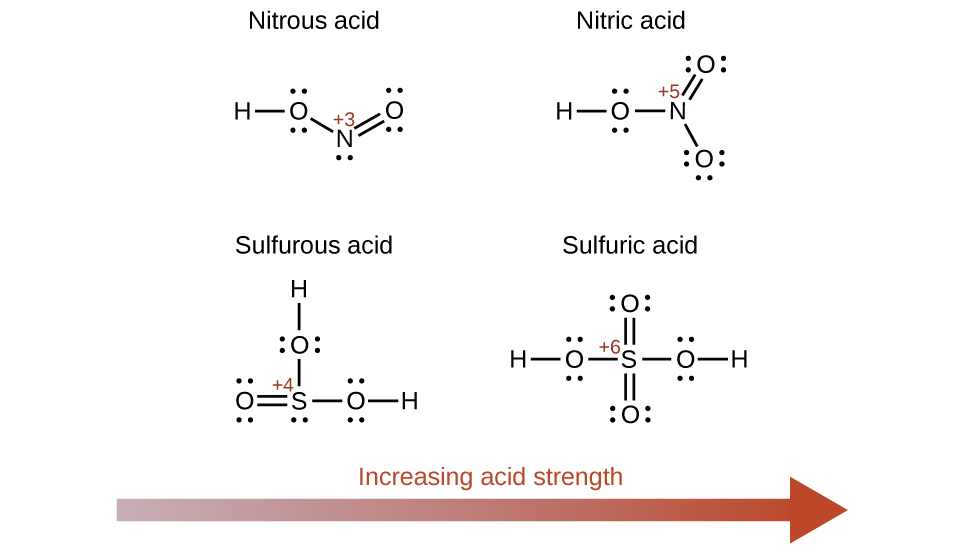
L'augmentation du nombre d'oxydation de l'atome central E augmente également l'acidité d'un oxyacide, car cela augmente l'attraction de E pour les électrons qu'il partage avec l'oxygène et affaiblit ainsi la liaison O-H. L'acide sulfurique, H 2 SO 4 ou O 2 S (OH) 2 (avec un indice d'oxydation du soufre de +6), est plus acide que l'acide sulfureux, H 2 SO 3 ou OS (OH) 2 (avec un indice d'oxydation du soufre de +4). De même, l'acide nitrique, HNO 3, ou O 2 NOH (indice d'oxydation N = +5), est plus acide que l'acide nitreux, HNO 2 ou ONOH (indice d'oxydation N = +3). Dans chacune de ces paires, le nombre d'oxydation de l'atome central est plus élevé pour l'acide le plus fort (Figure\(\PageIndex{7}\)).
Les composés hydroxylés d'éléments présentant des électronégativités intermédiaires et un nombre d'oxydation relativement élevé (par exemple, les éléments situés près de la diagonale séparant les métaux des non-métaux dans le tableau périodique) sont généralement amphotères. Cela signifie que les composés hydroxy agissent comme des acides lorsqu'ils réagissent avec des bases fortes et comme des bases lorsqu'ils réagissent avec des acides forts. L'amphotérisme de l'hydroxyde d'aluminium, qui existe généralement sous forme d'hydrate\(\ce{Al(H2O)3(OH)3}\), se reflète dans sa solubilité à la fois dans les acides forts et les bases fortes. Dans les bases fortes, l'hydroxyde d'aluminium hydraté\(\ce{Al(H2O)3(OH)3}\), relativement insoluble, est converti en ion soluble\(\ce{[Al(H2O)2(OH)4]-}\), par réaction avec l'ion hydroxyde :
\[[\ce{Al(H2O)3(OH)3}](aq)+\ce{OH-}(aq)⇌\ce{H2O}(l)+\ce{[Al(H2O)2(OH)4]-}(aq) \nonumber \]
Dans cette réaction, un proton est transféré de l'une des molécules de H 2 O liées à l'aluminium vers un ion hydroxyde en solution. Le\(\ce{Al(H2O)3(OH)3}\) composé agit donc comme un acide dans ces conditions. D'autre part, lorsqu'il est dissous dans des acides forts, il est converti en ion soluble\(\ce{[Al(H2O)6]^3+}\) par réaction avec l'ion hydronium :
\[\ce{3H3O+}(aq)+\ce{Al(H2O)3(OH)3}(aq)⇌\ce{Al(H2O)6^3+}(aq)+\ce{3H2O}(l) \nonumber \]
Dans ce cas, les protons sont transférés des ions hydronium en solution vers\(\ce{Al(H2O)3(OH)3}\), et le composé fonctionne comme une base.
Résumé
Les forces des acides et des bases de Brønsted-Lowry dans les solutions aqueuses peuvent être déterminées par leurs constantes d'ionisation des acides ou des bases. Les acides plus forts forment des bases conjuguées plus faibles, et les acides plus faibles forment des bases conjuguées plus fortes. Ainsi, les acides forts sont complètement ionisés en solution aqueuse car leurs bases conjuguées sont des bases plus faibles que l'eau. Les acides faibles ne sont que partiellement ionisés parce que leurs bases conjuguées sont suffisamment fortes pour concurrencer avec succès l'eau pour la possession de protons. Les bases fortes réagissent avec l'eau pour former quantitativement des ions hydroxyde. Les bases faibles ne produisent que de petites quantités d'ions hydroxyde. Les forces des acides binaires augmentent de gauche à droite au cours d'une période du tableau périodique (CH 4 < NH 3 < H 2 O < HF), et elles augmentent vers le bas d'un groupe (HF < HCl < HBr < HI). La force des oxyacides qui contiennent le même élément central augmente à mesure que le nombre d'oxydation de l'élément augmente (H 2 SO 3 < H 2 SO 4). Les forces des oxyacides augmentent également à mesure que l'électronégativité de l'élément central augmente [H 2 SeO 4 < H 2 SO 4].
Équations clés
- \(K_\ce{a}=\ce{\dfrac{[H3O+][A- ]}{[HA]}}\)
- \(K_\ce{b}=\ce{\dfrac{[HB+][OH- ]}{[B]}}\)
- \(K_a \times K_b = 1.0 \times 10^{−14} = K_w \,(\text{at room temperature})\)
- \(\textrm{Percent ionization}=\ce{\dfrac{[H3O+]_{eq}}{[HA]_0}}×100\)
Lexique
- constante d'ionisation acide (K a)
- constante d'équilibre pour l'ionisation d'un acide faible
- constante d'ionisation de base (K b)
- constante d'équilibre pour l'ionisation d'une base faible
- effet nivelant de l'eau
- tout acide plus fort que\(\ce{H3O+}\) OH − ou toute base plus forte que OH − réagira avec l'eau pour former\(\ce{H3O+}\), respectivement, ou OH − ; l'eau agit comme une base pour que tous les acides forts apparaissent aussi forts, et elle agit comme un acide pour faire apparaître toutes les bases fortes de la même force
- oxyacide
- composé contenant un groupe non métallique et un ou plusieurs groupes hydroxyle
- pourcentage d'ionisation
- rapport entre la concentration de l'acide ionisé et la concentration initiale en acide, multiplié par 100


