14.2 : pH et PoH

Objectifs d'apprentissage

• Expliquer la caractérisation des solutions aqueuses comme étant acides, basiques ou neutres
• Exprimer les concentrations d'hydronium et d'ions hydroxyde sur les échelles de pH et de PoH
• Effectuer des calculs relatifs au pH et au PoH

Comme indiqué précédemment, les ions hydronium et hydroxyde sont présents à la fois dans l'eau pure et dans toutes les solutions aqueuses, et leurs concentrations sont inversement proportionnelles, telles que déterminées par le produit ionique de l'eau (\(K_w\)). Les concentrations de ces ions dans une solution sont souvent des déterminants critiques des propriétés de la solution et du comportement chimique de ses autres solutés, et un vocabulaire spécifique a été développé pour décrire ces concentrations en termes relatifs. Une solution est neutre si elle contient des concentrations égales d'hydronium et d'ions hydroxyde ; acide si elle contient une plus grande concentration d'ions hydronium que d'ions hydroxyde ; et basique si elle contient une concentration moindre d'ions hydronium que d'ions hydroxyde.

L'utilisation d'une échelle logarithmique est un moyen courant d'exprimer des quantités dont les valeurs peuvent s'étendre sur de nombreux ordres de grandeur. L'une de ces échelles, très populaire pour les concentrations chimiques et les constantes d'équilibre, est basée sur la fonction p, définie comme indiqué où « X » est la quantité d'intérêt et « log » est le logarithme en base 10 :

\[\mathrm{pX=−\log X} \label{1} \]

Le pH d'une solution est donc défini comme indiqué ici, où [H ₃ O ⁺] est la concentration molaire en ion hydronium dans la solution :

\[\mathrm{pH=-\log[H_3O^+]}\label{\(\PageIndex{2}\)} \]

La réorganisation de cette équation pour isoler la molarité de l'ion hydronium donne l'expression équivalente :

\[\mathrm{[H_3O^+]=10^{−pH}}\label{\(\PageIndex{3}\)} \]

De même, la molarité de l'ion hydroxyde peut être exprimée en fonction p, ou PoH :

\[\mathrm{pOH=-\log [OH^−]}\label{\(\PageIndex{4}\)} \]

ou

\[\mathrm{[OH^-]=10^{−pOH}} \label{\(\PageIndex{5}\)} \]

Enfin, la relation entre ces deux concentrations ioniques exprimées en fonctions p est facilement dérivée de l'\(K_w\)expression :

\[K_\ce{w}=\ce{[H_3O^+][OH^- ]} \label{\(\PageIndex{6}\)} \]

\[-\log K_\ce{w}=\mathrm{-\log([H_3O^+][OH^−])=-\log[H_3O^+] + -\log[OH^-]}\label{\(\PageIndex{7}\)} \]

\[\mathrm{p\mathit{K}_w=pH + pOH} \label{\(\PageIndex{8}\)} \]

À 25 °C, la valeur de\(K_w\) est\(1.0 \times 10^{−14}\), et donc :

\[\mathrm{14.00=pH + pOH} \label{\(\PageIndex{9}\)} \]

La molarité des ions hydronium dans l'eau pure (ou dans toute solution neutre) est de 25\( 1.0 \times 10^{-7}\; M\) °C. Le pH et le pOH d'une solution neutre à cette température sont donc les suivants :

\[\mathrm{pH=-\log[H_3O^+]=-\log(1.0\times 10^{−7}) = 7.00} \label{10} \]

\[\mathrm{pOH=-\log[OH^−]=-\log(1.0\times 10^{−7}) = 7.00} \label{11} \]

Ainsi, à cette température, les solutions acides sont celles dont les molarités des ions hydronium sont supérieures à\( 1.0 \times 10^{-7}\; M\) et celles des ions hydroxyde inférieures à\( 1.0 \times 10^{-7}\; M\) (correspondant à des valeurs de pH inférieures à 7,00 et des valeurs de PoH supérieures à 7,00). Les solutions basiques sont celles dont les molarités des ions hydronium sont inférieures à\( 1.0 \times 10^{-7}\; M\) et celles des ions hydroxyde supérieures à\( 1.0 \times 10^{-7}\; M\) (correspondant à des valeurs de pH supérieures à 7,00 et des valeurs de PoH inférieures à 7,00).

Quand\(pH=7\) Solutions are not Neutral

Comme la constante\(K_w\) d'auto-ionisation dépend de la température, ces corrélations entre les valeurs du pH et les adjectifs acide/neutre/basique seront différentes à des températures autres que 25 °C. Par exemple, la molarité de l'hydronium de l'eau pure à 80 °C est de 4,9 × 10 ⁻⁷ M, qui correspond aux valeurs de pH et de PoH de :

\[\begin{align*} pH &=-\log[\ce{H_3O^+}] \\[4pt] &= -\log(4.9\times 10^{−7}) \\[4pt] &=6.31 \label{12} \end{align*} \]

\[\begin{align*} pOH &=-\log[\ce{OH^-}]\\[4pt] & =-\log(4.9\times 10^{−7}) \\[4pt] &=6.31 \label{13}\end{align*} \]

À cette température, les solutions neutres présentent donc un pH = PoH = 6,31, les solutions acides présentent un pH inférieur à 6,31 et un pOH supérieur à 6,31, tandis que les solutions basiques présentent un pH supérieur à 6,31 et un pH inférieur à 6,31. Cette distinction peut être importante lors de l'étude de certains processus qui se produisent à des températures non standard, tels que les réactions enzymatiques chez les organismes à sang chaud. Sauf indication contraire, les références aux valeurs de pH sont présumées être celles à la température standard (25 °C) (tableau\(\PageIndex{1}\)).

Tableau\(\PageIndex{1}\) : Résumé des relations entre les solutions acides, basiques et neutres

Classement	Concentrations ions relatives	pH à 25 °C
acide	[H 3 O ^+] > [OH ^−]	pH < 7
neutre	[H 3 O ^+] = [OH ^−]	pH = 7
de base	[H 3 O ^+] < [OH ^−]	pH > 7

La figure\(\PageIndex{1}\) montre les relations entre [H ₃ O ⁺], [OH ⁻], le pH et le PoH, et donne des valeurs pour ces propriétés à des températures standard pour certaines substances courantes.

Figure\(\PageIndex{1}\) : Les échelles de pH et de PoH représentent les concentrations de [H ₃ O ⁺] et de OH ⁻, respectivement. Les valeurs du pH et du PoH de certaines substances courantes à température standard (25 °C) sont présentées dans ce graphique.

Un tableau comporte 5 colonnes. La première colonne est intitulée « Crochet gauche H indice 3 O exposant plus crochet droit (M) ». Les puissances de dix sont listées dans la colonne commençant par 10 exposant 1, y compris 10 exposant 0 ou 1, 10 exposant moins 1, diminuant par des puissances simples de 10 à 10 exposants moins 15. La deuxième colonne est intitulée « crochet gauche O H exposant négatif crochet droit (M) ». Les puissances de dix sont répertoriées dans la colonne commençant par 10 exposant moins 15, puis augmentées par des puissances simples de 10 pour inclure 10 exposants 0 ou 1, et 10 exposants 1. La troisième colonne est intitulée « p H ». Les valeurs répertoriées dans cette colonne sont des nombres entiers commençant par moins 1 et augmentés par un, jusqu'à 14. La quatrième colonne est intitulée « p O H ». Les valeurs de cette colonne sont des nombres entiers commençant à 15 et décroissants jusqu'à moins 1. La cinquième colonne est intitulée « Exemple de solution ». Une ligne verticale à gauche de la colonne comporte des coches correspondant à chaque niveau p H du tableau. Les substances sont répertoriées à côté de ce segment de ligne, des segments de ligne les reliant à la ligne pour indiquer les valeurs approximatives de p H et de p O H. 1 M H C l est répertorié à un p H de 0. Les sucs gastriques sont listés à un pH d'environ 1,5. Le jus de lime est répertorié à un p H d'environ 2, suivi de 1 M C H indice 3 C O indice 2 H, suivi de l'acide gastrique à une valeur de p H de près de 3. Le vin est répertorié autour de 3,5. Le café est répertorié juste après 5. L'eau pure est répertoriée à un pH de 7. Le sang pur est juste au-delà de 7. Le lait de magnésie est répertorié juste après un pH de 10,5. L'ammoniac domestique est répertorié juste avant un pH de 12. 1 M N a O H est répertorié à un p H de 0. À droite de cette flèche étiquetée se trouve une flèche pointant vers le haut et vers le bas à travers la hauteur de la colonne. Une bande beige traverse la table et mène à cette flèche à deux pointes à p H 7. À gauche de la flèche à double pointe de cette bande beige se trouve l'étiquette « neutre ». Une étroite bande beige traverse la flèche. Juste au-dessus et en dessous de cette zone, la flèche est violette. Il devient progressivement rouge vif à mesure qu'il s'étend vers le haut. En haut de la flèche, près de la pointe de la flèche se trouve l'étiquette « acide ». De même, la région inférieure change de couleur du violet au bleu en se déplaçant vers le bas de la colonne. La tête à cette extrémité de la flèche est étiquetée « basique ».

Exemple\(\PageIndex{1}\): Calculation of pH from \(\ce{[H_3O^+]}\)

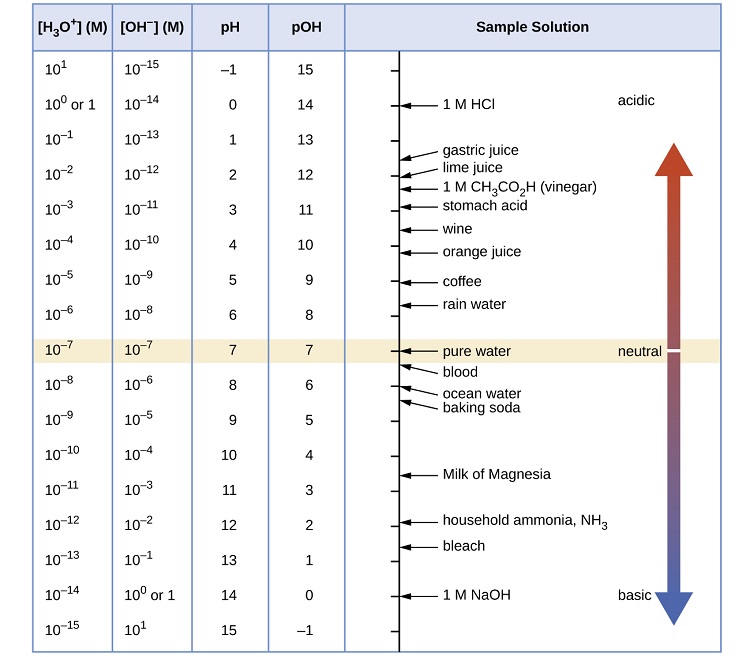
Quel est le pH de l'acide gastrique, une solution de HCl dont la concentration en ions hydronium est de\(1.2 \times 10^{−3}\; M\) ?

Solution

\[\begin{align*} pH &=-\log [H_3O^+] \\[4pt] &= -\log(1.2 \times 10^{−3}) \\[4pt] &=−(−2.92) \\[4pt]&=2.92 \end{align*} \nonumber \]

Exercice\(\PageIndex{1}\)

L'eau exposée à l'air contient de l'acide carbonique, H ₂ CO ₃, en raison de la réaction entre le dioxyde de carbone et l'eau :

\[\ce{CO2(aq) + H2O (l) \rightleftharpoons H2CO3(aq)} \nonumber \]

L'eau saturée d'air a une concentration en ions hydronium causée par la dissolution\(\ce{CO_2}\) de\(2.0 \times 10^{−6}\; M\), environ 20 fois supérieure à celle de l'eau pure. Calculer le pH de la solution à 25 °C.

Réponse

5,70

Exemple\(\PageIndex{2}\): Calculation of Hydronium Ion Concentration from pH

Calculez la concentration en ions hydronium du sang, dont le pH est de 7,3 (légèrement alcalin).

Solution

\[\mathrm{pH=-\log[H_3O^+]=7.3} \nonumber \]

\[\mathrm{\log[H_3O^+]=−7.3} \nonumber \]

\[\mathrm{[H_3O^+]=10^{−7.3}} \nonumber \]

ou

\[[\ce{H_3O^+}]=\textrm{antilog of} −7.3 \nonumber \]

\[[\ce{H_3O^+}]=5\times 10^{−8}\;M \nonumber \]

(Sur une calculatrice, prenez l'antilog, ou le logarithme « inverse », de −7.3, ou calculez 10 ^−7.3.)

Exercice\(\PageIndex{2}\)

Calculez la concentration en ions hydronium d'une solution ayant un pH de −1,07.

Réponse

12 M

Sciences de l'environnement

L'eau de pluie normale a un pH compris entre 5 et 6 en raison de la présence de CO ₂ dissous qui forme de l'acide carbonique :

\[\ce{H2O (l) + CO2(g) ⟶ H2CO3(aq)} \label{14} \]

\[\ce{H2CO3(aq) \rightleftharpoons H^+(aq) + HCO3^- (aq)} \label{15} \]

Les pluies acides sont des eaux de pluie dont le pH est inférieur à 5, en raison de la dissolution dans l'eau de divers oxydes non métalliques, notamment du CO ₂, du SO 2, du SO ₃, du NO et du NO ₂, qui réagissent avec elle pour former non seulement de l'acide carbonique, mais aussi de l'acide sulfurique et de l'acide nitrique. La formation et l'ionisation subséquente de l'acide sulfurique sont présentées ici :

\[\ce{H2O (l) + SO3(g) ⟶ H2SO4(aq)} \label{16} \]

\[\ce{H2SO4(aq) ⟶ H^+(aq) + HSO4^- (aq)} \label{17} \]

Le dioxyde de carbone est naturellement présent dans l'atmosphère parce que nous et la plupart des autres organismes le produisons sous forme de déchets du métabolisme. Le dioxyde de carbone se forme également lorsque les incendies libèrent du carbone stocké dans la végétation ou lorsque nous brûlons du bois ou des combustibles fossiles. Le trioxyde de soufre dans l'atmosphère est naturellement produit par l'activité volcanique, mais il provient également de la combustion de combustibles fossiles, qui contiennent des traces de soufre, et du processus de « torréfaction » des minerais de sulfures métalliques lors des processus d'affinage des métaux. Les oxydes d'azote se forment dans les moteurs à combustion interne où les températures élevées permettent à l'azote et à l'oxygène de l'air de se combiner chimiquement.

Les pluies acides constituent un problème particulier dans les zones industrielles où les produits de combustion et de fusion sont rejetés dans l'air sans être débarrassés des oxydes de soufre et d'azote. En Amérique du Nord et en Europe jusque dans les années 1980, elle a été responsable de la destruction de forêts et de lacs d'eau douce, lorsque l'acidité de la pluie a tué des arbres, endommagé les sols et rendu les lacs inhabitables pour toutes les espèces sauf pour les espèces les plus tolérantes aux acides. Les pluies acides corrodent également les façades des statues et des bâtiments en marbre et en calcaire (Figure\(\PageIndex{2}\)). Les réglementations limitant la quantité d'oxydes de soufre et d'azote qui peuvent être rejetés dans l'atmosphère par l'industrie et les automobiles ont réduit la gravité des dommages causés par l'acide aux environnements naturels et artificiels en Amérique du Nord et en Europe. C'est aujourd'hui un problème croissant dans les zones industrielles de la Chine et de l'Inde.

Figure\(\PageIndex{2}\) : (a) Les pluies acides rendent les arbres plus vulnérables à la sécheresse et aux infestations d'insectes, et épuisent les nutriments du sol. (b) Il s'agit également de statues corrodées sculptées dans du marbre ou du calcaire. (crédit a : modification de l'œuvre par Chris M Morris ; crédit b : modification de l'œuvre par « Eden, Janine et Jim » /Flickr)

Deux photos sont présentées. La photographie a sur la gauche montre la partie supérieure des arbres sur fond de ciel bleu vif. La cime de plusieurs arbres au centre de la photographie a des branches nues et semble morte. L'image b montre une statue d'un homme qui semble datant de l'époque de la guerre révolutionnaire, en marbre ou en calcaire.

Exemple\(\PageIndex{3}\): Calculation of pOH

Quels sont le pH et le pH d'une solution 0,0125 M d'hydroxyde de potassium, KOH ?

Solution

L'hydroxyde de potassium est un composé ionique hautement soluble qui se dissocie complètement lorsqu'il est dissous dans une solution diluée, donnant [OH ⁻] = 0,0125 M :

\[\mathrm{pOH=-\log[OH^− ]=-\log 0.0125} \nonumber \]

\[=−(−1.903)=1.903 \nonumber \]

Le pH peut être déterminé à partir de\(\ce{pOH}\) :

\[\mathrm{pH+pOH=14.00} \nonumber \]

\[\mathrm{pH=14.00−pOH=14.00−1.903=12.10} \nonumber \]

Exercice\(\PageIndex{3}\)

La concentration en ions hydronium du vinaigre est d'environ\(4 \times 10^{−3}\; M\). Quelles sont les valeurs correspondantes de PoH et de pH ?

Réponse

pH = 11,6,

pH = 14,00 - PoH = 2,4

L'acidité d'une solution est généralement évaluée expérimentalement en mesurant son pH. Le pH d'une solution n'est généralement pas mesuré, car il est facile de le calculer à partir d'une valeur de pH déterminée expérimentalement. Le pH d'une solution peut être directement mesuré à l'aide d'un pH-mètre (Figure\(\PageIndex{3}\)).

Figure\(\PageIndex{3}\) : (a) Un pH-mètre de recherche utilisé en laboratoire peut avoir une résolution de 0,001 unité de pH, une précision de ± 0,002 unité de pH et peut coûter plus de 1 000 dollars. (b) Un pH-mètre portable a une résolution inférieure (0,01 unité de pH), une précision moindre (± 0,2 unité de pH) et un prix bien inférieur. (crédit b : modification d'une œuvre de Jacopo Werther)

Cette figure contient deux images. La première, l'image a, est celle d'un pH-mètre numérique analytique installé sur un comptoir de laboratoire. La seconde, image b, est celle d'un pH-mètre numérique portatif.

Le pH d'une solution peut également être estimé visuellement à l'aide d'indicateurs colorés (Figure\(\PageIndex{3}\)).

Figure\(\PageIndex{4}\) : (a) Un indicateur universel suppose une couleur différente dans des solutions de différentes valeurs de pH. Ainsi, il peut être ajouté à une solution pour déterminer le pH de la solution. Les huit flacons contiennent chacun un indicateur universel et des solutions à 0,1 M d'acides de plus en plus faibles : HCl (pH = l), CH ₃ CO ₂ H (pH = 3) et NH ₄ Cl (pH = 5), de l'eau déionisée, une substance neutre (pH = 7) ; et des solutions 0,1 M de bases de plus en plus fortes : KCl (pH = 7), aniline, C ₆ H ₅ NH ₂ (pH = 9), NH ₃ (pH = 11) et NaOH (pH = 13). (b) Le papier sur le pH contient un mélange d'indicateurs qui donnent des couleurs différentes à des solutions ayant des valeurs de pH différentes. (source : modification de l'œuvre de Sahar Atwa).

Cette figure contient deux images. La première montre une variété de couleurs de solutions dans des béchers étiquetés. Une solution rouge dans un bécher est étiquetée « 0,10 M H C l. ». Une solution orange est étiquetée « 0,10 M C H indice 3 C O O H. » Une solution jaune-orange est étiquetée « 0,1 M N H indice 4 C l ». Une solution jaune est étiquetée « eau déionisée ». Un deuxième bécher de solution est étiqueté « 0,10 M K C l. ». Une solution verte est étiquetée « 0,10 M d'aniline ». Une solution bleue est étiquetée « 0,10 M N H indice 4 C l (a q) ». Un bécher final contenant une solution bleu foncé est étiqueté « 0,10 M N a O H. » L'image b montre du papier Phydrion utilisé pour mesurer le pH dans la plage de p H comprise entre 1 et 12. L'échelle de couleurs permettant d'identifier p H en fonction de la couleur est indiquée, ainsi que plusieurs des bandelettes de test utilisées pour évaluer p H.

Résumé

La concentration d'ion hydronium dans une solution d'un acide dans l'eau est supérieure\( 1.0 \times 10^{-7}\; M\) à 25 °C. La concentration d'ion hydroxyde dans une solution d'une base dans l'eau est supérieure\( 1.0 \times 10^{-7}\; M\) à 25 °C. La concentration de H ₃ O ⁺ dans une solution peut être exprimée comme le pH du solution ;\(\ce{pH} = -\log \ce{H3O+}\). La concentration de ^{OH -} peut être exprimée comme le PoH de la solution :\(\ce{pOH} = -\log[\ce{OH-}]\) Dans de l'eau pure, pH = 7,00 et pOH = 7,00

Équations clés

• \(\ce{pH}=-\log[\ce{H3O+}]\)
• \(\ce{pOH} = -\log[\ce{OH-}]\)
• [H ₃ O ⁺] = 10 ^−pH
• [OH ⁻] = 10 ^−POH
• pH + PoH = p K _w = 14,00 à 25 °C

Lexique

acide

décrit une solution dans laquelle [H ₃ O ⁺] > [OH ⁻]

de base

décrit une solution dans laquelle [H ₃ O ⁺] < [OH ⁻]

neutre

décrit une solution dans laquelle [H ₃ O ⁺] = [OH ⁻]

pH

mesure logarithmique de la concentration en ions hydronium dans une solution

PoH

mesure logarithmique de la concentration en ions hydroxyde dans une solution