12.5 : Théorie des collisions

Last updated
Save as PDF

Page ID: 193969

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objectifs d'apprentissage

Utiliser les postulats de la théorie des collisions pour expliquer les effets de l'état physique, de la température et de la concentration sur les vitesses de réaction
Définir les concepts d'énergie d'activation et d'état de transition
Utiliser l'équation d'Arrhenius dans les calculs reliant les constantes de vitesse à la température

Il ne faut pas s'étonner que des atomes, des molécules ou des ions doivent entrer en collision avant de pouvoir réagir les uns avec les autres. Les atomes doivent être proches les uns des autres pour former des liaisons chimiques. Cette prémisse simple est à la base d'une théorie très puissante qui explique de nombreuses observations concernant la cinétique chimique, y compris les facteurs influant sur les vitesses de réaction. La théorie des collisions est basée sur les postulats suivants :

Postulats de la théorie des collisions

La vitesse d'une réaction est proportionnelle à la vitesse des collisions de réactifs :\[\mathrm{reaction\: rate ∝ \dfrac{\#\,collisions}{time}} \nonumber \]
Les espèces réactives doivent entrer en collision dans une orientation qui permet le contact entre les atomes qui se lieront ensemble dans le produit.
La collision doit se produire avec une énergie suffisante pour permettre la pénétration mutuelle des couches de valence des espèces réactives afin que les électrons puissent se réarranger et former de nouvelles liaisons (et de nouvelles espèces chimiques).

Nous pouvons voir l'importance des deux facteurs physiques notés dans les postulats 2 et 3, l'orientation et l'énergie des collisions, lorsque nous examinons la réaction du monoxyde de carbone avec l'oxygène :

\[\ce{2CO}(g)+\ce{O2}(g)⟶\ce{2CO2}(g) \nonumber \]

Le monoxyde de carbone est un polluant produit par la combustion de combustibles hydrocarbonés. Pour réduire ce polluant, les automobiles sont équipées de convertisseurs catalytiques qui utilisent un catalyseur pour effectuer cette réaction. Il s'agit également d'une réaction secondaire de la combustion de poudre à canon qui provoque des éclats de bouche pour de nombreuses armes à feu. Si le monoxyde de carbone et l'oxygène sont présents en quantité suffisante, la réaction est spontanée à haute température et à haute pression.

La première étape de la réaction en phase gazeuse entre le monoxyde de carbone et l'oxygène est une collision entre les deux molécules :

\[\ce{CO}(g)+\ce{O2}(g)⟶\ce{CO2}(g)+\ce{O}(g) \nonumber \]

Bien qu'il existe de nombreuses orientations possibles différentes que les deux molécules peuvent avoir l'une par rapport à l'autre, considérez les deux présentées dans la Figure\(\PageIndex{1}\). Dans le premier cas, le côté oxygène de la molécule de monoxyde de carbone entre en collision avec la molécule d'oxygène. Dans le second cas, le côté carbone de la molécule de monoxyde de carbone entre en collision avec la molécule d'oxygène. Le second cas est clairement plus susceptible d'entraîner la formation de dioxyde de carbone, dont un atome de carbone central est lié à deux atomes d'oxygène\(\ce{(O=C=O)}\). Il s'agit d'un exemple assez simple de l'importance de l'orientation de la collision pour créer le produit souhaité de la réaction.

alt — Figure\(\PageIndex{1}\) : Deux collisions susceptibles de se produire entre des molécules de monoxyde de carbone et d'oxygène sont illustrées. L'orientation des molécules qui entrent en collision détermine partiellement si une réaction entre les deux molécules se produira.

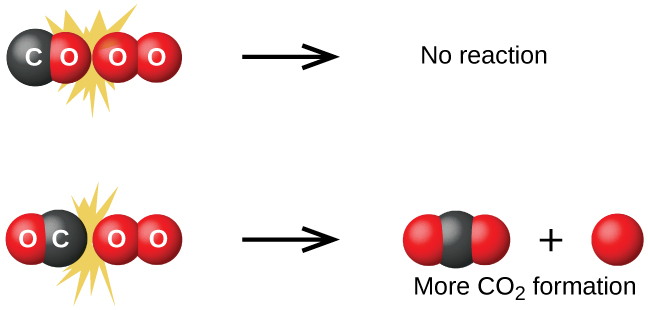
Si la collision se produit dans la bonne orientation, il n'y a toujours aucune garantie que la réaction se traduira par la formation de dioxyde de carbone. Chaque réaction nécessite une certaine quantité d'énergie d'activation pour qu'elle se déroule vers l'avant, produisant ainsi un complexe activé approprié en cours de route. Comme le\(\PageIndex{2}\) montre la figure, même une collision avec la bonne orientation peut ne pas former le produit de réaction. Dans l'étude des mécanismes de réaction, chacun de ces trois arrangements d'atomes est appelé complexe activé proposé ou état de transition.

alt — Figure\(\PageIndex{2}\) : États de transition possibles (complexes activés) pour le monoxyde de carbone réagissant avec l'oxygène pour former du dioxyde de carbone. Les lignes continues représentent les liaisons covalentes, tandis que les lignes pointillées représentent les chevauchements orbitaux instables qui peuvent ou non devenir des liaisons covalentes au fur et à mesure de la formation du produit. Dans les deux premiers exemples de cette figure, la double liaison O=O n'est pas affectée ; par conséquent, le dioxyde de carbone ne peut pas se former. Le troisième état de transition proposé entraînera la formation de dioxyde de carbone si le troisième atome d'oxygène « supplémentaire » se sépare du reste de la molécule.

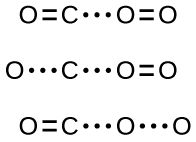
Dans la plupart des cas, il est impossible d'isoler ou d'identifier un état de transition ou un complexe activé. Lors de la réaction entre le monoxyde de carbone et l'oxygène pour former du dioxyde de carbone, les complexes activés n'ont été observés par spectroscopie que dans des systèmes utilisant un catalyseur hétérogène. La réaction en phase gazeuse se produit trop rapidement pour isoler un tel composé chimique.

La théorie des collisions explique pourquoi la plupart des taux de réaction augmentent lorsque les concentrations augmentent. Lorsque la concentration de toute substance réactive augmente, les risques de collisions entre molécules sont augmentés car il y a plus de molécules par unité de volume. Un plus grand nombre de collisions signifie une vitesse de réaction plus rapide, en supposant que l'énergie des collisions soit adéquate.

Énergie d'activation et équation d'Arrhenius

L'énergie minimale nécessaire pour former un produit lors d'une collision entre des réactifs est appelée énergie d'activation y (\(E_a\)). L'énergie cinétique des molécules de réactif joue un rôle important dans une réaction, car l'énergie nécessaire à la formation d'un produit est fournie par la collision d'une molécule de réactif avec une autre molécule de réactif. (Dans les réactions à un seul réactif, l'énergie d'activation peut être fournie par une collision de la molécule du réactif avec la paroi du récipient de réaction ou avec des molécules d'un contaminant inerte.) Si l'énergie d'activation est bien supérieure à l'énergie cinétique moyenne des molécules, la réaction se produira lentement : seules quelques molécules se déplaçant rapidement auront assez d'énergie pour réagir. Si l'énergie d'activation est bien inférieure à l'énergie cinétique moyenne des molécules, la fraction de molécules possédant l'énergie cinétique nécessaire sera importante ; la plupart des collisions entre molécules entraîneront une réaction, qui se produira rapidement.

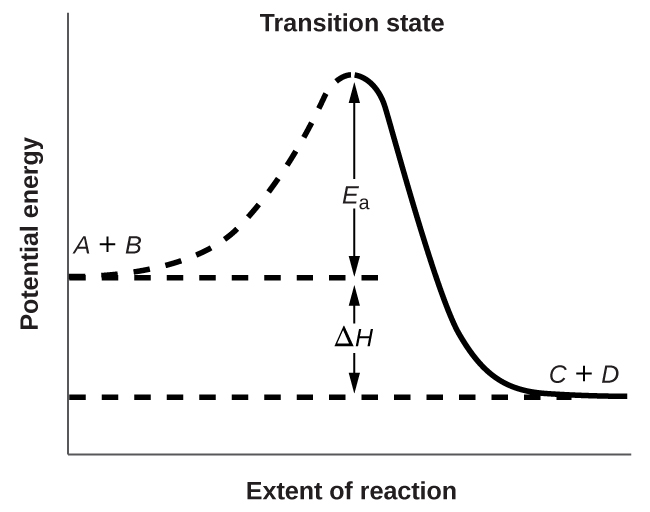
La figure\(\PageIndex{3}\) montre les relations énergétiques pour la réaction générale d'une molécule de\(A\) avec une molécule de\(B\) pour former des molécules de\(C\) et\(D\) :

\[A+B⟶C+D \nonumber \]

La figure montre que l'énergie de l'état de transition est supérieure à celle des réactifs\(A\) et\(B\) d'une quantité égale à\(E_a\) l'énergie d'activation. Ainsi, la somme des énergies cinétiques de\(A\) et\(B\) doit être égale ou supérieure à E _a pour atteindre l'état de transition. Une fois que l'état de transition a été atteint\(C\) et qu'il\(D\) commence à se former, le système perd de l'énergie jusqu'à ce que son énergie totale soit inférieure à celle du mélange initial. Cette énergie perdue est transférée à d'autres molécules, leur donnant suffisamment d'énergie pour atteindre l'état de transition. La réaction directe (celle entre les molécules\(A\) et\(B\)) a donc tendance à se produire facilement une fois que la réaction a commencé. Dans la figure\(\PageIndex{3}\),\(ΔH\) représente la différence d'enthalpie entre les réactifs (\(A\)et\(B\)) et les produits (\(C\)et\(D\)). La somme de\(E_a\) et\(ΔH\) représente l'énergie d'activation pour la réaction inverse :

\[C+D⟶A+B \nonumber \]

alt — Figure\(\PageIndex{3}\) : Ce graphique montre les relations énergétiques potentielles pour la réaction\(A+B⟶C+D\). La partie pointillée de la courbe représente l'énergie du système en présence d'une molécule de A et d'une molécule de B, et la partie solide l'énergie du système en présence d'une molécule de C et d'une molécule de D. L'énergie d'activation de la réaction directe est représentée par E _a. L'énergie d'activation pour la réaction inverse est supérieure à celle pour la réaction directe d'une quantité égale à ΔH. Le pic de la courbe représente l'état de transition.

Nous pouvons utiliser l'équation d'Arrhenius pour relier l'énergie d'activation et la constante de vitesse, k, d'une réaction donnée :

\[k=Ae^{−E_a/RT} \label{Arrhenius} \]

Dans cette équation,

\(R\)est la constante de gaz idéale, qui a une valeur de 8,314 J/mol/K,
\(T\)est la température sur l'échelle Kelvin,
\(E_a\)est l'énergie d'activation en joules par mole,
\(e\)est la constante 2,7183, et
\(A\)est une constante appelée facteur de fréquence, qui est liée à la fréquence des collisions et à l'orientation des molécules réactives.

Les deux postulats de la théorie des collisions concernant les vitesses de réaction sont pris en compte dans l'équation d'Arrhenius. Le facteur de fréquence A est lié à la vitesse à laquelle se produisent des collisions ayant la bonne orientation. Le terme exponentiel,\(e^{−E_a/RT}\), est lié à la fraction de collisions fournissant l'énergie suffisante pour surmonter la barrière d'activation de la réaction.

À un extrême, le système ne contient pas assez d'énergie pour que les collisions puissent surmonter la barrière d'activation. Dans de tels cas, aucune réaction ne se produit. À l'autre extrême, le système a tellement d'énergie que chaque collision avec la bonne orientation peut surmonter la barrière d'activation, provoquant ainsi la poursuite de la réaction. Dans de tels cas, la réaction est quasi instantanée.

L'équation d'Arrhenius (équation \ ref {Arrhenius}) décrit quantitativement une grande partie de ce que nous avons déjà discuté au sujet des vitesses de réaction. Pour deux réactions à la même température, la réaction ayant l'énergie d'activation la plus élevée a la constante de vitesse la plus faible et la vitesse la plus lente. La plus grande valeur de se\(E_a\) traduit par une valeur plus faible pour\(e^{−E_a/RT}\), reflétant la plus petite fraction de molécules ayant suffisamment d'énergie pour réagir. Sinon, la réaction avec le plus petit\(E_a\) produit une plus grande fraction de molécules ayant suffisamment d'énergie pour réagir. Cela se traduira par une valeur plus grande de\(e^{−E_a/RT}\), une constante de vitesse plus grande et une vitesse plus rapide pour la réaction.

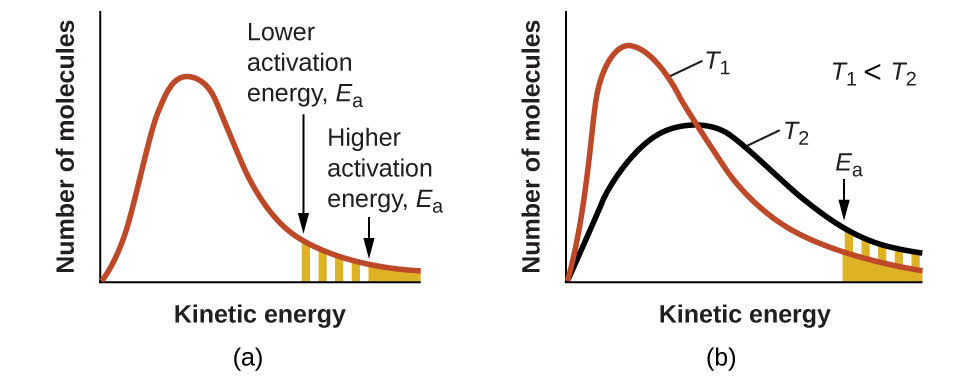
Figure\(\PageIndex{4}\) : (a) Lorsque l'énergie d'activation d'une réaction diminue, le nombre de molécules possédant au moins cette énergie augmente, comme le montrent les zones ombrées. (b) À une température plus élevée, T2, un plus grand nombre de molécules ont une énergie cinétique supérieure à Ea, comme le montre la zone ombrée en jaune.

Une augmentation de la température a le même effet qu'une diminution de l'énergie d'activation. Une plus grande fraction de molécules possède l'énergie nécessaire pour réagir (Figure\(\PageIndex{4}\)), comme l'indique une augmentation de la valeur de\(e^{−E_a/RT}\). La constante de vitesse est également directement proportionnelle au facteur de fréquence,\(A\). Ainsi, un changement des conditions ou des réactifs qui augmente le nombre de collisions avec une orientation favorable à la réaction entraîne une augmentation\(A\) et, par conséquent, une augmentation de\(k\).

Une approche pratique\(E_a\) pour déterminer une réaction consiste à mesurer\(k\) à différentes températures et à utiliser une version alternative de l'équation d'Arrhenius qui prend la forme d'une équation linéaire :

\ [\ begin {align*}
\ ln k&= \ left (\ dfrac {−e_A} {R} \ right) \ left (\ dfrac {1} {T} \ right) + \ ln A \ \
y&=mx+b
\ end {align*} \ nonumber \]

Ainsi, un diagramme de\(\ln k\) versus\(\dfrac{1}{T}\) donne une ligne droite avec la pente\(\dfrac{-E_\ce{a}}{R}\), à partir de laquelle E _a peut être déterminé. L'interception donne la valeur de\(\ln A\). C'est ce que l'on appelle parfois un complot d'Arrhenius.

Exemple\(\PageIndex{1}\)

Détermination de E _a La variation de la constante de vitesse en fonction de la température pour la décomposition de HI (g) en H ₂ (g) et I ₂ (g) est donnée ici. Quelle est l'énergie d'activation de la réaction ?

\[\ce{2HI}(g)⟶\ce{H2}(g)+\ce{I2}(g) \nonumber \]

variation de la constante de vitesse en fonction de la température pour la décomposition de HI (g) en H2 (g) et I2 (g)
*(Royaume-Uni)*	k (L/mol/s)
555	3,52 × 10 ⁻⁷
575	1,22 × 10 ⁻⁶
645	8,59 × 10 ⁻⁵
700	1,16 × 10 ⁻³
781	3,95 × 10 ⁻²

Solution

Les valeurs de\(\dfrac{1}{T}\) et ln k sont les suivantes :

Solutions à l'exemple 12.5.1
\(\mathrm{\dfrac{1}{T}\:(K^{−1})}\)	en Royaume-Uni
\ (\ mathrm {\ dfrac {1} {T} \ : (K^ {−1})} \) » style="text-align:center ; « >1,80 × 10 ⁻³	−14 860
\ (\ mathrm {\ dfrac {1} {T} \ : (K^ {−1})} \) » style="text-align:center ; « >1,74 × 10 ⁻³	−13 617
\ (\ mathrm {\ dfrac {1} {T} \ : (K^ {−1})} \) » style="text-align:center ; « >1,55 × 10 ⁻³	−9,362
\ (\ mathrm {\ dfrac {1} {T} \ : (K^ {−1})} \) » style="text-align:center ; « >1,43 × 10 ⁻³	−6 759
\ (\ mathrm {\ dfrac {1} {T} \ : (K^ {−1})} \) » style="text-align:center ; « >1,28 × 10 ⁻³	−3,231

La figure\(\PageIndex{5}\) est un graphique de ln k par rapport à\(\dfrac{1}{T}\). Pour déterminer la pente de la droite, nous avons besoin de deux valeurs de ln k, qui sont déterminées à partir de la droite à deux valeurs de\(\dfrac{1}{T}\) (une près de chaque extrémité de la ligne est préférable). Par exemple, la valeur de ln k déterminée à partir de la ligne où\(\dfrac{1}{T}=1.25×10^{−3}\) est de −2,593 ; la valeur quand\(\dfrac{1}{T}=1.78×10^{−3}\) est de −14,447.

alt — Figure\(\PageIndex{5}\) : Ce graphique montre la relation linéaire entre\(\ln k\) et\(\dfrac{1}{T}\) pour la réaction\(\ce{2HI ⟶ H2 + I2}\) selon l'équation d'Arrhenius.

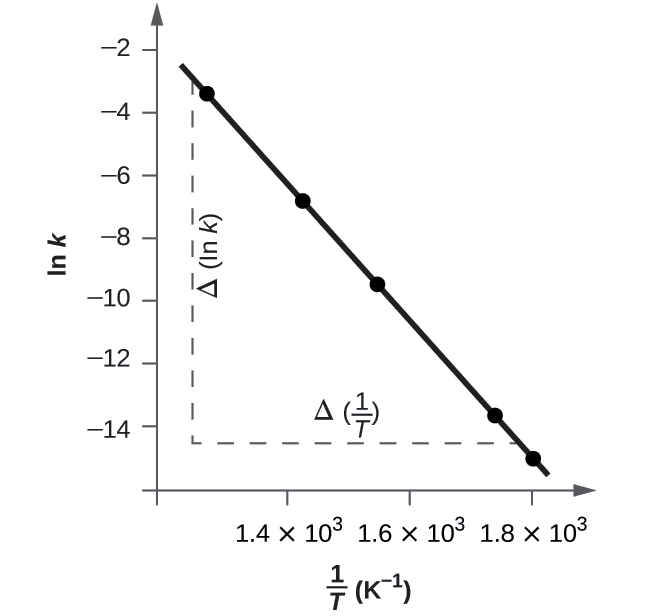
La pente de cette droite est donnée par l'expression suivante :

\ [\ begin {align*}
\ ce {Pente} &= \ dfrac {Δ (\ ln k)} {Δ \ left (\ dfrac {1} {T} \ right)} \ \
&= \ mathrm {\ dfrac {(−14,447) − (−2,593)} {(1,78 × 10^ {−3}} \ :K^ {−1}) − (1,78 × 10^ {−3} \ :K^ {−1}) − (1,78 × 10^ {−3} \ :K^ {−1}) − (1,78 × 10^ 25 × 10^ {−3} \ :K^ {−1})}} \ \
&= \ mathrm {\ dfrac {−11,854} {0,53 × 10^ {−3}} \ :K^ {−1}} =2,2 × 10^4 \ :K} \ \
&=− \ dfrac {E_ \ ce {a}} {R}
\ end {align*} \ nonumber \]

Ainsi :

\[ \begin{align*} E_\ce{a} &=\mathrm{−slope×\mathit R=−(−2.2×10^4\:K×8.314\: J\: mol^{−1}\:K^{−1})} \\[4pt] &=\mathrm{1.8×10^5\:J\: mol^{−1}} \end{align*} \nonumber \]

Dans de nombreuses situations, il est possible d'obtenir une estimation raisonnable de l'énergie d'activation sans passer par l'ensemble du processus de construction du diagramme d'Arrhenius. L'équation d'Arrhenius :

\[\ln k=\left(\dfrac{−E_\ce{a}}{R}\right)\left(\dfrac{1}{T}\right)+\ln A \nonumber \]

peut être réorganisé comme indiqué pour donner :

\[\dfrac{Δ(\ln k)}{Δ\left(\dfrac{1}{T}\right)}=−\dfrac{E_\ce{a}}{R} \nonumber \]

\[\ln\dfrac{k_1}{k_2}=\dfrac{E_\ce{a}}{R}\left(\dfrac{1}{T_2}−\dfrac{1}{T_1}\right) \nonumber \]

Cette équation peut être réorganisée pour donner un calcul en une étape afin d'obtenir une estimation de l'énergie d'activation :

\[E_\ce{a}=−R\left( \dfrac{\ln k_2−\ln k_1}{\left(\dfrac{1}{T_2}\right)−\left(\dfrac{1}{T_1}\right)}\right ) \nonumber \]

À l'aide des données expérimentales présentées ici, nous pouvons simplement sélectionner deux entrées de données. Pour cet exemple, nous sélectionnons la première et la dernière entrée :

Première et dernière entrée
(Royaume-Uni)	k (L/mol/s)	\(\dfrac{1}{T}\:(K^{-1})\)	en Royaume-Uni
555	3,52 × 10 ⁻⁷	\ (\ dfrac {1} {T} \ : (K^ {-1}) \) » style="text-align:center ; « >1,80 × 10 ⁻³	−14 860
781	3,95 × 10 ⁻²	\ (\ dfrac {1} {T} \ : (K^ {-1}) \) » style="text-align:center ; « >1,28 × 10 ⁻³	−3,231

Après avoir calculé\(\dfrac{1}{T}\) et ln k, on peut remplacer dans l'équation :

\[E_\ce{a}=\mathrm{−8.314\:J\:mol^{−1}\:K^{−1}\left(\dfrac{−3.231−(−14.860)}{1.28×10^{−3}\:K^{−1}−1.80×10^{−3}\:K^{−1}}\right)} \nonumber \]

et le résultat est E _a = 185 900 J/mol.

Cette méthode est très efficace, en particulier lorsqu'un nombre limité de constantes de vitesse dépendantes de la température sont disponibles pour la réaction d'intérêt.

Exercice\(\PageIndex{1}\)

La constante de vitesse pour la vitesse de décomposition de N ₂ O ₅ en NO et O ₂ en phase gazeuse est de 1,66 L/mol/s à 650 K et de 7,39 L/mol/s à 700 K :

\[\ce{2N2O5}(g)⟶\ce{4NO}(g)+\ce{3O2}(g) \nonumber \]

En supposant que la cinétique de cette réaction est conforme à l'équation d'Arrhenius, calculez l'énergie d'activation pour cette décomposition.

Réponse: 113 000 J/mol

Résumé

Les réactions chimiques nécessitent des collisions entre les espèces réactives. Ces collisions de réactifs doivent être correctement orientées et avoir une énergie suffisante pour entraîner la formation du produit. La théorie des collisions fournit une explication simple mais efficace de l'effet de nombreux paramètres expérimentaux sur les vitesses de réaction. L'équation d'Arrhenius décrit la relation entre la constante de vitesse d'une réaction et son énergie d'activation, sa température et sa dépendance à l'orientation de la collision.

Équations clés

\(k=Ae^{−E_a/RT}\)
\(\ln k=\left(\dfrac{−E_\ce{a}}{R}\right)\left(\dfrac{1}{T}\right)+\ln A\)
\(\ln\dfrac{k_1}{k_2}=\dfrac{E_\ce{a}}{R}\left(\dfrac{1}{T_2}−\dfrac{1}{T_1}\right)\)

Lexique

complexe activé: (également, état de transition) combinaison instable d'espèces réactives représentant l'état énergétique le plus élevé d'un système réactionnel

énergie d'activation (E _a): énergie nécessaire pour qu'une réaction ait lieu

Équation d'Arrhenius: relation mathématique entre la constante de vitesse et l'énergie d'activation d'une réaction

théorie des collisions: modèle qui met l'accent sur l'énergie et l'orientation des collisions moléculaires pour expliquer et prédire la cinétique des réactions

facteur de fréquence (A): constante de proportionnalité dans l'équation d'Arrhenius, liée au nombre relatif de collisions ayant une orientation susceptible de conduire à la formation de produits