Home
Français
Chimie 1e (OpenStax)
12 : Cinétique
12.6 : Mécanismes réactionnels

12.6 : Mécanismes réactionnels

Last updated
Save as PDF

Page ID: 193971

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

⦁

Objectifs d'apprentissage

Distinguer les réactions nettes des réactions élémentaires (étapes)
Identifier la moléculaire des réactions élémentaires
Ecrire une équation chimique équilibrée pour un processus en fonction de son mécanisme de réaction
Dériver la loi de vitesse compatible avec un mécanisme de réaction donné

Une équation équilibrée pour une réaction chimique indique ce qui réagit et ce qui est produit, mais elle ne révèle rien sur la manière dont la réaction se produit réellement. Le mécanisme de réaction (ou voie de réaction) est le processus, ou la voie, par lequel une réaction se produit. Une réaction chimique se produit souvent par étapes, bien qu'elle ne soit pas toujours évidente pour un observateur. La décomposition de l'ozone, par exemple, semble suivre un mécanisme en deux étapes :

\ [\ ce {O3} (g) ⟶ \ ce {O2} (g) + \ ce {O} \
\ ce {O} + \ ce {O3} (g) ⟶ \ ce {2O2} (g) \ étiquette {12,7.1} \]

Chaque étape d'un mécanisme de réaction est appelée réaction élémentaire. Les réactions élémentaires se produisent exactement telles qu'elles sont écrites et ne peuvent pas être décomposées en étapes plus simples. Les réactions élémentaires s'additionnent à la réaction globale qui, pour la décomposition, est la suivante :

\[\ce{2O3}(g)⟶\ce{3O2}(g) \label{12.7.2} \]

Notez que l'atome d'oxygène produit lors de la première étape de ce mécanisme est consommé lors de la deuxième étape et n'apparaît donc pas sous forme de produit dans la réaction globale. Les espèces produites en une étape et consommées lors d'une étape ultérieure sont appelées intermédiaires.

Alors que l'équation de réaction globale pour la décomposition de l'ozone indique que deux molécules d'ozone réagissent pour donner trois molécules d'oxygène, le mécanisme de la réaction n'implique pas la collision et la réaction de deux molécules d'ozone. Il s'agit plutôt d'une molécule d'ozone qui se décompose en une molécule d'oxygène et un atome d'oxygène intermédiaire ; l'atome d'oxygène réagit ensuite avec une deuxième molécule d'ozone pour donner deux molécules d'oxygène. Ces deux réactions élémentaires se produisent exactement comme le montre le mécanisme de réaction.

Réactions élémentaires unimoléculaires

La moléculaire d'une réaction élémentaire est le nombre d'espèces réactives (atomes, molécules ou ions). Par exemple, une réaction unimoléculaire implique le réarrangement d'une seule espèce réactive pour produire une ou plusieurs molécules de produit :

\[A⟶\ce{products} \label{12.7.2b} \]

L'équation de vitesse pour une réaction unimoléculaire est la suivante :

\[\ce{rate}=k[A] \label{12.7.3} \]

Une réaction unimoléculaire peut être l'une des nombreuses réactions élémentaires d'un mécanisme complexe. Par exemple, la réaction :

\[\ce{O3 ⟶ O2 + O} \label{12.7.4} \]

illustre une réaction élémentaire unimoléculaire qui se produit dans le cadre d'un mécanisme de réaction en deux étapes. Cependant, certaines réactions unimoléculaires peuvent n'avoir qu'une seule réaction dans le mécanisme de réaction. (En d'autres termes, une réaction élémentaire peut également être une réaction globale dans certains cas.) Par exemple, la décomposition en phase gazeuse du cyclobutane, C ₄ H ₈, en éthylène, C ₂ H ₄, se fait par un mécanisme unimoléculaire en une seule étape :

Dans cette figure, des formules structurales sont utilisées pour illustrer une réaction chimique. Sur la gauche, une formule structurale pour le cyclobutane est présentée. Cette structure est composée de 4 atomes de carbone reliés par des liaisons simples de forme carrée. Chaque atome de C est lié à deux autres atomes de C de la structure, laissant deux liaisons pour les atomes H pointant vers l'extérieur au-dessus, en dessous, à gauche et à droite. Une flèche pointe vers la droite vers deux molécules d'éthane identiques séparées par un symbole plus. Chacune de ces molécules contient deux atomes de carbone connectés par une double liaison orientée verticalement entre eux. L'atome C au sommet de ces molécules possède des atomes H liés au-dessus à droite et à gauche. De même, l'atome C inférieur possède deux atomes H liés en dessous à droite et à gauche.

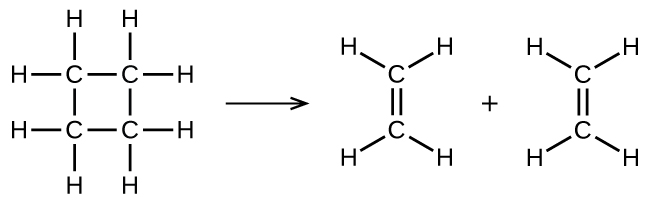
Pour que ces réactions unimoléculaires se produisent, il suffit de séparer les parties des molécules d'un seul réactif en produits.

Les liaisons chimiques ne s'effondrent pas simplement lors de réactions chimiques. De l'énergie est nécessaire pour rompre les liaisons chimiques. L'énergie d'activation pour la décomposition du C ₄ H ₈, par exemple, est de 261 kJ par mole. Cela signifie qu'il faut 261 kilojoules pour déformer une mole de ces molécules en complexes activés qui se décomposent en produits :

Dans cette figure, des formules structurales sont utilisées pour illustrer une réaction chimique, y compris une étape intermédiaire. Sur la gauche, une formule structurale pour le cyclobutane est présentée. Cette structure est composée de 4 atomes de carbone reliés par des liaisons simples de forme carrée. Chaque atome de C est lié à deux autres atomes de C de la structure, laissant deux liaisons pour les atomes H pointant vers l'extérieur au-dessus, en dessous, à gauche et à droite. Cette structure est étiquetée « Cyclohexane ». Une flèche pointe vers la droite vers une structure similaire dont les liaisons supérieure et inférieure sont remplacées par des rangées de 4 points. De même, des colonnes de 3 points apparaissent juste à l'intérieur des segments de ligne indiquant les liaisons simples orientées verticalement dans la structure. L'étiquette « Complexe activé » apparaît sous cette structure. Une deuxième flèche pointe vers la droite vers deux molécules d'éthane identiques séparées par un symbole plus. Chacune de ces molécules contient deux atomes de carbone connectés par une double liaison orientée verticalement entre eux. L'atome C au sommet de ces molécules possède des atomes H liés au-dessus à droite et à gauche. De même, l'atome C inférieur possède deux atomes H liés en dessous à droite et à gauche. Sous ces deux molécules apparaît l'étiquette « éthylène ».

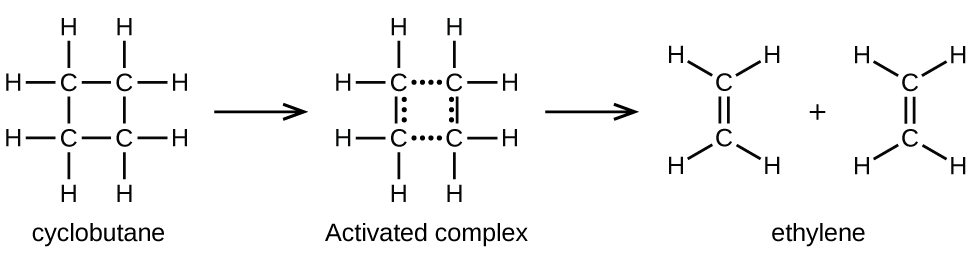
Dans un échantillon de C ₄ H ₈, quelques-unes des molécules de C ₄ H ₈ se déplaçant rapidement entrent en collision avec d'autres molécules se déplaçant rapidement et captent de l'énergie supplémentaire. Lorsque les molécules de C ₄ H ₈ gagnent suffisamment d'énergie, elles peuvent se transformer en un complexe activé et la formation de molécules d'éthylène peut se produire. En effet, une collision particulièrement énergétique fait entrer une molécule de C ₄ H ₈ dans la géométrie du complexe activé. Cependant, seule une petite fraction des molécules de gaz se déplace à des vitesses suffisamment élevées avec des énergies cinétiques suffisamment importantes pour y parvenir. Ainsi, à tout moment, seules quelques molécules captent suffisamment d'énergie lors des collisions pour réagir.

La vitesse de décomposition du C ₄ H ₈ est directement proportionnelle à sa concentration. Doubler la concentration de C ₄ H ₈ dans un échantillon permet d'obtenir deux fois plus de molécules par litre. Bien que la fraction de molécules ayant suffisamment d'énergie pour réagir reste la même, le nombre total de ces molécules est deux fois plus élevé. Par conséquent, il y a deux fois plus de C ₄ H ₈ par litre, et la vitesse de réaction est deux fois plus rapide :

\[\ce{rate}=−\dfrac{Δ[\ce{C4H8}]}{Δt}=k[\ce{C4H8}] \label{12.7.5} \]

Une relation similaire s'applique à toute réaction élémentaire unimoléculaire ; la vitesse de réaction est directement proportionnelle à la concentration du réactif et la réaction présente un comportement de premier ordre. La constante de proportionnalité est la constante de vitesse pour la réaction unimoléculaire particulière.

Réactions élémentaires bimoléculaires

La collision et la combinaison de deux molécules ou atomes pour former un complexe activé dans une réaction élémentaire sont appelées réaction bimoléculaire. Il existe deux types de réactions élémentaires bimoléculaires :

\[A+B⟶\ce{products} \label{12.7.6} \]

\[2A⟶\ce{products} \label{12.7.7} \]

Pour le premier type, dans lequel les deux molécules réactives sont différentes, la loi de vitesse est du premier ordre en A et du premier ordre en B :

\[\ce{rate}=k[A][B] \label{12.7.8} \]

Pour le second type, dans lequel deux molécules identiques entrent en collision et réagissent, la loi de vitesse est du second ordre dans A :

\[\ce{rate}=k[A][A]=k[A]^2 \label{12.7.9} \]

Certaines réactions chimiques ont des mécanismes qui consistent en une seule réaction élémentaire bimoléculaire. Un exemple est la réaction du dioxyde d'azote avec le monoxyde de carbone :

\[\ce{NO2}(g)+\ce{CO}(g)⟶\ce{NO}(g)+\ce{CO2}(g) \label{12.7.10} \]

(voir Figure\(\PageIndex{1}\))

Figure\(\PageIndex{1}\) : Le mécanisme probable de la réaction entre\(\ce{NO_2}\) et\(\ce{CO}\) pour donner\(\ce{NO}\) et\(\ce{CO_2}\).

Les réactions élémentaires bimoléculaires peuvent également être impliquées en tant qu'étapes d'un mécanisme de réaction à étapes multiples. La réaction de l'oxygène atomique avec l'ozone en est un exemple :

\[\ce{O}(g)+\ce{O3}(g)⟶\ce{2O2}(g) \label{12.7.12} \]

Réactions élémentaires termoléculaires

Une réaction termoléculaire élémentaire implique la collision simultanée de trois atomes, molécules ou ions. Les réactions élémentaires termoléculaires sont rares car la probabilité que trois particules entrent en collision simultanément est inférieure au millième de la probabilité que deux particules entrent en collision. Il existe cependant quelques réactions élémentaires termoléculaires établies. La réaction de l'oxyde nitrique avec l'oxygène semble impliquer des étapes termoléculaires :

\ [\ ce {2NO + O2 ⟶ 2NO2} \ \
\ ce {taux} =k [\ ce {NO}] ^2 [\ ce {O2}] \ étiquette {12.7.13} \]

De même, la réaction de l'oxyde nitrique avec le chlore semble impliquer des étapes termoléculaires :

\ [\ ce {2NO + Cl2 ⟶ 2NOCl} \
\ \ ce {taux} =k [\ ce {NO}] ^2 [\ ce {Cl2}] \ étiquette {12.7.14} \]

Associer les mécanismes de réaction aux lois des taux

Il arrive souvent qu'une étape d'un mécanisme de réaction en plusieurs étapes soit nettement plus lente que les autres. Comme une réaction ne peut pas se dérouler plus rapidement que son étape la plus lente, cette étape limitera la vitesse à laquelle la réaction globale se produit. L'étape la plus lente est donc appelée étape de limitation de vitesse (ou étape de détermination de la vitesse) de la réaction Figure\(\PageIndex{2}\).

Figure\(\PageIndex{2}\) : Un parachute à bétail est un exemple non chimique d'une étape qui détermine le taux. Le bétail ne peut être déplacé d'un enclos à l'autre que si un animal peut se frayer un chemin dans la goulotte. (crédit : Loren Kerns)

Comme décrit précédemment, les lois de vitesse peuvent être dérivées directement des équations chimiques pour les réactions élémentaires. Ce n'est toutefois pas le cas pour les réactions chimiques ordinaires. Les équations équilibrées les plus souvent rencontrées représentent le changement global d'un système chimique, et cela est très souvent le résultat de certains mécanismes de réaction en plusieurs étapes. Dans tous les cas, nous devons déterminer la loi des taux globale à partir de données expérimentales et en déduire le mécanisme à partir de la loi des taux (et parfois à partir d'autres données). La réaction du NO ₂ et du CO fournit un exemple illustratif :

\[\ce{NO2}(g)+\ce{CO}(g)⟶\ce{CO2}(g)+\ce{NO}(g) \nonumber \]

Pour les températures supérieures à 225 °C, la loi de vitesse s'est révélée être la suivante :

\[\ce{rate}=k[\ce{NO2}][\ce{CO}] \nonumber \]

La réaction est du premier ordre par rapport au NO ₂ et du premier ordre par rapport au CO. Ceci est compatible avec un mécanisme bimoléculaire en une seule étape et il est possible que ce soit le mécanisme de cette réaction à des températures élevées.

À des températures inférieures à 225 °C, la réaction est décrite par une loi de vitesse du second ordre par rapport au NO ₂ :

\[\ce{rate}=k[\ce{NO2}]^2 \nonumber \]

Ceci est conforme à un mécanisme qui implique les deux réactions élémentaires suivantes, dont la première est plus lente et constitue donc l'étape déterminante :

\ [\ ce {NO2} (g) + \ ce {NO2} (g) ⟶ \ ce {NO3} (g) + \ ce {NO} (g) \ : \ ce {(lent)} \
\ ce {NO3} (g) + \ ce {CO} (g) ⟶ \ ce {NO2} (g) + \ ce {CO2} (g) \ : \ ce {rapide)} \ aucun numéro \]

L'étape de détermination de la vitesse donne une loi de vitesse indiquant une dépendance du second ordre à l'égard de la concentration de NO ₂, et la somme des deux équations donne la réaction globale nette.

En général, lorsque l'étape de détermination de la vitesse (plus lente) est la première étape d'un mécanisme, la loi de vitesse pour la réaction globale est la même que la loi de vitesse pour cette étape. Toutefois, lorsque l'étape de détermination de la vitesse est précédée d'une étape impliquant une réaction d'équilibre, la loi de vitesse pour la réaction globale peut être plus difficile à déduire.

Une réaction élémentaire est à l'équilibre lorsqu'elle se déroule à la fois dans le sens avant et dans le sens inverse à des vitesses égales. Considérons la dimérisation de NO en N ₂ O ₂, avec k ₁ utilisé pour représenter la constante de vitesse de la réaction directe et k _-1 pour représenter la constante de vitesse de la réaction inverse :

\[\ce{NO + NO ⇌ N2O2} \nonumber \]

\[\ce{rate_{forward}=rate_{reverse}} \nonumber \]

\[k_1[\ce{NO}]^2=k_{−1}[\ce{N2O2}] \nonumber \]

Si N ₂ O ₂ était un intermédiaire dans un mécanisme, cette expression pourrait être réarrangée pour représenter la concentration de N _{2 O ₂} dans l'expression globale de la loi de vitesse à l'aide d'une manipulation algébrique :

\[\mathrm{\left(\dfrac{k_1[NO]^2}{k_{−1}}\right)=[N_2O_2]} \nonumber \]

Cependant, encore une fois, les intermédiaires ne peuvent pas être répertoriés dans l'expression globale de la loi de vitesse, bien qu'ils puissent être inclus dans une réaction élémentaire individuelle d'un mécanisme. L'exemple\(\PageIndex{1}\) illustrera comment dériver des lois de taux globales à partir de mécanismes impliquant des étapes d'équilibre précédant l'étape de détermination du taux.

Exemple\(\PageIndex{1}\): Deriving the Overall Rate Law Expression for a Multistep Reaction

Mécanisme Le chlorure de nitryle (NO ₂ Cl) se décompose en dioxyde d'azote (NO ₂) et en chlore gazeux (Cl ₂) selon le mécanisme suivant :

\(\ce{2NO2Cl}(g)⇌\ce{ClO2}(g)+\ce{N2O}(g)+\ce{ClO}(g)\)(rapide, k ₁ représente la constante de vitesse pour la réaction directe et k _-1 la constante de vitesse pour la réaction inverse)
\(\ce{N2O}(g)+\ce{ClO2}(g)⇌\ce{NO2}(g)+\ce{NOCl}(g)\)(rapide, k ₂ pour la réaction directe, k _-2 pour la réaction inverse)
\(\ce{NOCl + ClO ⟶ NO2 + Cl2}\)(lent, k ₃ la constante de vitesse pour la réaction directe)

Déterminez la réaction globale, écrivez l'expression de la loi de vitesse pour chaque réaction élémentaire, identifiez tout intermédiaire et déterminez l'expression globale de la loi de vitesse.

Solution

Pour la réaction globale, il suffit de faire la somme des trois étapes, d'annuler les intermédiaires et de combiner les formules similaires :

\[\ce{2NO2Cl}(g)⟶\ce{2NO2}(g)+\ce{Cl2}(g) \nonumber \]

Ensuite, écrivez l'expression de la loi de vitesse pour chaque réaction élémentaire. N'oubliez pas que pour les réactions élémentaires qui font partie d'un mécanisme, l'expression de la loi de vitesse peut être dérivée directement de la stœchiométrie :

\ [\ begin {align*}
k_1 \ ce {[NO2Cl] 2} &=k_ {−1} \ ce {[ClO2] [N2O] [ClO]} \ \
k_2 \ ce {[N2O] [ClO2]} &=k_ {−2} \ ce {[NO2] [NOcl]} \
\ ce {Taux} &=k_3 \ ce {[NoCl] [ClO]}
\ end {align*} \ nonnumber \]

La troisième étape, qui est l'étape lente, est l'étape qui détermine le taux. Par conséquent, l'expression globale de la loi de vitesse pourrait être écrite comme Rate = k ₃ [NOCl] [CLo]. Cependant, le NOCl et le ClO sont tous deux des intermédiaires. Des expressions algébriques doivent être utilisées pour représenter [NoCl] et [ClO] de telle sorte qu'aucun intermédiaire ne reste dans l'expression globale de la loi des taux.

En utilisant la réaction élémentaire 1,\(\ce{[ClO]}=\dfrac{k_1\ce{[NO2Cl]^2}}{k_{−1}\ce{[ClO2][N2O]}}\).
En utilisant la réaction élémentaire 2,\(\ce{[NOCl]}=\dfrac{k_2\ce{[N2O][ClO2]}}{k_{−2}\ce{[NO2]}}\).

Remplacez maintenant ces expressions algébriques dans l'expression globale de la loi des taux et simplifiez :

\ [\ begin {align*}
\ ce {taux} &=k_3 \ left (\ dfrac {k_2 \ ce {[N2O] [ClO2]}} {k_ {−2} \ ce {[NO2]}} \ right) \ left (\ dfrac {k_1 \ ce {[NO2Cl] ^2}} {k_ {−1} \ ce [ClO2] [N2O]}} \ droite) \ \
\ ce {taux} &= \ dfrac {k_3k_2k_1 \ ce {[NO2Cl] ^2}} {k_ {−2} k_ {−1} \ ce {[NO2]}}
\ end {align*} \ nonumber \]

Notez que cette loi de vitesse montre une dépendance inverse à la concentration de l'une des espèces de produits, ce qui correspond à la présence d'une étape d'équilibre dans le mécanisme de réaction.

Exercice\(\PageIndex{1}\)

Le chlore atomique présent dans l'atmosphère réagit avec l'ozone dans les deux réactions élémentaires suivantes :

\(\ce{Cl}+\ce{O3}(g)⟶\ce{ClO}(g)+\ce{O2}(g)\hspace{20px}(\textrm{rate constant }k_1)\)

\(\ce{ClO}(g)+\ce{O}⟶\ce{Cl}(g)+\ce{O2}(g)\hspace{20px}(\textrm{rate constant }k_2)\)

Réponse

réaction globale :\(\ce{O3}(g)+\ce{O}⟶\ce{2O2}(g)\)
taux ₁ = k ₁ [O ₃] [Cl] ; taux ₂ = k ₂ [ClO] [O]
intermédiaire : ClO (g)
taux global = k ₂ k ₁ [O ₃] [Cl] [O]

Résumé

La séquence des étapes individuelles, ou réactions élémentaires, par lesquelles les réactifs sont convertis en produits au cours d'une réaction est appelée mécanisme de réaction. La vitesse globale d'une réaction est déterminée par la vitesse de l'étape la plus lente, appelée étape déterminante de la vitesse. Les réactions élémentaires unimoléculaires ont des lois de vitesse du premier ordre, tandis que les réactions élémentaires bimoléculaires ont des lois de vitesse du second ordre. En comparant les lois de vitesse dérivées d'un mécanisme de réaction à celles déterminées expérimentalement, le mécanisme peut être considéré comme incorrect ou plausible.

Notes

Cette question est tirée de l'examen de placement avancé en chimie et est utilisée avec l'autorisation du Service des tests éducatifs.

Lexique

réaction bimoléculaire: réaction élémentaire impliquant la collision et la combinaison de deux espèces réactives

réaction élémentaire: réaction qui se produit exactement comme indiqué dans son équation chimique

intermédiaire: molécule ou ion produit lors d'une étape d'un mécanisme de réaction et consommé dans une autre

moléculaire: nombre d'espèces réactives (atomes, molécules ou ions) impliquées dans une réaction élémentaire

étape de détermination du taux: (également étape de limitation de vitesse) réaction élémentaire la plus lente d'un mécanisme de réaction ; détermine la vitesse de la réaction globale

mécanisme de réaction: séquence par étapes de réactions élémentaires par lesquelles se produit un changement chimique

réaction termoléculaire: réaction élémentaire impliquant la collision et la combinaison simultanées de trois espèces réactives

réaction unimoléculaire: réaction élémentaire impliquant le réarrangement d'une seule espèce réactive pour produire une ou plusieurs molécules de produit