12.4 : Lois tarifaires intégrées
- Page ID
- 193960
- Expliquer la forme et la fonction d'une loi tarifaire intégrée
- Effectuer des calculs intégrés de la loi de vitesse pour les réactions de zéro, de premier et de second ordre
- Définir la demi-vie et effectuer les calculs correspondants
- Déterminer l'ordre d'une réaction à partir des données de concentration/temps
Les lois de vitesse que nous avons vues jusqu'à présent relient le taux et les concentrations de réactifs. Nous pouvons également déterminer une deuxième forme de chaque loi de vitesse qui relie les concentrations de réactifs et le temps. Ces lois sont appelées lois tarifaires intégrées. Nous pouvons utiliser une loi de vitesse intégrée pour déterminer la quantité de réactif ou de produit présente après un certain temps ou pour estimer le temps requis pour qu'une réaction se produise dans une certaine mesure. Par exemple, une loi de débit intégrée est utilisée pour déterminer la durée pendant laquelle une matière radioactive doit être stockée pour que sa radioactivité atteigne un niveau sûr.
À l'aide du calcul, la loi de vitesse différentielle pour une réaction chimique peut être intégrée en fonction du temps pour donner une équation qui relie la quantité de réactif ou de produit présent dans un mélange réactionnel au temps écoulé de la réaction. Ce processus peut être très simple ou très complexe, selon la complexité de la loi des taux différentiels. À des fins de discussion, nous nous concentrerons sur les lois de taux intégrées qui en résultent pour les réactions d'ordre 1, 2 et zéro.
Réactions de premier ordre
Une équation reliant la constante de vitesse\(k\) à la concentration initiale\([A]_0\) et à la concentration\([A]_t\) présente après un certain temps\(t\) peut être dérivée pour une réaction du premier ordre et présentée comme suit :
\[\ln\left(\dfrac{[A]_t}{[A]_0}\right)=−kt \nonumber \]
ou bien
\[\ln\left(\dfrac{[A]_0}{[A]_t}\right)=kt \nonumber \]
ou
\[[A]=[A]_0e^{−kt} \nonumber \]
La constante de vitesse pour la décomposition du premier ordre du cyclobutane,\(\ce{C4H8}\) à 500 °C, est de 9,2 × 10 −3 s −1 :
\[\ce{C4H8⟶2C2H4} \nonumber \]
Combien de temps faudra-t-il pour que 80 % d'un échantillon de C 4 H 8 se décompose ?
Solution
Nous utilisons la forme intégrée de la loi tarifaire pour répondre aux questions concernant le temps :
\[\ln\left(\dfrac{[A]_0}{[A]}\right)=kt \nonumber \]
La loi des taux comporte quatre variables, donc si nous en connaissons trois, nous pouvons déterminer la quatrième. Dans ce cas, nous connaissons [A] 0, [A] et k, et nous devons trouver t.
La concentration initiale de C 4 H 8, [A] 0, n'est pas fournie, mais la condition selon laquelle 80,0 % de l'échantillon est décomposé est suffisante pour résoudre ce problème. Soit x la concentration initiale, auquel cas la concentration après une décomposition à 80,0 % est de 20,0 % de x ou 0,200 x. En réorganisant la loi des taux pour isoler t et en substituant les quantités fournies, on obtient :
\ [\ begin {align*}
t&= \ ln \ dfrac {[x]} {[0,200x]} × \ dfrac {1} {k} \ \ [4 points]
&= \ mathrm {\ ln \ dfrac {0,100 \ :mol \ : L^ {−1}} {0,020 \ :mol \ : L^ {−1}} × \ dfrac {1} {9,2 × 10^ {−3} \ :s^ {−1}}} \ \ [4 points]
&= \ mathrm {1,609× \ dfrac {1} {9,2 × 10^ {−3} \ :s^ {−1}}} \ \ [4 points]
&= \ mathrm {1,7 × 10^ 2 \ :s}
\ end {align*} \ nonumber \]
L'iode 131 est un isotope radioactif utilisé pour diagnostiquer et traiter certaines formes de cancer de la thyroïde. L'iode 131 se désintègre en xénon-131 selon l'équation :
\[\textrm{I-131 ⟶ Xe-131 + electron} \nonumber \]
La décroissance est du premier ordre avec une constante de vitesse de 0,138 d -1. Toute désintégration radioactive est de premier ordre. Combien de jours faudra-t-il pour que 90 % de l'iode 131 contenu dans une solution à 0,500 M de cette substance se désintègre en Xe-131 ?
- Réponse
-
16,7 jours
Nous pouvons utiliser des lois de vitesse intégrées avec des données expérimentales qui consistent en des informations sur le temps et la concentration pour déterminer l'ordre et la constante de vitesse d'une réaction. La loi de taux intégrée peut être réorganisée selon un format d'équation linéaire standard :
\ [\ begin {align}
\ ln [A] & =( −k) (t) + \ ln [A] _0 \ label {in1st} \ \ [4pt]
y&=mx+b
\ end {align} \ nonumber \]
Un diagramme de\(\ln[A]\) versus\(t\) pour une réaction de premier ordre est une ligne droite avec une pente\(−k\) et une intersection de\(\ln[A]_0\). Si un ensemble de données de vitesse est tracé de cette façon mais n'aboutit pas à une ligne droite, la réaction n'est pas du premier ordre\(A\).
Montrez que les données de cette figure peuvent être représentées par une loi de vitesse du premier ordre en représentant graphiquement ln [H 2 O 2] en fonction du temps. Déterminer la constante de vitesse pour la vitesse de décomposition de H 2 O 2 à partir de ces données.
Solution
Les données de cette figure additionnées des valeurs de ln [H 2 O 2] sont données dans la figure\(\PageIndex{1}\).
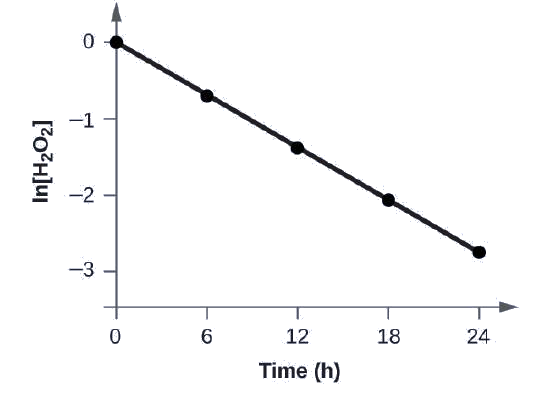
| Procès | Heure (h) | [H 2 O 2] (M) | ln [H 2 O 2] |
|---|---|---|---|
| 1 | 0 | 1 000 | 0,0 |
| 2 | 6,00 | 0,500 | −0,693 |
| 3 | 12h00 | 0,250 | −1,386 |
| 4 | 18h00 | 0,125 | −2 079 |
| 5 | 24,00 | 0,0625 | −2,772 |
Le diagramme de ln [H 2 O 2] en fonction du temps étant linéaire, nous avons vérifié que la réaction peut être décrite par une loi de vitesse du premier ordre.
La constante de vitesse pour une réaction du premier ordre est égale à la valeur négative de la pente du diagramme de ln [H 2 O 2] en fonction du temps où :
\[\ce{slope}=\dfrac{\textrm{change in }y}{\textrm{change in }x}=\dfrac{Δy}{Δx}=\dfrac{Δ\ln[\ce{H2O2}]}{Δt} \nonumber \]
Pour déterminer la pente de la droite, nous avons besoin de deux valeurs de ln [H 2 O 2] à des valeurs différentes de t (une à proximité de chaque extrémité de la ligne est préférable). Par exemple, la valeur de ln [H 2 O 2] lorsque t est de 6,00 h est de −0,693 ; la valeur lorsque t = 12,00 h est de −1,386 :
\ [\ begin {align*}
\ ce {pente} &= \ mathrm {\ dfrac {−1,386− (−0,693)} {12,00 \ : h−6,00 \ : h}} \ \ [4 points]
&= \ mathrm {\ dfrac {−0,693} {6,00 \ : h}} \ \ [4 points] &= \ mathrm {−0,693} {6,00 \ : h}} \ \ [4 points]
&= \ mathrm {−1,155 × 10^ {−2} \ :h^ {−1}} \ \ [4 points]
k&= \ mathrm {−slope=− (−1,155 × 10^ {−1} \ :h^ {−1}) =1,155 × 10^ {−1} \ :h^ {−1} }
\ end {align*} \ nonumber \]
Représentez graphiquement les données suivantes pour déterminer si la réaction\(A⟶B+C\) est de premier ordre.
| Procès | Heure (s) | [A] |
|---|---|---|
| 1 | 4,0 | 0,220 |
| 2 | 8,0 | 0,144 |
| 3 | 12,0 | 0,110 |
| 4 | 16,0 | 0,088 |
| 5 | 20,0 | 0,074 |
- Réponse
-
Le diagramme de ln [A] par rapport à t n'est pas une ligne droite. L'équation n'est pas de premier ordre :
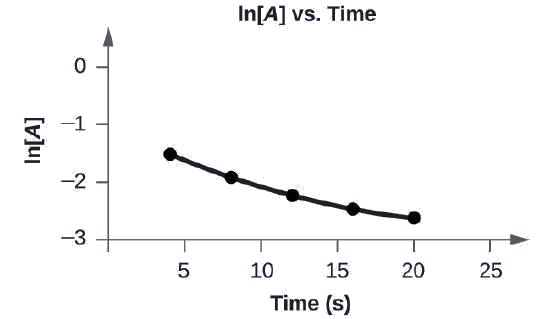
Un graphique, intitulé ci-dessus « l n [A] vs. Time » est affiché. L'axe X est étiqueté « Temps (s) » et l'axe y est étiqueté « l n [A] ». L'axe X montre les marquages à 5, 10, 15, 20 et 25 heures. L'axe Y montre les marques à moins 3, moins 2, moins 1 et 0. Une légère courbe est tracée reliant cinq points aux coordonnées approximatives (4, négatif 1,5), (8, négatif 2), (12, négatif 2,2), (16, négatif 2,4) et (20, négatif 2,6).
Réactions de second ordre
Les équations qui relient les concentrations de réactifs et la constante de vitesse des réactions de second ordre sont assez compliquées. Nous nous limiterons aux réactions de second ordre les plus simples, à savoir celles dont la vitesse dépend de la concentration d'un seul réactif et qui est décrite par la loi des vitesses différentielles :
\[\ce{Rate}=k[A]^2 \nonumber \]
Pour ces réactions de second ordre, la loi de vitesse intégrée est la suivante :
\[\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0} \label{int2nd} \]
où les termes de l'équation ont leur signification habituelle telle que définie précédemment.
La réaction du gaz butadiène (C 4 H 6) avec lui-même produit du gaz C 8 H 12 comme suit :
\[\ce{2C4H6}(g)⟶\ce{C8H12(g)} \nonumber \]
La réaction est du second ordre avec une constante de vitesse égale à 5,76 × 10 -2 L/mol/min dans certaines conditions. Si la concentration initiale de butadiène est de 0,200 M, quelle est la concentration restante après 10 min ?
Solution
Nous utilisons la forme intégrée de la loi tarifaire pour répondre aux questions concernant le temps. Pour une réaction de second ordre, nous avons :
\[\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0} \nonumber \]
Nous connaissons trois variables dans cette équation : [A] 0 = 0,200 mol/L, k = 5,76 × 10 −2 L/mol/min et t = 10,0 min. Par conséquent, nous pouvons résoudre pour [A], la quatrième variable :
\ [\ begin {align*}
\ dfrac {1} {[A]} &= \ mathrm {(5,76 × 10^ {−2} \ :L \ : mol^ {−1} \ :min^ {−1}) (10 \ :min) + \ dfrac {1} {0,200 \ :mol^ {−1}}} \ \ [4 points]
\ dfrac {1} 1} {[A]} &= \ mathrm {(5,76 × 10^ {−1}} \ :L \ : mol^ {−1}) +5,00 \ :L \ : mol^ {−1}} \ \ [4 points]
\ dfrac {1} {[A]} &= \ mathrm {5,58 \ :L \ : mol^ {−1}} \ \ [4 points]
[A] &= \ mathrm {1,79 × 10^ {−1} \ :mol \ : L^ {−1}}
\ end {align*} \ nonnumber \]
Il reste donc 0,179 mol/L de butadiène au bout de 10,0 min, contre 0,200 mol/L initialement présent.
Si la concentration initiale de butadiène est de 0,0200 M, quelle est la concentration restante après 20 min ?
- Réponse
-
0,0196 mol/L
La loi de vitesse intégrée pour nos réactions du second ordre prend la forme de l'équation d'une droite :
\ [\ begin {align*}
\ dfrac {1} {[A]} &=kt+ \ dfrac {1} {[A] _0} \ \ [4 points]
y&=mx+b
\ end {align*} \ nonnumber \]
Un diagramme de\(\dfrac{1}{[A]}\) versus t pour une réaction du second ordre est une droite avec une pente de k et une intersection de\(\dfrac{1}{[A]_0}\). Si le tracé n'est pas une ligne droite, alors la réaction n'est pas de second ordre.
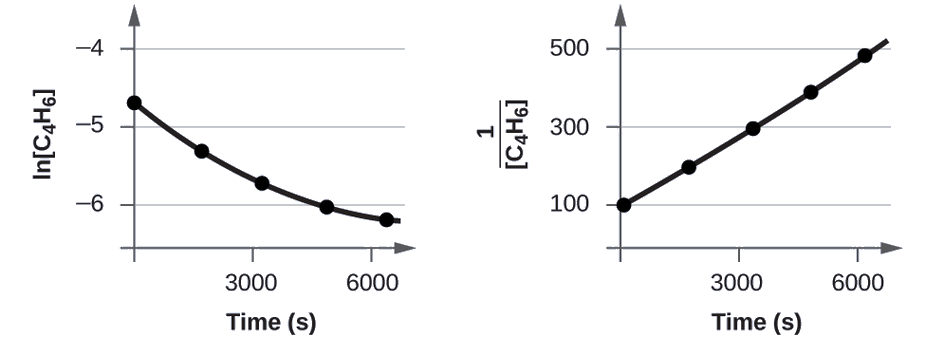
Testez les données fournies pour montrer si la dimérisation du C 4 H 6 est une réaction du premier ou du second ordre.
Solution
| Procès | Heure (s) | [C 4 H 6] (M) |
|---|---|---|
| 1 | 0 | 1,00 × 10 −2 |
| 2 | 1600 | 5,04 × 10 −3 |
| 3 | 3200 | 3,37 × 10 −3 |
| 4 | 4800 | 2,53 × 10 −3 |
| 5 | 6200 | 2,08 × 10 −3 |
Afin de distinguer une réaction de premier ordre d'une réaction de second ordre, nous tracons ln [C 4 H 6] par rapport à t et nous la comparons à un graphique de\(\mathrm{\dfrac{1}{[C_4H_6]}}\) versus t. Les valeurs nécessaires pour ces diagrammes sont présentées ci-dessous.
| Heure (s) | \(\dfrac{1}{[\ce{C4H6}]}\:(M^{−1})\) | sur [C 4 H 6] |
|---|---|---|
| 0 | \ (\ dfrac {1} {[\ ce {C4H6}]} \ : (M^ {−1}) \) » style="text-align:center ; « >100 | −4 605 |
| 1600 | \ (\ dfrac {1} {[\ ce {C4H6}]} \ : (M^ {−1}) \) » style="text-align:center ; « >198 | −5 289 |
| 3200 | \ (\ dfrac {1} {[\ ce {C4H6}]} \ : (M^ {−1}) \) » style="text-align:center ; « >296 | −5,692 |
| 4800 | \ (\ dfrac {1} {[\ ce {C4H6}]} \ : (M^ {−1}) \) » style="text-align:center ; « >395 | −5,978 |
| 6200 | \ (\ dfrac {1} {[\ ce {C4H6}]} \ : (M^ {−1}) \) » style="text-align:center ; « >481 | −6,175 |
Les diagrammes sont présentés dans la figure\(\PageIndex{2}\). Comme vous pouvez le constater, le diagramme de ln [C 4 H 6] par rapport à t n'est pas linéaire, donc la réaction n'est pas du premier ordre. Le diagramme de\(\dfrac{1}{[\ce{C4H6}]}\) versus t est linéaire, ce qui indique que la réaction est de second ordre.
Les données suivantes correspondent-elles à une loi tarifaire de second ordre ?
| Procès | Heure (s) | [A] (M) |
|---|---|---|
| 1 | 5 | 0,952 |
| 2 | 10 | 0,625 |
| 3 | 15 | 0,465 |
| 4 | 20 | 0,370 |
| 5 | 25 | 0,308 |
| 6 | 35 | 0,230 |
- Réponse
-
Oui. Le diagramme de\(\dfrac{1}{[A]}\) vs. t est linéaire :
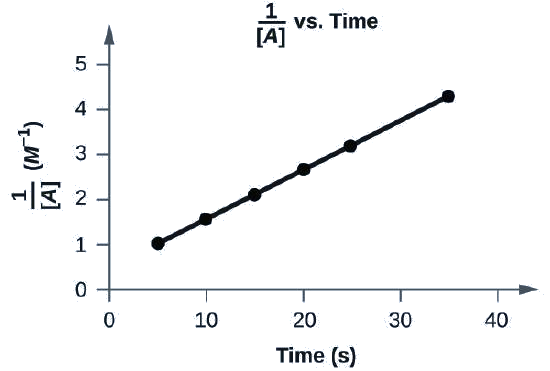
Un graphique intitulé « 1 divisé par [A] par rapport au temps » est présenté, avec l'étiquette « Temps (s) » sur l'axe des abscisses. L'étiquette « 1 divisé par [A] » apparaît à gauche de l'axe Y. L'axe X montre les marquages commençant à zéro et se poursuivant à des intervalles de 10 à 40 inclus. L'axe Y sur la gauche montre les marques commençant à 0 et augmentant par intervalles de 1 à 5 inclus. Une ligne présentant une tendance à la hausse est tracée à travers six points à environ (4, 1), (10, 1,5), (15, 2,2), (20, 2,8), (26, 3,4) et (36, 4,4).
Réactions d'ordre zéro
Pour les réactions d'ordre zéro, la loi du taux différentiel est la suivante :
\[\ce{Rate}=k[A]^0=k \nonumber \]
Une réaction d'ordre zéro présente donc une vitesse de réaction constante, quelle que soit la concentration de ses réactifs.
La loi de vitesse intégrée pour une réaction d'ordre zéro a également la forme de l'équation d'une droite :
\ [\ begin {align*}
[A] &=−kt+ [A] _0 \ label {intzero} \ \ [4 points]
y&=mx+b
\ end {align*} \ nonumber \]
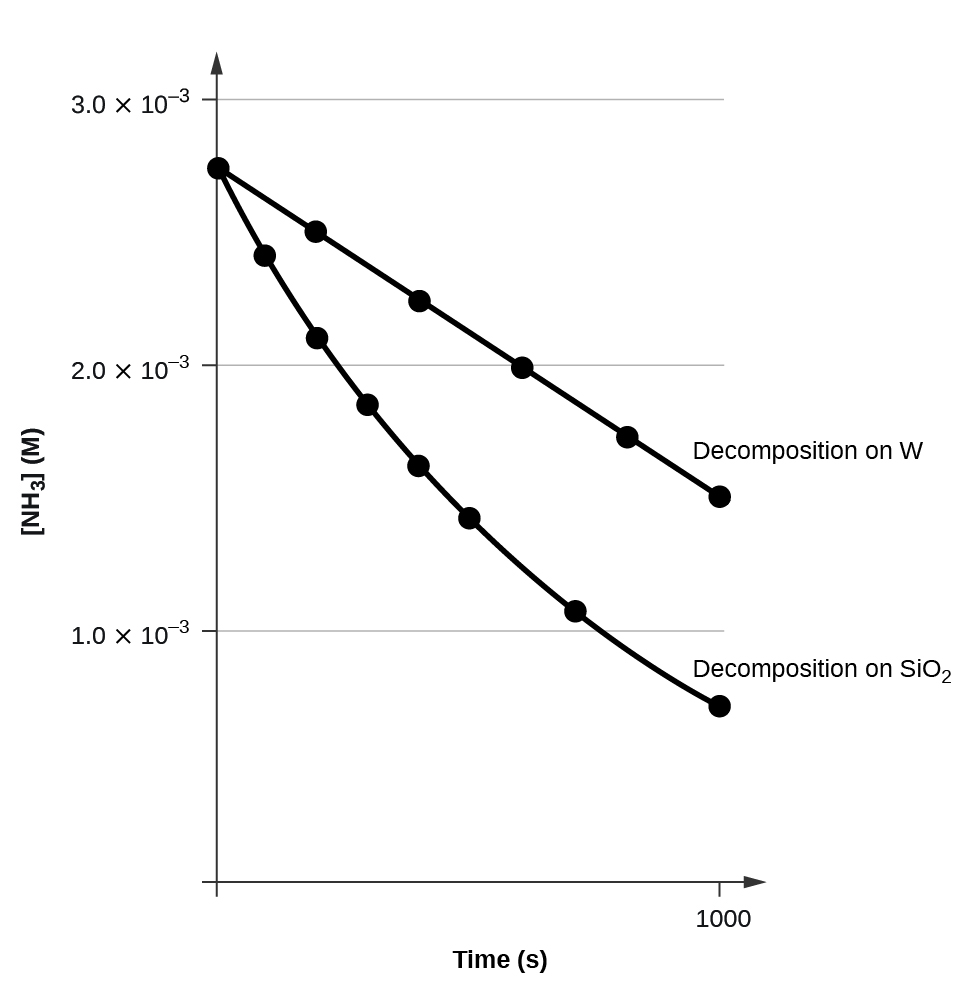
Un diagramme de\([A]\) versus\(t\) pour une réaction d'ordre zéro est une droite avec une pente de −k et une intersection de [A] 0. La figure\(\PageIndex{3}\) montre un graphique de [NH 3] en fonction de t pour la décomposition de l'ammoniac sur un fil de tungstène chaud et pour la décomposition de l'ammoniac sur du quartz chaud (SiO 2). La décomposition du NH 3 sur du tungstène chaud est d'ordre zéro ; le graphique est une ligne droite. La décomposition du NH 3 sur du quartz chaud n'est pas d'ordre zéro (c'est du premier ordre). À partir de la pente de la droite pour la décomposition d'ordre zéro, nous pouvons déterminer la constante de vitesse :
\[\ce{slope}=−k=\mathrm{1.3110^{−6}\:mol/L/s} \nonumber \]
La demi-vie d'une réaction
La demi-vie d'une réaction (t 1/2) est le temps nécessaire pour que la moitié d'une quantité donnée de réactif soit consommée. À chaque demi-vie suivante, la moitié de la concentration restante du réactif est consommée. En utilisant la décomposition du peroxyde d'hydrogène comme exemple, nous constatons que pendant la première demi-vie (de 0,00 heures à 6,00 heures), la concentration de H 2 O 2 diminue de 1 000 M à 0,500 M. Au cours de la deuxième demi-vie (de 6 heures à 12 heures), elle diminue de 0,500 M à 0,250 M ; pendant la troisième demi-vie, elle diminue de 0,250 M à 0,125 M. La concentration en H 2 O 2 diminue de moitié au cours de chaque période successive de 6,00 heures. La décomposition du peroxyde d'hydrogène est une réaction du premier ordre et, comme on peut le montrer, la demi-vie d'une réaction du premier ordre est indépendante de la concentration du réactif. Cependant, les demi-vies des réactions avec d'autres ordres dépendent des concentrations des réactifs.
Réactions de premier ordre
Nous pouvons déduire une équation pour déterminer la demi-vie d'une réaction de premier ordre à partir de la forme alternative de la loi de vitesse intégrée, comme suit :
\ [\ begin {align*}
\ ln \ dfrac {[A] _0} {[A]} &=kt \ \ [4pt]
t&= \ ln \ dfrac {[A] _0} {[A]} × \ dfrac {1} {k}
\ end {align*} \ nonnumber \]
Si l'on fixe le temps t à la demi-vie\(t_{1/2}\), la concentration correspondante de A à ce moment est égale à la moitié de sa concentration initiale. Par conséquent, quand\(t=t_{1/2}\),\([A]=\dfrac{1}{2}[A]_0\).
Par conséquent :
\ [\ begin {align*}
t_ {1/2} &= \ ln \ dfrac {[A] _0} {\ dfrac {1} {2} [A] _0} × \ dfrac {1} {k} \ \ [4pt]
&= \ ln 2× \ dfrac {1} {k} =0,693 × \ dfrac {1} \ k}
\ end {align*} \ nonnumber \]
Ainsi :
\[t_{1/2}=\dfrac{0.693}{k} \nonumber \]
Nous pouvons voir que la demi-vie d'une réaction du premier ordre est inversement proportionnelle à la constante de vitesse k. Une réaction rapide (demi-vie plus courte) aura un k plus grand ; une réaction lente (demi-vie plus longue) aura un k plus petit.
Calculer la constante de vitesse pour la décomposition du premier ordre du peroxyde d'hydrogène dans l'eau à 40 °C, en utilisant les données de la figure\(\PageIndex{4}\).
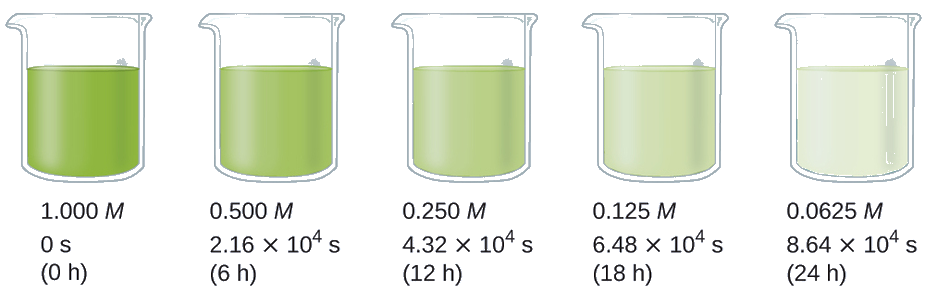
Solution La demi-vie pour la décomposition de H 2 O 2 est de 2,16 × 10 4 s :
\ [\ begin {align*}
t_ {1/2} &= \ dfrac {0,693} {k} \ \ [4 points]
k&= \ dfrac {0,693} {t_ {1/2}} = \ dfrac {0,693} {2,16 × 10^4 \ : \ ce s} =3,21 × 10^ {−5} \ : \ ce s^ {−1}
\ end {align*} \ nonumber \]
La désintégration radioactive du premier ordre de l'iode 131 présente une constante de vitesse de 0,138 d -1. Quelle est la demi-vie de cette décomposition ?
- Réponse
-
5,02 d.
Réactions de second ordre
Nous pouvons déduire l'équation pour calculer la demi-vie d'un second ordre comme suit :
\[\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0} \nonumber \]
ou
\[\dfrac{1}{[A]}−\dfrac{1}{[A]_0}=kt \nonumber \]
Si
\[t=t_{1/2} \nonumber \]
alors
\[[A]=\dfrac{1}{2}[A]_0 \nonumber \]
et nous pouvons écrire :
\ dfrac {1} {\ dfrac {1} {2} [A] _0} − \ dfrac {1} {[A] _0} &=kt_ {1/2} \ \ [4pt]
2 [A] _0− \ dfrac {1} {[A] _0} &=kt_ {1/2} \ \ [4pt]
\ dfrac {1} {[A] _0} &=kt_ {1/2}
\ end {align*} \)
Ainsi :
\[t_{1/2}=\dfrac{1}{k[A]_0} \nonumber \]
Pour une réaction de second ordre,\(t_{1/2}\) est inversement proportionnelle à la concentration du réactif, et la demi-vie augmente au fur et à mesure de la réaction parce que la concentration du réactif diminue. Par conséquent, nous trouvons que l'utilisation du concept de demi-vie est plus complexe pour les réactions de second ordre que pour les réactions de premier ordre. Contrairement aux réactions du premier ordre, la constante de vitesse d'une réaction du second ordre ne peut pas être calculée directement à partir de la demi-vie à moins que la concentration initiale ne soit connue.
Réactions d'ordre zéro
Nous pouvons dériver une équation pour calculer la demi-vie d'une réaction d'ordre zéro comme suit :
\[[A]=−kt+[A]_0 \nonumber \]
Lorsque la moitié de la quantité initiale de réactif a été consommée\(t=t_{1/2}\) et\([A]=\dfrac{[A]_0}{2}\). Ainsi :
\ [\ begin {align*}
\ dfrac {[A] _0} {2} &=−kt_ {1/2} + [A] _0 \ \ [4pt]
kt_ {1/2} &= \ dfrac {[A] _0} {2}
\ end {align*} \ nonnumber \]
et
\[t_{1/2}=\dfrac{[A]_0}{2k} \nonumber \]
La demi-vie d'une réaction d'ordre zéro augmente à mesure que la concentration initiale augmente. Les équations pour les lois de vitesse différentielles et intégrées et les demi-vies correspondantes pour les réactions de zéro, de premier et de second ordre sont résumées dans le tableau\(\PageIndex{1}\).
| Commande zéro | Première commande | Deuxième ordre | |
|---|---|---|---|
| loi sur les taux | taux = k | taux = k [A] | taux = k [A] 2 |
| unités de constante de vitesse | M est −1 | s −1 | M −1 x −1 |
| loi tarifaire intégrée | [A] = − kt + [A] 0 | ln [A] = − kt + ln [A] 0 | \(\dfrac{1}{[A]}=kt+\left(\dfrac{1}{[A]_0}\right)\) |
| diagramme nécessaire pour l'ajustement linéaire des données de taux | [A] contre t | Ln [A] contre t | \(\dfrac{1}{[A]}\)contre t |
| relation entre la pente du diagramme linéaire et la constante de vitesse | k = −pente | k = −pente | k = +pente |
| demi-vie | \(t_{1/2}=\dfrac{[A]_0}{2k}\) | \(t_{1/2}=\dfrac{0.693}{k}\) | \(t_{1/2}=\dfrac{1}{[A]_0k}\) |
Résumé
Les lois de taux différentiels peuvent être déterminées par la méthode des taux initiaux ou par d'autres méthodes. Nous mesurons les valeurs des vitesses initiales d'une réaction à différentes concentrations des réactifs. À partir de ces mesures, nous déterminons l'ordre de la réaction dans chaque réactif. Les lois de taux intégrées sont déterminées par intégration des lois de taux différentiels correspondantes. Les constantes de vitesse pour ces lois de vitesse sont déterminées à partir de mesures de concentration effectuées à différents moments au cours d'une réaction.
La demi-vie d'une réaction est le temps nécessaire pour réduire de moitié la quantité d'un réactif donné. La demi-vie d'une réaction d'ordre zéro diminue à mesure que la concentration initiale du réactif dans la réaction diminue. La demi-vie d'une réaction de premier ordre est indépendante de la concentration, et la demi-vie d'une réaction de second ordre diminue à mesure que la concentration augmente.
Équations clés
- loi de vitesse intégrée pour les réactions d'ordre zéro (équation \ ref {intzero}) :
\([A]=−kt+[A]_0\)avec\(t_{1/2}=\dfrac{[A]_0}{2k}\)
- loi de vitesse intégrée pour les réactions du premier ordre (équation \ ref {in1st}) :
\(\ln[A]=−kt+ \ln[A]_0\)avec\(t_{1/2}=\dfrac{0.693}{k}\)
- loi de vitesse intégrée pour les réactions du second ordre (équation \ ref {int2nd}) :
\(\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0}\)avec\(t_{1/2}=\dfrac{1}{[A]_0k}\)
Lexique
- demi-vie d'une réaction (t l/2)
- temps nécessaire pour que la moitié d'une quantité donnée de réactif soit consommée
- loi tarifaire intégrée
- équation qui relie la concentration d'un réactif au temps de réaction écoulé


