12.3 : Lois tarifaires
- Page ID
- 193965
- Expliquer la forme et la fonction d'une loi tarifaire
- Utiliser les lois de vitesse pour calculer les vitesses de réaction
- Utiliser les données de vitesse et de concentration pour identifier les ordres de réaction et établir des lois de vitesse
Comme décrit dans le module précédent, la vitesse d'une réaction est affectée par les concentrations de réactifs. Les lois ou équations de vitesse sont des expressions mathématiques qui décrivent la relation entre la vitesse d'une réaction chimique et la concentration de ses réactifs. En général, une loi de taux (ou loi de taux différentiel, comme on l'appelle parfois) prend la forme suivante :
\[\ce{rate}=k[A]^m[B]^n[C]^p… \nonumber \]
dans laquelle [A], [B] et [C] représentent les concentrations molaires des réactifs, et k est la constante de vitesse, qui est spécifique à une réaction particulière à une température donnée. Les exposants m, n et p sont généralement des entiers positifs (bien qu'il soit possible qu'ils soient des fractions ou des nombres négatifs). La constante de vitesse k et les exposants m, n et p doivent être déterminés expérimentalement en observant comment la vitesse d'une réaction change lorsque les concentrations des réactifs changent. La constante de vitesse k est indépendante de la concentration de A, B ou C, mais elle varie en fonction de la température et de la surface.
Les exposants d'une loi de vitesse décrivent les effets des concentrations de réactifs sur la vitesse de réaction et définissent l'ordre de la réaction. Considérons une réaction pour laquelle la loi des taux est la suivante :
\[\ce{rate}=k[A]^m[B]^n \nonumber \]
Si l'exposant m est égal à 1, la réaction est du premier ordre par rapport à A. Si m est égal à 2, la réaction est du second ordre par rapport à A. Si n est égal à 1, la réaction est du premier ordre dans B. Si n est égal à 2, la réaction est du second ordre dans B. Si m ou n est nul, la réaction est d'ordre zéro en A ou B, respectivement, et la vitesse de la réaction n'est pas affectée par la concentration de ce réactif. L'ordre de réaction global est la somme des ordres par rapport à chaque réactif. Si m = 1 et n = 1, l'ordre global de la réaction est du second ordre (m + n = 1 + 1 = 2).
La loi tarifaire :
\[\ce{rate}=k[\ce{H2O2}] \nonumber \]
décrit une réaction de premier ordre dans le peroxyde d'hydrogène et de premier ordre dans son ensemble. La loi tarifaire :
\[\ce{rate}=k[\ce{C4H6}]^2 \nonumber \]
décrit une réaction qui est du second ordre dans C 4 H 6 et du second ordre dans l'ensemble. La loi tarifaire :
\[\ce{rate}=k[\ce{H+}][\ce{OH-}] \nonumber \]
décrit une réaction qui est du premier ordre dans H +, du premier ordre dans OH − et du second ordre dans l'ensemble.
Une expérience montre que la réaction du dioxyde d'azote avec le monoxyde de carbone :
\[\ce{NO2}(g)+\ce{CO}(g)⟶\ce{NO}(g)+\ce{CO2}(g) \nonumber \]
est le second ordre dans le NO 2 et l'ordre zéro dans le CO à 100 °C. Quelle est la loi de vitesse de la réaction ?
Solution
La réaction aura la forme suivante :
\[\ce{rate}=k[\ce{NO2}]^m[\ce{CO}]^n \nonumber \]
La réaction est du second ordre dans le NO 2 ; donc m = 2. La réaction est d'ordre zéro dans le CO ; donc n = 0. La loi tarifaire est la suivante :
\[\ce{rate}=k[\ce{NO2}]^2[\ce{CO}]^0=k[\ce{NO2}]^2 \nonumber \]
Rappelez-vous qu'un nombre élevé à la puissance zéro est égal à 1, donc [CO] 0 = 1, c'est pourquoi nous pouvons simplement supprimer la concentration de CO de l'équation de vitesse : la vitesse de réaction dépend uniquement de la concentration de NO 2. Lorsque nous examinerons les mécanismes de vitesse plus loin dans ce chapitre, nous expliquerons comment la concentration d'un réactif peut n'avoir aucun effet sur une réaction malgré son implication dans la réaction.
La loi de vitesse de la réaction :
\[\ce{H2}(g)+\ce{2NO}(g)⟶\ce{N2O}(g)+\ce{H2O}(g) \nonumber \]
a été déterminé expérimentalement comme étant le taux = k [NO] 2 [H 2]. Quels sont les ordres relatifs à chaque réactif et quel est l'ordre général de la réaction ?
- Réponse
-
- ordre en NO = 2 ;
- ordre en H 2 = 1 ;
- commande globale = 3
Lors d'une réaction de transestérification, un triglycéride réagit avec un alcool pour former un ester et du glycérol. De nombreux étudiants découvrent la réaction entre le méthanol (CH 3 OH) et l'acétate d'éthyle (CH 3 CH 2 OCOCH 3) sous forme de réaction d'échantillon avant d'étudier les réactions chimiques qui produisent du biodiesel :
\[\ce{CH3OH + CH3CH2OCOCH3 ⟶ CH3OCOCH3 + CH3CH2OH} \nonumber \]
La loi de vitesse pour la réaction entre le méthanol et l'acétate d'éthyle est, dans certaines conditions, déterminée expérimentalement comme étant :
\[\ce{rate}=k[\ce{CH3OH}] \nonumber \]
Quel est l'ordre de réaction par rapport au méthanol et à l'acétate d'éthyle, et quel est l'ordre général des réactions ?
- Réponse
-
- ordre en CH 3 OH = 1 ;
- ordre dans CH 3 CH 2 OCOCH 3 = 0 ;
- commande globale = 1
Il est parfois utile d'utiliser une méthode algébrique plus explicite, souvent appelée méthode des taux initiaux, pour déterminer les ordres des lois des taux. Pour utiliser cette méthode, nous sélectionnons deux ensembles de données de vitesse dont la concentration d'un seul réactif diffère et nous établissons un ratio entre les deux taux et les deux lois de vitesse. Après avoir annulé les termes qui sont égaux, il nous reste une équation qui ne contient qu'une seule inconnue, le coefficient de la concentration qui varie. Nous résolvons ensuite cette équation pour le coefficient.
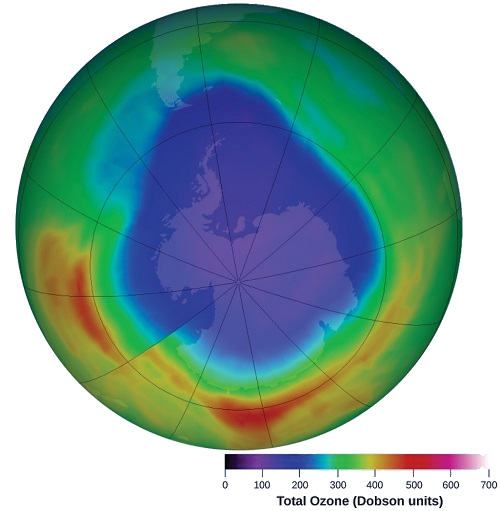
L'ozone de la haute atmosphère est appauvri lorsqu'il réagit avec les oxydes d'azote. Les vitesses des réactions des oxydes d'azote avec l'ozone sont des facteurs importants pour déterminer l'importance de ces réactions dans la formation du trou d'ozone au-dessus de l'Antarctique (Figure\(\PageIndex{1}\)). L'une de ces réactions est la combinaison du monoxyde d'azote (NO) avec de l'ozone (O 3) :
\[\ce{NO}(g)+\ce{O3}(g)⟶\ce{NO2}(g)+\ce{O2}(g) \nonumber \]
Cette réaction a été étudiée en laboratoire et les données de vitesse suivantes ont été déterminées à 25 °C.
| Procès | \([\ce{NO}]\)(mol/L) | \([\ce{O3}]\)(mol/L) | \(\dfrac{Δ[\ce{NO2}]}{Δt}\:\mathrm{(mol\:L^{−1}\:s^{−1})}\) |
|---|---|---|---|
| 1 | \ ([\ ce {NO}] \) (mol/L) » style="text-align:center ; vertical-align:middle ; « >1,00 × 10 −6 | \ ([\ ce {O3}] \) (mol/L) » style="text-align:center ; vertical-align:middle ; « >3,00 × 10 −6 | \ (\ dfrac {Δ [\ ce {NO2}]} {Δt} \ : \ mathrm {(mol \ :L^ {−1} \ :s^ {−1})} \) » style="text-align:center ; vertical-align:middle ; « >6,60 × 10 −5 |
| 2 | \ ([\ ce {NO}] \) (mol/L) » style="text-align:center ; vertical-align:middle ; « >1,00 × 10 −6 | \ ([\ ce {O3}] \) (mol/L) » style="text-align:center ; vertical-align:middle ; « >6,00 × 10 −6 | \ (\ dfrac {Δ [\ ce {NO2}]} {Δt} \ : \ mathrm {(mol \ :L^ {−1} \ :s^ {−1})} \) » style="text-align:center ; vertical-align:middle ; « >1,32 × 10 −4 |
| 3 | \ ([\ ce {NO}] \) (mol/L) » style="text-align:center ; vertical-align:middle ; « >1,00 × 10 −6 | \ ([\ ce {O3}] \) (mol/L) » style="text-align:center ; vertical-align:middle ; « >9,00 × 10 −6 | \ (\ dfrac {Δ [\ ce {NO2}]} {Δt} \ : \ mathrm {(mol \ :L^ {−1} \ :s^ {−1})} \) » style="text-align:center ; vertical-align:middle ; « >1,98 × 10 −4 |
| 4 | \ ([\ ce {NO}] \) (mol/L) » style="text-align:center ; vertical-align:middle ; « >2,00 × 10 −6 | \ ([\ ce {O3}] \) (mol/L) » style="text-align:center ; vertical-align:middle ; « >9,00 × 10 −6 | \ (\ dfrac {Δ [\ ce {NO2}]} {Δt} \ : \ mathrm {(mol \ :L^ {−1} \ :s^ {−1})} \) » style="text-align:center ; vertical-align:middle ; « >3,96 × 10 −4 |
| 5 | \ ([\ ce {NO}] \) (mol/L) » style="text-align:center ; vertical-align:middle ; « >3,00 × 10 −6 | \ ([\ ce {O3}] \) (mol/L) » style="text-align:center ; vertical-align:middle ; « >9,00 × 10 −6 | \ (\ dfrac {Δ [\ ce {NO2}]} {Δt} \ : \ mathrm {(mol \ :L^ {−1} \ :s^ {−1})} \) » style="text-align:center ; vertical-align:middle ; « >5,94 × 10 −4 |
Déterminer la loi de vitesse et la constante de vitesse pour la réaction à 25 °C.
Solution
La loi tarifaire aura la forme suivante :
\[\ce{rate}=k[\ce{NO}]^m[\ce{O3}]^n \nonumber \]
Nous pouvons déterminer les valeurs de m, n et k à partir des données expérimentales en utilisant le processus en trois étapes suivant :
- Déterminez la valeur de m à partir des données dans lesquelles [NO] varie et [O 3] est constant. Dans les trois dernières expériences, [NO] varie tandis que [O 3] reste constant. Lorsque [NO] double entre l'essai 3 et l'essai 4, le taux double, et lorsque [NON] triple entre l'essai 3 et l'essai 5, le taux triple également. Ainsi, le taux est également directement proportionnel à [NO], et m dans la loi des taux est égal à 1.
- Déterminez la valeur de n à partir de données dans lesquelles [O 3] varie et [NO] est constant. Dans les trois premières expériences, [NO] est constant et [O 3] varie. La vitesse de réaction varie en proportion directe de la variation de [O 3]. Lorsque [O 3] double entre l'essai 1 et l'essai 2, le taux double ; lorsque [O 3] triple entre l'essai 1 et 3, le taux augmente également par trois. Ainsi, le taux est directement proportionnel à [O 3], et n est égal à 1. La loi des taux est ainsi :
\[\ce{rate}=k[\ce{NO}]^1[\ce{O3}]^1=k[\ce{NO}][\ce{O3}] \nonumber \]
- Déterminez la valeur de k à partir d'un ensemble de concentrations et du taux correspondant.
\ [\ begin {align*}
k&= \ mathrm {\ dfrac {rate} {[NON] [O_3]}} \ \
&= \ mathrm {\ dfrac {6,60×10^ {−5} \ annuler {mol \ : L^ {−1}} \ :s^ {−1}} {(1,00×10^ {−6} \ annuler {mol \ : L^ {−1}}) (3,00 × 10^ {−6} \ :mol \ :L^ {−1})}} \ \
&= \ mathrm {2,20 × 10^7 \ :L \ :mol^ {−1} \ :s^ {−1}}
\ end {align*} \ nonumber \]La valeur élevée de k indique qu'il s'agit d'une réaction rapide qui pourrait jouer un rôle important dans l'appauvrissement de la couche d'ozone si [NO] est suffisamment important.
L'acétaldéhyde se décompose lorsqu'il est chauffé pour produire du méthane et du monoxyde de carbone selon l'équation suivante :
\[\ce{CH3CHO}(g)⟶\ce{CH4}(g)+\ce{CO}(g) \nonumber \]
Déterminer la loi de vitesse et la constante de vitesse de la réaction à partir des données expérimentales suivantes :
| Procès | \([\ce{CH3CHO}]\)(mol/L) | \(−\dfrac{Δ[\ce{CH3CHO}]}{Δt}\mathrm{(mol\:L^{−1}\:s^{−1})}\) |
|---|---|---|
| 1 | \ ([\ ce {CH3CHO}] \) (mol/L) » style="text-align:center ; « >1,75 × 10 −3 | \ (− \ dfrac {Δ [\ ce {CH3CHO}]} {Δt} \ mathrm {(mol \ :L^ {−1} \ :s^ {−1})} \) » style="text-align:center ; « >2,06 × 10 −11 |
| 2 | \ ([\ ce {CH3CHO}] \) (mol/L) » style="text-align:center ; « >3,50 × 10 −3 | \ (− \ dfrac {Δ [\ ce {CH3CHO}]} {Δt} \ mathrm {(mol \ :L^ {−1} \ :s^ {−1})} \) » style="text-align:center ; « >8,24 × 10 −11 |
| 3 | \ ([\ ce {CH3CHO}] \) (mol/L) » style="text-align:center ; « >7,00 × 10 −3 | \ (− \ dfrac {Δ [\ ce {CH3CHO}]} {Δt} \ mathrm {(mol \ :L^ {−1} \ :s^ {−1})} \) » style="text-align:center ; « >3,30 × 10 −10 −10 |
- Réponse
-
\(\ce{rate}=k[\ce{CH3CHO}]^2\)avec k = 6,73 × 10 −6 L/mol/s
À l'aide de la méthode des vitesses initiales et des données expérimentales, déterminez la loi de vitesse et la valeur de la constante de vitesse pour cette réaction :
\[\ce{2NO}(g)+\ce{Cl2}(g)⟶\ce{2NOCl}(g) \nonumber \]
| Procès | [NON] (mol/L) | \([Cl_2]\)(mol/L) | \(−\dfrac{Δ[\ce{NO}]}{2Δt}\mathrm{(mol\:L^{−1}\:s^{−1})}\) |
|---|---|---|---|
| 1 | 0,10 | \ ([Cl_2] \) (mol/L) » style="text-align:center ; « >0,10 | \ (− \ dfrac {Δ [\ ce {NO}]} {2Δt} \ mathrm {(mol \ :L^ {−1}} \ :s^ {−1})} \) » style="text-align:center ; « >0,00300 |
| 2 | 0,10 | \ ([Cl_2] \) (mol/L) » style="text-align:center ; « >0,15 | \ (− \ dfrac {Δ [\ ce {NO}]} {2Δt} \ mathrm {(mol \ :L^ {−1}} \ :s^ {−1})} \) » style="text-align:center ; « >0,00450 |
| 3 | 0,15 | \ ([Cl_2] \) (mol/L) » style="text-align:center ; « >0,10 | \ (− \ dfrac {Δ [\ ce {NO}]} {2Δt} \ mathrm {(mol \ :L^ {−1}} \ :s^ {−1})} \) » style="text-align:center ; « >0,00675 |
Solution
La loi de vitesse pour cette réaction aura la forme suivante :
\[\ce{rate}=k[\ce{NO}]^m[\ce{Cl2}]^n \nonumber \]
Comme dans l'exemple\(\PageIndex{2}\), nous pouvons aborder ce problème par étapes, en déterminant les valeurs de m et de n à partir des données expérimentales, puis en utilisant ces valeurs pour déterminer la valeur de k. Dans cet exemple, nous utiliserons toutefois une approche différente pour déterminer les valeurs de m et de n :
Déterminez la valeur de m à partir des données dans lesquelles [NO] varie et [Cl 2] est constant. Nous pouvons écrire les ratios avec les indices x et y pour indiquer les données de deux essais différents :
\[\dfrac{\ce{rate}_x}{\ce{rate}_y}=\dfrac{k[\ce{NO}]^m_x[\ce{Cl2}]^n_x}{k[\ce{NO}]^m_y[\ce{Cl2}]^n_y} \nonumber \]
En utilisant le troisième essai et le premier essai, dans lesquels [Cl 2] ne varie pas, on obtient :
\[\mathrm{\dfrac{rate\: 3}{rate\: 1}}=\dfrac{0.00675}{0.00300}=\dfrac{k(0.15)^m(0.10)^n}{k(0.10)^m(0.10)^n} \nonumber \]
Après avoir annulé les termes équivalents dans le numérateur et le dénominateur, il nous reste :
\[\dfrac{0.00675}{0.00300}=\dfrac{(0.15)^m}{(0.10)^m} \nonumber \]ce qui permet de :
\[2.25=(1.5)^m \nonumber \]
Nous pouvons utiliser des logarithmes naturels pour déterminer la valeur de l'exposant m :
\ ln (2,25) &=m \ ln (1,5)
\ dfrac {\ ln (2,25)} {\ ln (1,5)} &=m
2&=m
\ end {align*} \)
Nous pouvons facilement confirmer le résultat, car :
- Déterminez la valeur de n à partir de données dans lesquelles [Cl 2] varie et [NO] est constant. \[\mathrm{\dfrac{rate\: 2}{rate\: 1}}=\dfrac{0.00450}{0.00300}=\dfrac{k(0.10)^m(0.15)^n}{k(0.10)^m(0.10)^n} \nonumber \]
L'annulation donne :
\[\dfrac{0.0045}{0.0030}=\dfrac{(0.15)^n}{(0.10)^n} \nonumber \]
ce qui permet de :
\[1.5=(1.5)^n \nonumber \]
Ainsi, n doit être égal à 1, et la forme de la loi des taux est la suivante :
\[\ce{Rate}=k[\ce{NO}]^m[\ce{Cl2}]^n=k[\ce{NO}]^2[\ce{Cl2}] \nonumber \]
- Déterminez la valeur numérique de la constante de vitesse k avec les unités appropriées. Les unités de la vitesse d'une réaction sont mol/L/s. Les unités de k sont ce qui est nécessaire pour que la substitution dans l'expression de la loi de vitesse donne les unités appropriées pour la vitesse. Dans cet example, les unités de concentration sont mol 3 /L 3. Les unités de k doivent être mol −2 L 2 /s afin que le taux soit exprimé en mol/L/s.
Pour déterminer la valeur de k une fois que l'expression de la loi des taux a été résolue, il suffit d'intégrer les valeurs du premier essai expérimental et de résoudre pour k :
\ (\ begin {align*}
\ mathrm {0,00300 \ :mol \ :L^ {−1}} \ :s^ {−1}} &=k \ mathrm {(0,10 \ :mol \ :L^ {−1}) ^2 (0,10 \ :mol \ :mol \ :L^ {−1}) ^1} \ \ k&= \ mathrm {3.0 \ :mol^ {−1}) ^1} \ \
k&= \ mathrm {3.0 \ :mol^ {−1} 2} \ :L^2 \ :s^ {−1}}
\ end {align*} \)
Utilisez les données de vitesse initiale fournies pour dériver la loi de vitesse de la réaction dont l'équation est la suivante :
\[\ce{OCl-}(aq)+\ce{I-}(aq)⟶\ce{OI-}(aq)+\ce{Cl-}(aq) \nonumber \]
| Procès | [Col −] (mol/L) | [I −] (mol/L) | Taux initial (mol/L/s) |
|---|---|---|---|
| 1 | 0,0040 | 0,0020 | 0,00184 |
| 2 | 0,0020 | 0,0040 | 0,00092 |
| 3 | 0,0020 | 0,0020 | 0,00046 |
Déterminez l'expression de la loi de vitesse et la valeur de la constante de vitesse k avec les unités appropriées pour cette réaction.
- Réponse
-
\(\mathrm{\dfrac{rate\: 2}{rate\: 3}}=\dfrac{0.00092}{0.00046}=\dfrac{k(0.0020)^x(0.0040)^y}{k(0.0020)^x(0.0020)^y}\)
2,00 = 2,00 g
y = 1
\(\mathrm{\dfrac{rate\: 1}{rate\: 2}}=\dfrac{0.00184}{0.00092}=\dfrac{k(0.0040)^x(0.0020)^y}{k(0.0020)^x(0.0040)^y}\)
\ (\ begin {align*}
2,00&= \ dfrac {2^x} {2^y} \ \
2,00&= \ dfrac {2^x} {2^1} \ \
4,00&=2^x \ \
x&=2
\ end {align*} \)
En substituant les données de concentration de l'essai 1 et en résolvant pour k, on obtient :
\ (\ begin {align*}
\ ce {taux} &=k [\ ce {OCl-}] ^2 [\ ce {I-}] ^1 \ \
0,00184&=k (0,0040) ^2 (0,0020) ^1 \ \
k&= \ mathrm {5,75 × 10^4 \ :mol^ {−2} \ :L^2 \ :s^ {−1}}
\ end {align*} \)
Unités constantes d'ordre et de vitesse de réaction
Dans certains de nos exemples, les ordres de réaction dans la loi de vitesse sont les mêmes que les coefficients de l'équation chimique de la réaction. Ce n'est qu'une coïncidence et, bien souvent, ce n'est pas le cas. Les lois de vitesse peuvent présenter des ordres fractionnaires pour certains réactifs, et des ordres de réaction négatifs sont parfois observés lorsqu'une augmentation de la concentration d'un réactif entraîne une diminution de la vitesse de réaction. Quelques exemples illustrant ces points sont fournis :
\ (\ ce {NO2 + CONO + CO2} \ hspace {20th} \ ce {taux} =k [\ ce {NO2}] ^2 \ \
\ ce {CH3CHOCH4 + CO} \ hspace {20th} \ ce {taux} =k [\ ce {CH3CHO}] ^2 \ \
\ ce {2N2O52NO2 + O2} \ hspace {20th} \ ce {taux} =k [\ ce {N2O5}] \ \
\ ce {2NO2 + F22NO2F} \ hspace {20th} \ ce {taux} =k [\ ce {NO2}] [\ ce {F2}] \ \ \ ce {2}] \
\ ce {2 NO2Cl2NO2+Cl2} \ hspace {1080p} \ ce {taux} =k [\ ce {NO2Cl}] \)
Il est important de noter que les lois de vitesse sont déterminées uniquement par expérience et ne sont pas prédites de manière fiable par la stœchiométrie des réactions.
Les ordres de réaction jouent également un rôle dans la détermination des unités de la constante de vitesse k. Dans l'exemple\(\PageIndex{2}\), une réaction du second ordre, nous avons trouvé que les unités de k étaient\(\mathrm{L\:mol^{-1}\:s^{-1}}\), alors que dans l'exemple\(\PageIndex{3}\), une réaction du troisième ordre, nous avons trouvé que les unités de k étaient mol −2 L 2 /s. Plus généralement, les unités de la constante de vitesse pour a réaction d'ordre\( (m+n)\) sont\(\ce{mol}^{1−(m+n)}\ce L^{(m+n)−1}\ce s^{−1}\). \(\PageIndex{1}\)Le tableau résume les unités de constante de vitesse pour les ordres de réaction courants.
| Ordre des réactions | Unités de k |
|---|---|
| \( (m+n)\) | \(\ce{mol}^{1−(m+n)}\ce L^{(m+n)−1}\ce s^{−1}\) |
| zéro | Mol/L/s |
| premier | s −1 |
| seconde | L/mol/s |
| troisième | mol −2 L 2 x −1 |
Notez que les unités du tableau peuvent également être exprimées en termes de molarité (M) au lieu de mol/L. De plus, des unités de temps autres que la seconde (telles que les minutes, les heures, les jours) peuvent être utilisées, selon la situation.
Résumé
Les lois des taux fournissent une description mathématique de la façon dont les variations de la quantité d'une substance influent sur la vitesse d'une réaction chimique. Les lois de vitesse sont déterminées expérimentalement et ne peuvent pas être prédites par la stoechiométrie des réactions. L'ordre de réaction décrit dans quelle mesure un changement de la quantité de chaque substance affecte la vitesse globale, et l'ordre général d'une réaction est la somme des ordres pour chaque substance présente dans la réaction. Les ordres de réaction sont généralement du premier ordre, du deuxième ordre ou de l'ordre zéro, mais des ordres fractionnaires et même négatifs sont possibles.
Lexique
- méthode des taux initiaux
- utilisation d'une méthode algébrique plus explicite pour déterminer les ordres d'une loi des taux
- ordre global des réactions
- somme des ordres de réaction pour chaque substance représentée dans la loi des taux
- constante de vitesse (k)
- constante de proportionnalité dans la relation entre la vitesse de réaction et les concentrations de réactifs
- loi sur les taux
- (également, équation de vitesse) équation mathématique montrant la dépendance de la vitesse de réaction par rapport à la constante de vitesse et à la concentration d'un ou de plusieurs réactifs
- ordre des réactions
- valeur d'un exposant dans une loi de taux, exprimée sous forme de nombre ordinal (par exemple, ordre zéro pour 0, premier ordre pour 1, deuxième ordre pour 2, etc.)


