12.1 : Taux de réaction chimique
- Page ID
- 193961
- Définir la vitesse de réaction chimique
- Dériver les expressions de vitesse à partir de l'équation équilibrée pour une réaction chimique donnée
- Calculer les taux de réaction à partir de données
Un taux est une mesure de la façon dont certains biens varient dans le temps. La vitesse est un taux familier qui exprime la distance parcourue par un objet dans un laps de temps donné. Le salaire est un taux qui représente le montant d'argent gagné par une personne travaillant pendant une période donnée. De même, la vitesse d'une réaction chimique est une mesure de la quantité de réactif consommée, ou de la quantité de produit produite, par la réaction dans un laps de temps donné.
La vitesse de réaction est la variation de la quantité d'un réactif ou d'un produit par unité de temps. Les vitesses de réaction sont donc déterminées en mesurant la dépendance temporelle de certaines propriétés qui peuvent être liées aux quantités de réactif ou de produit. Les vitesses des réactions qui consomment ou produisent des substances gazeuses, par exemple, sont facilement déterminées en mesurant les variations de volume ou de pression. Pour les réactions impliquant une ou plusieurs substances colorées, les taux peuvent être surveillés par des mesures de l'absorption de la lumière. Pour les réactions impliquant des électrolytes aqueux, les vitesses peuvent être mesurées en fonction des modifications de la conductivité d'une solution.
Pour les réactifs et les produits en solution, leurs quantités relatives (concentrations) sont utilisées de manière pratique pour exprimer les vitesses de réaction. Si nous mesurons la concentration de peroxyde d'hydrogène, H 2 O 2, dans une solution aqueuse, nous constatons qu'elle change lentement au fil du temps à mesure que le H 2 O 2 se décompose, selon l'équation :
\[\ce{2H2O2}(aq)⟶\ce{2H2O}(l)+\ce{O2}(g) \nonumber \]
La vitesse à laquelle le peroxyde d'hydrogène se décompose peut être exprimée en termes de vitesse de variation de sa concentration, comme indiqué ici :
\ [\ begin {align*}
\ ce {taux \ : de \ : décomposition \ : de \ : H_2O_2}
&= \ mathrm {− \ dfrac {changement \ : in \ : concentration \ : de \ : réactif} {temps \ : intervalle}} \ \ [4pt] &=− \ dfrac {[\ ce {H2O2}] _ {t_2}
− [4pt] &=− \ dfrac {[\ ce {H2O2}] _ {t_2} − [\ ce {H2O2}] _ {t_1}} {t_2−t_1} \ \ [4 points]
&=− \ dfrac {Δ [\ ce {H2O2}]} {Δt}
\ end {align*} \ nonumber \]
Cette représentation mathématique de l'évolution de la concentration en espèces au fil du temps est l'expression de la vitesse de la réaction. Les parenthèses indiquent les concentrations molaires et le symbole delta (Δ) indique la « variation ». Ainsi,\([\ce{H2O2}]_{t_1}\) représente la concentration molaire de peroxyde d'hydrogène à un moment t 1 ; de même,\([\ce{H2O2}]_{t_2}\) représente la concentration molaire de peroxyde d'hydrogène à un moment t 2 ultérieur ; et Δ [H 2 O 2] représente la variation de concentration molaire en peroxyde d'hydrogène pendant l'intervalle de temps Δ t (c'est-à-dire t 2 - t 1). Comme la concentration du réactif diminue au fur et à mesure de la réaction, Δ [H 2 O 2] est une quantité négative ; nous plaçons un signe négatif devant l'expression car les vitesses de réaction sont, par convention, des quantités positives. La figure\(\PageIndex{1}\) fournit un exemple de données collectées lors de la décomposition de H 2 O 2.
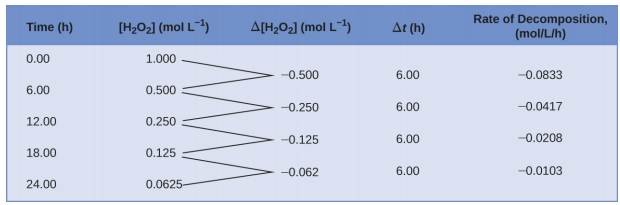
Pour obtenir les résultats tabulés de cette décomposition, la concentration de peroxyde d'hydrogène a été mesurée toutes les 6 heures au cours d'une journée à une température constante de 40 °C. Les taux de réaction ont été calculés pour chaque intervalle de temps en divisant la variation de concentration par l'incrément de temps correspondant, comme illustré ici pour la première période de 6 heures :
\[\dfrac{−Δ[\ce{H2O2}]}{Δt}=\mathrm{\dfrac{−(0.500\: mol/L−1.000\: mol/L)}{(6.00\: h−0.00\: h)}=0.0833\: mol\:L^{−1}\:h^{−1}} \nonumber \]
Notez que les vitesses de réaction varient avec le temps et diminuent au fur et à mesure de la réaction. Les résultats des 6 dernières heures donnent une vitesse de réaction de :
\[\dfrac{−Δ[\ce{H2O2}]}{Δt}=\mathrm{\dfrac{−(0.0625\:mol/L−0.125\:mol/L)}{(24.00\:h−18.00\:h)}=0.0104\:mol\:L^{−1}\:h^{−1}} \nonumber \]
Ce comportement indique que la réaction ralentit continuellement avec le temps. L'utilisation des concentrations au début et à la fin d'une période pendant laquelle la vitesse de réaction change permet de calculer une vitesse moyenne pour la réaction sur cet intervalle de temps. À tout moment précis, la vitesse à laquelle se déroule une réaction est connue sous le nom de vitesse instantanée. La vitesse instantanée d'une réaction au « temps zéro », lorsque la réaction commence, est sa vitesse initiale. Prenons l'analogie d'une voiture qui ralentit à l'approche d'un panneau d'arrêt. La vitesse initiale du véhicule, analogue au début d'une réaction chimique, serait la valeur mesurée par le compteur de vitesse au moment où le conducteur commence à appuyer sur les freins (t 0). Quelques instants plus tard, le rythme instantané à un moment précis (appelez-le t 1) serait un peu plus lent, comme l'indique la lecture du compteur de vitesse à ce moment-là. Au fil du temps, la vitesse instantanée continuera de baisser jusqu'à ce qu'elle atteigne zéro, lorsque la voiture (ou la réaction) s'arrête. Contrairement à la vitesse instantanée, la vitesse moyenne de la voiture n'est pas indiquée par le compteur de vitesse, mais elle peut être calculée comme le rapport entre la distance parcourue et le temps nécessaire pour arrêter complètement le véhicule (Δ t). Comme dans le cas d'une voiture qui décélère, la vitesse moyenne d'une réaction chimique se situe quelque part entre sa vitesse initiale et sa vitesse finale.
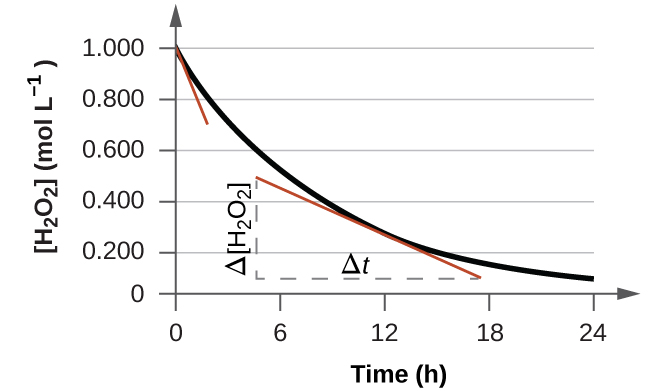
La vitesse instantanée d'une réaction peut être déterminée de deux manières. Si les conditions expérimentales permettent de mesurer les variations de concentration sur de très courts intervalles de temps, les taux moyens calculés comme décrit précédemment fournissent des approximations raisonnablement bonnes des taux instantanés. Il est également possible d'utiliser une procédure graphique qui, en fait, donne les résultats qui seraient obtenus si des mesures par intervalles de temps courts étaient possibles. Si nous tracons la concentration de peroxyde d'hydrogène en fonction du temps, le taux instantané de décomposition de H 2 O 2 à tout moment t est donné par la pente d'une droite tangente à la courbe à ce moment (Figure\(\PageIndex{2}\)). Nous pouvons utiliser le calcul pour évaluer les pentes de telles lignes tangentes, mais la procédure pour le faire dépasse le cadre de ce chapitre.
Les médecins utilisent souvent des bandelettes de test jetables pour mesurer les quantités de diverses substances présentes dans l'urine d'un patient (Figure\(\PageIndex{2}\)). Ces bandelettes de test contiennent divers réactifs chimiques, intégrés dans de petits tampons situés à différents endroits le long de la bandelette, qui changent de couleur lorsqu'ils sont exposés à des concentrations suffisantes de substances spécifiques. Les instructions d'utilisation des bandelettes de test soulignent souvent qu'un temps de lecture approprié est essentiel pour des résultats optimaux. L'accent mis sur le temps de lecture suggère que les aspects cinétiques des réactions chimiques qui se produisent sur la bandelette réactive sont des considérations importantes.
Le test de glycémie urinaire repose sur un processus en deux étapes représenté par les équations chimiques présentées ici :
\[\ce{C6H12O6 + O2}\underset{\large\textrm{catalyst}}{\xrightarrow{\hspace{45px}}}\ce{C6H10O6 + H2O2} \label{eq1} \]
\[\ce{2H2O2 + 2I-}\underset{\large\textrm{catalyst}}{\xrightarrow{\hspace{45px}}}\ce{I2 + 2H2O + O2} \label{eq2} \]
L'équation\(\ref{eq1}\) décrit l'oxydation du glucose dans l'urine pour produire de la glucolactone et du peroxyde d'hydrogène. Le peroxyde d'hydrogène produit ensuite oxyde l'ion iodure incolore pour produire de l'iode brun (équation\(\ref{eq2}\)), qui peut être détecté visuellement. Certaines bandelettes contiennent une substance supplémentaire qui réagit avec l'iode pour produire un changement de couleur plus distinct.
Les deux réactions de test présentées ci-dessus sont intrinsèquement très lentes, mais leur vitesse est augmentée par des enzymes spéciales intégrées dans la bandelette réactive. Il s'agit d'un exemple de catalyse, sujet abordé plus loin dans ce chapitre. Une bandelette de test de glucose typique destinée à être utilisée avec de l'urine nécessite environ 30 secondes pour terminer les réactions de formation de couleur. Une lecture trop précoce du résultat pourrait amener à conclure que la concentration de glucose de l'échantillon d'urine est inférieure à ce qu'elle est réellement (résultat faussement négatif). Attendre trop longtemps pour évaluer le changement de couleur peut entraîner un faux positif en raison de l'oxydation plus lente (non catalysée) de l'ion iodure par d'autres substances présentes dans l'urine.

Taux de réaction relatifs
La vitesse d'une réaction peut être exprimée en termes de variation de la quantité de tout réactif ou produit, et peut être simplement dérivée de la stœchiométrie de la réaction. Considérez la réaction représentée par l'équation suivante :
\[\ce{2NH3}(g)⟶\ce{N2}(g)+\ce{3H2}(g) \nonumber \]
Les facteurs stœchiométriques dérivés de cette équation peuvent être utilisés pour relier les vitesses de réaction de la même manière qu'elles sont utilisées aux quantités de réactif et de produit connexes. La relation entre les vitesses de réaction exprimées en termes de production d'azote et de consommation d'ammoniac, par exemple, est la suivante :
\[\mathrm{−\dfrac{Δmol\: NH_3}{Δ\mathit t}×\dfrac{1\: mol\: N_2}{2\: mol\: NH_3}=\dfrac{Δmol\:N_2}{Δ\mathit t}} \nonumber \]
Nous pouvons exprimer cela plus simplement sans montrer les unités du facteur stœchiométrique :
\[−\dfrac{1}{2}\dfrac{\mathrm{Δmol\:NH_3}}{Δt}=\dfrac{\mathrm{Δmol\:N_2}}{Δt} \nonumber \]
Notez qu'un signe négatif a été ajouté pour tenir compte des signes opposés des deux changements de quantité (la quantité de réactif diminue alors que la quantité de produit augmente). Si les réactifs et les produits sont présents dans la même solution, les quantités molaires peuvent être remplacées par des concentrations :
\[−\dfrac{1}{2}\dfrac{Δ[\ce{NH3}]}{Δt}=\dfrac{Δ[\ce{N2}]}{Δt} \nonumber \]
De même, la vitesse de formation de H 2 est trois fois la vitesse de formation de N 2 car trois moles de H 2 se forment pendant le temps nécessaire à la formation d'une mole de N 2 :
\[\dfrac{1}{3}\dfrac{Δ[\ce{H2}]}{Δt}=\dfrac{Δ[\ce{N2}]}{Δt} \nonumber \]
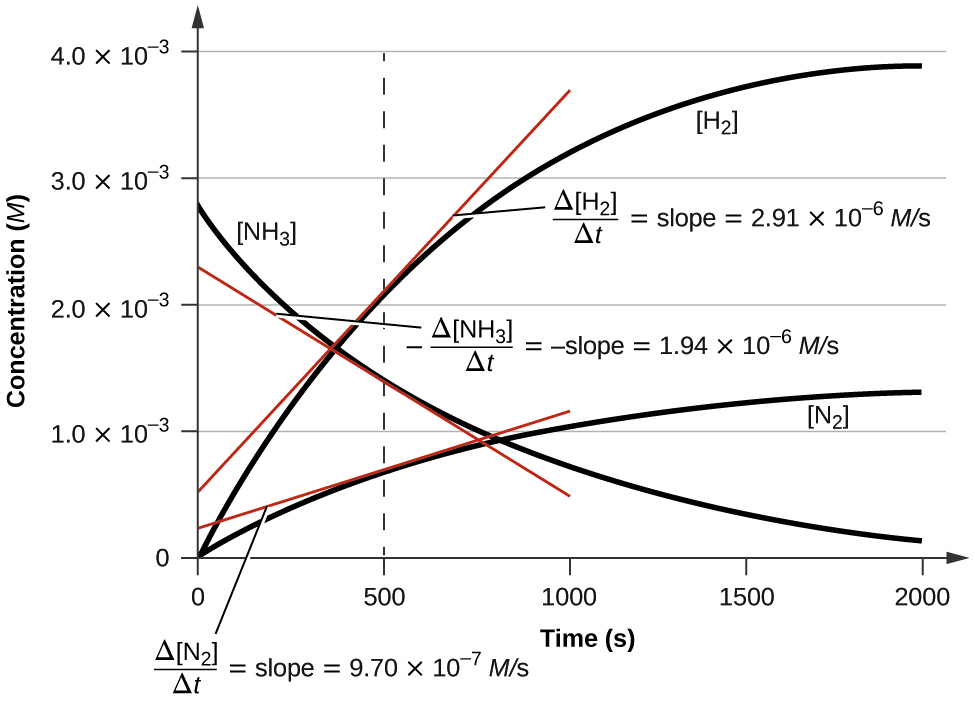
La figure\(\PageIndex{3}\) illustre l'évolution des concentrations au fil du temps pour la décomposition de l'ammoniac en azote et en hydrogène à 1100 °C. Nous pouvons voir, à partir des pentes des tangentes tracées à t = 500 secondes, que les taux de variation instantanés des concentrations des réactifs et des produits sont liés par leurs facteurs stœchiométriques. Le taux de production d'hydrogène, par exemple, est observé comme étant trois fois supérieur à celui de la production d'azote :
\[\dfrac{2.91×10^{−6}\:M/\ce s}{9.71×10^{−6}\:M/\ce s}≈3 \nonumber \]
La première étape de la production d'acide nitrique est la combustion de l'ammoniac :
\[\ce{4NH3}(g)+\ce{5O2}(g)⟶\ce{4NO}(g)+\ce{6H2O}(g) \nonumber \]
Écrivez les équations qui relient les taux de consommation des réactifs et les taux de formation des produits.
Solution
Compte tenu de la stœchiométrie de cette réaction homogène, les vitesses de consommation de réactifs et de formation de produits sont les suivantes :
\[−\dfrac{1}{4}\dfrac{Δ[\ce{NH3}]}{Δt}=−\dfrac{1}{5}\dfrac{Δ[\ce{O2}]}{Δt}=\dfrac{1}{4}\dfrac{Δ[\ce{NO}]}{Δt}=\dfrac{1}{6}\dfrac{Δ[\ce{H2O}]}{Δt} \nonumber \]
Le taux de formation de Br 2 est de 6,0 × 10 −6 mol/L/s dans une réaction décrite par l'équation ionique nette suivante :
\[\ce{5Br- + BrO3- + 6H+ ⟶ 3Br2 + 3H2O} \nonumber \]
Écrivez les équations qui relient les taux de consommation des réactifs et les taux de formation des produits.
- Réponse
-
\[−\dfrac{1}{5}\dfrac{Δ[\ce{Br-}]}{Δt}=−\dfrac{Δ[\ce{BrO3-}]}{Δt}=−\dfrac{1}{6}\dfrac{Δ[\ce{H+}]}{Δt}=\dfrac{1}{3}\dfrac{Δ[\ce{Br2}]}{Δt}=\dfrac{1}{3}\dfrac{Δ[\ce{H2O}]}{Δt} \nonumber \]
Le graphique de la figure\(\PageIndex{3}\) montre le taux de décomposition de H 2 O 2 au fil du temps :
\[\ce{2H2O2 ⟶ 2H2O + O2} \nonumber \]
Sur la base de ces données, la vitesse instantanée de décomposition de H 2 O 2 à t = 11,1 h est déterminée comme étant de 3,20 × 10 −2 mol/l/h, soit :
\[−\dfrac{Δ[\ce{H2O2}]}{Δt}=\mathrm{3.20×10^{−2}\:mol\: L^{−1}\:h^{−1}} \nonumber \]
Quel est le taux de production instantané d'H 2 O et d'O 2 ?
Solution
En utilisant la stœchiométrie de la réaction, nous pouvons déterminer que :
\[−\dfrac{1}{2}\dfrac{Δ[\ce{H2O2}]}{Δt}=\dfrac{1}{2}\dfrac{Δ[\ce{H2O}]}{Δt}=\dfrac{Δ[\ce{O2}]}{Δt} \nonumber \]
Par conséquent :
et
\[\dfrac{Δ[\ce{O2}]}{Δt}=\mathrm{1.60×10^{−2}\:mol\:L^{−1}\:h^{−1}} \nonumber \]
Si le taux de décomposition de l'ammoniac, NH 3, à 1150 K est de 2,10 × 10 −6 mol/L/s, quel est le taux de production d'azote et d'hydrogène ?
- Réponse
-
1,05 × 10 −6 mol/L/s, N 2 et 3,15 × 10 −6 mol/L/s, H 2.
Résumé
La vitesse d'une réaction peut être exprimée soit en termes de diminution de la quantité d'un réactif, soit en termes d'augmentation de la quantité d'un produit par unité de temps. Les relations entre les différentes expressions de vitesse pour une réaction donnée sont dérivées directement des coefficients stœchiométriques de l'équation représentant la réaction.
Lexique
- taux moyen
- taux d'une réaction chimique calculé comme le rapport entre un changement mesuré de la quantité ou de la concentration de la substance et l'intervalle de temps au cours duquel le changement s'est produit
- taux initial
- vitesse instantanée d'une réaction chimique à t = 0 s (immédiatement après le début de la réaction)
- taux instantané
- vitesse d'une réaction chimique à tout instant, déterminée par la pente de la droite tangente à un graphique de concentration en fonction du temps
- vitesse de réaction
- mesure de la vitesse à laquelle se produit une réaction chimique
- expression du taux
- représentation mathématique reliant la vitesse de réaction aux changements de quantité, de concentration ou de pression du réactif ou de l'espèce de produit par unité de temps


