9.4 : Épanchement et diffusion de gaz
- Page ID
- 194061
⋅
- Définir et expliquer l'effusion et la diffusion
- Énoncez la loi de Graham et utilisez-la pour calculer les propriétés pertinentes du gaz
Si vous vous êtes déjà rendu dans une pièce lors de la livraison d'une pizza très chaude, vous avez été informé du fait que des molécules gazeuses peuvent se répandre rapidement dans une pièce, comme en témoigne l'arôme agréable qui atteint rapidement votre nez. Bien que les molécules gazeuses se déplacent à des vitesses énormes (des centaines de mètres par seconde), elles entrent en collision avec d'autres molécules gazeuses et se déplacent dans de nombreuses directions différentes avant d'atteindre la cible souhaitée. À température ambiante, une molécule gazeuse subit des milliards de collisions par seconde. La trajectoire libre moyenne est la distance moyenne parcourue par une molécule entre deux collisions. Le trajet libre moyen augmente avec la diminution de la pression ; en général, le trajet libre moyen d'une molécule gazeuse sera des centaines de fois le diamètre de la molécule
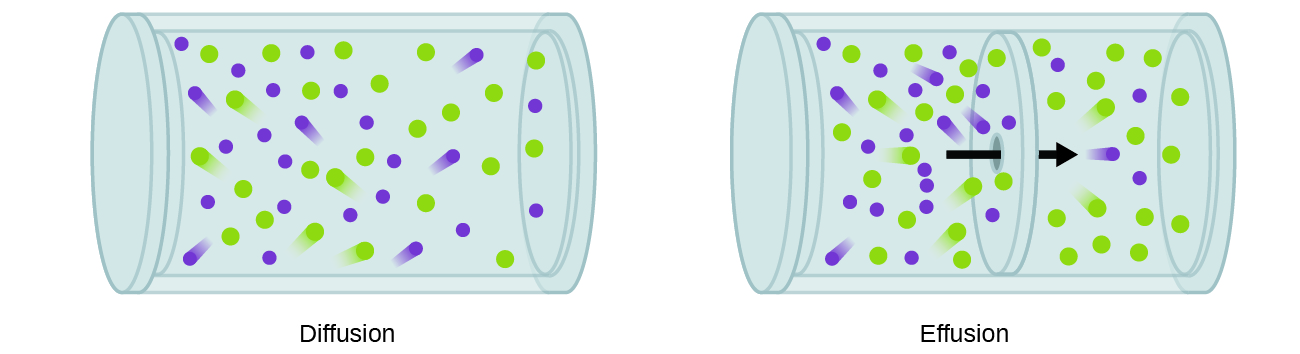
En général, nous savons que lorsqu'un échantillon de gaz est introduit dans une partie d'un récipient fermé, ses molécules se dispersent très rapidement dans tout le récipient ; ce processus par lequel les molécules se dispersent dans l'espace en réponse à des différences de concentration est appelé diffusion (illustré sur la figure\(\PageIndex{1}\)) . Les atomes ou molécules gazeux ne sont évidemment pas conscients de tout gradient de concentration ; ils se déplacent simplement de manière aléatoire : les régions à forte concentration contiennent plus de particules que les régions à faible concentration, ce qui entraîne un mouvement net d'espèces des zones à forte concentration vers les zones à faible concentration. Dans un environnement fermé, la diffusion se traduira finalement par des concentrations de gaz égales dans l'ensemble, comme le montre la Figure\(\PageIndex{1}\). Les atomes et les molécules gazeux continuent de se déplacer, mais comme leurs concentrations sont les mêmes dans les deux ampoules, les taux de transfert entre les ampoules sont égaux (aucun transfert net de molécules ne se produit).

Nous nous intéressons souvent au taux de diffusion, à la quantité de gaz traversant une zone par unité de temps :
\[\textrm{rate of diffusion}=\dfrac{\textrm{amount of gas passing through an area}}{\textrm{unit of time}} \nonumber \]
Le taux de diffusion dépend de plusieurs facteurs : le gradient de concentration (augmentation ou diminution de la concentration d'un point à un autre), la quantité de surface disponible pour la diffusion et la distance que les particules de gaz doivent parcourir. Notez également que le temps nécessaire pour que la diffusion se produise est inversement proportionnel à la vitesse de diffusion, comme le montre l'équation du taux de diffusion.
Un processus impliquant le mouvement d'espèces gazeuses similaire à la diffusion est l'effusion, c'est-à-dire l'échappement de molécules de gaz par un minuscule trou, tel qu'un trou d'épingle dans un ballon, dans le vide (Figure\(\PageIndex{1}\)). Bien que les taux de diffusion et d'effusion dépendent tous deux de la masse molaire du gaz impliqué, leurs vitesses ne sont pas égales ; cependant, les rapports de leurs vitesses sont les mêmes.
Si un mélange de gaz est placé dans un récipient à parois poreuses, les gaz s'échappent par les petites ouvertures des parois. Les gaz les plus légers passent par les petites ouvertures plus rapidement (à une vitesse plus élevée) que les plus lourds (Figure\(\PageIndex{2}\)). En 1832, Thomas Graham a étudié les taux d'effusion de différents gaz et a formulé la loi d'effusion de Graham : La vitesse d'effusion d'un gaz est inversement proportionnelle à la racine carrée de la masse de ses particules :
\[\textrm{rate of effusion}∝\dfrac{1}{\sqrt{ℳ}} \nonumber \]
Cela signifie que si deux gaz A et B sont à la même température et à la même pression, le rapport de leurs taux d'effusion est inversement proportionnel au rapport des racines carrées des masses de leurs particules :
\[\dfrac{\textrm{rate of effusion of B}}{\textrm{rate of effusion of A}}=\dfrac{\sqrt{ℳ_\ce{A}}}{\sqrt{ℳ_\ce{B}}} \nonumber \]

Calculez le rapport entre le taux d'effusion d'hydrogène et le taux d'effusion d'oxygène.
Solution
D'après la loi de Graham, nous avons :
\[\dfrac{\textrm{rate of effusion of hydrogen}}{\textrm{rate of effusion of oxygen}}=\mathrm{\dfrac{\sqrt{1.43\cancel{g\: L^{−1}}}}{\sqrt{0.0899\cancel{g\: L^{−1}}}}=\dfrac{1.20}{0.300}=\dfrac{4}{1}} \nonumber \]
En utilisant des masses molaires :
\[\dfrac{\textrm{rate of effusion of hydrogen}}{\textrm{rate of effusion of oxygen}}=\mathrm{\dfrac{32\cancel{g\: mol^{−1}}}{2\cancel{g\: mol^{−1}}}=\dfrac{\sqrt{16}}{\sqrt{1}}=\dfrac{4}{1}} \nonumber \]
L'hydrogène s'évapore quatre fois plus rapidement que l'oxygène.
À une pression et à une température particulières, l'azote s'écoule à une vitesse de 79 ml/s. À quelle vitesse le dioxyde de soufre s'écoulera-t-il en utilisant le même appareil à la même température et à la même pression ?
- Réponse
-
52 mL/s
Voici un autre exemple qui montre en quoi la détermination des temps diffère de la détermination des taux.
Il faut 243 s pour que 4,46 × 10 −5 mol Xe s'écoule à travers un petit trou. Dans les mêmes conditions, combien de temps faudra-t-il pour que 4,46 × 10 −5 mol Ne s'effuse ?
Solution
Il est important de résister à la tentation d'utiliser directement les temps et de se rappeler comment la vitesse est liée au temps et comment elle est liée à la masse. Rappelons la définition du taux d'effusion :
\[\textrm{rate of effusion}=\dfrac{\textrm{amount of gas transferred}}{\textrm{time}}\nonumber \]
et combinez-la avec la loi de Graham :
\[\dfrac{\textrm{rate of effusion of gas Xe}}{\textrm{rate of effusion of gas Ne}}=\dfrac{\sqrt{ℳ_\ce{Ne}}}{\sqrt{ℳ_\ce{Xe}}}\nonumber \]
Pour obtenir :
\[\dfrac{\dfrac{\textrm{amount of Xe transferred}}{\textrm{time for Xe}}}{\dfrac{\textrm{amount of Ne transferred}}{\textrm{time for Ne}}}=\dfrac{\sqrt{ℳ_\ce{Ne}}}{\sqrt{ℳ_\ce{Xe}}}\nonumber \]
En notant que la quantité de A = quantité de B, et en résolvant en fonction du temps pour Ne :
\[\dfrac{\dfrac{\cancel{\textrm{amount of Xe}}}{\textrm{time for Xe}}}{\dfrac{\cancel{\textrm{amount of Ne}}}{\textrm{time for Ne}}}=\dfrac{\textrm{time for Ne}}{\textrm{time for Xe}}=\dfrac{\sqrt{ℳ_\ce{Ne}}}{\sqrt{ℳ_\ce{Xe}}}=\dfrac{\sqrt{ℳ_\ce{Ne}}}{\sqrt{ℳ_\ce{Xe}}} \nonumber \]
et valeurs de substitution :
\[\mathrm{\dfrac{time\: for\: Ne}{243\:s}=\sqrt{\dfrac{20.2\cancel{g\: mol}}{131.3\cancel{g\: mol}}}=0.392}\nonumber \]
Enfin, déterminez la quantité souhaitée :
\[\mathrm{time\: for\: Ne=0.392×243\:s=95.3\:s}\nonumber \]
Notez que cette réponse est raisonnable : Comme Ne est plus léger que Xe, le taux d'effusion pour Ne sera plus important que celui pour\(\ce{Xe}\), ce qui signifie que le temps d'effusion pour Ne sera plus court que pour Xe.
Un ballon de fête rempli d'hélium se dégonfle pour\(\dfrac{2}{3}\) retrouver son volume d'origine en 8 heures. Combien de temps faudra-t-il à un ballon identique rempli du même nombre de moles d'air (= 28,2 g/mol) pour\(\dfrac{1}{2}\) atteindre son volume initial ?
- Réponse
-
32 h
Enfin, voici un autre exemple montrant comment calculer la masse molaire à partir des données sur le taux d'effusion.
Un gaz inconnu s'échappe 1,66 fois plus rapidement que le CO 2. Quelle est la masse molaire du gaz inconnu ? Pouvez-vous deviner raisonnablement son identité ?
Solution
D'après la loi de Graham, nous avons :
\[\mathrm{\dfrac{rate\: of\: effusion\: of\: Unknown}{rate\: of\: effusion\: of\: CO_2}}=\dfrac{\sqrt{ℳ_\mathrm{CO_2}}}{\sqrt{ℳ_{Unknown}}} \nonumber \]
Branchez les données connues :
\[\dfrac{1.66}{1}=\dfrac{\sqrt{44.0\:\ce{g/mol}}}{\sqrt{ℳ_{Unknown}}} \nonumber \]
Résoudre :
\[ℳ_{Unknown}=\mathrm{\dfrac{44.0\:g/mol}{(1.66)^2}=16.0\:g/mol} \nonumber \]
Le gaz pourrait bien être du CH 4, le seul gaz ayant cette masse molaire.
L'hydrogène s'écoule à travers un contenant poreux 8,97 fois plus vite qu'un gaz inconnu. Estimez la masse molaire du gaz inconnu.
- Réponse
-
163 g/mol
La diffusion gazeuse a été utilisée pour produire de l'uranium enrichi destiné à être utilisé dans des centrales nucléaires et des armes. L'uranium naturel ne contient que 0,72 % de 235 U, le type d'uranium « fissile », c'est-à-dire capable de supporter une réaction de fission en chaîne nucléaire. Les réacteurs nucléaires nécessitent un combustible contenant entre 2 et 5 % de 235 U, et les bombes nucléaires nécessitent des concentrations encore plus élevées. L'un des moyens d'enrichir l'uranium aux niveaux souhaités est de tirer parti de la loi de Graham. Dans une usine d'enrichissement par diffusion gazeuse, l'hexafluorure d'uranium (UF 6, le seul composé d'uranium suffisamment volatil pour fonctionner) est pompé lentement dans de grands récipients cylindriques appelés diffuseurs, qui contiennent des barrières poreuses dotées d'ouvertures microscopiques. Il s'agit d'un processus de diffusion car l'autre côté de la barrière n'est pas évacué. Les 235 molécules d'UF 6 ont une vitesse moyenne plus élevée et diffusent à travers la barrière un peu plus rapidement que les 238 molécules d'UF 6 plus lourdes. Le gaz qui a traversé la barrière est légèrement enrichi en 235 UF 6 et le gaz résiduel est légèrement appauvri. La faible différence de poids moléculaire entre 235 UF 6 et 238 UF 6 (enrichissement d'environ 0,4 % seulement) est obtenue dans un seul diffuseur (Figure\(\PageIndex{4}\)). Mais en connectant de nombreux diffuseurs en une séquence d'étapes (appelée cascade), le niveau d'enrichissement souhaité peut être atteint.

La séparation à grande échelle du 235 UF 6 gazeux et du 238 UF 6 a été réalisée pour la première fois pendant la Seconde Guerre mondiale, dans l'installation d'énergie atomique d'Oak Ridge, dans le Tennessee, dans le cadre du projet Manhattan (développement de la première bombe atomique). Bien que la théorie soit simple, cela a nécessité de surmonter de nombreux défis techniques redoutables pour qu'elle fonctionne dans la pratique. La barrière doit comporter de petits trous uniformes (environ 10 à 6 cm de diamètre) et être suffisamment poreuse pour produire des débits élevés. Tous les matériaux (la barrière, les tubes, les revêtements de surface, les lubrifiants et les joints) doivent pouvoir contenir l'UF 6 hautement réactif et corrosif, mais ne pas réagir avec lui.
Comme les installations de diffusion gazeuse nécessitent de très grandes quantités d'énergie (pour comprimer le gaz aux pressions élevées requises et le faire passer dans la cascade du diffuseur, pour éliminer la chaleur produite lors de la compression, etc.), elles sont désormais remplacées par la technologie de centrifugation à gaz, qui nécessite beaucoup moins d'énergie. L'une des questions politiques actuelles est de savoir comment refuser cette technologie à l'Iran, afin de l'empêcher de produire suffisamment d'uranium enrichi pour qu'il puisse l'utiliser pour fabriquer des armes nucléaires.
Résumé
Les atomes et les molécules gazeux se déplacent librement et de manière aléatoire dans l'espace. La diffusion est le processus par lequel les atomes et les molécules gazeux sont transférés de régions de concentration relativement élevée vers des régions de concentration relativement faible. L'effusion est un processus similaire dans lequel des espèces gazeuses passent d'un récipient à un vide par de très petits orifices. Les taux d'effusion des gaz sont inversement proportionnels aux racines carrées de leurs densités ou aux racines carrées de leurs masses atomes/molécules (loi de Graham).
Équations clés
- \(\textrm{rate of diffusion}=\dfrac{\textrm{amount of gas passing through an area}}{\textrm{unit of time}}\)
- \(\dfrac{\textrm{rate of effusion of gas A}}{\textrm{rate of effusion of gas B}}=\dfrac{\sqrt{m_B}}{\sqrt{m_A}}=\dfrac{\sqrt{ℳ_B}}{\sqrt{ℳ_A}}\)
Résumé
- dispersion
- mouvement d'un atome ou d'une molécule d'une région de concentration relativement élevée vers une région de concentration relativement faible (discuté dans ce chapitre en ce qui concerne les espèces gazeuses, mais applicable aux espèces présentes dans n'importe quelle phase)
- effusion
- transfert d'atomes ou de molécules gazeux d'un récipient vers un vide par de très petites ouvertures
- La loi de Graham sur l'effusion
- les taux de diffusion et d'effusion des gaz sont inversement proportionnels aux racines carrées de leurs masses moléculaires
- chemin libre moyen
- distance moyenne parcourue par une molécule entre deux collisions
- taux de diffusion
- quantité de gaz diffusant à travers une zone donnée pendant un temps donné


