9.3 : Stoechiométrie des substances gazeuses, des mélanges et des réactions
- Page ID
- 194053
⦁
- Utilisez la loi des gaz idéale pour calculer les densités de gaz et les masses molaires
- Effectuer des calculs stœchiométriques impliquant des substances gazeuses
- Énoncez la loi de Dalton sur les pressions partielles et utilisez-la dans des calculs impliquant des mélanges gazeux
L'étude du comportement chimique des gaz a été à la base de la révolution chimique peut-être la plus fondamentale de l'histoire. Le noble français Antoine Lavoisier, largement considéré comme le « père de la chimie moderne », a fait passer la chimie d'une science qualitative à une science quantitative grâce à ses travaux sur les gaz. Il a découvert la loi de conservation de la matière, découvert le rôle de l'oxygène dans les réactions de combustion, déterminé la composition de l'air, expliqué la respiration en termes de réactions chimiques, etc. Il a été victime de la Révolution française, guillotiné en 1794. À propos de sa mort, le mathématicien et astronome Joseph-Louis Lagrange a déclaré : « Il n'a fallu qu'un instant à la foule pour retirer sa tête ; un siècle ne suffira pas à la reproduire ».
Comme décrit dans un chapitre précédent de ce texte, nous pouvons nous tourner vers la stœchiométrie chimique pour obtenir des réponses à de nombreuses questions qui demandent « Quelle quantité ? » Nous pouvons répondre à la question avec des masses de substances ou des volumes de solutions. Cependant, nous pouvons également répondre à cette question d'une autre manière : avec des volumes de gaz. Nous pouvons utiliser l'équation du gaz idéal pour relier la pression, le volume, la température et le nombre de moles d'un gaz. Nous allons ici combiner l'équation du gaz idéal avec d'autres équations pour déterminer la densité du gaz et la masse molaire. Nous traiterons des mélanges de différents gaz et calculerons les quantités de substances lors de réactions impliquant des gaz. Cette section ne présentera aucun nouveau matériel ni aucune nouvelle idée, mais fournira des exemples d'applications et de moyens d'intégrer des concepts dont nous avons déjà parlé.
Densité d'un gaz
Rappelons que la densité d'un gaz est son rapport masse/volume,\(ρ=\dfrac{m}{V}\). Par conséquent, si nous pouvons déterminer la masse d'un certain volume d'un gaz, nous obtiendrons sa densité. La densité d'un gaz inconnu peut être utilisée pour déterminer sa masse molaire et ainsi aider à son identification. La loi du gaz idéal, PV = NRt, nous fournit un moyen de dériver une telle formule mathématique pour relier la densité d'un gaz à son volume dans la preuve présentée dans l'exemple\(\PageIndex{1}\).
Utilisez PV = nRT pour obtenir une formule pour la densité du gaz en g/L
Une solution
\[PV = nRT \nonumber \]
Réorganisez pour obtenir (mol/L) :
\[\dfrac{n}{v}=\dfrac{P}{RT} \nonumber \]
Multipliez chaque côté de l'équation par la masse molaire,. Lorsque les moles sont multipliées par en g/mol, on obtient g :
\[(ℳ)\left(\dfrac{n}{V}\right)=\left(\dfrac{P}{RT}\right)(ℳ) \nonumber \]
\[ℳ/V=ρ=\dfrac{Pℳ}{RT} \nonumber \]
On a découvert qu'un gaz avait une densité de 0,0847 g/L à 17,0 °C et une pression de 760 torr. Quelle est sa masse molaire ? Qu'est-ce que le gaz ?
- Réponse
-
\[ρ=\dfrac{Pℳ}{RT} \nonumber \]
\[\mathrm{0.0847\:g/L=760\cancel{torr}×\dfrac{1\cancel{atm}}{760\cancel{torr}}×\dfrac{\mathit{ℳ}}{0.0821\: L\cancel{atm}/mol\: K}×290\: K} \nonumber \]
= 2,02 g/mol ; par conséquent, le gaz doit être de l'hydrogène (H 2, 2,02 g/mol)
Nous devons spécifier à la fois la température et la pression d'un gaz lors du calcul de sa densité, car le nombre de moles d'un gaz (et donc la masse du gaz) dans un litre varie avec la température ou la pression. Les densités de gaz sont souvent signalées au STP.
En utilisant la loi du gaz idéal et la densité d'un gaz, le cyclopropane, un gaz autrefois utilisé avec de l'oxygène comme anesthésique général, est composé de 85,7 % de carbone et de 14,3 % d'hydrogène en masse. Trouvez la formule empirique. Si 1,56 g de cyclopropane occupe un volume de 1,00 L à 0,984 atm et à 50 °C, quelle est la formule moléculaire du cyclopropane ?
Solution
Stratégie :
Résolvez d'abord le problème des formules empiriques en utilisant les méthodes décrites précédemment Supposons 100 g et convertissez le pourcentage de chaque élément en grammes. Déterminez le nombre de moles de carbone et d'hydrogène dans l'échantillon de 100 g de cyclopropane. Divisez par le plus petit nombre de moles pour relier le nombre de moles de carbone au nombre de moles d'hydrogène. Dans la dernière étape, sachez que le plus petit ratio de nombres entiers est la formule empirique :
\[\mathrm{85.7\: g\: C×\dfrac{1\: mol\: C}{12.01\: g\: C}=7.136\: mol\: C\hspace{20px}\dfrac{7.136}{7.136}=1.00\: mol\: C} \nonumber \]
\[\mathrm{14.3\: g\: H×\dfrac{1\: mol\: H}{1.01\: g\: H}=14.158\: mol\: H\hspace{20px}\dfrac{14.158}{7.136}=1.98\: mol\: H} \nonumber \]
La formule empirique est CH 2 [masse empirique (EM) de 14,03 g/unité empirique].
Ensuite, utilisez l'équation de densité liée à la loi des gaz idéaux pour déterminer la masse molaire :
\[d=\dfrac{Pℳ}{RT}\hspace{20px}\mathrm{\dfrac{1.56\: g}{1.00\: L}=0.984\: atm×\dfrac{ℳ}{0.0821\: L\: atm/mol\: K}×323\: K} \nonumber \]
= 42,0 g/mol\(\dfrac{ℳ}{Eℳ}=\dfrac{42.0}{14.03}=2.99\), donc (3) (CH 2) = C 3 H 6 (formule moléculaire)
L'acétylène, combustible utilisé pour les torches de soudage, est composé de 92,3 % de C et de 7,7 % de H en masse. Trouvez la formule empirique. Si 1,10 g d'acétylène occupe un volume de 1,00 L à 1,15 atm et à 59,5 °C, quelle est la formule moléculaire de l'acétylène ?
- Réponse
-
Formule empirique, CH ; Formule moléculaire, C 2 H 2
Masse molaire d'un gaz
Une autre application utile de la loi des gaz idéaux concerne la détermination de la masse molaire. Par définition, la masse molaire d'une substance est le rapport entre sa masse en grammes, m, et sa quantité en moles, n :
\[ℳ=\mathrm{\dfrac{grams\: of\: substance}{moles\: of\: substance}}=\dfrac{m}{n} \nonumber \]
L'équation du gaz idéal peut être réarrangée pour isoler n :
\[n=\dfrac{PV}{RT} \nonumber \]
puis combiné à l'équation de masse molaire pour obtenir :
\[ℳ=\dfrac{mRT}{PV} \nonumber \]
Cette équation peut être utilisée pour déduire la masse molaire d'un gaz à partir de mesures de sa pression, de son volume, de sa température et de sa masse.
La masse molaire approximative d'un liquide volatil peut être déterminée par :
- Chauffer un échantillon du liquide dans un flacon percé d'un petit trou dans la partie supérieure, qui transforme le liquide en gaz susceptible de s'échapper par le trou
- Retirer le flacon du feu au moment où le dernier morceau de liquide se transforme en gaz, moment auquel le flacon sera rempli uniquement d'un échantillon gazeux à pression ambiante
- Sceller le flacon et laisser l'échantillon gazeux se condenser en liquide, puis peser le flacon pour déterminer la masse de l'échantillon (Figure\(\PageIndex{1}\))

En utilisant cette procédure, un échantillon de gaz chloroformique pesant 0,494 g est prélevé dans un flacon d'un volume de 129 cm 3 à 99,6 °C lorsque la pression atmosphérique est de 742,1 mm Hg. Quelle est la masse molaire approximative du chloroforme ?
Solution
Depuis
\[ℳ=\dfrac{m}{n} \nonumber \]
et
\[n=\dfrac{PV}{RT} \nonumber \]
la substitution et le réarrangement donnent
\[ℳ=\dfrac{mRT }{PV} \nonumber \]
alors
\[ℳ=\dfrac{mRT}{PV}=\mathrm{\dfrac{(0.494\: g)×0.08206\: L⋅atm/mol\: K×372.8\: K}{0.976\: atm×0.129\: L}=120\:g/mol} \nonumber \]
Un échantillon de phosphore pesant 3,243 × 10 −2 g exerce une pression de 31,89 kPa dans une ampoule de 56,0 ml à 550 °C. Quelles sont la masse molaire et la formule moléculaire de la vapeur de phosphore ?
- Réponse
-
124 g/mol de P 4
La pression d'un mélange de gaz : la loi de Dalton
À moins qu'ils ne réagissent chimiquement entre eux, les gaz individuels d'un mélange de gaz n'affectent pas la pression de l'autre. Chaque gaz d'un mélange exerce la même pression que s'il était présent seul dans le récipient (Figure\(\PageIndex{2}\)). La pression exercée par chaque gaz individuel dans un mélange est appelée pression partielle. Cette observation est résumée par la loi de Dalton sur les pressions partielles : La pression totale d'un mélange de gaz idéaux est égale à la somme des pressions partielles des gaz composants :
\[P_{Total}=P_A+P_B+P_C+...=\sum_iP_i \nonumber \]
Dans l'équation P Total est la pression totale d'un mélange de gaz, P A est la pression partielle du gaz A ; P B est la pression partielle du gaz B ; P C est la pression partielle du gaz C ; et ainsi de suite.

La pression partielle du gaz A est liée à la pression totale du mélange gazeux via sa fraction molaire (X), une unité de concentration définie comme le nombre de moles d'un composant d'une solution divisé par le nombre total de moles de tous les composants :
\[P_A=X_A×P_{Total}\hspace{20px}\ce{where}\hspace{20px}X_A=\dfrac{n_A}{n_{Total}} \nonumber \]
où P A, X A et n A sont la pression partielle, la fraction molaire et le nombre de moles du gaz A, respectivement, et n Total est le nombre de moles de tous les composants du mélange.
Un récipient de 10,0 L contient 2,50 × 10 −3 mol de H 2, 1,00 × 10 −3 mol de He et 3,00 × 10 −4 mol de Ne à 35 °C.
- Quelles sont les pressions partielles de chacun des gaz ?
- Quelle est la pression totale dans les atmosphères ?
Solution
Les gaz se comportent indépendamment, de sorte que la pression partielle de chaque gaz peut être déterminée à partir de l'équation du gaz idéal, en utilisant\(P=\dfrac{nRT}{V}\) :
\[P_\mathrm{H_2}=\mathrm{\dfrac{(2.50×10^{−3}\:mol)(0.08206\cancel{L}atm\cancel{mol^{−1}\:K^{−1}})(308\cancel{K})}{10.0\cancel{L}}=6.32×10^{−3}\:atm} \nonumber \]
\[P_\ce{He}=\mathrm{\dfrac{(1.00×10^{−3}\cancel{mol})(0.08206\cancel{L}atm\cancel{mol^{−1}\:K^{−1}})(308\cancel{K})}{10.0\cancel{L}}=2.53×10^{−3}\:atm} \nonumber \]
\[P_\ce{Ne}=\mathrm{\dfrac{(3.00×10^{−4}\cancel{mol})(0.08206\cancel{L}atm\cancel{mol^{−1}\:K^{−1}})(308\cancel{K})}{10.0\cancel{L}}=7.58×10^{−4}\:atm} \nonumber \]
La pression totale est donnée par la somme des pressions partielles :
\[P_\ce{T}=P_\mathrm{H_2}+P_\ce{He}+P_\ce{Ne}=\mathrm{(0.00632+0.00253+0.00076)\:atm=9.61×10^{−3}\:atm} \nonumber \]
Un flacon de 5,73 L à 25 °C contient 0,0388 mol de N 2, 0,147 mol de CO et 0,0803 mol de H 2. Quelle est la pression totale dans le flacon en atmosphères ?
- Réponse
-
1,137 atm
Voici un autre exemple de ce concept, mais traitant du calcul des fractions molaires.
Un mélange gazeux utilisé pour l'anesthésie contient 2,83 mol d'oxygène, O 2, et 8,41 mol d'oxyde nitreux, N 2 O. La pression totale du mélange est de 192 kPa.
- Quelles sont les fractions molaires de O 2 et de N 2 O ?
- Quelles sont les pressions partielles de O 2 et de N 2 O ?
Solution
La fraction molaire est donnée par
\[X_A=\dfrac{n_A}{n_{Total}} \nonumber \]
et la pression partielle est
\[P_A = X_A \times P_{Total} \nonumber \]
Pour O 2,
\[X_{O_2}=\dfrac{n_{O_2}}{n_{Total}}=\mathrm{\dfrac{2.83 mol}{(2.83+8.41)\:mol}=0.252} \nonumber \]
et
\[P_{O_2}=X_{O_2}×P_{Total}=\mathrm{0.252×192\: kPa=48.4\: kPa} \nonumber \]
Pour N 2 O,
\[X_{N_2O}=\dfrac{n_{N_2O}}{n_{Total}}=\mathrm{\dfrac{8.41\: mol}{(2.83+8.41)\:mol}=0.748} \nonumber \]
et
\[P_{N_2O}=X_{N_2O}×P_{Total}=\mathrm{(0.748)×192\: kPa = 143.6 \: kPa} \nonumber \]
Quelle est la pression d'un mélange de 0,200 g de H 2, de 1,00 g de N 2 et de 0,820 g d'Ar dans un récipient d'un volume de 2,00 L à 20 °C ?
- Réponse
-
1,87 atm
Collecte de gaz au-dessus de l'eau
Un moyen simple de collecter les gaz qui ne réagissent pas avec l'eau est de les capturer dans une bouteille remplie d'eau et retournée dans un plat rempli d'eau. La pression du gaz à l'intérieur de la bouteille peut être rendue égale à la pression de l'air extérieur en soulevant ou en abaissant la bouteille. Lorsque le niveau d'eau est le même à l'intérieur et à l'extérieur de la bouteille (Figure\(\PageIndex{3}\)), la pression du gaz est égale à la pression atmosphérique, qui peut être mesurée à l'aide d'un baromètre.
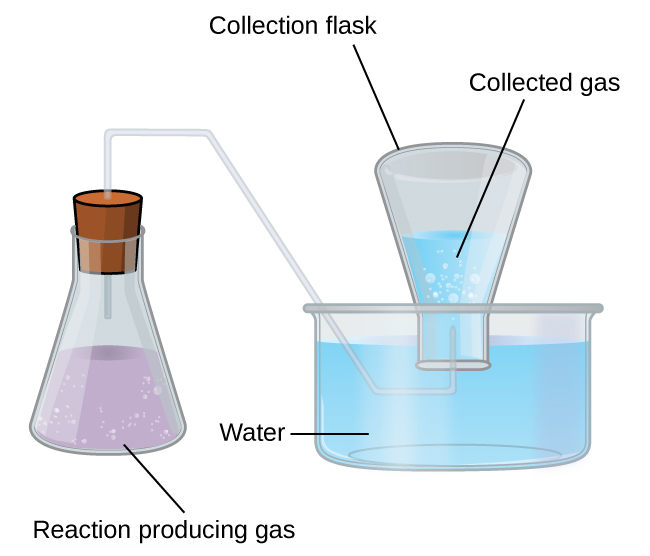
Cependant, il y a un autre facteur à prendre en compte lorsque nous mesurons la pression du gaz par cette méthode. L'eau s'évapore et il y a toujours de l'eau gazeuse (vapeur d'eau) au-dessus d'un échantillon d'eau liquide. Lorsqu'un gaz est collecté au-dessus de l'eau, il devient saturé de vapeur d'eau et la pression totale du mélange est égale à la pression partielle du gaz plus la pression partielle de la vapeur d'eau. La pression du gaz pur est donc égale à la pression totale moins la pression de la vapeur d'eau, c'est ce que l'on appelle la pression du gaz « sec », c'est-à-dire la pression du gaz uniquement, sans vapeur d'eau.
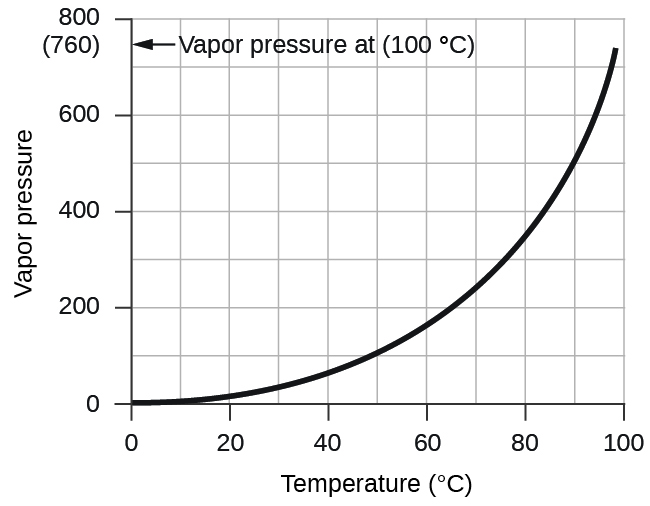
La pression de vapeur de l'eau, qui est la pression exercée par la vapeur d'eau en équilibre avec l'eau liquide dans un récipient fermé, dépend de la température (Figure\(\PageIndex{4}\)) ; des informations plus détaillées sur la dépendance de la vapeur d'eau en fonction de la température peuvent être trouvées dans le tableau\(\PageIndex{1}\) et la vapeur la pression sera abordée plus en détail dans le prochain chapitre sur les liquides.
| Température (°C) | Pression (torr) | Température (°C) | Pression (torr) | Température (°C) | Pression (torr) | ||
|---|---|---|---|---|---|---|---|
| —10 | 1,95 | 18 | 15,5 | 30 | 31,8 | ||
| —5 | 3,0 | 19 | 16,5 | 35 | 42,2 | ||
| —2 | 3.9 | 20 | 17,5 | 40 | 55,3 | ||
| 0 | 4.6 | 21 | 18,7 | 50 | 92,5 | ||
| 2 | 5.3 | 22 | 19,8 | 60 | 149,4 | ||
| 4 | 6.1 | 23 | 21,1 | 70 | 233,7 | ||
| 6 | 7,0 | 24 | 22,4 | 80 | 355,1 | ||
| 8 | 8,0 | 25 | 23,8 | 90 | 525,8 | ||
| 10 | 9.2 | 26 | 25,2 | 95 | 633,9 | ||
| 12 | 10,5 | 27 | 26,7 | 99 | 733,2 | ||
| 14 | 12,0 | 28 | 28,3 | 100,0 | 760,0 | ||
| 16 | 13,6 | 29 | 30,0 | 101,0 | 787,6 |
Si 0,200 L d'argon sont collectés au-dessus de l'eau à une température de 26 °C et à une pression de 750 torr dans un système tel que celui illustré à la figure\(\PageIndex{3}\), quelle est la pression partielle de l'argon ?
Solution
Selon la loi de Dalton, la pression totale dans la bouteille (750 torr) est la somme de la pression partielle de l'argon et de la pression partielle de l'eau gazeuse :
\[P_\ce{T}=P_\ce{Ar}+P_\mathrm{H_2O} \nonumber \]
La réorganisation de cette équation pour résoudre la pression de l'argon donne :
\[P_\ce{Ar}=P_\ce{T}−P_\mathrm{H_2O} \nonumber \]
La pression de la vapeur d'eau au-dessus d'un échantillon d'eau liquide à 26 °C est de 25,2 torr (annexe E), donc :
\[P_\ce{Ar}=\mathrm{750\:torr−25.2\:torr=725\:torr} \nonumber \]
Un échantillon d'oxygène prélevé sur de l'eau à une température de 29,0 °C et à une pression de 764 torr a un volume de 0,560 L. Quel volume aurait l'oxygène sec dans les mêmes conditions de température et de pression ?
- Réponse
-
0,583 L
Stoechiométrie chimique et gaz
La stœchiométrie chimique décrit les relations quantitatives entre les réactifs et les produits dans les réactions chimiques. Nous avons déjà mesuré les quantités de réactifs et de produits en utilisant les masses des solides et les volumes en conjonction avec la molarité des solutions ; maintenant, nous pouvons également utiliser les volumes de gaz pour indiquer les quantités. Si nous connaissons le volume, la pression et la température d'un gaz, nous pouvons utiliser l'équation de gaz idéale pour calculer le nombre de moles de gaz présentes. Si nous savons combien de moles d'un gaz sont impliquées, nous pouvons calculer le volume d'un gaz à n'importe quelle température et pression.
La loi d'Avogadro revisitée
Parfois, nous pouvons tirer parti d'une caractéristique simplificatrice de la stœchiométrie des gaz que ne présentent pas les solides et les solutions : tous les gaz qui présentent un comportement idéal contiennent le même nombre de molécules dans le même volume (à la même température et à la même pression). Ainsi, les rapports des volumes de gaz impliqués dans une réaction chimique sont donnés par les coefficients de l'équation de la réaction, à condition que les volumes de gaz soient mesurés à la même température et à la même pression.
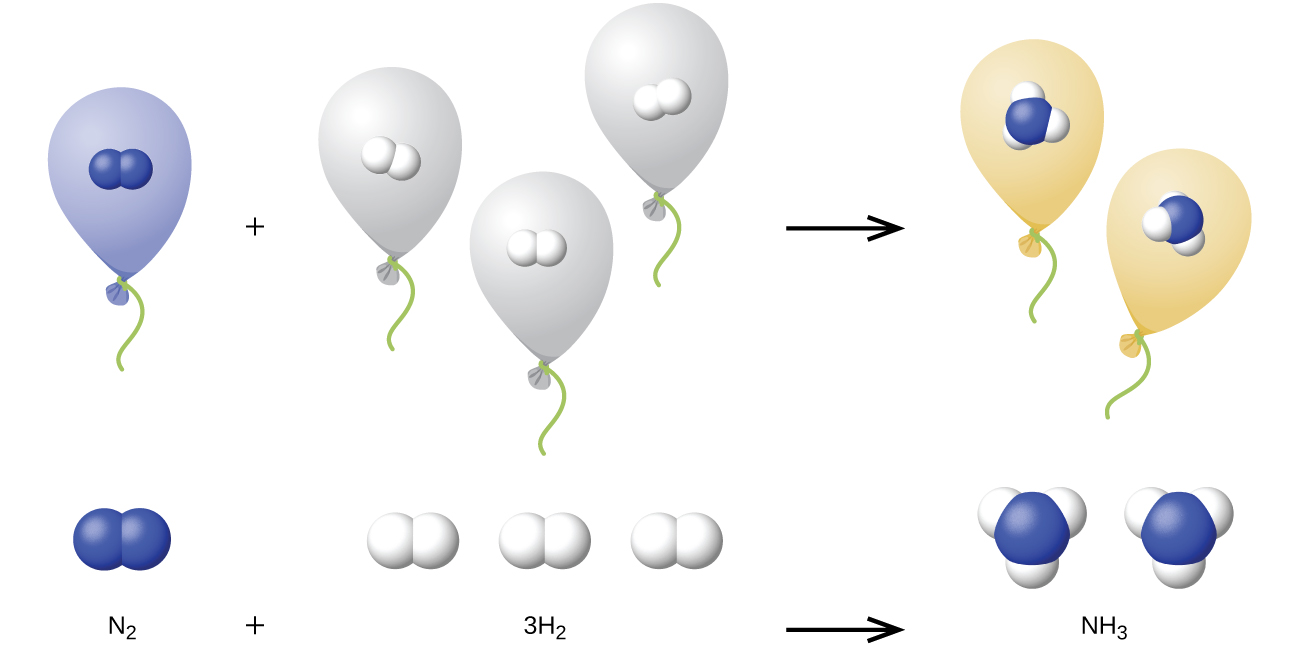
Nous pouvons étendre la loi d'Avogadro (selon laquelle le volume d'un gaz est directement proportionnel au nombre de moles du gaz) aux réactions chimiques avec les gaz : les gaz se combinent, ou réagissent, dans des proportions volumiques définies et simples, à condition que tous les volumes de gaz soient mesurés à la même température et à la même pression. Par exemple, étant donné que les gaz d'azote et d'hydrogène réagissent pour produire de l'ammoniac selon
\[\ce{N2}(g)+\ce{3H2}(g)⟶\ce{2NH3}(g) \nonumber \]
un volume donné d'azote gazeux réagit avec trois fois ce volume d'hydrogène gazeux pour produire deux fois ce volume d'ammoniac, si la pression et la température restent constantes.
L'explication de cette situation est illustrée dans la figure\(\PageIndex{4}\). Selon la loi d'Avogadro, des volumes égaux de N 2, H 2 et NH 3 gazeux, à la même température et à la même pression, contiennent le même nombre de molécules. Comme une molécule de N 2 réagit avec trois molécules de H 2 pour produire deux molécules de NH 3, le volume de H 2 requis est trois fois le volume de N 2 et le volume de NH 3 produit est deux fois le volume de N 2.
Le propane, C 3 H 8 (g), est utilisé dans les grils à gaz pour fournir la chaleur nécessaire à la cuisson. Quel volume d'O 2 (g) mesuré à 25 °C et 760 torr est nécessaire pour réagir avec 2,7 L de propane mesurés dans les mêmes conditions de température et de pression ? Supposons que le propane subit une combustion complète.
Solution
Le rapport des volumes de C 3, H 8 et O 2 sera égal au rapport de leurs coefficients dans l'équation équilibrée de la réaction :
\ [\ begin {align}
& \ ce {C3H8} (g) + \ ce {5O2} (g) ⟶ && \ ce {3CO2} (g) + \ ce {4H2O} (l) \ \
\ ce {&1 \ : volume + 5 \ : volumes &&3 \ : volumes + 4 \ : volumes}
\ end {align} \ nonnumber \]
À partir de l'équation, nous voyons qu'un volume de C 3 H 8 va réagir avec cinq volumes d'O 2 :
\[\mathrm{2.7\cancel{L\:C_3H_8}×\dfrac{5\: L\:\ce{O2}}{1\cancel{L\:C_3H_8}}=13.5\: L\:\ce{O2}} \nonumber \]
Un volume de 13,5 L d'O 2 sera nécessaire pour réagir avec 2,7 L de C 3 H 8.
Un réservoir d'acétylène pour torche de soudage à l'oxyacétylène fournit 9340 L d'acétylène gazeux, C 2 H 2, à 0 °C et à 1 atm. Combien de réservoirs d'oxygène, fournissant chacun 7,00 × 10 3 L d'O 2 à 0 °C et 1 atm, seront nécessaires pour brûler l'acétylène ?
\[\ce{2C2H2 + 5O2⟶4CO2 + 2H2O} \nonumber \]
- Réponse
-
3,34 réservoirs (2,34 × 10 4 L)
L'ammoniac est un engrais et un produit chimique industriel importants. Supposons qu'un volume de 683 milliards de pieds cubes d'ammoniac gazeux, mesuré à 25 °C et à 1 atm, ait été fabriqué. Quel volume de H 2 (g), mesuré dans les mêmes conditions, a été nécessaire pour préparer cette quantité d'ammoniac par réaction avec du N 2 ?
\[\ce{N2}(g)+\ce{3H2}(g)⟶\ce{2NH3}(g) \nonumber \]
Solution
Comme des volumes égaux de H 2 et de NH 3 contiennent un nombre égal de molécules et que chacune des trois molécules de H 2 qui réagissent produit deux molécules de NH 3, le rapport des volumes de H 2 et de NH 3 sera égal à 3:2. Deux volumes de NH 3, en l'occurrence en unités de milliards de pieds 3, seront formés à partir de trois volumes de H 2 :
\[\mathrm{683\cancel{billion\:ft^3\:NH_3}×\dfrac{3\: billion\:ft^3\:H_2}{2\cancel{billion\:ft^3\:NH_3}}=1.02×10^3\:billion\:ft^3\:H_2} \nonumber \]
La fabrication de 683 milliards de pieds 3 de NH 3 a nécessité 1 020 milliards de pieds 3 de H 2. (À 25 °C et 1 atm, il s'agit du volume d'un cube dont l'arête a une longueur d'environ 3 km.)
Quel volume d'O 2 (g) mesuré à 25 °C et 760 torr est nécessaire pour réagir avec 17,0 L d'éthylène, C 2 H 4 (g), mesuré dans les mêmes conditions de température et de pression ? Les produits sont du CO 2 et de la vapeur d'eau.
- Réponse
-
51,0 L
Quel volume d'hydrogène à 27 °C et 723 torr peut être préparé par réaction de 8,88 g de gallium avec un excès d'acide chlorhydrique ?
\[\ce{2Ga}(s)+\ce{6HCl}(aq)⟶\ce{2GaCl3}(aq)+\ce{3H2}(g) \nonumber \]
Solution en solo
Pour passer de la masse de gallium au volume de H 2 (g), nous devons faire quelque chose comme ceci :

Les deux premières conversions sont les suivantes :
\[\mathrm{8.88\cancel{g\: Ga}×\dfrac{1\cancel{mol\: Ga}}{69.723\cancel{g\: Ga}}×\dfrac{3\: mol\:H_2}{2\cancel{mol\: Ga}}=0.191\:mol\: H_2} \nonumber \]
Enfin, nous pouvons utiliser la loi des gaz idéale :
\[V_\mathrm{H_2}=\left(\dfrac{nRT}{P}\right)_\mathrm{H_2}=\mathrm{\dfrac{0.191\cancel{mol}×0.08206\: L\cancel{atm\:mol^{−1}\:K^{−1}}×300\: K}{0.951\:atm}=4.94\: L} \nonumber \]
Le dioxyde de soufre est un intermédiaire dans la préparation de l'acide sulfurique. Quel volume de SO 2 à 343 °C et 1,21 atm est produit en brûlant 100 kg de soufre dans de l'oxygène ?
- Réponse
-
1,30 × 10 3 L
La fine couche de notre atmosphère empêche la Terre de devenir une planète de glace et la rend habitable. En fait, cela est dû à moins de 0,5 % des molécules d'air. De l'énergie solaire qui atteint la Terre, elle\(\dfrac{1}{3}\) est presque réfléchie dans l'espace, le reste étant absorbé par l'atmosphère et la surface de la Terre. Une partie de l'énergie absorbée par la Terre est réémise sous forme de rayonnement infrarouge (IR), dont une partie est renvoyée dans l'atmosphère vers l'espace. Cependant, la majeure partie de ce rayonnement infrarouge est absorbée par certaines substances présentes dans l'atmosphère, appelées gaz à effet de serre, qui réémettent cette énergie dans toutes les directions et retiennent une partie de la chaleur. Cela permet de maintenir des conditions de vie favorables : sans atmosphère, la température moyenne mondiale de 14 °C (57 °F) serait d'environ —19 °C (—2 °F). Les principaux gaz à effet de serre (GES) sont la vapeur d'eau, le dioxyde de carbone, le méthane et l'ozone. Depuis la révolution industrielle, l'activité humaine a augmenté les concentrations de GES, ce qui a modifié le bilan énergétique et altère de manière significative le climat de la Terre (Figure\(\PageIndex{6}\)).
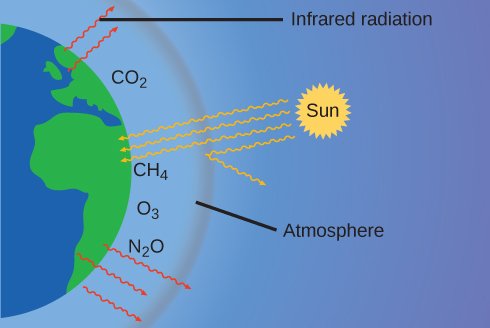
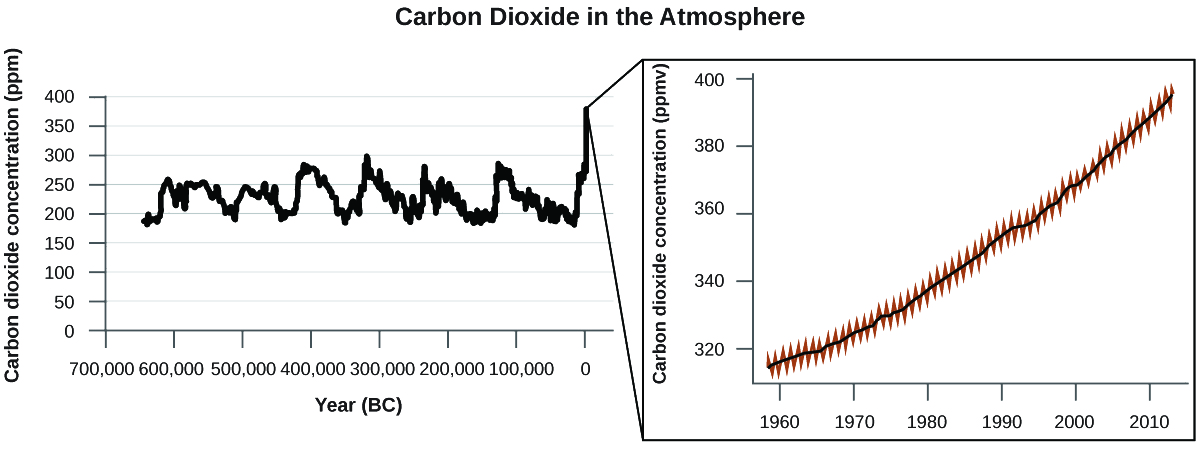
Il existe des preuves solides provenant de sources multiples que l'augmentation des niveaux atmosphériques de CO 2 est due à l'activité humaine, la combustion de combustibles fossiles étant à l'origine\(\dfrac{3}{4}\) de la récente augmentation du CO 2. Des données fiables provenant de carottes de glace révèlent que la concentration de CO 2 dans l'atmosphère a atteint son niveau le plus élevé au cours des 800 000 dernières années ; d'autres preuves indiquent qu'elle pourrait être à son niveau le plus élevé depuis 20 millions d'années. Ces dernières années, la concentration de CO 2 est passée de niveaux historiques inférieurs à 300 ppm à près de 400 ppm aujourd'hui (Figure\(\PageIndex{7}\)).
Résumé
La loi des gaz idéaux peut être utilisée pour dériver un certain nombre d'équations pratiques reliant les quantités directement mesurées aux propriétés présentant un intérêt pour les substances et mélanges gazeux. Un réarrangement approprié de l'équation du gaz idéal peut être effectué pour permettre le calcul des densités de gaz et des masses molaires. La loi des pressions partielles de Dalton peut être utilisée pour relier les pressions de gaz mesurées pour les mélanges gazeux à leurs compositions. La loi d'Avogadro peut être utilisée dans les calculs stœchiométriques pour les réactions chimiques impliquant des réactifs ou des produits gazeux.
Équations clés
- P Total = P A + P B + P C +... = i P i
- P A = X A P Total
- \(X_A=\dfrac{n_A}{n_{Total}}\)
Notes
- « Quotations de Joseph-Louis Lagrange », modifié pour la dernière fois en février 2006, consulté le 10 février 2015, www-history.mcs.st-andrews.ac... /Lagrange.html
Résumé
- La loi des pressions partielles de Dalton
- la pression totale d'un mélange de gaz idéaux est égale à la somme des pressions partielles des gaz constitutifs.
- fraction molaire (X)
- unité de concentration définie comme le rapport entre la quantité molaire d'un composant du mélange et le nombre total de moles de tous les composants du mélange
- pression partielle
- pression exercée par un gaz individuel dans un mélange
- pression de vapeur de l'eau
- pression exercée par la vapeur d'eau en équilibre avec de l'eau liquide dans un récipient fermé à une température spécifique


