9.2 : Relation de la pression, du volume, de la quantité et de la température - La loi des gaz idéaux

⦁

Objectifs d'apprentissage

• Identifier les relations mathématiques entre les différentes propriétés des gaz
• Utilisez la loi des gaz idéaux et les lois des gaz connexes pour calculer les valeurs de diverses propriétés du gaz dans des conditions spécifiées

Au cours des XVIIe et surtout XVIIIe siècles, animés à la fois par le désir de comprendre la nature et par la recherche de ballons dans lesquels ils pourraient voler (Figure\(\PageIndex{1}\)), un certain nombre de scientifiques ont établi les relations entre les propriétés physiques macroscopiques des gaz, à savoir la pression, le volume, température et quantité de gaz. Bien que leurs mesures n'aient pas été précises par rapport aux normes actuelles, ils ont pu déterminer les relations mathématiques entre les paires de ces variables (par exemple, pression et température, pression et volume) qui sous-tendent un gaz idéal, une construction hypothétique sous laquelle les gaz réels se situent certaines conditions. Finalement, ces lois individuelles ont été combinées en une seule équation, la loi des gaz idéaux, qui relie les quantités de gaz aux gaz et qui est assez précise pour les basses pressions et les températures modérées. Nous examinerons les principaux développements des relations individuelles (pour des raisons pédagogiques qui ne sont pas tout à fait dans l'ordre historique), puis les regrouperons dans la loi du gaz idéale.

Figure\(\PageIndex{1}\) : En 1783, le premier (a) vol en montgolfière remplie d'hydrogène, (b) vol habité en montgolfière et (c) vol habité en montgolfière rempli d'hydrogène a eu lieu. Lorsque le ballon rempli d'hydrogène représenté en (a) a atterri, les villageois effrayés de Gonesse l'auraient détruit à l'aide de fourches et de couteaux. Le lancement de ce dernier aurait été vu par 400 000 personnes à Paris.

Cette figure comprend trois images. L'image a est une image en noir et blanc d'un ballon à hydrogène apparemment dégonflé par une foule de personnes. Sur l'image b, un ballon bleu, doré et rouge est maintenu au sol à l'aide de cordes alors qu'il est positionné au-dessus d'une plate-forme d'où de la fumée s'élève sous le ballon. En c, une image est représentée en gris sur un fond couleur pêche d'un ballon gonflé avec des bandes verticales en l'air. Il semble avoir un panier fixé sur sa face inférieure. Un grand bâtiment majestueux apparaît en arrière-plan.

Pression et température : loi d'Amontons

Imaginez que vous remplissiez de gaz un contenant rigide fixé à un manomètre, puis que vous fermiez le récipient de manière à ce qu'aucun gaz ne s'échappe. Si le récipient est refroidi, le gaz à l'intérieur se refroidit également et on observe une diminution de la pression. Le récipient étant rigide et hermétiquement fermé, le volume et le nombre de moles de gaz restent constants. Si nous chauffons la sphère, le gaz à l'intérieur devient plus chaud (Figure\(\PageIndex{2}\)) et la pression augmente.

Figure\(\PageIndex{2}\) : Effet de la température sur la pression du gaz : Lorsque la plaque chauffante est éteinte, la pression du gaz dans la sphère est relativement faible. Lorsque le gaz est chauffé, la pression du gaz dans la sphère augmente.

Cette figure inclut trois diagrammes similaires. Dans le premier schéma à gauche, un récipient sphérique rigide contenant un gaz auquel est fixé un manomètre en haut est placé dans un grand bécher rempli d'eau, indiqué en bleu clair, au-dessus d'une plaque chauffante. L'aiguille du manomètre pointe à l'extrême gauche du manomètre. Le diagramme est étiqueté « P bas » ci-dessus et « plaque chauffante éteinte » ci-dessous. Le deuxième schéma similaire montre également le récipient de gaz sphérique rigide placé dans un grand bécher à partir duquel des segments de lignes ondulées bleu clair partent du haut du liquide contenu dans le bécher. Le bécher est situé au-dessus d'une zone circulaire légèrement rougie. L'aiguille du manomètre pointe vers le haut ou vers le milieu du manomètre. Le diagramme est étiqueté « moyen P » ci-dessus et « plaque chauffante sur support » ci-dessous. Le troisième schéma montre également le récipient de gaz sphérique rigide placé dans un grand bécher dans lequel des bulles apparaissent près de la surface du liquide et plusieurs segments de ligne bleu clair ondulés partent de la surface et sortent du bécher. Le bécher est situé au-dessus d'une zone circulaire rouge vif. L'aiguille du manomètre pointe à l'extrême droite du manomètre. Le diagramme est étiqueté « haut P » ci-dessus et « plaque chauffante en haut » ci-dessous.

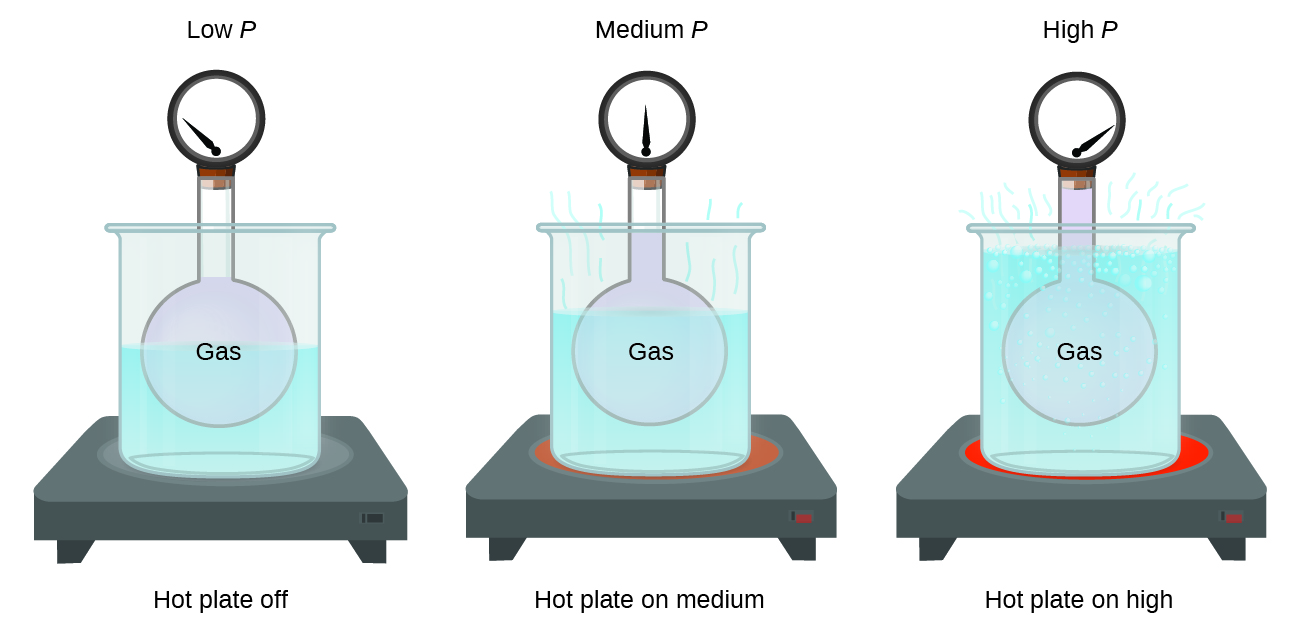
Cette relation entre température et pression est observée pour tout échantillon de gaz confiné à un volume constant. Un exemple de données expérimentales de pression/température est présenté pour un échantillon d'air dans ces conditions sur la figure\(\PageIndex{3}\). Nous constatons que la température et la pression sont liées de manière linéaire, et si la température est sur l'échelle du kelvin, alors P et T sont directement proportionnels (là encore, lorsque le volume et les moles de gaz sont maintenus constants) ; si la température sur l'échelle des kelvins augmente d'un certain facteur, la pression du gaz augmente du même facteur.

Figure\(\PageIndex{3}\) : Pour un volume et une quantité d'air constants, la pression et la température sont directement proportionnelles, à condition que la température soit exprimée en kelvins. (Les mesures ne peuvent pas être effectuées à des températures plus basses en raison de la condensation du gaz.) Lorsque cette droite est extrapolée à des pressions plus basses, elle atteint une pression de 0 à —273 °C, soit 0 sur l'échelle des kelvins et la température la plus basse possible, appelée zéro absolu.

Cette figure comprend un tableau et un graphique. Le tableau comporte 3 colonnes et 7 lignes. La première ligne est un en-tête qui indique les colonnes « Température, degrés C », « Température, K » et « Pression, k P a ». La première colonne contient les valeurs de haut en bas : moins 150, moins 100, moins 50, 0, 50 et 100. La deuxième colonne contient les valeurs de haut en bas 173, 223, 273, 323, 373 et 423. La troisième colonne contient les valeurs 36,0, 46,4, 56,7, 67,1, 77,5 et 88,0. Un graphique apparaît à droite du tableau. L'axe horizontal est étiqueté « Température (K) ». Des marques et des étiquettes sont fournies pour les multiples de 100 commençant à 0 et se terminant à 500. L'axe vertical est étiqueté « Pression (k P a) » avec des marques et des étiquettes fournies pour les multiples de 10, commençant à 0 et se terminant à 100. Six points de données du tableau sont tracés sur le graphique avec des points noirs. Ces points sont reliés par une ligne noire continue. Une ligne pointillée s'étend du point de données le plus à gauche jusqu'à l'origine. Le graphique montre une tendance linéaire positive.

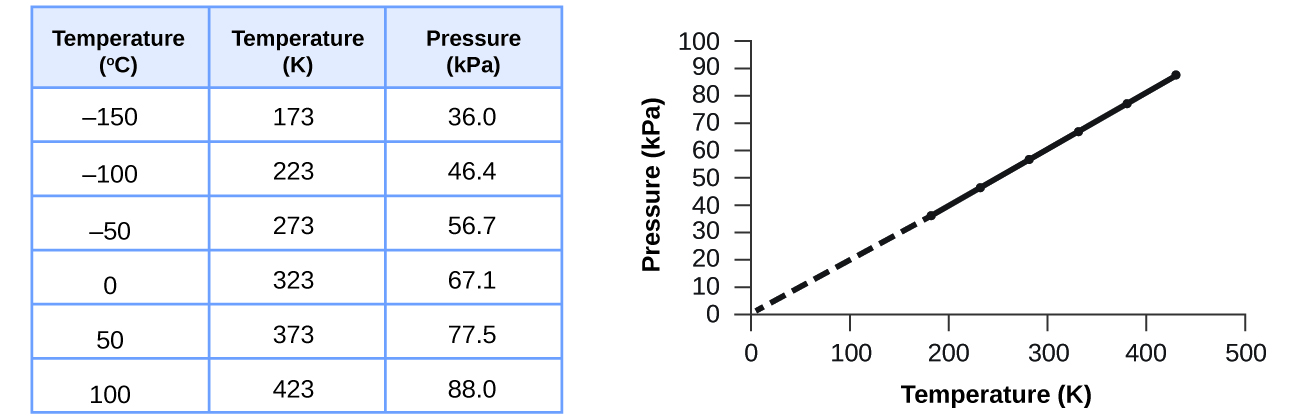
Guillaume Amontons a été le premier à établir empiriquement la relation entre la pression et la température d'un gaz (~1700), et Joseph Louis Gay-Lussac a déterminé la relation plus précisément (~1800). Pour cette raison, la relation P - T pour les gaz est connue sous le nom de loi d'Amontons ou de loi de Gay-Lussac. Sous l'un ou l'autre nom, il indique que la pression d'une quantité donnée de gaz est directement proportionnelle à sa température sur l'échelle du kelvin lorsque le volume est maintenu constant. Mathématiquement, cela peut s'écrire :

\[P∝T\ce{\:or\:}P=\ce{constant}×T\ce{\:or\:}P=k×T \nonumber \]

où n1 signifie « est proportionnel à » et k est une constante de proportionnalité qui dépend de l'identité, de la quantité et du volume du gaz.

Pour un volume de gaz confiné et constant, le rapport\(\dfrac{P}{T}\) est donc constant (c'est-à-dire,\(\dfrac{P}{T}=k\)). Si le gaz est initialement dans la « condition 1 » (avec P = P ₁ et T = T ₁), puis passe en « condition 2 » (avec P = P ₂ et T = T ₂), nous avons \(\dfrac{P_1}{T_1}=k\)et\(\dfrac{P_2}{T_2}=k\), qui se réduit à\(\dfrac{P_1}{T_1}=\dfrac{P_2}{T_2}\). Cette équation est utile pour les calculs de pression/température pour un gaz confiné à volume constant. Notez que les températures doivent être sur l'échelle des kelvins pour tout calcul de la loi des gaz (0 sur l'échelle des kelvins et la température la plus basse possible est appelée zéro absolu). (Notez également qu'il existe au moins trois manières de décrire comment la pression d'un gaz change à mesure que sa température change : nous pouvons utiliser un tableau de valeurs, un graphique ou une équation mathématique.)

Exemple\(\PageIndex{1}\): Predicting Change in Pressure with Temperature

Un flacon de spray capillaire est utilisé jusqu'à ce qu'il soit vide, à l'exception du gaz propulseur, l'isobutane.

1. Sur la boîte se trouve l'avertissement « Conserver uniquement à des températures inférieures à 120 °F (48,8 °C). Ne pas incinérer. » Pourquoi ?
2. Le gaz contenu dans le bidon est initialement à 24 °C et 360 kPa, et le bidon a un volume de 350 ml. Si le bidon est laissé dans une voiture qui atteint 50 °C par temps chaud, quelle est la nouvelle pression dans le bidon ?

Solution

1. La boîte contient une quantité de gaz isobutane à volume constant, donc si la température augmente par chauffage, la pression augmentera proportionnellement. Une température élevée peut entraîner une pression élevée et provoquer l'éclatement de la boîte. (De plus, l'isobutane étant combustible, l'incinération peut provoquer l'explosion du bidon.)
2. Nous recherchons un changement de pression dû à un changement de température à volume constant, nous utiliserons donc la loi d'Amontons/Gay-Lussac. En prenant P ₁ et T ₁ comme valeurs initiales, T ₂ comme la température pour laquelle la pression est inconnue et P ₂ comme pression inconnue, et en convertissant °C en K, nous avons :

\(\dfrac{P_1}{T_1}=\dfrac{P_2}{T_2}\textrm{ which means that }\dfrac{360\:\ce{kPa}}{297\:\ce K}=\dfrac{P_2}{323\:\ce K}\)

La réorganisation et la résolution donnent :

\(P_2=\mathrm{\dfrac{360\:kPa×323\cancel{K}}{297\cancel{K}}=390\:kPa}\)

Exercice\(\PageIndex{1}\)

Un échantillon d'azote, N ₂, occupe 45,0 ml à 27 °C et 600 torr. Quelle pression aura-t-il s'il est refroidi à —73 °C alors que le volume reste constant ?

Réponse

400 torr

Volume et température : loi de Charles

Si nous remplissons un ballon d'air et que nous le scellons, le ballon contient une quantité spécifique d'air à la pression atmosphérique, disons 1 atm. Si nous mettons le ballon dans un réfrigérateur, le gaz à l'intérieur se refroidit et le ballon se rétracte (bien que la quantité de gaz et sa pression restent constantes). Si on fait très froid au ballon, il rétrécira beaucoup et il se dilatera à nouveau lorsqu'il se réchauffera.

Vidéo\(\PageIndex{1}\) : Cette vidéo montre comment le refroidissement et le chauffage d'un gaz entraînent une diminution ou une augmentation de son volume, respectivement.

Ces exemples de l'effet de la température sur le volume d'une quantité donnée d'un gaz confiné à pression constante sont généralement vrais : le volume augmente lorsque la température augmente et diminue lorsque la température diminue. Les données volume-température pour un échantillon de 1 mole de méthane à 1 atm sont répertoriées et représentées graphiquement sur la figure\(\PageIndex{2}\).

Figure\(\PageIndex{4}\) : Le volume et la température sont liés de manière linéaire pour 1 mole de méthane à une pression constante de 1 atm. Si la température est exprimée en kelvins, le volume et la température sont directement proportionnels. La droite s'arrête à 111 K parce que le méthane se liquéfie à cette température ; une fois extrapolée, elle coupe l'origine du graphique, ce qui représente une température nulle absolue.

Cette figure comprend un tableau et un graphique. Le tableau comporte 3 colonnes et 6 lignes. La première ligne est un en-tête qui indique les colonnes « Température, degrés C », « Température, K » et « Pression, k P a ». La première colonne contient les valeurs de haut en bas, moins 100, moins 50, 0, 100 et 200. La deuxième colonne contient les valeurs de haut en bas 173, 223, 273, 373 et 473. La troisième colonne contient les valeurs 14,10, 18,26, 22,40, 30,65 et 38,88. Un graphique apparaît à droite du tableau. L'axe horizontal est étiqueté « Température (K) ». Des marques et des étiquettes sont fournies pour les multiples de 100 commençant à 0 et se terminant à 300. L'axe vertical est étiqueté « Volume (L) » avec un marquage et des étiquettes prévus pour les multiples de 10, commençant à 0 et se terminant à 30. Cinq points de données du tableau sont tracés sur le graphique avec des points noirs. Ces points sont reliés par une ligne noire continue. Le graphique montre une tendance linéaire positive.

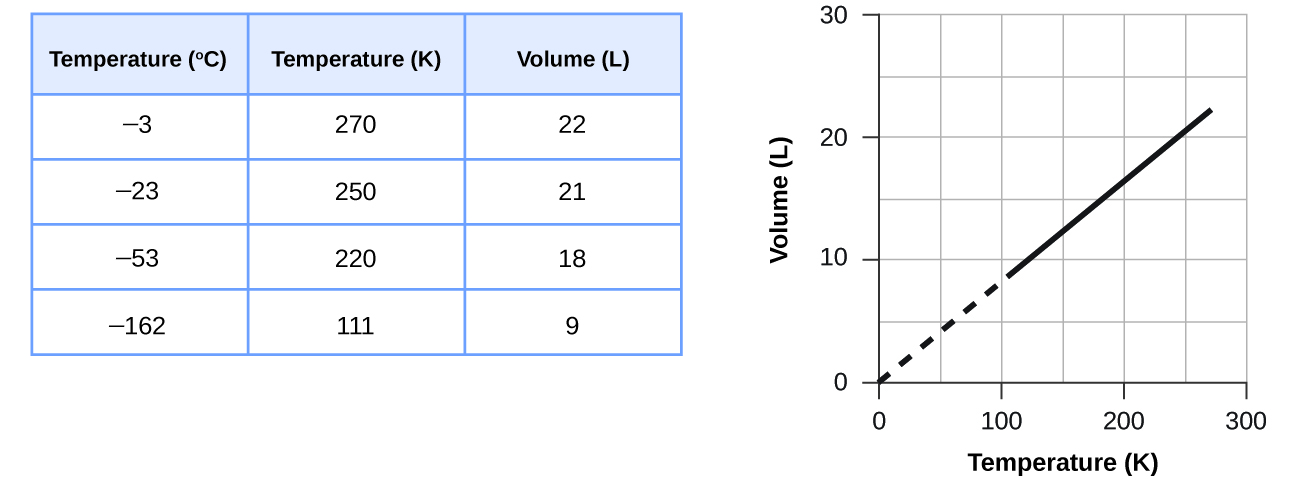
La relation entre le volume et la température d'une quantité donnée de gaz à pression constante est connue sous le nom de loi de Charles en reconnaissance du scientifique français et pionnier du vol en montgolfière Jacques Alexandre César Charles. La loi de Charles stipule que le volume d'une quantité donnée de gaz est directement proportionnel à sa température sur l'échelle des kelvins lorsque la pression est maintenue constante.

Mathématiquement, cela peut être écrit comme suit :

\[VαT\ce{\:or\:}V=\ce{constant}·T\ce{\:or\:}V=k·T \nonumber \]

avec k étant une constante de proportionnalité qui dépend de la quantité et de la pression du gaz.

Pour un échantillon de gaz confiné et à pression constante,\(\dfrac{V}{T}\) est constant (c'est-à-dire le rapport = k), et comme le montre la relation P - T, cela conduit à une autre forme de loi de Charles :\(\dfrac{V_1}{T_1}=\dfrac{V_2}{T_2}\).

Exemple\(\PageIndex{2}\): Predicting Change in Volume with Temperature

Un échantillon de dioxyde de carbone, le CO ₂, occupe 0,300 L à 10 °C et 750 torr. Quel volume aura le gaz à 30 °C et 750 torr ?

Solution

Comme nous recherchons le changement de volume provoqué par un changement de température à pression constante, cela relève de la loi de Charles. En prenant V ₁ et T ₁ comme valeurs initiales, T ₂ comme la température à laquelle le volume est inconnu et V ₂ comme volume inconnu, et en convertissant °C en K, nous avons :

\(\dfrac{V_1}{T_1}=\dfrac{V_2}{T_2}\textrm{ which means that }\dfrac{0.300\:\ce L}{283\:\ce K}=\dfrac{V_2}{303\:\ce K}\)

La réorganisation et la résolution donnent :\(V_2=\mathrm{\dfrac{0.300\:L×303\cancel{K}}{283\cancel{K}}=0.321\:L}\)

Cette réponse confirme notre attente selon la loi de Charles, à savoir que l'augmentation de la température du gaz (de 283 K à 303 K) à une pression constante entraînera une augmentation de son volume (de 0,300 L à 0,321 L).

Exercice\(\PageIndex{2}\)

Un échantillon d'oxygène, O ₂, occupe 32,2 ml à 30 °C et 452 torr. Quel volume occupera-t-il à —70 °C et à la même pression ?

Réponse

21,6 ml

Exemple\(\PageIndex{3}\): Measuring Temperature with a Volume

La température de changement est parfois mesurée à l'aide d'un thermomètre à gaz en observant l'évolution du volume du gaz lorsque la température change à pression constante. L'hydrogène contenu dans un thermomètre à hydrogène donné a un volume de 150,0 cm ³ lorsqu'il est immergé dans un mélange de glace et d'eau (0,00 °C). Immergé dans de l'ammoniac liquide bouillant, le volume d'hydrogène, à la même pression, est de 131,7 cm ³. Déterminez la température de l'ammoniac bouillant sur les échelles Kelvin et Celsius.

Solution

Un changement de volume provoqué par un changement de température à pression constante signifie que nous devons utiliser la loi de Charles. En prenant V ₁ et T ₁ comme valeurs initiales, T ₂ comme la température à laquelle le volume est inconnu et V ₂ comme volume inconnu, et en convertissant °C en K, nous avons :

\[\dfrac{V_1}{T_1}=\dfrac{V_2}{T_2}\textrm{ which means that }\mathrm{\dfrac{150.0\:cm^3}{273.15\:K}}=\dfrac{131.7\:\ce{cm}^3}{T_2} \nonumber \]

Le réarrangement donne\(T_2=\mathrm{\dfrac{131.7\cancel{cm}^3×273.15\:K}{150.0\:cm^3}=239.8\:K}\)

En soustrayant 273,15 de 239,8 K, nous trouvons que la température de l'ammoniac bouillant sur l'échelle Celsius est de —33,4 °C.

Exercice\(\PageIndex{3}\)

Quel est le volume d'un échantillon d'éthane à 467 K et 1,1 atm s'il occupe 405 ml à 298 K et 1,1 atm ?

Réponse

635 ml

 

Volume et pression : la loi de Boyle

Si nous remplissons partiellement une seringue hermétique d'air, la seringue contient une quantité spécifique d'air à température constante, disons 25 °C. Si nous enfonçons lentement le piston tout en maintenant la température constante, le gaz contenu dans la seringue est comprimé dans un volume plus petit et sa pression augmente ; si nous retirons le piston, le volume augmente et la pression diminue. Cet exemple de l'effet du volume sur la pression d'une quantité donnée d'un gaz confiné est vrai en général. La diminution du volume d'un gaz contenu augmentera sa pression, et l'augmentation de son volume diminuera sa pression. En effet, si le volume augmente d'un certain facteur, la pression diminue du même facteur, et vice versa. Les données de pression volumique pour un échantillon d'air à température ambiante sont illustrées dans la figure\(\PageIndex{5}\).

Figure\(\PageIndex{5}\) : Lorsqu'un gaz occupe un volume plus petit, il exerce une pression plus élevée ; lorsqu'il occupe un volume plus important, il exerce une pression plus faible (en supposant que la quantité de gaz et la température ne changent pas). Puisque P et V sont inversement proportionnels, un graphique de\(\dfrac{1}{P}\) vs. V est linéaire.

Cette figure contient un diagramme et deux graphiques. Le schéma montre une seringue étiquetée à l'aide d'une échelle en m l ou c c avec des multiples de 5 marqués commençant à 5 et se terminant à 30. Les marquages à mi-chemin entre ces mesures sont également fournis. Sur la partie supérieure de la seringue se trouve un manomètre avec une échelle de cinq, de 40 à gauche à 5 à droite. L'aiguille de la jauge repose entre 10 et 15, légèrement plus près de 15. La position du piston de la seringue indique une mesure du volume à mi-chemin entre 10 et 15 m l ou c. Le premier graphique est marqué « V (m L) » sur l'axe horizontal et « P (p s i) » sur l'axe vertical. Les points sont étiquetés à 5, 10, 15, 20 et 25 m L avec des valeurs correspondantes de 39,0, 19,5, 13,0, 9,8 et 6,5 p s. Les points sont reliés par une courbe lisse qui diminue à un taux de variation décroissant. Le deuxième graphique est étiqueté « V (m L) » sur l'axe horizontal et « 1 divisé par P (p s i) » sur l'axe vertical. L'axe horizontal est marqué par des multiples de 5, commençant à zéro et s'étendant jusqu'à 35 m L. L'axe vertical est marqué par des multiples de 0,02, commençant à 0 et s'étendant jusqu'à 0,18. Six points indiqués par des points noirs sur ce graphique sont reliés par un segment de ligne noire indiquant une tendance linéaire positive.

Contrairement aux relations P-T et V-T, la pression et le volume ne sont pas directement proportionnels l'un à l'autre. Au lieu de cela,\(P\) et faites\(V\) preuve d'une proportionnalité inverse : l'augmentation de la pression entraîne une diminution du volume du gaz. Mathématiquement, cela peut s'écrire :

\[P \propto \dfrac{1}{V} \nonumber \]

ou

\[P=k⋅ \dfrac{1}{V} \nonumber \]

ou

\[PV=k \nonumber \]

ou

\[P_1V_1=P_2V_2 \nonumber \]

avec le\(k\) fait d'être une constante. Graphiquement, cette relation est illustrée par la droite qui apparaît lorsque l'on trace l'inverse de la pression\(\left(\dfrac{1}{P}\right)\) par rapport au volume (V), ou l'inverse du volume\(\left(\dfrac{1}{V}\right)\) par rapport à la pression (\(P\)). Les graphes à lignes courbes sont difficiles à lire avec précision à des valeurs faibles ou élevées des variables, et ils sont plus difficiles à utiliser pour ajuster des équations et des paramètres théoriques aux données expérimentales. Pour ces raisons, les scientifiques essaient souvent de trouver un moyen de « linéariser » leurs données. Si nous tracons P par rapport à V, nous obtenons une hyperbole (Figure\(\PageIndex{6}\)).

Figure\(\PageIndex{6}\) : La relation entre la pression et le volume est inversement proportionnelle. (a) Le graphe de P contre V est une hyperbole, tandis que (b) le graphique de\(\left(\dfrac{1}{P}\right)\) contre V est linéaire.

Ce diagramme montre deux graphiques. Dans a, un graphique est représenté avec le volume sur l'axe horizontal et la pression sur l'axe vertical. Une ligne courbe est présentée sur le graphique montrant une tendance à la baisse avec un taux de variation décroissant. En b, un graphique est représenté avec le volume sur l'axe horizontal et un graphique divisé par la pression sur l'axe vertical. Un segment de ligne, commençant à l'origine du graphique, indique une tendance linéaire positive.

La relation entre le volume et la pression d'une quantité donnée de gaz à température constante a été publiée pour la première fois par le philosophe naturel anglais Robert Boyle il y a plus de 300 ans. Elle est résumée dans la déclaration maintenant connue sous le nom de loi de Boyle : le volume d'une quantité donnée de gaz maintenu à température constante est inversement proportionnel à la pression sous laquelle il est mesuré.

Exemple\(\PageIndex{4}\): Volume of a Gas Sample

L'échantillon de gaz a un volume de 15,0 ml à une pression de 13,0 psi. Déterminer la pression du gaz à un volume de 7,5 ml en utilisant :

1. le graphique P-V de la figure\(\PageIndex{6a}\)
2. le graphique\(\dfrac{1}{P}\) par rapport à V dans la figure\(\PageIndex{6b}\)
3. l'équation de la loi de Boyle

Donnez votre avis sur la précision probable de chaque méthode.

Solution

1. L'estimation à partir du graphique P-V donne une valeur pour P d'environ 27 psi.
2. L'estimation à partir du graphique\(\dfrac{1}{P}\) par rapport à V donne une valeur d'environ 26 psi.
3. D'après la loi de Boyle, nous savons que le produit de la pression et du volume (PV) pour un échantillon de gaz donné à température constante est toujours égal à la même valeur. Nous avons donc P ₁ V ₁ = k et P ₂ V ₂ = k, ce qui signifie que P ₁ V ₁ = P ₂ V ₂.

En utilisant P ₁ et V ₁ comme valeurs connues 13,0 psi et 15,0 ml, P ₂ comme pression à laquelle le volume est inconnu et V ₂ comme volume inconnu, nous avons :

\[P_1V_1=P_2V_2\mathrm{\:or\:13.0\:psi×15.0\:mL}=P_2×7.5\:\ce{mL} \nonumber \]

Résoudre :

\[P_2=\mathrm{\dfrac{13.0\:psi×15.0\cancel{mL}}{7.5\cancel{mL}}=26\:psi} \nonumber \]

Comme il était plus difficile de bien estimer à partir du graphique P-V, (a) est probablement plus inexact que (b) ou (c). Le calcul sera aussi précis que l'équation et les mesures le permettent.

Exercice\(\PageIndex{4}\)

L'échantillon de gaz a un volume de 30,0 ml à une pression de 6,5 psi. Déterminez le volume du gaz à une pression de 11,0 psi en utilisant :

1. le graphique P-V de la figure\(\PageIndex{6a}\)
2. le graphique\(\dfrac{1}{P}\) par rapport à V dans la figure\(\PageIndex{6b}\)
3. l'équation de la loi de Boyle

Donnez votre avis sur la précision probable de chaque méthode.

Répondez à une

environ 17 à 18 ml

Réponse b

~18 ml

Réponse c

17,7 ml ; il était plus difficile de bien estimer à partir du graphique P-V, donc (a) est probablement plus inexact que (b) ; le calcul sera aussi précis que l'équation et les mesures le permettent

La respiration et la loi de Boyle

Que faites-vous environ 20 fois par minute pendant toute votre vie, sans pause, et souvent sans même vous en rendre compte ? La réponse, bien sûr, est la respiration, ou la respiration. Comment fonctionne-t-il ? Il s'avère que les lois sur le gaz s'appliquent ici. Vos poumons absorbent les gaz dont votre corps a besoin (oxygène) et éliminent les gaz résiduaires (dioxyde de carbone). Les poumons sont constitués de tissu spongieux et extensible qui se dilate et se contracte lorsque vous respirez. Lorsque vous inspirez, votre diaphragme et vos muscles intercostaux (les muscles situés entre vos côtes) se contractent, ce qui dilate la cavité thoracique et augmente le volume de vos poumons. L'augmentation du volume entraîne une diminution de la pression (loi de Boyle). Cela provoque la circulation de l'air dans les poumons (d'une pression élevée à une pression basse). Lorsque vous expirez, le processus s'inverse : les muscles de votre diaphragme et de vos côtes se relâchent, votre cavité thoracique se contracte et le volume de vos poumons diminue, provoquant une augmentation de la pression (encore une fois la loi de Boyle) et l'air s'écoule hors des poumons (d'une pression élevée à une pression basse). Vous inspirez et expirez encore et encore, en répétant ce cycle de la loi de Boyle pour le reste de votre vie (Figure\(\PageIndex{7}\)).

Figure\(\PageIndex{7}\) : La respiration se produit parce que l'expansion et la contraction du volume pulmonaire créent de petites différences de pression entre les poumons et l'environnement, ce qui entraîne l'aspiration et l'expulsion de l'air dans les poumons.

Cette figure contient deux diagrammes d'une coupe transversale de la tête et du torse humains. Le premier diagramme sur la gauche s'intitule « Inspiration ». Il montre des flèches incurvées en gris qui traversent les voies nasales et la bouche jusqu'aux poumons. Une flèche pointe vers le bas à partir du diaphragme, qui est relativement plat, juste sous les poumons. Cette flèche est intitulée « Le diaphragme se contracte ». À l'entrée de la bouche et des voies nasales, une étiquette indiquant que « poumons en indice P est égal à 1 tiret 3 torr plus bas » est apposée. Le second diagramme similaire, intitulé « Expiration », inverse le sens des deux flèches. Les flèches s'étendent des poumons vers l'extérieur en passant par les voies nasales et la bouche. De même, une flèche pointe vers le diaphragme, montrant un diaphragme incurvé et des poumons dont la taille a été réduite par rapport à l'image précédente. Cette flèche est intitulée « Le diaphragme se détend ». À l'entrée de la bouche et des voies nasales, une étiquette indiquant que « poumons en indice P est égal à 1 tiret 3 torr plus » est apposée.

 

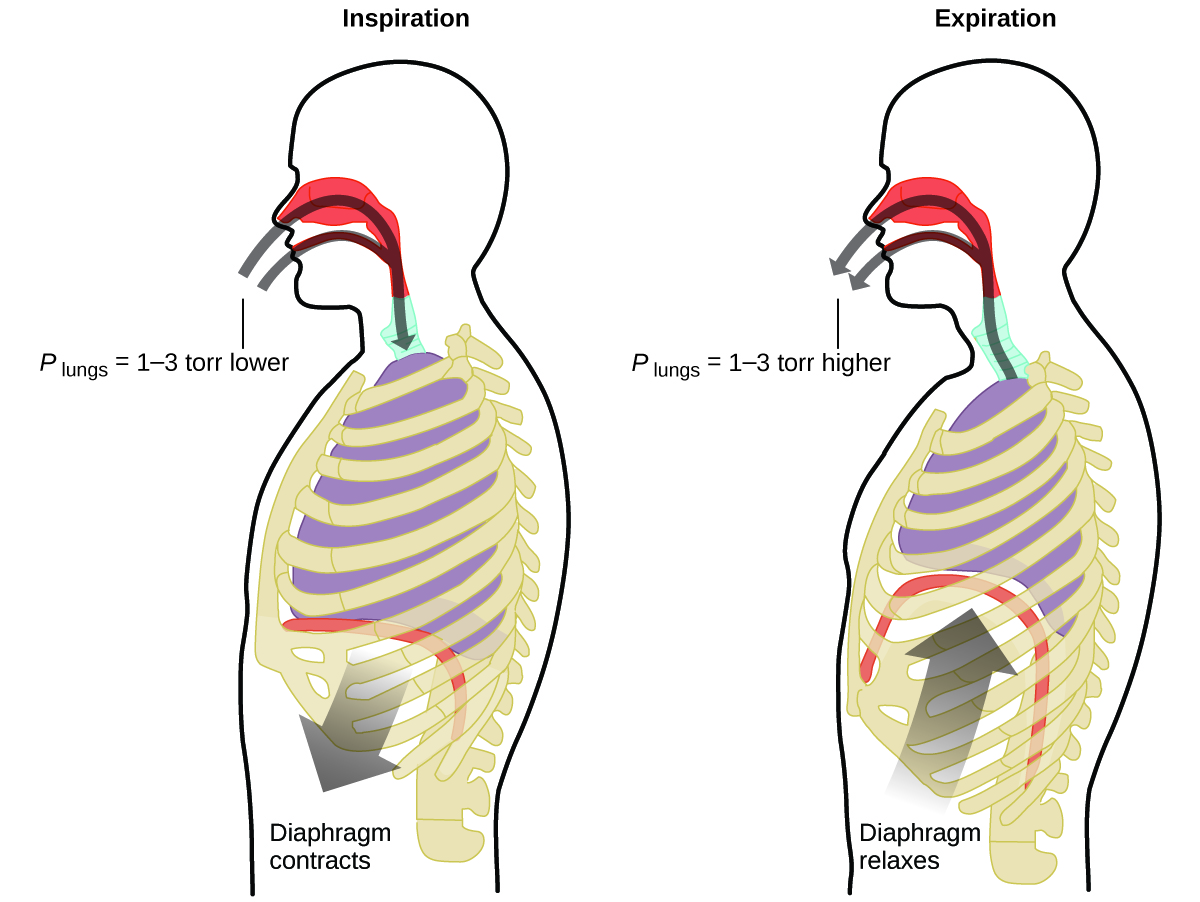
Moles de gaz et volume : la loi d'Avogadro

Le scientifique italien Amedeo Avogadro a avancé une hypothèse en 1811 pour expliquer le comportement des gaz, affirmant que des volumes égaux de tous les gaz, mesurés dans les mêmes conditions de température et de pression, contiennent le même nombre de molécules. Au fil du temps, cette relation a été confirmée par de nombreuses observations expérimentales telles qu'exprimées par la loi d'Avogadro : pour un gaz confiné, le volume (V) et le nombre de moles (n) sont directement proportionnels si la pression et la température restent constantes.

Sous forme d'équation, cela s'écrit comme suit :

\[V∝n\textrm{ or }V=k×n\textrm{ or }\dfrac{V_1}{n_1}=\dfrac{V_2}{n_2} \nonumber \]

Des relations mathématiques peuvent également être déterminées pour les autres paires de variables, telles que P contre n et n contre T.

Consultez cette simulation PhET interactive pour étudier les relations entre la pression, le volume, la température et la quantité de gaz. Utilisez la simulation pour examiner l'effet de la modification d'un paramètre sur un autre tout en maintenant les autres paramètres constants (comme décrit dans les sections précédentes sur les différentes lois des gaz).

La loi idéale sur le gaz

À ce stade, quatre lois distinctes ont été discutées qui concernent la pression, le volume, la température et le nombre de moles du gaz :

• Loi de Boyle : PV = constante à T et n constants
• Loi d'Amontons :\(\dfrac{P}{T}\) = constante à V et n constants
• Loi de Charles :\(\dfrac{V}{T}\) = constante à P et n constants
• Loi d'Avogadro :\(\dfrac{V}{n}\) = constante à P et T constants

La combinaison de ces quatre lois permet d'obtenir la loi des gaz idéale, une relation entre la pression, le volume, la température et le nombre de moles d'un gaz :

\[PV=nRT \nonumber \]

où P est la pression d'un gaz, V est son volume, n est le nombre de moles du gaz, T est sa température sur l'échelle du kelvin et R est une constante appelée constante de gaz idéale ou constante de gaz universelle. Les unités utilisées pour exprimer la pression, le volume et la température détermineront la forme appropriée de la constante de gaz, comme l'exige l'analyse dimensionnelle, les valeurs les plus fréquemment rencontrées étant 0,08206 L atm mol ^{—1 K —1} et 8,3145 kPa L mol ^—1 K ^—1.

La loi des gaz idéaux est facile à mémoriser et à appliquer pour résoudre les problèmes, à condition d'utiliser les valeurs et les unités appropriées pour la constante de gaz, R.

Les gaz dont les propriétés de P, V et T sont décrites avec précision par la loi des gaz idéaux (ou les autres lois des gaz) sont considérés comme présentant un comportement idéal ou comme se rapprochant des caractéristiques d'un gaz idéal. Un gaz idéal est une construction hypothétique qui peut être utilisée conjointement avec la théorie moléculaire cinétique pour expliquer efficacement les lois des gaz, comme cela sera décrit dans un module ultérieur de ce chapitre. Bien que tous les calculs présentés dans ce module supposent un comportement idéal, cette hypothèse n'est raisonnable que pour les gaz dans des conditions de pression relativement basse et de température élevée. Dans le dernier module de ce chapitre, une loi modifiée sur les gaz sera présentée pour tenir compte du comportement non idéal observé pour de nombreux gaz à des pressions relativement élevées et à des températures basses.

L'équation des gaz idéaux contient cinq termes : la constante de gaz R et les propriétés variables P, V, n et T. La spécification de quatre de ces termes permettra d'utiliser la loi du gaz idéal pour calculer le cinquième terme, comme le montrent les exemples d'exercices suivants.

Exemple\(\PageIndex{5}\): Using the Ideal Gas Law

Le méthane, le CH ₄, est envisagé comme carburant automobile de remplacement pour remplacer l'essence. Un gallon d'essence pourrait être remplacé par 655 g de CH ₄. Quel est le volume de cette quantité de méthane à 25 °C et 745 torr ?

Solution

Exercice\(\PageIndex{5}\)

Calculez la pression en bar de 2 520 moles d'hydrogène gazeux stockées à 27 °C dans le réservoir de 180 L d'une voiture moderne à hydrogène.

Réponse

350 bars

 

Si le nombre de moles d'un gaz idéal est maintenu constant dans deux ensembles de conditions différents, une relation mathématique utile appelée loi des gaz combinés est obtenue :\(\dfrac{P_1V_1}{T_1}=\dfrac{P_2V_2}{T_2}\) en utilisant les unités de atm, L et K. Les deux ensembles de conditions sont égaux au produit de n × R (où n = le nombre de moles du gaz et R est la constante de la loi du gaz idéale).

Exemple\(\PageIndex{6}\): Using the Combined Gas Law

Lorsqu'il est rempli d'air, un réservoir de plongée classique d'un volume de 13,2 L a une pression de 153 atm (Figure\(\PageIndex{8}\)). Si la température de l'eau est de 27 °C, combien de litres d'air un tel réservoir fournira-t-il aux poumons d'un plongeur à une profondeur d'environ 70 pieds dans l'océan où la pression est de 3,13 atm ?

Figure\(\PageIndex{8}\) : Les plongeurs utilisent de l'air comprimé pour respirer lorsqu'ils sont sous l'eau. (source : modification de l'œuvre de Mark Goodchild)

Cette photographie montre un plongeur sous-marin avec un réservoir sur le dos et des bulles sortant de l'appareil respiratoire.

Soit 1 représente l'air dans le réservoir de plongée et 2 représente l'air dans les poumons, et en notant que la température corporelle (la température à laquelle l'air sera dans les poumons) est de 37 °C, nous avons :

\[\dfrac{P_1V_1}{T_1}=\dfrac{P_2V_2}{T_2}⟶\mathrm{\dfrac{(153\:atm)(13.2\:L)}{(300\:K)}=\dfrac{(3.13\:atm)(\mathit{V}_2)}{(310\:K)}} \nonumber \]

Résoudre pour V ₂ :

\[V_2=\mathrm{\dfrac{(153\cancel{atm})(13.2\:L)(310\cancel{K})}{(300\cancel{K})(3.13\cancel{atm})}=667\:L} \nonumber \]

(Remarque : Sachez que cet exemple particulier est un exemple dans lequel l'hypothèse d'un comportement idéal des gaz n'est pas très raisonnable, car il s'agit de gaz à des pressions relativement élevées et à des températures basses. Malgré cette limite, le volume calculé peut être considéré comme une bonne estimation « approximative ».)

Exercice\(\PageIndex{6}\)

Un échantillon d'ammoniac occupe 0,250 L dans des conditions de laboratoire de 27 °C et 0,850 atm. Déterminez le volume de cet échantillon à 0 °C et à 1,00 atm.

Réponse

0,193 L

L'interdépendance entre la profondeur et la pression de l'océan en plongée sous-marine

Qu'il s'agisse de faire de la plongée sous-marine sur la Grande Barrière de Corail en Australie (illustrée dans la figure\(\PageIndex{9}\)) ou dans les Caraïbes, les plongeurs doivent comprendre comment la pression affecte un certain nombre de problèmes liés à leur confort et à leur sécurité.

Figure\(\PageIndex{9}\) : Les plongeurs, que ce soit dans la Grande Barrière de Corail ou dans les Caraïbes, doivent être conscients de la flottabilité, de l'égalisation de la pression et du temps qu'ils passent sous l'eau afin d'éviter les risques associés à la présence de gaz sous pression dans le corps. (crédit : Kyle Taylor).

Cette photo montre des coraux sous-marins et des anémones colorés dans des tons de jaune, d'orange, de vert et de brun, entourés d'eau de couleur bleue.

La pression augmente avec la profondeur de l'océan, et elle change le plus rapidement lorsque les plongeurs atteignent la surface. La pression subie par un plongeur est la somme de toutes les pressions au-dessus du plongeur (provenant de l'eau et de l'air). La plupart des mesures de pression sont données en unités d'atmosphère, exprimées en « atmosphères absolues » ou ATA dans la communauté des plongeurs : chaque 33 pieds d'eau salée représente 1 ATA de pression en plus de 1 ATA de pression provenant de l'atmosphère au niveau de la mer. Lorsque le plongeur descend, l'augmentation de la pression provoque la compression des poches d'air du corps situées dans les oreilles et les poumons ; lors de la montée, la diminution de la pression provoque l'expansion de ces poches d'air, ce qui peut provoquer la rupture des tympans ou l'éclatement des poumons. Les plongeurs doivent donc effectuer une égalisation en ajoutant de l'air dans les espaces aériens corporels lors de la descente en respirant normalement et en ajoutant de l'air au masque en respirant par le nez ou en ajoutant de l'air aux oreilles et aux sinus par des techniques d'égalisation ; le corollaire est également vrai en montée, les plongeurs doivent libérer de l'air du corps pour maintenir l'égalisation. La flottabilité, ou la capacité de contrôler si un plongeur coule ou flotte, est contrôlée par le compensateur de flottabilité (BCD). Si un plongeur monte, l'air de son BCD se dilate en raison de la baisse de la pression selon la loi de Boyle (la diminution de la pression des gaz augmente le volume). L'air en expansion augmente la flottabilité du plongeur et celui-ci commence à monter. Le plongeur doit évacuer l'air du BCD sous peine de risquer une remontée incontrôlée qui pourrait provoquer une rupture des poumons. En descente, l'augmentation de la pression provoque la compression de l'air dans le BCD et le plongeur s'enfonce beaucoup plus rapidement ; le plongeur doit ajouter de l'air au BCD sous peine de risquer une descente incontrôlée, face à des pressions beaucoup plus élevées près du fond de l'océan. La pression influe également sur la durée pendant laquelle un plongeur peut rester sous l'eau avant de monter. Plus un plongeur plonge profondément, plus l'air respiré est comprimé en raison de l'augmentation de la pression : si un plongeur plonge de 33 pieds, la pression est de 2 ATA et l'air sera comprimé à la moitié de son volume initial. Le plongeur utilise l'air disponible deux fois plus vite qu'à la surface.

 

Conditions standard de température et de pression

Nous avons vu que le volume d'une quantité donnée de gaz et le nombre de molécules (moles) dans un volume de gaz donné varient en fonction des variations de pression et de température. Les chimistes font parfois des comparaisons avec une température et une pression standard (STP) pour signaler les propriétés des gaz : 273,15 K (0,00 °C) et 1 atm (101,325 kPa). Au STP, un gaz idéal a un volume d'environ 22,4 L, ce que l'on appelle le volume molaire standard (Figure\(\PageIndex{10}\)).

Figure\(\PageIndex{10}\) : Étant donné que le nombre de moles dans un volume de gaz donné varie en fonction des variations de pression et de température, les chimistes utilisent la température et la pression standard (273,15 K et 1 atm ou 101,325 kPa) pour indiquer les propriétés des gaz.

Cette figure montre trois bulles remplies chacune avec H e, N H indice 2 et O indice 2 respectivement. Sous le premier ballon se trouve l'étiquette « 4 g de He ». Sous le second ballon se trouve l'étiquette « 15 g de N H indice 2 ». Sous le troisième ballon se trouve l'étiquette « 32 g d'indice O 2 ». Chaque ballon contient le même nombre de molécules de leurs gaz respectifs.

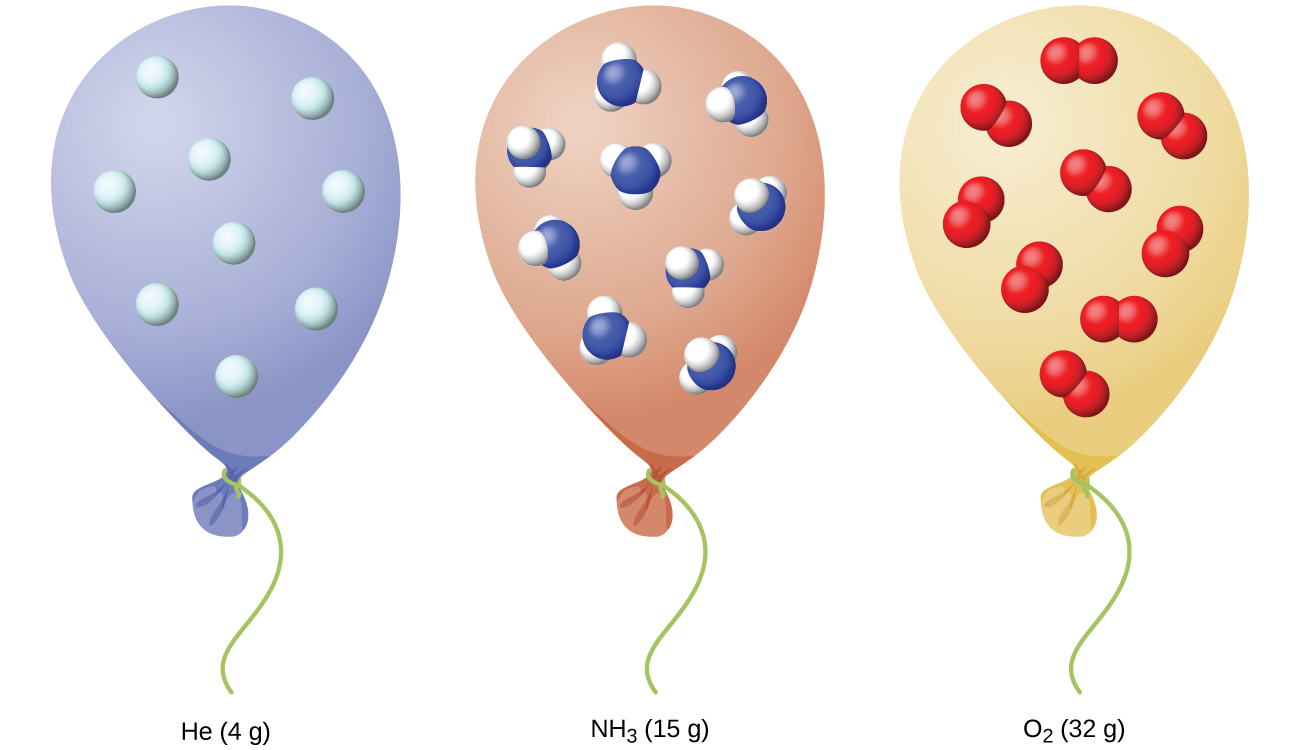
Résumé

Le comportement des gaz peut être décrit par plusieurs lois basées sur des observations expérimentales de leurs propriétés. La pression d'une quantité donnée de gaz est directement proportionnelle à sa température absolue, à condition que le volume ne change pas (loi d'Amontons). Le volume d'un échantillon de gaz donné est directement proportionnel à sa température absolue à pression constante (loi de Charles). Le volume d'une quantité donnée de gaz est inversement proportionnel à sa pression lorsque la température est maintenue constante (loi de Boyle). Dans les mêmes conditions de température et de pression, des volumes égaux de tous les gaz contiennent le même nombre de molécules (loi d'Avogadro).

Les équations décrivant ces lois sont des cas particuliers de la loi des gaz idéaux, PV = nRT, où P est la pression du gaz, V est son volume, n est le nombre de moles du gaz, T est sa température en kelvins et R est la constante de gaz idéale (universelle).

Équations clés

• PV = NRT

Résumé

zéro absolu

température à laquelle le volume d'un gaz serait nul selon la loi de Charles.

Loi d'Amontons

(également, loi de Gay-Lussac) la pression d'un nombre donné de moles de gaz est directement proportionnelle à sa température en kelvins lorsque le volume est maintenu constant

Loi d'Avogadro

le volume d'un gaz à température et pression constantes est proportionnel au nombre de molécules de gaz

Loi de Boyle

le volume d'un nombre donné de moles de gaz maintenu à température constante est inversement proportionnel à la pression sous laquelle il est mesuré

Loi de Charles

le volume d'un nombre donné de moles de gaz est directement proportionnel à sa température en kelvins lorsque la pression est maintenue constante

gaz idéal

gaz hypothétique dont les propriétés physiques sont parfaitement décrites par les lois des gaz

constante de gaz idéale (R)

constante dérivée de l'équation des gaz idéaux R = 0,08226 L atm mol ^—1 K ^—1 ou 8,314 L kPa mol ^—1 K ^—1

loi idéale sur les gaz

relation entre la pression, le volume, la quantité et la température d'un gaz dans des conditions dérivées par combinaison des lois simples des gaz

conditions standard de température et de pression (STP)

273,15 K (0 °C) et 1 atm (101,325 kPa)

volume molaire standard

volume de 1 mole de gaz à la station d'épuration, environ 22,4 L pour les gaz se comportant de manière idéale