9.6 : Comportement non idéal des gaz
- Page ID
- 194060
- Décrire les facteurs physiques qui entraînent des écarts par rapport au comportement idéal des gaz
- Expliquer comment ces facteurs sont représentés dans l'équation de Van der Waals
- Définir la compressibilité (Z) et décrire comment sa variation avec la pression reflète un comportement non idéal
- Quantifier le comportement non idéal en comparant les calculs des propriétés des gaz à l'aide de la loi du gaz idéal et de l'équation de Van der Waals
Jusqu'à présent, la loi des gaz idéaux, PV = NrT, a été appliquée à différents types de problèmes, allant de la stœchiométrie des réactions aux problèmes de formules empiriques et moléculaires, en passant par la détermination de la densité et de la masse molaire d'un gaz. Comme indiqué dans les modules précédents de ce chapitre, cependant, le comportement d'un gaz n'est souvent pas idéal, ce qui signifie que les relations observées entre sa pression, son volume et sa température ne sont pas décrites avec précision par les lois des gaz. Dans cette section, les raisons de ces écarts par rapport au comportement idéal des gaz sont examinées.
L'une des manières d'évaluer la précision de PV = nRT est de comparer le volume réel d'une mole de gaz (son volume molaire, Vm) au volume molaire d'un gaz idéal à la même température et à la même pression. Ce rapport est appelé facteur de compressibilité (Z) avec :
\[\mathrm{Z=\dfrac{molar\: volume\: of\: gas\: at\: same\:\mathit{T}\:and\:\mathit{P}}{molar\: volume\: of\: ideal\: gas\: at\: same\:\mathit{T}\:and\:\mathit{P}}}=\left(\dfrac{PV_m}{RT}\right)_\ce{measured} \nonumber \]
Le comportement idéal du gaz est donc indiqué lorsque ce rapport est égal à 1, et tout écart par rapport à 1 indique un comportement non idéal. La figure\(\PageIndex{1}\) montre des diagrammes de Z sur une large plage de pression pour plusieurs gaz courants.
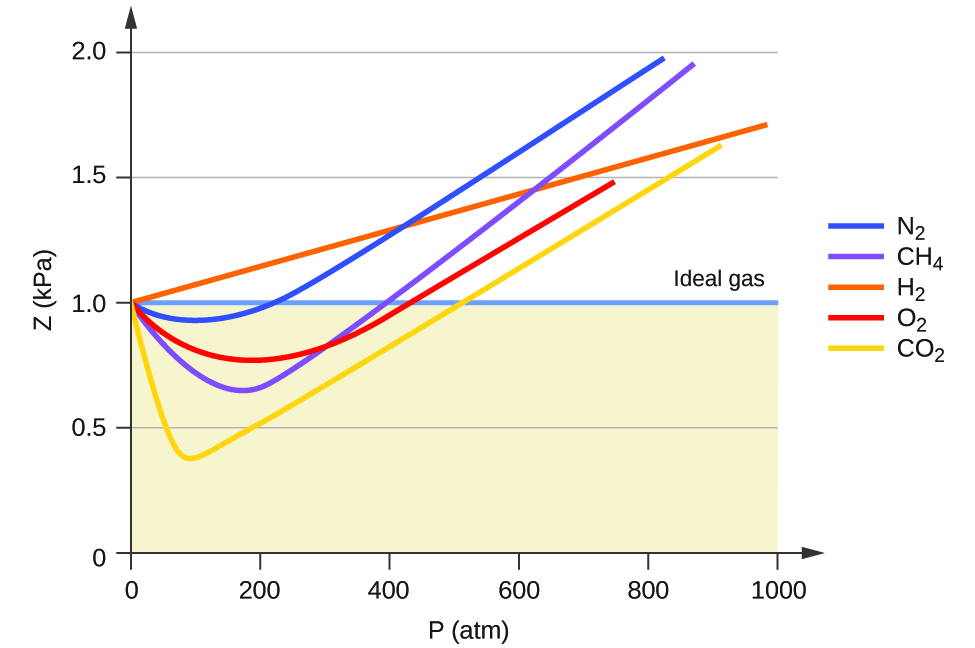
Comme le montre la figure\(\PageIndex{1}\), la loi des gaz idéaux ne décrit pas bien le comportement du gaz à des pressions relativement élevées. Pour déterminer pourquoi il en est ainsi, considérez les différences entre les propriétés réelles du gaz et ce que l'on attend d'un gaz idéal hypothétique.
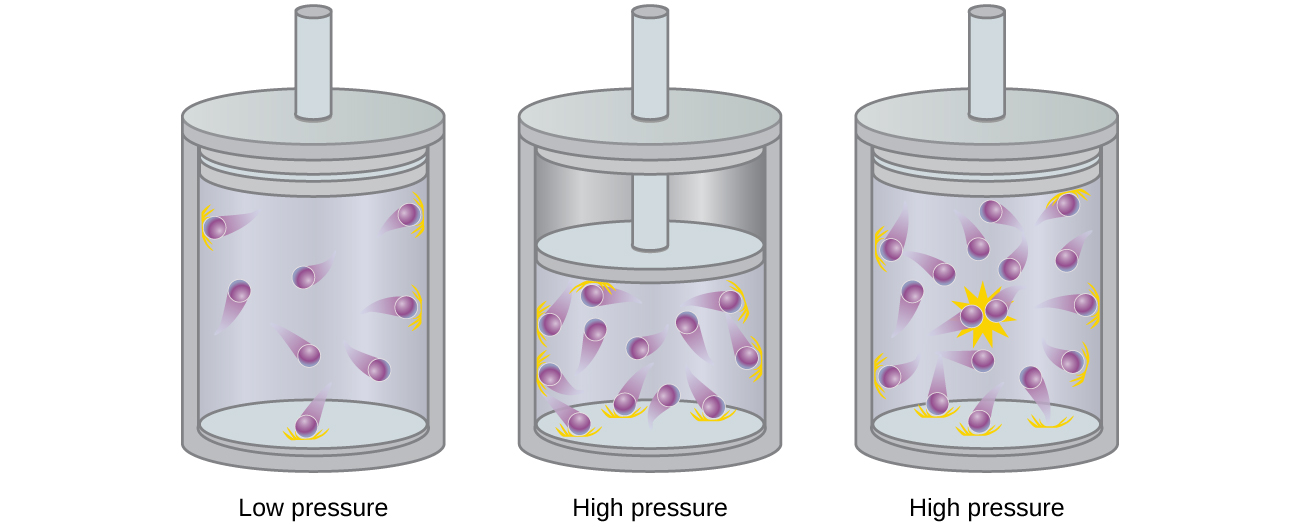
Les particules d'un gaz idéal hypothétique n'ont pas de volume significatif et ne s'attirent ni ne se repoussent. En général, les gaz réels se rapprochent de ce comportement à des pressions relativement basses et à des températures élevées. Cependant, à des pressions élevées, les molécules d'un gaz sont rapprochées les unes des autres et la quantité d'espace vide entre les molécules est réduite. À ces pressions plus élevées, le volume des molécules de gaz elles-mêmes devient appréciable par rapport au volume total occupé par le gaz (Figure\(\PageIndex{2}\)). Le gaz devient donc moins compressible à ces pressions élevées, et bien que son volume continue de diminuer avec l'augmentation de la pression, cette diminution n'est pas proportionnelle comme le prédit la loi de Boyle.
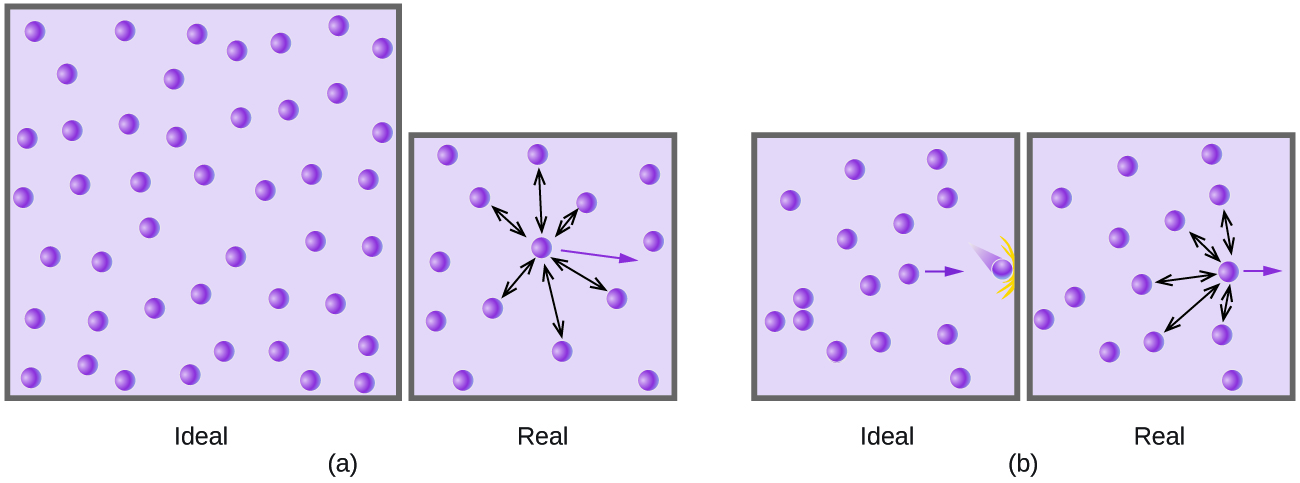
À des pressions relativement basses, les molécules de gaz ne sont pratiquement pas attirées les unes pour les autres parce qu'elles sont (en moyenne) très éloignées les unes des autres et qu'elles se comportent presque comme les particules d'un gaz idéal. Cependant, à des pressions plus élevées, la force d'attraction n'est plus négligeable. Cette force rapproche légèrement les molécules, diminuant légèrement la pression (si le volume est constant) ou diminuant le volume (à pression constante) (Figure\(\PageIndex{3}\)). Ce changement est plus prononcé à basse température car les molécules ont un KE plus faible par rapport aux forces d'attraction, et elles sont donc moins efficaces pour surmonter ces attraits après une collision les unes avec les autres.
Il existe plusieurs équations différentes qui donnent une meilleure idée du comportement des gaz que ne le fait la loi des gaz idéaux. Le premier, et le plus simple, a été développé par le scientifique néerlandais Johannes van der Waals en 1879. L'équation de Van der Waals améliore la loi des gaz idéaux en ajoutant deux termes : l'un pour rendre compte du volume des molécules de gaz et l'autre pour les forces d'attraction entre elles.

La constante a correspond à l'intensité de l'attraction entre les molécules d'un gaz particulier, et la constante b correspond à la taille des molécules d'un gaz particulier. La « correction » du terme de pression dans la loi des gaz idéaux est\(\dfrac{n^2a}{V^2}\), et la « correction » du volume est nb. Notez que lorsque V est relativement grand et n est relativement petit, ces deux termes de correction deviennent négligeables, et l'équation de Van der Waals se réduit à la loi des gaz idéaux, PV = NRt. Une telle condition correspond à un gaz dans lequel un nombre relativement faible de molécules occupe un volume relativement important, c'est-à-dire un gaz à une pression relativement basse. Les valeurs expérimentales des constantes de Van der Waals de certains gaz courants sont données dans le tableau\(\PageIndex{1}\).
| Gaz | a (L 2 atm/mol 2) | b (L/mol) |
|---|---|---|
| N° 2 | 1,39 | 0,0391 |
| O 2 | 1,36 | 0,0318 |
| CO 2 | 3,59 | 0,0427 |
| H 2 O | 5,46 | 0,0305 |
| Il | 0,0342 | 0,0237 |
| CCl 4 | 20,4 | 0,1383 |
À basse pression, la correction de l'attraction intermoléculaire, a, est plus importante que celle du volume moléculaire, b. À des pressions élevées et à de faibles volumes, la correction du volume des molécules devient importante car les molécules elles-mêmes sont incompressibles et constituent une fraction appréciable du volume total. À une certaine pression intermédiaire, les deux corrections ont des influences opposées et le gaz semble suivre la relation donnée par PV = NRt sur une petite plage de pressions. Ce comportement se reflète dans les « creux » de plusieurs des courbes de compressibilité illustrées sur la figure\(\PageIndex{1}\). La force d'attraction entre les molécules rend initialement le gaz plus compressible qu'un gaz idéal, à mesure que la pression augmente (Z diminue avec l'augmentation de P). À des pressions très élevées, le gaz devient moins compressible (Z augmente avec P), car les molécules de gaz commencent à occuper une fraction de plus en plus importante du volume total de gaz.
À proprement parler, l'équation du gaz idéal fonctionne bien lorsque les attractions intermoléculaires entre les molécules de gaz sont négligeables et que les molécules de gaz elles-mêmes n'occupent pas une partie appréciable du volume total. Ces critères sont satisfaits dans des conditions de basse pression et de température élevée. Dans de telles conditions, on dit que le gaz se comporte de manière idéale et que les écarts par rapport aux lois sur les gaz sont suffisamment faibles pour être ignorés, mais ce n'est souvent pas le cas.
Un flacon de 4,25 L contient 3,46 mol de CO 2 à 229 °C. Calculez la pression de cet échantillon de CO 2 :
- à partir de la loi du gaz idéal
- à partir de l'équation de Van der Waals
- Expliquez la ou les raisons de la différence.
Solution
a) À partir de la loi sur les gaz idéaux :
(b) À partir de l'équation de Van der Waals :
\(\left(P+\dfrac{n^2a}{V^2}\right)×(V−nb)=nRT⟶P=\dfrac{nRT}{(V−nb)}−\dfrac{n^2a}{V^2}\)
\(P=\mathrm{\dfrac{3.46\:mol×0.08206\:L\:atm\:mol^{−1}\:K^{−1}×502\: K}{(4.25\:L−3.46\:mol×0.0427\:L\:mol^{−1})}−\dfrac{(3.46\:mol)^2×3.59\:L^2\:atm\:mol^2}{(4.25\:L)^2}}\)
Cela donne finalement P = 32,4 atm.
(c) Cette valeur n'est pas très différente de la valeur de la loi des gaz idéaux car la pression n'est pas très élevée et la température n'est pas très basse. La valeur est quelque peu différente parce que les molécules de CO 2 ont un certain volume et des attraits entre les molécules, et la loi des gaz idéaux suppose qu'elles n'ont pas de volume ni d'attractions.
Un flacon de 560 ml contient 21,3 g de N 2 à 145 °C. Calculez la pression de N 2 :
- à partir de la loi du gaz idéal
- à partir de l'équation de Van der Waals
- Expliquez la ou les raisons de la différence.
- Répondez à une
-
46,562 atm
- Réponse b
-
46,594 atm
- Réponse c
-
L'équation de Van der Waals prend en compte le volume des molécules de gaz elles-mêmes ainsi que les attractions intermoléculaires.
Résumé
Les molécules de gaz possèdent un volume limité et subissent des forces d'attraction les unes pour les autres. Par conséquent, le comportement du gaz n'est pas nécessairement bien décrit par la loi du gaz idéal. Dans des conditions de basse pression et de température élevée, ces facteurs sont négligeables, l'équation du gaz idéal est une description précise du comportement du gaz, et le gaz est censé présenter un comportement idéal. Cependant, à des températures plus basses et à des pressions plus élevées, des corrections du volume moléculaire et des attractions moléculaires sont nécessaires pour tenir compte de la taille moléculaire finie et des forces d'attraction. L'équation de Van der Waals est une version modifiée de la loi des gaz idéaux qui peut être utilisée pour tenir compte du comportement non idéal des gaz dans ces conditions.
Équations clés
- \(\mathrm{Z=\dfrac{molar\:volume\: of\: gas\: at\: same\:\mathit{T}\:and\:\mathit{P}}{molar\: volume\: of\: ideal\: gas\: at\: same\:\mathit{T}\:and\:\mathit{P}}}=\left(\dfrac{P×V_m}{R×T}\right)_\ce{measured}\)
- \(\left(P+\dfrac{n^2a}{V^2}\right)×(V−nb)=nRT\)
Lexique
- facteur de compressibilité (Z)
- rapport entre le volume molaire mesuré expérimentalement pour un gaz et son volume molaire, tel que calculé à partir de l'équation du gaz idéal
- Équation de Van der Waals
- version modifiée de l'équation du gaz idéal contenant des termes supplémentaires pour tenir compte du comportement non idéal du gaz


