9.E : Gaz (exercices)

Last updated
Save as PDF

Page ID: 194045

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

9.1 : Pression de gaz

Q9.1.1

Pourquoi les couteaux tranchants sont-ils plus efficaces que les couteaux émoussés (Conseil : pensez à la définition de la pression) ?

9.1.1

Le tranchant d'un couteau aiguisé a une surface plus petite que celle d'un couteau émoussé. Comme la pression est une force par unité de surface, un couteau bien aiguisé exercera une pression plus élevée avec la même force et tranchera le matériau plus efficacement.

Q9.1.2

Pourquoi certains petits ponts ont-ils des limites de poids qui dépendent du nombre de roues ou d'essieux du véhicule qui traverse ?

Q9.1.3

Pourquoi devriez-vous rouler ou ramper le ventre plutôt que de marcher sur un étang gelé ?

9.1.3

En position couchée, vous répartissez votre poids sur une plus grande surface, en exerçant moins de pression sur la glace que lorsque vous êtes debout. Si vous exercez moins de pression, vous risquez moins de percer la glace mince.

Q9.1.4

La pression barométrique typique à Redding, en Californie, est d'environ 750 mm Hg. Calculez cette pression en atm et en kPa.

Q9.1.5

La pression barométrique typique à Denver, au Colorado, est de 615 mm Hg. Quelle est cette pression en atmosphères et en kilopascals ?

9.1.5

0,809 atm ; 82,0 kPa

Q9.1.6

La pression barométrique typique à Kansas City est de 740 torr. Quelle est cette pression dans les atmosphères, en millimètres de mercure et en kilopascals ?

Q9.1.7

Les manomètres canadiens sont indiqués en unités de kilopascals. Quelle lecture sur une telle jauge correspond à 32 psi ?

9.1.7

2,2 × 10 ² kPa

Q9.1.8

Lors de l'atterrissage des Vikings sur Mars, il a été déterminé que la pression atmosphérique était en moyenne d'environ 6,50 millibars (1 bar = 0,987 atm). Quelle est cette pression en torr et en kPa ?

Q9.1.9

La pression de l'atmosphère à la surface de la planète Vénus est d'environ 88,8 atm. Comparez cette pression en psi à la pression normale sur Terre au niveau de la mer en psi.

9.1.9

Terre : 14,7 livres en ^—2 ; Vénus : 13,1 × 10 ³ livres en ⁻²

Q9.1.10

Un catalogue de laboratoire médical décrit la pression dans une bouteille de gaz à 14,82 MPa. Quelle est la pression de ce gaz en atmosphère et en torr ?

Q9.1.11

Envisagez ce scénario et répondez aux questions suivantes : Un jour de mi-août dans le nord-est des États-Unis, les informations suivantes ont été publiées dans le journal local : pression atmosphérique au niveau de la mer 29,97 pouces, 1013,9 mbar.

Quelle était la pression en kPa ?
La pression près de la côte, dans le nord-est des États-Unis, est généralement signalée à près de 30,0 pouces. Hg. Lors d'un ouragan, la pression peut chuter à près de 28 pouces. Hg. Calculez la chute de pression en torr.

9.1.11

a) 101,5 kPa ; b) Chute de 15 torr

Q9.1.12

Pourquoi est-il nécessaire d'utiliser un liquide non volatil dans un baromètre ou un manomètre ?

Q9.1.13

La pression d'un échantillon de gaz est mesurée au niveau de la mer à l'aide d'un manomètre à extrémité fermée. Le liquide contenu dans le manomètre est du mercure. Déterminez la pression du gaz dans :

torr
Pennsylvanie
bar

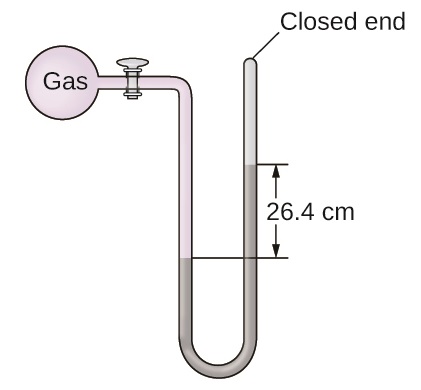
9.1.13

a) 264 torr ; b) 35 200 Pa ; c) 0,352 bar

Q9.1.14

La pression d'un échantillon de gaz est mesurée à l'aide d'un manomètre à extrémité ouverte, représenté partiellement à droite. Le liquide contenu dans le manomètre est du mercure. En supposant que la pression atmosphérique est de 29,92 pouces. Hg, déterminez la pression du gaz dans :

torr
Pennsylvanie
bar

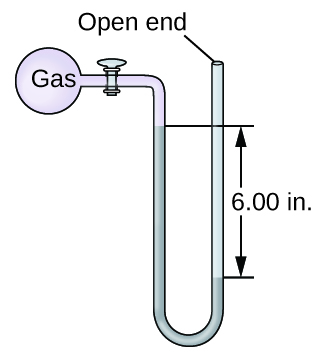
Q9.1.15

La pression d'un échantillon de gaz est mesurée au niveau de la mer à l'aide d'un manomètre à mercure à extrémité ouverte. En supposant que la pression atmosphérique est de 760,0 mm Hg, déterminez la pression du gaz dans :

mm Hg
guichet automatique
kPa

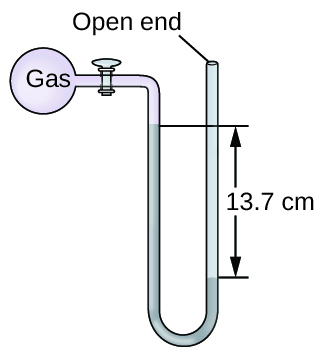
9.1.15

a) 623 mm de mercure ; b) 0,820 atm ; c) 83,1 kPa

Q9.1.16

La pression d'un échantillon de gaz est mesurée au niveau de la mer à l'aide d'un manomètre à mercure à extrémité ouverte. En supposant que la pression atmosphérique est de 760 mm Hg, déterminez la pression du gaz dans :

mm Hg
guichet automatique
kPa

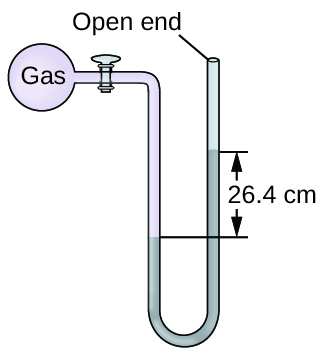
Q9.1.17

Comment l'utilisation d'un liquide volatil affecterait-elle la mesure d'un gaz à l'aide de manomètres à extrémité ouverte par rapport à des manomètres à extrémité fermée ?

9.1.17

Avec un manomètre à extrémité fermée, aucun changement ne serait observé, car le liquide vaporisé produirait des pressions égales et opposées dans les deux bras du tube du manomètre. Cependant, avec un manomètre ouvert, une lecture de pression du gaz plus élevée que prévu serait obtenue, puisque P _gas = P _atm + P _{vol liquide}.

9.2 : Relation de la pression, du volume, de la quantité et de la température : la loi des gaz idéaux

Q9.2.1

Parfois, laisser un vélo au soleil par une chaude journée peut provoquer une éruption cutanée. Pourquoi ?

Q9.2.2

Expliquez comment le volume des bulles évacuées par un plongeur (Figure) change lorsqu'elles remontent à la surface, en supposant qu'elles restent intactes.

9.2.2

Lorsque les bulles montent, la pression diminue, de sorte que leur volume augmente, comme le suggère la loi de Boyle.

Q9.2.3

Une façon d'énoncer la loi de Boyle est que « toutes choses étant égales par ailleurs, la pression d'un gaz est inversement proportionnelle à son volume ». a) Que signifie le terme « inversement proportionnel » ? (b) Quelles sont les « autres choses » qui doivent être égales ?

Q9.2.4

Une autre façon d'énoncer la loi d'Avogadro est la suivante : « Toutes choses étant égales par ailleurs, le nombre de molécules dans un gaz est directement proportionnel au volume du gaz ».

Que signifie le terme « directement proportionnel » ?
Quelles sont les « autres choses » qui doivent être égales ?

9.2.4

(a) Le nombre de particules dans le gaz augmente à mesure que le volume augmente. (b) température, pression

Q9.2.5

Comment le graphique de la figure changerait-il si le nombre de moles de gaz dans l'échantillon utilisé pour déterminer la courbe était doublé ?

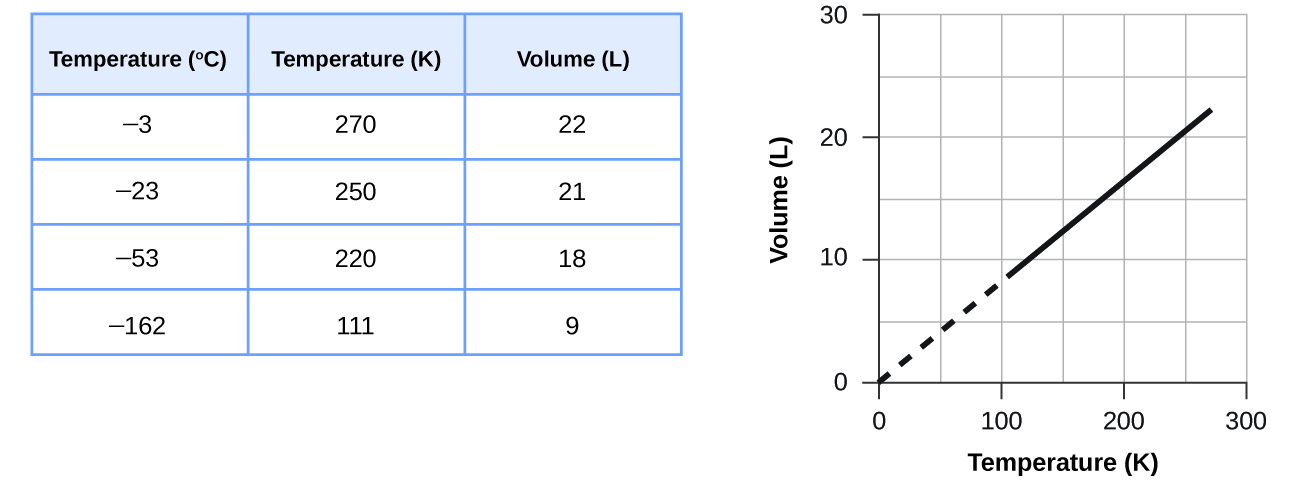
Le volume et la température sont liés de manière linéaire pour 1 mole de méthane à une pression constante de 1 atm. Si la température est exprimée en kelvins, le volume et la température sont directement proportionnels. La droite s'arrête à 111 K parce que le méthane se liquéfie à cette température ; une fois extrapolée, elle coupe l'origine du graphique, ce qui représente une température nulle absolue.

Q9.2.6

Comment le graphique de la figure changerait-il si le nombre de moles de gaz dans l'échantillon utilisé pour déterminer la courbe était doublé ?

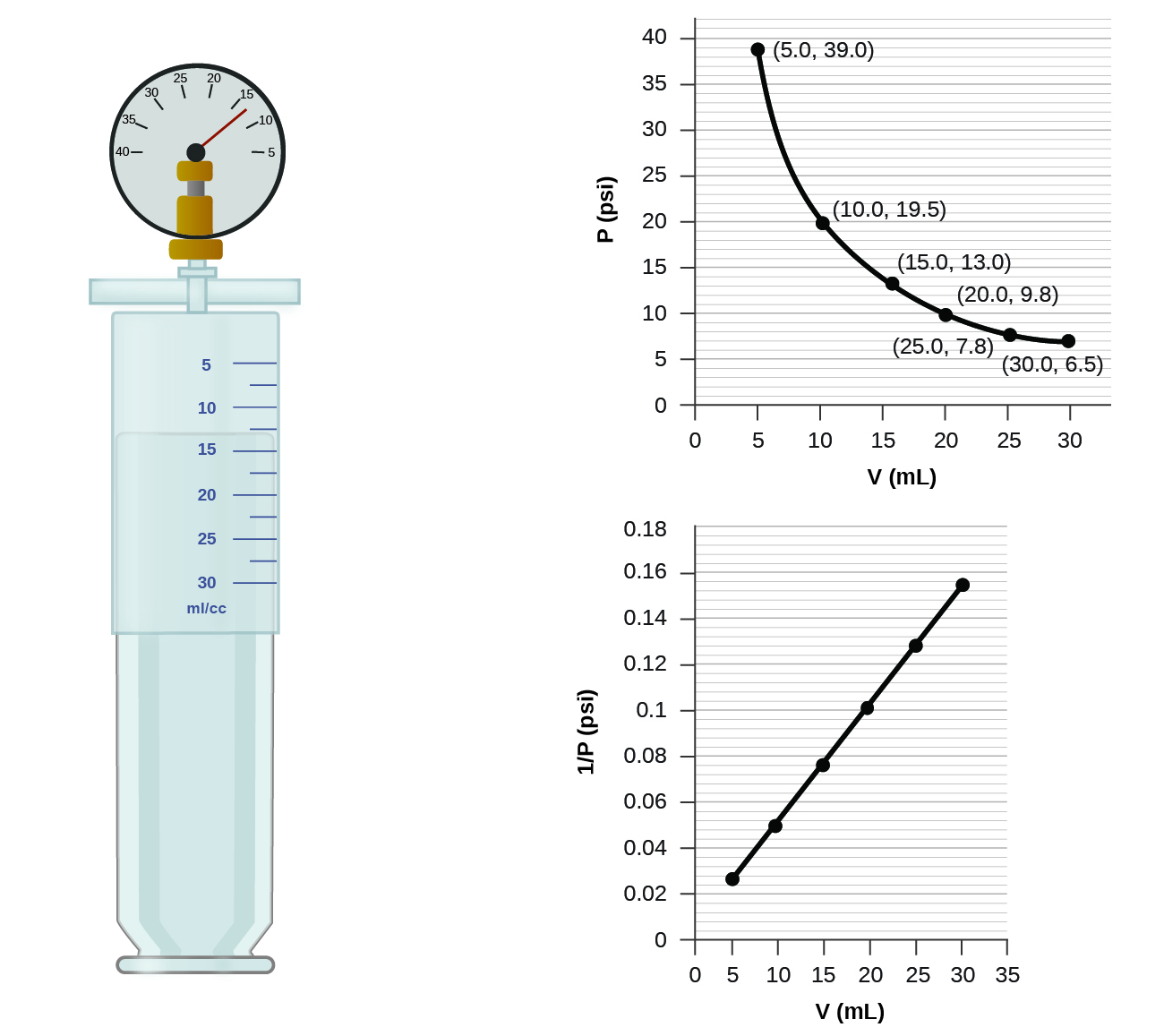
Lorsqu'un gaz occupe un volume plus petit, il exerce une pression plus élevée ; lorsqu'il occupe un volume plus important, il exerce une pression plus faible (en supposant que la quantité de gaz et la température ne changent pas). Puisque P et V sont inversement proportionnels, un graphique de\(1/P\) vs.\(V\) est linéaire.

9.2.6

La courbe serait plus à droite et plus haut, mais aurait la même forme de base.

Q9.2.7

Outre les données de la Figure, de quelles autres informations avons-nous besoin pour déterminer la masse de l'échantillon d'air utilisé pour déterminer le graphique ?

Q9.2.8

Déterminez le volume de 1 mol de gaz CH ₄ à 150 K et 1 atm, à l'aide de la Figure.

9.2.8

16,3 à 16,5 L

Q9.2.9

Déterminez la pression du gaz dans la seringue illustrée à la figure lorsque son volume est de 12,5 ml, en utilisant :

le graphique approprié
Loi de Boyle

Q9.2.10

Un aérosol est utilisé jusqu'à ce qu'il soit vide, à l'exception du gaz propulseur, qui a une pression de 1344 torr à 23 °C. Si le bidon est jeté dans un feu (T = 475 °C), quelle sera la pression dans le bidon chaud ?

9.2.10

3,40 × 10 ³ torr

Q9.2.11

Quelle est la température d'un échantillon de 11,2 L de monoxyde de carbone, CO, à 744 torr s'il occupe 13,3 L à 55 °C et 744 torr ?

9.2.11

nous devons utiliser\(\dfrac{P_1V_1}{T_1} =\dfrac{P_2V_2}{T_2}\) et résoudre\(T_1\)

\(T_1 = \dfrac{P_1V_1T_2}{P_2V_2}\)

Où :

\(P_1 = 744\: torr\)

\(V_1 = 11.2\: L\)

\(P_2 = 744\: torr\)

\(V_2 = 13.3\: L\)

\(T_2 = 328.15°\: K\)

\(\dfrac{(744\: torr)(11.2\: L)(328.15°\: K)}{(744\: torr)(13.3\: L)} = 276°\: K\)

276 °K ; 3 °C

Q9.2.12

Un volume de 2,50 L d'hydrogène mesuré à —196 °C est chauffé à 100 °C. Calculer le volume du gaz à la température la plus élevée, en supposant qu'il n'y a pas de changement de pression.

9.2.13

12,1 L

Q9.2.14

Un ballon gonflé avec trois respirations d'air a un volume de 1,7 L. À la même température et à la même pression, quel est le volume du ballon si cinq autres respirations de même taille sont ajoutées au ballon ?

Q9.2.15

Un ballon météo contient 8,80 moles d'hélium à une pression de 0,992 atm et à une température de 25 °C au niveau du sol. Quel est le volume du ballon dans ces conditions ?

9.2.15

217 L

Q9.2.16

Le volume d'un sac gonflable d'automobile était de 66,8 L lorsqu'il était gonflé à 25 °C avec 77,8 g d'azote gazeux. Quelle était la pression dans le sac en kPa ?

Q9.2.17

Combien de moles de trifluorure de bore gazeux, BF ₃, sont contenues dans une ampoule de 4,3410 L à 788,0 K si la pression est de 1,220 atm ? Combien de grammes de BF ₃ ?

9.2.17

8,190 × 10 ^—2 mol ; 5,53 g

Q9.2.18

L'iode, I ₂, est un solide à température ambiante mais se sublime (se transforme d'un solide en gaz) lorsqu'il est réchauffé. Quelle est la température dans une ampoule de 73,3 ml contenant 0,292 g de vapeur d'I ₂ à une pression de 0,462 atm ?

9.2.18

1.) Utilisez l'équation\(PV =nRT\) and solve for \(T\)

\(T= \dfrac{PV}{nR}\)

2.) convert grams of I₂ to moles of I₂ and convert mL to L

\(0.292g\: \ce{I2}\times \dfrac{1\: mole\: \ce{I2}}{253.8g\: \ce{I2}} = 1.15 \times10^{-3}\: moles\: \ce{I2}\)

\(73.3\:mL = 0.0733\:L\)

3.) Use these values along with \(R= 0.08206\: \dfrac{atm\:L}{mole\:°K}\) to solve for \(T\)

\(T= \dfrac{(0.462\: \cancel{atm})(0.0733\:\cancel{L})}{(1.15\times10^{-3}\: \cancel{moles})(0.08206\: \dfrac{\cancel{atm}\:\cancel{L}}{\cancel{mole}\:°K})} = 359\: °K \)

359°K ; 86°C

Q9.2.19

How many grams of gas are present in each of the following cases?

0.100 L of CO₂ at 307 torr and 26 °C
8.75 L of C₂H₄, at 378.3 kPa and 483 K
221 mL of Ar at 0.23 torr and –54 °C

S9.2.19

(a) 7.24 × 10^–2 g; (b) 23.1 g; (c) 1.5 × 10^–4 g

Q9.2.20

A high altitude balloon is filled with 1.41 × 10⁴ L of hydrogen at a temperature of 21 °C and a pressure of 745 torr. What is the volume of the balloon at a height of 20 km, where the temperature is –48 °C and the pressure is 63.1 torr?

Q9.2.21

A cylinder of medical oxygen has a volume of 35.4 L, and contains O₂ at a pressure of 151 atm and a temperature of 25 °C. What volume of O₂ does this correspond to at normal body conditions, that is, 1 atm and 37 °C?

S9.2.21

5561 L

Q9.2.22

A large scuba tank (Figure) with a volume of 18 L is rated for a pressure of 220 bar. The tank is filled at 20 °C and contains enough air to supply 1860 L of air to a diver at a pressure of 2.37 atm (a depth of 45 feet). Was the tank filled to capacity at 20 °C?

Q9.2.23

A 20.0-L cylinder containing 11.34 kg of butane, C₄H₁₀, was opened to the atmosphere. Calculate the mass of the gas remaining in the cylinder if it were opened and the gas escaped until the pressure in the cylinder was equal to the atmospheric pressure, 0.983 atm, and a temperature of 27 °C.

S9.2.23

46.4 g

Q9.2.24

While resting, the average 70-kg human male consumes 14 L of pure O₂ per hour at 25 °C and 100 kPa. How many moles of O₂ are consumed by a 70 kg man while resting for 1.0 h?

Q9.2.25

For a given amount of gas showing ideal behavior, draw labeled graphs of:

the variation of P with V
the variation of V with T
the variation of P with T
the variation of \(\dfrac{1}{P}\) with V

Q9.2.26

For a gas exhibiting ideal behavior:

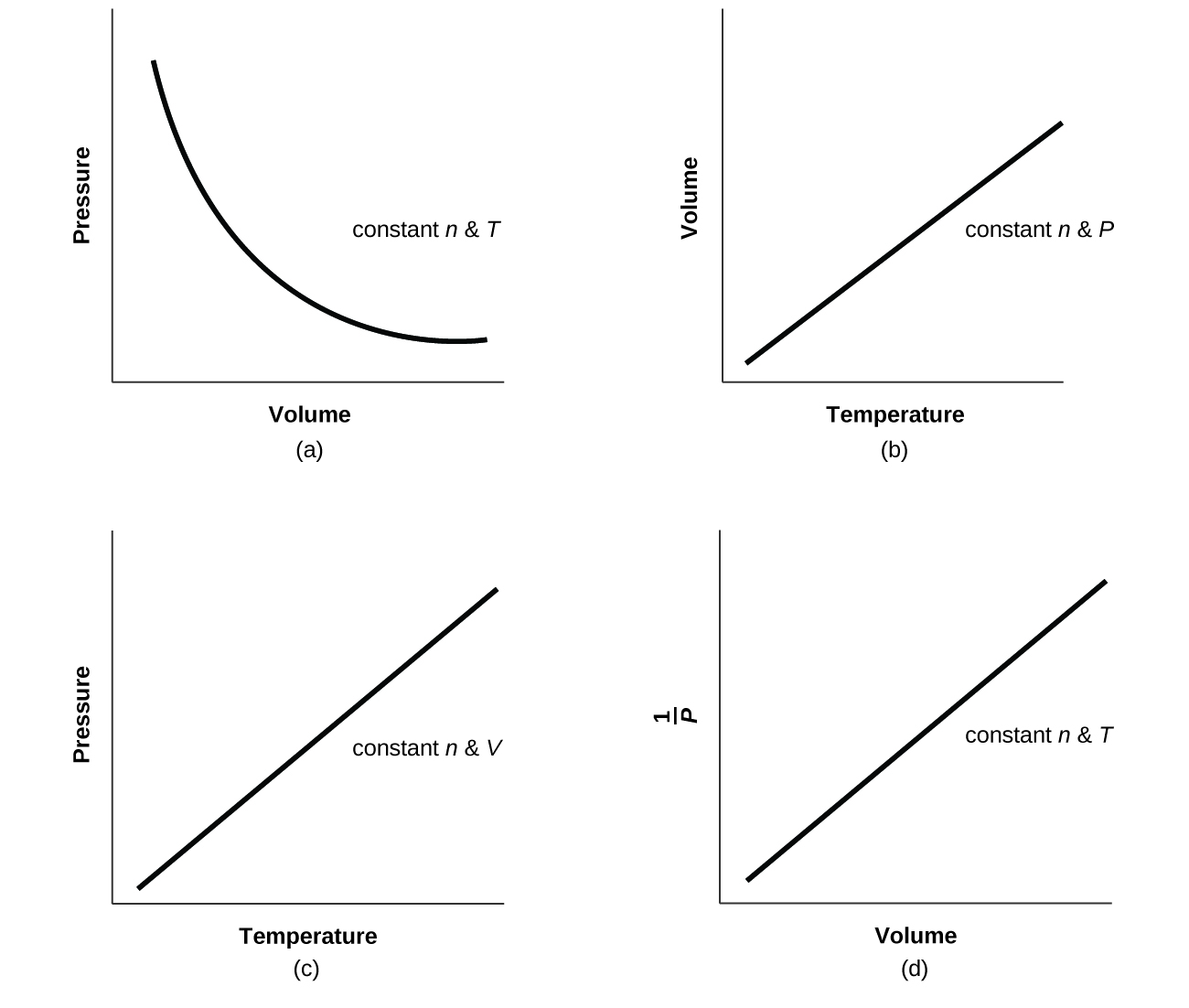
Q9.2.27

Un litre de méthane, CH ₄, à la STP contient plus d'atomes d'hydrogène qu'un litre d'hydrogène pur, H ₂, à la STP. En utilisant la loi d'Avogadro comme point de départ, expliquez pourquoi.

Q9.2.28

L'effet des chlorofluorocarbones (tels que le CCl ₂ F ₂) sur l'appauvrissement de la couche d'ozone est bien connu. L'utilisation de substituts, tels que le CH ₃ CH ₂ F (g), pour les chlorofluorocarbones a largement corrigé le problème. Calculer le volume occupé par 10,0 g de chacun de ces composés au STP :

CCl _₂ F (g)
CH ₃ CH ₂ F (g)

9.2.28

a) 1,85 L de CCl ₂ F ₂ ; b) 4,66 L de CH ₃ CH ₂ F

Q9.2.29

À mesure que 1 g de radium, un élément radioactif, se désintègre en 1 an, il produit 1,16 × 10 ¹⁸ particules alpha (noyaux d'hélium). Chaque particule alpha devient un atome d'hélium gazeux. Quelle est la pression en pascal de l'hélium gazeux produit s'il occupe un volume de 125 ml à une température de 25 °C ?

Q9.2.30

Un ballon de 100,21 L à 21 °C et 0,981 atm est lâché et franchit à peine le sommet du mont Crumpet en Colombie-Britannique. Si le volume final du ballon est de 144,53 L à une température de 5,24 °C, quelle est la pression subie par le ballon lorsqu'il franchit le mont Crumpet ?

9.2.30

0,644 atm

Q9.2.31

Si la température d'une quantité fixe d'un gaz est doublée à volume constant, qu'advient-il de la pression ?

Q9.2.32

Si le volume d'une quantité fixe d'un gaz est triplé à température constante, qu'advient-il de la pression ?

9.2.32

La pression diminue d'un facteur 3.

9.3 : Stoechiométrie des substances gazeuses, des mélanges et des réactions

Q9.3.1

Quelle est la densité du gaz hilarant, le monoxyde de diazote, N ₂ O, à une température de 325 K et à une pression de 113,0 kPa ?

9.3.1

1.) Convertissez d'abord kPa en atm

\(113.0\:kPa\times\dfrac{1\:atm}{101.325\:kPa}=1.115\:atm\)

2.) Ensuite, utilisez l'équation\(d=\dfrac{PM}{RT}\) où d = densité en g L ^-1 et M = masse molaire en g mol ^-1

\(d=\dfrac{(1.115\:atm)(44.02\dfrac{g}{\cancel{mol}})}{(0.08206\: \dfrac{\cancel{atm}\:L}{\cancel{mole}\:\cancel{°K}})(325\:\cancel{°K})}=1.84\:\dfrac{g}{L}\)

Q9.3.2

Calculer la densité du fréon 12, CF ₂ Cl ₂, à 30,0 °C et 0,954 atm.

9.3.2

4,64 g L ^-1

Q9.3.3

Quel est le plus dense à la même température et à la même pression, de l'air sec ou de l'air saturé en vapeur d'eau ? Expliquez.

Q9.3.4

Un cylindre d'O ₂ (g) utilisé pour respirer par les patients atteints d'emphysème a un volume de 3,00 L à une pression de 10,0 atm. Si la température de la bouteille est de 28,0 °C, quelle est la masse d'oxygène contenue dans la bouteille ?

9.3.4

38,8 g

Q9.3.5

Quelle est la masse molaire d'un gaz si 0,0494 g du gaz occupe un volume de 0,100 L à une température de 26 °C et à une pression de 307 torr ?

9.3.5

1.) convertir torr en atm et °C en °K

\(307\:torr=0.404atm\)

\(26°C= 300.°K\)

2.) Utilisez l'équation\(PV=nRT\) et résolvez pour\(n\)

\(n=\dfrac{PV}{RT}\)

\(n=\dfrac{(0.404\:\cancel{atm})(0.100\:\cancel{L})}{(0.08206\dfrac{\cancel{atm}\:\cancel{L}}{mol\:\cancel{°K}})(300.\cancel{°K})}=0.00165\:moles\)

3.) Divisez ensuite les grammes par le nombre de moles pour obtenir la masse molaire :

\(\dfrac{0.0494g}{0.00165\:moles}=30.0\dfrac{g}{mole}\)

Q9.3.6

Quelle est la masse molaire d'un gaz si 0,281 g du gaz occupe un volume de 125 ml à une température de 126 °C et à une pression de 777 torr ?

9.3.6

72,0 g mol ^-1

Q9.3.7

Comment pouvez-vous démontrer expérimentalement que la formule moléculaire du propène est C ₃ H ₆, et non CH ₂ ?

Q9.3.8

La densité d'un certain fluorure gazeux de phosphore est de 3,93 g/L à la STP. Calculez la masse molaire de ce fluorure et déterminez sa formule moléculaire.

9.3.8

88,1 g mol ^-1 ; PF ₃

Q9.3.9

Réfléchissez à cette question : Quelle est la formule moléculaire d'un composé contenant 39 % de C, 45 % de N et 16 % de H si 0,157 g du composé occupe 125 ml sous une pression de 99,5 kPa à 22 °C ?

Décrivez les étapes nécessaires pour répondre à la question.
Réponds à la question.

Q9.3.10

Une bouteille de 36 L d'un gaz utilisé pour l'étalonnage des analyseurs de gaz sanguins dans les laboratoires médicaux contient 350 g de CO ₂, 805 g d'O ₂ et 4 880 g de N ₂. À 25 degrés C, quelle est la pression dans le cylindre en atmosphère ?

9.3.10

141 atm

Q9.3.11

Une bouteille d'un mélange de gaz utilisée pour l'étalonnage des analyseurs de gaz sanguins dans les laboratoires médicaux contient 5,0 % de CO ₂, 12,0 % d'O ₂ et le reste de N ₂ à une pression totale de 146 atm. Quelle est la pression partielle de chaque composant de ce gaz ? (Les pourcentages indiqués indiquent le pourcentage de la pression totale due à chaque composant.)

Q9.3.12

Un échantillon de gaz isolé à partir de pétrole non raffiné contient 90,0 % de CH ₄, 8,9 % de C ₂ H ₆ et 1,1 % de C ₃ H ₈ à une pression totale de 307,2 kPa. Quelle est la pression partielle de chaque composant de ce gaz ? (Les pourcentages indiqués indiquent le pourcentage de la pression totale due à chaque composant.)

9.3.12

CH ₄ : 276 kPa ; C ₂ H ₆ : 27 kPa ; C ₃ H ₈ : 3,4 kPa

Q9.3.13

Un mélange de 0,200 g de H ₂, 1,00 g de N ₂ et 0,820 g d'Ar est stocké dans un récipient fermé au STP. Déterminez le volume du récipient, en supposant que les gaz présentent un comportement idéal.

Q9.3.14

La plupart des mélanges d'hydrogène et d'oxygène gazeux sont explosifs. Toutefois, un mélange contenant moins de 3,0 % d'O ₂ ne l'est pas. Si une quantité suffisante d'O ₂ est ajoutée à une bouteille de H ₂ à 33,2 atm pour porter la pression totale à 34,5 atm, le mélange est-il explosif ?

9.3.14

Oui

Q9.3.15

Un analyseur de vapeur de mercure commercial peut détecter, dans l'air, des concentrations d'atomes de mercure gazeux (qui sont toxiques) aussi faibles que 2 × 10 ⁻⁶ mg/L d'air. À cette concentration, quelle est la pression partielle du mercure gazeux si la pression atmosphérique est de 733 torr à 26 °C ?

Q9.3.16

Un échantillon de monoxyde de carbone a été prélevé au-dessus de l'eau à une pression totale de 756 torr et à une température de 18 °C. Quelle est la pression du monoxyde de carbone ? (Voir le tableau pour la pression de vapeur de l'eau.)

9.3.16

740 torr

Q9.3.17

Lors d'une expérience menée dans un laboratoire de chimie générale, un étudiant a prélevé un échantillon de gaz au-dessus de l'eau. Le volume du gaz était de 265 ml à une pression de 753 torr et à une température de 27 °C. La masse du gaz était de 0,472 g. Quelle était la masse molaire du gaz ?

Q9.3.18

Joseph Priestley a d'abord préparé de l'oxygène pur en chauffant de l'oxyde mercurique, HgO :

\(\ce{2HgO}(s)⟶\ce{2Hg}(l)+\ce{O2}(g)\)

Décrivez les étapes nécessaires pour répondre à la question suivante : Quel volume d'O ₂ à 23 °C et 0,975 atm est produit par la décomposition de 5,36 g de HgO ?
Réponds à la question.

9.3.18

a) Déterminer les moles de HgO qui se décomposent ; à l'aide de l'équation chimique, déterminer les moles d'O ₂ produites par la décomposition de cette quantité de HgO ; et déterminer le volume d'O ₂ à partir des moles d'O ₂, de la température et de la pression. (b) 0,308 L

Q9.3.19

Cavendish a préparé de l'hydrogène en 1766 en utilisant la nouvelle méthode consistant à faire passer de la vapeur à travers un canon de pistolet chauffé au rouge :

\[\ce{4H2O}(g)+\ce{3Fe}(s)⟶\ce{Fe3O4}(s)+\ce{4H2}(g)\]

Décrivez les étapes nécessaires pour répondre à la question suivante : Quel volume de H ₂ à une pression de 745 torr et à une température de 20 °C peut être préparé à partir de la réaction de 15,O g de H ₂ O ?
Réponds à la question.

Q9.3.20

Le chlorofluorocarbone CCl ₂ F ₂ peut être recyclé en un composé différent par réaction avec l'hydrogène pour produire du CH ₂ F ₂ (g), un composé utile dans la fabrication chimique :

\[\ce{CCl2F2}(g)+\ce{4H2}(g)⟶\ce{CH2F2}(g)+\ce{2HCl}(g)\]

Décrivez les étapes nécessaires pour répondre à la question suivante : Quel volume d'hydrogène à 225 atm et 35,5 °C serait nécessaire pour réagir avec 1 tonne (1 000 × 10 ³ kg) de CCl ₂ F ₂ ?
Réponds à la question.

9.3.20

Déterminer la masse molaire du CCl ₂ F ₂. À partir de l'équation équilibrée, calculez les moles de H ₂ nécessaires à la réaction complète. À partir de la loi des gaz idéaux, convertissez les moles de H ₂ en volume.
3,72 × 10 ³ L

Q9.3.21

Les coussins gonflables des automobiles sont gonflés avec de l'azote gazeux, qui est formé par la décomposition de l'azoture de sodium solide (NaN ₃). L'autre produit est du sodium métallique. Calculer le volume d'azote gazeux à 27 °C et 756 torr formé par la décomposition de 125 g d'azoture de sodium.

Q9.3.2

La chaux, CaO, est produite en chauffant du carbonate de calcium, CaCO ₃ ; le dioxyde de carbone est l'autre produit.

Décrivez les étapes nécessaires pour répondre à la question suivante : Quel volume de dioxyde de carbone à 875 °C et 0,966 atm est produit par la décomposition d'une tonne (1 000 × 10 ³ kg) de carbonate de calcium ?
Réponds à la question.

9.3.2

(a) Équilibrer l'équation. Déterminez les grammes de CO ₂ produits et le nombre de moles. À partir de la loi du gaz idéal, déterminez le volume de gaz. (b) 7,43 × 10 ⁵ L

Q9.3.23

Avant que les petites batteries ne soient disponibles, des lampes au carbure étaient utilisées pour les feux de vélo. De l'acétylène gazeux, du C ₂ H ₂, et de l'hydroxyde de calcium solide ont été formés par réaction du carbure de calcium, CaC ₂, avec de l'eau. L'allumage du gaz acétylène a fourni la lumière. Actuellement, les mêmes lampes sont utilisées par certains spéléologues et le carbure de calcium est utilisé pour produire de l'acétylène pour les canons en carbure.

Décrivez les étapes nécessaires pour répondre à la question suivante : Quel volume de C ₂ H ₂ à 1,005 atm et 12,2 °C est formé par la réaction de 15,48 g de CaC ₂ avec de l'eau ?
Réponds à la question.

Q9.3.24

Calculer le volume d'oxygène nécessaire pour brûler 12,00 L d'éthane, C ₂ H ₆, afin de produire du dioxyde de carbone et de l'eau, si les volumes de C ₂ H ₆ et d'O ₂ sont mesurés dans les mêmes conditions de température et de pression.

9.3.24

42,00 L

Q9.3.25

Quel volume d'O ₂ à la STP est nécessaire pour oxyder 8,0 L de NO à la STP en NO ₂ ? Quel volume de NO ₂ est produit par STP ?

Q9.3.26

Réfléchissez aux questions suivantes :

Quel est le volume total de CO ₂ (g) et de H ₂ O (g) à 600 °C et 0,888 atm produits par la combustion de 1 L de C ₂ H ₆ (g) mesuré au STP ?
Quelle est la pression partielle de H ₂ O dans les gaz produits ?

9.3.26

a) 18,0 L ; b) 0,533 atm

Q9.3.27

Le méthanol, CH ₃ OH, est produit industriellement par la réaction suivante :

\[\ce{CO}(g)+\ce{2H2}(g)\xrightarrow{\textrm{ copper catalyst 300 °C, 300 atm }}\ce{CH3OH}(g)\]

Q9.3.28

En supposant que les gaz se comportent comme des gaz idéaux, déterminez le rapport entre le volume total des réactifs et le volume final.

Q9.3.29

Quel volume d'oxygène à 423,0 K et à une pression de 127,4 kPa est produit par la décomposition de 129,7 g de BaO ₂ en BaO et O ₂ ?

9.3.29

10,57 L DE ₂

Q9.3.30

Un échantillon de 2,50 L d'un gaz incolore à la STP s'est décomposé pour donner 2,50 L de N ₂ et 1,25 L d'O ₂ à la STP. Qu'est-ce que le gaz incolore ?

Q9.3.31

L'éthanol, C ₂ H ₅ OH, est produit industriellement à partir de l'éthylène, C ₂ H ₄, par la séquence de réactions suivante :

\[\ce{3C2H4 + 2H2SO4⟶C2H5HSO4 + (C2H5)2SO4}\]

\[\ce{C2H5HSO4 + (C2H5)2SO4 + 3H2O⟶3C2H5OH + 2H2SO4}\]

Quel volume d'éthylène au STP est nécessaire pour produire 1 000 tonnes métriques (1 000 kg) d'éthanol si le rendement global en éthanol est de 90,1 % ?

9.3.31

5,40 × 10 ⁵ L

Q9.3.32

Une molécule d'hémoglobine se combinera à quatre molécules d'oxygène. Si 1,0 g d'hémoglobine se combine à 1,53 ml d'oxygène à la température corporelle (37 °C) et à une pression de 743 torr, quelle est la masse molaire de l'hémoglobine ?

Q9.3.3

Un échantillon d'un composé de xénon et de fluor a été confiné dans une ampoule à une pression de 18 torr. De l'hydrogène a été ajouté à l'ampoule jusqu'à ce que la pression soit de 72 torr. Le passage d'une étincelle électrique à travers le mélange produit du Xe et du HF. Après élimination du HF par réaction avec du KOH solide, la pression finale du xénon et de l'hydrogène n'ayant pas réagi dans l'ampoule était de 36 torr. Quelle est la formule empirique du fluorure de xénon dans l'échantillon original ? (Remarque : les fluorures de xénon ne contiennent qu'un seul atome de xénon par molécule.)

9.3.3

XeF ₂

Q9.3.34

L'une des méthodes d'analyse des acides aminés est la méthode de Van Slyke. Les groupes aminés caractéristiques (−NH ₂) de la matière protéique peuvent réagir avec l'acide nitreux, HNO ₂, pour former du N ₂ gazeux. À partir du volume du gaz, la quantité d'acide aminé peut être déterminée. Un échantillon de 0,0604 g d'un échantillon biologique contenant de la glycine, CH ₂ (NH ₂) COOH, a été analysé par la méthode de van Slyke et a donné 3,70 ml de N ₂ collectés sur de l'eau à une pression de 735 torr et à 29 °C. Quel était le pourcentage de glycine dans l'échantillon ?

\(\ce{CH2(NH2)CO2H + HNO2⟶CH2(OH)CO2H + H2O + N2}\)

9.4 : Épanchement et diffusion de gaz

Q9.4.1

Un ballon rempli d'hélium met 6 heures à se dégonfler à 50 % de son volume initial. Combien de temps faudra-t-il pour qu'un ballon identique rempli du même volume d'hydrogène gazeux (au lieu d'hélium) diminue son volume de 50 % ?

9.4.1

4,2 heures

Q9.4.2

Expliquez pourquoi le nombre de molécules n'est pas identique dans les ampoules gauche et droite illustrées dans l'illustration centrale de la figure.

Q9.4.3

En commençant par la définition du taux d'effusion et les résultats de Graham établissant un lien entre le taux et la masse molaire, montrez comment dériver l'équation de la loi de Graham, reliant les taux relatifs d'effusion de deux gaz à leurs masses moléculaires.

9.4.3

L'effusion peut être définie comme le processus par lequel un gaz s'échappe dans le vide par un trou d'épingle. La loi de Graham stipule qu'avec un mélange de deux gaz A et B :\(\mathrm{\left(\dfrac{rate\: A}{rate\: B}\right)=\left(\dfrac{molar\: mass\: of\: B}{molar\: mass\: of\: A}\right)^{1/2}}\). A et B se trouvent tous deux dans le même récipient à la même température et auront donc la même énergie cinétique :

\(\mathrm{KE_A=KE_BKE}=\dfrac{1}{2}mv^2\) Par conséquent,\(\dfrac{1}{2}m_\ce{A}v^2_\ce{A}=\dfrac{1}{2}m_\ce{B}v^2_\ce{B}\) \(\dfrac{v^2_\ce{A}}{v^2_\ce{B}}=\dfrac{m_\ce{B}}{m_\ce{A}}\) \(\left(\dfrac{v^2_\ce{A}}{v^2_\ce{B}}\right)^{1/2}=\left(\dfrac{m_\ce{B}}{m_\ce{A}}\right)^{1/2}\) \(\dfrac{v_\ce{A}}{v_\ce{B}}=\left(\dfrac{m_\ce{B}}{m_\ce{A}}\right)^{1/2}\)

Q9.4.4

L'eau lourde, D ₂ O (masse molaire = 20,03 g mol ^—1), peut être séparée de l'eau ordinaire, H ₂ O (masse molaire = 18,01), en raison de la différence entre les vitesses relatives de diffusion des molécules en phase gazeuse. Calculer les taux relatifs de diffusion de H ₂ O et de D ₂ O.

Q9.4.5

Lequel des gaz suivants diffuse plus lentement que l'oxygène ? F ₂, Ne, N ₂ O, C ₂ H ₂, NO, Cl ₂, H ₂ S

9.4.5

F ₂, N ₂ O, Cl ₂, H ₂ S

Q9.4.6

Au cours de la discussion sur la diffusion gazeuse pour enrichir l'uranium, il a été affirmé que ²³⁵ UF ₆ diffusait 0,4 % plus rapidement que ²³⁸ UF ₆. Afficher le calcul qui soutient cette valeur. La masse molaire de ²³⁵ UF ₆ = 235,043930 + 6 × 18,998403 = 349,034348 g/mol, et la masse molaire de ²³⁸ UF ₆ = 238,050788 + 6 × 18,998403 = 352,041206 g/mol.

Q9.4.7

Calculer le taux de diffusion relatif de ¹ H ₂ (masse molaire 2,0 g/mol) par rapport à celui de ² H ₂ (masse molaire 4,0 g/mol) et le taux de diffusion relatif de O ₂ (masse molaire 32 g/mol) par rapport à celui de O ₃ (masse molaire 48 g/mol).

9.4.7

1,4 ; 1,2

Q9.4.8

Un gaz d'identité inconnue diffuse à un débit de 83,3 mL/s dans un appareil de diffusion dans lequel le dioxyde de carbone diffuse à une vitesse de 102 mL/s. Calculez la masse moléculaire du gaz inconnu.

Q9.4.9

Lorsque deux bouchons de coton, l'un humidifié avec de l'ammoniaque et l'autre avec de l'acide chlorhydrique, sont insérés simultanément aux extrémités opposées d'un tube de verre de 87,0 cm de long, un anneau blanc de NH ₄ Cl se forme là où le NH ₃ gazeux et le HCl gazeux entrent en contact pour la première fois. (Conseil : calculez les vitesses de diffusion du NH ₃ et du HCl, et découvrez à quel point le NH ₃ diffuse plus rapidement que le HCl.)

\[\ce{NH3}(g)+\ce{HCl}(g)⟶\ce{NH4Cl}(s)\]

Q9.4.10

À quelle distance environ du bouchon humidifié à l'ammoniac cela se produit-il ?

9.4.10

51,7 cm

9.5 : La théorie cinético-moléculaire

Q9.5.1

À l'aide des postulats de la théorie moléculaire cinétique, expliquez pourquoi un gaz remplit uniformément un contenant de n'importe quelle forme.

Q9.5.2

La vitesse d'une molécule donnée dans un gaz peut-elle doubler à température constante ? Expliquez votre réponse.

9.5.2

Oui. À tout instant donné, il existe une gamme de valeurs de vitesses moléculaires dans un échantillon de gaz. Chaque molécule peut accélérer ou ralentir lorsqu'elle entre en collision avec d'autres molécules. La vitesse moyenne de toutes les molécules est constante à température constante.

Q9.5.3

Décrivez ce qu'il advient de l'énergie cinétique moyenne des molécules de gaz idéales lorsque les conditions changent comme suit :

La pression du gaz est augmentée en réduisant le volume à température constante.
La pression du gaz est augmentée en augmentant la température à volume constant.
La vitesse moyenne des molécules est augmentée d'un facteur 2.

Q9.5.4

La distribution des vitesses moléculaires dans un échantillon d'hélium est illustrée à la figure. Si l'échantillon est refroidi, la distribution des vitesses ressemblera-t-elle davantage à celle de H ₂ ou de H ₂ O ? Expliquez votre réponse.

9.5.4

H ₂ O. Le refroidissement ralentit les vitesses des atomes de He, les amenant à se comporter comme s'ils étaient plus lourds.

Q9.5.5

Quel est le rapport entre l'énergie cinétique moyenne d'une molécule de SO ₂ et celle d'une molécule d'O ₂ dans un mélange de deux gaz ? Quel est le rapport entre les vitesses quadratiques moyennes des racines, u _rms, des deux gaz ?

Q9.5.6

Un échantillon de 1 L de CO initialement au STP est chauffé à 546 °C, et son volume est augmenté à 2 L.

Quel est l'effet de ces changements sur le nombre de collisions des molécules du gaz par unité de surface de la paroi du récipient ?
Quel est l'effet sur l'énergie cinétique moyenne des molécules ?
Quel est l'effet sur la vitesse quadratique moyenne des molécules ?

9.5.6

a) Le nombre de collisions par unité de surface de la paroi du conteneur est constant. (b) L'énergie cinétique moyenne double. (c) La vitesse quadratique moyenne de la racine augmente jusqu'à 4\(\sqrt{2}\) fois sa valeur initiale ; u _rms est proportionnel à\(\mathrm{KE_{avg}}\).

Q9.5.7

La vitesse quadratique moyenne des molécules de H ₂ à 25 °C est d'environ 1,6 km/s. Quelle est la vitesse quadratique moyenne d'une molécule de N ₂ à 25 °C ?

Q9.5.8

Répondez aux questions suivantes :

La pression du gaz dans la montgolfière indiquée au début de ce chapitre est-elle supérieure, inférieure ou égale à celle de l'atmosphère à l'extérieur de la montgolfière ?
La densité du gaz dans la montgolfière illustrée au début de ce chapitre est-elle supérieure, inférieure ou égale à celle de l'atmosphère à l'extérieur de la montgolfière ?
À une pression de 1 atm et à une température de 20 °C, l'air sec a une densité de 1,2256 g/L. Quelle est la masse molaire (moyenne) de l'air sec ?
La température moyenne du gaz dans une montgolfière est de 1,30 × 10 ² °F. Calculez sa densité en supposant que la masse molaire est égale à celle de l'air sec.
La capacité de levage d'une montgolfière est égale à la différence entre la masse de l'air froid déplacé par le ballon et la masse du gaz dans le ballon. Quelle est la différence entre la masse de 1,00 L de l'air froid dans la partie (c) et de l'air chaud dans la partie (d) ?
Un ballon moyen a un diamètre de 60 pieds et un volume de 1,1 × 10 ⁵ pieds ³. Quel est le pouvoir de levage d'un tel ballon ? Si le poids du ballon et de son gréement est de 500 livres, quelle est sa capacité de transport de passagers et de marchandises ?
Un ballon transporte 40 gallons de propane liquide (densité 0,5005 g/L). Quel volume de CO ₂ et de H ₂ O est produit par la combustion de ce propane ?
Un vol en montgolfière peut durer environ 90 minutes. Si tout le carburant est brûlé pendant cette période, quel est le taux approximatif de perte de chaleur (en kJ/min) due à l'air chaud contenu dans le sac pendant le vol ?

9.5.1

(a) égal ; (b) inférieur à ; (c) 29,48 g mol ⁻¹ ; (d) 1,0966 g L ⁻¹ ; (e) 0,129 g/L ; (f) 4,01 × 10 ⁵ g ; capacité de levage nette = 384 lb ; (g) 270 L ; (h) 39,1 kJ min ⁻¹

Q9.5.1

Montrez que le rapport entre la vitesse de diffusion du gaz 1 et la vitesse de diffusion du gaz 2\(\dfrac{R_1}{R_2}\), est le même à 0 °C et à 100 °C.

9.6 : Comportement non idéal des gaz

Q9.6.1

Des graphiques montrant le comportement de plusieurs gaz différents suivent. Lequel de ces gaz présente un comportement significativement différent de celui attendu pour les gaz idéaux ?

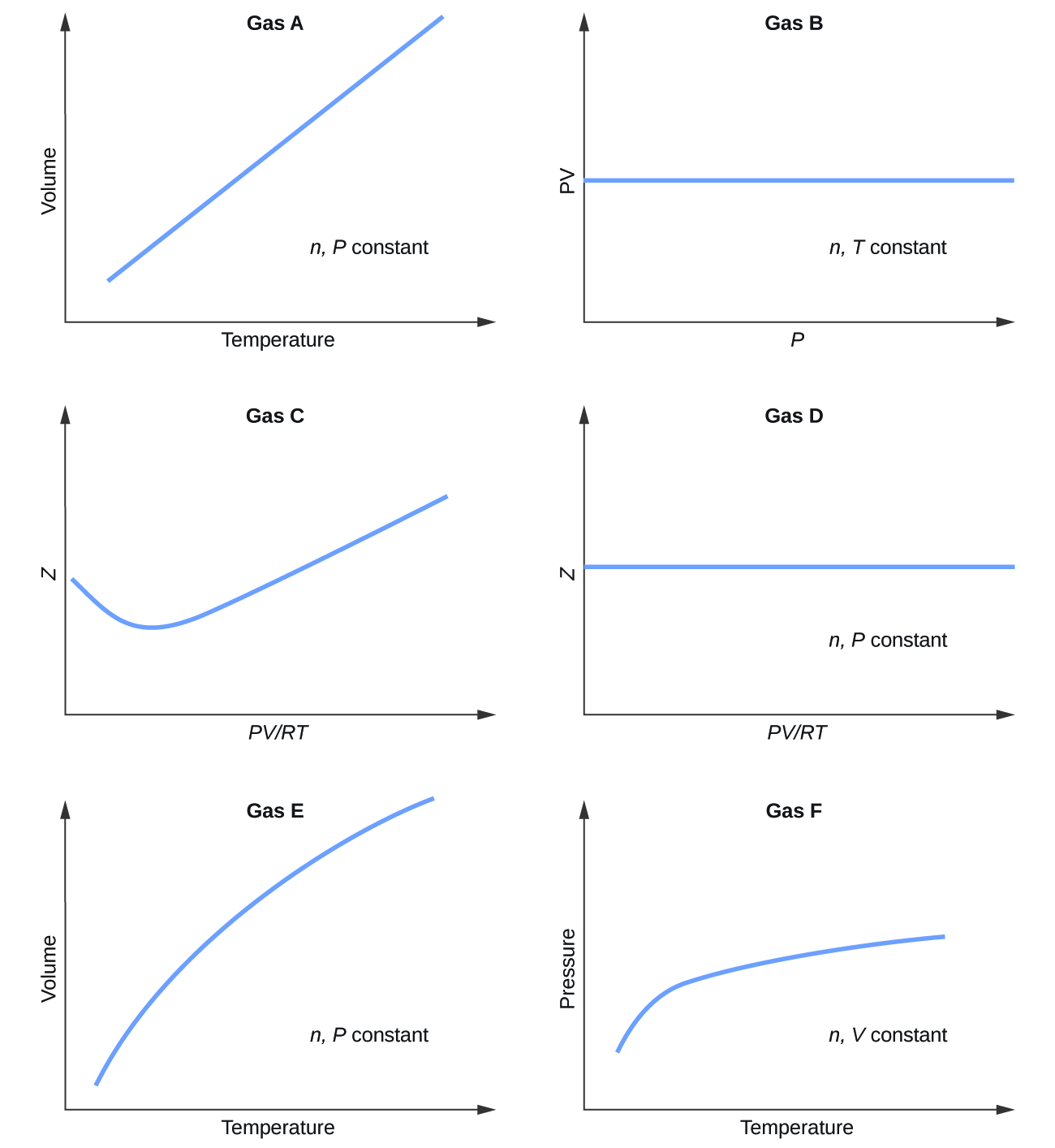
9.6.1

Gaz C, E et F

Q9.6.3

Expliquez pourquoi le diagramme du PV pour le CO ₂ diffère de celui d'un gaz idéal.

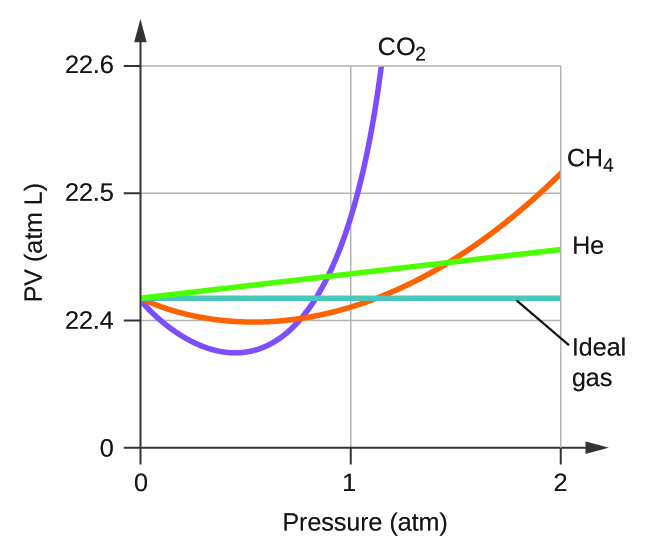
Q9.6.3

Dans laquelle des ensembles de conditions suivants un gaz réel se comporte-t-il le plus comme un gaz idéal, et dans quelles conditions un gaz réel devrait-il s'écarter du comportement idéal ? Expliquez.

haute pression, petit volume
haute température, basse pression
basse température, haute pression

9.6.3

Le comportement du gaz le plus proche d'un gaz idéal se produira dans les conditions décrites en (b). Les molécules ont des vitesses élevées et se déplacent sur de plus grandes distances entre les collisions ; elles ont également des temps de contact plus courts et les interactions sont moins probables. Des écarts se produisent dans les conditions décrites aux points (a) et (c). Dans les conditions de (a), certains gaz peuvent se liquéfier. Dans les conditions de (c), la plupart des gaz se liquéfieront.

Q9.6.4

Décrire les facteurs responsables de l'écart entre le comportement des gaz réels et celui d'un gaz idéal.

Q9.6.5

Pour lequel des gaz suivants la correction du volume moléculaire devrait-elle être la plus importante : CO, CO ₂, H ₂, He, NH ₃, SF ₆ ?

9.6.6

SF ₆

Q9.6.7

Un flacon de 0,245 L contient 0,467 mol de CO ₂ à 159 °C. Calculer la pression :

en utilisant la loi idéale sur les gaz
à l'aide de l'équation de Van der Waals
Expliquez la raison de la différence.
Déterminez quelle correction (celle pour P ou V) est dominante et pourquoi.

Q9.6.8

Répondez aux questions suivantes :

Si XX se comportait comme un gaz idéal, à quoi ressemblerait son graphique entre Z et P ?
Pendant la majeure partie de ce chapitre, nous avons effectué des calculs traitant les gaz comme étant idéaux. Cela était-il justifié ?
Quel est l'effet du volume des molécules de gaz sur Z ? Dans quelles conditions cet effet est-il faible ? Quand est-ce grand ? Expliquez à l'aide d'un schéma approprié.
Quel est l'effet des attractions intermoléculaires sur la valeur de Z ? Dans quelles conditions cet effet est-il faible ? Quand est-ce grand ? Expliquez à l'aide d'un schéma approprié.
En général, dans quelles conditions de température vous attendriez-vous à ce que Z présente les plus grands écarts par rapport au Z pour un gaz idéal ?

9.6.8

(a) Une ligne horizontale droite à 1,0 ; (b) Lorsque les gaz réels se trouvent à de basses pressions et à des températures élevées, ils se comportent suffisamment près des gaz idéaux pour être approximés comme tels. Cependant, dans certains cas, nous constatons qu'à une pression et à une température élevées, l'approximation du gaz idéal se décompose et est différente de la pression calculée par l'équation de Van der Waals (c) Plus la compressibilité est grande, plus le volume est important. À basse pression, le facteur de correction des attractions intermoléculaires est plus significatif, et l'effet du volume des molécules de gaz sur Z serait une légère diminution de la compressibilité. À des pressions plus élevées, l'effet du volume des molécules de gaz elles-mêmes sur Z augmenterait la compressibilité (voir Figure) (d) Encore une fois, à basse pression, l'effet des attractions intermoléculaires sur Z serait plus important que le facteur de correction du volume des molécules de gaz eux-mêmes, même s'ils sont peut-être encore petits. À des pressions plus élevées et à des températures basses, l'effet des attractions intermoléculaires serait plus important. Voir la figure. (e) basses températures

9.6 : Comportement non idéal des gaz

Exercices

Des graphiques montrant le comportement de plusieurs gaz différents suivent. Lequel de ces gaz présente un comportement significativement différent de celui attendu pour les gaz idéaux ?

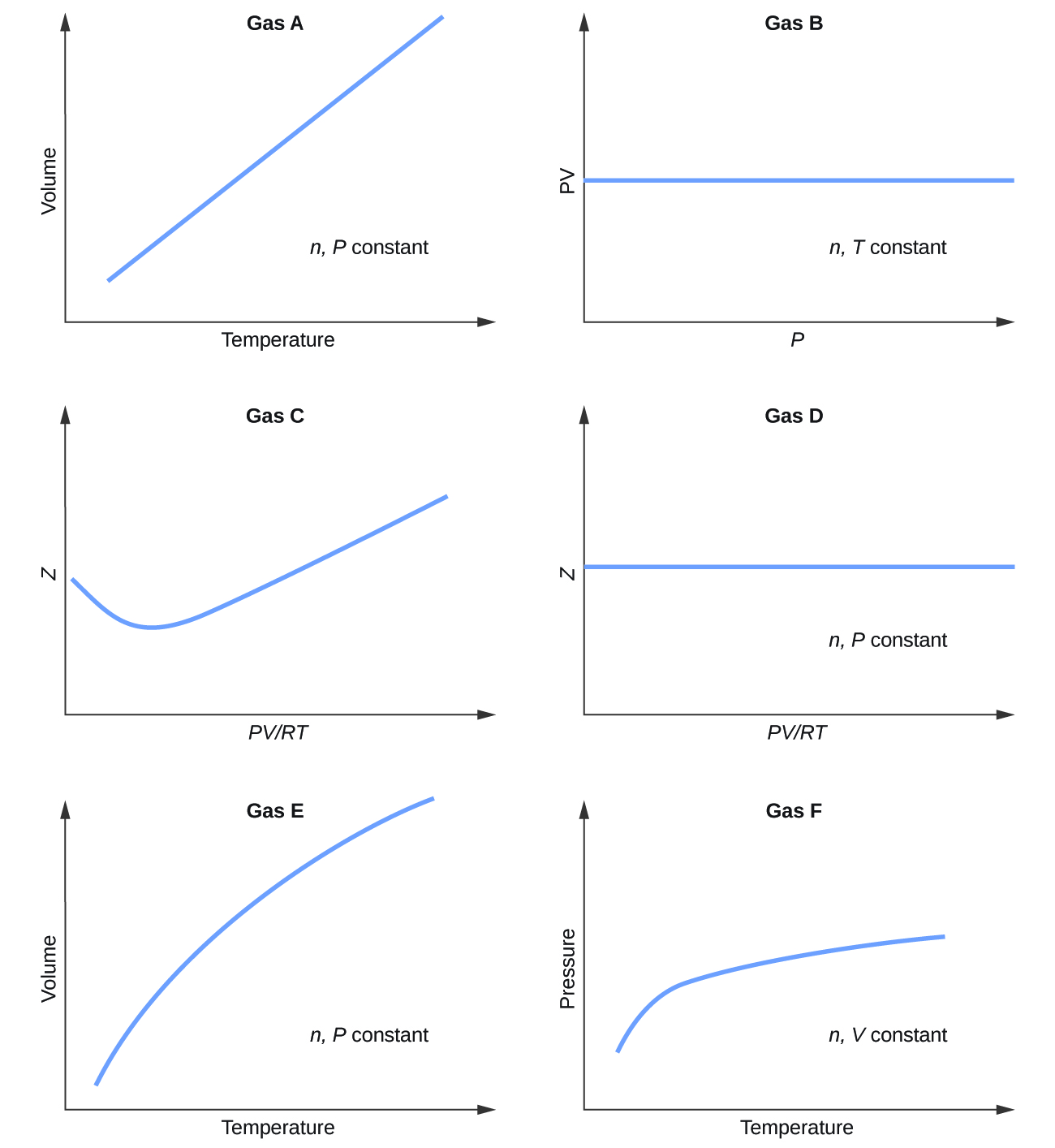
Gaz C, E et F

Expliquez pourquoi le diagramme du PV pour le CO ₂ diffère de celui d'un gaz idéal.

a) haute pression, petit volume

(b) haute température, basse pression

Décrire les facteurs responsables de l'écart entre le comportement des gaz réels et celui d'un

gaz idéal.

Pour lequel des gaz suivants la correction du volume moléculaire doit être la plus importante :

CO, CO ₂, H ₂, He, NH ₃, SF ₆ ?

SF ₆

Un flacon de 0,245 L contient 0,467 mol de CO ₂ à 159 °C. Calculer la pression :

a) en utilisant la loi du gaz idéal

(b) en utilisant l'équation de Van der Waals

(d) Déterminer quelle correction (celle pour P ou V) est dominante et pourquoi.

Répondez aux questions suivantes :

(a) Si XX se comportait comme un gaz idéal, à quoi ressemblerait son graphique entre Z et P ?

(b) Pendant la majeure partie de ce chapitre, nous avons effectué des calculs traitant les gaz comme étant idéaux. Cela était-il justifié ?

(c) Quel est l'effet du volume des molécules de gaz sur Z ? Dans quelles conditions cet effet est-il faible ? Quand est-ce grand ? Expliquez à l'aide d'un schéma approprié.

(d) Quel est l'effet des attractions intermoléculaires sur la valeur de Z ? Dans quelles conditions cet effet est-il faible ? Quand est-ce grand ? Expliquez à l'aide d'un schéma approprié.

(e) En général, dans quelles conditions de température vous attendriez-vous à ce que Z présente les plus grands écarts par rapport au Z pour un gaz idéal ?