6.3 : Développement de la théorie quantique
- Page ID
- 193932
- Étendre également à la matière le concept de dualité onde-particule observé dans le rayonnement électromagnétique
- Comprendre l'idée générale de la description mécanique quantique des électrons dans un atome, et comprendre qu'elle utilise la notion de fonctions d'onde tridimensionnelles, ou orbitales, qui définissent la distribution des probabilités pour trouver un électron dans une partie particulière de l'espace
- Énumérer et décrire les traits des quatre nombres quantiques qui constituent la base pour spécifier complètement l'état d'un électron dans un atome
Le modèle de Bohr expliquait les données expérimentales pour l'atome d'hydrogène et a été largement accepté, mais il a également soulevé de nombreuses questions. Pourquoi les électrons tournaient-ils uniquement à des distances fixes définies par un seul nombre quantique n = 1, 2, 3, etc., mais jamais entre les deux ? Pourquoi le modèle a-t-il si bien fonctionné pour décrire l'hydrogène et les ions à un électron, mais n'a-t-il pas pu prédire correctement le spectre d'émission de l'hélium ou de tout autre atome plus gros ? Pour répondre à ces questions, les scientifiques ont dû revoir complètement leur conception de la matière.
Comportement dans le monde microscopique
Nous savons comment se comporte la matière dans le monde macroscopique : les objets suffisamment grands pour être vus à l'œil nu suivent les règles de la physique classique. Une boule de billard qui se déplace sur une table se comporte comme une particule : elle continue en ligne droite, sauf si elle entre en collision avec une autre balle ou le coussin de la table, ou si elle est soumise à une autre force (telle que la friction). La balle a une position et une vitesse bien définies (ou un moment bien défini\(p = mv\), défini par la masse\(m\) et la vitesse\(v\)) à tout moment. En d'autres termes, la balle se déplace selon une trajectoire classique. C'est le comportement typique d'un objet classique.
Lorsque les ondes interagissent les unes avec les autres, elles présentent des modèles d'interférence qui ne sont pas visibles par des particules macroscopiques telles que la boule de billard. Par exemple, les ondes en interaction à la surface de l'eau peuvent produire des modèles d'interférence similaires à ceux illustrés sur la figure\(\PageIndex{1}\). Il s'agit d'un cas de comportement des ondes à l'échelle macroscopique, et il est clair que les particules et les ondes sont des phénomènes très différents dans le domaine macroscopique.

À mesure que les progrès technologiques ont permis aux scientifiques de sonder le monde microscopique plus en détail, il est devenu de plus en plus évident dans les années 1920 que les très petits morceaux de matière suivent un ensemble de règles différent de celles que nous observons pour les objets de grande taille. La séparation incontestable des ondes et des particules n'était plus le cas dans le monde microscopique.
Louis de Broglie a été l'une des premières personnes à prêter attention au comportement particulier du monde microscopique. Il a posé la question suivante : si le rayonnement électromagnétique peut avoir le caractère de particules, les électrons et autres particules submicroscopiques peuvent-ils présenter un caractère ondulatoire ? Dans sa thèse de doctorat de 1925, de Broglie a étendu la dualité onde-particule de la lumière qu'Einstein a utilisée pour résoudre le paradoxe de l'effet photoélectrique aux particules matérielles. Il a prédit qu'une particule ayant une masse m et une vitesse v (c'est-à-dire avec un moment linéaire p) devrait également présenter le comportement d'une onde avec une valeur de longueur d'onde λ, donnée par cette expression dans laquelle h est la constante de Planck familière
\[\lambda=\dfrac{h}{mv}=\dfrac{h}{p} \label{6.4.1} \]
C'est ce qu'on appelle la longueur d'onde de Broglie. Contrairement aux autres valeurs de λ discutées dans ce chapitre, la longueur d'onde de de Broglie est une caractéristique des particules et d'autres corps, et non du rayonnement électromagnétique (notez que cette équation implique la vitesse [v, m/s], et non la fréquence [v/Hz]). Bien que ces deux symboles soient identiques, ils signifient des choses très différentes). Alors que Bohr avait postulé que l'électron était une particule orbitant autour du noyau sur des orbites quantifiées, de Broglie a soutenu que l'hypothèse de quantification de Bohr peut être expliquée si l'électron n'est pas considéré comme une particule, mais plutôt comme une onde circulaire stationnaire telle que seul un nombre entier de longueurs d'onde pourrait s'adapter exactement à l'orbite (Figure\(\PageIndex{2}\)).
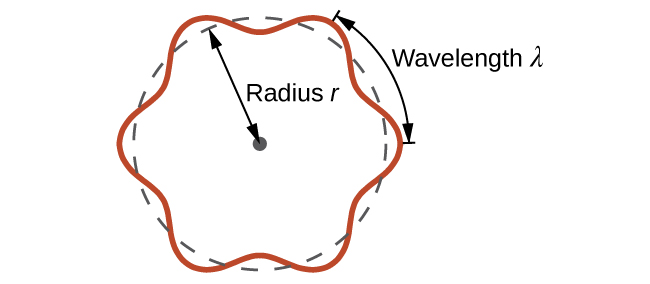
Pour une orbite circulaire de rayon r, la circonférence est de 2πr, et donc la condition de Broglie est la suivante :
\[2πr=nλ \label{6.4.3} \]
avec\(n=1,2,3,...\)
Puisque l'expression de de Broglie relie la longueur d'onde à l'impulsion et, par conséquent, à la vitesse, cela implique :
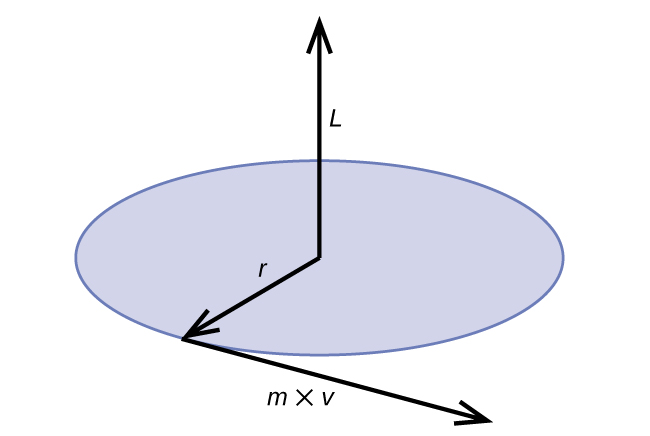
\[2πr=nλ=\dfrac{nh}{p}=\dfrac{nh}{mv}=\dfrac{nhr}{mvr}=\dfrac{nhr}{L} \label{6.4.3b} \]
Cette expression peut être réarrangée pour donner la formule de Bohr pour la quantification du moment cinétique :
\[L=\dfrac{nh}{2π}=n \hbar \label{6.4.4} \]
Le moment cinétique classique L pour un mouvement circulaire est égal au produit du rayon du cercle et du moment de la particule en mouvement p.
\[L=rp=rmv \;\;\; \text{(for a circular motion)} \label{6.4.5} \]
Peu de temps après que de Broglie ait proposé la nature ondulatoire de la matière, deux scientifiques des laboratoires Bell, C. J. Davisson et L. H. Germer, ont démontré expérimentalement que les électrons peuvent présenter un comportement ondulatoire en montrant un schéma d'interférence pour les électrons se déplaçant dans un motif atomique dans un cristal. Les couches atomiques régulièrement espacées ont servi de fentes, comme celles utilisées dans d'autres expériences d'interférence. Comme l'espacement entre les couches servant de fentes doit être similaire à la longueur d'onde de l'onde testée pour qu'un motif d'interférence se forme, Davisson et Germer ont utilisé une cible de nickel cristallin pour leurs « fentes », car l'espacement des atomes au sein du réseau était à peu près le même que le Broglie les longueurs d'onde des électrons qu'ils ont utilisés. La figure\(\PageIndex{4}\) montre un schéma d'interférence.
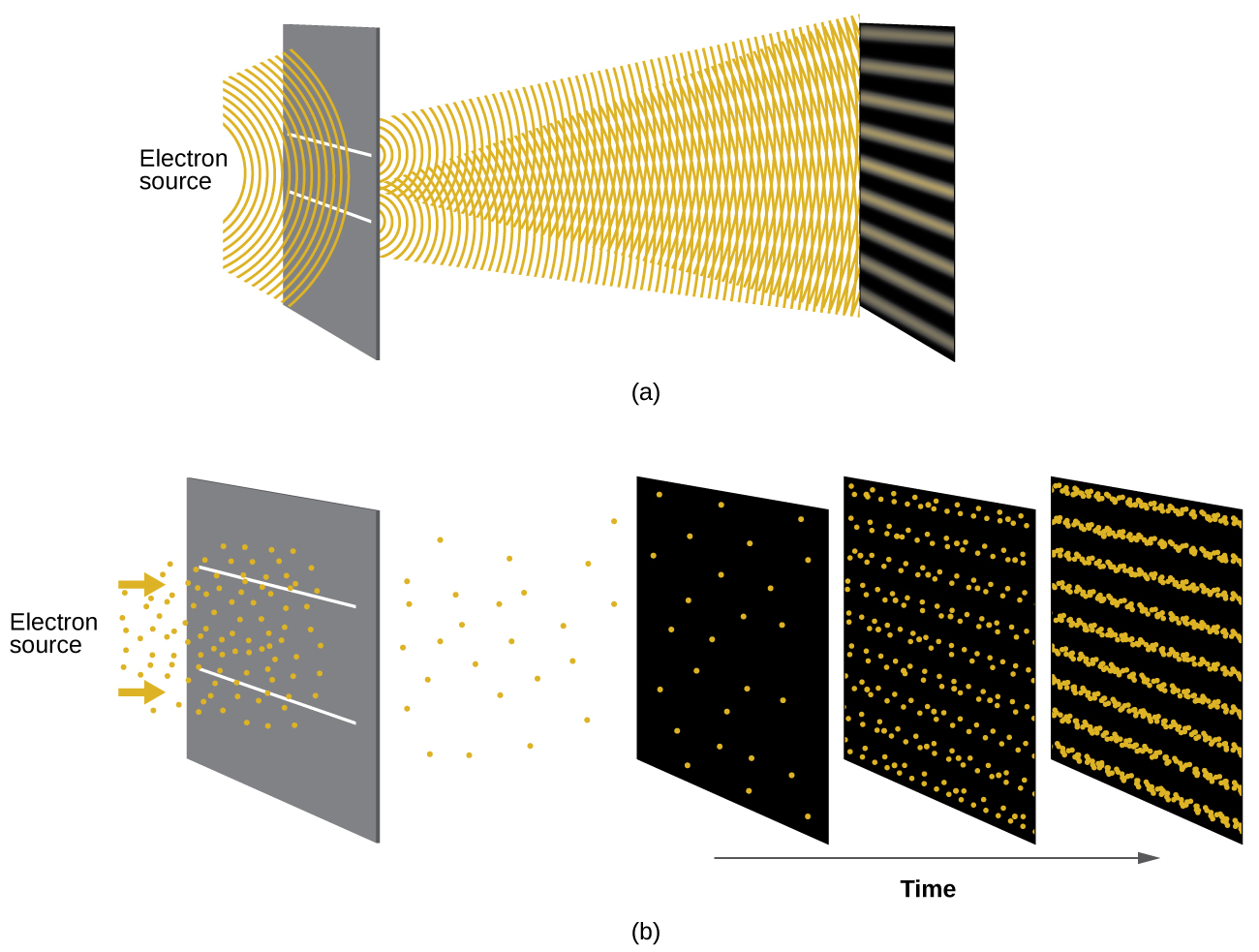
La dualité onde-particule de la matière peut être observée en observant ce qui se passe si des collisions d'électrons sont enregistrées sur une longue période. Au départ, lorsque seuls quelques électrons ont été enregistrés, ils se comportent clairement comme des particules, étant arrivés en petits paquets localisés qui semblent être aléatoires. Au fur et à mesure que de plus en plus d'électrons arrivaient et étaient enregistrés, un schéma d'interférence clair, caractéristique du comportement ondulatoire, est apparu. Il semble donc que, bien que les électrons soient de petites particules localisées, leur mouvement ne suit pas les équations de mouvement sous-entendues par la mécanique classique, mais qu'il est régi par une sorte d'équation d'onde qui régit une distribution de probabilité même pour le mouvement d'un seul électron. Ainsi, la dualité onde-particule observée pour la première fois avec les photons est en fait un comportement fondamental intrinsèque à toutes les particules quantiques.
Si un électron se déplace à une vitesse de 1 000 × 10 7 m s —1 et a une masse de 9,109 × 10 —28 g, quelle est sa longueur d'onde ?
Solution
Nous pouvons utiliser l'équation de Broglie pour résoudre ce problème, mais nous devons d'abord effectuer une conversion unitaire de la constante de Planck. Vous avez appris plus tôt que 1 J = 1 kg m 2 /s 2. Ainsi, on peut écrire h = 6,626 × 10 —34 J s comme étant 6,626 × 10 —34 kg m 2 /s.
\[\begin{align*} λ&=\dfrac{h}{mv} \\[4pt] &=\mathrm{\dfrac{6.626×10^{−34}\:kg\: m^2/s}{(9.109×10^{−31}\:kg)(1.000×10^7\:m/s)}}\\[4pt] &= \mathrm{7.274×10^{−11}\:m} \end{align*} \nonumber \]
Cette valeur est faible, mais elle est nettement supérieure à la taille d'un électron dans la vue classique (particule). Cette taille est du même ordre de grandeur que la taille d'un atome. Cela signifie que le comportement des ondes électroniques sera perceptible dans un atome.
Calculez la longueur d'onde d'une balle de softball d'une masse de 100 g se déplaçant à une vitesse de 35 m s —1, en supposant qu'elle puisse être modélisée sous la forme d'une particule unique.
- Réponse
-
1,9 × 10 —34 m.
On ne pense jamais qu'une balle de softball lancée ait une longueur d'onde, puisque cette longueur d'onde est si petite qu'elle est impossible à détecter pour nos sens ou pour aucun instrument connu (à proprement parler, la longueur d'onde d'une vraie balle de baseball correspondrait aux longueurs d'onde de ses atomes et molécules constitutifs, qui, bien que beaucoup plus grandes) que cette valeur, serait encore microscopiquement minuscule). La longueur d'onde de Broglie n'est appréciable que pour les matières qui ont une masse très faible et/ou une vitesse très élevée.
Werner Heisenberg a examiné les limites de la précision avec laquelle nous pouvons mesurer les propriétés d'un électron ou d'autres particules microscopiques. Il a déterminé qu'il existe une limite fondamentale à la précision avec laquelle on peut mesurer simultanément la position et la quantité de mouvement d'une particule. Plus nous mesurons la quantité de mouvement d'une particule avec précision, moins nous pouvons déterminer avec précision sa position à ce moment-là, et vice versa. Cela se résume dans ce que nous appelons aujourd'hui le principe d'incertitude de Heisenberg : il est fondamentalement impossible de déterminer simultanément et exactement à la fois la quantité de mouvement et la position d'une particule. Pour une particule de masse m se déplaçant avec une vitesse v x dans la direction x (ou de manière équivalente avec le moment p x), le produit de l'incertitude sur la position, Δ x, et de l'incertitude sur la quantité de mouvement, Δ p x, doit être supérieur ou égal à\(\dfrac{ℏ}{2}\) (rappelons que\(ℏ=\dfrac{h}{2π}\) la valeur de la constante de Planck divisée par 2 π).
\[Δx×Δp_x=(Δx)(mΔv)≥\dfrac{ℏ}{2} \nonumber \]
Cette équation nous permet de calculer la limite de la précision avec laquelle nous pouvons connaître à la fois la position simultanée d'un objet et sa quantité de mouvement. Par exemple, si nous améliorons notre mesure de la position d'un électron de telle sorte que l'incertitude de la position (Δ x) ait une valeur de, disons, 1 pm (10 —12 m, environ 1 % du diamètre d'un atome d'hydrogène), alors notre détermination de sa quantité de mouvement doit avoir une incertitude d'une valeur d'au moins
\[\left [Δp=mΔv=\dfrac{h}{(2Δx)} \right ]=\mathrm{\dfrac{(1.055×10^{−34}\:kg\: m^2/s)}{(2×1×10^{−12}\:m)}=5×10^{−23}\:kg\: m/s.} \nonumber \]
La valeur de n'étant pas grande, l'incertitude quant à la position ou à l'impulsion d'un objet macroscopique tel qu'une balle de baseball est trop insignifiante pour être observée. Cependant, la masse d'un objet microscopique tel qu'un électron est suffisamment petite pour que l'incertitude puisse être grande et significative.
Il convient de noter que le principe d'incertitude de Heisenberg ne se limite pas aux incertitudes de position et de momentum, mais qu'il relie également d'autres variables dynamiques. Par exemple, lorsqu'un atome absorbe un photon et passe d'un état énergétique à un autre, l'incertitude quant à l'énergie et l'incertitude quant au temps requis pour la transition sont liées de la même manière, comme Δ E Δ t ≥\(\dfrac{ℏ}{2}\). Comme nous le verrons plus loin, même les composantes vectorielles du moment cinétique ne peuvent pas toutes être spécifiées exactement simultanément.
Le principe de Heisenberg impose des limites ultimes à ce que l'on peut connaître en science. On peut démontrer que le principe d'incertitude est une conséquence de la dualité onde-particule, qui est au cœur de ce qui distingue la théorie quantique moderne de la mécanique classique. Rappelons que les équations du mouvement obtenues à partir de la mécanique classique sont des trajectoires dans lesquelles, à tout instant, la position et la quantité de mouvement d'une particule peuvent être déterminées avec précision. Le principe d'incertitude de Heisenberg implique qu'une telle vision est intenable dans le domaine microscopique et qu'il existe des limites fondamentales qui régissent le mouvement des particules quantiques. Cela ne signifie pas que les particules microscopiques ne se déplacent pas dans des trajectoires, mais simplement que les mesures des trajectoires sont limitées dans leur précision. Dans le domaine de la mécanique quantique, les mesures introduisent des changements dans le système observé.
Le modèle mécanique quantique d'un atome
Peu de temps après que de Broglie ait publié ses idées selon lesquelles l'électron d'un atome d'hydrogène pourrait être mieux considéré comme une onde stationnaire circulaire plutôt que comme une particule se déplaçant sur des orbites circulaires quantifiées, comme l'avait soutenu Bohr, Erwin Schrödinger a étendu les travaux de de Broglie en incorporant la relation de Broglie dans un équation d'onde, dérivant ce que l'on appelle aujourd'hui l'équation de Schrödinger. Lorsque Schrödinger a appliqué son équation à des atomes semblables à l'hydrogène, il a pu reproduire l'expression de Bohr pour l'énergie et, par conséquent, la formule de Rydberg régissant les spectres de l'hydrogène, et il l'a fait sans avoir à invoquer les hypothèses de Bohr concernant les états stationnaires et les orbites quantifiées, les moments angulaires et les énergies ; la quantification dans la théorie de Schrödinger était une conséquence naturelle des mathématiques sous-jacentes à l'équation des vagues. Comme de Broglie, Schrödinger a d'abord considéré l'électron contenu dans l'hydrogène comme une onde physique plutôt que comme une particule, mais lorsque de Broglie a pensé à l'électron en termes d'ondes circulaires stationnaires, Schrödinger a correctement pensé en termes d'ondes stationnaires tridimensionnelles, ou fonctions d'onde, représenté par la lettre grecque psi, ψ. Quelques années plus tard, Max Born a proposé une interprétation de la fonction d'onde φ qui est toujours acceptée aujourd'hui : les électrons sont toujours des particules, de sorte que les ondes représentées par φ ne sont pas des ondes physiques mais des amplitudes de probabilité complexes. Le carré de l'amplitude d'une fonction d'onde\(∣ψ∣^2\) décrit la probabilité que la particule quantique soit présente à proximité d'un certain endroit dans l'espace. Cela signifie que les fonctions d'onde peuvent être utilisées pour déterminer la distribution de la densité de l'électron par rapport au noyau d'un atome. Dans sa forme la plus générale, l'équation de Schrödinger peut être écrite comme suit :
\[\hat{H}ψ=Eψ \nonumber \]
\(\hat{H}\)est l'opérateur hamiltonien, un ensemble d'opérations mathématiques représentant l'énergie totale de la particule quantique (comme un électron dans un atome), φ est la fonction d'onde de cette particule qui peut être utilisée pour déterminer la distribution spéciale de la probabilité de trouver la particule, et \(E\)est la valeur réelle de l'énergie totale de la particule.
Les travaux de Schrödinger, ainsi que ceux de Heisenberg et de nombreux autres scientifiques qui suivent leurs traces, sont généralement appelés mécanique quantique.
Comprendre la théorie quantique des électrons dans les atomes
L'objectif de cette section est de comprendre les orbitales des électrons (localisation des électrons dans les atomes), leurs différentes énergies et d'autres propriétés. L'utilisation de la théorie quantique permet de mieux comprendre ces sujets. Ces connaissances sont un précurseur de la liaison chimique.
Comme cela a été décrit précédemment, les électrons dans les atomes ne peuvent exister qu'à des niveaux d'énergie discrets, mais pas entre eux. On dit que l'énergie d'un électron dans un atome est quantifiée, c'est-à-dire qu'elle ne peut être égale qu'à certaines valeurs spécifiques et peut sauter d'un niveau d'énergie à un autre sans passer en douceur ou rester entre ces niveaux.
Les niveaux d'énergie sont marqués par une valeur n, où n = 1, 2, 3,... D'une manière générale, l'énergie d'un électron dans un atome est plus grande pour des valeurs de n. Ce nombre, n, est appelé le nombre quantique principal. Le nombre quantique principal définit l'emplacement du niveau d'énergie. Il s'agit essentiellement du même concept que le n dans la description de l'atome de Bohr. Un autre nom pour le nombre quantique principal est le numéro de coque. Les coquilles d'un atome peuvent être considérées comme des cercles concentriques émanant du noyau. Les électrons qui appartiennent à une couche spécifique sont les plus susceptibles de se trouver dans la zone circulaire correspondante. Plus on s'éloigne du noyau, plus le nombre de coquilles est élevé et donc plus le niveau d'énergie est élevé (Figure\(\PageIndex{5}\)). Les protons chargés positivement dans le noyau stabilisent les orbitales électroniques par attraction électrostatique entre les charges positives des protons et les charges négatives des électrons. Ainsi, plus l'électron est éloigné du noyau, plus son énergie est importante.
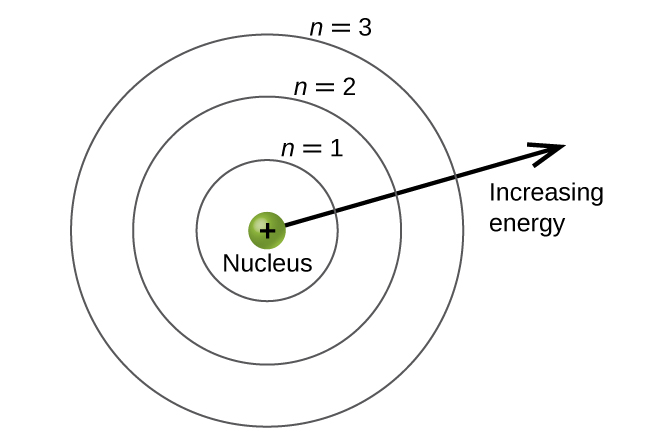
Ce modèle de mécanique quantique de la localisation des électrons dans un atome peut être utilisé pour examiner les transitions électroniques, c'est-à-dire les événements lorsqu'un électron passe d'un niveau d'énergie à un autre. Si la transition se fait vers un niveau d'énergie plus élevé, l'énergie est absorbée et le changement d'énergie a une valeur positive. Pour obtenir la quantité d'énergie nécessaire à la transition vers un niveau d'énergie supérieur, un photon est absorbé par l'atome. Une transition vers un niveau d'énergie inférieur implique une libération d'énergie, et le changement d'énergie est négatif. Ce processus s'accompagne de l'émission d'un photon par l'atome. L'équation suivante résume ces relations et est basée sur l'atome d'hydrogène :
\[ \begin{align*} ΔE &=E_\ce{final}−E_\ce{initial} \\[4pt] &=−2.18×10^{−18}\left(\dfrac{1}{n^2_\ce f}−\dfrac{1}{n^2_\ce i}\right)\:\ce J \end{align*} \nonumber \]
Les valeurs n f et n i sont les états énergétiques final et initial de l'électron.
Le nombre quantique principal est l'un des trois nombres quantiques utilisés pour caractériser une orbitale. Une orbitale atomique, distincte d'une orbite, est une région générale d'un atome à l'intérieur de laquelle un électron est le plus susceptible de résider. Le modèle de mécanique quantique précise la probabilité de trouver un électron dans l'espace tridimensionnel autour du noyau et est basé sur des solutions de l'équation de Schrödinger. De plus, le nombre quantique principal définit l'énergie d'un électron dans un atome d'hydrogène ou similaire à l'hydrogène ou un ion (un atome ou un ion avec un seul électron) et la région générale dans laquelle se situent les niveaux d'énergie discrets des électrons dans des atomes et des ions à plusieurs électrons.
Un autre nombre quantique est l, le nombre quantique du moment cinétique. C'est un entier qui définit la forme de l'orbitale et prend les valeurs, l = 0, 1, 2,..., n — 1. Cela signifie qu'une orbitale avec n = 1 ne peut avoir qu'une seule valeur de l, l = 0, alors que n = 2 permet l = 0 et l = 1, et ainsi de suite. Le nombre quantique principal définit la taille et l'énergie générales de l'orbite. La valeur l indique la forme de l'orbitale. Les orbitales ayant la même valeur de l forment une sous-couche. De plus, plus le nombre quantique du moment cinétique est élevé, plus le moment cinétique d'un électron sur cette orbitale est élevé.
Les orbitales avec l = 0 sont appelées orbitales s (ou sous-couches s). La valeur l = 1 correspond aux orbitales p. Pour un n donné, les orbitales p constituent une sous-couche p (par exemple, 3 p si n = 3). Les orbitales avec l = 2 sont appelées orbitales d, suivies des orbitales f-, g- et h- pour l = 3, 4, 5, et il y a des valeurs plus élevées que nous ne prendrons pas en compte.
À certaines distances du noyau, la densité de probabilité de trouver un électron situé sur une orbitale particulière est nulle. En d'autres termes, la valeur de la fonction d'onde φ est nulle à cette distance pour cette orbitale. Une telle valeur de rayon r est appelée nœud radial. Le nombre de nœuds radiaux dans une orbitale est n — l — 1.
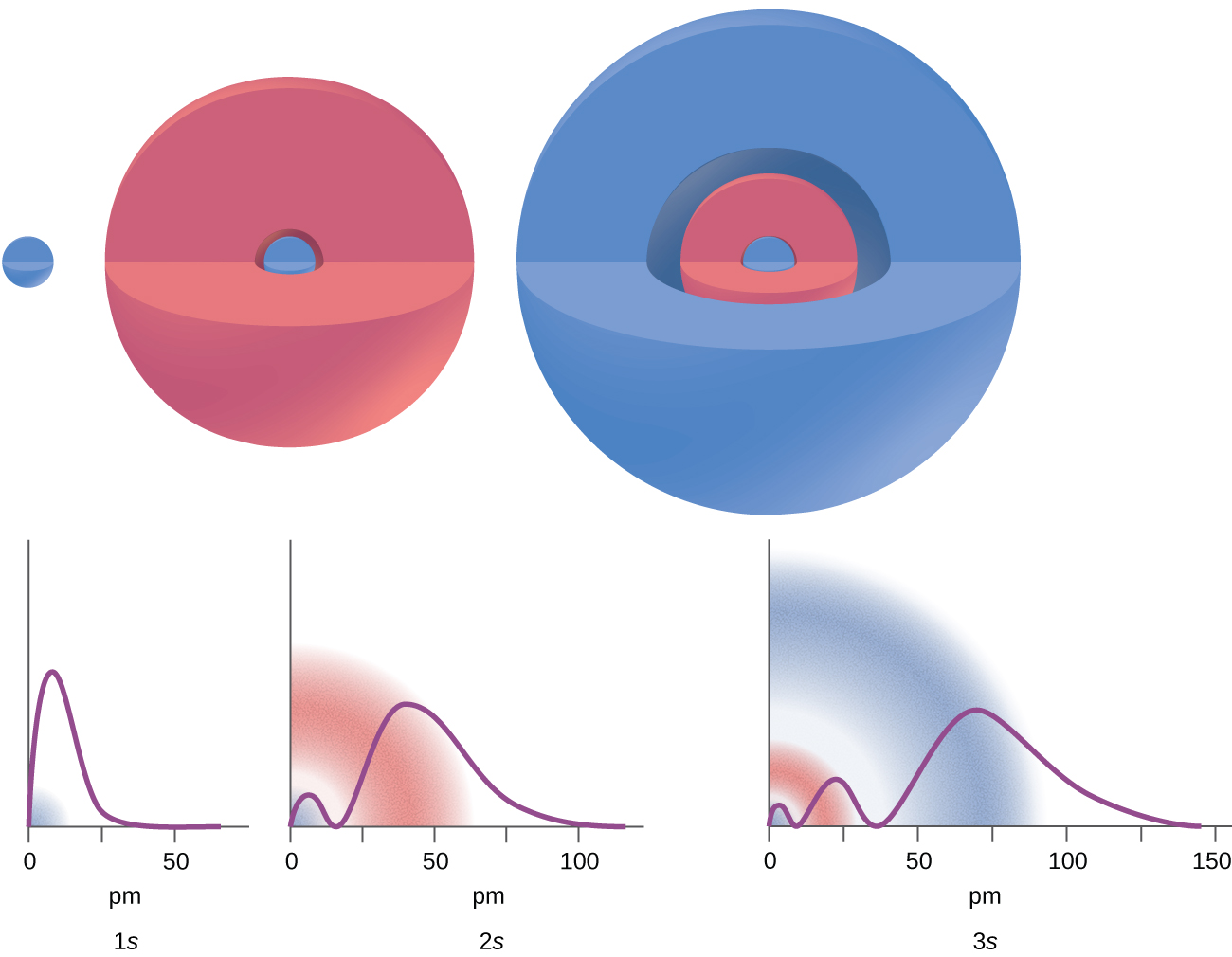
Examinez les exemples de la figure\(\PageIndex{7}\). Les orbitales représentées sont du type s, donc l = 0 pour toutes. Les graphes des densités de probabilité montrent qu'il y a 1 — 0 — 1 = 0 endroits où la densité est nulle (nœuds) pendant 1 s (n = 1), 2 — 0 — 1 = 1 nœud pendant 2 s et 3 — 0 — 1 = 1 = 2 nœuds pour les orbitales de 3 s.
La distribution de densité électronique de la sous-couche s est sphérique et la sous-couche p a une forme d'haltère. Les orbitales d et f sont plus complexes. Ces formes représentent les régions tridimensionnelles dans lesquelles l'électron est susceptible de se trouver.
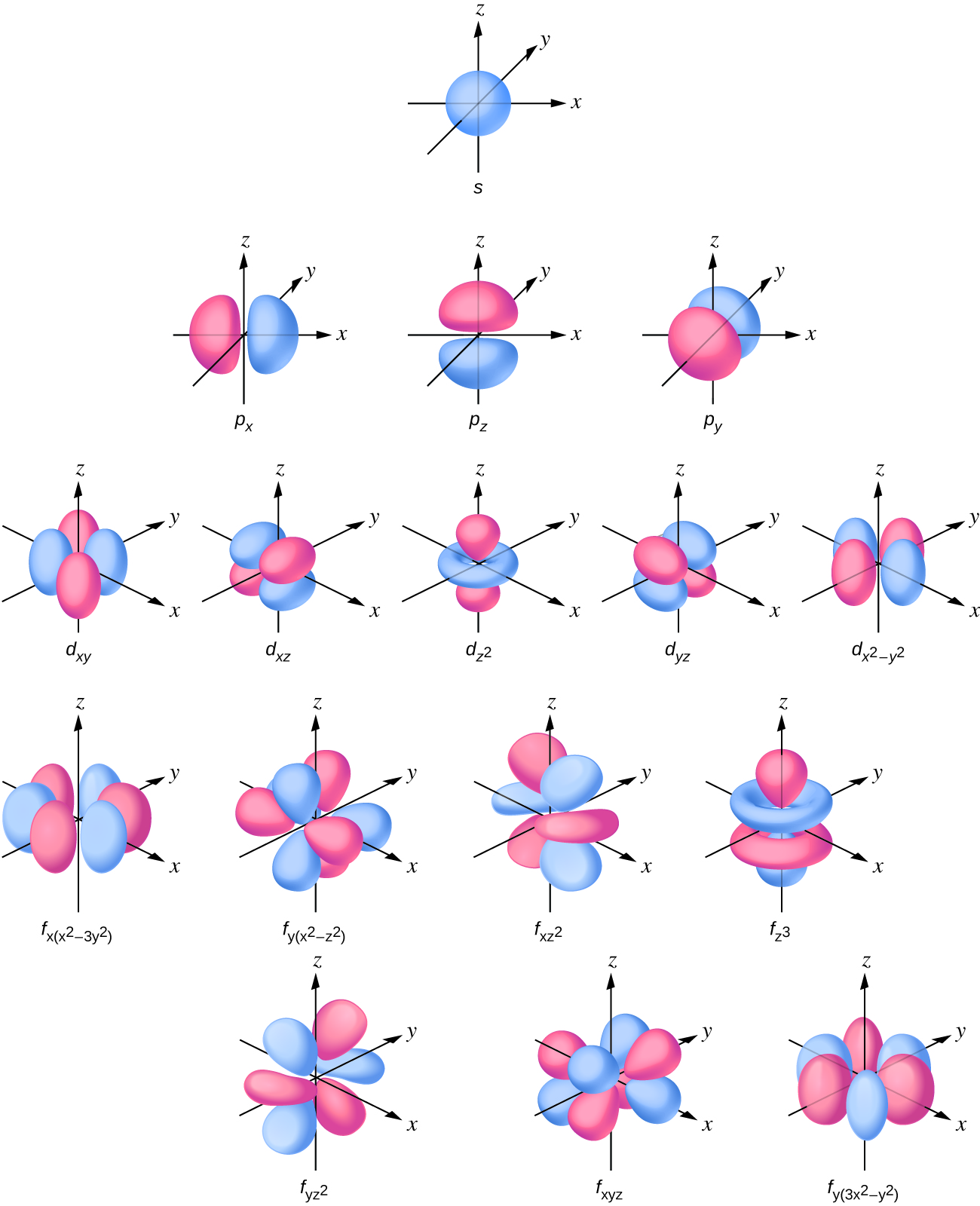
Si un électron possède un moment cinétique (l ↓ 0), alors ce vecteur peut pointer dans différentes directions. De plus, la composante z du moment cinétique peut avoir plusieurs valeurs. Cela signifie que si un champ magnétique est appliqué dans la direction z, les orbitales ayant des valeurs différentes de la composante z du moment cinétique auront des énergies différentes résultant de l'interaction avec le champ. Le nombre quantique magnétique, appelé m l, indique la composante z du moment cinétique pour une orbitale donnée. Par exemple, pour une orbitale s, l = 0, et la seule valeur de m l est zéro. Pour les orbitales p, l = 1 et m l peut être égal à —1, 0 ou +1. D'une manière générale, m l peut être égal à — l, — (l — 1),..., —1, 0, +1,..., (l — 1), l. Le nombre total d'orbitales possibles ayant la même valeur de l (une sous-couche) est de 2 l+1. Ainsi, il y a une orbitale s pour ml = 0, il y a trois orbitales p pour ml = 1, cinq orbitales d pour ml = 2, sept orbitales f pour ml = 3, et ainsi de suite. Le nombre quantique principal définit la valeur générale de l'énergie électronique. Le nombre quantique du moment cinétique détermine la forme de l'orbitale. Et le nombre quantique magnétique indique l'orientation de l'orbitale dans l'espace, comme on peut le voir sur la figure\(\PageIndex{7}\).
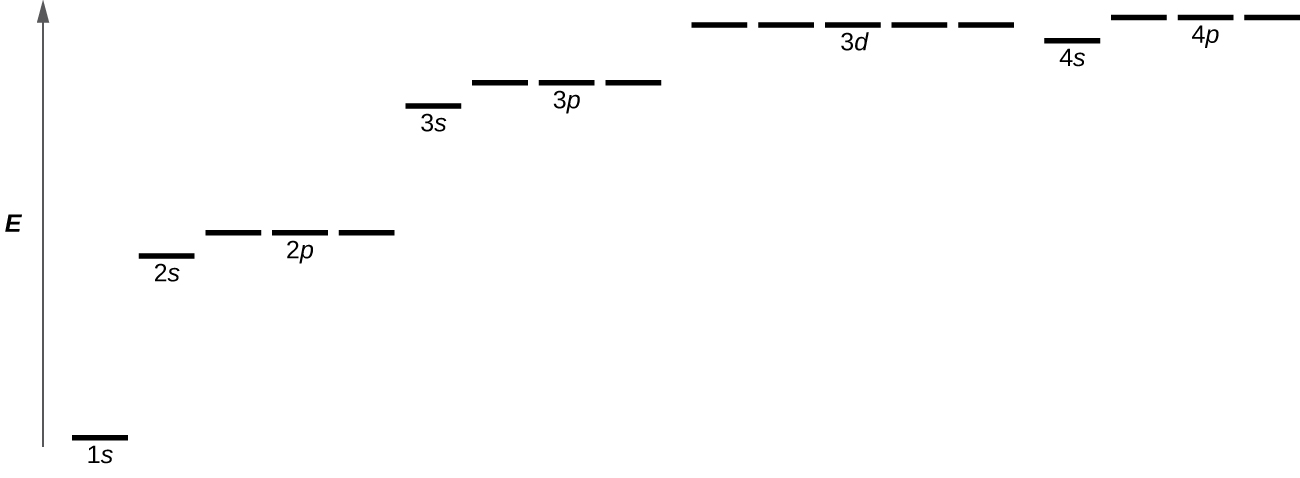
La figure\(\PageIndex{8}\) illustre les niveaux d'énergie pour différentes orbitales. Le nombre précédant le nom de l'orbite (par exemple 2 s, 3 p, etc.) représente le nombre quantique principal, n. La lettre du nom de l'orbite définit la sous-couche avec un nombre quantique de moment cinétique spécifique l = 0 pour les orbitales s, 1 pour les orbitales p, 2 pour les orbitales d. Enfin, il existe plusieurs orbitales possibles pour l ≥ 1, chacune correspondant à une valeur spécifique de m l. Dans le cas d'un atome d'hydrogène ou d'un ion à un électron (comme He +, Li 2 +, etc.), les énergies de toutes les orbitales ayant le même n sont les mêmes. C'est ce qu'on appelle une dégénérescence, et les niveaux d'énergie pour le même nombre quantique principal, n, sont appelés niveaux d'énergie dégénérés. Cependant, dans les atomes contenant plus d'un électron, cette dégénérescence est éliminée par les interactions électron—électron, et les orbitales appartenant à différentes sous-couches ont des énergies différentes. Les orbitales au sein d'une même sous-couche (par exemple ns, np, nd, nf, telles que 2 p, 3 s) sont toujours dégénérées et ont la même énergie.
Bien que les trois nombres quantiques discutés dans les paragraphes précédents fonctionnent bien pour décrire les orbitales électroniques, certaines expériences ont montré qu'ils n'étaient pas suffisants pour expliquer tous les résultats observés. Il a été démontré dans les années 1920 que lorsque les spectres des raies d'hydrogène sont examinés à très haute résolution, certaines raies ne sont pas en fait des pics uniques mais plutôt des paires de raies rapprochées. C'est ce que l'on appelle la structure fine du spectre, et cela implique qu'il existe de petites différences supplémentaires dans les énergies des électrons, même lorsqu'ils sont situés sur la même orbitale. Ces observations ont amené Samuel Goudsmit et George Uhlenbeck à proposer que les électrons possèdent un quatrième nombre quantique. Ils l'ont appelé le nombre quantique de spin, ou m s.
Les trois autres nombres quantiques, n, l et m l, sont des propriétés d'orbitales atomiques spécifiques qui définissent également dans quelle partie de l'espace un électron est le plus susceptible de se trouver. Les orbitales sont le résultat de la résolution de l'équation de Schrödinger pour les électrons dans les atomes. Le spin des électrons est une propriété différente. Il s'agit d'un phénomène complètement quantique qui n'a aucun analogue dans le domaine classique. De plus, elle ne peut pas être dérivée de la résolution de l'équation de Schrödinger et n'est pas liée aux coordonnées spatiales normales (telles que les coordonnées cartésiennes x, y et z). Le spin électronique décrit une « rotation » ou une « rotation » intrinsèque d'un électron. Chaque électron agit comme un minuscule aimant ou un petit objet rotatif avec un moment cinétique, même si cette rotation ne peut pas être observée en termes de coordonnées spatiales.
L'amplitude du spin global de l'électron ne peut avoir qu'une seule valeur, et un électron ne peut « tourner » que dans l'un des deux états quantifiés. L'un est appelé état α, la composante z du spin étant dans la direction positive de l'axe z. Cela correspond au nombre quantique de spin\(m_s=\dfrac{1}{2}\). L'autre est appelé état β, la composante z du spin étant négative et\(m_s=−\dfrac{1}{2}\). Tout électron, quelle que soit l'orbite atomique dans laquelle il se trouve, ne peut avoir qu'une seule de ces deux valeurs du nombre quantique de spin. Les énergies des électrons ayant\(m_s=−\dfrac{1}{2}\) et\(m_s=\dfrac{1}{2}\) sont différentes si un champ magnétique externe est appliqué.
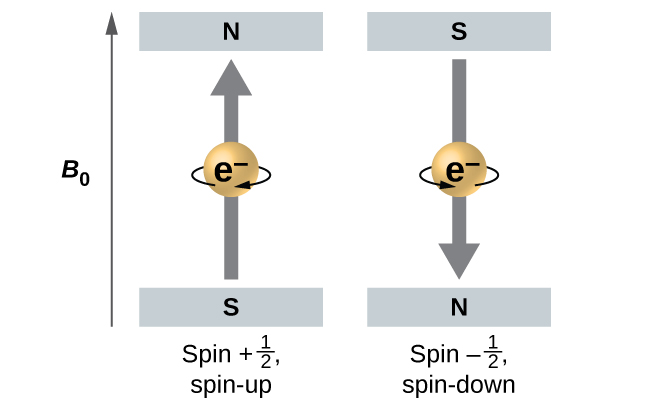
La figure\(\PageIndex{9}\) illustre ce phénomène. Un électron agit comme un minuscule aimant. Son moment est dirigé vers le haut (dans la direction positive de l'axe z) pour le nombre quantique de\(\dfrac{1}{2}\) spin et vers le bas (dans la direction z négative) pour le nombre quantique de spin de\(−\ce{1/2}\). Un aimant a une énergie plus faible si son moment magnétique est aligné avec le champ magnétique externe (l'électron gauche) et une énergie plus élevée lorsque le moment magnétique est opposé au champ appliqué. C'est pourquoi un électron avec\(m_s=\dfrac{1}{2}\) a une énergie légèrement plus faible dans un champ externe dans la direction z positive, et un électron avec\(m_s=−\dfrac{1}{2}\) une énergie légèrement plus élevée dans le même champ. Cela est vrai même pour un électron occupant la même orbitale dans un atome. Une raie spectrale correspondant à une transition pour des électrons provenant de la même orbitale mais ayant des nombres quantiques de spin différents possède deux valeurs d'énergie possibles ; ainsi, la raie du spectre présentera une fine division de structure.
Le principe d'exclusion de Pauli
Un électron dans un atome est complètement décrit par quatre nombres quantiques : n, l, m l et m s. Les trois premiers nombres quantiques définissent l'orbitale et le quatrième nombre quantique décrit la propriété intrinsèque des électrons appelée spin. Le physicien autrichien Wolfgang Pauli a formulé un principe général qui fournit la dernière information dont nous avons besoin pour comprendre le comportement général des électrons dans les atomes. Le principe d'exclusion de Pauli peut être formulé comme suit : Deux électrons d'un même atome ne peuvent pas avoir exactement le même ensemble des quatre nombres quantiques. Cela signifie que les électrons peuvent partager la même orbitale (le même ensemble de nombres quantiques n, l et m l), mais uniquement si leurs nombres quantiques de spin m s ont des valeurs différentes. Comme le nombre quantique de spin ne peut avoir que deux valeurs\(\left(±\dfrac{1}{2}\right)\), pas plus de deux électrons ne peuvent occuper la même orbitale (et si deux électrons sont situés sur la même orbitale, ils doivent avoir des spins opposés). Par conséquent, toute orbite atomique ne peut être peuplée que par zéro, un ou deux électrons. Les propriétés et la signification des nombres quantiques d'électrons dans les atomes sont brièvement résumées dans le tableau\(\PageIndex{1}\).
| Nom | symbole | Valeurs autorisées | Signification physique |
|---|---|---|---|
| nombre quantique principal | n | 1, 2, 3, 4,... | coque, la région générale de la valeur de l'énergie d'un électron sur l'orbite |
| moment cinétique ou nombre quantique azimutal | l | 0 ≤ l ≤ n — 1 | sous-coque, la forme de l'orbite |
| nombre quantique magnétique | m l | — l ≤ m l ≤ l | orientation de l'orbite |
| nombre quantique de spin | m s | \(\dfrac{1}{2},\:−\dfrac{1}{2}\) | direction du « spin » quantique intrinsèque de l'électron |
Indiquez le nombre de sous-couches, le nombre d'orbitales dans chaque sous-couche et les valeurs de l et m l pour les orbitales de la couche n = 4 d'un atome.
Solution
Pour n = 4, l peut avoir des valeurs de 0, 1, 2 et 3. Ainsi, les sous-couches s, p, d et f se trouvent dans la couche n = 4 d'un atome. Pour l = 0 (le sous-shell s), m l ne peut être que 0. Il n'y a donc qu'une seule orbitale de 4 s. Pour l = 1 (orbitales de type p), m peut avoir des valeurs de -1, 0, +1, donc nous trouvons trois orbitales 4 p. Pour l = 2 (orbitales de type d), m l peut avoir des valeurs de —2, —1, 0, +1, +2, donc nous avons cinq orbitales 4 d. Lorsque l = 3 (orbitales de type f), m l peut avoir des valeurs de —3, —2, —1, 0, +1, +2, +3, et nous pouvons avoir sept orbitales 4 f. Ainsi, nous trouvons un total de 16 orbitales dans la couche n = 4 d'un atome.
Identifiez la sous-couche dans laquelle se trouvent des électrons ayant les nombres quantiques suivants :
- n = 3, l = 1 ;
- n = 5, l = 3 ;
- n = 2, l = 0.
- Répondez à une
-
3 p.
- Réponse b
-
5 f
- Réponse c
-
2
Calculez le nombre maximum d'électrons pouvant occuper une couche avec (a) n = 2, (b) n = 5 et (c) n comme variable. Notez que vous ne regardez que les orbitales avec la valeur n spécifiée, pas celles à des énergies plus faibles.
Solution
(a) Lorsque n = 2, il existe quatre orbitales (une seule orbitale de 2 s et trois orbitales étiquetées 2 p). Ces quatre orbitales peuvent contenir huit électrons.
(b) Lorsque n = 5, il y a cinq sous-couches d'orbitales que nous devons additionner :
& \ phantom {+} \ textrm {1 étiquetée orbitale} 5s \ \
& \ phantom {+} \ textrm {3 orbitales étiquetées} 5p \ \
& \ phantom {+} \ textrm {5 orbitales étiquetées} 5d \ \
& \ phantom {+} \ textrm {7 orbitales étiquetées} 5f \ \
& \ soulignement {+ \ texte {9 orbitales étiquetées} 5g} \ \
& \, \ textrm {25 orbitales au total}
\ end {align*} \)
Encore une fois, chaque orbitale contient deux électrons, donc 50 électrons peuvent entrer dans cette coque.
(c) Le nombre d'orbitales dans toute couche n sera égal à n 2. Il peut y avoir jusqu'à deux électrons sur chaque orbitale, de sorte que le nombre maximum d'électrons sera de 2 × n 2
Si une couche contient au maximum 32 électrons, quel est le principal nombre quantique, n ?
- Réponse
-
n = 4
Complétez le tableau suivant pour les orbitales atomiques :
| Orbitale | n | l | Je suis une dégénérescence | Nœuds radiaux (nombre) |
|---|---|---|---|---|
| 4 f | ||||
| 4 | 1 | |||
| 7 | 7 | 3 | ||
| 5 d |
Solution
Le tableau peut être complété selon les règles suivantes :
- La désignation orbitale est nl, où l = 0, 1, 2, 3, 4, 5,... est mappé à la séquence de lettres s, p, d, f, g, h,...,
- La dégénérescence m l est le nombre d'orbitales au sein d'une sous-couche l, de même que 2 l + 1 (il y a une orbitale s, trois orbitales p, cinq orbitales d, sept orbitales f, etc.).
- Le nombre de nœuds radiaux est égal à n — l — 1.
| Orbitale | n | l | Je suis une dégénérescence | Nœuds radiaux (nombre) |
|---|---|---|---|---|
| 4 f | 4 | 3 | 7 | 0 |
| 4 p. | 4 | 1 | 3 | 2 |
| 7 f | 7 | 3 | 7 | 3 |
| 5 d | 5 | 2 | 5 | 2 |
Combien d'orbitales ont l = 2 et n = 3 ?
- Réponse
-
Les cinq orbitales 3D dégénérées
Résumé
Les objets macroscopiques agissent comme des particules. Les objets microscopiques (tels que les électrons) possèdent les propriétés d'une particule et d'une onde. Leurs trajectoires exactes ne peuvent être déterminées. Le modèle mécanique quantique des atomes décrit la position tridimensionnelle de l'électron de manière probabiliste selon une fonction mathématique appelée fonction d'onde, souvent désignée par φ. Les fonctions d'ondes atomiques sont également appelées orbitales. L'amplitude carrée de la fonction d'onde décrit la distribution de la probabilité de trouver l'électron dans une région particulière de l'espace. Par conséquent, les orbitales atomiques décrivent les zones d'un atome où les électrons sont le plus susceptibles de se trouver.
Une orbitale atomique est caractérisée par trois nombres quantiques. Le nombre quantique principal, n, peut être n'importe quel entier positif. La région générale de la valeur de l'énergie de l'orbitale et la distance moyenne entre un électron et le noyau sont liées à n. Les orbitales ayant la même valeur de n sont dites se trouver dans la même coque. Le nombre quantique du moment cinétique, l, peut avoir n'importe quelle valeur entière comprise entre 0 et n — 1. Ce nombre quantique décrit la forme ou le type de l'orbite. Les orbitales ayant le même nombre quantique principal et la même valeur l appartiennent à la même sous-couche. Le nombre quantique magnétique, m l, avec 2 valeurs l+1 comprises entre — l et + l, décrit l'orientation de l'orbitale dans l'espace. De plus, chaque électron possède un nombre quantique de spin, m s, qui peut être égal à\(±\dfrac{1}{2}\). Deux électrons d'un même atome ne peuvent pas avoir le même ensemble de valeurs pour les quatre nombres quantiques.
Lexique
- nombre quantique de moment cinétique (l)
- nombre quantique distinguant les différentes formes des orbitales ; c'est aussi une mesure du moment cinétique orbital
- orbitale atomique
- fonction mathématique qui décrit le comportement d'un électron dans un atome (également appelée fonction d'onde), elle peut être utilisée pour déterminer la probabilité de localiser un électron dans une région spécifique autour du noyau, ainsi que d'autres variables dynamiques
- d orbital
- région de l'espace à haute densité d'électrons qui est soit à quatre lobes, soit contenant une forme d'haltère et de tore ; décrit les orbitales avec l = 2. Un électron sur cette orbitale est appelé électron d
- densité d'électrons
- une mesure de la probabilité de localiser un électron dans une région particulière de l'espace, elle est égale à la valeur absolue au carré de la fonction d'onde φ
- f orbital
- région multilobée de l'espace à haute densité électronique, décrit les orbitales avec l = 3. Un électron sur cette orbitale est appelé électron f.
- Principe d'incertitude de Heisenberg
- règle stipulant qu'il est impossible de déterminer exactement à la fois certaines propriétés dynamiques conjuguées telles que la quantité de mouvement et la position d'une particule en même temps. Le principe d'incertitude est une conséquence du fait que les particules quantiques présentent une dualité onde-particule.
- nombre quantique magnétique (m l)
- nombre quantique signifiant l'orientation d'une orbitale atomique autour du noyau ; les orbitales ayant des valeurs différentes de m l mais la même valeur de sous-couche de l ont la même énergie (sont dégénérées), mais cette dégénérescence peut être supprimée par l'application d'un aimant externe champ
- p orbital
- région de l'espace en forme d'haltère à haute densité d'électrons, décrit les orbitales avec l = 1. Un électron sur cette orbitale est appelé électron p
- Principe d'exclusion de Pauli
- précise que deux électrons d'un atome ne peuvent pas avoir la même valeur pour les quatre nombres quantiques
- nombre quantique principal (n)
- nombre quantique spécifiant la couche qu'un électron occupe dans un atome
- mécanique quantique
- domaine d'étude qui inclut la quantification de l'énergie, la dualité onde-particule et le principe d'incertitude de Heisenberg pour décrire la matière
- s orbital
- région sphérique de l'espace à haute densité d'électrons, décrit les orbitales avec l = 0. Un électron sur cette orbitale est appelé électron s
- coquille
- ensemble d'orbitales ayant le même nombre quantique principal, n
- nombre quantique de spin (m s)
- nombre spécifiant la direction du spin de l'électron,\(+\dfrac{1}{2}\) soit\(−\dfrac{1}{2}\)
- sous-coque
- ensemble d'orbitales dans un atome ayant les mêmes valeurs de n et de l
- fonction d'onde (φ)
- description mathématique d'une orbitale atomique qui décrit la forme de l'orbitale ; elle peut être utilisée pour calculer la probabilité de trouver l'électron à un endroit donné de l'orbitale, ainsi que des variables dynamiques telles que l'énergie et le moment cinétique


