5.3 : Enthalpie

Objectifs d'apprentissage

• Énoncer la première loi de la thermodynamique
• Définissez l'enthalpie et expliquez sa classification en tant que fonction d'état
• Écrire et équilibrer des équations thermochimiques
• Calculer les variations d'enthalpie pour diverses réactions chimiques
• Expliquez la loi de Hess et utilisez-la pour calculer les enthalpies de réaction

La thermochimie est une branche de la thermodynamique chimique, la science qui traite des relations entre la chaleur, le travail et d'autres formes d'énergie dans le contexte de processus chimiques et physiques. Alors que nous nous concentrons sur la thermochimie dans ce chapitre, nous devons prendre en compte certains concepts de thermodynamique largement utilisés.

Les substances agissent comme des réservoirs d'énergie, ce qui signifie que de l'énergie peut y être ajoutée ou retirée. L'énergie est stockée dans une substance lorsque l'énergie cinétique de ses atomes ou de ses molécules augmente. La plus grande énergie cinétique peut prendre la forme d'une augmentation des translations (déplacements ou mouvements en ligne droite), des vibrations ou des rotations des atomes ou des molécules. Lorsque l'énergie thermique est perdue, l'intensité de ces mouvements diminue et l'énergie cinétique diminue. Le total de tous les types d'énergie possibles présents dans une substance est appelé énergie interne (U), parfois symbolisée par E.

Au fur et à mesure qu'un système subit un changement, son énergie interne peut changer et l'énergie peut être transférée du système vers l'environnement, ou de l'environnement vers le système. L'énergie est transférée dans un système lorsqu'il absorbe la chaleur (q) de l'environnement ou lorsque l'environnement agit (w) sur le système. Par exemple, l'énergie est transférée dans un fil métallique à température ambiante s'il est immergé dans de l'eau chaude (le fil absorbe la chaleur de l'eau) ou si vous le pliez rapidement d'avant en arrière (le fil devient plus chaud à cause du travail effectué dessus). Les deux processus augmentent l'énergie interne du fil, ce qui se traduit par une augmentation de la température du fil. À l'inverse, l'énergie est transférée hors d'un système lorsque de la chaleur est perdue ou lorsque le système fonctionne sur l'environnement.

La relation entre l'énergie interne, la chaleur et le travail peut être représentée par l'équation suivante :

\[ΔU=q+w \label{5.4.1} \]

comme le montre la figure\(\PageIndex{1}\). Il s'agit d'une version de la première loi de la thermodynamique, qui montre que l'énergie interne d'un système change par le flux de chaleur entrant ou sortant du système (q positif est le flux de chaleur entrant ; négatif q est le flux de chaleur sortant) ou par le travail effectué sur ou par le système. Le travail, w, est positif s'il est effectué sur le système et négatif s'il est effectué par le système.

Figure\(\PageIndex{1}\) : L'énergie interne, U, d'un système peut être modifiée par le flux de chaleur et le travail. _{Si de la chaleur entre dans le système, q entre, ou si un travail est effectué sur le système, w on, son énergie interne augmente, ΔU > 0.} Si la chaleur s'écoule hors du système, q _sort, ou si un travail est effectué par le système, w _by, son énergie interne diminue, ΔU < 0.

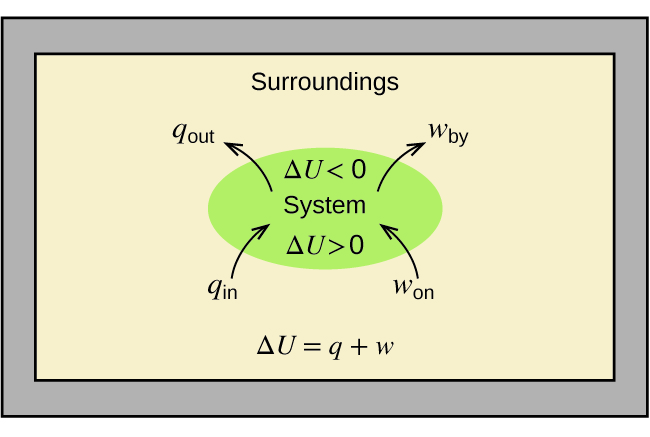
Un type de travail appelé travail d'expansion (ou travail pression/volume) se produit lorsqu'un système repousse l'environnement contre une pression de retenue, ou lorsque l'environnement comprime le système. Cela se produit par exemple lors du fonctionnement d'un moteur à combustion interne. La réaction de l'essence et de l'oxygène est exothermique. Une partie de cette énergie est émise sous forme de chaleur et une autre fonctionne en poussant le piston dans le cylindre. Les substances impliquées dans la réaction sont le système, tandis que le moteur et le reste de l'univers sont l'environnement. Le système perd de l'énergie à la fois en chauffant et en travaillant sur l'environnement, et son énergie interne diminue. (Le moteur est capable de maintenir la voiture en mouvement car ce processus est répété plusieurs fois par seconde pendant que le moteur tourne.) Nous verrons comment déterminer la quantité de travail nécessaire à un changement chimique ou physique dans le chapitre sur la thermodynamique.

Comme nous l'avons vu, la relation entre l'énergie interne, la chaleur et le travail peut être représentée par Δ U = q + w. L'énergie interne est un type de quantité connu sous le nom de fonction d'état (ou variable d'état), alors que la chaleur et le travail ne sont pas des fonctions d'état. La valeur d'une fonction d'état dépend uniquement de l'état dans lequel se trouve un système, et non de la manière dont cet état est atteint. Si une quantité n'est pas une fonction d'état, sa valeur dépend de la manière dont l'état est atteint. L'altitude ou l'altitude sont un exemple de fonction d'état. Si vous vous trouvez au sommet du mont. Kilimandjaro, vous êtes à une altitude de 5895 m, et peu importe que vous y ayez fait de la randonnée ou du parachute. La distance que vous avez parcourue jusqu'au sommet du Kilimandjaro n'est toutefois pas une fonction de l'État. Vous pouvez monter au sommet par un itinéraire direct ou par un chemin plus circulaire et sinueux (Figure\(\PageIndex{2}\)). Les distances parcourues seraient différentes (la distance n'est pas une fonction d'état) mais l'altitude atteinte serait la même (l'altitude est une fonction d'état).

Figure\(\PageIndex{2}\) : Les chemins X et Y représentent deux itinéraires différents jusqu'au sommet du mont. Kilimandjaro. Les deux ont le même changement d'altitude (l'altitude ou l'altitude sur une montagne est une fonction d'état ; cela ne dépend pas de la trajectoire), mais les distances parcourues sont très différentes (la distance parcourue n'est pas une fonction d'état ; elle dépend du chemin). (crédit : modification de l'œuvre de Paul Shaffner)

Une photo aérienne montre une vue du mont Kilimandjaro. Une flèche verte droite étiquetée X est dessinée depuis le terme « base », écrit au bas de la montagne, jusqu'au terme « sommet », écrit au sommet de la montagne. Une autre flèche nommée Y est tracée de la base jusqu'au sommet à côté de la flèche verte, mais cette flèche est rose et comporte trois grandes courbes en forme de S sur sa longueur.

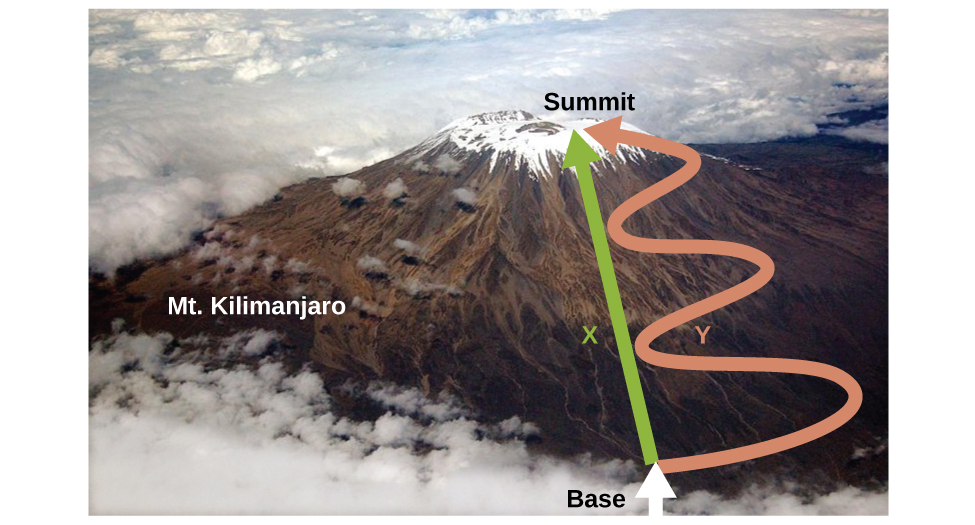
Les chimistes utilisent généralement une propriété appelée enthalpie (\(H\)) pour décrire la thermodynamique des processus chimiques et physiques. L'enthalpie est définie comme la somme de l'énergie interne (\(U\)) d'un système et du produit mathématique de sa pression (\(P\)) et de son volume (\(V\)) :

\[H=U+PV \label{5.4.2} \]

Comme elle est dérivée de trois fonctions d'état (\(U\),\(P\), et\(V\)), l'enthalpie est également une fonction d'état. Les valeurs d'enthalpie pour des substances spécifiques ne peuvent pas être mesurées directement ; seules les variations d'enthalpie liées à des processus chimiques ou physiques peuvent être déterminées. Pour les processus qui se déroulent à pression constante (condition courante pour de nombreux changements chimiques et physiques), le changement d'enthalpie (\(ΔH\)) est le suivant :

\[ΔH=ΔU+PΔV\label{5.4.3} \]

Le produit mathématique\(PΔV\) représente le travail (\(w\)), à savoir le travail d'expansion ou de pression/volume, comme indiqué. Selon leurs définitions, les signes arithmétiques de ΔV et w seront toujours opposés :

\[PΔV=−w \label{5.4.4} \]

En remplaçant l'équation \ ref {5.4.4} et la définition de l'énergie interne (Équation \ ref {5.4.1}) par l'équation \ ref {5.4.3}, on obtient :

\[ \begin{align} ΔH&=ΔU+PΔV \\[4pt] &=q_\ce{p}+\cancel{w}−\cancel{w} \\[4pt] &=q_\ce{p} \label{5.4.5} \end{align} \]

où\(q_p\) est la chaleur de réaction dans des conditions de pression constante.

Ainsi, si un processus chimique ou physique est effectué à pression constante et que le seul travail effectué est dû à une expansion ou à une contraction, alors le flux thermique (\(q_\ce{p}\)) et le changement d'enthalpie (\(ΔH\)) du processus sont égaux.

La chaleur dégagée lorsque vous faites fonctionner un brûleur Bunsen est égale au changement d'enthalpie de la réaction de combustion du méthane qui a lieu, puisqu'elle se produit à une pression essentiellement constante de l'atmosphère. D'autre part, la chaleur produite par une réaction mesurée dans un calorimètre à bombe n'est pas égale\(ΔH\) car le récipient métallique fermé à volume constant empêche tout travail d'expansion. Les chimistes effectuent généralement des expériences dans des conditions atmosphériques normales, à pression externe constante\(q = ΔH\), ce qui fait de l'enthalpie le choix le plus pratique pour déterminer la chaleur.

Les conventions suivantes s'appliquent lorsque nous utilisons\(ΔH\) :

1. Les chimistes utilisent une équation thermochimique pour représenter les changements de matière et d'énergie. Dans une équation thermochimique, le changement d'enthalpie d'une réaction est représenté par une valeur Δ H suivant l'équation de la réaction. Cette\(ΔH\) valeur indique la quantité de chaleur associée à la réaction impliquant le nombre de moles de réactifs et de produits, comme indiqué dans l'équation chimique. Par exemple, considérez cette équation :\[\ce{H2(g) + 1/2 O2(g) ⟶ H2O (l)} \;\; ΔH=\mathrm{−286\:kJ} \label{5.4.6} \] cette équation indique que lorsqu'une mole d'hydrogène gazeux et 12 mole d'oxygène gazeux à une certaine température et pression passent à 1 mole d'eau liquide à la même température et à la même pression, 286 kJ de chaleur sont libérés dans l'environnement. Si les coefficients de l'équation chimique sont multipliés par un facteur, le changement d'enthalpie doit être multiplié par ce même facteur (ΔH est une propriété étendue).

\[\begin {align*} &\textrm{(two-fold increase in amounts)}\label{5.4.7}\\ &\ce{2H2}(g)+\ce{O2}(g)⟶\ce{2H2O}(l)\hspace{20px}ΔH=\mathrm{2×(−286\:kJ)=−572\:kJ}\\ &\textrm{(two-fold decrease in amounts)}\\ &\frac{1}{2}\ce{H2}(g)+\dfrac{1}{4}\ce{O2}(g)⟶\frac{1}{2}\ce{H2O}(l)\hspace{20px}ΔH=\mathrm{\frac{1}{2}×(−286\:kJ)=−143\:kJ} \end {align*} \label{5.4.6B} \]

2. Le changement d'enthalpie d'une réaction dépend de l'état physique des réactifs et des produits de la réaction (qu'il s'agisse de gaz, de liquides, de solides ou de solutions aqueuses), ils doivent donc être indiqués. Par exemple, lorsqu'une mole d'hydrogène gazeux et 12 mole d'oxygène gazeux se transforment en 1 mole d'eau liquide à la même température et à la même pression, 286 kJ de chaleur sont libérés. Si de l'eau gazeuse se forme, seuls 242 kJ de chaleur sont libérés.

\[\ce{ H2(g) + 1/2 O2(g) ⟶ H2O(g)} \;\;\; ΔH=\ce{−242\:kJ} \label{5.4.7B} \]

 

3. Une valeur négative d'un changement d'enthalpie, Δ H, indique une réaction exothermique ; une valeur positive de Δ H indique une réaction endothermique. Si le sens d'une équation chimique est inversé, le signe arithmétique de son Δ H est modifié (un processus endothermique dans un sens est exothermique dans le sens opposé).

Exemple\(\PageIndex{1}\): Measurement of an Enthalpy Change

Lorsque 0,0500 mol de HCl (aq) réagit avec 0,0500 mol de NaOH (aq) pour former 0,0500 mol de NaCl (aq), 2,9 kJ de chaleur sont produits. Qu'est-ce que ΔH, le changement d'enthalpie, par mole d'acide réagissant, pour la réaction acide-base exécutée dans les conditions décrites ?

\[\ce{HCl (aq) + NaOH(aq) \rightarrow NaCl (aq) + H2O(l)} \nonumber \]

Solution

Pour la réaction de 0,0500 mol d'acide (HCl), q = −2,9 kJ. Ce ratio

\[\mathrm{\dfrac{−2.9 \; kJ}{0.0500\; mol\; HCl}} \nonumber \]

peut être utilisé comme facteur de conversion pour déterminer la chaleur produite lorsqu'une mole de HCl réagit :

\[ΔH =\mathrm{1\; \cancel{mol\; HCl} \times \dfrac{ −2.9\; kJ}{0.0500 \;\cancel{ mol\; HCl}} =−58\; kJ} \nonumber \]

Le changement d'enthalpie lorsqu'une mole de HCl réagit est de −58 kJ. Comme il s'agit du nombre de moles dans l'équation chimique, nous écrivons l'équation thermochimique comme suit :

\[\ce{HCl}_{(aq)}+\ce{NaOH}_{(aq)}⟶\ce{NaCl}_{(aq)}+\ce{H_2O}_{(l)} \;\;\; ΔH=\mathrm{−58\;kJ} \nonumber \]

Exercice\(\PageIndex{1}\)

Lorsque 1,34 g de Zn (s) réagit avec 60,0 ml de 0,750 M HCl (aq), 3,14 kJ de chaleur sont produits. Déterminer le changement d'enthalpie par mole de zinc réagissant pour la réaction :

\[ \ce{Zn}_{(s)}+\ce{2HCl}_{(aq)}⟶\ce{ZnCl}_{(aq)}+\ce{H}_{2(g)} \nonumber \]

Réponse

ΔH = −153 kJ

Assurez-vous de prendre en compte à la fois la stœchiométrie et les réactifs limitants lors de la détermination du Δ H pour une réaction chimique.

Exemple\(\PageIndex{2}\): Another Example of the Measurement of an Enthalpy Change

Un ourson en gélatine contient 2,67 g de saccharose, C ₁₂ H ₂₂ O ₁₁. Lorsqu'il réagit avec 7,19 g de chlorate de potassium, KClO ₃, 43,7 kJ de chaleur sont produits. Déterminer le changement d'enthalpie pour la réaction

\[\ce{C12H22O11}(aq)+\ce{8KClO3}(aq)⟶\ce{12CO2}(g)+\ce{11H2O}(l)+\ce{8KCl}(aq) \nonumber \]

Une solution

Nous avons à\(\mathrm{2.67\:\cancel{g}×\dfrac{1\:mol}{342.3\:\cancel{g}}=0.00780\:mol\:C_{12}H_{22}O_{11}}\) votre disposition, et

\(\mathrm{7.19\:\cancel{g}×\dfrac{1\:mol}{122.5\:\cancel{g}}=0.0587\:mol\:KClO_3}\)disponible.

Depuis

\(\mathrm{0.0587\:mol\:KClO_3×\dfrac{1\:mol\:\ce{C12H22O11}}{8\:mol\:KClO_3}=0.00734\:mol\:\ce{C12H22O11}}\)

est nécessaire, C ₁₂ H ₂₂ O ₁₁ est le réactif en excès et KClO ₃ est le réactif limite.

La réaction utilise 8 mol de KClO ₃, et le facteur de conversion est\(\mathrm{\dfrac{−43.7\:kJ}{0.0587\:mol\:KClO_3}}\), donc nous l'avons fait\(ΔH=\mathrm{8\:mol×\dfrac{−43.7\:kJ}{0.0587\:mol\:KClO_3}=−5960\:kJ}\). Le changement d'enthalpie pour cette réaction est de −5960 kJ, et l'équation thermochimique est la suivante :

\[\ce{C12H22O11 + 8KClO3⟶12CO2 + 11H2O + 8KCl}\hspace{20px}ΔH=\ce{−5960\:kJ} \nonumber \]

Exercice\(\PageIndex{2}\)

Lorsque 1,42 g de fer réagit avec 1,80 g de chlore, 3,22 g\(\ce{FeCl}_{2(s)}\) et 8,60 kJ de chaleur sont produits. Quel est le changement d'enthalpie de la réaction lorsqu'une mole de\(\ce{FeCl2(s)}\) est produite ?

Réponse

ΔH = −338 kJ

Les variations d'enthalpie sont généralement présentées sous forme de tableaux pour les réactions dans lesquelles les réactifs et les produits se trouvent dans les mêmes conditions. Un état standard est un ensemble communément accepté de conditions utilisées comme point de référence pour la détermination de propriétés dans d'autres conditions différentes. Pour les chimistes, l'état standard de l'IUPAC fait référence à des matériaux sous une pression de 1 bar et à des solutions à 1 M, sans spécifier de température (il est également utilisé). De nombreux tableaux thermochimiques listent des valeurs avec un état standard de 1 atm. Comme le Δ H d'une réaction change très peu avec de si faibles variations de pression (1 bar = 0,987 atm), les valeurs de Δ H (à l'exception des valeurs mesurées les plus précisément) sont essentiellement les mêmes dans les deux ensembles de conditions standard. Nous allons inclure un « o » en exposant dans le symbole de changement d'enthalpie pour désigner l'état standard. Comme la température habituelle (mais pas techniquement standard) est de 298,15 K, nous utiliserons l'indice « 298 » pour désigner cette température. Ainsi, le symbole (\(ΔH^\circ_{298}\)) est utilisé pour indiquer un changement d'enthalpie pour un processus se produisant dans ces conditions. (Le symbole Δ H est utilisé pour indiquer un changement d'enthalpie pour une réaction survenant dans des conditions non standard.)

Les changements d'enthalpie pour de nombreux types de processus chimiques et physiques sont disponibles dans la littérature de référence, y compris ceux relatifs aux réactions de combustion, aux transitions de phase et aux réactions de formation. Lorsque nous discutons de ces quantités, il est important de prêter attention à la nature étendue de l'enthalpie et des changements d'enthalpie. Comme le changement d'enthalpie pour une réaction donnée est proportionnel aux quantités de substances impliquées, il peut être indiqué sur cette base (c'est-à-dire sous la forme de Δ H pour des quantités spécifiques de réactifs). Cependant, nous trouvons souvent plus utile de diviser une propriété étendue (Δ H) par une autre (quantité de substance) et de déclarer une valeur intensive par quantité de Δ H, souvent « normalisée » par mole. (Notez que cela revient à déterminer la chaleur spécifique intensive de la propriété à partir de la capacité thermique étendue de la propriété, comme nous l'avons vu précédemment.)

Enthalpie de combustion

L'enthalpie standard de combustion (\(ΔH_C^\circ\)) est le changement d'enthalpie lorsqu'une mole d'une substance brûle (se combine vigoureusement à l'oxygène) dans des conditions d'état standard ; elle est parfois appelée « chaleur de combustion ». Par exemple, l'enthalpie de combustion de l'éthanol, −1366,8 kJ/mol, est la quantité de chaleur produite lorsqu'une mole d'éthanol subit une combustion complète à 25 °C et à une pression atmosphérique, produisant des produits également à 25 °C et 1 atm.

\[\ce{C2H5OH}(l)+\ce{3O2}(g)⟶\ce{2CO2}+\ce{3H2O}(l)\hspace{20px}ΔH_{298}^\circ=\mathrm{−1366.8\: kJ} \label{5.4.8} \]

Les enthalpies de combustion de nombreuses substances ont été mesurées ; quelques-unes d'entre elles sont répertoriées dans le tableau\(\PageIndex{1}\). De nombreuses substances facilement disponibles avec de grandes enthalpies de combustion sont utilisées comme combustibles, notamment l'hydrogène, le carbone (sous forme de charbon ou de charbon de bois) et les hydrocarbures (composés contenant uniquement de l'hydrogène et du carbone), tels que le méthane, le propane et les principaux composants de l'essence.

Tableau\(\PageIndex{1}\) : Enthalpies molaires standard de combustion

Substance	Réaction de combustion	Enthalpie de combustion\(ΔH_c^\circ \left(\mathrm{\dfrac{kJ}{mol} \:at\:25°C}\right)\)
carbone	\(\ce{C}(s)+\ce{O2}(g)⟶\ce{CO2}(g)\)	\ (ΔH_C^ \ circ \ left (\ mathrm {\ dfrac {kJ} {mol} \ :at \ :25°C} \ right) » style="text-align:center ; « >−393.5
hydrogène	\(\ce{H2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{H2O}(l)\)	\ (ΔH_C^ \ circ \ left (\ mathrm {\ dfrac {kJ} {mol} \ :at \ :25°C} \ right) » style="text-align:center ; « >−285.8
magnésium	\(\ce{Mg}(s)+\frac{1}{2}\ce{O2}(g)⟶\ce{MgO}(s)\)	\ (ΔH_C^ \ circ \ left (\ mathrm {\ dfrac {kJ} {mol} \ :at \ :25°C} \ right) » style="text-align:center ; « >−601.6
soufre	\(\ce{S}(s)+\ce{O2}(g)⟶\ce{SO2}(g)\)	\ (ΔH_C^ \ circ \ left (\ mathrm {\ dfrac {kJ} {mol} \ :at \ :25°C} \ right) » style="text-align:center ; « >−296.8
monoxyde de carbone	\(\ce{CO}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{CO2}(g)\)	\ (ΔH_C^ \ circ \ left (\ mathrm {\ dfrac {kJ} {mol} \ :at \ :25°C} \ right) » style="text-align:center ; « >−283.0
méthane	\(\ce{CH4}(g)+\ce{2O2}(g)⟶\ce{CO2}(g)+\ce{2H2O}(l)\)	\ (ΔH_C^ \ circ \ left (\ mathrm {\ dfrac {kJ} {mol} \ :at \ :25°C} \ right) » style="text-align:center ; « >−890,8
acétylène	\(\ce{C2H2}(g)+\dfrac{5}{2}\ce{O2}(g)⟶\ce{2CO2}(g)+\ce{H2O}(l)\)	\ (ΔH_C^ \ circ \ left (\ mathrm {\ dfrac {kJ} {mol} \ :at \ :25°C} \ right) » style="text-align:center ; « >−1301.1
éthanol	\(\ce{C2H5OH}(l)+\ce{3O2}(g)⟶\ce{CO2}(g)+\ce{3H2O}(l)\)	\ (ΔH_C^ \ circ \ left (\ mathrm {\ dfrac {kJ} {mol} \ :at \ :25°C} \ right) » style="text-align:center ; « >−1366.8
méthanol	\(\ce{CH3OH}(l)+\dfrac{3}{2}\ce{O2}(g)⟶\ce{CO2}(g)+\ce{2H2O}(l)\)	\ (ΔH_C^ \ circ \ left (\ mathrm {\ dfrac {kJ} {mol} \ :at \ :25°C} \ right) » style="text-align:center ; « >−726.1
isooctane	\(\ce{C8H18}(l)+\dfrac{25}{2}\ce{O2}(g)⟶\ce{8CO2}(g)+\ce{9H2O}(l)\)	\ (ΔH_C^ \ circ \ left (\ mathrm {\ dfrac {kJ} {mol} \ :at \ :25°C} \ right) » style="text-align:center ; « >−5461

Exemple\(\PageIndex{3}\): Using Enthalpy of Combustion

Comme le\(\PageIndex{3}\) suggère la figure, la combustion de l'essence est un processus hautement exothermique. Déterminons la quantité approximative de chaleur produite par la combustion de 1,00 L d'essence, en supposant que l'enthalpie de combustion de l'essence soit la même que celle de l'isooctane, un composant courant de l'essence. La densité de l'isooctane est de 0,692 g/mL.

Figure\(\PageIndex{3}\) : La combustion de l'essence est très exothermique. (crédit : modification de l'œuvre par « AlexEagle » /Flickr)

Solution

À partir d'une quantité connue (1,00 L d'isooctane), nous pouvons effectuer des conversions entre les unités jusqu'à obtenir la quantité de chaleur ou d'énergie souhaitée. L'enthalpie de combustion de l'isooctane fournit l'une des conversions nécessaires. Le tableau\(\PageIndex{1}\) donne cette valeur sous la forme de -5460 kJ pour 1 mole d'isooctane (C ₈ H ₁₈).

À l'aide de ces données,

\[\mathrm{1.00\:\cancel{L\:\ce{C8H18}}×\dfrac{1000\:\cancel{mL\:\ce{C8H18}}}{1\:\cancel{L\:\ce{C8H18}}}×\dfrac{0.692\:\cancel{g\:\ce{C8H18}}}{1\:\cancel{mL\:\ce{C8H18}}}×\dfrac{1\:\cancel{mol\:\ce{C8H18}}}{114\:\cancel{g\:\ce{C8H18}}}×\dfrac{−5460\:kJ}{1\:\cancel{mol\:\ce{C8H18}}}=−3.31×10^4\:kJ} \nonumber \]

La combustion de 1,00 L d'isooctane produit 33 100 kJ de chaleur. (Cette quantité d'énergie est suffisante pour faire fondre 99,2 kg, soit environ 218 livres, de glace.)

Remarque : Si vous effectuez ce calcul étape par étape, vous trouverez :

\ (\ begin {align*}
& \ mathrm {1,00 \ :L \ : \ ce {C8H18} 1,00 × 10^3 \ :ml \ : \ ce {C8H18}} \ \
& \ mathrm {1,00 × 10^3 \ :ml \ : \ ce {C8H18} 692 \ :g \ : \ ce {C8H18}} \
& \ mathrm {692 \ :g \ : \ ce {C8H18} 6,07 \ :mol \ : \ ce {C8H18}} \ \
& \ mathrm {692 \ :g \ : \ ce {C8H18} −3,31 × 10^4 \ :kJ}
\ end {align*} \)

Exercice\(\PageIndex{3}\)

Quelle est la quantité de chaleur produite par la combustion de 125 g d'acétylène ?

Réponse

6,25 × 10 ³ kJ

Technologies énergétiques émergentes basées sur les algues (biocarburants)

À mesure que les réserves de combustibles fossiles diminuent et deviennent plus coûteuses à extraire, la recherche de sources de combustibles de remplacement pour l'avenir se poursuit. Parmi les biocarburants les plus prometteurs figurent ceux dérivés d'algues (Figure\(\PageIndex{4}\)). Les espèces d'algues utilisées sont non toxiques, biodégradables et figurent parmi les organismes qui se développent le plus rapidement au monde. Environ 50 % du poids des algues est constitué de pétrole, qui peut être facilement converti en carburant tel que le biodiesel. Les algues peuvent produire 26 000 gallons de biocarburant par hectare, soit beaucoup plus d'énergie par acre que les autres cultures. Certaines souches d'algues peuvent se développer dans des eaux saumâtres qui ne sont pas utilisables pour d'autres cultures. Les algues peuvent produire du biodiesel, de la biogessence, de l'éthanol, du butanol, du méthane et même du carburéacteur.

Figure\(\PageIndex{4}\) : (a) De minuscules organismes algaux peuvent être (b) cultivés en grande quantité et éventuellement (c) transformés en carburant utile tel que le biodiesel. (crédit a : modification d'une œuvre par Micah Sittig ; crédit b : modification d'œuvre par Robert Kerton ; crédit c : modification d'une œuvre par John F. Williams)

Selon le ministère américain de l'Énergie, seuls 39 000 kilomètres carrés (environ 0,4 % de la masse terrestre des États-Unis ou moins que la superficie utilisée pour la culture\(\dfrac{1}{7}\) du maïs) peuvent produire suffisamment de combustible algal pour remplacer tous les combustibles à base de pétrole utilisés aux États-Unis. Le coût des carburants à base d'algues devient de plus en plus compétitif. Par exemple, l'US Air Force produit du carburéacteur à partir d'algues pour un coût total inférieur à 5 dollars le gallon. Le processus utilisé pour produire du combustible algal est le suivant : faire pousser les algues (qui utilisent la lumière du soleil comme source d'énergie et le CO ₂ comme matière première) ; récolter les algues ; extraire les composés combustibles (ou composés précurseurs) ; procéder selon les besoins (par exemple, effectuer une réaction de transestérification pour fabriquer du biodiesel) ; purifier et distribuer (Figure\(\PageIndex{5}\)).

Figure\(\PageIndex{5}\) : Les algues convertissent la lumière du soleil et le dioxyde de carbone en huile qui est récoltée, extraite, purifiée et transformée en divers carburants renouvelables.

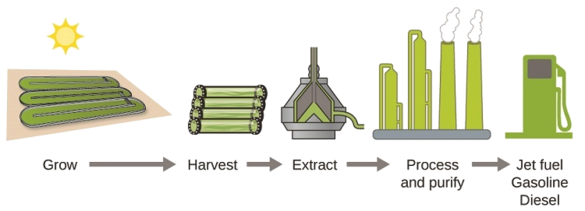
Enthalpie standard de formation

Une enthalpie de formation standard\(ΔH^\circ_\ce{f}\) est un changement d'enthalpie pour une réaction dans laquelle exactement 1 mole d'une substance pure est formée à partir d'éléments libres dans leurs états les plus stables dans des conditions d'état standard. Ces valeurs sont particulièrement utiles pour calculer ou prévoir les changements d'enthalpie pour des réactions chimiques peu pratiques ou dangereuses à réaliser, ou pour des procédés pour lesquels il est difficile d'effectuer des mesures. Si nous avons des valeurs pour les enthalpies standard de formation appropriées, nous pouvons déterminer le changement d'enthalpie pour n'importe quelle réaction, ce que nous allons pratiquer dans la section suivante sur la loi de Hess.

L'enthalpie standard de formation de CO ₂ (g) est de -393,5 kJ/mol. Voici le changement d'enthalpie pour la réaction exothermique :

\[\ce{C}(s)+\ce{O2}(g)⟶\ce{CO2}(g)\hspace{20px}ΔH^\circ_\ce{f}=ΔH^\circ_{298}=−393.5\:\ce{kJ} \label{5.4.9} \]

en commençant par les réactifs à une pression de 1 atm et 25 °C (le carbone étant présent sous forme de graphite, la forme de carbone la plus stable dans ces conditions) et en terminant par une mole de CO ₂, également à 1 atm et 25 °C. Pour le dioxyde d'azote,\(\ce{NO}_{2(g)}\),\(ΔH^\circ_\ce{f}\) est de 33,2 kJ/mol. Voici le changement d'enthalpie de la réaction :

\[\frac{1}{2}\ce{N2}(g)+\ce{O2}(g)⟶\ce{NO2}(g)\hspace{20px}ΔH^\circ_\ce{f}=ΔH^\circ_{298}=+33.2\: \ce{kJ} \label{5.4.10} \]

Une équation de réaction avec une\(\frac{1}{2}\) mole de N ₂ et une mole d'O ₂ est correcte dans ce cas car l'enthalpie standard de formation fait toujours référence à 1 mole de produit, NO ₂ (g).

Vous trouverez un tableau des enthalpies standard de formation de nombreuses substances courantes dans les tableaux T1 et T2. Ces valeurs indiquent que les réactions de formation vont de très exothermiques (par exemple −2984 kJ/mol pour la formation de P ₄ O ₁₀) à fortement endothermiques (par exemple +226,7 kJ/mol pour la formation d'acétylène, C ₂ H ₂). Par définition, l'enthalpie standard de formation d'un élément dans sa forme la plus stable est égale à zéro dans les conditions standard, soit 1 atm pour les gaz et 1 M pour les solutions.

Exemple\(\PageIndex{4}\): Evaluating an Enthalpy of Formation

L'ozone, O ₃ (g), se forme à partir de l'oxygène, O ₂ (g), par un processus endothermique. Le rayonnement ultraviolet est la source d'énergie qui entraîne cette réaction dans la haute atmosphère. En supposant que les réactifs et les produits de la réaction sont à l'état standard, déterminer l'enthalpie standard de formation\(ΔH^\circ_\ce{f}\) de l'ozone à partir des informations suivantes :

\[\ce{3O2}(g)⟶\ce{2O3}(g)\hspace{20px}ΔH^\circ_{298}=+286\: \ce{kJ} \nonumber \]

S olutio n\(ΔH^\circ_\ce{f}\) est le changement d'enthalpie pour la formation d'une mole d'une substance à l'état standard à partir des éléments à leur état standard. Ainsi,\(ΔH^\circ_\ce{f}\) pour O ₃ (g) est le changement d'enthalpie de la réaction :

\[\dfrac{3}{2}\ce{O2}(g)⟶\ce{O3}(g) \nonumber \]

Pour la formation de 2 moles de O ₃ (g),\(ΔH^\circ_{298}=+286\: \ce{kJ}\). Ce rapport peut être utilisé comme facteur de conversion pour déterminer la chaleur produite lors de la formation d'une mole d'O ₃ (g), qui est l'enthalpie de formation de O ₃ (g) :\(\mathrm{\left(\dfrac{286\:kJ}{2\:mol\:O_3}\right)}\)

\[ΔH^\circ \ce{\:for\:1\:mole\: of\:O_3}(g)=\mathrm{1\:\cancel{mol\:O_3}×\dfrac{286\:kJ}{2\:\cancel{mol\:O_3}}=143\:kJ} \nonumber \]

Par conséquent,\(ΔH^\circ_\ce{f}[\ce{O3}(g)]=\ce{+143\: kJ/mol}\).

Exercice\(\PageIndex{4}\)

L'hydrogène gazeux, H ₂, réagit de manière explosive avec le chlore gazeux, Cl ₂, pour former du chlorure d'hydrogène, HCl (g). Quel est le changement d'enthalpie pour la réaction d'une mole de H ₂ (g) avec 1 mole de Cl ₂ (g) si les réactifs et les produits se trouvent dans des conditions d'état standard ? L'enthalpie standard de formation de HCl (g) est de −92,3 kJ/mol.

Réponse

Pour la réaction

\[\ce{H2}(g)+\ce{Cl2}(g)⟶\ce{2HCl}(g)\hspace{20px}ΔH^\circ_{298}=\mathrm{−184.6\:kJ} \nonumber \]

Exemple\(\PageIndex{5}\): Writing Reaction Equations for \(ΔH^\circ_\ce{f}\)

Écrivez les équations de la réaction de chaleur de formation pour :

1. \(\ce{C2H_5OH}_{(l)}\)
2. \(\ce{Ca_3(PO_4)}_{2(s)}\)

Solution

En se souvenant que les équations de\(ΔH^\circ_\ce{f}\) réaction visent à former 1 mole du composé à partir de ses éléments constitutifs dans des conditions standard, nous avons :

1. \(\ce{2C}(s,\:\ce{graphite})+\ce{3H2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{C2H5OH}(l)\)
2. \(\ce{3Ca}(s)+\frac{1}{2}\ce{P4}(s)+\ce{4O2}(g)⟶\ce{Ca3(PO4)2}(s)\)

Remarque : L'état standard du carbone est le graphite, et le phosphore existe sous forme de\(P_4\).

Exercice\(\PageIndex{5}\)

Écrivez les équations de la réaction de chaleur de formation pour :

1. \(\ce{C_2H_5OC_2H}_{5(l)}\)
2. \(\ce{Na_2CO}_{3(s)}\)

Répondez à

\(\ce{4C}(s,\:\ce{graphite})+\ce{5H2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{C2H5OC2H5}(l)\);

Réponse b

\(\ce{2Na}(s)+\ce{C}(s,\:\ce{graphite})+\dfrac{3}{2}\ce{O2}(g)⟶\ce{Na2CO3}(s)\)

Loi de Hess

Il existe deux manières de déterminer la quantité de chaleur impliquée dans un changement chimique : la mesurer expérimentalement ou la calculer à partir d'autres changements d'enthalpie déterminés expérimentalement. Certaines réactions sont difficiles, voire impossibles, à étudier et à effectuer des mesures précises de manière expérimentale. Et même lorsqu'une réaction n'est pas difficile à réaliser ou à mesurer, il est pratique de pouvoir déterminer la chaleur impliquée dans une réaction sans avoir à effectuer d'expérience.

Ce type de calcul implique généralement l'utilisation de la loi de Hess, qui stipule que : Si un processus peut être écrit comme la somme de plusieurs processus par étapes, la variation d'enthalpie du processus total est égale à la somme des variations d'enthalpie des différentes étapes. La loi de Hess est valide parce que l'enthalpie est une fonction d'état : les changements d'enthalpie dépendent uniquement du point de départ et de fin d'un processus chimique, mais pas du chemin qu'il emprunte du début à la fin. Par exemple, nous pouvons penser que la réaction du carbone avec l'oxygène pour former du dioxyde de carbone se produit soit directement, soit par un processus en deux étapes. Le processus direct est écrit :

\[\ce{C}_{(s)}+\ce{O}_{2(g)}⟶\ce{CO}_{2(g)}\;\;\;ΔH^∘_{298}=\mathrm{−394\;kJ} \label{ 5.4.11} \]

Dans le procédé en deux étapes, le premier monoxyde de carbone est formé :

\[\ce{C}_{(s)}+\dfrac{1}{2}\ce{O}_{2(g)}⟶\ce{CO}_{(g)}\;\;\;ΔH^∘_{298}=\mathrm{−111\;kJ} \label{ 5.4.12} \]

Ensuite, le monoxyde de carbone réagit davantage pour former du dioxyde de carbone :

\[\ce{CO} {(g)}+\dfrac{1}{2}\ce{O2}(g)⟶\ce{CO}_2 {(g)}\;\;\;ΔH^∘_{298}=\mathrm{−283\;kJ} \label{ 5.4.13} \]

L'équation décrivant la réaction globale est la somme de ces deux changements chimiques :

\[\begin {align*} &\textrm{Step 1:} \:\ce{C}(s)+\frac{1}{2}\ce{O2}(g)⟶\ce{CO}(g)\\ &\underline{\textrm{Step 2:} \:\ce{CO}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{CO2}(g)}\\ &\textrm{Sum:} \:\ce{C}(s)+\frac{1}{2}\ce{O2}(g)+\ce{CO}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{CO}(g)+\ce{CO2}(g) \end {align*} \label{5.4.14} \]

Comme le CO produit à l'étape 1 est consommé à l'étape 2, la variation nette est la suivante :

\[\ce{C}_{(s)}+\ce{O}_{2(g)}⟶\ce{CO}_{2(g)} \label{5.4.15} \]

Selon la loi de Hess, le changement d'enthalpie de la réaction sera égal à la somme des variations d'enthalpie des étapes. Nous pouvons appliquer les données des enthalpies expérimentales de combustion du tableau\(\PageIndex{1}\) pour déterminer le changement d'enthalpie de l'ensemble de la réaction à partir de ses deux étapes :

\ [\ begin {align*}
& \ ce {C} (s) + \ frac {1} {2} \ ce {O2} (g) ⟶ \ ce {CO} (g) &ΔH^ \ circ_ {298} = \ mathrm {−111 \ :kJ} \ \
& \ ce {CO} (g) + \ frac {1} {2} \ ce {O2} (g) ⟶ \ ce {CO2} (g) &ΔH^ \ circ_ {298} = \ mathrm {−283 \ :kJ} \ \
& \ overline {\ ce {C} (s) + \ ce {O2} (g) ⟶ \ ce {CO2} (g) \ hspace {25px}} et ; & \ overline {ΔH^ \ circ_ {298} = \ mathrm {−394 \ :kJ}}
 \ end {align*} \ label {5.4.16} \]

Le résultat est illustré dans la figure\(\PageIndex{6}\). Nous voyons que le ΔH de la réaction globale est le même, qu'elle se produise en une ou deux étapes. Ce résultat (ΔH global pour la réaction = somme des valeurs de Δ H pour les « étapes » de la réaction globale) est généralement vrai pour les processus chimiques et physiques.

Figure\(\PageIndex{6}\) : La formation de CO ₂ (g) à partir de ses éléments peut être considérée comme se produisant en deux étapes, dont la somme correspond à la réaction globale, comme décrit par la loi de Hess. Les lignes bleues horizontales représentent les enthalpies. Dans le cas d'un procédé exothermique, les produits présentent une enthalpie inférieure à celle des réactifs.

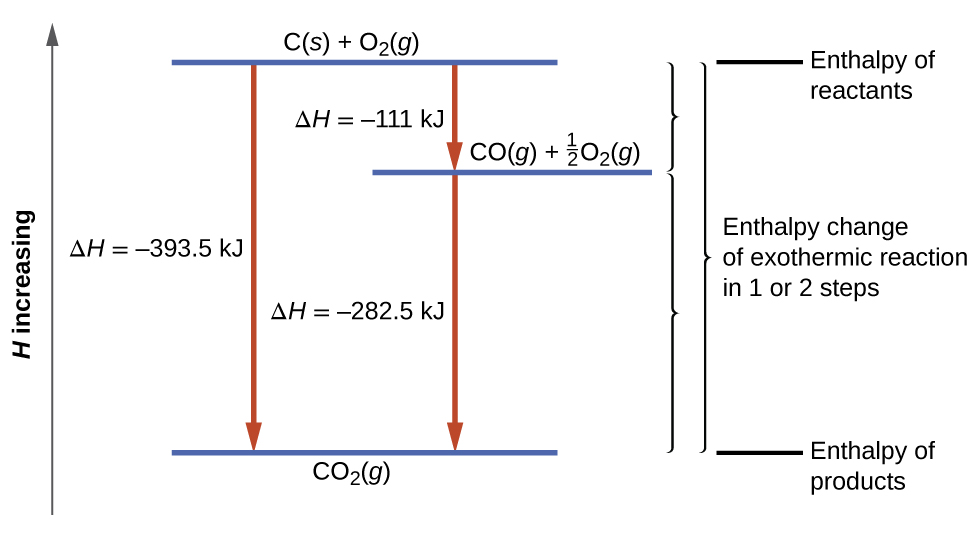
Avant de nous entraîner davantage à utiliser la loi de Hess, rappelons deux caractéristiques importantes du Δ H.

1. Δ H est directement proportionnel aux quantités de réactifs ou de produits. Par exemple, le changement d'enthalpie pour la réaction formant 1 mole de NO ₂ (g) est de +33,2 kJ :\[\frac{1}{2}\ce{N2}(g)+\ce{O2}(g)⟶\ce{NO2}(g)\hspace{20px}ΔH=\mathrm{+33.2\: kJ} \label{5.4.17} \]

   Lorsque 2 moles de NO ₂ (deux fois plus) se forment, le Δ H sera deux fois plus grand :\[\ce{N2}(g)+\ce{2O2}(g)⟶\ce{2NO2}(g)\hspace{20px}ΔH=\mathrm{+66.4\: kJ} \label{5.4.18} \]

   En général, si nous multiplions ou divisons une équation par un nombre, le changement d'enthalpie doit également être multiplié ou divisé par le même nombre.

2. Δ H pour une réaction dans un sens est égal en amplitude et en signe opposé à Δ H pour la réaction dans le sens inverse. Par exemple, étant donné que :\[\ce{H2}(g)+\ce{Cl2}(g)⟶\ce{2HCl}(g)\hspace{20px}ΔH=\mathrm{−184.6\:kJ} \label{5.4.19} \]

   Ensuite, pour la réaction « inverse », le changement d'enthalpie est également « inversé » :\[\ce{2HCl}(g)⟶\ce{H2}(g)+\ce{Cl2}(g)\hspace{20px}ΔH=\mathrm{+184.6\: kJ} \label{5.4.20} \]

Exemple\(\PageIndex{6}\): Stepwise Calculation of \(ΔH^\circ_\ce{f}\)

À l'aide de la loi de Hess\(ΔH^\circ_\ce{f}\), déterminez l'enthalpie de formation du FeCl ₃ (s) à partir des variations d'enthalpie du processus en deux étapes suivant qui se produit dans des conditions d'état standard :

\[\ce{Fe}(s)+\ce{Cl2}(g)⟶\ce{FeCl2}(s)\hspace{20px}ΔH°=\mathrm{−341.8\:kJ} \nonumber \]

\[\ce{FeCl2}(s)+\frac{1}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{20px}ΔH°=\mathrm \nonumber{−57.7\:kJ} \nonumber \]

Solution

Nous essayons de déterminer l'enthalpie standard de formation de FeCl3 (s), qui est égale à ΔH° pour la réaction :

\[\ce{Fe}(s)+\frac{3}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{20px}ΔH^\circ_\ce{f}=\:? \nonumber \]

En regardant les réactions, nous voyons que la réaction pour laquelle nous voulons trouver Δ H° est la somme des deux réactions dont les valeurs de Δ H sont connues, nous devons donc additionner leurs Δ H s :

\[\ce{Fe}(s)+\ce{Cl2}(g)⟶\ce{FeCl2}(s)\hspace{59px}ΔH°=\mathrm{−341.8\:kJ}\\ \underline{\ce{FeCl2}(s)+\frac{1}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{20px}ΔH°=\mathrm{−57.7\:kJ}}\\ \ce{Fe}(s)+\frac{1}{2}\ce{Cl2}(g)⟶\ce{FeCl3}(s)\hspace{43px}ΔH°=\mathrm{−399.5\:kJ} \nonumber \]

L'enthalpie de formation du FeCl ₃ (s) est de −399,5 kJ/mol.\(ΔH^\circ_\ce{f}\)

Exercice\(\PageIndex{6}\)

Calculez ΔH pour le processus :

\[\ce{N2}(g)+\ce{2O2}(g)⟶\ce{2NO2}(g) \nonumber \]

à partir des informations suivantes :

\[\ce{N2}(g)+\ce{O2}(g)⟶\ce{2NO}(g)\hspace{20px}ΔH=\mathrm{180.5\:kJ} \nonumber \]

\[\ce{NO}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{NO2}(g)\hspace{20px}ΔH=\mathrm{−57.06\:kJ} \nonumber \]

Réponse

6,4 kJ

Voici un exemple moins simple qui illustre le processus de réflexion impliqué dans la résolution de nombreux problèmes juridiques de Hess. Il montre comment on peut trouver de nombreuses enthalpies de formation standard (et d'autres valeurs de Δ H) si elles sont difficiles à déterminer expérimentalement.

Exemple\(\PageIndex{7}\): A More Challenging Problem

Selon la loi de Hess, le monofluorure de chlore peut réagir avec le fluor pour former du trifluorure de chlore :

(i)\(\ce{ClF}(g)+\ce{F2}(g)⟶\ce{ClF3}(g)\hspace{20px}ΔH°=\:?\)

Utilisez les réactions ci-dessous pour déterminer le ΔH° de la réaction (i) :

(ii)\(\ce{2OF2}(g)⟶\ce{O2}(g)+\ce{2F2}(g)\hspace{20px}ΔH^\circ_{(ii)}=\mathrm{−49.4\:kJ}\)

(iii)\(\ce{2ClF}(g)+\ce{O2}(g)⟶\ce{Cl2O}(g)+\ce{OF2}(g)\hspace{20px}ΔH^\circ_{(iii)}=\mathrm{+205.6\: kJ}\)

(iv)\(\ce{ClF3}(g)+\ce{O2}(g)⟶\frac{1}{2}\ce{Cl2O}(g)+\dfrac{3}{2}\ce{OF2}(g)\hspace{20px}ΔH^\circ_{(iv)}=\mathrm{+266.7\: kJ}\)

Solution

Notre objectif est de manipuler et de combiner les réactions (ii), (iii) et (iv) de manière à ce qu'elles s'additionnent à la réaction (i). En allant de gauche à droite dans (i), nous voyons d'abord que\(\ce{ClF}_{(g)}\) c'est nécessaire en tant que réactif. Cela peut être obtenu en multipliant la réaction (iii) par\(\frac{1}{2}\), ce qui signifie que la variation de ΔH° est également multipliée par\(\frac{1}{2}\) :

\[\ce{ClF}(g)+\frac{1}{2}\ce{O2}(g)⟶\frac{1}{2}\ce{Cl2O}(g)+\frac{1}{2}\ce{OF2}(g)\hspace{20px} ΔH°=\frac{1}{2}(205.6)=+102.8\: \ce{kJ} \nonumber \]

Ensuite, nous voyons que cela\(\ce{F_2}\) est également nécessaire en tant que réactif. Pour ce faire, inversez et réduisez de moitié la réaction (ii), ce qui signifie que le ΔH° change de signe et est réduit de moitié :

\[\frac{1}{2}\ce{O2}(g)+\ce{F2}(g)⟶\ce{OF2}(g)\hspace{20px}ΔH°=+24.7\: \ce{kJ} \nonumber \]

Pour obtenir le ClF ₃ sous forme de produit, inversez (iv) en modifiant le signe de ΔH° :

\[\frac{1}{2}\ce{Cl2O}(g)+\dfrac{3}{2}\ce{OF2}(g)⟶\ce{ClF3}(g)+\ce{O2}(g)\hspace{20px}ΔH°=\mathrm{−266.7\: kJ} \nonumber \]

Vérifiez maintenant que ces réactions s'additionnent à la réaction que nous voulons :

\ [\ begin {align*}
& \ ce {ClF} (g) + \ frac {1} {2} \ ce {O2} (g) ⟶ \ frac {1} {2} \ ce {Cl2O} (g) + \ frac {1} {2} \ ce {OF2} (g) &ΔH°= \ mathrm {+102,8 \ : kJ} \
& \ frac {1} {2} \ ce {O2} (g) + \ ce {F2} (g) ⟶ \ ce {OF2} (g) &ΔH°= \ mathrm {+24,7 \ : kJ} \ \
& \ frac {1} {2} \ ce {Cl2O} (g) + \ dfrac {3} {2} \ ce {OF2} (g) ⟶ \ ce {ClF3} (g) + \ ce {O2} (g) &ΔH°= \ mathrm {−266,7 \ :kJ} \ \
& \ overline {\ ce {ClF} (g) + \ ce {F2} ⟶ \ ce {ClF3} (g) \ hspace {130px}} && \ overline {ΔH2} ⟶ \ ce {ClF3} (g) \ hspace {130px}} °= \ mathrm {−139.2 \ :kJ}}
 \ end {align*} \ nonnumber \]

Réactifs\(\frac{1}{2}\ce{O2}\) et\(\frac{1}{2}\ce{O2}\) annulent le produit O ₂ ;\(\frac{1}{2}\ce{Cl2O}\) le produit annule le réactif\(\frac{1}{2}\ce{Cl2O}\) ; et le réactif\(\dfrac{3}{2}\ce{OF2}\) est annulé par les produits\(\frac{1}{2}\ce{OF2}\) et OF ₂. Il ne reste donc que les réactifs ClF (g) et F ₂ (g) et le produit ClF ₃ (g), qui sont ce que nous voulons. Puisque la somme de ces trois réactions modifiées donne la réaction qui nous intéresse, la somme des trois valeurs de ΔH° modifiées donnera le ΔH° souhaité :

\(ΔH°=\mathrm{(+102.8\:kJ)+(24.7\:kJ)+(−266.7\:kJ)=−139.2\:kJ}\)

Exercice\(\PageIndex{7}\)

Le chlorure d'aluminium peut être formé à partir de ses éléments :

(i)\(\ce{2Al}(s)+\ce{3Cl2}(g)⟶\ce{2AlCl3}(s)\hspace{20px}ΔH°=\:?\)

Utilisez les réactions ci-dessous pour déterminer le ΔH° de la réaction (i) :

(ii)\(\ce{HCl}(g)⟶\ce{HCl}(aq)\hspace{20px}ΔH^\circ_{(ii)}=\mathrm{−74.8\:kJ}\)

(iii)\(\ce{H2}(g)+\ce{Cl2}(g)⟶\ce{2HCl}(g)\hspace{20px}ΔH^\circ_{(iii)}=\mathrm{−185\:kJ}\)

(iv)\(\ce{AlCl3}(aq)⟶\ce{AlCl3}(s)\hspace{20px}ΔH^\circ_{(iv)}=\mathrm{+323\:kJ/mol}\)

(v)\(\ce{2Al}(s)+\ce{6HCl}(aq)⟶\ce{2AlCl3}(aq)+\ce{3H2}(g)\hspace{20px}ΔH^\circ_{(v)}=\mathrm{−1049\:kJ}\)

Réponse

−1407 kJ

Nous pouvons également utiliser la loi de Hess pour déterminer le changement d'enthalpie de toute réaction si les enthalpies correspondantes de formation des réactifs et des produits sont disponibles. Les réactions par étapes que nous considérons sont les suivantes : (i) les décompositions des réactifs en leurs éléments constitutifs (pour lesquelles les variations d'enthalpie sont proportionnelles à la négative des enthalpies de formation des réactifs), suivie de (ii) des recombinaisons des éléments pour donner les produits (avec l'enthalpie) changements proportionnels aux enthalpies de formation des produits). La variation d'enthalpie standard de la réaction globale est donc égale à : (ii) la somme des enthalpies standard de formation de tous les produits plus (i) la somme des négatifs des enthalpies standard de formation des réactifs. Ceci est généralement légèrement réorganisé pour être écrit comme suit,\(\sum\) représentant « la somme de » et n représentant les coefficients stœchiométriques :

\[ΔH^\circ_\ce{reaction}=\sum n×ΔH^\circ_\ce{f}\ce{(products)}−\sum n×ΔH^\circ_\ce{f}\ce{(reactants)} \label{5.4.20B} \]

L'exemple suivant montre en détail pourquoi cette équation est valide et comment l'utiliser pour calculer le changement d'enthalpie pour une réaction d'intérêt.

Exemple\(\PageIndex{8}\): Using Hess’s Law

Quel est le changement d'enthalpie standard pour la réaction :

\[\ce{3NO2}(g)+\ce{H2O}(l)⟶\ce{2HNO3}(aq)+\ce{NO}(g)\hspace{20px}ΔH°=\:? \nonumber \]

Solution 1 : utilisation de l'équation

Nous pourrions également utiliser la forme spéciale de la loi de Hess donnée précédemment :

\[ΔH^\circ_\ce{reaction}=∑n×ΔH^\circ_\ce{f}\ce{(products)}−∑n×ΔH^\circ_\ce{f}\ce{(reactants)} \nonumber \]

\[\begin {align*} &=\mathrm{\left[2\:\cancel{mol\:HNO_3}×\dfrac{−207.4\:kJ}{\cancel{mol\:HNO_3\:(\mathit{aq})}}+1\:\cancel{mol\: NO\:(\mathit{g})}×\dfrac{+90.2\: kJ}{\cancel{mol\: NO\:(\mathit{g})}}\right]}\\ &\mathrm{\:−\,\left[3\:\cancel{mol\:NO_2(\mathit{g})}×\dfrac{+33.2\: kJ}{\cancel{mol\:NO_2\:(\mathit{g})}}+1\:\cancel{mol\:H_2O\:(\mathit{l})}×\dfrac{−285.8\:kJ}{\cancel{mol\:H_2O\:(\mathit{l})}}\right]}\\ &=\mathrm{2(−207.4\:kJ)+1(+90.2\: kJ)−3(+33.2\: kJ)−1(−285.8\:kJ)}\\ &=\mathrm{−138.4\:kJ}\end {align*} \nonumber \]

Solution 2 : Expliquer pourquoi l'équation générale est valide

Nous pouvons écrire cette réaction comme la somme des décompositions de 3NO ₂ (g) et de 1H ₂ O (l) en leurs éléments constitutifs, et de la formation de 2 HNO ₃ (aq) et de 1 NO (g) à partir de leurs éléments constitutifs. En écrivant ces réactions et en notant leurs relations avec les\(ΔH^\circ_\ce{f}\) valeurs de ces composés (tirées des tableaux T1 et T2), nous avons :

\[\ce{3NO2}(g)⟶ \dfrac{3}{2} \ce{N2}(g)+ 3 \ce{O2}(g)\hspace{20px}ΔH^\circ_{1}=\mathrm{−99.6\:kJ} \nonumber \]

\[\ce{H2O}(l)⟶\ce{H2}(g)+\frac{1}{2}\ce{O2}(g)\hspace{20px}ΔH^\circ_{2}=+285.8\: \ce{kJ}\:[−1×ΔH^\circ_\ce{f}(\ce{H2O})] \nonumber \]

\[\ce{H2}(g)+\ce{N2}(g)+ 3 \ce{O2}(g)⟶\ce{2HNO3}(aq)\hspace{20px}ΔH^\circ_{3}=−414.8\:kJ\:[2×ΔH^\circ_\ce{f}(\ce{HNO3 \nonumber})] \nonumber \]

\[\frac{1}{2}\ce{N2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{NO}(g)\hspace{20px}ΔH^\circ \nonumber_{4}=+90.2\: \ce{kJ}\:[1×(\ce{NO})] \nonumber \]

La somme de ces équations de réaction donne la réaction qui nous intéresse :

\[\ce{3NO2}(g)+\ce{H2O}(l)⟶\ce{2HNO3}(aq)+\ce{NO}(g) \nonumber \]

La somme de leurs variations d'enthalpie donne la valeur que nous voulons déterminer :

\[\begin {align*} ΔH^\circ_\ce{rxn}&=ΔH^\circ_1+ΔH^\circ_2+ΔH^\circ_3+ΔH^\circ_4=\mathrm{(−99.6\:kJ)+(+285.8\: kJ)+(−414.8\:kJ)+(+90.2\: kJ)}\\ &=\mathrm{−138.4\:kJ} \end {align*} \nonumber \]

Le changement d'enthalpie standard pour cette réaction est donc Δ H° = −138,4 kJ.

Notez que ce résultat a été obtenu par :

1. en multipliant le\(ΔH^\circ_\ce{f}\) de chaque produit par son coefficient stœchiométrique et en additionnant ces valeurs,
2. en multipliant le\(ΔH^\circ_\ce{f}\) de chaque réactif par son coefficient stœchiométrique et en additionnant ces valeurs, puis
3. soustraire le résultat trouvé à l'étape 2 du résultat trouvé à l'étape 1.

C'est également la procédure à suivre pour utiliser l'équation générale, comme indiqué.

Exercice\(\PageIndex{8}\)

Calculez la chaleur de combustion d'une mole d'éthanol, C ₂ H ₅ OH (l), lorsque du H ₂ O (l) et du CO ₂ (g) se forment. Utiliser les enthalpies de formation suivantes : C ₂ H ₅ OH (l), −278 kJ/mol ; H ₂ O (l), −286 kJ/mol ; et CO ₂ (g), −394 kJ/mol.

Réponse

−1368 kJ/mol

Résumé

Si un changement chimique est effectué à pression constante et que le seul travail effectué est dû à une expansion ou à une contraction, q pour le changement est appelé changement d'enthalpie avec le symbole Δ H, ou\(ΔH^\circ_{298}\) pour les réactions se produisant dans des conditions d'état standard. La valeur de Δ H pour une réaction dans un sens est égale en amplitude, mais de signe opposé, à Δ H pour la réaction dans la direction opposée, et Δ H est directement proportionnel à la quantité de réactifs et de produits. Des exemples de changements d'enthalpie incluent l'enthalpie de combustion, l'enthalpie de fusion, l'enthalpie de vaporisation et l'enthalpie standard de formation. L'enthalpie standard de formation,\(ΔH^\circ_\ce{f}\), est le changement d'enthalpie accompagnant la formation d'une mole d'une substance à partir des éléments dans leur état le plus stable à 1 bar (état standard). La plupart des procédés sont effectués à 298,15 K. Si les enthalpies de formation sont disponibles pour les réactifs et les produits d'une réaction, le changement d'enthalpie peut être calculé à l'aide de la loi de Hess : Si un processus peut être écrit comme la somme de plusieurs processus par étapes, le changement d'enthalpie de l'ensemble du processus est égal à la somme des variations d'enthalpie des différentes étapes.

Équations clés

• \(ΔU=q+w\)
• \(ΔH^\circ_\ce{reaction}=∑n×ΔH^\circ_\ce{f}\ce{(products)}−∑n×ΔH^\circ_\ce{f}\ce{(reactants)}\)

Notes

1. 1 Pour en savoir plus sur les combustibles algaux, consultez le site www.theguardian.com/environme... n-fuel-problem.

Lexique

thermodynamique chimique

domaine scientifique qui traite des relations entre la chaleur, le travail et toutes les formes d'énergie associées aux processus chimiques et physiques

enthalpie (H)

somme de l'énergie interne d'un système et du produit mathématique de sa pression et de son volume

changement d'enthalpie (Δ H)

chaleur dégagée ou absorbée par un système sous pression constante au cours d'un processus chimique ou physique

travaux d'expansion (travail pression/volume)

le travail effectué lorsque le système se développe ou se contracte face à la pression extérieure

première loi de la thermodynamique

l'énergie interne d'un système change en raison du flux de chaleur entrant ou sortant du système ou du travail effectué sur ou par le système

Loi de Hess

si un processus peut être représenté comme la somme de plusieurs étapes, le changement d'enthalpie du processus est égal à la somme des changements d'enthalpie des étapes

hydrocarbure

composé composé uniquement d'hydrogène et de carbone, principal composant des combustibles fossiles

énergie interne (U)

total de tous les types d'énergie possibles présents dans une ou plusieurs substances

enthalpie de combustion standard (\(ΔH^\circ_\ce{c}\))

chaleur dégagée lorsqu'une mole d'un composé subit une combustion complète dans des conditions standard

enthalpie de formation standard (\(ΔH^\circ_\ce{f}\))

changement d'enthalpie d'une réaction chimique dans laquelle 1 mole d'une substance pure est formée à partir de ses éléments dans leurs états les plus stables dans des conditions d'état standard

état standard

ensemble de conditions physiques acceptées comme conditions de référence communes pour la déclaration des propriétés thermodynamiques ; 1 bar de pression et solutions à une concentration molaire, généralement à une température de 298,15 K

fonction d'état

propriété dépendant uniquement de l'état d'un système, et non du chemin emprunté pour atteindre cet état