5.2 : Calorimétrie
- Page ID
- 194055
- Expliquer la technique de la calorimétrie
- Calculer et interpréter la chaleur et les propriétés connexes à l'aide de données calorimétriques classiques
L'une des techniques que nous pouvons utiliser pour mesurer la quantité de chaleur impliquée dans un processus chimique ou physique est la calorimétrie. La calorimétrie est utilisée pour mesurer les quantités de chaleur transférées vers ou depuis une substance. Pour ce faire, la chaleur est échangée avec un objet calibré (calorimètre). La variation de température de la partie de mesure du calorimètre est convertie en quantité de chaleur (puisque l'étalonnage précédent a été utilisé pour établir sa capacité calorifique). La mesure du transfert de chaleur à l'aide de cette approche nécessite la définition d'un système (la ou les substances soumises à la modification chimique ou physique) et de son environnement (les autres composants de l'appareil de mesure qui servent à fournir de la chaleur au système ou absorber la chaleur du système). La connaissance de la capacité thermique de l'environnement et les mesures minutieuses des masses du système et de l'environnement et de leurs températures avant et après le processus permettent de calculer la chaleur transférée comme décrit dans cette section.
Un calorimètre est un appareil utilisé pour mesurer la quantité de chaleur impliquée dans un processus chimique ou physique. Par exemple, lorsqu'une réaction exothermique se produit en solution dans un calorimètre, la chaleur produite par la réaction est absorbée par la solution, ce qui augmente sa température. Lorsqu'une réaction endothermique se produit, la chaleur requise est absorbée par l'énergie thermique de la solution, ce qui fait baisser sa température (Figure\(\PageIndex{1}\)). Le changement de température, ainsi que la chaleur et la masse spécifiques de la solution, peuvent ensuite être utilisés pour calculer la quantité de chaleur impliquée dans les deux cas.
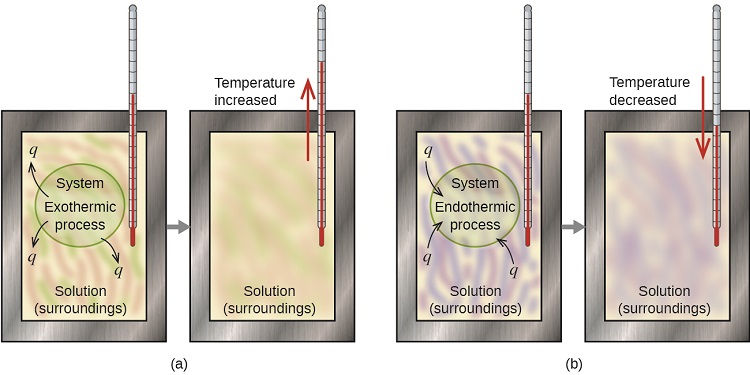
Par convention, q reçoit un signe négatif (-) lorsque le système libère de la chaleur dans l'environnement (exothermique) ; q reçoit un signe positif (+) lorsque le système absorbe la chaleur de l'environnement (endothermique).
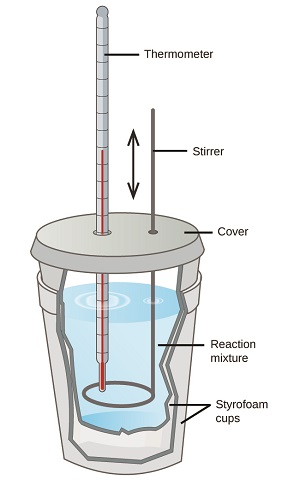
Les scientifiques utilisent des calorimètres bien isolés qui empêchent presque tout transfert de chaleur entre le calorimètre et son environnement. Cela permet de déterminer avec précision la chaleur impliquée dans les processus chimiques, le contenu énergétique des aliments, etc. Les étudiants en chimie générale utilisent souvent de simples calorimètres fabriqués à partir de gobelets en polystyrène (Figure\(\PageIndex{2}\)). Ces calorimètres « tasses à café » faciles à utiliser permettent un meilleur échange de chaleur avec leur environnement et produisent donc des valeurs énergétiques moins précises.
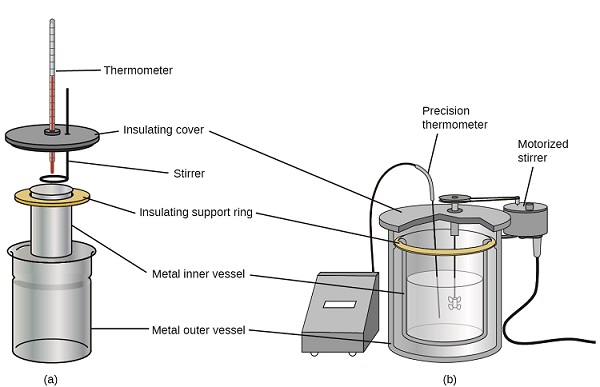
Des calorimètres à solution commerciale sont également disponibles. Les calorimètres relativement peu coûteux se composent souvent de deux cuvettes à paroi mince imbriquées de manière à minimiser le contact thermique pendant l'utilisation, ainsi que d'un couvercle isolé, d'un agitateur portatif et d'un simple thermomètre. Les calorimètres plus coûteux utilisés pour l'industrie et la recherche sont généralement équipés d'une cuve de réaction entièrement fermée et bien isolée, d'un mécanisme d'agitation motorisé et d'un capteur de température plus précis (Figure\(\PageIndex{3}\)).
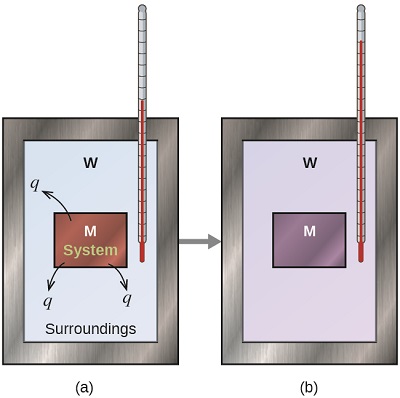
Avant de pratiquer les problèmes de calorimétrie impliquant des réactions chimiques, considérez un exemple simple qui illustre l'idée de base de la calorimétrie. Supposons que nous ayons initialement une substance à haute température, telle qu'un morceau de métal chaud (M), et une substance à basse température, telle que de l'eau froide (W). Si nous plaçons le métal dans l'eau, la chaleur circulera de M vers W. La température de M diminuera et la température de W augmentera, jusqu'à ce que les deux substances atteignent la même température, c'est-à-dire lorsqu'elles atteignent l'équilibre thermique (Figure\(\PageIndex{4}\)). Si cela se produit dans un calorimètre, idéalement, tout ce transfert de chaleur se produit entre les deux substances, sans gain ni perte de chaleur ni par le calorimètre ni par l'environnement du calorimètre. Dans ces circonstances idéales, le changement de chaleur net est nul :
\[q_\mathrm{\,substance\: M} + q_\mathrm{\,substance\: W}=0 \label{5.3.1} \]
Cette relation peut être réarrangée pour montrer que la chaleur gagnée par la substance M est égale à la chaleur perdue par la substance W :
\[q_\mathrm{\,substance\: M}=-q_\mathrm{\,substance\: W} \label{5.3.2} \]
L'amplitude de la chaleur (changement) est donc la même pour les deux substances, et le signe négatif indique simplement que\(q_{substance\, M}\) et\(q_{substance\, W}\) sont opposées dans le sens du flux de chaleur (gain ou perte) mais n'indique pas le signe arithmétique de l'une ou l'autre des valeurs q (c'est-à-dire déterminée par le fait que la matière en question gagne ou perd de la chaleur, selon la définition). Dans la situation spécifique décrite,\(q_{substance\, M}\) est une valeur négative et\(q_{substance\, W}\) positive, car la chaleur est transférée de M à W.
Une barre d'armature chaude de 360 g (une tige d'acier utilisée pour le renforcement du béton) est déposée dans 425 ml d'eau à 24,0 °C. La température finale de l'eau est mesurée à 42,7 °C. Calculez la température initiale de la pièce d'armature. Supposons que la chaleur spécifique de l'acier est approximativement la même que celle du fer (tableau T4) et que tout le transfert de chaleur se produit entre les barres d'armature et l'eau (il n'y a aucun échange de chaleur avec l'environnement).
Solution
La température de l'eau augmente de 24,0 °C à 42,7 °C, de sorte que l'eau absorbe la chaleur. Cette chaleur provenait de la pièce d'armature, qui était initialement à une température plus élevée. En supposant que tout le transfert de chaleur s'est fait entre les barres d'armature et l'eau, sans « perte » de chaleur vers l'environnement, alors la chaleur dégagée par les barres d'armature = − chaleur absorbée par l'eau, ou :
\[q_\ce{rebar}=−q_\ce{water} \nonumber \]
Comme nous savons comment la chaleur est liée à d'autres quantités mesurables, nous avons :
\[(c×m×ΔT)_\ce{rebar}=−(c×m×ΔT)_\ce{water} \nonumber \]
En laissant f = final et i = initial, sous forme développée, cela devient :
\[ c_\ce{rebar}×m_\ce{rebar}×(T_\mathrm{f,rebar}−T_\mathrm{i,rebar})=−c_\ce{water}×m_\ce{water}×(T_\mathrm{f,water}−T_\mathrm{i,water}) \nonumber \]
La densité de l'eau est de 1,0 g/mL, donc 425 mL d'eau = 425 g. Si l'on tient compte du fait que la température finale des barres d'armature et de l'eau est de 42,7 °C, la substitution de valeurs connues donne :
\[ \mathrm{(0.449\:J/g\: °C)(360g)(42.7°C−\mathit T_\mathrm{i,rebar})=-(4.184\:J/g\: °C)(425\:g)(42.7°C−24.0°C)} \nonumber \]
\[\mathrm{\mathit T_{i,rebar}=\dfrac{(4.184\:J/g\: °C)(425\:g)(42.7°C−24.0°C)}{(0.449\:J/g\: °C)(360\:g)}+42.7°C} \nonumber \]
La résolution de ce problème donne Ti, barre d'armature = 248 °C, donc la température initiale de la barre d'armature était de 248 °C.
Un morceau de cuivre de 248 g est déposé dans 390 ml d'eau à 22,6 °C. La température finale de l'eau a été mesurée à 39,9 °C. Calculez la température initiale du morceau de cuivre. Supposons que tous les transferts de chaleur se produisent entre le cuivre et l'eau.
- Réponse
-
La température initiale du cuivre était de 335,6 °C.
Un morceau de cuivre de 248 g initialement à 314 °C est jeté dans 390 ml d'eau, initialement à 22,6 °C. En supposant que tout le transfert de chaleur se produit entre le cuivre et l'eau, calculez la température finale.
- Réponse
-
La température finale (atteinte à la fois par le cuivre et par l'eau) est de 38,7 °C.
Cette méthode peut également être utilisée pour déterminer d'autres grandeurs, telles que la chaleur spécifique d'un métal inconnu.
Un morceau de métal de 59,7 g qui avait été immergé dans de l'eau bouillante a été rapidement transféré dans 60,0 ml d'eau, initialement à 22,0 °C. La température finale est de 28,5 °C. Utilisez ces données pour déterminer la chaleur spécifique du métal. Utilisez ce résultat pour identifier le métal.
Solution
En supposant un transfert de chaleur parfait, la chaleur dégagée par le métal = −chaleur absorbée par l'eau, ou :
\[q_\ce{metal}=−q_\ce{water} \nonumber \]
Sous forme développée, il s'agit de :
\[c_\ce{metal}×m_\ce{metal}×(T_\mathrm{f,metal}−T_\mathrm{i, metal})=−c_\ce{water}×m_\ce{water}×(T_\mathrm{f,water}−T_\mathrm{i,water}) \nonumber \]
En notant que puisque le métal a été immergé dans de l'eau bouillante, sa température initiale était de 100,0 °C ; et que pour l'eau, 60,0 ml = 60,0 g ; nous avons :
\[\mathrm{(\mathit c_{metal})(59.7\:g)(28.5°C−100.0°C)=−(4.18\:J/g\: °C)(60.0\:g)(28.5°C−22.0°C)} \nonumber \]
Pour résoudre ce problème :
\[\mathrm{\mathit c_{metal}=\dfrac{−(4.184\:J/g\: °C)(60.0\:g)(6.5°C)}{(59.7\:g)(−71.5°C)}=0.38\:J/g\: °C} \nonumber \]
En comparant cela aux valeurs du tableau T4, notre chaleur spécifique expérimentale est la plus proche de la valeur pour le cuivre (0,39 J/g °C). Nous avons donc identifié le métal comme étant du cuivre.
Un morceau de 92,9 g d'un métal gris et argenté est chauffé à 178,0 °C, puis transféré rapidement dans 75,0 ml d'eau, initialement à 24,0 °C. Après 5 minutes, le métal et l'eau ont atteint la même température : 29,7 °C. Déterminez la chaleur spécifique et l'identité du métal. (Remarque : vous devriez constater que la chaleur spécifique est proche de celle de deux métaux différents. Expliquez comment vous pouvez déterminer en toute confiance l'identité du métal).
- Réponse
-
\(c_{metal}= 0.13 \;J/g\; °C\)
Cette chaleur spécifique est proche de celle de l'or ou du plomb. Il serait difficile de déterminer quel métal il s'agissait en se basant uniquement sur les valeurs numériques. Cependant, l'observation selon laquelle le métal est argenté/gris en plus de la valeur de la chaleur spécifique indique que le métal est du plomb.
Lorsque nous utilisons la calorimétrie pour déterminer la chaleur impliquée dans une réaction chimique, les mêmes principes que ceux dont nous avons discuté s'appliquent. La quantité de chaleur absorbée par le calorimètre est souvent suffisamment faible pour que nous puissions la négliger (mais pas pour des mesures très précises, comme nous le verrons plus loin), et le calorimètre minimise les échanges d'énergie avec l'environnement. Comme l'énergie n'est ni créée ni détruite lors d'une réaction chimique, il n'y a pas de changement énergétique global au cours de la réaction. La chaleur produite ou consommée lors de la réaction (le « système »), de la réaction q, plus la chaleur absorbée ou perdue par la solution (l' « environnement »)\(q_{solution}\), doivent totaliser zéro :
\[q_\ce{reaction}+q_\ce{solution}=0\ \label{ 5.3.10} \]
Cela signifie que la quantité de chaleur produite ou consommée dans la réaction est égale à la quantité de chaleur absorbée ou perdue par la solution :
\[q_\ce{reaction}=−q_\ce{solution} \label{5.3.11} \]
Ce concept est au cœur de tous les problèmes et de tous les calculs calorimétriques.
Lorsque 50,0 ml de HCl (aq) 0,10 M et 50,0 ml de NaOH (aq) 1,00 M, tous deux à 22,0 °C, sont ajoutés à un calorimètre pour tasse à café, la température du mélange atteint un maximum de 28,9 °C. Quelle est la quantité approximative de chaleur produite par cette réaction ?
\[\ce{HCl}(aq)+\ce{NaOH}(aq)⟶\ce{NaCl}(aq)+\ce{H2O}(l) \nonumber \]
Une solution
Pour visualiser ce qui se passe, imaginez que vous pouvez combiner les deux solutions si rapidement qu'aucune réaction ne se produit pendant le mélange ; puis, après le mélange, la réaction a eu lieu. Au moment du mélange, vous avez 100,0 ml d'un mélange de HCl et de NaOH à 22,0 °C. Le HCl et le NaOH réagissent ensuite jusqu'à ce que la température de la solution atteigne 28,9 °C.
La chaleur dégagée par la réaction est égale à celle absorbée par la solution. Par conséquent :
\[q_\ce{reaction}=−q_\ce{solution} \nonumber \]
(Il est important de se rappeler que cette relation n'est valable que si le calorimètre n'absorbe aucune chaleur provenant de la réaction et qu'il n'y a aucun échange de chaleur entre le calorimètre et son environnement.)
Ensuite, nous savons que la chaleur absorbée par la solution dépend de sa chaleur, de sa masse et de son changement de température spécifiques :
\[q_\ce{solution}=(c×m×ΔT)_\ce{solution} \nonumber \]
Pour procéder à ce calcul, nous devons faire quelques hypothèses ou approximations plus raisonnables. Comme la solution est aqueuse, nous pouvons procéder comme s'il s'agissait d'eau en termes de chaleur et de masse spécifiques. La densité de l'eau étant d'environ 1,0 g/mL, 100,0 mL ont une masse d'environ 1,0 × 10 2 g (deux chiffres significatifs). La chaleur spécifique de l'eau est d'environ 4,18 J/g °C, nous l'utilisons donc pour la chaleur spécifique de la solution. La substitution de ces valeurs donne :
\[\mathrm{\mathit q_{solution}=(4.184\:J/g\: °C)(1.0×10^2\:g)(28.9°C−22.0°C)=2.89×10^3\:J} \nonumber \]
Enfin, puisque nous cherchons à trouver la chaleur de la réaction, nous avons :
\[q_\ce{reaction}=−q_\ce{solution}=−2.89×10^3\:J \nonumber \]
Le signe négatif indique que la réaction est exothermique. Il produit 2,89 kJ de chaleur.
Lorsque 100 ml de NaCl à 0,200 M (aq) et 100 ml de 0,200 M d'AgNO 3 (aq), tous deux à 21,9 °C, sont mélangés dans un calorimètre à tasse à café, la température augmente à 23,5 °C lorsque du AgCl solide se forme. Quelle quantité de chaleur est produite par cette réaction de précipitation ? Quelles hypothèses avez-vous faites pour déterminer votre valeur ?
- Réponse
-
\(1.34 \times 10^3\; J\); supposons qu'aucune chaleur n'est absorbée par le calorimètre, qu'aucune chaleur n'est échangée entre le calorimètre et son environnement, et que la chaleur et la masse spécifiques de la solution sont les mêmes que celles de l'eau
Lorsque vous travaillez ou jouez à l'extérieur par temps froid, vous pouvez utiliser un chauffe-mains pour vous réchauffer les mains (Figure\(\PageIndex{5}\)). Un chauffe-mains réutilisable courant contient une solution sursaturée de NaC 2 H 3 O 2 (acétate de sodium) et un disque métallique. La flexion du disque crée des sites de nucléation autour desquels le NaC 2 H 3 O 2 métastable cristallise rapidement (un chapitre sur les solutions étudiera plus en détail la saturation et la sursaturation).
Le processus\(\ce{NaC2H3O2}(aq)⟶\ce{NaC2H3O2}(s)\) est exothermique et la chaleur produite par ce processus est absorbée par vos mains, les réchauffant ainsi (au moins pendant un certain temps). Si le chauffe-mains est réchauffé, le NaC 2 H 3 O 2 se redissout et peut être réutilisé.

Un autre chauffe-mains courant produit de la chaleur lorsqu'il est ouvert, exposant ainsi le fer et l'eau contenus dans le chauffe-mains à l'oxygène de l'air. Une version simplifiée de cette réaction exothermique est
\[\ce{2Fe(s) + 3/2 O2(g) ⟶ Fe2O3(s)}.\ n\nonumber \]
Le sel contenu dans le chauffe-mains catalyse la réaction, ce qui permet de produire de la chaleur plus rapidement ; la cellulose, la vermiculite et le charbon actif aident à répartir la chaleur de manière uniforme. D'autres types de chauffe-mains utilisent un liquide plus léger (un catalyseur au platine aide le liquide à briquet à s'oxyder de manière exothermique), du charbon de bois (le charbon s'oxyde dans un cas particulier) ou des unités électriques qui produisent de la chaleur en faisant passer le courant électrique d'une batterie à travers des fils résistifs.
Lorsque le nitrate d'ammonium solide se dissout dans l'eau, la solution devient froide. C'est la base d'une « banquise instantanée » (Figure\(\PageIndex{5}\)). Lorsque 3,21 g de NH 4 NO 3 solide se dissolvent dans 50,0 g d'eau à 24,9 °C dans un calorimètre, la température diminue à 20,3 °C.
Calculez la valeur de q pour cette réaction et expliquez la signification de son signe arithmétique. Énoncez toutes les hypothèses que vous avez faites.

Solution
Nous supposons que le calorimètre empêche le transfert de chaleur entre la solution et son environnement extérieur (y compris le calorimètre lui-même), auquel cas :
\[q_\ce{rxn}=−q_\ce{soln} \nonumber \]
avec « rxn » et « soln » utilisés comme abréviations pour « réaction » et « solution », respectivement.
En supposant également que la chaleur spécifique de la solution est la même que celle de l'eau, nous avons :
\[\begin{align*} q_\ce{rxn} &=−q_\ce{soln}=−(c×m×ΔT)_\ce{soln}\\ &=\mathrm{−[(4.184J/g\: °C)×(53.2\:g)×(20.3°C−24.9°C)]}\\ &=\mathrm{−[(4.184J/g\: °C)×(53.2\:g)×(−4.6°C)]}\\ &+\mathrm{1.0×10^3\:J=+1.0\:kJ} \end{align*}\]
Le signe positif de q indique que la dissolution est un processus endothermique.
Lorsqu'un échantillon de 3,00 g de KCl a été ajouté à 3,00 × 10 2 g d'eau dans un calorimètre à tasse à café, la température a diminué de 1,05 °C. Quelle est la quantité de chaleur impliquée dans la dissolution du KCl ? Quelles hypothèses avez-vous formulées ?
- Réponse
-
1,33 kJ ; supposons que le calorimètre empêche le transfert de chaleur entre la solution et son environnement extérieur (y compris le calorimètre lui-même) et que la chaleur spécifique de la solution est la même que celle de l'eau.
Si la quantité de chaleur absorbée par un calorimètre est trop importante pour être négligée ou si nous avons besoin de résultats plus précis, nous devons prendre en compte la chaleur absorbée à la fois par la solution et par le calorimètre.
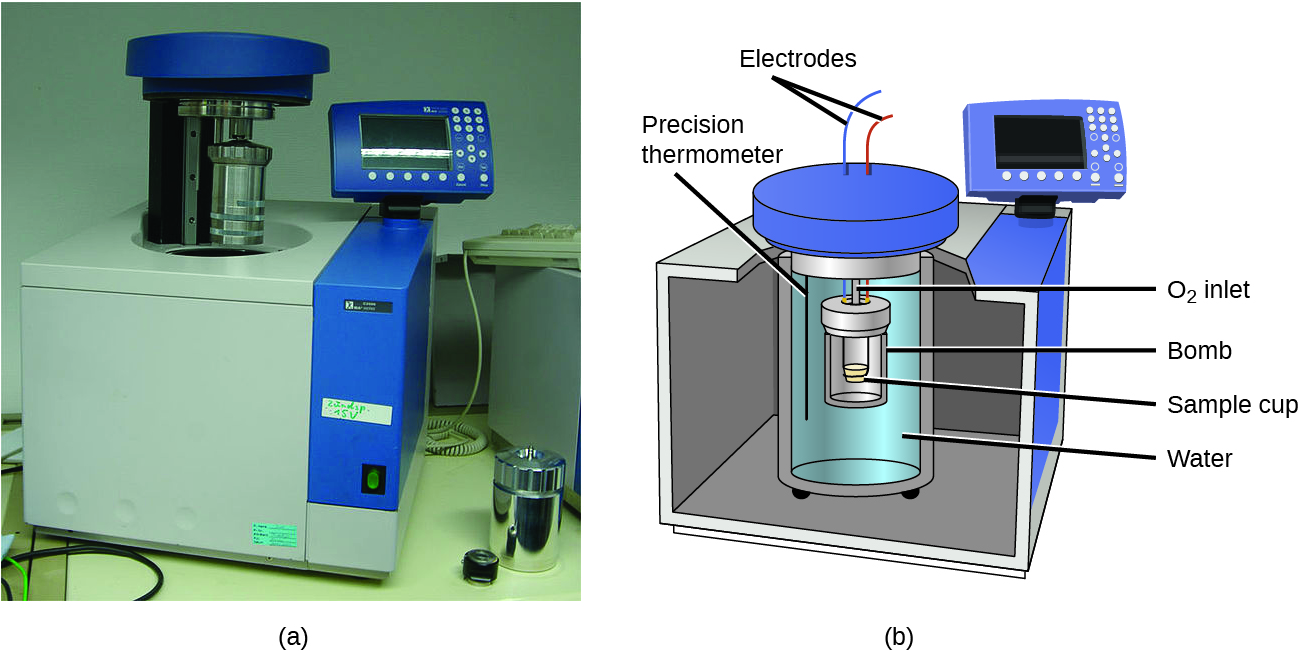
Les calorimètres décrits sont conçus pour fonctionner à pression (atmosphérique) constante et sont pratiques pour mesurer le flux de chaleur accompagnant les processus qui se produisent en solution. Un autre type de calorimètre qui fonctionne à volume constant, communément appelé calorimètre à bombe, est utilisé pour mesurer l'énergie produite par les réactions qui produisent de grandes quantités de chaleur et de produits gazeux, tels que les réactions de combustion. (Le terme « bombe » vient de l'observation que ces réactions peuvent être suffisamment fortes pour ressembler à des explosions qui endommageraient d'autres calorimètres.) Ce type de calorimètre consiste en un récipient en acier robuste (la « bombe ») qui contient les réactifs et qui est lui-même immergé dans l'eau (Figure\(\PageIndex{6}\)). L'échantillon est placé dans la bombe, qui est ensuite remplie d'oxygène à haute pression. Une petite étincelle électrique est utilisée pour enflammer l'échantillon. L'énergie produite par la réaction est piégée dans la bombe en acier et dans l'eau environnante. L'augmentation de température est mesurée et, associée à la capacité thermique connue du calorimètre, est utilisée pour calculer l'énergie produite par la réaction. Les calorimètres à bombe doivent être étalonnés pour déterminer la capacité thermique du calorimètre et garantir des résultats précis. L'étalonnage est effectué en utilisant une réaction avec un q connu, tel qu'une quantité mesurée d'acide benzoïque allumée par une étincelle provenant d'un fil de fusible en nickel qui est pesé avant et après la réaction. Le changement de température produit par la réaction connue est utilisé pour déterminer la capacité thermique du calorimètre. L'étalonnage est généralement effectué à chaque fois avant que le calorimètre ne soit utilisé pour recueillir des données de recherche.
Vidéo\(\PageIndex{1}\) : Vidéo montrant comment un calorimètre à bombe est préparé pour l'action.
Lorsque 3,12 g de glucose, C 6 H 12 O 6, sont brûlés dans un calorimètre à bombe, la température du calorimètre augmente de 23,8 °C à 35,6 °C. Le calorimètre contient 775 g d'eau et la bombe elle-même a une capacité calorifique de 893 J/°C. Quelle quantité de chaleur a été produite par combustion de l'échantillon de glucose ?
Solution
La combustion produit de la chaleur qui est principalement absorbée par l'eau et la bombe. (Les quantités de chaleur absorbées par les produits de réaction et l'excès d'oxygène n'ayant pas réagi sont relativement faibles et leur traitement dépasse le cadre de ce texte. Nous les négligerons dans nos calculs.)
La chaleur produite par la réaction est absorbée par l'eau et la bombe :
\ [\ begin {align*}
&q_ \ ce {rxn} =− (q_ \ ce {eau} +q_ \ ce {bombe}) \ \
&= \ mathrm {− [(4,184 \ :J/g \ : °C) × (775 \ :g) × (35,6 °C−23,8 °C) +893 \ :J/°C× (35,6 °C−23,8°C) +893 \ :J/°C× (35,6 °C−23,8°C) °C)} \ \
&= \ mathrm {− (38 300 \ :J+10 500 \ :J)} \ \
&= \ mathrm {−48 800 \ : J=−48,8 \ : kJ}
\ end { align*} \ nonnumber \]
Cette réaction a libéré 48,7 kJ de chaleur lorsque 3,12 g de glucose ont été brûlés.
Lorsque 0,963 g de benzène, C 6 H 6, sont brûlés dans un calorimètre à bombe, la température du calorimètre augmente de 8,39 °C. La bombe a une capacité thermique de 784 J/°C et est immergée dans 925 ml d'eau. Quelle quantité de chaleur a été produite par la combustion de l'échantillon de glucose ?
Réponse-
39,0 kJ
Depuis la construction du premier en 1899, 35 calorimètres ont été construits pour mesurer la chaleur produite par une personne vivante. 1 Ces calorimètres destinés à l'ensemble du corps, de différentes conceptions, sont suffisamment grands pour contenir un être humain. Plus récemment, les calorimètres utilisés pour l'ensemble de la pièce permettent d'effectuer des activités relativement normales, et ces calorimètres génèrent des données qui reflètent plus fidèlement le monde réel. Ces calorimètres sont utilisés pour mesurer le métabolisme de personnes soumises à différentes conditions environnementales, à différents régimes alimentaires et à différents problèmes de santé, tels que le diabète. Chez l'homme, le métabolisme se mesure généralement en calories par jour. Une calorie nutritionnelle (calorie) est l'unité énergétique utilisée pour quantifier la quantité d'énergie dérivée du métabolisme des aliments ; une calorie est égale à 1 000 calories (1 kcal), la quantité d'énergie nécessaire pour chauffer 1 kg d'eau à 1 °C.
Dans votre vie de tous les jours, vous connaissez peut-être mieux l'énergie fournie sous forme de calories, ou de calories nutritionnelles, qui sont utilisées pour quantifier la quantité d'énergie contenue dans les aliments. Une calorie (cal) = exactement 4,184 joules, et une calorie (notez la capitalisation) = 1000 cal, soit 1 kcal. (Il s'agit approximativement de la quantité d'énergie nécessaire pour chauffer 1 kg d'eau à 1 °C.)
Les macronutriments contenus dans les aliments sont les protéines, les glucides et les graisses ou huiles. Les protéines fournissent environ 4 calories par gramme, les glucides environ 4 calories par gramme, et les graisses et les huiles fournissent environ 9 calories/g. Les étiquettes nutritionnelles des emballages alimentaires indiquent le contenu calorique d'une portion de l'aliment, ainsi que la répartition en calories de chacun des trois macronutriments ( \(\PageIndex{7}\)Chiffre).

Pour l'exemple illustré en (b), l'énergie totale par portion de 228 g est calculée comme suit :
\[\mathrm{(5\:g\: protein×4\:Calories/g)+(31\:g\: carb×4\:Calories/g)+(12\:g\: fat×9\:Calories/g)=252\:Calories} \label{5.3.X} \]
Vous pouvez donc utiliser les étiquettes des aliments pour compter vos calories. Mais d'où viennent ces valeurs ? Et quelle est leur précision ? Le contenu calorique des aliments peut être déterminé en utilisant la calorimétrie à la bombe, c'est-à-dire en brûlant les aliments et en mesurant l'énergie qu'ils contiennent. Un échantillon de nourriture est pesé, mélangé dans un mélangeur, lyophilisé, broyé en poudre et transformé en pastille. La pastille est brûlée à l'intérieur d'un calorimètre à bombe et le changement de température mesuré est converti en énergie par gramme de nourriture.
Aujourd'hui, le contenu calorique sur les étiquettes des aliments est calculé à l'aide d'une méthode appelée système Atwater qui utilise le contenu calorique moyen des différents constituants chimiques des aliments, des protéines, des glucides et des graisses. Les quantités moyennes sont celles indiquées dans l'équation et sont dérivées des divers résultats obtenus par calorimétrie à la bombe pour les aliments entiers. La quantité de glucides est réduite d'une certaine quantité pour la teneur en fibres, qui sont des glucides non digestibles. Pour déterminer le contenu énergétique d'un aliment, les quantités de glucides, de protéines et de matières grasses sont multipliées par la moyenne des calories par gramme pour chacun et les produits sont additionnés pour obtenir l'énergie totale.
Résumé
La calorimétrie est utilisée pour mesurer la quantité d'énergie thermique transférée lors d'un processus chimique ou physique. Cela nécessite de mesurer avec soin le changement de température qui se produit pendant le processus et les masses du système et de l'environnement. Ces quantités mesurées sont ensuite utilisées pour calculer la quantité de chaleur produite ou consommée dans le processus à l'aide de relations mathématiques connues. Les calorimètres sont conçus pour minimiser les échanges d'énergie entre le système étudié et son environnement. Ils vont de simples calorimètres à tasse de café utilisés par les étudiants débutants en chimie à des calorimètres sophistiqués utilisés pour déterminer le contenu énergétique des aliments.
Notes
- 1 Francis D. Reardon et coll. « Le calorimètre humain Snellen revisité, repensé et amélioré : caractéristiques de conception et de performance. » Génie médical et biologique et informatique 8 (2006) 721—28, Le calorimètre humain Snellen revisité, repensé et amélioré : caractéristiques de conception et de performance [link.springer.com].
Lexique
- calorimètre à bombe
- dispositif conçu pour mesurer le changement d'énergie lors de processus se déroulant dans des conditions de volume constant ; couramment utilisé pour les réactions impliquant des réactifs ou des produits solides et gazeux
- calorimètre
- appareil utilisé pour mesurer la quantité de chaleur absorbée ou libérée lors d'un processus chimique ou physique
- calorimétrie
- procédé de mesure de la quantité de chaleur impliquée dans un processus chimique ou physique
- calorie nutritionnelle (Calorie)
- unité utilisée pour quantifier l'énergie fournie par la digestion des aliments, définie comme 1000 cal ou 1 kcal
- environs
- toute matière autre que le système étudié
- système
- partie de la matière soumise à une modification chimique ou physique étudiée


